Вычисление кубического корня : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Побережный Александр |
| ||
29/07/08 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Батороев |
| ||
23/01/07 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| obar |
| |||
13/04/11 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| alex1910 |
| ||
21/07/10 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Простые и не очень способы того, как вычислить кубический корень :: SYL.
 ru
ruСколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «аn».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа.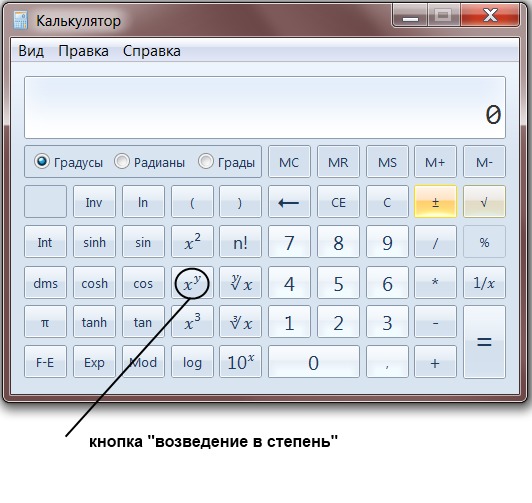 В то время, как вычислить кубический корень из отрицательной величины не составит труда.
В то время, как вычислить кубический корень из отрицательной величины не составит труда.
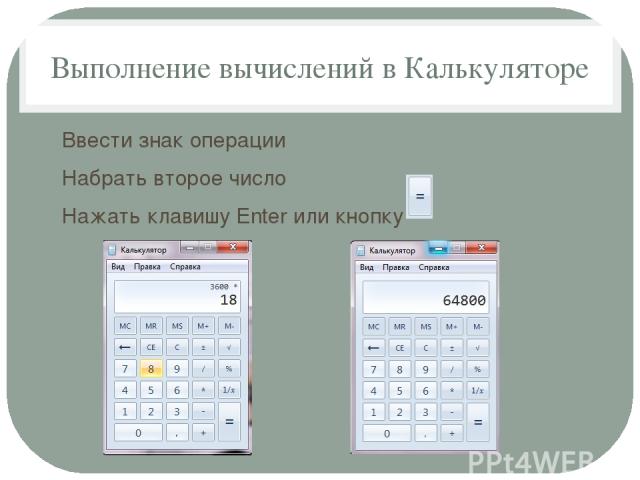
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
- Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а2 * 300 * х + а * 30 * х2 + х3. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.

- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 23, значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 22 * 300 * х +2 * 30 * х2 + х3 < 7000, или 1200 х + 60 х2 + х3< 7000.
- Методом подбора получается, что х = 4.
 1200 * 4 + 60 * 16 + 64 = 5824.
1200 * 4 + 60 * 16 + 64 = 5824. - Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х2 + х3< 1176000.
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х2 + х3< 113064000.
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Как вычислить кубический корень из любого числа
Как вычислить кубический корень из любого числа
Напишите на калькуляторе число
. Нажмите кнопку квадратного корня 12 раз
Вычесть 1
Разделите на n, где n — корень n-й степени. Например, если вы находите кубический корень числа, n будет равно 3.
Добавить 1
Нажмите «кнопку умножения, а затем кнопку равно» 12 раз
т.е. умножить равно на умножить равно….. \
И вы получите свой кубический корень!
Также помните, что когда вы нажимаете кнопку «умножить» и ставите знак «равно» вместе на простом калькуляторе , вы фактически пытаетесь получить квадратный корень из квадратных чисел, то есть для таких чисел, как (1) ∧ 2, (1) ∧ 4, (1) ∧8вы будете получать результаты.
Но когда вы просто используете знак множественного числа один раз, а затем постоянно используете только знак равенства и множественное число, то фактически вы получаете (1) ∧ 2, (1) ∧ 3, (1) ∧ 4, (1) ∧ 5, ( 1)∧6, (1)∧7.
На финансовом калькуляторе (BA II PLUS CALCULATORS)
Начните с очистки всех последних записей калькулятора
Прежде чем что-либо делать, нажмите следующие кнопки, чтобы убедиться, что ваш калькулятор понятен:
«2-й», а затем «Работа CLR». Вторая кнопка находится в левом верхнем углу калькулятора, а кнопка CLR Work — в левом нижнем углу калькулятора.
Два метода простых вопросов возведения в квадрат
Когда вам нужно рассчитать 10², у вас есть два варианта.
Опция 1
Введите «10», затем нажмите кнопку «x²». кнопка x² находится вверху в центре калькулятора.
Опция 2
Нажмите «10», затем нажмите кнопку «yˆx», а затем «2» и знак «равно». Кнопка «yˆx» находится в верхней и правой части вашего калькулятора.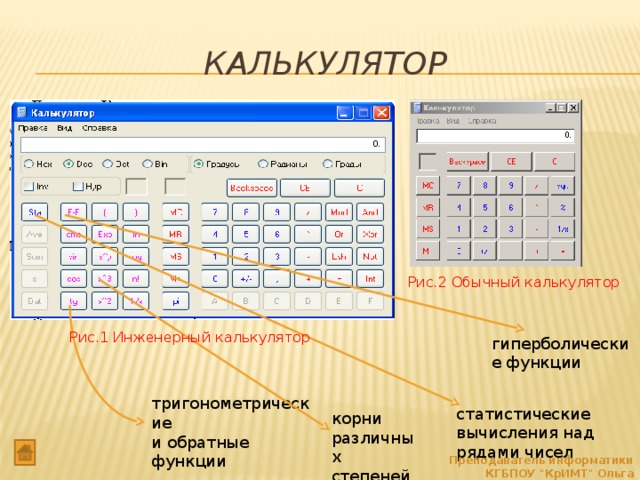
Оба сценария должны дать вам 100.
Вычисление больших значений экспоненты
Для таких задач, как вычисление 10³, у вас есть только один вариант.
Введите «10», перейдите к кнопке «yˆx», введите «3» и, наконец, нажмите знак «равно».
У вас должно получиться значение 1000.
Вычисление кубического корня на BA II Plus
Кубические корни может быть немного сложнее сделать правильно. Убедитесь, что вы выполнили четкую работу, прежде чем начинать новую формулу. Есть также несколько вариантов того, как вы можете рассчитать эти значения на своем калькуляторе. Мы начнем с 1000, чтобы упростить задачу.
Опция 1
Введите «1000».
Используйте кнопку «yˆx».
Введите «3».
Нажмите «1/x» (находится в правом верхнем углу).
Нажмите «равно».
Опция 2
Начните с «1000».
Используйте кнопку «yˆx».
Нажмите кнопку «(» (расположена в левом центре калькулятора).
Введите «1», «÷», «3».
Используйте кнопку «)», чтобы закрыть скобки.
Наконец нажмите знак «равно».
В любом случае вы получите 10 баллов. Лучше использовать вариант 1, так как в нем немного меньше шагов, а значит, меньше места для ошибок.
- Предыдущий
- Следующий
Вы не вошли в систему. Пожалуйста, войдите, чтобы оставлять комментарии.
- О нас
- Артикул
- Новости
- Форум
- Регистр
- Вакансии
- Связаться с нами
- Политика конфиденциальности
СВЯЗАТЬСЯ С НАМИ
- Электронная почта: [email protected]
Далал-стрит, Форт,
Мумбаи — 400001.

СЛЕДУЙТЕ ЗА НАМИ
Забыли пароль ?
Зарегистрироваться
Подписывайтесь на нашу новостную рассылку
Авторские права © Все права защищены.
Калькулятор кубического корня| Пример | Определение
Калькулятор кубического корня — это инструмент, который можно использовать для вычисления кубического корня любого положительного числа, чья заданная площадь больше нуля. CalCon Cube Root Calculator работает по принципу ввода числа, корень которого вычисляем, затем вводим степень корня, после чего результат показывается автоматически. Таким образом, кроме кубического корня третьей степени, вы можете найти корень любой другой степени, например, квадратный или корень пятой степени и так далее.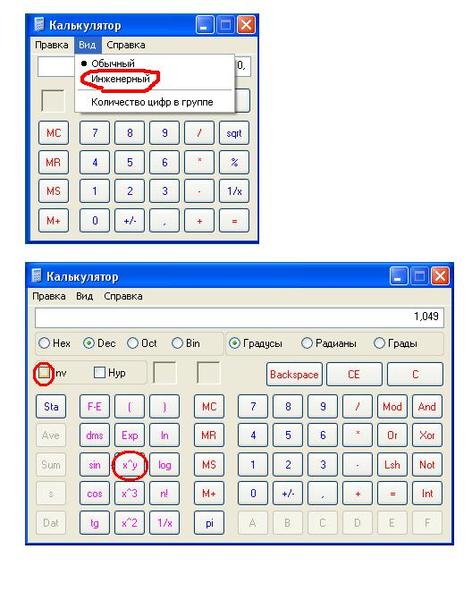 CalCon Cube Root Calculator доступен на этом веб-сайте через приложения для Android и iOS, которые можно загрузить через Play Store или App Store.
CalCon Cube Root Calculator доступен на этом веб-сайте через приложения для Android и iOS, которые можно загрузить через Play Store или App Store.
В продолжении этой статьи мы покажем, что такое корень числа вообще, определение кубического корня, функцию корня и кубический корень. Мы также покажем несколько советов при вычислении корня и приблизительном расчете без использования этого калькулятора. См. также наш Калькулятор корней.
Что такое корень числа?
Корень числа х это другое число, которое при умножении само на себя определенное количество раз равно х . Так, например, второй корень из 9 равен 3, потому что 3×3 = 9.
- Второй корень обычно называют квадратным корнем. См. наш калькулятор квадратного корня для получения дополнительной информации.
- Третий корень обычно называют кубическим корнем.
- Их тогда называют n-м корнем, например, 5-й корень, 7-й корень и т. д.
История
По данным Университета Сент-Луиса, древние египтяне создали корень и использовали его для архитектуры, строительства пирамиды и другие повседневные действия, требующие математики.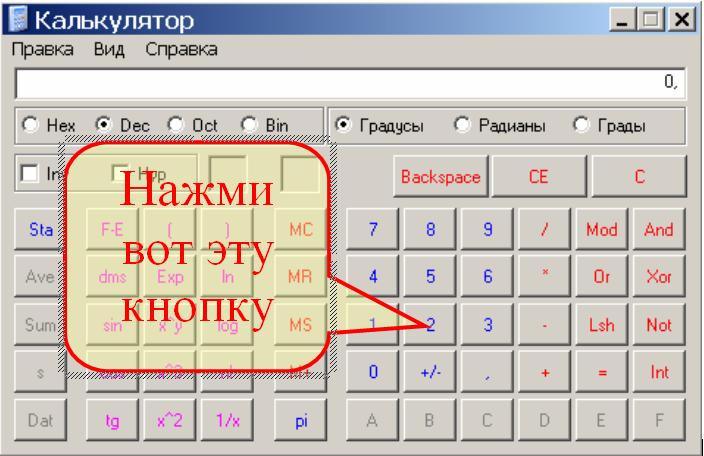 Большая часть сегодняшних знаний о египетской математике исходит из папирусов, написанных во времена 12-й династии. Считается, что у древних египтян была табличка с корнем из нескольких цифр, которая использовалась в качестве ориентира.
Большая часть сегодняшних знаний о египетской математике исходит из папирусов, написанных во времена 12-й династии. Считается, что у древних египтян была табличка с корнем из нескольких цифр, которая использовалась в качестве ориентира.
Поскольку не было дано никаких подробных объяснений корней, антропологи собрали информацию о нем. Например, египетское название корня называлось kenbet , и оно выглядело как угол в 90 градусов, подобно текущему символу корня. Считается, что форма прямого угла была представлением о том, что корень подобен углу коробки; это был «корень» области, потому что они имели одинаковую длину.
В дополнение к египетской истории исчисления корней в математике, есть также записи исчисления, из которых видно, что исчисление корней практиковалось как древними греками, так и вавилонянами с древними калькуляторами.
Что такое кубический корень?
Когда мы произносим слова «куб» и «корень», первый образ, который может прийти на ум, — это куб и корни дерева.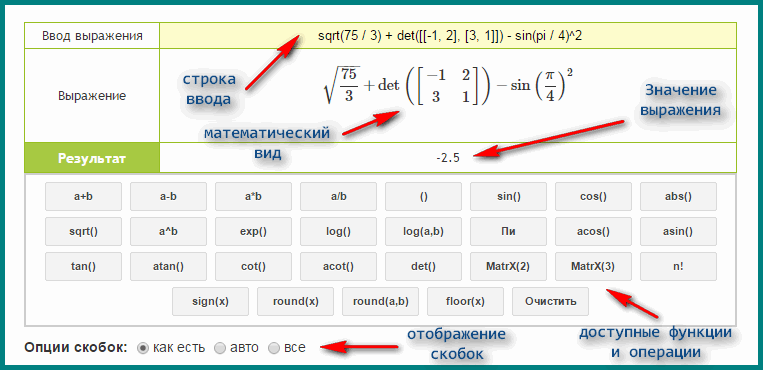 Ну идея очень похожа. Корень означает первоисточник или происхождение. Математическое определение кубического корня гласит: « Кубический корень — это число, которое нужно трижды умножить само на себя, чтобы получить исходное число. » Давайте теперь посмотрим на формулу кубического корня, где y — это кубический корень из х . 9{1/3}
Ну идея очень похожа. Корень означает первоисточник или происхождение. Математическое определение кубического корня гласит: « Кубический корень — это число, которое нужно трижды умножить само на себя, чтобы получить исходное число. » Давайте теперь посмотрим на формулу кубического корня, где y — это кубический корень из х . 9{1/3}
Кубический корень — это операция, обратная кубу числа, пример которой приведен ниже.
Например, корень третьей степени (также называемый кубическим корнем) из 64 равен 4, потому что если вы умножите три 4 вместе, вы получите 64:
4 х 4 х 4 = 64
Это будет представлено как:
\sqrt[3]{64}=4
Приведенный выше пример будет задан как «корень в третьей степени из 64 равен 4» или «кубический корень из 64 равен 4».
Символы
Подкоренное число
Выражение, для которого нужно найти корень.
Радикальный символ
Символ √, означающий «корень». Длина горизонтальной линии имеет важное значение, потому что все, что находится под ней, представляет собой то, для чего вам нужен корень.
Градус
Сколько раз подкоренное число умножалось само на себя. 2 означает квадратный корень, 3 означает кубический корень. После этого они называются 4-м корнем, 5-м корнем и т. д. Предполагается, что это 2-квадратный корень, если он отсутствует. 9{1/n}
Функция кубического корня и график
Функция квадратного корня — это функция с переменной ниже корня. Точно так же функция кубического корня — это функция с переменной ниже кубического корня. Самые основные из этих функций — √( x ) и 3 √( x ) соответственно. Мы можем построить эти основные функции, найдя точки, удовлетворяющие каждой функции, нарисовав их и соединив точки.
Основные функции квадратного и кубического корня можно представить так, как показано на следующем фото.
Однако, если появляется гораздо более сложная функция, нет смысла рисовать наизусть, а логичнее использовать основные правила и шаги для расчета основных элементов функций и построения графиков, либо с помощью нашего калькулятора или обычные математические калькуляторы с расширенным набором функций.
Ниже приведены примеры функций кубического корня:
Что такое кубический корень из…?
Кубический корень из любого положительного числа легко найти с помощью нашего Калькулятора кубического корня. Введите любое число, чтобы увидеть его кубический корень или любую другую степень корня. Например, кубический корень из 729.равно 9.
В отличие от квадратного корня, имейте в виду, что можно найти кубический корень из отрицательного числа . В конце концов, отрицательное число, возведенное в третью степень, остается отрицательным, например, (-9) ³ = -729.
С помощью калькуляторов можно найти только положительный кубический корень, но имейте в виду, что вы можете ввести абсолютное значение числа, кубический корень которого вы ищете, и добавить отрицательный символ к конечному результату, если исходное число отрицательное .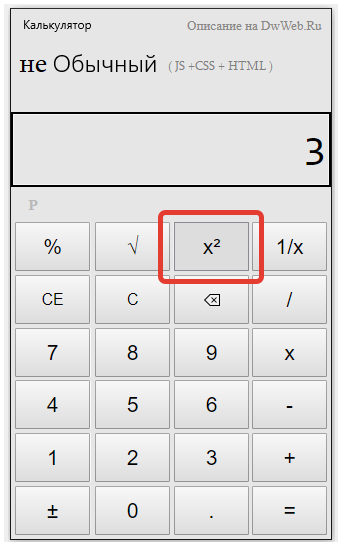
Однако вы должны помнить, что любое ненулевое число имеет три кубических корня: как минимум один действительный и два мнимых. Поэтому этот калькулятор кубического корня имеет дело только с действительными числами.
Совершенные кубы
Совершенные кубы — это целые числа, и перечисленные числа, умноженные на три, дают совершенный куб.
| Числа | Совершенные кубики Кубики | Числа | Совершенные кубики |
| 0 | 0 | 8 | 512 |
| 1 | 1 900 26 | 9 | 729 |
| 2 | 8 | 10 | 1000 |
| 3 | 27 | 11 | 1331 |
| 4 | 64 9 0278 | 12 | 1728 |
| 5 | 125 | 13 | 2197 |
| 6 | 216 | 14 | 274 4 |
| 7 | 343 | 15 | 3375 |
Это легко вычислить кубический корень совершенного куба без калькулятора, но вычислить другие кубические корни очень сложно.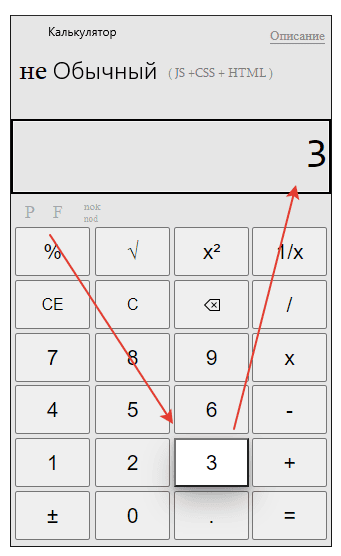 Основные шаги, которые вы можете сделать, чтобы начать вычисление кубических корней без калькулятора, будут представлены ниже.
Основные шаги, которые вы можете сделать, чтобы начать вычисление кубических корней без калькулятора, будут представлены ниже.
Как вычислить кубический корень?
Вычисление кубического корня с помощью Калькулятора кубического корня CalCon является полностью интерактивным и простым, поскольку все, что вам нужно сделать, это:
- Введите число, из которого вы хотите вычислить кубический корень ) в поле
- Прочитать результат
Если вы хотите вычислить другие корни (степень корня) с помощью этого калькулятора, вам нужно изменить число 3 на нужную степень на втором шаге.
Оценка корня
Метод простой простой факторизации используется для определения кубического корня числа. Чтобы найти кубический корень, вы можете начать с факторизации заданного числа, используя основные математические законы. Затем разделите полученные факторы на группы, содержащие по три одинаковых фактора. Затем удалите степень кубического корня и умножьте множители, чтобы получить ответ. Предположим, что остался какой-то фактор, который нельзя разделить поровну на группы по три. В этом случае данное число не является полным кубом, как описано выше, и мы не можем найти кубический корень этого числа вручную, а должны использовать калькулятор.
Предположим, что остался какой-то фактор, который нельзя разделить поровну на группы по три. В этом случае данное число не является полным кубом, как описано выше, и мы не можем найти кубический корень этого числа вручную, а должны использовать калькулятор.
Пример:
Кубический корень из 64 =?
Таким образом, простая факторизация числа 64 равна
. 2 х 2 х 2 х 2 х 2 х 2
Мы ищем кубический корень из 64, полный кубический корень, поэтому мы разделим простые множители на три одинаковые группы.
Обратите внимание, что мы можем переставить множители следующим образом:
64 = 2 х 2 х 2 х 2 х 2 х 2 = (2 х 2) х (2 х 2) х (2 х 2) 9{3} = 64
Третий корень числа 64 равен 4.
Оценка n
th Root Вычисление n th корня может быть выполнено с использованием аналогичного метода, с изменениями для решения н. Вычисление n-го корня без калькулятора требует значительных усилий.



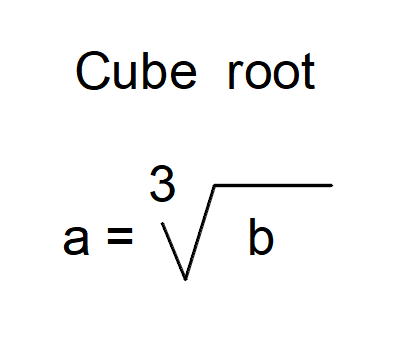

 01 (точное значение 1.7099).
01 (точное значение 1.7099).


 1200 * 4 + 60 * 16 + 64 = 5824.
1200 * 4 + 60 * 16 + 64 = 5824.