Сумма, разность векторов, произведение вектора на число. Свойства этих операций.
Линейные операции над векторами.
Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.
b
a+b
a Замечание. Такое правило сложения векторов называют правилом треугольника.
Свойство 1. a + b = b + a.
Свойство 2. (a+b)+c=a+(b+c).
Свойство 3.
Для
любого вектора а существует нулевой вектор О такой, что а+О=а.
Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.
a a—b
b
Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.
Свойство 1. k(a + b) = ka + kb.
Свойство
2. (k
+ m)a = ka +
ma.
Свойство 3. k(ma) = (km)a.
Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.
Угол между векторами.
Угол между векторами
Вычисление ортогональной проекции.
Так как , каждый вектор однозначно раскладывается в сумму векторов и . Вектор х1 называется ортогональной проекцией х на .Легко видеть, что х2 – ортогональная проекция х на .
Найдем
ортогональную проекцию х на
в
предположении, что в
задан
некоторый ортогональный базис h1,…,hk.
Дополним этот базис до ортогонального
базиса в пространстве ε, присоединив к
нему произвольный ортогональный базис
hk
получаем: .
Если k = 1, проекция имеет вид х1 = ((х, h)/|h|2)h, и мы видим, что правая часть формулы – сумма проекций на ортогональные одномерные пространства, натянутые на h1,…,hk. Так же истолковывается формула , а значит, равенство Парсеваля является обобщением теоремы Пифагора.
Из (х1, х2) = 0 следует .
Длина |х2| ортогональной проекции х на обладает следующим свойством минимальности, обобщающую теорему о длине перпендикуляра и наклонной из элементарной геометрии.
Предположение: Пусть х1 – ортогональная проекция х на . Тогда для любого вектора , отличного от х 1, выполнено
.
Доказательство. Обозначив х1 – у через z, имеем: .
Но (z, x2) = 0, так как , и, следовательно,
Отсюда
непосредственно вытекает доказываемое
утверждение.
Ортогональная проекция суммы векторов и произведения вектора на число.
Линейная комбинация векторов, линейно независимые вектора. Условия линейной зависимости векторов.
Линейной комбинацией векторов а1, а2,…,аn называется выражение вида: k1a1 + k2a2 +…+ knan, где ki – числа.
Векторы а1, а2,…,аn
при
ki не равных нулю одновременно, т. е. k12 + k22 +…+ kn2 ≠
0.
е. k12 + k22 +…+ kn2 ≠
0.
Если же равенство (2) возможно только при всех ki = 0, векторы называются линейно независимыми.
Замечание 1. Если система векторов содержит нулевой вектор , то она линейно зависима.
Замечание 2. Если среди n векторов какие-либо (n-1) линейно зависимы, то и все n векторов линейно зависимы. (Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.)
Замечание 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Замечание
4.
Необходимым и достаточным условием
линейной зависимости трех векторов
является их компланарность.
Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.
Графические методы – Колледж физики, главы 1-17
3 Двумерная кинематика
Резюме
- Понимание правил сложения, вычитания и умножения векторов.
- Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.
Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление – [латекс]\жирныйсимвол{\тета}.[/латекс]
ВЕКТОРА В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .
Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6.Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7. Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины. )
)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9о}[/latex]северо-восток. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, обозначив первый[latex]\textbf{A},[/latex]второй[latex]\textbf{B},[/latex]и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 8.(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9.(3) Нарисуйте результирующий вектор,[latex]\textbf{R}.[/latex]
Рисунок 10. (4) Используйте линейку для измерения величины[latex]\ textbf{R},[/latex]и транспортир для измерения направления[latex]\textbf{R}.[/latex]Хотя направление вектора можно задать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9о}[/latex]юго-восток.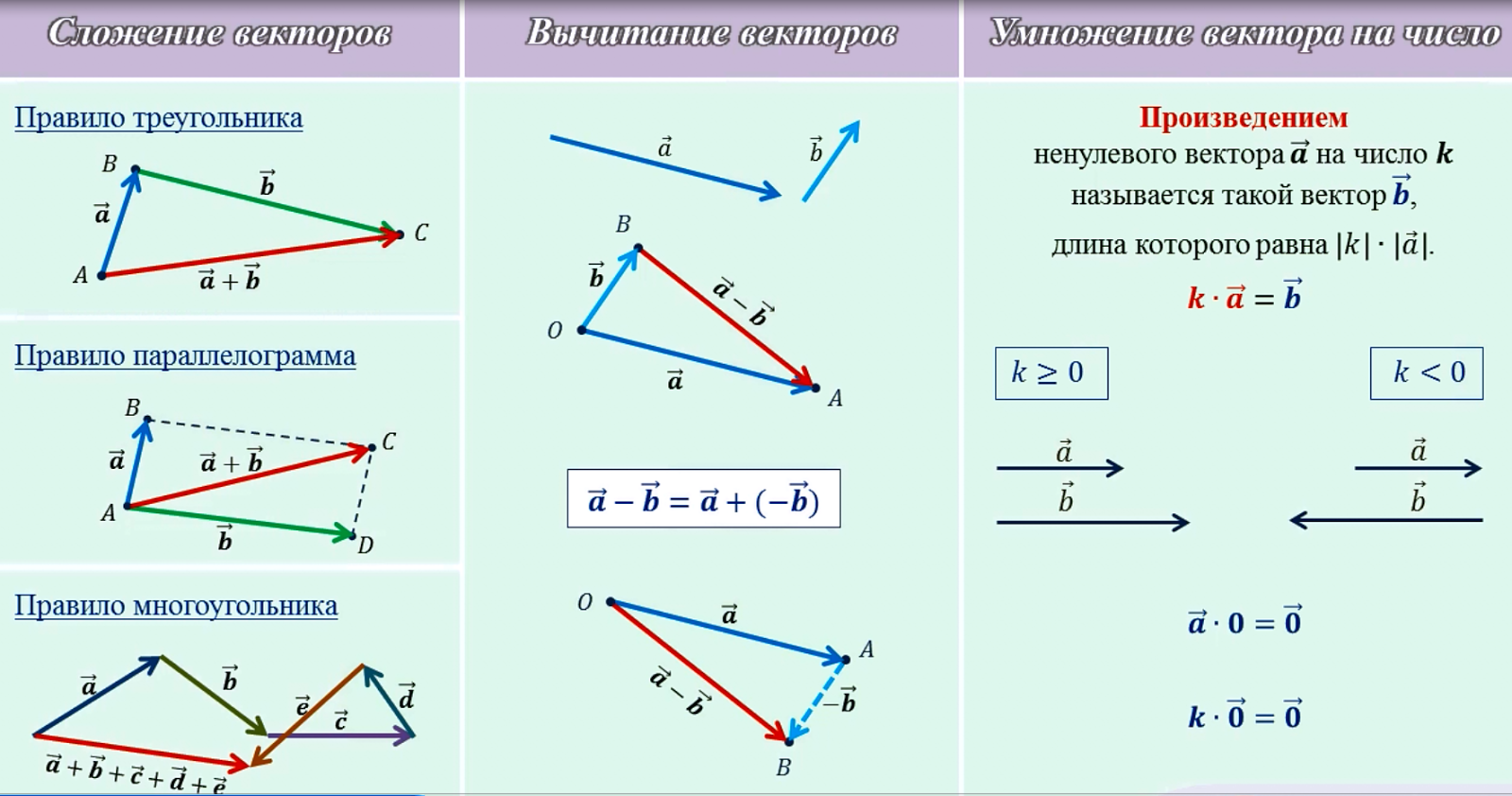
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Рисунок 12.Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это верно для сложения обычных чисел как хорошо — вы получите тот же результат, если вы добавите, например, [латекс]\жирныйсимвол{2+3}[/латекс]или [латекс]\жирныйсимвол{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0021 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0021 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
 o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока. Рисунок 14.
o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока. Рисунок 14. Стратегия
Мы можем представить первый этап поездки с помощью вектора[latex]\textbf{A},[/latex], а второй этап поездки с помощью вектора[latex] \textbf{B}.[/latex]Док расположен в месте[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]Если женщина по ошибке путешествует в напротив 9о}[/latex]юго-восток. Мы представляем это как[latex]\boldsymbol{-\textbf{B}},[/latex], как показано ниже. Вектор[latex]\boldsymbol{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [латекс]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]или[латекс]\boldsymbol{\textbf{A}-\textbf {B}}.[/latex]
Рисунок 15. Выполним сложение векторов для сравнения расположения дока,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/ латекс]с местом, куда по ошибке прибыла женщина,[латекс]\boldsymbol{\textbf{A}+(-\textbf{B})}. [/latex]
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы[latex]\textbf{A}[/latex]и[latex]\boldsymbol{-\textbf{B}} .[/latex]
(2) Поместите векторы от начала до конца.
(3) Нарисуйте результирующий вектор[latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.о}[/latex]юго-восток. 9о}[/latex]северо-восток.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше первого этапа пути, рассмотренного в предыдущем примере, то мы бы прошли[latex]\boldsymbol{3 \times 27,5\textbf{ м}},[/latex]или 82,5 м, в направлении[латекс]\boldsymbol{66. o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: Когда вектор[латекс]\текстбф{А}[/латекс] умножается на скаляр[латекс]\жирныйсимвол{с},[/латекс]
- модуль вектора становится абсолютным значением[latex]\boldsymbol{cA},[/latex]
- , если [latex]\boldsymbol{c}[/latex] положительный, направление вектора не меняется,
- , если [латекс]\boldsymbol{c}[/латекс]отрицательно, направление меняется на противоположное.
В нашем случае [латекс]\boldsymbol{c=3}[/latex]и[латекс]\boldsymbol{\textbf{A}=27,5\textbf{м}}.[/latex]Вектора умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x – и y , или компонентов север-юг и восток-запад. 9o}[/latex]к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод сложения векторов [latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex] включает в себя рисование векторов на графике и их сложение с использованием прямого метод хвоста.
 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно. - графический метод вычитания вектора [latex]\textbf{B}[/latex]из [latex]\textbf{A}[/latex]предполагает добавление противоположного вектора[latex]\textbf{B},[/latex] ] который определяется как [латекс]\boldsymbol{-\textbf{B}}.[/latex]В этом случае [латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A} +(-\textbf{B})=\textbf{R}}.[/latex]Затем обычным методом сложения головы к хвосту получается результирующий вектор[latex]\textbf{R }.[/латекс]
- Сложение векторов коммутативно так, что [латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора.
 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора. - Если вектор[latex]\textbf{A}[/latex] умножается на скалярную величину[latex]\boldsymbol{c},[/latex]величина произведения определяется как[latex]\boldsymbol{cA }.[/latex]Если [латекс]\boldsymbol{c}[/латекс] положителен, направление произведения указывает на то же направление, что и [латекс]\текстбф{А};[/латекс]если[латекс] \boldsymbol{c}[/latex]отрицательно, направление произведения указывает на направление, противоположное [latex]\textbf{A}.[/latex]
- компонент (двумерного вектора)
- часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов 90 336
- коммутативный
- относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 336
- направление (вектора)
- ориентация вектора в пространстве
- голова (вектора)
- конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
- метод «голова к хвосту»
- метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора
- величина (вектора)
- длина или размер вектора; величина является скалярной величиной
- результат
- сумма двух или более векторов
- результирующий вектор
- векторная сумма двух или более векторов
- скаляр
- количество с величиной, но без направления
- хвост
- начальная точка вектора; напротив наконечника или наконечника стрелки
Разница между двумя векторами в R
В этой статье мы увидим, как найти разницу между двумя векторами в языке программирования R.
Разница (A-B) между двумя векторами в R Programming эквивалентна элементам, присутствующим в A, но отсутствующим в B. Результирующие элементы всегда являются подмножеством A. В случае, если оба набора не пересекаются, возвращается весь набор A.
Метод 1: использование setdiff() методМетод setdiff() в R используется для извлечения элементов вектора X, которые не содержатся в Y. Этот метод может применяться, когда два векторы также могут принадлежать к разным типам данных, где элементы первого вектора-аргумента возвращаются без изменений. В случае, если входные векторы эквивалентны, то есть содержат одни и те же элементы, результирующий вектор будет иметь нулевые записи и ссылаться на выходные данные типа данных (0). Также разные типы результатов получаются при изменении порядка векторов во время вызова функции.
Syntax:
setdiff( X, Y)
Example:
R
|
Output
[1] "Исходный вектор1" [1] 1 2 3 4 5 [1] "Исходный вектор2" [1] 4 5 6 7 8 [1] «Век1-Век2» [1] 1 2 3
Этот метод работает и для строковых векторов.
Example:
R
|
Output
[1] “Original vector1 “
[1] «Geeksforgeeks» «Интервью» «Наука»
[1] «Исходный вектор2»
[1] «Алгоритмы» «Наука» «размещения» »
[1] «Алгоритмы» «размещения» «структуры данных»
Также этот метод автоматически возвращает уникальные элементы результирующего вектора.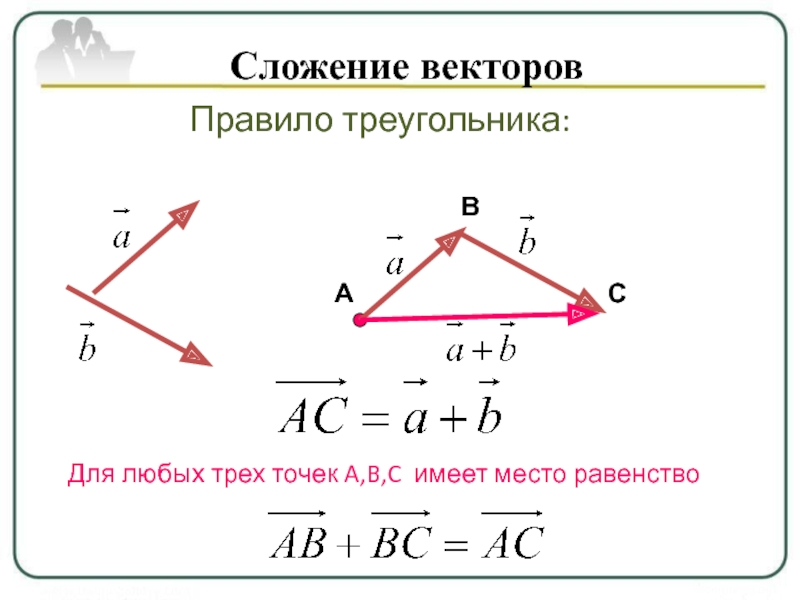 Любые повторяющиеся элементы удаляются.
Любые повторяющиеся элементы удаляются.
Пример:
Ч
|
Output
[1] "Original vector1 " [1] «Geeksforgeeks» «Интервью» «Наука» [1] "Исходный вектор2" [1] 1 2 3 5 5 [1] "Век2 - Век1" [1] 1 2 3 5Способ 2: Использование оператора %in%
Оператор %in% можно использовать для проверки наличия элемента в списке. Этот подход сначала проверяет, какие индексы вектора1 не находятся в векторе2, а затем возвращаются соответствующие элементы вектора1. Затем следует применение метода unique(), который возвращает только уникальные элементы результирующего вектора.
Этот подход сначала проверяет, какие индексы вектора1 не находятся в векторе2, а затем возвращаются соответствующие элементы вектора1. Затем следует применение метода unique(), который возвращает только уникальные элементы результирующего вектора.
Синтаксис:
vec1[! vec1 %in% vec2]
Example:
R
|
Выход
[1] «Оригинальный вектор1» «
[1]« Гекс -фрукты »« Интервью »« Наука »
[1]« Оригинальный вектор 2 »
[1]« Алгоритмы »« Наука ».
места размещения» «структуры данных»
[1] «Vec1 – Vec2»
[1] «Geeksforgeeks» «Интервью»
Этот подход также совместим с векторами, принадлежащими к разным типам данных. В этом случае возвращаются элементы vec1.
Example:
R
|

 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.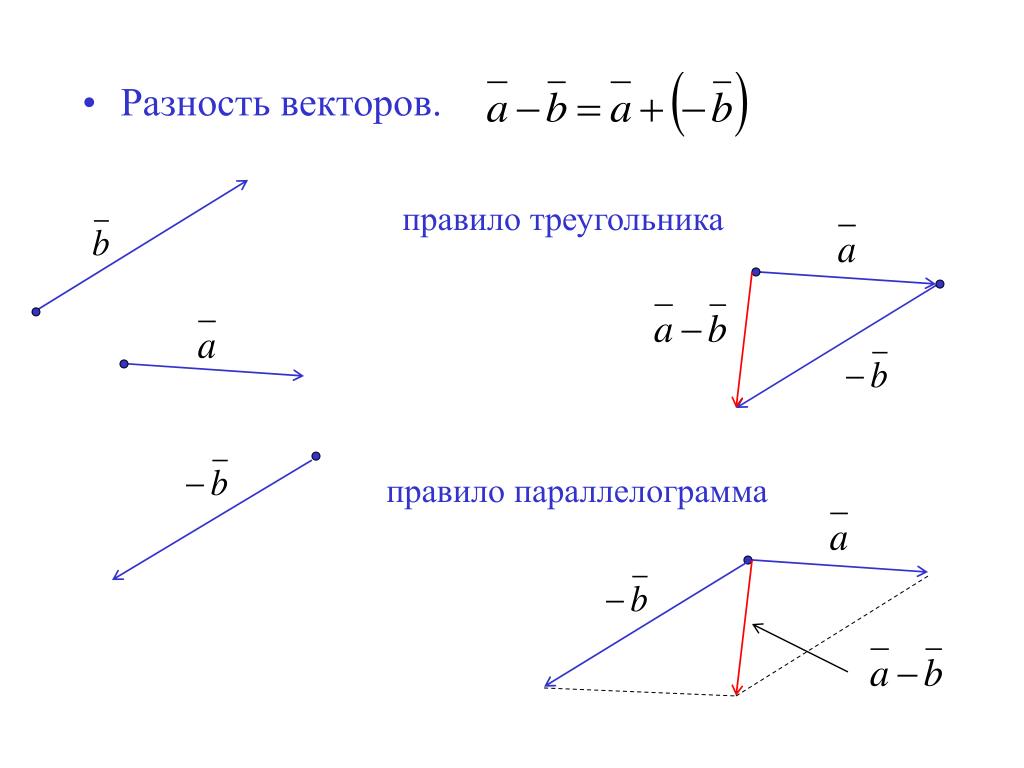 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора. места размещения» «структуры данных»
места размещения» «структуры данных»