1 смежные вертикальные углы. «смежные и вертикальные углы». Получившийся угол АОС является смежным для угла АОВ
§ 1 Смежные углы. Определение, свойство
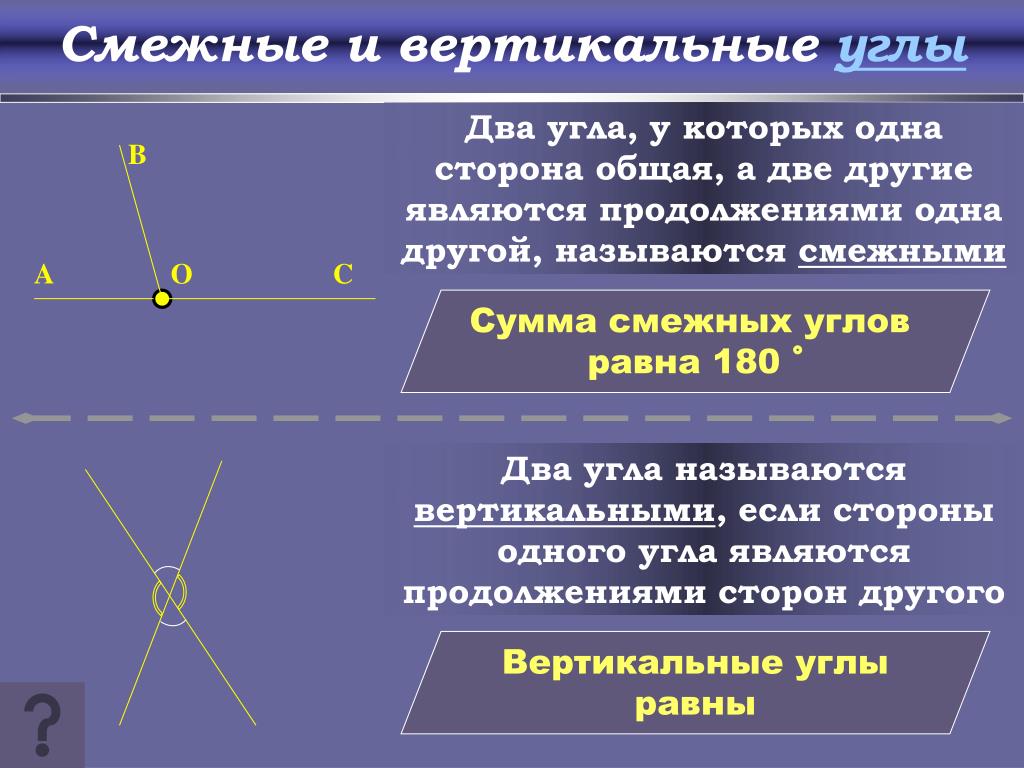
Рассмотрим развернутый угол АОВ, величина которого равна 180°. Проведем из вершины угла О луч ОС. Этот луч разделил развернутый угол на два угла АОС и ВОС. Такие углы называются смежными.
Определение: два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Так как лучи ОА и ОВ образуют развернутый угол, то ∠АОС + ∠ВОС = ∠АОВ = 180°.
Значит, сумма смежных углов равна 180°. Запомним это важное свойство.
§ 2 Вертикальные углы. Определение, свойство
Предположим, что ученику предложили построить угол, равный данному углу АОВ, только с помощью линейки и карандаша. Он поступил так: построил лучи ОС и ОD, как продолжение соответственно лучам ОВ и ОА, и заявил, что угол СОD= углу АОВ. Прав ли он? Докажем, что он прав.
Чтобы установить равенство углов СОD и АОВ, т. е. углов 1 и 2, докажем, что их градусные меры равны. Угол 1 и угол DОВ смежные, значит, их сумма равна 180° (∠1 + ∠DОВ = 180°). Аналогично, угол 2 и угол ДОВ смежные, значит, и их сумма равна 180° (∠2 + ∠DОВ = 180°).
е. углов 1 и 2, докажем, что их градусные меры равны. Угол 1 и угол DОВ смежные, значит, их сумма равна 180° (∠1 + ∠DОВ = 180°). Аналогично, угол 2 и угол ДОВ смежные, значит, и их сумма равна 180° (∠2 + ∠DОВ = 180°).
Из полученных равенств выразим угол 1 и угол 2, получаем:
∠1 = 180° — ∠DOВ,
∠2 = 180° — ∠DOВ.
Таким образом, градусные меры углов 1 и 2, т.е. углов СОD и АОВ равны. Ученик оказался прав. Эти углы называются вертикальными.
Определение: два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Запомним важное свойство вертикальных углов: вертикальные углы равны.
§ 3 Перпендикулярные прямые
В жизни вы не раз встречались с четырьмя неразвернутыми углами, которые образуются при пересечении прямых. Выясним, какими углами окажутся все эти углы, если один из них будет прямым. Как называют в этом случае пересекающиеся прямые?
Построим прямой угол АОВ. Проведем лучи ОС и ОD, как продолжение лучам ОА и ОВ соответственно, получим две пересекающиеся прямые АС и ВD и четыре угла АОВ, АОD, СОD, СОВ.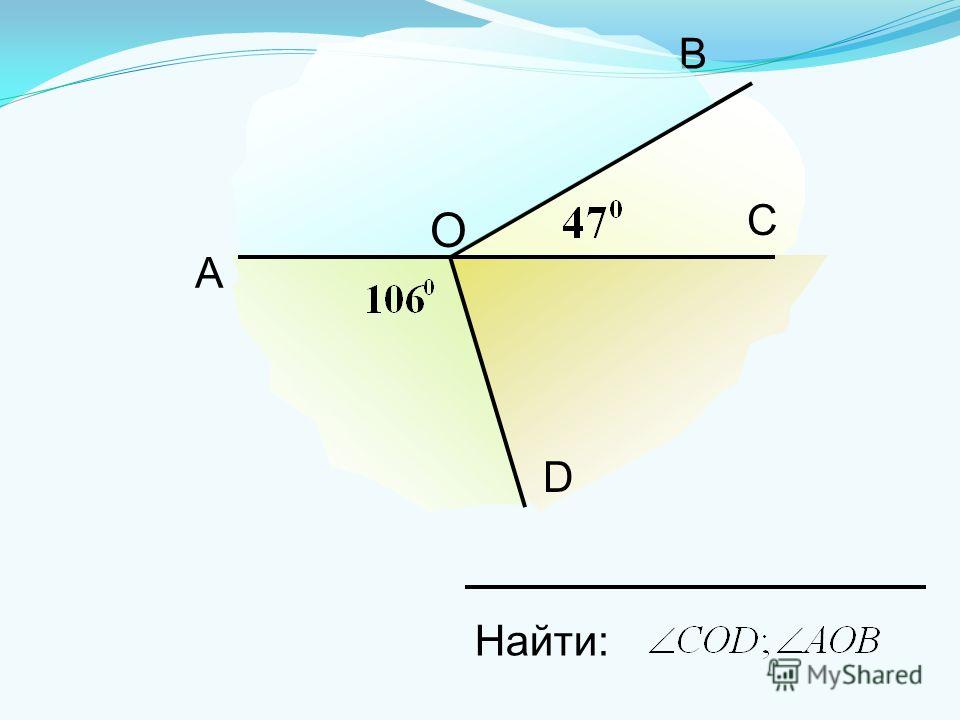
Определение: две пересекающие прямые называются перпендикулярными(или взаимно перпендикулярными), если они образуют четыре прямых угла.
О таких прямых также говорят, что они пересекаются под прямым углом. На чертеже прямой угол отмечают квадратом.
Перпендикулярность прямых записывается так: АС⊥ВD, читается: «прямая АС перпендикулярна к прямой ВD».
Отметим важное утверждение: две прямые, перпендикулярные к третьей, не пересекаются.
Для проведения перпендикулярных прямых используют чертежный угольник и линейку.
В геодезии для построения прямых углов используют прибор теодолит.
§ 4 Решение задачи по теме урока
Рассмотрим задачу.
Задача: Один из смежных углов на 16° больше другого.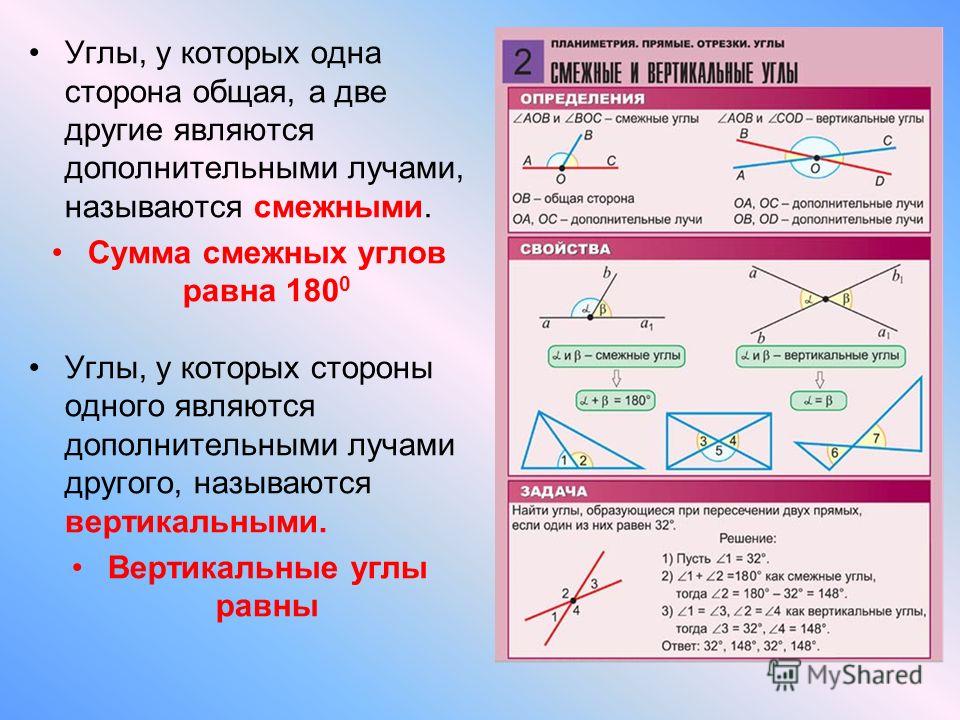 Найти величину каждого угла.
Найти величину каждого угла.
Пусть меньший угол СОВ = х градусов, тогда угол АОС = х + 16°. Углы АОС и ВОС — смежные, значит, их сумма равна 180°.
Получаем: х + х + 16° = 180°
Решая это уравнение, находим неизвестное: х = 82°. Значит, угол СОВ = 82°, а угол АОС = 82° + 16° = 98°.
Ответ: угол ВОС = 82°, угол АОС = 98°.
Список использованной литературы:
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с. : ил.
- Гаврилова Н.Ф. Поурочные разработки по геометрии 7 класс. — М.: «ВАКО», 2004, 288с. – (В помощь школьному учителю)
- Белицкая О.В. Геометрия. 7 класс. Ч.1. Тесты. – Саратов: Лицей, 2014. – 64 с.
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD.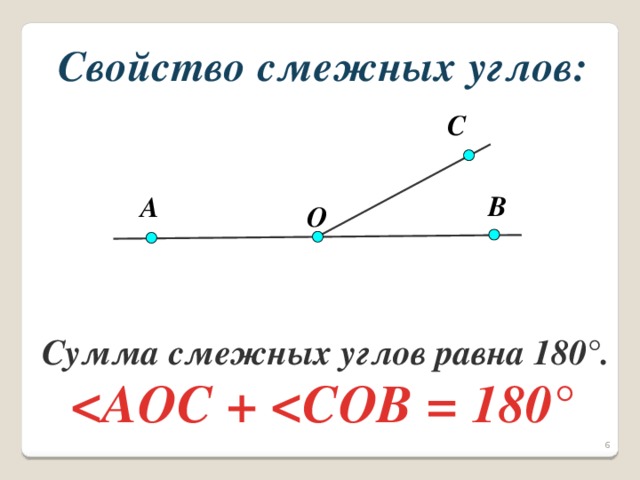 Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α.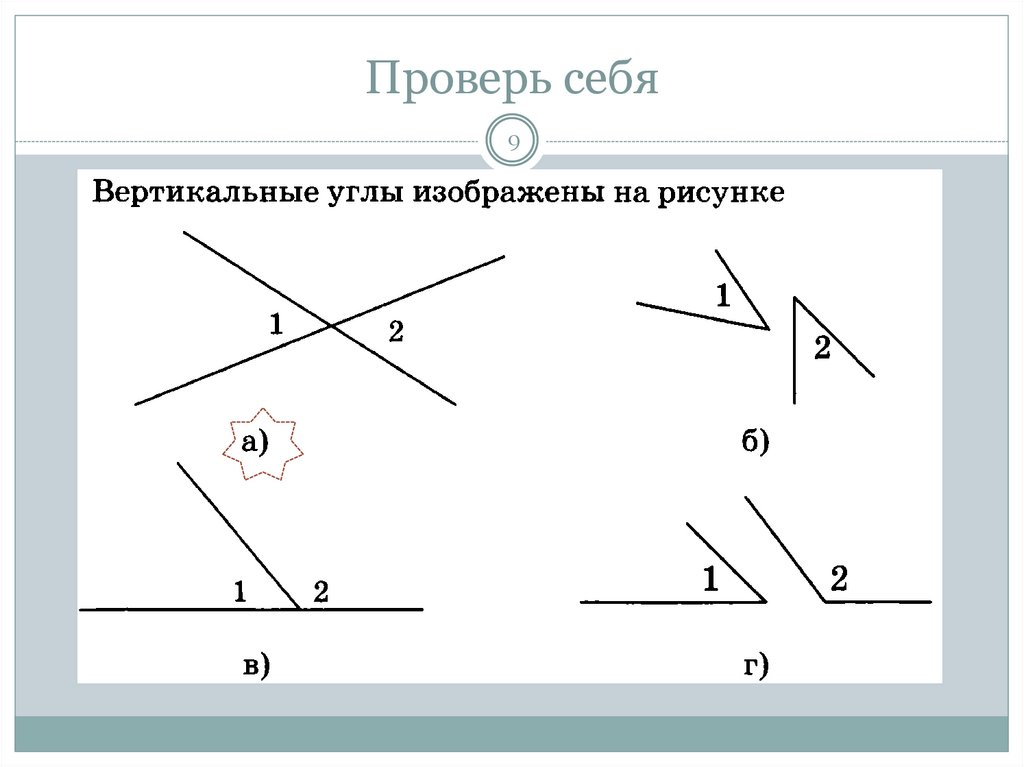 То есть они будут равны между собой.
То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().
- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
Тема урока: «Смежные и вертикальные углы. »
»
Цель урока: познакомить с понятием «смежные и вертикальные углы
Задачи:
Учебные – закрепить понятие угла, правила измерения и построения углов; на основе выделенных признаков научить объединять углы по группам; научить вести исследование с опорой на алгоритм действий, анализировать полученные данные и делать выводы; закрепить полученные на уроке знания в ходе решения задач.
Развивающие – используя возможности мультимедийной презентации и электронного учебника повысить интерес к изучаемому предмету; развивать геометрическую интуицию, умение контролировать внимание на всех этапах урока.
Воспитательные –воспитать любовь к Родине, любовь к матери, воспитать аккуратность, прилежание.
Оборудование: компьютер, мультимедийный проектор, электронный учебник, учебник «Геометрия 7-9 класс, автор Л.С.Атанасян», карточки-задания, карточки для проведения рефлексии, таблицы «Вертикальные и смежные углы».
ХОД УРОКА
Организационный момент (Слайд 1 )
А.П.Чехов говорил: «Нужно стремиться к тому,
чтобы каждый видел и знал больше,
чем видел и знал его отец и дед»
Мы начинаем урок геометрии. У всех на столе: учебник, тетрадь, карандаш, ручка, линейка, транспортир.
(Эмоциональный настрой на урок. Стихотворение Евгения Винокурова. )
(Слайды 2)
О Петр, ведь ты построил город
Не для умерших – для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых.
Недвижимы аллеи парков.
Прямы проспекты, как стрела.
Сильней божественных монархов
Здесь геометрия была.
(Слайд 3)
Гуляют каменные финны.
Курятся трубки из бород.
Вот и построили Афины
Средь топей северных болот!
Налево львы. И львы направо.
А у заставы инвалид,
Штык держит вертикально прямо.
Как геометрия велит.
II. Подготовка к восприятию темы
Сегодня мы продолжаем наше путешествие по стране «Геометрия» и поговорим об углах. А вот о каких углах сегодня пойдет речь, мы постараемся выяснить в ходе нашего урока. Для этого мы вытащим из тайников памяти кое-что ценное и восхитимся глубокими знаниями, которые пригодятся нам сегодня на уроке. (Слайд 4 – план урока ). Для разминки я предлагаю провести «Мозговой штурм». Да, я совсем забыла сказать, что на уроке можно ошибаться, сомневаться, консультироваться. Но при этом, вы должны дать себе установку (Слайд 5) «понять и быть тем первым, который увидит ход решения и даст правильный ответ» . Каждый правильный ответ вы будите отмечать в листке контроля. Это мне поможет выставить оценки за урок. Тот кто наберет больше баллов, тот и получит лучше оценку. Никто без поощрения не останется. Итак, мы начинаем.
III. Актуализация знаний учащихся. «Мозговой штурм» (Слайд 6)
– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (На прошлом уроке мы говорили об угле)
Какая фигура называется углом? (Геометрическая фигура, которая состоит из двух лучей, исходящих из одной точки, называется угол)
— Что такое вершина и стороны угла? (Общая точка называется вершиной угла, а лучи сторонами)
— )
С помощью какого инструмента измеряют углы?(Углы измеряют с помощью транспортира)
(Слайд 7 )
— Какие это углы?
Угол, градусная мера которого меньше 90 0 , называется острым)
(Угол, градусная мера которого больше 90, но меньше 180 0 , называется тупым)
Какие углы называются прямыми?(Угол называется прямым, если он равен 90 0 )
-Как выглядит прямой угол.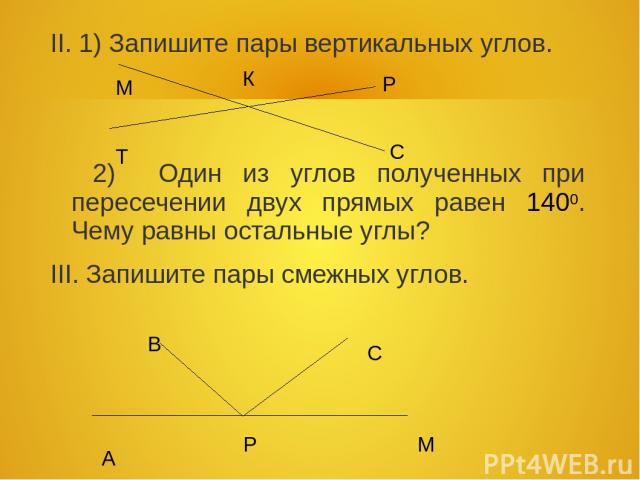
Угол называется развернутым, если он равен 180 0)
(Слайд 8)
А сейчас мы решим несколько задач на вычисление градусной меры угла. Каждый выбирает себе задание по силам. Для 1 уровня- это задача на рисунке 1. Её решение мы разберем на доске, для 2 уровня задача на рисунке 2. Её я предлагаю решить самостоятельно. Те кто выберет самостоятельное решение, каждый получит плюс в карточку учета, если ответ будет верным. Кто выбирает задачу на рисунке 2, работают самостоятельно. Кто выбирает задачу на рисунке 1 и желает ее решить у доски.
Сколько углов мы видим на рисунке?(На рисунке 3 угла)
-Н азови и покажи их? (угол АОС, угол АОВ, угол ВОС )
Что мы можем сказать о градусной мере угла ВОС?(
Запишем это и найдем градусную меру угла ВОС. Запишем ответ.
Проверим наши ответы. Кто работал самостоятельно оцените свою работу, если ответы сошлись, то поставьте плюс в карточку учета.
Итак подведем итог.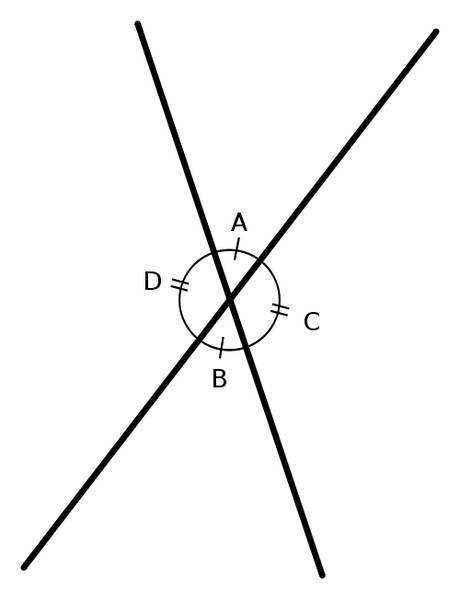
(Слайд 9)
По какому признаку мы делим углы? (Углы разделяются в зависимость от величины)
Какие это углы?(О).
IV. Практическая работа исследовательского характера
– А сейчас познакомимся со второй группой углов и попробуем выяснить, по какому признаку можно ее выделить. Перед вами карточки с изображением углов. Ваша задача – выполнить следующие действия для карточки № 1.
(Слайд 10 – алгоритм действий ).
-Какой вывод сделали? (Сумма углов равна 180 градусов )
(Слайд 11)
Как бы вы назвали эти углы?(Смежные )
По какому признаку мы выделили этот вид углов? (Этот вид углов мы выделили по взаимному расположению)
Давайте запишем определение
(Слайд 12 )
Постройте острый, прямой и тупой углы. Продолжите одну из сторон и укажите получившиеся смежные углы.
3 ученика у доски, остальные в тетради.
Для любого угла можно построить ему смежный угол? (Да)
-Повторите алгоритм действия для карточки №2.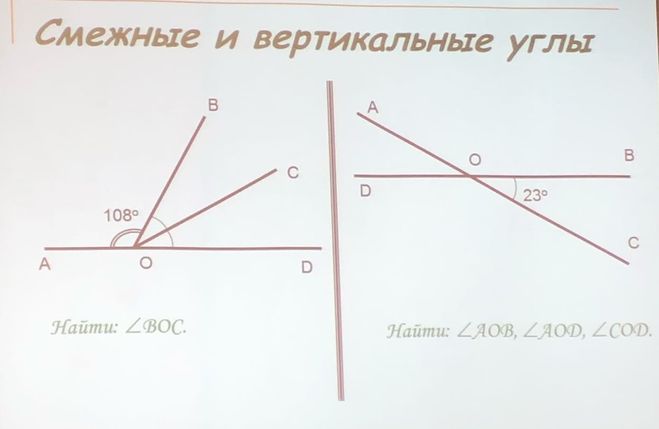
(Слайд 13)
-Какой вывод можно сделать?.(Углы равны )
(Слайд 14)
Как бы вы назвали данный вид углов?(Вертикальные )
-Запишем определение.
(Слайд 15)
Посмотрите на правило построения вертикальных углов и выполните построение в тетради.
(Слайд 16)
-Посмотрите на чертежи и назовите вертикальные углы
(Слайд 17)
-Вернёмся к схеме, которую мы рассматривали в начале урока, и подведем итог.
(Слайд 18)
-По каким признакам мы делим углы? (Углы делятся по величине угла и по их взаимному расположению )
Какие углы по величине градусной меры мы знаем?(По величине градусной меры углы бывают: острые, тупые, прямые, развернутые)
Какие углы по взаимному расположению мы изучили сегодня? (По взаимному расположению углы бывают: смежные и вертикальные).
Не забывайте отмечать свои верные ответы в карточке учета.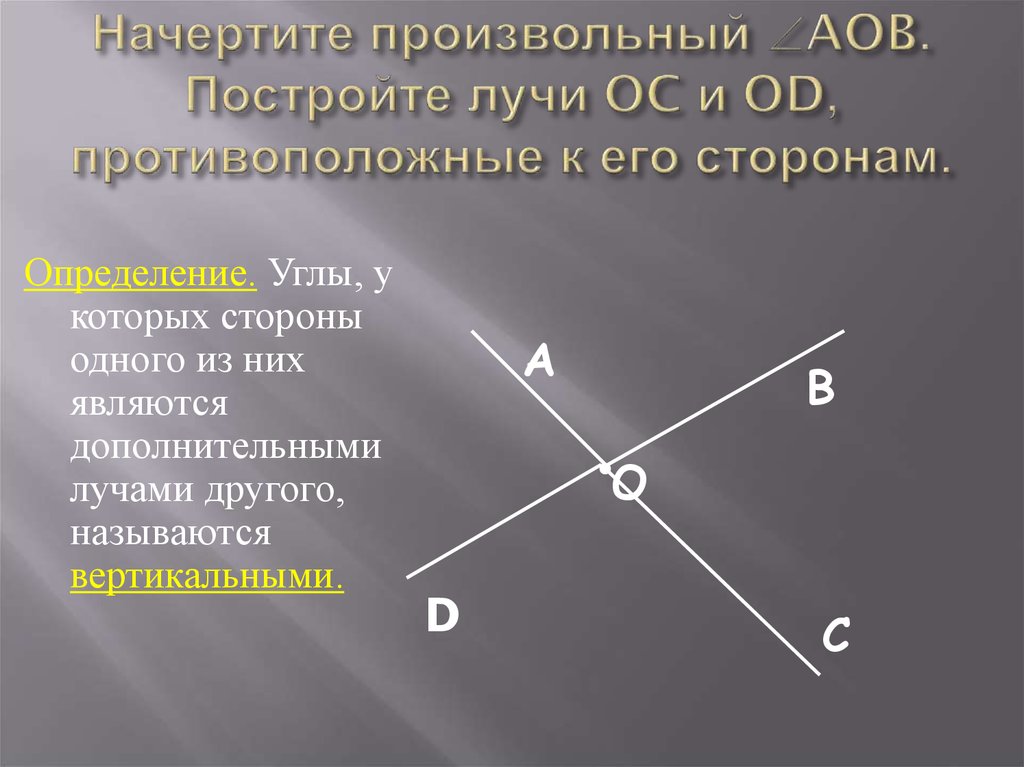
-Как же теперь мы сформулировали тему нашего сегодняшнего урока(«Смежные и вертикальные углы» ).
Правильно. «Смежные и вертикальные углы». Посмотрите, как в Санкт-Петербурге это хорошо видно.
(Слайд 19)
V . Физкукльтминутка.
Вы устали? Давайте отдохнём.
(Слайд 20)
1.Голова идет по кругу.
2.Руки в стороны.(Развернутый угол, прямой угол).
3.Руки с соседом. (Смежные углы).
4.Спиной к соседу.(Вертикальные углы).
V I . Работа по отработке ЗУН. Практикум
А теперь посмотрим на практике, как вы усвоили тему сегодняшнего урока.
1.Устная работа
(Слайд 21).
Запишите ответы на вопросы в тетрадь. Проверьте свои ответы. Отметьте верные ответы в карточке учета.
2.Решение задач.
А сейчас мы вновь разделимся на группы. Каждая группа выбирает себе задание по силам.
1уровень- выполняет тест на доске.
(Слайды 22, 23, 24)
2 уровень- самостоятельно решает задачи из учебника на стр. 24 №58(а, б) и №66(а). Проверить ответы можно на обратной стороне карточки, которая лежит у вас на парте.
3 уровень- выполняет тест из электронного учебного.(работа на компьютерах )
Каждый из вас может получить ещё 3 плюса.
Отметьте верные ответы в карточке учета.
Какую установку мы давали себе на урок?
(Слайд 25)
Подсчитаем плюсы. Кто набрал 10 плюсов? Вы получаете оценку «5». Кто набрал 7 плюсов? Вы получаете оценку «4». Остальные, я думаю, подучат эту тему дома и на следующем уроке получат хорошие оценки.
VI. Итоговая рефлексия
– Подошло к концу наше путешествие.
О какой фигуре мы говорили на уроке?
Что нового вы сегодня узнали на уроке?
Где в жизни мы видели смежные и вертикальные углы?
(Слайд 26)
(Слайд 27)
Если вы все поняли прикрепите цветочки с углами красного цвета к нашей корзинке, если вас, что-то заставило задуматься – жёлтого цвета и если остались вопросы – синего.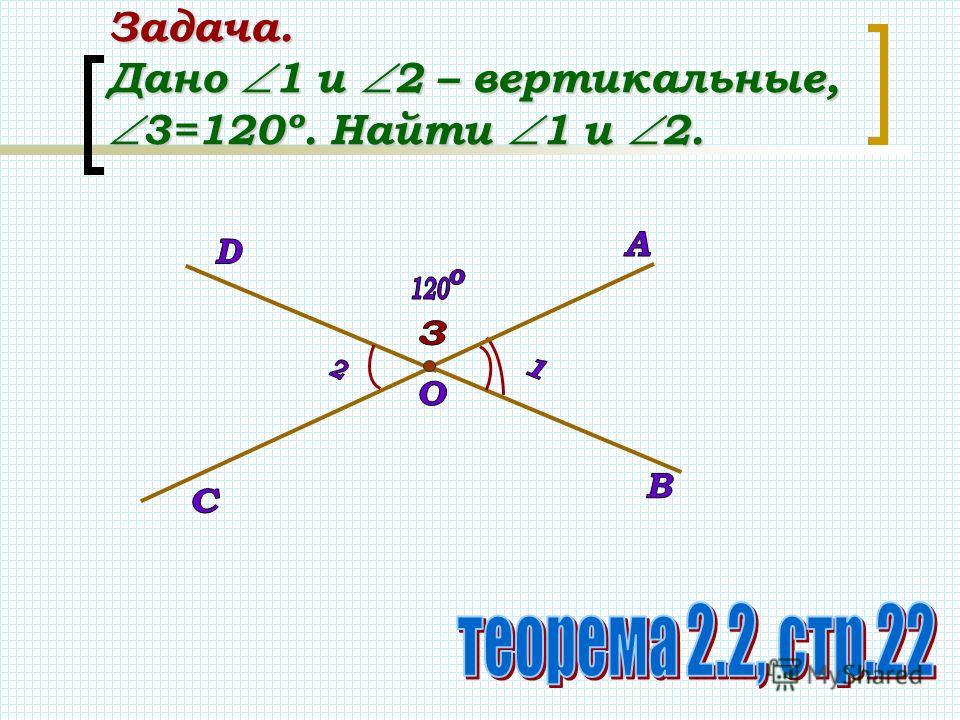 Этот букет мы подарим нашим мамам, бабушкам, сестрам в воскресенье на день матери.
Этот букет мы подарим нашим мамам, бабушкам, сестрам в воскресенье на день матери.
VII. Запись домашнего задания.
А сейчас запишем домашнее задание
(Слайд 28)
1.п. 11 ,вопросы 17,18.
2.Решить задачи: 1 уровень-№42,45,46 из рабочей тетради
2 уровень- № 64, № 61 (а, б) из учебника
3. Творческое задание: сочините сказку о смежных и вертикальных углах.
– Спасибо всем за урок!
(Слайд 29 )
1)– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (Об угле)
— Назовите единицу измерения углов?(За единицу измерения углов принимают градус )
– Что называется градусной мерой угла?(Положительное число, которое показывает, сколько раз градус и его части укладывается в данном угле )
– По какому признаку мы разделим углы на группы? (В зависимости от величины угла)
— Какие это углы? (Острый, тупой, прямой, развернутый)
– Какие углы называются острыми? (Угол градусная мера которого меньше 90 0 )
Выберите его изображение из предложенных вам вариантов углов.
Какие углы называются тупыми? (Угол градусная мера которого больше 90, но меньше 180 0 )
Покажите изображение тупого угла.
Какие углы называются прямыми?(Угол в 90 0)
-Как выглядит прямой угол.
Какие углы называются развернутыми?( (Угол градусная мера которого равна 180 0)
-Как построить развернутый угол? (Провести прямую, отметить вершину, подписать стороны )
2)-Что мы можем сказать о градусной мере угла ВОС?(Его градусная мера равна разности градусных мер углов АОС и АОВ)
Почему?(Луч ОВ делит угол АОС на два угла: АОВ и ВОС)
— Сколько получим?(49 0 )
— Что мы скажем про угол СОN?(Его градусная мера равна 180 0 минус градусная мера угла АОС и минус градусная мера угла BON )
— Почему 180 0 минус?(Потому что угол АОВ- развернутый угол и его градусная мера равна 180 0 )
Сколько получаем?(94 0 )
Итак подведем итог. Углы, в зависимости от величины угла, делятся: на какие?(Острые, тупые, прямые и развернутые ).
Углы, в зависимости от величины угла, делятся: на какие?(Острые, тупые, прямые и развернутые ).
3)Углы, в зависимости от величины угла, делятся: (на острые, тупые, прямые и развернутые ). В зависимости от их взаимного расположения на (смежные и вертикальные).
Тема урока: «Смежные и вертикальные углы.»
Цель урока: познакомить с понятием «смежные и вертикальные углы
Задачи:
Учебные – закрепить понятие угла, правила измерения и построения углов; на основе выделенных признаков научить объединять углы по группам; научить вести исследование с опорой на алгоритм действий, анализировать полученные данные и делать выводы; закрепить полученные на уроке знания в ходе решения задач.
Развивающие – используя возможности мультимедийной презентации и электронного учебника повысить интерес к изучаемому предмету; развивать геометрическую интуицию, умение контролировать внимание на всех этапах урока.
Воспитательные –воспитать любовь к Родине, любовь к матери, воспитать аккуратность, прилежание.
Оборудование: компьютер, мультимедийный проектор, электронный учебник, учебник «Геометрия 7-9 класс, автор Л.С.Атанасян», карточки-задания, карточки для проведения рефлексии, таблицы «Вертикальные и смежные углы».
ХОД УРОКА
Организационный момент (Слайд 1 )
А.П.Чехов говорил: «Нужно стремиться к тому,
чтобы каждый видел и знал больше,
чем видел и знал его отец и дед»
Мы начинаем урок геометрии. У всех на столе: учебник, тетрадь, карандаш, ручка, линейка, транспортир.
(Эмоциональный настрой на урок. Стихотворение Евгения Винокурова. )
(Слайды 2)
О Петр, ведь ты построил город
Не для умерших – для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых.
Недвижимы аллеи парков.
Прямы проспекты, как стрела.
Сильней божественных монархов
Здесь геометрия была.
(Слайд 3)
Гуляют каменные финны.
Курятся трубки из бород.
Вот и построили Афины
Средь топей северных болот!
Налево львы. И львы направо.
А у заставы инвалид,
Штык держит вертикально прямо.
Как геометрия велит.
II. Подготовка к восприятию темы
Сегодня мы продолжаем наше путешествие по стране «Геометрия» и поговорим об углах. А вот о каких углах сегодня пойдет речь, мы постараемся выяснить в ходе нашего урока. Для этого мы вытащим из тайников памяти кое-что ценное и восхитимся глубокими знаниями, которые пригодятся нам сегодня на уроке. (Слайд 4 – план урока ). Для разминки я предлагаю провести «Мозговой штурм». Да, я совсем забыла сказать, что на уроке можно ошибаться, сомневаться, консультироваться.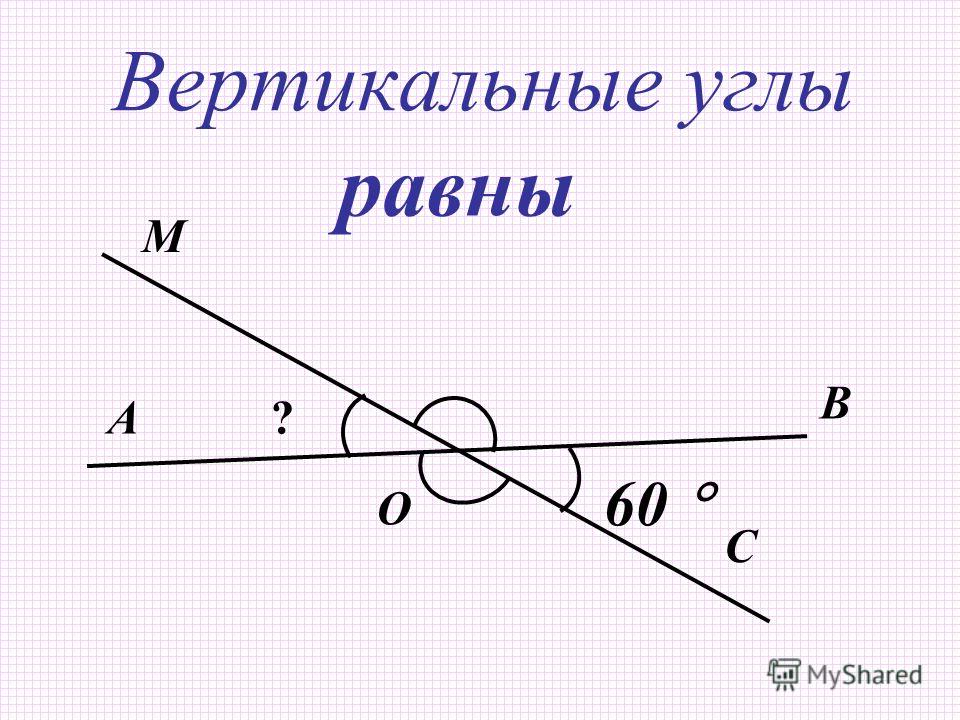 Но при этом, вы должны дать себе установку (Слайд 5) «понять и быть тем первым, который увидит ход решения и даст правильный ответ» . Каждый правильный ответ вы будите отмечать в листке контроля. Это мне поможет выставить оценки за урок. Тот кто наберет больше баллов, тот и получит лучше оценку. Никто без поощрения не останется. Итак, мы начинаем.
Но при этом, вы должны дать себе установку (Слайд 5) «понять и быть тем первым, который увидит ход решения и даст правильный ответ» . Каждый правильный ответ вы будите отмечать в листке контроля. Это мне поможет выставить оценки за урок. Тот кто наберет больше баллов, тот и получит лучше оценку. Никто без поощрения не останется. Итак, мы начинаем.
III. Актуализация знаний учащихся. «Мозговой штурм» (Слайд 6)
– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (На прошлом уроке мы говорили об угле)
Какая фигура называется углом? (Геометрическая фигура, которая состоит из двух лучей, исходящих из одной точки, называется угол)
— Что такое вершина и стороны угла? (Общая точка называется вершиной угла, а лучи сторонами)
— )
С помощью какого инструмента измеряют углы?(Углы измеряют с помощью транспортира)
(Слайд 7 )
— Какие это углы?
Угол, градусная мера которого меньше 90 0 , называется острым)
(Угол, градусная мера которого больше 90, но меньше 180 0 , называется тупым)
Какие углы называются прямыми?(Угол называется прямым, если он равен 90 0 )
-Как выглядит прямой угол.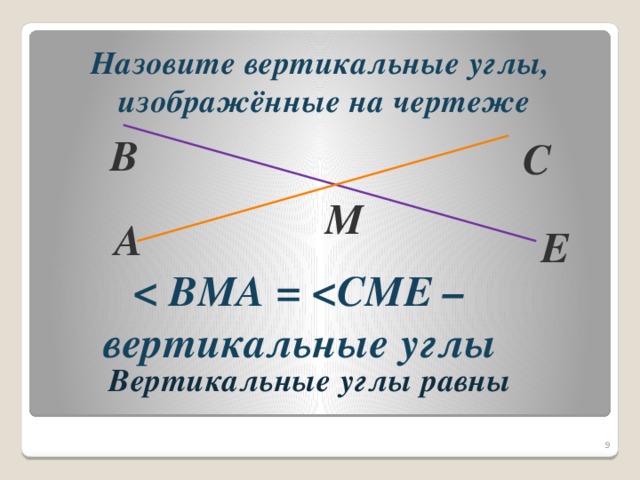
Угол называется развернутым, если он равен 180 0)
(Слайд 8)
А сейчас мы решим несколько задач на вычисление градусной меры угла. Каждый выбирает себе задание по силам. Для 1 уровня- это задача на рисунке 1. Её решение мы разберем на доске, для 2 уровня задача на рисунке 2. Её я предлагаю решить самостоятельно. Те кто выберет самостоятельное решение, каждый получит плюс в карточку учета, если ответ будет верным. Кто выбирает задачу на рисунке 2, работают самостоятельно. Кто выбирает задачу на рисунке 1 и желает ее решить у доски.
Сколько углов мы видим на рисунке?(На рисунке 3 угла)
-Н азови и покажи их? (угол АОС, угол АОВ, угол ВОС )
Что мы можем сказать о градусной мере угла ВОС?(
Запишем это и найдем градусную меру угла ВОС. Запишем ответ.
Проверим наши ответы. Кто работал самостоятельно оцените свою работу, если ответы сошлись, то поставьте плюс в карточку учета.
Итак подведем итог.
(Слайд 9)
По какому признаку мы делим углы? (Углы разделяются в зависимость от величины)
Какие это углы?(О).
IV. Практическая работа исследовательского характера
– А сейчас познакомимся со второй группой углов и попробуем выяснить, по какому признаку можно ее выделить. Перед вами карточки с изображением углов. Ваша задача – выполнить следующие действия для карточки № 1.
(Слайд 10 – алгоритм действий ).
-Какой вывод сделали? (Сумма углов равна 180 градусов )
(Слайд 11)
Как бы вы назвали эти углы?(Смежные )
По какому признаку мы выделили этот вид углов? (Этот вид углов мы выделили по взаимному расположению)
Давайте запишем определение
(Слайд 12 )
Постройте острый, прямой и тупой углы. Продолжите одну из сторон и укажите получившиеся смежные углы.
3 ученика у доски, остальные в тетради.
Для любого угла можно построить ему смежный угол? (Да)
-Повторите алгоритм действия для карточки №2.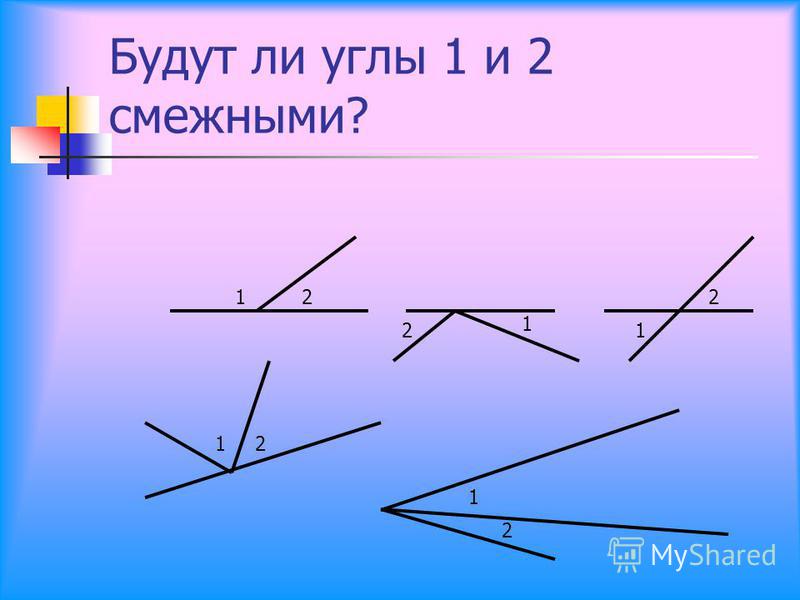
(Слайд 13)
-Какой вывод можно сделать?.(Углы равны )
(Слайд 14)
Как бы вы назвали данный вид углов?(Вертикальные )
-Запишем определение.
(Слайд 15)
Посмотрите на правило построения вертикальных углов и выполните построение в тетради.
(Слайд 16)
-Посмотрите на чертежи и назовите вертикальные углы
(Слайд 17)
-Вернёмся к схеме, которую мы рассматривали в начале урока, и подведем итог.
(Слайд 18)
-По каким признакам мы делим углы? (Углы делятся по величине угла и по их взаимному расположению )
Какие углы по величине градусной меры мы знаем?(По величине градусной меры углы бывают: острые, тупые, прямые, развернутые)
Какие углы по взаимному расположению мы изучили сегодня? (По взаимному расположению углы бывают: смежные и вертикальные).
Не забывайте отмечать свои верные ответы в карточке учета.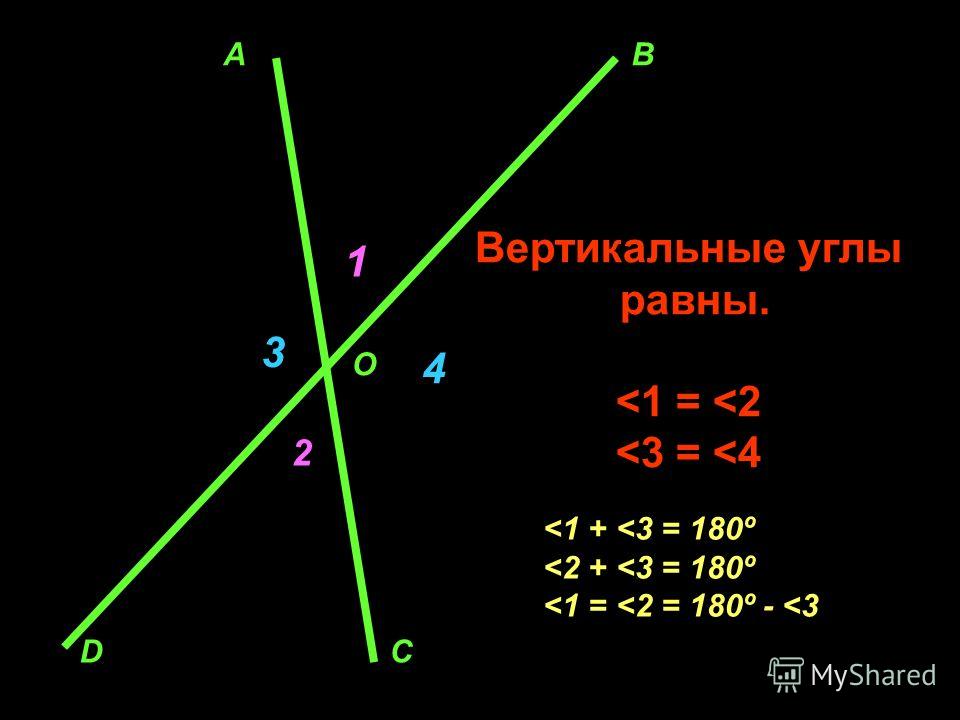
-Как же теперь мы сформулировали тему нашего сегодняшнего урока(«Смежные и вертикальные углы» ).
Правильно. «Смежные и вертикальные углы». Посмотрите, как в Санкт-Петербурге это хорошо видно.
(Слайд 19)
V . Физкукльтминутка.
Вы устали? Давайте отдохнём.
(Слайд 20)
1.Голова идет по кругу.
2.Руки в стороны.(Развернутый угол, прямой угол).
3.Руки с соседом. (Смежные углы).
4.Спиной к соседу.(Вертикальные углы).
V I . Работа по отработке ЗУН. Практикум
А теперь посмотрим на практике, как вы усвоили тему сегодняшнего урока.
1.Устная работа
(Слайд 21).
Запишите ответы на вопросы в тетрадь. Проверьте свои ответы. Отметьте верные ответы в карточке учета.
2.Решение задач.
А сейчас мы вновь разделимся на группы. Каждая группа выбирает себе задание по силам.
1уровень- выполняет тест на доске.
(Слайды 22, 23, 24)
2 уровень- самостоятельно решает задачи из учебника на стр. 24 №58(а, б) и №66(а). Проверить ответы можно на обратной стороне карточки, которая лежит у вас на парте.
3 уровень- выполняет тест из электронного учебного.(работа на компьютерах )
Каждый из вас может получить ещё 3 плюса.
Отметьте верные ответы в карточке учета.
Какую установку мы давали себе на урок?
(Слайд 25)
Подсчитаем плюсы. Кто набрал 10 плюсов? Вы получаете оценку «5». Кто набрал 7 плюсов? Вы получаете оценку «4». Остальные, я думаю, подучат эту тему дома и на следующем уроке получат хорошие оценки.
VI. Итоговая рефлексия
– Подошло к концу наше путешествие.
О какой фигуре мы говорили на уроке?
Что нового вы сегодня узнали на уроке?
Где в жизни мы видели смежные и вертикальные углы?
(Слайд 26)
(Слайд 27)
Если вы все поняли прикрепите цветочки с углами красного цвета к нашей корзинке, если вас, что-то заставило задуматься – жёлтого цвета и если остались вопросы – синего.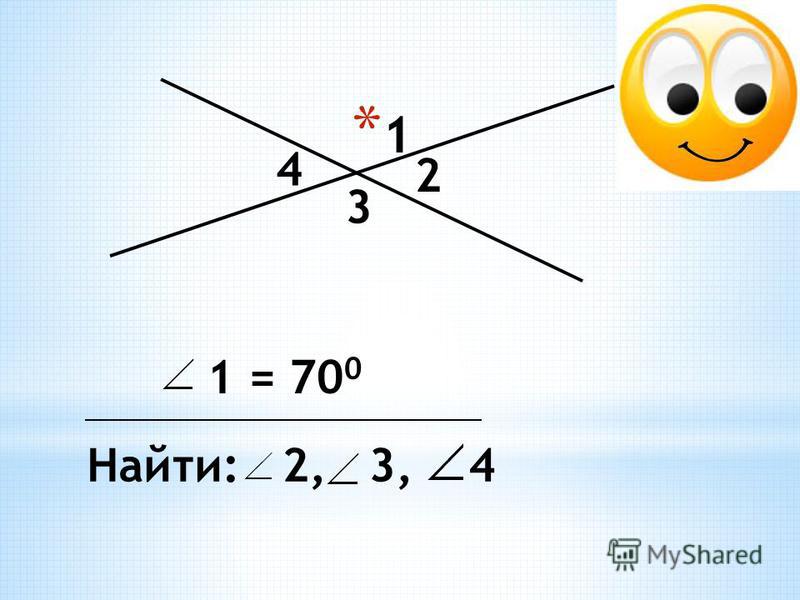 Этот букет мы подарим нашим мамам, бабушкам, сестрам в воскресенье на день матери.
Этот букет мы подарим нашим мамам, бабушкам, сестрам в воскресенье на день матери.
VII. Запись домашнего задания.
А сейчас запишем домашнее задание
(Слайд 28)
1.п. 11 ,вопросы 17,18.
2.Решить задачи: 1 уровень-№42,45,46 из рабочей тетради
2 уровень- № 64, № 61 (а, б) из учебника
3. Творческое задание: сочините сказку о смежных и вертикальных углах.
– Спасибо всем за урок!
(Слайд 29 )
1)– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (Об угле)
— Назовите единицу измерения углов?(За единицу измерения углов принимают градус )
– Что называется градусной мерой угла?(Положительное число, которое показывает, сколько раз градус и его части укладывается в данном угле )
– По какому признаку мы разделим углы на группы? (В зависимости от величины угла)
— Какие это углы? (Острый, тупой, прямой, развернутый)
– Какие углы называются острыми? (Угол градусная мера которого меньше 90 0 )
Выберите его изображение из предложенных вам вариантов углов.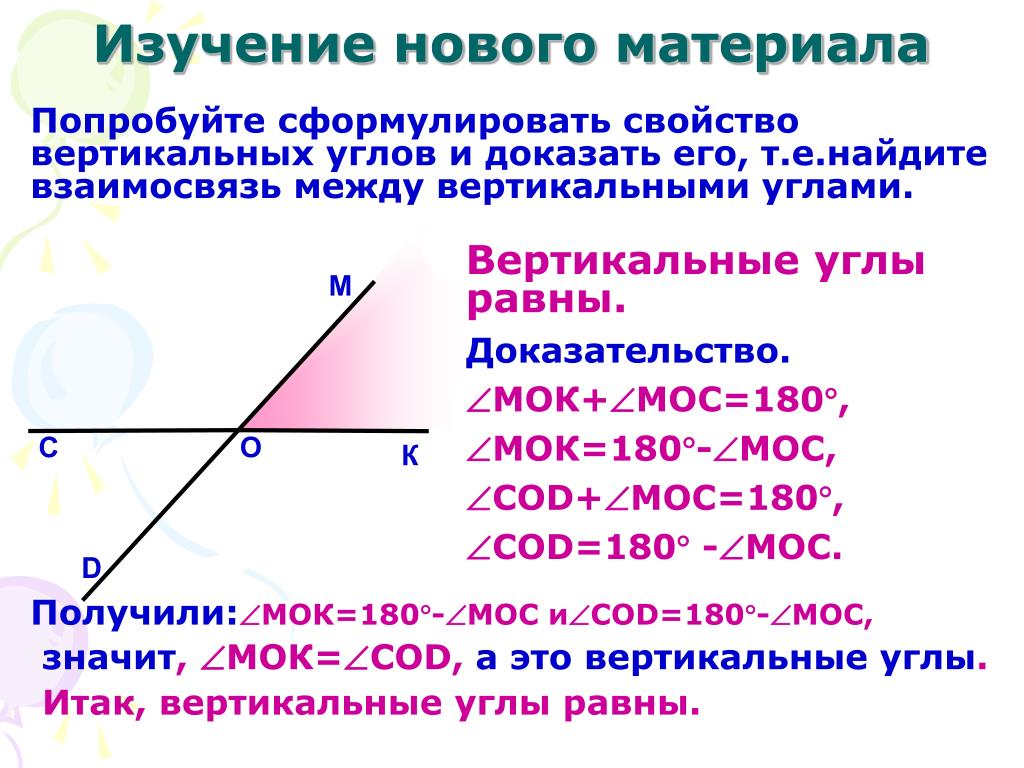
Какие углы называются тупыми? (Угол градусная мера которого больше 90, но меньше 180 0 )
Покажите изображение тупого угла.
Какие углы называются прямыми?(Угол в 90 0)
-Как выглядит прямой угол.
Какие углы называются развернутыми?( (Угол градусная мера которого равна 180 0)
-Как построить развернутый угол? (Провести прямую, отметить вершину, подписать стороны )
2)-Что мы можем сказать о градусной мере угла ВОС?(Его градусная мера равна разности градусных мер углов АОС и АОВ)
Почему?(Луч ОВ делит угол АОС на два угла: АОВ и ВОС)
— Сколько получим?(49 0 )
— Что мы скажем про угол СОN?(Его градусная мера равна 180 0 минус градусная мера угла АОС и минус градусная мера угла BON )
— Почему 180 0 минус?(Потому что угол АОВ- развернутый угол и его градусная мера равна 180 0 )
Сколько получаем?(94 0 )
Итак подведем итог. Углы, в зависимости от величины угла, делятся: на какие?(Острые, тупые, прямые и развернутые ).
Углы, в зависимости от величины угла, делятся: на какие?(Острые, тупые, прямые и развернутые ).
3)Углы, в зависимости от величины угла, делятся: (на острые, тупые, прямые и развернутые ). В зависимости от их взаимного расположения на (смежные и вертикальные).
Углы которые всегда равны называется. Развернутый, тупой, вертикальный и неразвернутый: виды углов геометрии
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников.
 Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей. - В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.

Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются.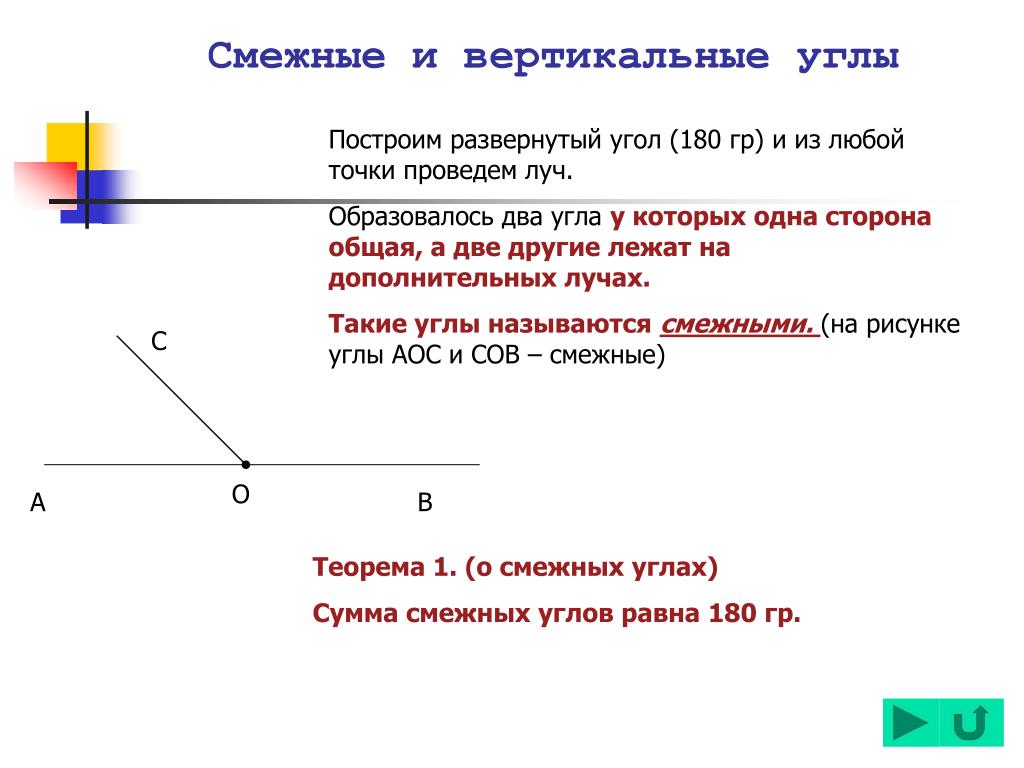 Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним.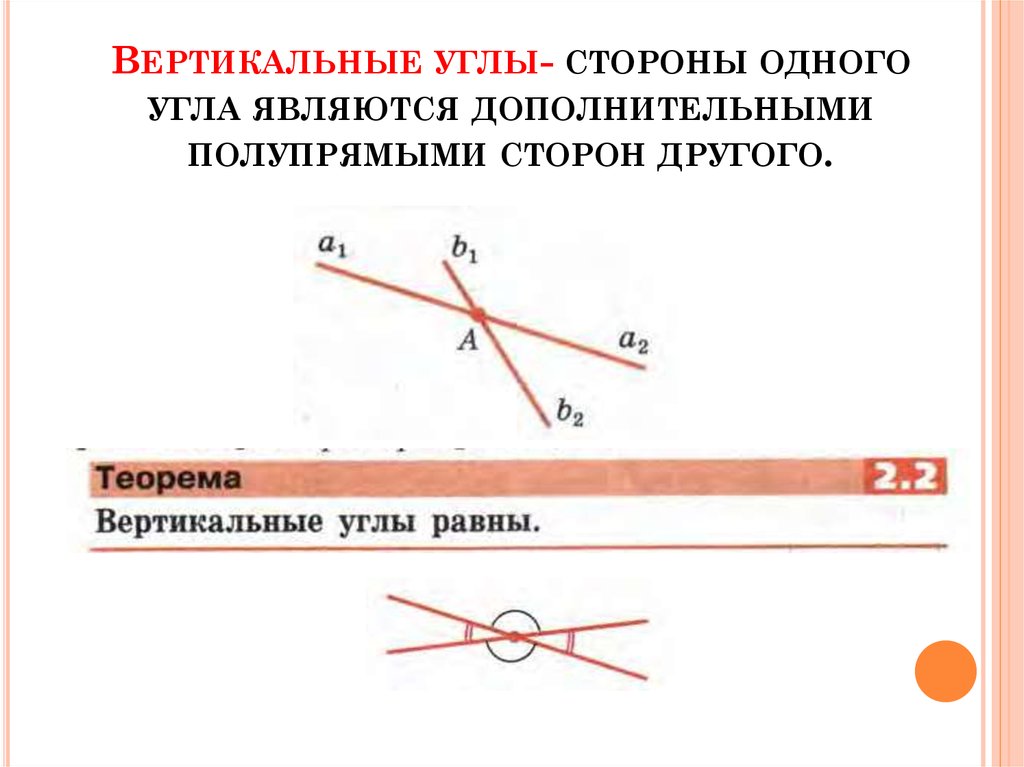 Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p
или луч k
), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА
или луч СD
). Покажем изображение и обозначение лучей на чертеже.
Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.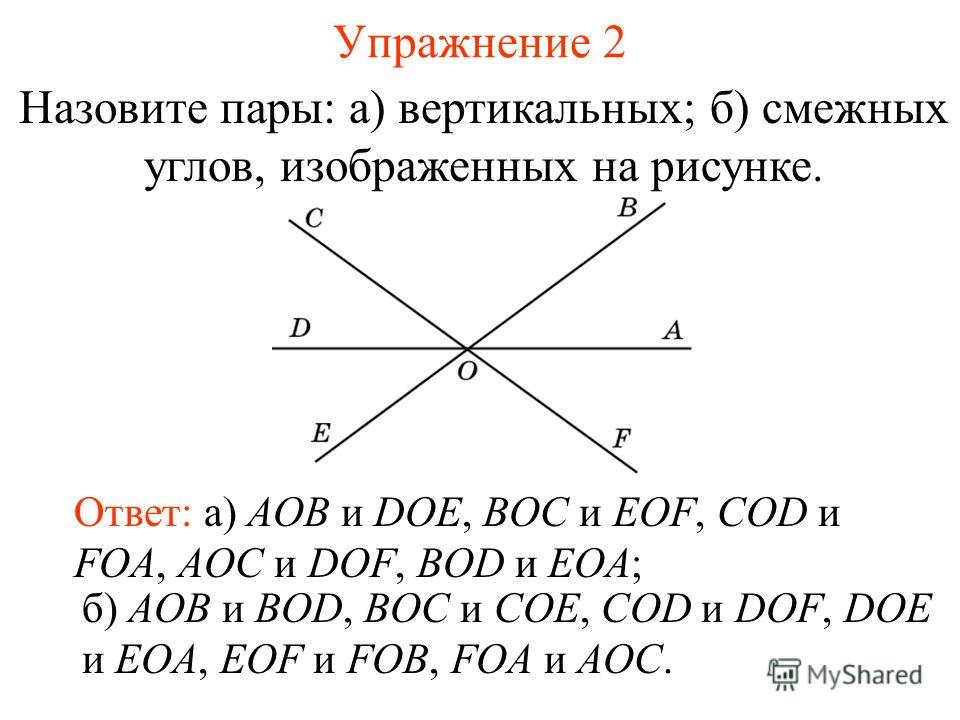
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.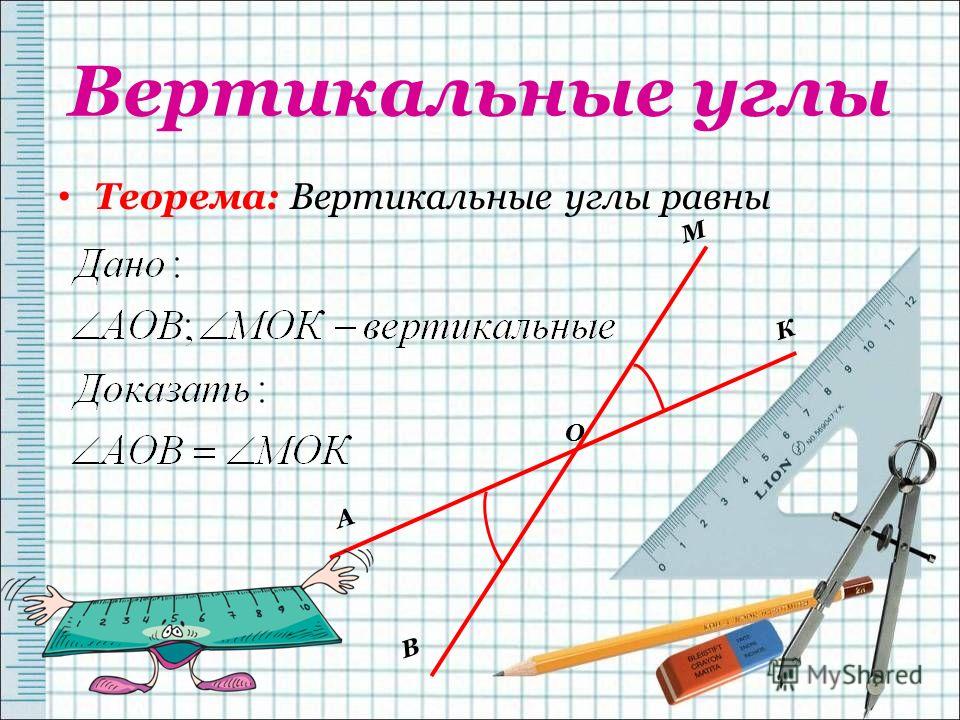
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .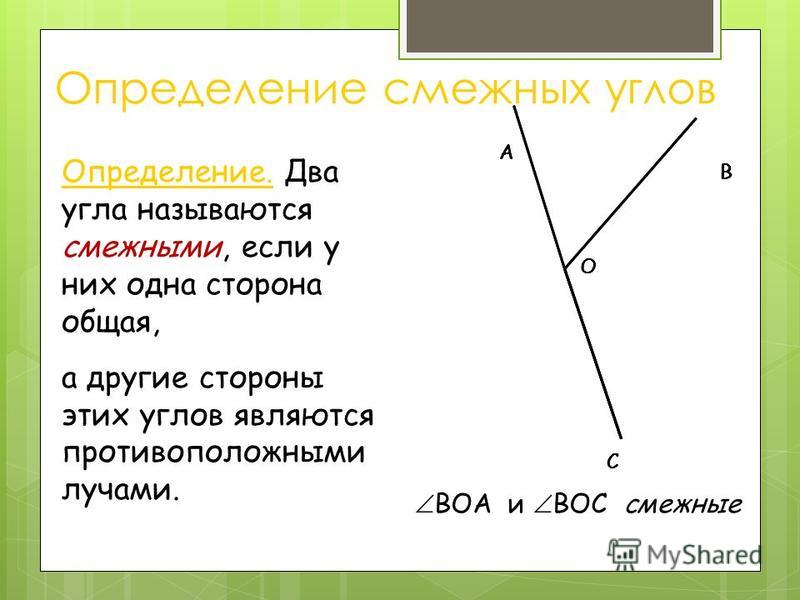
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения).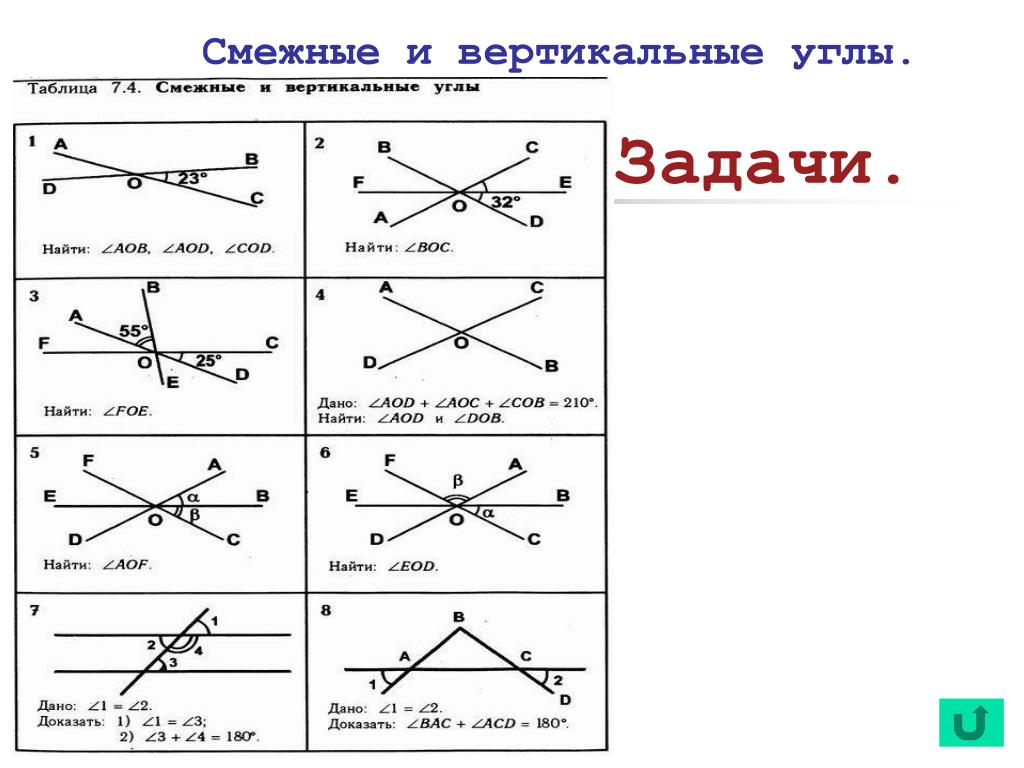 Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.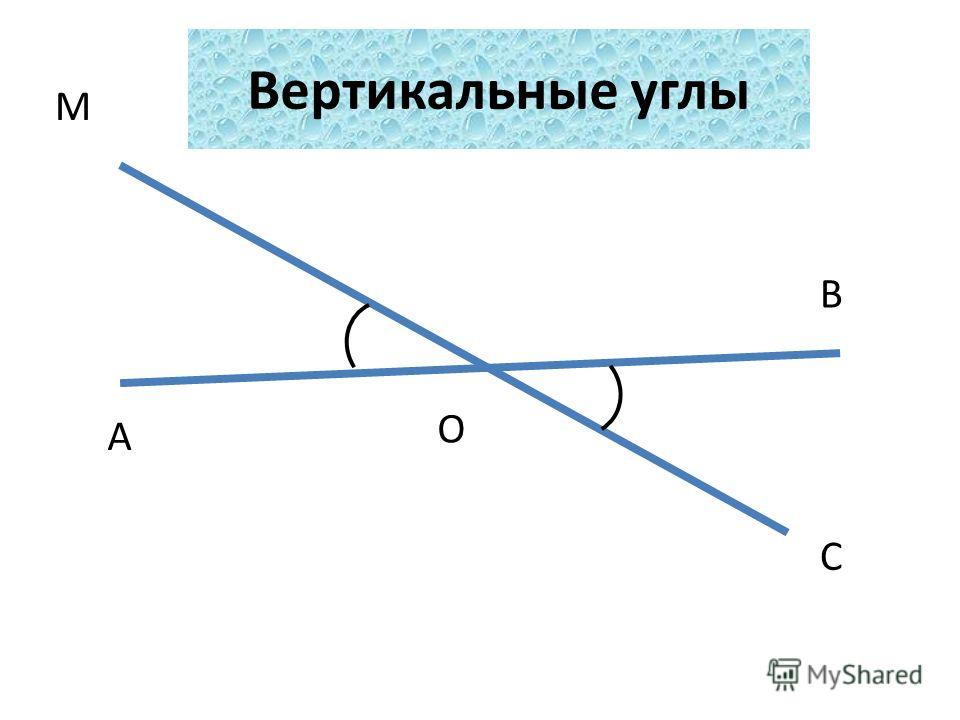 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад».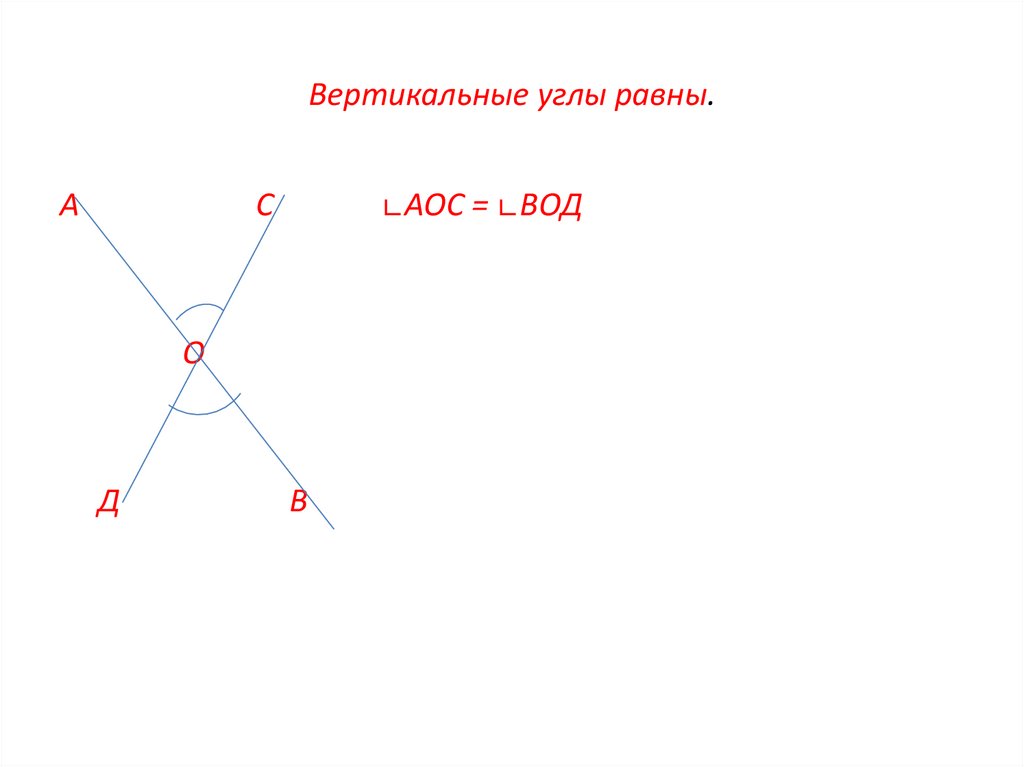 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.

На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах.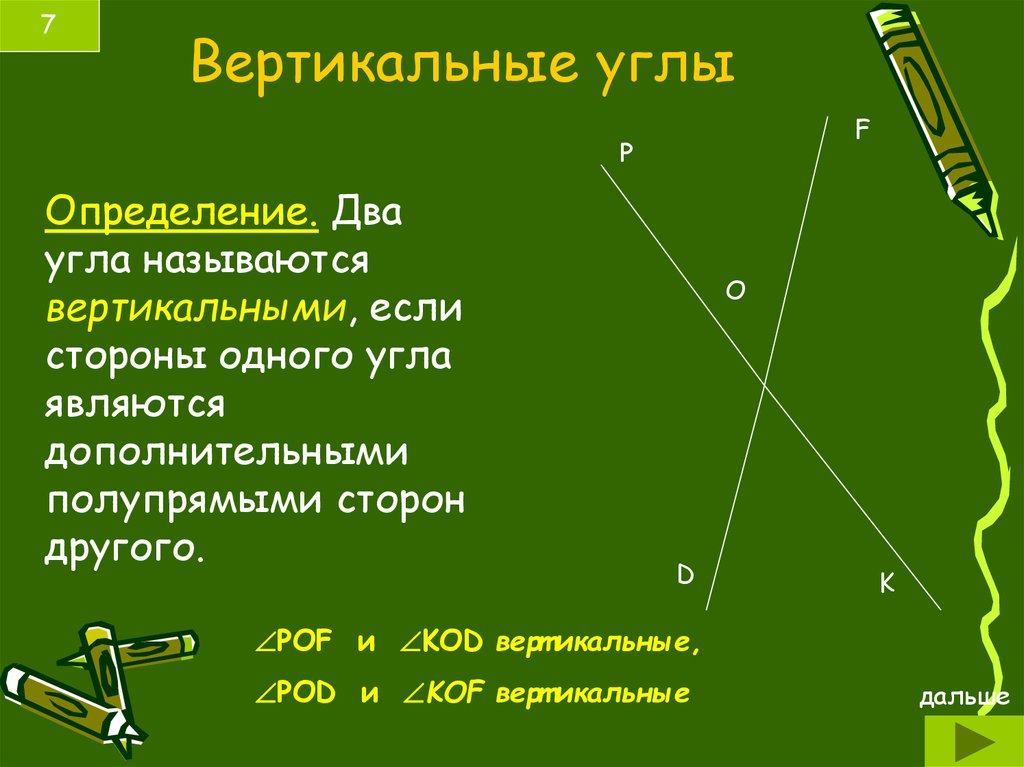 Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Yandex.RTB R-A-339285-1 Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу.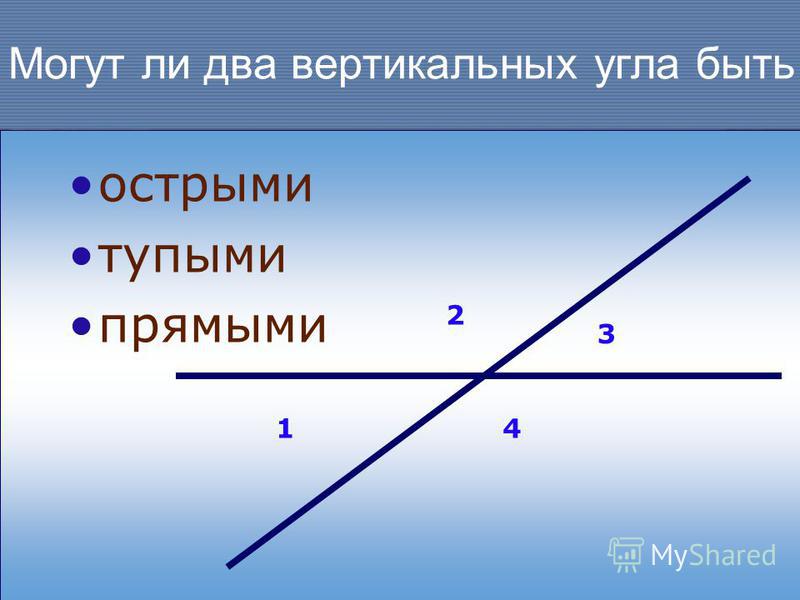 Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».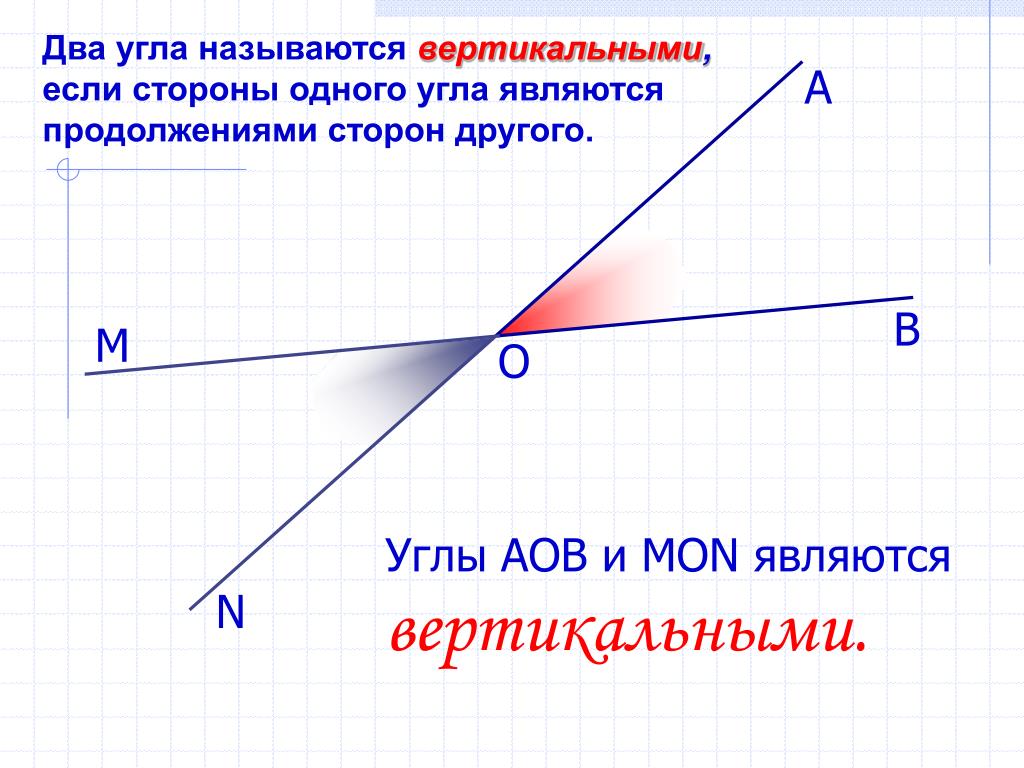
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.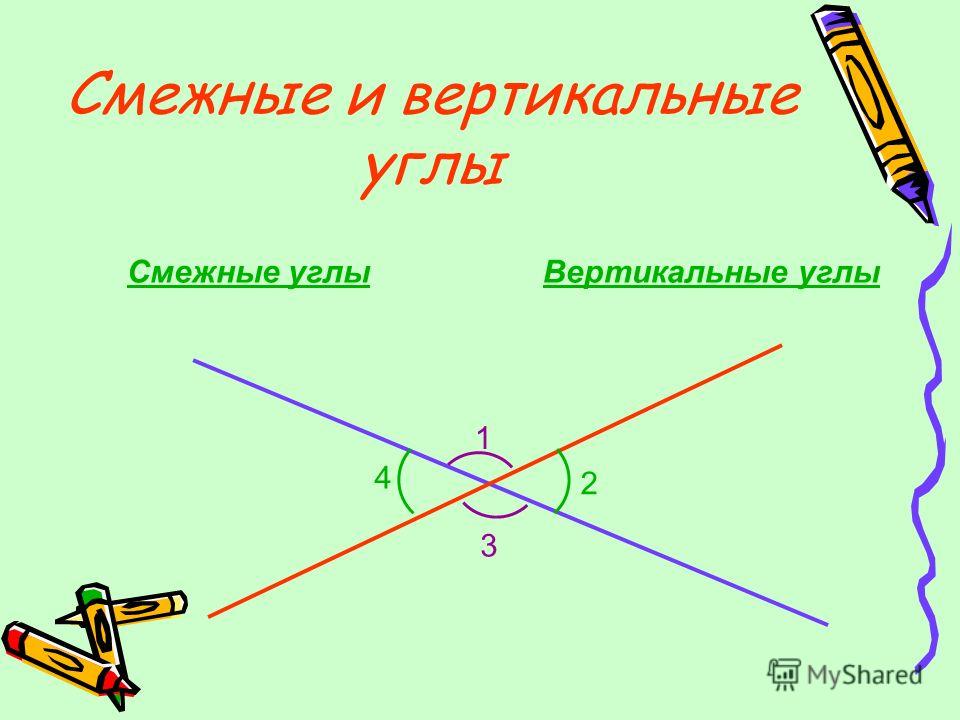
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Игро+матика: января 2015
Углы при параллельных прямых. Их свойства
В заметке «Углы при пересечении двух прямых третьей» мы разобрали какие углы при этом пересечении будут получаться и как они будут называться. Заметим, что речь шла о любых двух прямых. Если же эти прямые параллельны, то рассмотренные нами углы, обладают определенными свойствами. Перечислим их:
Перечислим их:
Наглядно представить себе углы, получаемые при параллельных прямых и повторить их названия, можно здесь.
А сейчас, выполните интерактивные задания, чтобы проверить, как хорошо вы усвоили свойства углов.
Найдите один из углов при параллельных прямых, если известен какой-то другой
А это интерактивный тест с проверкой, содержит три уровня сложности.
Найди неизвестный угол
В этом (или этом) тренажере, вам придется применить свои знания не только о свойствах углов, полученных при пересечении параллельных прямых секущей, но и свойства смежных и вертикальных углов.
И в заключение, еще одна игра, в которую можно играть самому, или с кем-то из друзей
Танковая атака
Если хотите выиграть танковое сражение, то, используя свойства углов при параллельных прямых, правильно определите неизвестный угол.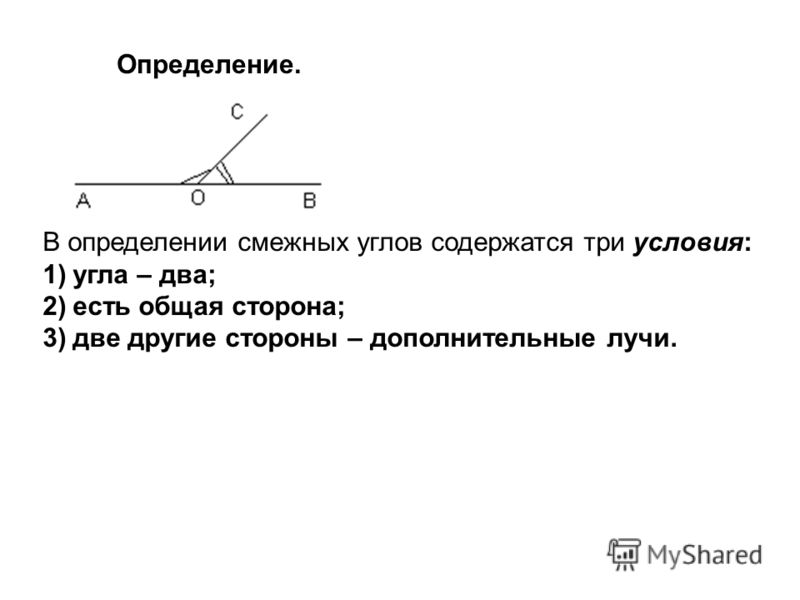
И, в заключение, еще три небольших игры: 1, 2, 3, 4.
В предпоследней игре необходимо вначале ответить на вопрос будут ли указанные углы равны, или будут в сумме составлять 180 градусов, а затем правильно их назвать. А в последней — вам придется использовать все, полученные по данной теме знания.
Углы при пересечении двух прямых третьей
Продолжаем тему углов, начатую в заметках «Виды углов» и «Вертикальные и смежные углы».
Найди один из углов. Тренажеры
Повторите свойства смежных углов и выполните задания. В случае ошибки посмотрите верное решение.
Ваши знания об углах поможет проверить следующий тест
С помощью следующего теста можно повторить все о вертикальных, смежных и развернутых углах. Решайте последовательно каждый уровень, начиная с первого, или сразу переходите к смешанным задачам на четвертом уровне.
Очень простой тренажер, но работа идет на время, так что долго думать не получится, считать нужно очень быстро
А в этом тренажере необходимо подобрать пары смежных углов.
Здесь задача уже потруднее: из множества углов, необходимо выбрать угол, смежный данному.
Смежные и вертикальные углы. Их свойства
В заметке «Виды углов», мы выяснили, что в зависимости от величины градусной меры угла, различают острые, прямые, тупые и развернутые углы.
Это была классификация по градусной мере угла. Сегодня рассмотрим виды углов, отличающихся от других расположением своих сторон.
На рисунке изображены два угла: Ð АOС и Ð СOВ. Луч OС является как стороной одного, так и другого угла. Лучи OА и OВ – другие стороны углов – составляют прямую линию. Для таких углов в математике есть специальное название.
Два угла, у которых имеется общая сторона, а две другие составляют прямую, называются СМЕЖНЫМИ.
Будьте внимательны при работе со смежными углами!
Изображённые на рисунке углы ADB и BDC не являются смежными. Хотя они и имеют общую сторону DB, но две другие стороны DA и DC не образуют прямую.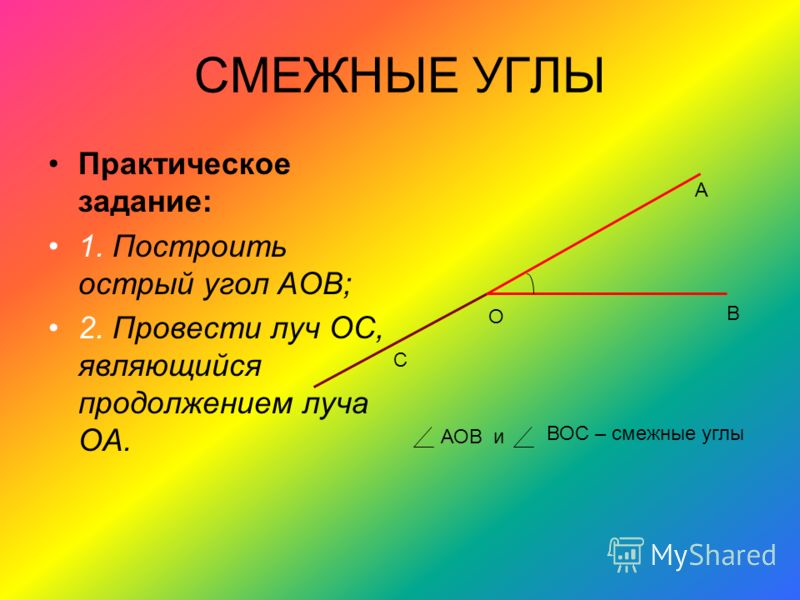 По той же причине углы KNL и LNM нельзя назвать смежными.
По той же причине углы KNL и LNM нельзя назвать смежными.
Стороны углов EPF и GPH образуют прямую (лучи PE и PH), но эти углы не имеют общей стороны и поэтому не являются смежными. Тем не менее, для этих углов можно указать смежные: для угла EPF смежным является угол FPH, а для угла GPH — угол EPG.
Смежные углы обладают замечательным свойством: поскольку одна сторона у них общая, а две другие образуют прямую, то сумма этих углов равна развёрнутому углу. А градусная мера развёрнутого угла равна 180°.
Значит, СУММА СМЕЖНЫХ УГЛОВ равна 180°.
ÐАОС + ÐСОВ = 180°.
(Убедиться в этом поможет Динамическая модель. Передвигайте стрелку, меняйте значения углов и наблюдайте за результатом)
Угол, смежный с прямым углом, тоже прямой угол; смежный с острым углом — тупой; смежный с тупым углом — острый угол.
Посмотрите на картинку слева. На нем две пересекающиеся прямые образуют две пары углов с общей вершиной в точке О так, что стороны одного угла, являются продолжением сторон другого.
Такие углы называются ВЕРТИКАЛЬНЫМИ. ВЕРТИКАЛЬНЫЕ углы РАВНЫ.
ÐАОВ = ÐCOD
Углы АОС и ВОD также являются равными вертикальными углами.
(Понаблюдайте за величиной вертикальных углов на динамической модели)
А теперь, примените полученные знания при нахождении недостающего угла, занимаясь с тренажерами.
Здесь потребуется найти значение неизвестного вертикального угла
Здесь придется определить какой угол неизвестен: смежный или вертикальный и найти его.
Примените свойство углов, о том, что градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами через вершину данного угла при вычислении градусной меры неизвестных углов.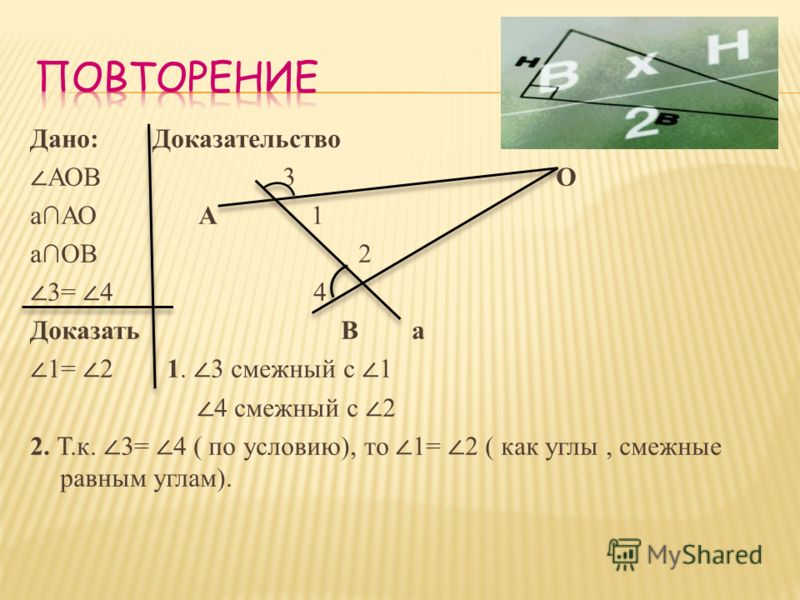
Виды углов
Посмотрите на картинку. Звери на ней несут различные углы, каждый из которых имеет свое название. Повторим их.
Угол называется РАЗВЕРНУТЫМ, если его стороны вместе образуют прямую.
Величина развернутого угла равна 180°.
Угол, который равен половине развернутого угла, называется ПРЯМЫМ.
Величина прямого угла равна 90°.
ОСТРЫЙ угол — это угол, который меньше прямого.
Величина острого угла < 90°.
ТУПОЙ угол — это угол, который больше прямого, но меньше развернутого.
Величина тупого угла > 90° и < 180°
Обобщим все сказанное, на рисунке:
А теперь с помощью несложных тестов и тренажеров проверьте, насколько хорошо вы усвоили данные понятия.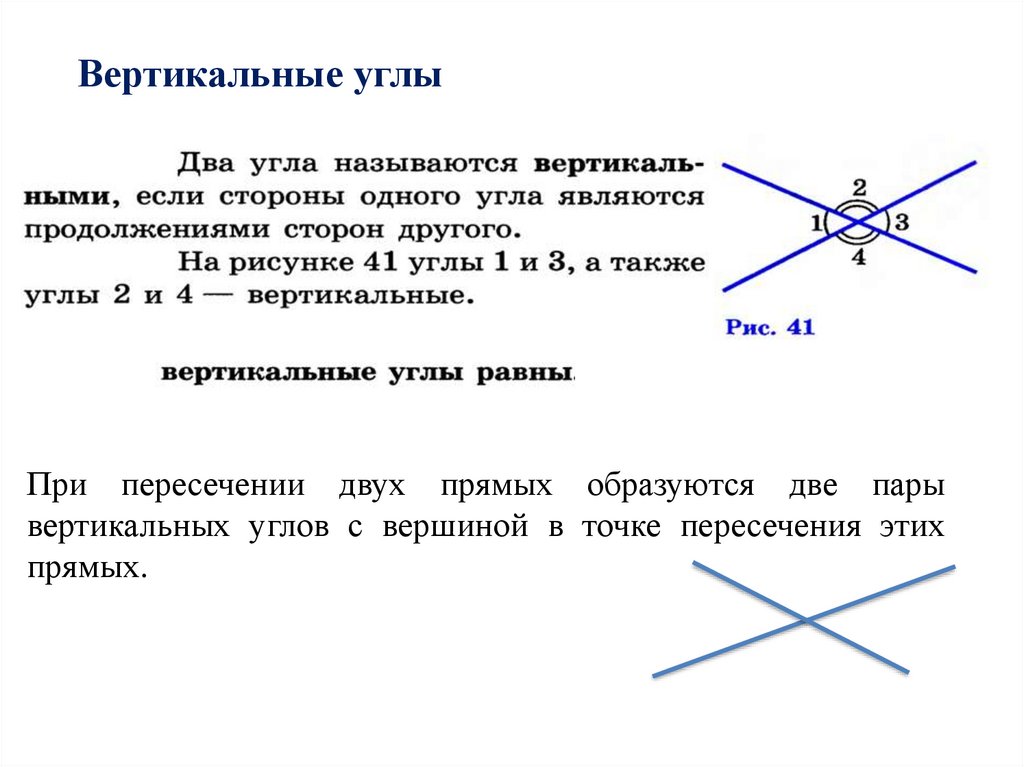
Какой это угол?
Посмотрите на чертеж и определите, какой это угол: острый, прямой или тупой.
Еще один, очень похожий тренажер, в котором для узнавания добавлен еще и развернутый угол.
А это аналогичный русскоязычный ресурс, но для работы с ним требуется регистрация
Попади в нужный угол
Для работы с этим тренажером выберите верхний раздел меню. В открывшемся окне, вы должны выбрать угол, тип которого указан на прицеле, навести на него курсор и кликнуть мышкой. В случае правильного попадания, угол исчезнет. Типы углов указаны по английски, но можно легко запомнить, что RIGHT — это прямой угол, ACUTE — острый, OBTUSE — тупой.
В этой флеш игре вы должны показать насколько хорошо вы знакомы с такими понятиями как острый, тупой и прямой угол. Робот будет задавать вам задания. Постарайтесь каждый раз выбирать правильный ответ. Игра на английском языке. Заодно можно подтянуть свои знания языка.
Играть втроем и вдвоем тоже можно!
Робот передвигается к нужному углу с помощью стрелок управления курсором; выстрел — клавиша — «Пробел». Acute — острый угол; Obtuse — тупой угол; Right -прямой угол.
Ответь на вопросы.
При работе с этим тестом, включите автоматический перевод страниц, чтобы вопросы отображались по-русски
Быстро считаем, не позволяя мухам сесть на пиццу
Замечательный тренажер устного счета. Сначала выбирайте действие, на которое будете решать примеры. Можно выбрать только сложение или только деление, а можно все действия сразу. Затем выберите диапазон, в котором будут изменяться числа. Рекомендую вам начать с чисел от 0 до 10, потом перейти к числам от 0 до 20 или 50, а закончить самым сложным разделом от 0 до 100.
После установки настроек перейдите по стрелке и решайте примеры. Не позволяйте мухам състь пиццу, но помните, что можно убить только ту муху, на которой написан правильный ответ!
Углы и их градусная мера
Фигура, образованная двумя лучами с общим началом, называется УГЛОМ. Также углом называют и часть плоскости, ограниченную этими лучами.
Также углом называют и часть плоскости, ограниченную этими лучами.
Общее начало лучей называется вершиной угла, а сами лучи — сторонами угла.
Для измерения углов применяют транспортир. Нужно приложить верхний край линейки к одной из сторон угла, так, чтобы центр совпал с вершиной угла. Затем нужно посмотреть, сколько градусных делений содержится между сторонами угла. Число таких делений называют градусной мерой угла, или, по-другому, величиной угла.
Углы называют равными, если у них одна и та же величина. Равные углы — углы, которые совпадают при наложении.
А теперь попробуйте сами с помощью транспортира определить градусную меру углов. Можете попробовать работать с любым из интерактивных ресурсов.
Вот еще один Онлайн транспортир
В игре, ссылка на которую расположена ниже, вам, наоборот, придется сами устанавливать величину угла, чтобы запустив ракету, сбить монстра.
Аналогичный ресурс, но теперь, устанавливая величину угла, вы будете кормить кролика.
И. в заключение, итоговый тест, на измерение углов с помощью транспортира.
Правильные и неправильные дроби
Обыкновенные дроби, в зависимости от величины числителя и знаменателя делятся на две группы, называемые правильными и неправильными дробями.
Дробь, в которой числитель меньшезнаменателя, называется правильной.
Правильная дробь всегда меньше 1.
Дробь, в которой числитель больше или равен знаменателю, называется неправильной.
Неправильная дробь ≥ 1.
Для того, чтобы легче было запомнить, какая из дробей правильная, а какая неправильная, представьте себе пирамиду из человеческих тел.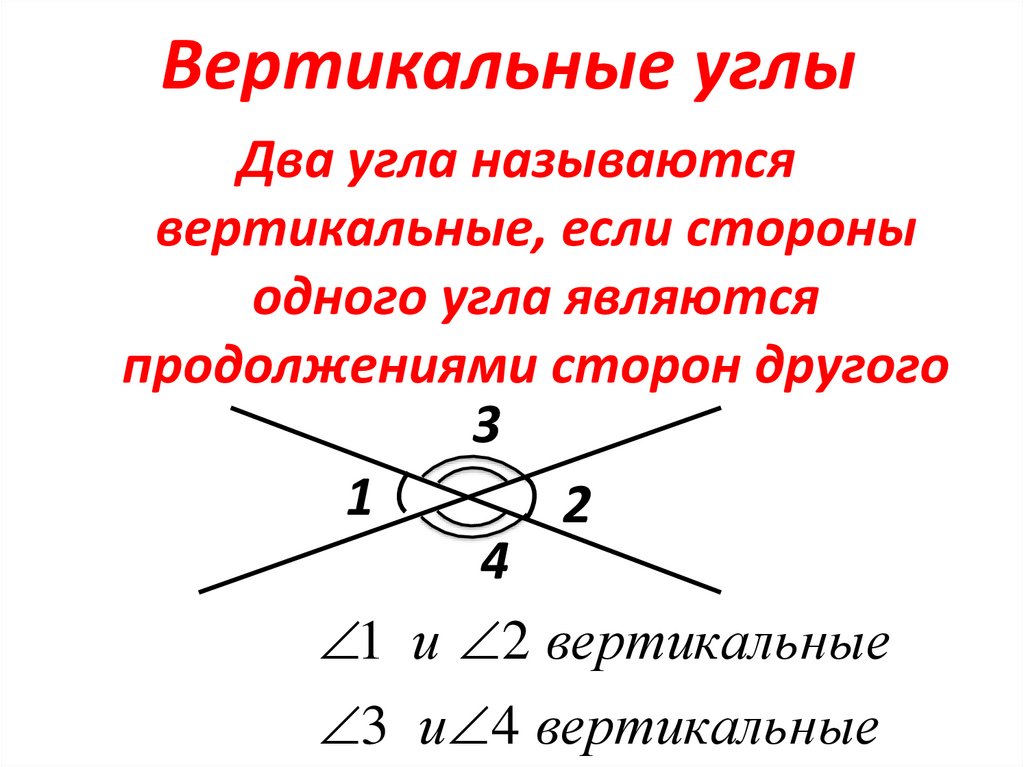 Естественно, правильно, привычно выглядит пирамида, когда взрослый держит ребенка, т.е. внизу большой, а сверху маленький человек. И нам трудно себе представить ситуацию, когда взрослый заберется на плечи ребенку. Любой скажет, что это неправильно. Такая же ситуация и у дробей.
Естественно, правильно, привычно выглядит пирамида, когда взрослый держит ребенка, т.е. внизу большой, а сверху маленький человек. И нам трудно себе представить ситуацию, когда взрослый заберется на плечи ребенку. Любой скажет, что это неправильно. Такая же ситуация и у дробей.
Если вы сможете запомнить эту аналогию, то вы всегда безошибочно будете определять, какая из дробей правильная, а какая неправильная.
Понятие обыкновенной дроби
Представьте себе, что вечером придут гости и вы испекли для них пирог. Вот вы разрезали его на 8 равных частей, т.е. 1 поделили на 8. Математически результат этого действия можно записать так: 1:8, но чаще деление одной целой части на несколько более мелких частей записывают в виде дроби, заменяя знак деления дробной чертой —
Пока все куски лежат на блюде это пирога, поэтому .
А если вы съели три куска из восьми, то это записывается в виде .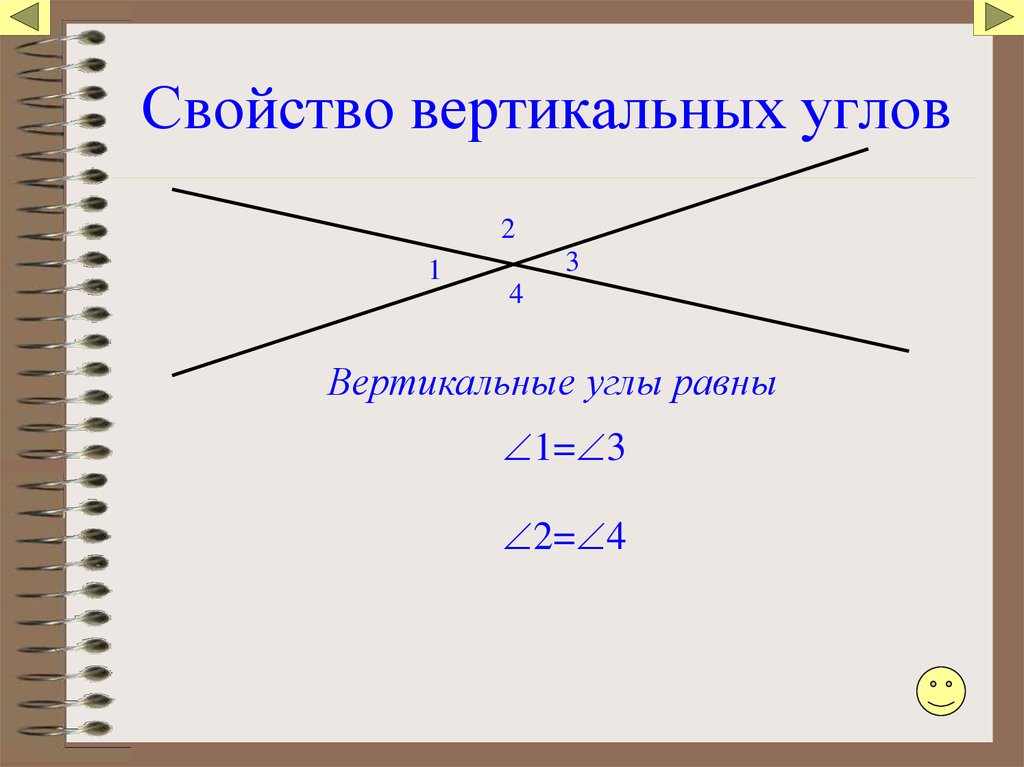 Таким образом, число, которое записывается под дробной чертой (его называют знаменатель) показывает на сколько равных частей было разделено целое, а число над чертой (оно называется числитель) говорит о том, сколько таких частей взяли. Видим, что на тарелке осталось пять из восьми кусков, то есть пирога.
Таким образом, число, которое записывается под дробной чертой (его называют знаменатель) показывает на сколько равных частей было разделено целое, а число над чертой (оно называется числитель) говорит о том, сколько таких частей взяли. Видим, что на тарелке осталось пять из восьми кусков, то есть пирога.
Посмотрите этот весёлый
фильм о дробях и тогда вам все станет совсем понятно.А теперь попробуйте сами, работая на тренажерах, записать по рисунку различные дроби.
Переберись на другой берег
Сопоставьте дробь и рисунок
Первый уровень Второй уровень
Найди и попади!
Нужно сбить модель, соответствующую дроби, записанной на прицеле. В открывшемся меню для игры кликните на третьем или четвертом рисунке.
Рассортируй дроби
Следующие Предыдущие Главная страница
Подписаться на: Сообщения (Atom)
Вертикальные углы равны.
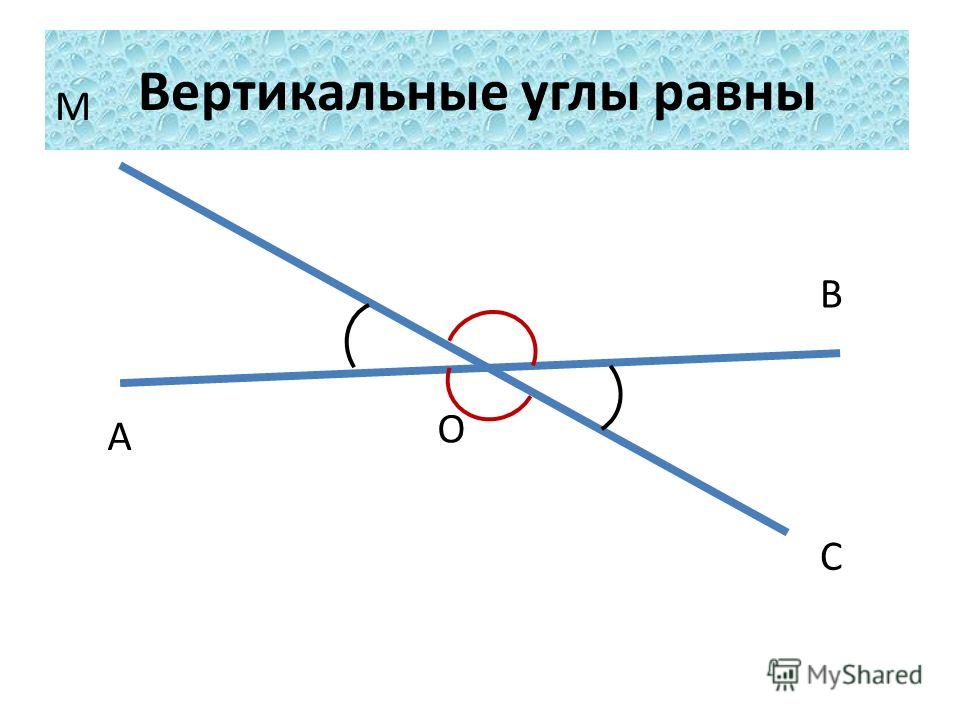 Какие углы вертикальные. Определение вертикальных углов.
Какие углы вертикальные. Определение вертикальных углов.- Альфашкола
- Статьи
- Вертикальные углы
В геометрии пары углов могут относиться друг к другу разными способами, в этой статье мы объясним что такое вертикальные углы
Когда две линии пересекаются, противоположные углы образуют вертикальные углы или вертикально противоположные углы. Они называются вертикальными углами, так как имеют одну и ту же вершину. Снизу рисунок вертикальных углов \(y\) и \(y\), \(x\) и \(x\):
Вертикальные углы равны. Заметьте также, что сумма углов \(x\) и \(y\) равна \(180°\). Прокрутите страницу вниз для получения дополнительных примеров и решений.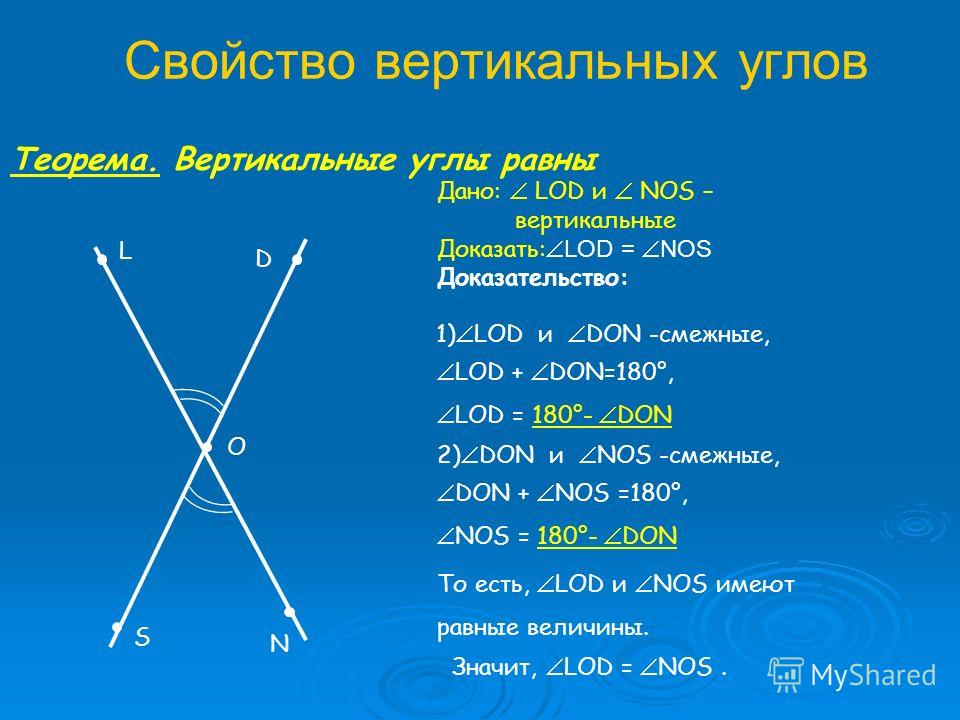
Пример 1. Найти \(x\):
Решение:
\( х + 65° = 180° ⇒ х = 180° – 65° = 115° \)
Найти \(z\):
\(z\) и \(x\) — вертикальные углы, поэтому они равны 115° .
Найти y:
y и \(65°\) вертикальные углы.
Поэтому \(y = 65°\)
Ответ: \(x = 115°, y = 65° , z = 115° \)
Пример 1. \(AEC \) и \(DEB\) прямые линии, которые пересекаются в точке \(E\). \(∠DEC\) \(=135°\). Найти \(q\).
Решение:
\(∠AEB\) = \(∠DEC\) вертикальные углы \(—>\) \( q + 45= 135\)
\(q=\) \( 135 – 45 = 90\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Тамара Ростиславовна Промская
Репетитор по математике
Стаж (лет)
Образование:
ГГУ им.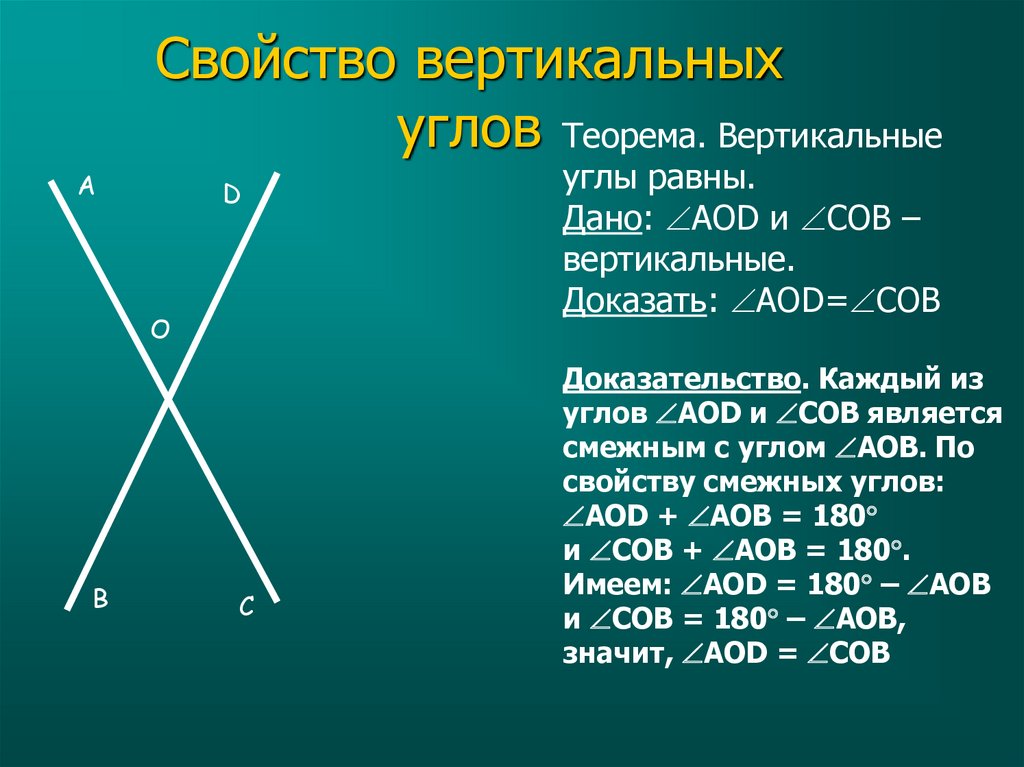 Я.Купалы
Я.Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-5 классов и русскому языку 1-4 классов. Учитываю индивидуальность каждого ученика, даю возможность роста, уверенности в себе. Такт, терпение, требовательность, доброжелательность. Объясняю простым и доступным языком. Учу ребят рассуждать, говорить, мыслить и анализировать. Даю детям прочные знания. С любовью отношусь к своему делу и прививаю любовь к обучению детям. Вместе мы достигнем поставленной цели.
Марина Валериевна Петрова
Репетитор по математике
Стаж (лет)
Образование:
Курский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-4 классы и русскому языку 1-4 классы.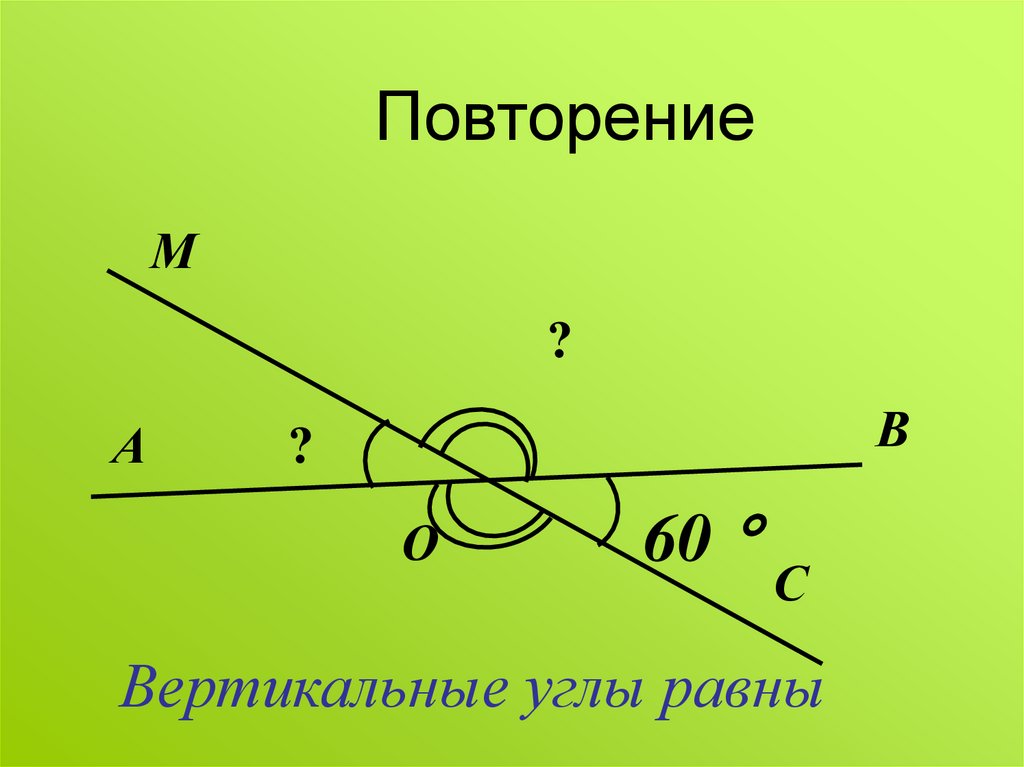 Математика — точная наука, которая развивает логическое мышление, учит думать и является основой для дальнейшего изучения школьных предметов в старшей школе.
Главное, чтобы ребенок перестал боятся задач, «трудных» уравнений и «длинных» примеров. Результат работы — мои ученики победители и призеры муниципальных и краевых олимпиад.
Сейчас работаю по программе «Школа России». Есть несколько выпусков по программе»ХХI век» и опыт работы по учебнику математики Л.Петерсон.
Математика — точная наука, которая развивает логическое мышление, учит думать и является основой для дальнейшего изучения школьных предметов в старшей школе.
Главное, чтобы ребенок перестал боятся задач, «трудных» уравнений и «длинных» примеров. Результат работы — мои ученики победители и призеры муниципальных и краевых олимпиад.
Сейчас работаю по программе «Школа России». Есть несколько выпусков по программе»ХХI век» и опыт работы по учебнику математики Л.Петерсон.
Михаил Николаевич Макеев
Репетитор по математике
Стаж (лет)
Образование:
Московский энергетический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Учитель по физике 7-11 классов, подготовка к ЕГЭ и ОГЭ. Физика в рамках школьной программы. Буду вашим гидом в онлайн режиме. Помогу с домашним заданием по программе 7-11 классов. Подготовлю по любым темам для сдачи ЕГЭ. Основой успешного обучения считаю доверительный и комфортный контакт между преподавателем и учеником.
Физика в рамках школьной программы. Буду вашим гидом в онлайн режиме. Помогу с домашним заданием по программе 7-11 классов. Подготовлю по любым темам для сдачи ЕГЭ. Основой успешного обучения считаю доверительный и комфортный контакт между преподавателем и учеником.
Похожие статьи
- Все, что нужно знать об олимпиаде «Кенгуру»
- Векторы
- Объем прямоугольной призмы
- Площадь прямоугольной пирамиды
- РУДН: Прикладная информатика (учебный план, проходной балл)
- Как строить графики функций с модулем из ОГЭ
- Нужно ли носить шапку зимой?
- Вымершие животные, которые могли существовать, если бы не деятельность человека
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Что такое угол? Виды углов.
 Острый угол как найти
Острый угол как найтиАвтор Historian Просмотров 77 Опубликовано
Углы могут быть обозначены разными цветами. Главное, чтобы она была простой и запоминающейся. Не все углы должны быть отмечены. Только те углы, которые необходимы для решения проблемы.
Содержание
- Определение угла
- Виды углов
- Сравнение углов
- Теорема Пифагора
- Проверка прямого угла
- Калькулятор расчета диагонали прямого угла
- Как разметить прямой угол рулеткой
- Углы в 30 и 45 градусов
- Коротко главном
- Градусная мера вписанного угла
- Градусная мера углов треугольника
- Смежные углы
- Вертикальные углы
- Пример:
Определение угла
Углы — это простые геометрические фигуры. Определение угла напрямую связано со значением радиуса.
Радиус — это прямая линия, которая имеет начало, но не имеет конца и простирается только в одном направлении.
Если дана прямая A на плоскости и точка o на этой прямой, то она преобразуется в две части. Каждая часть линии представляет собой радиус с началом в точке o.
Радиус символизируется буквой латинского алфавита или двумя строчными буквами. Например.
Угол — это часть уровня между двумя прямыми линиями, начинающимися из одной точки. Обе стороны угла являются радиусами, а вершина — общим принципом сторон.
Что такое вершина и стороны угла?
В математике существует специальный символ для обозначения углов — ¶.
Когда стороны угла называются маленькими латинскими буквами, они пишутся после символа. Например, ∠AB или ∠BA.
Когда стороны угла обозначаются заглавными буквами, символ угла и три буквы составляют угол, при этом вершина всегда пишется посередине. Если стороны угла равны OA и OB, то названия угла записываются как ∠AOB и NOBOA. Вы также можете назвать угол с большой буквы, обозначающей вершину.
Может быть цифровая идентификация — это тоже возможно.
Например, все способы наименования угла:.
Если угол делит уровень на две части, то одна будет внутренней областью угла, а другая — внешней. Например:.
Единицей измерения угла является градус. Символ для обозначения градуса угла: °.
Виды углов
Существует несколько типов углов, и каждый имеет свое название.
В геометрии важно различать типы углов. Это можно сделать на глаз или с помощью линейки.
Прямые углы — это углы, стороны которых перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два соседних угла равны между собой, то каждый из них является прямым углом. Для удобства прямые углы символизируются углами. Например, так:.
На изображении показаны два правильных угла Шипл — AOC и NOCOB. Общая сторона OC перпендикулярна прямой AB, а точка O является основанием перпендикуляра.
Острые углы — это прямые углы, т.е. углы с малыми углами.
Открытый угол — это открытый угол, образованный двумя лучами света, равный сумме двух правильных углов. Открытый угол равен 180°. Как выглядит разработанный угол, показано на первом рисунке.
Открытый угол равен 180°. Как выглядит разработанный угол, показано на первом рисунке.
Когда развернутый угол делится на плоскости, каждая часть угла считается внутренней областью развернутого угла.
Неравный угол — это любой угол, который не является вычитаемым углом. Другими словами, она не равна 180°.
Тупые углы — это углы, которые больше прямых, но являются углами развития (меньше 90°).
Выпуклый угол — это угол, который больше прямого угла, но меньше полного (180°).
Полные углы — это углы, обе стороны которых имеют одинаковый радиус. Это равно сумме четырех правильных углов, т.е. = 360°.
Смежные углы — это пары углов с общей вершиной и стороной, причем другая сторона находится на противоположной стороне от общей стороны.
На рисунке изображены два смежных угла anob и ∠BOC, с общей вершиной o, общей ob.
Это определение может быть сформулировано по-разному. Если радиус вычитается из вершины угла, делящего угол на два, то образовавшиеся углы являются смежными.
Чтобы разделить угол на радиус, прибавьте угол. Из этого можно выделить следующие корректные различия.
Углы называются прямыми, если они равны 90°, острыми, если они меньше 90°, и тупыми, если они больше 90° и меньше 180°. Открытый угол равен 180°.
Онлайн-школа Skysmart поощряет детей и подростков к занятиям математикой. За интересные задачи, знание новых приложений и хорошие оценки!
Сравнение углов
Для сравнения углов можно использовать метод наложения, который является самым простым методом в учебной программе 4 класса. Для этого сопоставьте две вершины и одну сторону одного угла с одной стороной другого. Если стороны определенного угла совпадают, то углы равны. Если нет, то угол внутри другого угла будет меньше. Ниже приведены два наглядных примера равных и неравных углов.
Ракурсы для разработки всегда одни и те же.
Углы ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 расположены следующим образом.
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если другие стороны также совпадают, то углы равны: ∠𝐴𝐵𝐶=∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶
Углы также можно сравнивать, измеряя их значения. Для построения и измерения углов вам понадобится специальный инструмент — транспортир. Вот как это выглядит:.
Чтобы понять взаимосвязь между объектами, изучите отношения между различными частями. Определяя отношения между ними, вы найдете синус, косинус (что это такое?), тангенс (что это такое?), касательную (что это такое?). ), вводятся понятия тангенса и катагонали.
Теорема Пифагора
Теорема основана на утверждении, что в прямоугольном треугольнике сумма квадратов длин перпендикулярных линий равна квадрату длины гипотенузы. В пресс-релизе говорится, что
Стороны a и b — катеты, угол между которыми составляет ровно 90 градусов. Таким образом, сторона c является косой. Подставив две известные величины в это уравнение, можно рассчитать третью неизвестную величину. В результате можно регистрировать и контролировать правильный угол.
В результате можно регистрировать и контролировать правильный угол.
Теорема Пифагора также известна как «египетский треугольник». Это треугольник со сторонами 3, 4 и 5; единицы длины не имеют значения. Расстояние между сторонами 3 и 4 составляет ровно 90 градусов. Проверим это утверждение с помощью приведенного выше уравнения: a²+b²=c²= (3 x 3) + (4 x 4) = 9 + 16 = (5 x 5) = 25- все сходится!
Теперь давайте применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — контроля прямых углов с помощью теоремы Пифагора. Самый распространенный пример в отделке и строительстве — проверка перпендикулярности стен. Вертикальные стены — это стены, расположенные под углом 90° друг к другу.
Возьмите внутренний угол, который вы хотите контролировать. Обратите внимание на длину обеих стен (одинаковой высоты) или пола. Длина этих секций не является обязательной. Если возможно, следует разметить как можно больше, но полезно измерить диагонали между отметками на стенах. Например, отметьте 2,5 метра (или 250 см) на одной стене и 3 метра (или 300 см) на другой. Затем возведите в квадрат длину каждого участка стены (умножьте на себя) и сложите полученное произведение. Результат: (2,5 x 2,5) + (3 x 3) = 15,25 — это квадрат диагонали. Теперь вычтите квадратный корень из этого числа. √15,25 ≈ 3,90 — 3,9 метра — диагональ между точками. Если рулетка показывает разную длину диагонали, то контролируемый угол поворачивается и происходит отклонение на 90°.
Например, отметьте 2,5 метра (или 250 см) на одной стене и 3 метра (или 300 см) на другой. Затем возведите в квадрат длину каждого участка стены (умножьте на себя) и сложите полученное произведение. Результат: (2,5 x 2,5) + (3 x 3) = 15,25 — это квадрат диагонали. Теперь вычтите квадратный корень из этого числа. √15,25 ≈ 3,90 — 3,9 метра — диагональ между точками. Если рулетка показывает разную длину диагонали, то контролируемый угол поворачивается и происходит отклонение на 90°.
Калькулятор расчета диагонали прямого угла
Экспорт квадратных корней мне не понравился — простые люди не могут обойтись без калькуляторов. Не все мобильные расчеты можно экспортировать. Поэтому можно использовать упрощенный метод. Необходимо помнить, что прямой угол ровно 100 см является диагональю 141,4 см. Таким образом, для прямого угла со стороной 2 м. — Диагональ составляет 282,8 см. Это означает, что каждое измерение составляет 141,4 см. У этого метода есть недостатки. На обеих стенах должно быть измерено одинаковое расстояние, и оно должно быть кратно 1 метру. Я не могу сказать наверняка, но в моей скромной практике это гораздо удобнее. Не следует полностью забывать о первоначальном методе, но в некоторых случаях он очень важен.
Я не могу сказать наверняка, но в моей скромной практике это гораздо удобнее. Не следует полностью забывать о первоначальном методе, но в некоторых случаях он очень важен.
Сразу возникает вопрос: какое отклонение от расчетной длины диагонали считается нормальным (ошибкой), а какое — нет? Если угол, контролируемый отмеченным краем 1 м, составляет 89°, диагональ уменьшается до 140 см. Понимая эту взаимосвязь, можно сделать объективный вывод, что ошибка диагонали 141,4 см в несколько миллиметров не дает расхождения в общей оценке.
Как я могу проверить внешние углы? Наружный контроль в основном такой же, просто проденьте каждую линию стены до пола (или до земли с помощью кабеля) и измерьте внутренние углы обычным способом.
Как разметить прямой угол рулеткой
Разметка основана либо на общей теореме Пифагора, либо на началах «египетского треугольника». Однако, хотя теоретически на бумаге проектируются только линии, «поймать» все выбранные размеры с помощью шнуров или линий, протянутых на полу, — более сложная задача.
Поэтому рекомендуется упрощенный метод, основанный на диагоналях 141,4 см треугольника со сторонами 100 см. Вся последовательность раскладки показана на следующих рисунках. Важно помнить. Диагональ 141,4 см нужно умножить на количество измерений в секции AB. Отрезки AB и AB должны быть равны и соответствовать целым числам метров. Нажмите на картинку, чтобы увеличить ее!
Значение. Два угла называются перпендикулярными, если сторона одного угла равна дополнительной половине стороны другого угла.
Углы в 30 и 45 градусов
Выбор одного из способов вычисления угла 90° с помощью ленты не затрудняет формирование трех различных острых углов. 45 градусов возникает независимо от того, является ли треугольник равнобедренным или нет. Для 30 градусов подчиненный должен быть вытянут. Это равно двум коротким вертикалям. Здесь угол между ними остается равным 60 градусам.
В этом видео учитель делится своим опытом экспорта прямых углов с помощью теоремы Пифагора и египетского треугольника.
Коротко главном
В помещениях часто необходимо спроектировать прямые углы под мебелью и гидравлическими компонентами.
Существует три способа контроля угла 90° с помощью одной ленты: если соединительная линия между стенами длиной 1 метр равна 141,4 см, то стороны составляют 3/4/5 частей.
Ленты также достаточно для образования трех углов в 30, 45 и 60 градусов.
Кроме того, для выставления оценок могут потребоваться только калькулятор и карандаш.
Угол — это геометрическая фигура, образованная двумя лучами света (сторонами угла), исходящими из одной точки (называемой вершиной угла). Уровень, содержащий обе стороны одного угла, разделен на две зоны.
Градусная мера вписанного угла
Тогда градусная оценка угла регистрации равна половине градусной оценки смычка и половине градусной оценки угла на том же смычке.
Выгравированный угол будет равен 0,5 метра лука на дуге, на которой он расположен.
Рисунок 2.
Различают также различные типы углов.
Прямые углы равны 90 градусам. Острые углы меньше 90 градусов. А тупые углы — это углы больше 90 градусов и меньше 180 градусов. Так как же важно уметь считать углы и градусы? Он полезен при проведении следующих исследований Астрономия. Например, вычисление положения различных тел в пространстве. Чтобы попрактиковаться в этом, нужно нарисовать много углов, отличающихся друг от друга. Также важно практиковаться в рисовании. Вы также можете попрактиковаться в построении углов с произвольными числами с помощью транспортира.
Существует также концепция перегородок.
Биссектриса — это радиус, исходящий из вершины этого угла и делящий его посередине.
Пример 1. Разделы и экстенсивные угловые задачи.
Рисунок 3.
Рис. 3. Лучи DE и DF парализованы, соответствуют углам ADB и BDC.
Найдите угол ADC, угол EDF = 75°.
Ответ. Угол EDF равен половине угла ADB и BDC. Это означает, что EDF составляет половину угла ADC. Теперь угол ADC = 75 умножается на 2 = 150°.
Теперь угол ADC = 75 умножается на 2 = 150°.
Пример 2. Биссектрисы углов и прямые углы.
Рисунок 4.
На рисунке 4 видно, что угол ABC является правильным, а угол ABE EBD DBC — равным. Необходимо найти углы, образованные бисекторами ABE и DBC.
Решение: угол ABC правильный и поэтому равен 90°. Угол EBD = 90/3 = 30°. Согласно правилам, углы ABE EBD DBC равны и поэтому каждый из них = 30°. Более того, оказывается, что бисектор любого из трех углов разделит любой из этих углов на два угла, равных 15°. Поскольку оба угла ABE и DBC связаны с найденными углами, можно смело утверждать, что вычисляемый угол равен 30+15+15 = 60°.
Градусная мера углов треугольника
Каждая геометрическая фигура, кроме круглой, имеет угол. Рассматривая углы треугольника, мы видим, что Сумма углов треугольника всегда равна 180°. Рассматривая прямоугольный треугольник, мы видим, что один из углов равен 90°. Сумма двух других углов также равна 90°.
Поэтому, если мы знаем, сколько градусов составляет один из острых углов треугольника, второй угол можно найти по типу.
Два других угла — острые, так как прямоугольные треугольники имеют прямые углы.
Острые углы объясняются следующим образом. Острые углы — это углы менее 90 градусов.
Рисунок 5: Прямоугольный треугольник
Из вышесказанного следует, что прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками. Эти участки связаны с тремя точками. Все их углы — внутренние, один из которых прямой и соответствует 90°. Пример показан на рисунке 5.
2. если два луча света параллельны, но не лежат на одной прямой, начертите уровень, проходящий через принцип и разделяющий пространство на два полудома. Если лучи находятся в одном из этих полудомов, то они находятся под совместным надзором (рис. 2.51). Если лучи света находятся в разных полушариях, они имеют противоположные направления (рис. 2.52).
Смежные углы
Значение. Если два угла имеют одну общую плоскость и противоположные стороны этих углов являются дополнительными полуплоскостями, то такие углы называются смежными.
На рисунке 2.77
Сумма смежных углов равна 180°.
Следующий результат вытекает из Теоремы 4, т.е. из свойства смежных углов.
Последующее 1. Если два угла равны, то смежные углы равны.
Последующее 2. Угол, касательный к прямому углу, является прямым углом.
Впоследствии 3. Углы, касательные к острым углам, являются тупыми, а углы, касательные к тупым углам, являются острыми.
Вертикальные углы
На рисунке 2.78 изображены две пересекающиеся в точке О прямые АВ и CD. При пересечении этих прямых образовалось четыре угла:
Значение. Два угла называются перпендикулярными, если сторона одного угла равна дополнительной половине стороны другого угла.
На рисунке 2.78 углы 1 и 3, 2 и 4 перпендикулярны.
Очевидно, что две пересекающиеся прямые образуют смежный вертикальный угол и перпендикулярный угол. Смежные углы дополняют друг друга до 180°. Меньший угол из двух называется углом между линиями.
Пример:
На рисунке 2. 79 угол треска равен 30°. Чему равны углы AOC и DOK?
79 угол треска равен 30°. Чему равны углы AOC и DOK?
1. прямые CK и AD пересекаются в точке O
2.
4. угол между COD и AOK является вертикальным (1, определение вертикального угла).
5.
6. угол dok содержит угол cod (1, определение тангенса угла).
7.
Эта лекция взята со страницы с полным текстом урока «Математика».
См. также дополнительные лекции по предмету математика.
Отправляйте задания в любое время дня и ночи.
Официальный сайт Брилионо Банаталия Валерий Эвант Профессор Екатеринбургского государственного института.
Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.
Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.
Наталья Брилёнова не предлагает и не оказывает товары и услуги.
При копировании материалов ссылка на сайт Natalibrilenova.ru обязательна.
Проекции панорамных изображений
Проекция изображения происходит всякий раз, когда плоское изображение отображается на изогнутой поверхности или наоборот, и в частности, проекции повсеместно используются в панорамной фотографии. Проекция осуществляется, когда картограф отображает сферический глобус Земли на плоском листе бумаги, например. Поскольку полное поле зрения вокруг нас может рассматриваться как поверхность сферы (для всех углов зрения), для фотографий, которые будут показаны на плоском мониторе или отпечатаны, требуется аналогичная проекция сферы в плоскость.
| Узкий угол зрения (сетка практически квадратична) | Широкий угол зрения (сетка сильно искажена) |
Для малых углов зрения отобразить изображение на плоском листе бумаги относительно легко, поскольку обозреваемый сектор практически плоский. При отображении сферического изображения на плоской поверхности некоторые искажения неустранимы, поэтому каждый тип проекции пытается минимизировать один тип искажения за счёт остальных. По мере расширения угла зрения рассматриваемые сектора становятся всё более изогнутыми, и следовательно, разница между типами панорамных проекций становится более выраженной. Момент использования каждой из проекций зависит преимущественно от изображаемого предмета и применения; здесь мы сфокусируемся на нескольких типах проекций, которые наиболее распространены в цифровой фотографии. Многие типы проекций, обсуждаемые в данной главе, могут использоваться в качестве выходного формата в нескольких пакетах программ сборки панорам; PTAssembler позволяет использовать все перечисленные проекции.
При отображении сферического изображения на плоской поверхности некоторые искажения неустранимы, поэтому каждый тип проекции пытается минимизировать один тип искажения за счёт остальных. По мере расширения угла зрения рассматриваемые сектора становятся всё более изогнутыми, и следовательно, разница между типами панорамных проекций становится более выраженной. Момент использования каждой из проекций зависит преимущественно от изображаемого предмета и применения; здесь мы сфокусируемся на нескольких типах проекций, которые наиболее распространены в цифровой фотографии. Многие типы проекций, обсуждаемые в данной главе, могут использоваться в качестве выходного формата в нескольких пакетах программ сборки панорам; PTAssembler позволяет использовать все перечисленные проекции.
Типы проекции изображений в фотографии
| Сетка, отображающая поле зрения (зритель в центре) | |||
| Плоская проекция: | |||
| Выберите тип проекции: | Эквидистантная (100% покрытия) | ||
| Прямоугольная | Цилиндрическая | ||
| Меркатора | Рыбий глаз | ||
| Синусоидальная | Стереографическая | ||
Если все эти типы проекции изображений выглядят несколько обескураживающе, попробуйте сперва прочитать и осознать различие между прямоугольной и цилиндрической проекциями (выделены), поскольку они наиболее широко используются при сборке цифровых панорам.
Эквидистантная проекция отображает координаты широты и долготы сферического глобуса непосредственно на горизонтальные и вертикальные координаты сетки, где сетка имеет ширину примерно вдвое больше высоты. Горизонтальное растяжение, как следствие, усиливается по направлению к полюсам, так что северный и южный полюсы оказываются растянуты на всю верхнюю и нижнюю границы плоской сетки, соответственно. Эквидистантные проекции могут показать полный вертикальный и горизонтальный углы вплоть до 360 градусов.
Цилиндрическая проекция изображения аналогична эквидистантной, за исключением того, что по мере приближения к северному и южному полюсам объекты также растягиваются по вертикали так что на полюсах достигается бесконечное растяжение по вертикали (так что горизонтальная линия наверху и внизу плоской сетки отсутствует). Именно по этой причине цилиндрические проекции непригодны для изображений с большим вертикальным углом зрения. Цилиндрические проекции также являются стандартным типом, отображаемым традиционными панорамными плёночными камерами с поворотным объективом. Цилиндрические проекции сохраняют более точные относительные размеры объектов, чем прямоугольные, однако достигается это за счёт искривления линий, параллельных линии зрения (которые иначе оставались бы прямыми).
Цилиндрические проекции сохраняют более точные относительные размеры объектов, чем прямоугольные, однако достигается это за счёт искривления линий, параллельных линии зрения (которые иначе оставались бы прямыми).
Прямоугольная проекция изображения имеет основное преимущество в том, что отображает прямые линии в трёхмерном пространстве в прямые линии на плоской двумерной сетке. Этот тип проекции соответствует тому, который создаёт большинство обычных широкоугольных объективов, так что она, вероятно, является наиболее понятной. Её основной недостаток состоит в том, что она может существенно преувеличить перспективу по мере увеличения угла обзора, что приводит к видимому завалу объектов к границам кадра. Именно по этой причине прямоугольные проекции обычно не рекомендуются для углов зрения, которые существенно превышают 120 градусов.
Рыбий глаз — это проекция изображения, целью которой является создание плоской сетки, где расстояние от центра сетки примерно пропорционально действительному углу зрения; она образует изображение, которое выглядит похоже на отражение от металлической сферы. Как правило такая проекция не используется в качестве выходного формата панорамной фотографии, но вместо того она может представлять исходные изображения, если для съёмки таковых использовался объектив типа «рыбий глаз». Эта проекция к тому же ограничена вертикальным и горизонтальным углом обзора 180 градусов или менее, порождая изображение, которое помещается в круг. Её характеризует нарастающее искривление линий (которые иначе были бы прямыми) по мере удаления от центра изображения. Камера с объективом типа «рыбий глаз» исключительно полезна при создании панорам, которые покрывают всю сферу зрения, поскольку достаточно будет собрать небольшое число снимков.
Как правило такая проекция не используется в качестве выходного формата панорамной фотографии, но вместо того она может представлять исходные изображения, если для съёмки таковых использовался объектив типа «рыбий глаз». Эта проекция к тому же ограничена вертикальным и горизонтальным углом обзора 180 градусов или менее, порождая изображение, которое помещается в круг. Её характеризует нарастающее искривление линий (которые иначе были бы прямыми) по мере удаления от центра изображения. Камера с объективом типа «рыбий глаз» исключительно полезна при создании панорам, которые покрывают всю сферу зрения, поскольку достаточно будет собрать небольшое число снимков.
Проекция Меркатора наиболее близко соотносится с цилиндрической и эквидистантной проекциями; она является компромиссом между этими двумя типами, обеспечивая меньшее растяжение по вертикали и более широкий употребимый угол зрения, чем цилиндрическая проекция, но с более сильным искривлением линий. Эта проекция, вероятно, является наиболее узнаваемой, поскольку используется в плоских картах мира. Отметим также, что альтернативная форма этой проекции (поперечный Меркатор) может использоваться для вертикальных панорам большой высоты.
Отметим также, что альтернативная форма этой проекции (поперечный Меркатор) может использоваться для вертикальных панорам большой высоты.
Синусоидальная проекция изображения пытается сохранить равные площади во всех участках сетки. Если развернуть глобус в плоскость, можно вообразить, что такую проекцию можно свернуть обратно, чтобы сформировать сферу, которая будет идентична исходной по форме и площади поверхности. Характеристика равной площади полезна, поскольку если записывать плоскую проекцию сферического изображения, она сохранит неизменное горизонтальное и вертикальное разрешение по всему изображению. Эта проекция подобна рыбьему глазу и стереографической, за вычетом того, что сохраняет абсолютно горизонтальные линии из исходной сферы.
Стереографическая проекция очень похожа на рыбий глаз, но при этом сохраняет лучшее ощущение перспективы, увеличивая растяжение объектов по мере их удаления от точки перспективы. Подобная выделяющая перспективу характеристика в чём-то похожа на прямоугольную проекцию, хотя здесь она менее выражена.
Примеры: широкое горизонтальное поле зрения
Как все эти проекции изображения в действительности влияют на панорамную фотографию? Следующая серия снимков используется для наглядной демонстрации различий между двумя типами проекции, которые наиболее часто встречаются в программах сборки панорам: прямоугольной и цилиндрической. Снимки подобраны так, чтобы показать только различия в искажениях для широкого горизонтального угла зрения; вертикальные панорамы подобраны далее для иллюстрации разницы в вертикальных искажениях между другими типами проекций.
Первый пример демонстрирует, как прямоугольная проекция могла бы отобразить фотопанораму из трёх снимков, показанных выше.
Обратите внимание на значительные искажения по краям угла зрения, вдобавок к драматической потере разрешения вследствие растягивания изображения. Следующий снимок демонстрирует, как выглядело бы сильно искажённое изображение, показанное выше, если бы его обрезали по горизонтальному углу зрения, составляющему всего 120 градусов.
Как можно видеть, такая кадрированная прямоугольная проекция производит вполне приятное впечатление, поскольку все прямые архитектурные линии в сборке остаются прямыми. С другой стороны, это достигается за счёт относительного размера объектов в пределах угла зрения; объекты на границах угла зрения (левый и правый края) значительно увеличены по сравнению с объектами в центре (башня со входом внизу).
Следующий пример демонстрирует, как выглядел бы результат сборки с использованием цилиндрической проекции. Её преимущество заключается в относительно равномерном распределении разрешения, а кроме того, она требует минимального кадрирования. Вдобавок, разница между цилиндрической и эквидистантной проекциями пренебрежимо мала для фотографий, которые не имеют исключительно большого вертикального угла зрения (как в следующем примере).
Примеры: высокое вертикальное поле зрения
Следующие примеры иллюстрируют разницу между типами проекций для вертикальной панорамы (с большим вертикальным полем зрения). Она даёт шанс показать разницу между эквидистантной, цилиндрической и проекцией Меркатора, которые в предыдущем примере выглядели бы практически одинаково (для широкого горизонтального угла зрения).
Она даёт шанс показать разницу между эквидистантной, цилиндрической и проекцией Меркатора, которые в предыдущем примере выглядели бы практически одинаково (для широкого горизонтального угла зрения).
| цилиндрическая | Меркатора | эквидистантная | |
Примечание: точка перспективы для этой панорамы установлена в основании башни, и как следствие, действительный вертикальный угол зрения выглядит так, как если бы поле зрения составляло 140 градусов (как если бы точка перспективы была на половинной высоте).
| Поперечный Меркатор |
Такой большой вертикальный угол зрения позволяет нам чётко увидеть, как каждая из выбранных проекций изображения отличается по степени вертикального растяжения/сжатия. Эквидистантная проекция сжимает вертикальную перспективу настолько сильно, что теряет ощущение огромной высоты, которое посещает непосредственного наблюдателя. По этой причине эквидистантная проекция рекомендуется, только когда это абсолютно необходимо (как например, для панорам с широчайшим полем зрения как по вертикали, так и по горизонтали).
По этой причине эквидистантная проекция рекомендуется, только когда это абсолютно необходимо (как например, для панорам с широчайшим полем зрения как по вертикали, так и по горизонтали).
Все три показанных проекции призваны сохранить практически прямые вертикальные линии; поперечная проекция Меркатора справа вносит некоторое скругление с целью сохранить более реалистичную (субъективно) перспективу. Этот тип проекции часто используется для экстремально больших вертикальных углов зрения. Заметим также, насколько хорошо эта проекция сохраняет исходный вид каждого из исходных снимков.
Разница между прямоугольной и цилиндрической проекциями для такого узкого горизонтального угла зрения едва заметна, так что прямоугольная проекция пропущена.
Калькуляторы панорамного поля зрения
Следующий калькулятор можно использовать для оценки горизонтального и вертикального углов зрения вашей камеры при использовании объективов с различными фокусными расстояниями, что может помочь в оценке подходящего типа проекции.
| Калькулятор панорамного поля зрения | ||
|---|---|---|
| Фокусное расстояние объектива: | мм | |
| Снимков по горизонтали: | 12345678910 | |
| Снимков по вертикали: | 12345678910 | |
| Ориентация камеры: | ландшафтнаяпортретная | |
| Процент перекрытия: | % | |
| Тип камеры:цифровая зеркальная, кроп-фактор 1.6цифровая компактная с сенсором 1/3″цифровая компактная с сенсором 1/2″цифровая компактная с сенсором 1/1.8″цифровая компактная с сенсором 2/3″цифровая зеркальная с сенсором 4/3″цифровая зеркальная, кроп-фактор 1.5APSцифровая зеркальная, кроп-фактор 1.335 мм6×4.5 см 6×6 см6×7 см5×4 дюйма10×8 дюймов | ||
| Поле зрения: x (горизонталь x вертикаль) | ||
Примечание: калькуляторы не предназначены для макросъёмки. Все результаты приблизительны, поскольку на угол зрения также влияет (в меньшей степени) дистанция фокусировки. Вдобавок, поле зрения подразумевает, что объектив осуществляет прямоугольную проекцию изображения; объективы с большими бочкообразными или подушкообразными искажениями могут показать несколько другие результаты.
Вдобавок, поле зрения подразумевает, что объектив осуществляет прямоугольную проекцию изображения; объективы с большими бочкообразными или подушкообразными искажениями могут показать несколько другие результаты.
Следующий калькулятор оценивает количество снимков, необходимых для получения кругового горизонтального обзора, исходя из фокусного расстояния, ориентации камеры, процента перекрытия и размера сенсора цифровой камеры.
| Калькулятор круговой панорамы | ||
|---|---|---|
| Фокусное расстояние: | мм | |
| Ориентация камеры: | ландшафтнаяпортретная | |
| Процент перекрытия: | % | |
Тип камеры:цифровая зеркальная, кроп-фактор 1.6цифровая компактная с сенсором 1/3″цифровая компактная с сенсором 1/2″цифровая компактная с сенсором 1/1.8″цифровая компактная с сенсором 2/3″цифровая зеркальная с сенсором 4/3″цифровая зеркальная, кроп-фактор 1.5APSцифровая зеркальная, кроп-фактор 1. 335 мм6×4.5 см 6×6 см6×7 см5×4 дюйма10×8 дюймов 335 мм6×4.5 см 6×6 см6×7 см5×4 дюйма10×8 дюймов | ||
| Необходимое число снимков по горизонтали: | ||
Примечание: кроп-фактор описывает относительный размер сенсора камеры по сравнению с камерой
35 мм. Подробности по этой теме читайте в главе, посвящённой размерам сенсоров цифровых камер.
В следующей таблице представлена сводка применения различных типов проекции:
| Тип проекции | Рекомендации по размеру поля зрения | Прямые линии? | ||
|---|---|---|---|---|
| горизонтальное | вертикальное | горизонтальные | вертикальные | |
| Прямоугольная | <120° | <120° | да | да |
| Цилиндрическая | ~120-360° | <120° | нет | да |
| Меркатора | ~120-360° | <150° | нет | да |
| Эквидистантная | ~120-360° | 120-180° | нет | да |
| Рыбий глаз | <180° | <180° | нет | нет |
Примечание: все замечания по прямым линиям исключают горизонтальные и вертикальные линии в самом центре; поле зрения подразумевает, что точка перспективы расположена в центре угла зрения.
Основы создания цифровых панорам изложены в предыдущих частях этой главы:
часть 1: общие понятия и съёмка
часть 2: программное обеспечение
Вертикальные углы — Теорема, доказательство, Вертикально противоположные углы
Вертикальные углы образуются, когда две линии встречаются в одной точке. Они всегда равны друг другу. Другими словами, всякий раз, когда две прямые пересекаются или пересекаются друг с другом, образуются 4 угла. Мы можем заметить, что два угла, которые противоположны друг другу, равны, и они называются вертикальными углами. Их также называют «вертикально противоположными углами», поскольку они лежат напротив друг друга.
| 1. | Что такое вертикальные углы? |
| 2. | Теоремао вертикальных углах |
| 3. | Вертикально противоположные углы Рабочий лист |
| 4. | Часто задаваемые вопросы о вертикальных углах |
Что такое вертикальные углы?
При пересечении двух прямых образуются четыре угла. Имеются две пары несмежных углов. Эти пары называются вертикальными углами. На изображении ниже (∠1, ∠3) и (∠2, ∠4) две пары вертикальных углов.
Имеются две пары несмежных углов. Эти пары называются вертикальными углами. На изображении ниже (∠1, ∠3) и (∠2, ∠4) две пары вертикальных углов.
Вертикальные углы Определение
Вертикальные углы представляют собой пару несмежных углов, образованных пересечением двух прямых линий. Проще говоря, вертикальные углы расположены друг напротив друга в углах «Х», образованных двумя прямыми линиями. Их также называют вертикально противоположными углами, так как они расположены друг напротив друга.
Теорема о вертикальных углах
Теорема о вертикальных углах или теорема о вертикально противоположных углах утверждает, что два противоположных вертикальных угла, образованных при пересечении двух прямых, всегда равны (конгруэнтны) друг другу. Давайте узнаем о теореме о вертикальных углах и ее доказательстве в деталях.
Утверждение : Вертикальные углы (противоположные углы, образующиеся при пересечении двух прямых) равны.
Доказательство вертикальных углов
Доказательство простое и основано на прямых углах. Мы уже знаем, что сумма углов на прямой составляет 180°.
Итак, на рисунке выше
∠1 + ∠2 = 180° (поскольку они представляют собой линейную пару углов) ——— (1)
∠1 +∠4 = 180° (поскольку они представляют собой линейную пару углов) ——— (2)
Из уравнений (1) и (2) ∠1 + ∠2 = 180° = ∠1 +∠4.
Согласно свойству транзитивности, если a = b и b = c, то a = c.
Следовательно, мы можем переписать утверждение как ∠1 + ∠2 = ∠1 +∠4. ———(3)
Исключив ∠1 в обеих частях уравнения (3), мы получим ∠2 = ∠4.
Сходным образом. мы можем использовать тот же набор утверждений, чтобы доказать, что ∠1 = ∠3. Отсюда делаем вывод, что вертикально противоположные углы всегда равны.
Чтобы найти меру углов на рисунке, мы используем свойство прямого угла и теорему о вертикальном угле одновременно. Давайте посмотрим на некоторые решенные примеры, чтобы понять это.
Вертикально противоположные углы Рабочий лист
Следующая таблица состоит из рабочих листов творческих вертикальных углов. Эти рабочие листы легко и бесплатно скачать. Попробуйте и отработайте несколько вопросов, основанных на вертикально противоположных углах, и улучшите знания по теме.
Вертикальные углы Рабочий лист — 1 | Скачать PDF |
Вертикальные углы Рабочий лист — 2 | Скачать PDF |
Вертикальные углы Рабочий лист — 3 | Скачать PDF |
Вертикальные углы Рабочий лист — 4 | Скачать PDF |
Важные примечания
- Вертикальные углы всегда равны.
- Вертикальные углы могут быть как дополнительными, так и взаимодополняющими.
- Вертикальные углы всегда несмежны.

Темы, относящиеся к вертикальным углам
Ознакомьтесь с некоторыми интересными статьями, посвященными вертикальным углам.
- Уголки
- Альтернативные углы
- Альтернативные внутренние углы Теорема
- Дополнительные углы
- Калькулятор дополнительных углов
- Дополнительные уголки
- Геометрия
Примеры вертикальных углов
Пример 1: Найдите меру ∠f по рисунку, используя теорему о вертикальных углах.
Решение:
На приведенном ниже изображении мы видим, что AE и DC представляют собой две прямые линии. Здесь ∠DOE и ∠AOC — вертикальные углы.
∠DOE = ∠AOC
118° = 90° + ∠f
∠f = 118° — 90°
∠f = 28°
Следовательно, ∠90 28°
Пример 2: На приведенном ниже рисунке ∠f равен 79°, так как противоположные по вертикали углы равны. Верно ли утверждение? Обосновать ответ.

Решение:
Здесь 79° и f расположены напротив, но не являются вертикальными углами, так как углы не образуются при пересечении двух прямых. Здесь BD не является прямой линией. Следовательно, ∠f не равно 79° . Данное утверждение неверно.
Пример 3. Если угол b в три раза больше угла a, найдите значения углов a и b, используя теорему о вертикальных углах.
Решение:
Из рисунка видно, что 80° и сумма углов a и b вертикально противоположны. Это означает, что ∠a + ∠b = 80°. Дано, что ∠b = 3∠a. Подставляя значения в уравнение ∠a + ∠b = 80°, получаем, ∠a + 3∠a = 80°
4∠a = 80°
∠a= 80°/4
∠a= 20°
Так как ∠b = 3∠a, ∠b = 3 × 20°
2°3 090 = 60 0 9090 Следовательно, ∠a= 20° и ∠b= 60°
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по вертикальным углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о вертикальных углах
Что такое вертикальные углы в геометрии?
Вертикальные углы образуются при пересечении двух прямых. Из 4 образованных углов углы, противоположные друг другу, являются вертикальными углами. Их также называют «вертикально противоположными углами». Эти углы всегда равны.
☛Также читайте
- Пары углов
- Секущие и связанные углы
- Внутренние уголки
Вертикальные углы равны?
При пересечении двух прямых линий образуются вертикальные углы. Вертикальные углы всегда конгруэнтны и равны. Вертикальные углы конгруэнтны, так как две пары несмежных углов, образованные пересечением двух прямых, накладываются друг на друга.
☛Проверьте и прочитайте
- Равные углы
- Конгруэнтность
- Конгруэнтные треугольники
Дополняют ли вертикальные углы?
Когда сумма любых двух углов равна 180°, мы называем их дополнительными углами. Если есть случай, когда вертикальные углы прямые или равны 90°, то каждый вертикальный угол равен 90°. Следовательно, сумма этих двух углов будет равна 180°. Так что в таких случаях можно сказать, что вертикальные углы являются дополнительными. Следует отметить, что это частный случай, когда вертикальные углы являются дополнительными. В противном случае во всех остальных случаях, когда значение каждого из вертикальных углов меньше или больше 90 градусов, они не являются дополнительными.
☛Обратите внимание на разницу между:
- Дополнительные уголки
- Дополнительные углы
- Линейная пара углов
Что такое теорема о вертикальном угле?
Теорема о вертикальном угле утверждает, что углы, образованные двумя пересекающимися прямыми, которые называются вертикальными углами, равны. Вертикальные углы имеют равные измерения. Например, если ∠a, ∠b, ∠c, ∠d — это 4 угла, образованные двумя пересекающимися прямыми, и ∠a вертикально противоположна ∠b, а ∠c вертикально противоположна ∠d, то ∠a конгруэнтна ∠ b и ∠c конгруэнтно ∠d.
Вертикальные углы имеют равные измерения. Например, если ∠a, ∠b, ∠c, ∠d — это 4 угла, образованные двумя пересекающимися прямыми, и ∠a вертикально противоположна ∠b, а ∠c вертикально противоположна ∠d, то ∠a конгруэнтна ∠ b и ∠c конгруэнтно ∠d.
Могут ли вертикальные углы быть прямыми?
Да, вертикальные углы могут быть прямыми. Если два противоположных вертикальных угла равны 90° каждый, то вертикальные углы называются прямыми. Это можно наблюдать по линиям оси x и оси y декартова графика.
☛Оформить заказ
- Прямоугольный
- Угол 90 градусов
- Угол 180 градусов
Как измерить значение вертикального угла?
При решении таких случаев в первую очередь нужно внимательно следить за заданными параметрами. Если задан угол, следующий за вертикальным углом, то легко определить значение вертикальных углов, вычитая данное значение из 180 градусов до Так как в геометрии доказано, что вертикальный угол и смежный с ним угол являются дополнительными (180°) друг другу.
Как определить, является ли угол смежным или вертикальным?
Вертикальные углы — это углы, образованные при пересечении двух прямых. Противоположные углы, образованные этими линиями, называются вертикально противоположными углами. Принимая во внимание, что смежные углы — это два угла, которые имеют одну общую сторону и вершину.
Могут ли вертикальные углы быть смежными?
Вертикальные углы противоположны друг другу, тогда как смежные углы — это углы, расположенные рядом друг с другом. Таким образом, вертикальные углы никогда не могут быть смежными друг с другом.
Всегда ли вертикальные углы равны?
Да, вертикальные углы всегда равны. Пересечение двух прямых дает 4 угла. При этом образуются две пары вертикальных углов. Они равны по мере и конгруэнтны.
Что такое вертикальные углы? — [Объяснение теоремы и примеров вычислений]
Теорема о вертикальных углах и расчеты с примерами
Что такое вертикальные углы в геометрии?
Содержание
- Что такое вертикальные углы в геометрии?
- Теорема о вертикальном угле
- Характеристики
- Применение
- Важность
- Формула вертикального угла
- Конгруэнтны ли вертикальные углы?
- Примеры вертикального угла
- Пример 1
- Пример 2
- Расчет вертикальных угнет из двух пересекающихся прямых.

Вертикальные углы также определяются как пара несмежных углов, образованных двумя пересекающимися линиями. Вертикальные углы также известны как вертикально противоположные углы, потому что углы противоположны друг другу и имеют одну и ту же вершину.
В геометрии при пересечении двух прямых линий они образуют четыре угла. Углы, противоположные друг другу, являются вертикальными углами. В этом контексте вертикаль означает, что они имеют одну и ту же вершину.
Теорема о вертикальном угле
Характеристики
Вертикальные углы , образованные при пересечении двух прямых. Они противоположны друг другу. Они имеют следующие характеристики:
- Вертикальные углы имеют одну и ту же вершину (общую угловую точку), но не могут иметь общую сторону.
- Вертикальные углы всегда равны друг другу в градусах и поэтому называются конгруэнтными углами.
Использование
Вертикальные углы используются во многих сценариях реальной жизни.
 Например:
Например:- Знаки перехода через железнодорожные пути, обнаруженные на проезжей части вблизи железных дорог
- Письмо Х.
- Открытые ножницы
- В воздушном змее, который держится на двух деревянных палках.
- Точка пересечения потолочных балок в форме буквы X.
- В некоторых конструкциях полов линии пересекаются, образуя вертикальные углы.
- Пересекающиеся линии на мишени для дротиков образуют 10 пар вертикальных углов. Вершиной служит бычий глаз в центре доски.
Важность
Вертикальные углы являются важной частью геометрии.
Они чрезвычайно важны в треугольниках, углах, образованных между двумя параллельными прямыми и секущей, а иногда также полезны при решении вопросов, связанных с подшипниками.
Вертикальный угол
ФормулаЕсли углы вертикальные, то они конгруэнтны, что означает, что они равны в градусах. Если две прямые пересекаются под углом 90°, то вертикальные углы являются дополнительными углами.
 Вертикальные углы в перпендикулярных линиях в сумме составляют 180,
Вертикальные углы в перпендикулярных линиях в сумме составляют 180,Вертикальные углы не являются дополнительными, если линии не перпендикулярны друг другу. Как известно, при пересечении двух прямых они образуют четыре угла. Обе пары вертикальных углов (всего четыре угла) всегда дают в сумме полный угол 360.
Вертикальные углы конгруэнтны?
Да, Вертикальные углы всегда конгруэнтны , то есть равны по мере. Вертикальные углы — это несмежные углы, они имеют одну вершину, но не один и тот же луч, поэтому они равны по размеру.
Вертикальный угол
ПримерыПример 1
На приведенном выше рисунке пересекаются две линии. Четыре угла образованы этим пересечением двух линий.
∠a и ∠d являются смежными углами, а ∠c и ∠b также являются смежными углами, поскольку они имеют общий луч. ∠a и ∠b — несмежные углы, а ∠c и ∠d — также несмежные углы, поскольку они не имеют общего луча.
Как мы знаем, вертикальные углы — это пара несмежных углов, образованных двумя пересекающимися прямыми, поэтому ∠a и ∠b — одна пара вертикальных углов, а ∠c и ∠d — вторая пара вертикальных углов.

Вертикальные углы всегда равны. Следовательно, на приведенном выше рисунке:
∠a = ∠b
∠c = ∠d
Пример 2
На приведенном выше рисунке прямые AD и прямые BC пересекаются друг с другом в точке O. Четыре угла равны сформировалась в этот момент.
«О» — вершина. ∠AOB и ∠COD — несмежные углы и вертикальные углы. Есть равные по мере 70°. Точно так же ∠AOC и ∠BOD являются несмежными углами и являются вертикальными углами.
Есть равные по размеру 110°. ∠AOB и ∠COD — одна пара вертикальных углов. Они конгруэнтны.
∠AOB = ∠COD
∠AOC и ∠BOD — еще одна пара вертикальных углов. Они также конгруэнтны.
∠AOC = ∠BOD В сумме некоторые из них составляют полный угол 360°.
↑AOB + ↑COD + ↑AOC + ↑BOD = 360 °
70 ° + 70 ° + 110 ° + 110 ° = 360 °
Расчет вертикальных углов
Пример 1
9002. , ∠b и ∠cРешение: ∠b и 47° — вертикальные углы, поэтому они равны.

∠b = 47°
∠a и ∠c также являются вертикальными углами, поэтому они равны.
∠a = ∠c
Предположим, что они равны x°
∠a = ∠c = x°
Суммарно их сумма равна полному углу 360°
∠a + ∠cb + ∠ + 47° = 360°
x° + x° + 47° + 47° = 360°
2x° = 266°
x = 133
∠a = 133°, ∠b = 47°, ∠c = 133°
Пример 2Найдите x, следовательно, найдите угол 5x.
Решение: 5x и 2x + 24 — вертикальные углы, поэтому они равны.
5x = 2x + 24
Вычесть 2x с обеих сторон
3x = 24
Разделить обе стороны на 3
x = 8
Следовательно, угол 5x = 5(8) = 40°.
Вертикальные углы
Учащиеся смогут узнать и понять, что такое вертикальные углы, а также как вычислять вертикальные углы с помощью решенных примеров, интересных фактов и ответов на наиболее часто задаваемые вопросы о вертикальных углах.
 Прежде чем мы узнаем о вертикальных углах, давайте сначала разберемся с несколькими основными понятиями, которые также важно понимать.
Прежде чем мы узнаем о вертикальных углах, давайте сначала разберемся с несколькими основными понятиями, которые также важно понимать.Что такое пересекающиеся линии?
Когда две или более прямых пересекают друг друга на плоскости, они называются пересекающимися прямыми. Все пересекающиеся линии будут встречаться друг с другом в одной точке, поскольку они пересекают друг друга, эта общая точка на пересекающихся линиях называется точкой пересечения или точкой пересечения.
Свойства пересекающихся линий
Всегда будет одна общая точка, даже если есть две или более линий, пересекающих друг друга. Эти линии могут пересекаться друг с другом под любым углом, но угол всегда больше 0° и меньше 180°. Эти две пересекающиеся прямые, пересекающиеся друг с другом на плоскости, образуют пару вертикальных углов и имеют общую вершину или общую точку пересечения.
Например, ножницы имеют два конца, и эти два конца образуют пересекающиеся линии, имеющие общую точку пересечения.
 Перекрестки также являются отличным примером пересекающихся линий, поскольку это две разные дороги, пересекающиеся в одной точке.
Перекрестки также являются отличным примером пересекающихся линий, поскольку это две разные дороги, пересекающиеся в одной точке.Интересные факты о пересекающихся линиях
Если есть линия, которая пересекает более одной точки или пересекает более одной точки, это не прямые линии, а изогнутые линии.
Когда две линии пересекаются под углом 90 градусов, проведенные в одной плоскости, они называются перпендикулярными линиями. Перпендикулярные прямые являются исключительным случаем пересекающихся прямых.
Что такое параллельные линии?
Параллельные прямые противоположны пересекающимся. Там, где пересекающиеся прямые пересекаются, параллельные прямые не пересекаются на плоскости и находятся на одинаковом расстоянии друг от друга. Параллельные линии могут быть горизонтальными, вертикальными или даже диагональными линиями.
Свойства параллельных линий
Например, линии, которые мы видим в наших тетрадях, являются параллельными линиями.
 Они не встречаются друг с другом и также находятся на равном расстоянии друг от друга. Точно так же железнодорожные пути и пешеходный переход также являются примерами параллельных линий.
Они не встречаются друг с другом и также находятся на равном расстоянии друг от друга. Точно так же железнодорожные пути и пешеходный переход также являются примерами параллельных линий.Интересные факты о параллельных линиях
Каждая линия может иметь несколько параллельных линий. Нет установленных номеров для идентификации параллельной линии. Если линии не пересекаются и находятся на одинаковом расстоянии, они параллельны.
Даже если вы продолжите параллельную линию, вы можете делать это бесконечно, и они все равно не встретятся и не пересекутся ни в одной точке.
Что такое дополнительные и дополнительные углы?
Углы можно разделить на два основных типа на основе вращения и на основе их величины. Помимо этих двух основных типов углов у нас также есть еще одна основная категория углов, называемая дополнительными и дополнительными углами.
Дополнительные углы всегда будут иметь сумму 180° для двух углов.
 Тогда как в дополнительных углах сумма двух углов будет 90 °.
Тогда как в дополнительных углах сумма двух углов будет 90 °.Что такое вертикальные углы?
В геометрии при пересечении двух прямых образуются четыре угла. Вертикальные углы — это углы, которые противоположны друг другу. Любые две пересекающиеся прямые образуют две пары вертикальных углов, противоположных друг другу.
Углы, противоположные друг другу при пересечении двух прямых, называются вертикальными углами.
Термин «Вертикальный» в данном случае означает, что они имеют одну и ту же вершину или одну и ту же (угловую точку).
Пример: Загружено в ближайшее время)
Интересно, что вертикальные углы равны:
Угол A ° = Угол B °
Факты о вертикальных углах-
9 88888878
9 888888888888888888888888888888888888878 Congruent Congruent Congruent Congruent
88888888888888888888888888888878 Congruent Congruent Congruent.
 0538 Вертикальные углы всегда конгруэнтны, если они имеют одинаковую меру.
0538 Вертикальные углы всегда конгруэнтны, если они имеют одинаковую меру.Сумма вертикальных углов
Обе пары вертикальных углов (всего четыре угла) всегда дают в сумме 360 градусов.
Смежные углы
Углы каждой пары вертикальных углов называются смежными и являются дополнительными (сумма углов составляет 180 градусов).
Теорема о вертикальных углах-
Теорема о вертикальных углах утверждает, что вертикальные углы, т. е. углы, противоположные друг другу и образованные двумя пересекающимися прямыми, равны. Вертикальные углы всегда равны.
Все ли вертикальные углы равны?
Согласно теореме о вертикальном угле, как бы мы ни бросали карандаши, чтобы они пересеклись, или как бы ни пересекались любые две пересекающиеся прямые, вертикальные (противоположные) углы всегда будут конгруэнтны, или, другими словами, равны друг другу.
 В математике это известно как теорема о вертикальных углах.
В математике это известно как теорема о вертикальных углах.Смежны ли вертикальные углы?
По определению вертикальные углы не могут быть смежными (рядом друг с другом). Поскольку вертикальные углы противоположны друг другу, они не могут быть рядом друг с другом. Смежные углы берут один угол из одной пары вертикальных углов, а другой угол берут из другой пары вертикальных углов.
Все ли вертикальные углы дополняют друг друга?
Углы, которые противоположны друг другу при пересечении двух прямых, называются вертикальными углами. Две пары вертикальных углов равны друг другу. Две пары соседних углов являются дополнительными, то есть углы в сумме составляют 180 градусов.
Будем рассматривать углы как а, так как вертикальные углы всегда равны, оба угла можно записать как 2а,
2а = 180° (дополнительные углы = 180°), а = 90°
Смежные углы всегда являются дополнительными тогда как вертикальные углы не всегда являются дополнительными.
 Если мы возьмем любые два смежных угла из четырех углов, образованных двумя пересекающимися линиями, то сумма этих двух смежных углов всегда будет равна 180°.
Если мы возьмем любые два смежных угла из четырех углов, образованных двумя пересекающимися линиями, то сумма этих двух смежных углов всегда будет равна 180°.Вот схема для лучшего понимания,
(изображение будет загружено в ближайшее время)
На приведенной выше диаграмме ∠x = 75° и ∠y = 105°.
Из диаграммы видно, что если два угла вертикальны, то они равны (конгруэнтны). Обратите внимание, что x и y являются дополнительными углами, которые в сумме составляют 180 градусов.
∠x +∠y = 105° + 75° = 180°
Вертикальные углы дополняют друг друга?
Дополнительные углы — это углы, которые в сумме дают 90 градусов. Будем рассматривать углы как а, так как вертикальные углы всегда равны, оба угла можно записать как 2а,
2a = 90° (дополнительные углы = 90°), a = 45°
Только когда вертикальные углы измеряют 45°, они могут быть дополнительными.

Что такое вертикальные или пересекающиеся линии?
Когда две линии встречаются в точке на плоскости, они называются пересекающимися линиями или вертикальными линиями. Параллельные прямые — это прямые, которые не пересекаются ни в одной точке плоскости. На приведенном ниже рисунке показаны параллельные прямые и пересекающиеся прямые.
(изображения будут загружены в ближайшее время)
Применение вертикальных углов
Мы видим или испытываем множество применений вертикальных углов в нашей повседневной жизни.
Для правильной работы американские горки располагаются под определенным углом. Эти углы настолько критичны, что если они сместятся на градус влево или вправо, может произойти авария. Максимальный вертикальный угол американских горок (Mumbo Jumbo, Flamingo Land) составляет 112 градусов.
На авиашоу мы видим два паровых следа, пересекающихся и образующих вертикальные углы.

Для безопасности автомобилистов на проезжей части установлены знаки железнодорожного переезда (Х).
Воздушный змей с двумя деревянными палками, перекрещивающимися друг с другом и удерживающими змея на месте.
Бычий глаз — это виртуальная вершина на мишени для дротиков, имеющая десять пар вертикальных углов.
Вопросы для решения по вертикальным углам-
Вопрос 1) Найдите значение x из приведенного ниже рисунка, когда значение y равно 75.
(изображение будет загружено в ближайшее время)
Решение) Значение угол y = 75° ,
Так как x и y являются дополнительными углами (Сумма дополнительных углов = 180°)
Следовательно, значение угла x равно
∠ x+∠y = 180⁰
∠ x = 180⁰- ∠y
∠ x = 180⁰- 75⁰
9053Вопрос 2) Найдите градусную меру углов a°, b° и c°:
(изображение скоро будет загружено)
Поскольку b° вертикально противоположно 40°, оно также должно быть 40° (как вертикальные углы конгруэнтны)
Полный круг равен 360°,
Значит,
360° − 2×40° = 280°
Угол a° и угол c° также являются вертикальными углами, поэтому они равны, что означает, что углы a и c равны 140° каждый.

Следовательно, углы измеряются: a = 140°, b = 40° и c = 140°.
Интересные факты!
Вертикальные углы образуют Х-образную форму.
Два смежных угла равны 180 градусам.
Вертикальные углы образованы двумя пересекающимися линиями.
Обе пары вертикальных углов в сумме дают 360 градусов.
Они имеют общую вершину (общую точку)
Заключение
Полное понимание концепций вертикальных углов в деталях с Решением вопросов также важно для футуристического обучения. Студенты могут пройти через понятия пересекающихся линий, дополнительных углов и многое другое. Вам следует внимательно обращаться к определениям и вопросам и понимать концепции, используемые для решения этих вопросов.
 Это очень поможет студентам на экзаменах.
Это очень поможет студентам на экзаменах.Как выглядят вертикальные углы?
от anstoall2021
Как выглядят вертикальные углы? Углы, противоположные друг другу при пересечении двух прямых. Они всегда равны. В этом примере a° и b° являются вертикальными углами. «Вертикаль» относится к вершине (где они пересекаются), а НЕ вверх/вниз.
Что является примером вертикального угла? Вертикальные углы являются дополнительными углами, когда прямые пересекаются перпендикулярно. Например, ∠W и ∠Y — вертикальные углы, которые также являются дополнительными углами. Точно так же ∠X и ∠Z являются дополнительными вертикальными углами.
Сумма вертикальных углов равна 180? Факты о вертикальных углах. Вертикальные углы всегда конгруэнтны, если они имеют одинаковую меру. Обе пары вертикальных углов (всего четыре угла) всегда дают в сумме 360 градусов.
 Углы от каждой пары вертикальных углов называются смежными углами и являются дополнительными (сумма углов составляет 180 градусов).
Углы от каждой пары вертикальных углов называются смежными углами и являются дополнительными (сумма углов составляет 180 градусов).Каков вертикальный угол ∠ 4? Нахождение мер углов
Углы 1 и 2 представляют собой линейную пару, поэтому их сумма составляет 180 градусов; следовательно, угол 2 равен 180 – 115 = 65 градусов. Угол 4 равен 65 градусам, потому что углы 2 и 4 представляют собой пару вертикальных углов.
Содержание
- 1 Как выглядят вертикальные углы? – Связанные вопросы
- 1.1 Вертикальные углы равны 90°?
- 1.2 Вертикальные углы равны друг другу?
- 1.3 Что должны иметь вертикальные углы?
- 1.4 Равны ли вертикальные углы в окружности?
- 1.5 В чем разница между горизонтальным и вертикальным?
- 1.6 Что означает вертикальный угол?
- 1.7 Какие вертикальные углы никогда?
- 1.8 Какой тип пары углов 1 и 3?
- 1.9 Почему вертикальные углы никогда не бывают смежными?
- 1.
 10 Могут ли вертикальные углы быть прямыми?
10 Могут ли вертикальные углы быть прямыми? - 1.11 Почему вертикальные углы всегда равны?
- 1.12 Какие два угла в сумме дают 90 градусов?
- 1.13 В чем разница между конгруэнтными углами и вертикальными углами?
- 1.14 Что такое горизонтальный и вертикальный угол?
- 1.15 Как выглядят односторонние внутренние углы?
- 1.16 Какие существуют типы вертикальных углов?
- 1.17 Вертикально вверх или вниз?
- 1.18 Что является примером вертикальных отношений?
- 1.19 Как называются вертикально противоположные углы?
- 1.20 Какая линия вертикальная?
- 1.21 Всегда ли вертикальные углы являются дополнительными?
Вертикальные углы равны 90?
Вертикальные углы — это углы, которые противоположны друг другу при пересечении двух прямых. Две пары противоположных углов равны друг другу. Две пары соседних углов являются дополнительными, то есть в сумме они составляют 180 градусов.
 Дополнительными углами называются два угла, сумма которых равна 9.0 градусов.
Дополнительными углами называются два угла, сумма которых равна 9.0 градусов.Вертикальные углы равны между собой?
Вертикальные углы образуются, когда две прямые пересекаются в одной точке. Они всегда равны друг другу. Другими словами, всякий раз, когда две прямые пересекаются или пересекаются друг с другом, образуются 4 угла.
Какие должны быть вертикальные углы?
Вертикальные углы всегда конгруэнтны — они всегда имеют одну и ту же меру угла. Если один угол равен 40 градусов, вертикальный угол напротив него также будет равен 40 градусам. Поскольку они также вертикальны, они должны иметь одинаковую меру угла.
Вертикальные углы в окружности равны?
Если две хорды пересекаются внутри окружности, то мера образуемого угла равна половине суммы меры дуг, пересекаемых углом, и его вертикального угла. В окружности две хорды ¯PR и ¯QS пересекаются внутри окружности. Поскольку вертикальные углы равны, m∠1=m∠3 и m∠2=m∠4.
В чем разница между горизонтальной и вертикальной?
Вертикальная линия — это любая линия, параллельная вертикальному направлению.
 Горизонтальная линия — это любая линия, перпендикулярная вертикальной линии. Горизонтальные линии не пересекаются. Вертикальные линии не пересекаются.
Горизонтальная линия — это любая линия, перпендикулярная вертикальной линии. Горизонтальные линии не пересекаются. Вертикальные линии не пересекаются.Что означает вертикальный угол?
: любой из двух углов, лежащих по разные стороны от двух пересекающихся прямых.
Какие вертикальные углы никогда?
никогда. Вертикальные углы имеют общую вершину. всегда. Точка снаружи одного из двух вертикальных углов находится внутри другого.
Какой тип пары углов 1 и 3?
Эти пары называются вертикальными углами, и они всегда имеют одинаковую меру. ∠1 и ∠3 — вертикальные углы.
Почему вертикальные углы никогда не бывают смежными?
Если два угла имеют общую вершину и общую сторону, они называются смежными углами. При пересечении двух прямых образуются вертикальные углы, которые также являются несмежными углами. Имеются две пары вертикальных углов. Эти углы также имеют общую вершину, но никогда не имеют общей стороны.
Могут ли вертикальные углы быть прямыми?
Объяснение: Вертикальные углы образованы двумя пересекающимися линиями.
 В одном частном случае, когда вертикальные углы являются прямыми углами (т. е. линии, образующие эту пару вертикальных углов, перпендикулярны), их сумма равна прямому углу и, следовательно, они являются дополнительными.
В одном частном случае, когда вертикальные углы являются прямыми углами (т. е. линии, образующие эту пару вертикальных углов, перпендикулярны), их сумма равна прямому углу и, следовательно, они являются дополнительными.Почему вертикальные углы всегда равны?
Несмежные углы называются вертикальными или противоположными . Кроме того, каждая пара смежных углов образует прямую линию, и эти два угла являются дополнительными. Поскольку любой из пары вертикальных углов является дополнительным к любому из соседних углов, вертикальные углы равны по величине или размеру.
Какие два угла в сумме дают 90 градусов?
Два угла называются дополнительными, если сумма их величин равна 90 градусов.
В чем разница между конгруэнтными углами и вертикальными углами?
Когда две прямые пересекаются, они образуют две пары противоположных углов, A + C и B + D. Другое название противоположных углов — вертикальные углы. Вертикальные углы всегда конгруэнтны, что означает, что они равны.
 Смежные углы – это углы, выходящие из одной вершины.
Смежные углы – это углы, выходящие из одной вершины.Что такое горизонтальный и вертикальный угол?
Горизонтальные углы используются для определения пеленгов и направлений при контрольных съемках, для определения местоположения деталей при картировании и для разметки всех типов сооружений. Вертикальные углы используются при определении высоты точек и для расчета поправок на уклон.
Как выглядят внутренние углы с одинаковыми сторонами?
Односторонние внутренние углы, образованные при пересечении двух параллельных прямых секущей. Внутренние углы одинаковых сторон могут быть равны только тогда, когда каждый угол равен 90 градусам, потому что тогда сумма внутренних углов одинаковых сторон равна 180 градусам.
Какие бывают типы вертикальных углов?
Резюме урока
В обзоре вертикальные углы — это углы, образованные пересечением двух прямых, в то время как альтернативные внутренние углы, альтернативные внешние углы, соответствующие углы и последовательные внутренние углы образуются пересечением двух прямых и поперечной.

Вертикально вверх или вниз?
Вертикаль описывает что-то, что поднимается прямо вверх от горизонтальной линии или плоскости. Термины «вертикальный» и «горизонтальный» часто описывают направления: вертикальная линия идет вверх и вниз, а горизонтальная — поперек. Вы можете запомнить, какое направление является вертикальным, по букве «v», которая указывает вниз.
Что является примером вертикальных отношений?
Вертикальные отношения — это отношения, в которых один из участников имеет большее положение, будь то благодаря силе и авторитету или знаниям и мудрости. Отношения бабушек и дедушек, родителей и детей являются наиболее распространенными. Эти семейные отношения также известны как отношения между поколениями.
Как называются вертикально противоположные углы?
Точка, в которой они встречаются, называется вершиной. При пересечении двух прямых противоположные углы (X) равны. На приведенной выше диаграмме два зеленых угла равны и два желтых угла равны.
 Эти углы X называются вертикально противоположными углами, потому что они противоположны друг другу в вершине.
Эти углы X называются вертикально противоположными углами, потому что они противоположны друг другу в вершине.Какая линия вертикальная?
В координатной плоскости линия, параллельная оси Y, называется вертикальной линией. Это прямая линия, идущая сверху вниз и снизу вверх. Любая точка на этой линии будет иметь одинаковое значение координаты x.
Всегда ли вертикальные углы являются дополнительными?
Вертикальные углы всегда конгруэнтны или равны. На рисунке выше угол от каждой пары вертикальных углов является смежным и дополнительным (добавьте к 180°).
#вертикаль #угол
Категории Ответить на всевертикальных углов | Что?, Определение, Теорема, Примеры
Что я узнаю из этой статьи?
Прочитав эту статью, вы сможете:
- определить вертикальный угол;
- сформулируйте теорему о вертикальном угле;
- доказать теорему о вертикальном угле;
- определяют вертикальные углы на разных фигурах; и
- решают задачи, связанные с вертикальными углами.

Что такое вертикальный угол?
Вертикальные углы представляют собой пары противоположных или несмежных углов, образованных пересечением двух различных линий. «Вертикальный» стал синонимом «вертикального» или полной противоположности горизонтальному. Однако в данном случае речь идет больше о термине «вершина». Вертикальные углы получили свое название из-за того, что они имеют общую вершину.
Вертикальные углы, говоря простым языком, расположены друг напротив друга в углах «X», образованных двумя прямыми линиями. Их также называют вертикально противоположными углами из-за того, что они расположены напротив друг друга.
Скажем, например,
На рисунке ∠1 вертикально напротив ∠3, а ∠2 вертикально напротив ∠4. Кроме того, мы можем заметить, что углы 1, 2, 3 и 4 имеют одну и ту же точку вершины.
Что такое теорема о вертикальном угле?
Теорема о вертикальном угле утверждает, что:
Если две пересекающиеся прямые образуют углы, противоположные друг другу, то они конгруэнтны.

Какое доказательство теоремы о вертикальном угле?
Евдем Родосский приписал Фалесу Милетскому доказательство теоремы о вертикальном угле. Предложение показало, что, поскольку обе пары вертикальных углов являются дополнительными к обоим смежным углам, вертикальные углы равны по мере.
Согласно исторической заметке, Фалес заметил, что когда египтяне чертили две пересекающиеся линии, они измеряли вертикальные углы, чтобы убедиться, что они равны. Фалес пришел к выводу, что можно установить, что все вертикальные углы равны, если принять некоторые общие положения, такие как:
- Все прямые углы равны.
- Равные, добавленные к равным, равны.
- Равные, вычтенные из равных, равны.
Чтобы доказать теорему о вертикальном угле, предположим, что ∠1 и ∠2 — два смежных угла, образующих прямую. Тогда по постулату линейной пары они дополняют друг друга.
Таким образом, ∠1 + ∠2=180°.
Аналогично, если ∠1 и ∠4 — два смежных угла, образующих прямую, ∠1 + ∠4=180°.

Тогда по транзитивному свойству равенства и исключения
∠1 + ∠2= ∠1 + ∠4
∠2=∠4Поскольку углы ∠1 и ∠3, ∠1 и ∠4 смежны углов, следует то же утверждение, что ∠1=∠3.
Что известно о вертикальных углах?
В таблице ниже приведены другие сведения о вертикальных углах.
Равные углы Вертикальные углы всегда равны. Сумма вертикальных углов Обе пары вертикальных углов (4 угла, имеющих одну и ту же вершину) всегда дают в сумме 360°. Смежные углы Смежные углы, образованные каждой парой вертикальных углов, являются дополнительными (сумма углов равна 180°). Как определить вертикальные углы?
Для определения вертикальных углов необходимо учитывать следующее?
- Линии прямые?
- Линии между ними пересекаются?
- Они находятся на одной линии?
- Углы имеют одну и ту же вершину?
См.
 примеры вертикально противоположных углов в таблице ниже.
примеры вертикально противоположных углов в таблице ниже.Пара вертикально противоположных углов Не пара вертикальных углов
∠1 и ∠2 являются парой вертикальных углов, так как они имеют одну вершину и противоположны друг другу.
∠5 и ∠6 не являются парой вертикальных углов, поскольку они не противоположны друг другу, даже если имеют одну и ту же вершину. Однако ∠5 и ∠6 — это пара смежных углов.
∠3 и ∠4 являются парой вертикальных углов, так как они имеют одну вершину и противоположны друг другу.
∠7 и ∠8 не являются парой вертикальных углов, потому что, хотя они противоположны друг другу и имеют одну и ту же вершину, две пересекающиеся линии не являются прямой линией.Пример #1
Назовите пару вертикальных углов, представленных на рисунке ниже.

Решение
Даны прямые A и B, которые пересекаются в точке P, пара вертикальных углов равна:
Как показано на рисунке, мы можем назвать углы, образованные при пересечении двух прямых. Таким образом,
- ∠1 вертикально противоположно ∠2; а
- ∠3 вертикально противоположна ∠4 с той же вершиной в точке P.
Пример #2
Назовите углы, образованные при пересечении прямых N и P с прямыми L и M. Определите пары вертикальных углов на рисунке ниже.
Решение
Как показано на рисунке, когда линии N и P пересекаются с линиями L и M, создаются 4 точки вершины. Таким образом, мы можем назвать созданные углы как:
Следовательно, исходя из показанного рисунка,
- ∠A вертикально противоположно углу ∠C;
- ∠B вертикально противоположен углу ∠D;
- Углы A, B, C и D имеют одну вершину;
- ∠E вертикально противоположен углу ∠H;
- ∠G вертикально противоположен углу ∠F;
- Углы E, F, G и H имеют одну вершину;
- ∠I вертикально противоположен углу ∠J;
- ∠K вертикально противоположен углу ∠O;
- Углы I, J, K и O имеют одну вершину;
- ∠S вертикально противоположен углу ∠T;
- ∠U вертикально противоположен углу ∠V; и
- Углы S, T, U и V имеют одну вершину.

Как мы решаем задачи, связанные с вертикальными углами?
Для решения задач, связанных с вертикальными углами,
- Определите пары вертикальных углов.
- Используйте теорему о вертикальном угле, чтобы связать отношения между мерами вертикальных углов.
Пример #1
Определите значение x и угловые меры двух углов, если эти два угла являются вертикальными углами.
Решение
Шаг 1: Найдите значение x. Поскольку два заданных угла называются вертикальными, то по теореме о вертикальном угле:
2x – 13 = x + 17
2x – x = 17 + 13
x = 30Шаг 2: Таким образом, значение x равно 30. Подстановкой мера двух углов равна:
- , если ∠=2x-13, то
2x – 13 = 2 (30) – 13
= 60 – 13
= 47- если ∠=x+17, то
x + 17 = 30 + 17
= 47Так как оба угла равны 47°, то верно, что они вертикально противоположны друг другу.

Следовательно, значение x равно 30, а угловая мера вертикально противоположного угла равна 47°.
Пример #2Если флаг Ямайки образует пары вертикально противоположных углов, каково значение x на основе данной цифры?
Решение
Шаг 1: Найдите значение x. Поскольку образованные углы вертикально противоположны друг другу, то по теореме о вертикальном угле
65° = 2x + 15°
2x = 65° – 15°
2x = 50°
$\frac{2x}{2} = \frac{(50°)}{2}$
x = 25°Шаг 2: Проверьте, даст ли 2x + 15 65°, если мы подставим x = 25. Таким образом,
2x + 15 = 2(25) + 15
= 50 + 15
= 65Следовательно, значение х равно 25°.
Обратите внимание:
- Вертикальные углы всегда имеют одну и ту же вершину.
- Вертикальные углы всегда равны.
- Вертикальные углы всегда несмежны.
Какое значение имеют вертикальные углы?
Реальные настройки, в которых используются вертикальные углы, включают в себя;
- знак железнодорожного переезда,
- буква « X » и
- открытые плоскогубцы-ножницы.

Вертикальные углы также можно найти, когда человек скрещивает руки в форме буквы X, и их также очень легко найти в дизайне полов, где линии пересекаются, образуя пару вертикальных углов. Еще один очень распространенный реальный пример вертикально противоположных углов — это пересекающиеся линии мишени для дротиков, которые помогают создать десять пар вертикальных углов.
Рекомендуемые рабочие листы
Понимание дополнительных, дополнительных, вертикальных и прилегающих углов. Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Вертикальные углы (что это такое и почему они равны)
Вертикальные углы — это просто вертикально противоположные углы, образованные при пересечении двух прямых в одной точке, которую мы называем вершиной. Это один из первых типов углов, которые вы изучите в геометрии, и в конечном итоге вы будете работать с более сложными темами.
 Поняв определение и свойства вертикальных углов, вы получите доступ к большему количеству свойств, приложений и инструментов.
Поняв определение и свойства вертикальных углов, вы получите доступ к большему количеству свойств, приложений и инструментов.В этой статье мы рассмотрим основы, необходимые для определения вертикальных углов на данной диаграмме. Мы также покажем вам, почему вертикальные углы равны, и продемонстрируем методы, необходимые для нахождения неизвестных величин вертикальных углов.
Что такое вертикальные углы?
Вертикальные углы — это две пары противоположных углов, образованные при пересечении двух прямых в одной вершине. Каждая пара вертикальных углов всегда будет равна друг другу. Вот пример двух пар вертикальных углов, образованных пересекающимися прямыми m и n.
Эти две линии образуют форму «X», а пары углов, обращенных друг к другу, называются вертикальными углами. Это означает, что каждая пара углов будет иметь одинаковую меру:
\begin{выровнено}\угол 1 &= \угол 2\\\угол 3 &= \угол 4 \end{выравнивание}
Некоторые примеры реальных объектов, образующих вертикальные углы: 1) знаки перекрестка, подобные показанному ниже, и 2) вертикальные углы, образованные парой открытых ножниц.
 В точке пересечения или точки поворота пересекающиеся линии образуют вертикальные углы, где каждая пара всегда будет равна.
В точке пересечения или точки поворота пересекающиеся линии образуют вертикальные углы, где каждая пара всегда будет равна.Мы показали вам основное определение и концепцию, которые вам необходимо знать о вертикальных углах. Прежде чем мы углубимся в более сложные примеры и проблемы, давайте попробуем определить вертикальные углы на разных примерах.
Задача 1
Запишите все пары вертикальных углов, которые вы можете найти на следующих рисунках.
Напомним, что вертикальные углы — это противоположные углы, встречающиеся на пересечении двух пересекающихся прямых.
Давайте сначала сосредоточимся на верхней половине нашей диаграммы: мы видим две пересекающиеся линии, образующие четыре угла. Определите пары вертикальных углов, обращенных друг к другу, таким образом, мы имеем следующие вертикальные углы:
\begin{выровнено}\угол a &= \угол d\\\угол b &= \угол c \end{выровнено}
Теперь примените аналогичный процесс, чтобы найти вертикальные углы, указанные в нижней половине диаграммы.
 Отсюда имеем следующие вертикальные углы:
Отсюда имеем следующие вертикальные углы:\begin{выровнено}\угол e &= \угол h\\\угол f &= \угол g \end{выровнено}
Это означает, что из диаграммы мы можем назвать четыре пары вертикальных углов:
- \угол a и \угол d
- \угол b и \угол c
- \угол e и \угол h
- \угол f и \угол g
Понимание теоремы о вертикальном угле и ее доказательство
К этому моменту вы уже знаете, что когда углы вертикальны, их меры равны. Это утверждение фактически является теоремой о вертикальном угле. Согласно теореме, когда два противоположных угла имеют общую вершину, образованную двумя пересекающимися прямыми, их угловые меры всегда будут равны.
«Вертикальные углы всегда равны».
Доказать эту теорему несложно — нам просто нужно применить свойство линейных углов и свойство транзитивности в математике. Начнем с того, что поскольку это прямые, то сумма углов, образующих прямую, всегда будет равна 180 или .

Это означает, что мы имеем следующие уравнения:
\угол 1 + \угол 4 = 180\градус \угол 1 + \угол 3 = 180\градус
Теперь, по свойству транзитивности (a =b и b =c, тогда 1 =c), мы можем приравнять правые части каждого из уравнений друг к другу.
\begin{align}\угол 1 + \угол 4 &= 180\градус\\\угол 1 + \угол 3 &= 180\градус\\\угол 1 + \угол 4 &= \угол 1 + \угол 3\ \\угол 4 &= \угол 3 \end{выровнено}
Таким образом, мы показали, что пара вертикальных углов \угол 3 и \угол 4 равны, что подтверждает половину теоремы о вертикальном угле. Мы просто применяем тот же процесс, чтобы подтвердить, что \угол 1 = \угол 2. Это устанавливает теорему о вертикальном угле и подтверждает, что каждая пара вертикальных углов имеет одинаковую угловую меру.
Как использовать вертикальные углы?
Мы можем применить определение и свойства вертикальных углов для решения текстовых задач и поиска неизвестных углов на данной диаграмме.
 При использовании вертикальных углов помните о следующих указателях:
При использовании вертикальных углов помните о следующих указателях:- Сначала подтвердите, являются ли два угла, над которыми мы работаем, вертикальными углами.
- Вертикальные углы всегда равны.
При решении задач, связанных с вертикальными углами, определите меры вертикальных углов, затем приравняйте их друг к другу, чтобы найти неизвестные. В этом разделе мы сосредоточимся на других примерах задач, связанных с вертикальными углами.
Задача 2
Определите величины трех углов: \{\угол 1, \угол 2, \угол 3\}.
Во-первых, давайте найдем меру угла 1, используя тот факт, что он образует прямую с углом 4 = 80 градусов. Это означает, что они имеют общую сумму 180\степень.
\begin{выровнено} \угол 1 + \угол 4 &= 180\градус \,\,{\color{Орхидея} \text{Линейные углы}}\\\угол 1 + 80\градус &= 180\градус\\ \угол &- 180\градус – 80\градус\\&=100\градус \конец{выровнено}
Поскольку прямые a и b являются пересекающимися прямыми, они образуют две пары вертикальных углов: \угол 1 и \угол 2, а также \угол 3 и \угол 4.
 Это означает, что каждая пара вертикальных углов будет иметь одинаковую меру.
Это означает, что каждая пара вертикальных углов будет иметь одинаковую меру.\begin{выровнено} \угол 1 &= \угол 2\\&= 100\градус\\\угол 3 &= \угол 4\\&= 80\градус \end{выровнено}
На самом деле мы будем использовать аналогичный мыслительный процесс при решении более сложной задачи, связанной с вертикальными углами.
Задача 3
Предположим, что прямые \overline{AB} и \overline{CD} пересекаются друг с другом в точке O. Если \угол ВОС = 140\градус, какова угловая мера угла АОС?
Первым шагом при решении подобных задач является набросок диаграммы, показывающей наши углы и представленной так, как показано ниже.
Мы знаем, что \угол ВПК и \угол ВОС являются линейными углами и образуют прямую, поэтому \угол ВПК + \угол ВОС = 180\градус . Так как \угол ВОС = 140\градус, то имеем:
\begin{align} \угол БПК + \угол ВОС &= 180\градус\\\угол БПК + 140\градус&= 180\градус\\\угол БПК&= 180-140\градус\\&=40\градус \end {выровнено}
Теперь мы знаем, что \угол BOD и \угол AOC являются вертикальными углами, поэтому их угловые меры должны быть равны.
 Это означает, что \угол AOC также должен быть равен 40\градусам.
Это означает, что \угол AOC также должен быть равен 40\градусам.Бывают случаи, когда мы решаем задачу по алгебре, в которой участвуют углы, особенно вертикальные углы. Используйте тот же метод при определении вертикальных углов и приравняйте соответствующие вертикальные углы, чтобы найти любые неизвестные значения. Вот несколько примеров задач, над которыми вы можете поработать, чтобы проверить свое понимание.
Задача 4
Определите значение неизвестных для каждой из диаграмм, показанных ниже.
а.
Поскольку две прямые пересекаются друг с другом, образуя две пары вертикально противоположных углов. Это означает, что каждая пара вертикальных углов будет иметь одну и ту же меру.
Нам нужно сосредоточиться только на паре вертикальных углов, содержащих наше неизвестное значение: меры 4x и 6x -12 будут равны. Приравняйте каждое алгебраическое выражение, затем найдите x.
\begin{align} 6x — 12 &= 4x\\ 6x — 4x &= 12\\2x &= 12\\\dfrac{2x}{2} &= \dfrac{12}{2}\\x&= 6 \end{выровнено}
Это означает, что x равно 6.

b.
На этот раз нам дано два неизвестных. Не волнуйтесь, мы применим аналогичный подход, чтобы найти значения x и y. Во-первых, давайте определим пары вертикальных углов на диаграмме:
- \угол DOB = \угол AOC
- \угол AOD = \угол BOC
Теперь приравняйте алгебраические выражения, соответствующие каждому из углов, затем решите два полученных уравнения. В таблице ниже приведены шаги по нахождению x и y.
\begin{aligned}\boldsymbol{x}\end{align} \begin{aligned}\boldsymbol{y}\end{align} \begin{align} \angle DOB & = \угол AOC\\12x + 5 &= 44 — x\\12x + x &= 44 — 5\\13x &= 39\\\dfrac{13x}{3} &= \dfrac{39}{3}\\x&= 3 \end{aligned} \begin{align} \angle AOD &= \angle BOC\\6y +24 &= 4y +56\\6y — 4y&= 56 — 24\\2y &= 12\\\dfrac{2y}{2} &= \dfrac{12}{2}\\y &= 6 \end{aligned } Следовательно, x = 3 и y = 6.
c.
На данный момент мы знаем, что у нас есть следующие пары вертикальных углов для показанной диаграммы.

- \угол DOB = \угол AOC
- \угол AOD = \угол BOC
Кроме того, линейные углы \угол DOB и \угол BOC будут иметь сумму 180\градусов.
\begin{выровнено} \угол DOB + \угол BOC &= 180\градус\\\угол DOB + 36\степень&= 180\градус\\\угол DOB&= 180-36\градус\\&=144\градус \end {выровнено}
Теперь давайте приравняем выражения каждой пары вертикальных углов, чтобы найти x и y. Это означает, что у нас есть два уравнения: x – 6 = 36 и 3y + 6 = 144. Решите уравнения, чтобы найти значения x и y.
\begin{aligned}\boldsymbol{x}\end{align} \begin{aligned}\boldsymbol{y}\end{align} \begin{aligned} \angle AOD & = \угол BOC\\x — 6 &= 36\\x&= 36 + 6\\x&= 42 \end{выровнено} \begin{выровнено}\угол AOD &= \угол DOB\\3y +6 & = 144\\3y&= 144 -6\\3y &= 138\\\dfrac{3y}{3} &= \dfrac{138}{3}\\y &= 46 \end{выровнено} Это показывает, что x = 42 и y = 46.


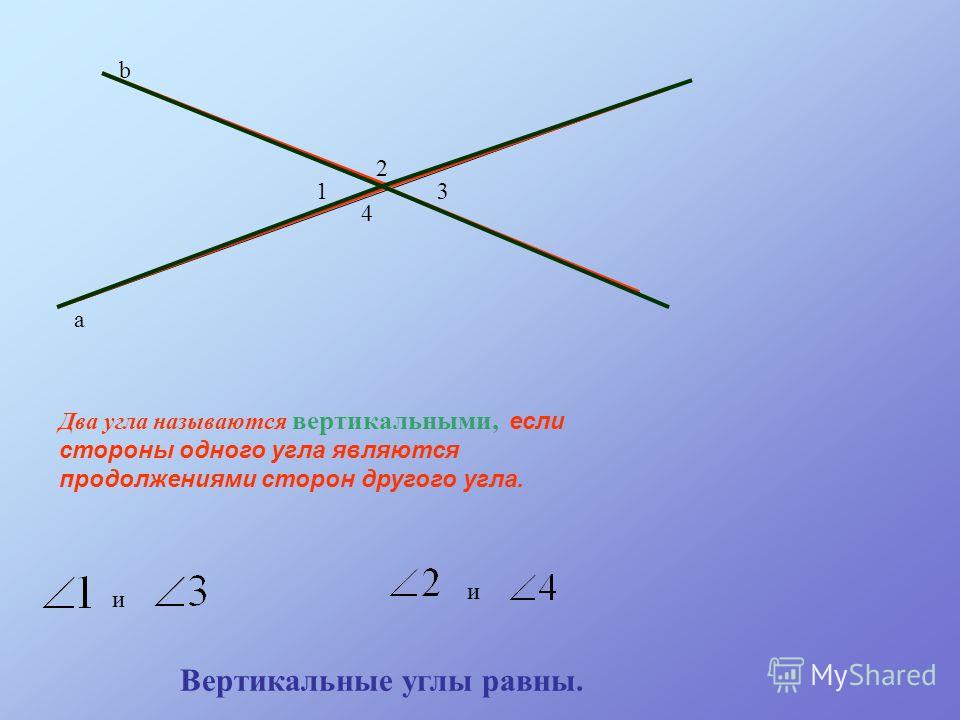
 Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
