Формула векторного произведения векторов: определения, свойства, формулы, примеры и решения

Содержание

определения, свойства, формулы, примеры и решения

Определение векторного произведения

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.

Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.

Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Определение 1

Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы a→ и b→ коллинеарны, он будет нулевым;
он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz

Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

антикоммутативность a→×b→=-b→×a→;
дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .

Пример 1

Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.

Решение

С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.

Ответ: 1522.

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.

Ответ: a→×b→=-2i→-2j→-2k→.

Пример 3

Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.

Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.

Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.

Ответ: i→-j→×i→+j→+k→=6. .

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.

Решение

Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.

Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→

Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→. .

Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..

Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.

По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.

Ответ: 3·a→-b→×a→-2·b→=60.

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Определение 3

Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Векторное произведение векторов. Определение и его смысл

Данная операция определена для двух пространственных векторов, пусть это будут нетленные буквы .

Обозначение: , существуют и другие варианты

И сразу вопрос: в чём отличие векторного произведения от произведения скалярного? Явное отличие, прежде всего, в РЕЗУЛЬТАТЕ:

– Результатом скалярного произведения векторов является ЧИСЛО:

– Результатом векторного произведения векторов является ВЕКТОР:
, то есть, умножаем векторы и получаем снова вектор.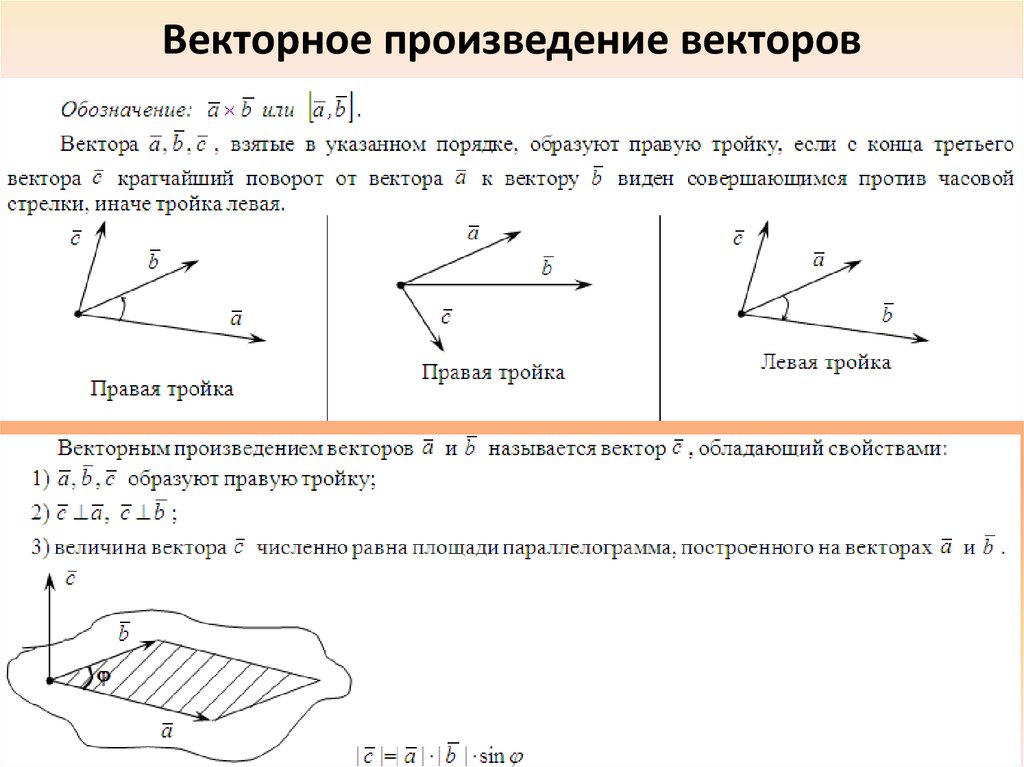

В учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .

Определение: векторным произведением неколлинеарных векторов , взятых в данном порядке, называется ВЕКТОР , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию.
Разберём определение «по косточкам»:

1) Исходные векторы , обозначенные красными стрелками, не коллинеарны.

2) Векторы взяты в строго определённом порядке: – «а» умножается на «бэ», а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .

3)Геометрический смысл векторного произведения. Это очень важный пункт! ДЛИНА «синего» вектора численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом. Длина «малинового» вектора , естественно, равна этой же площади.

Примечание: чертёж является схематическим, и поэтому номинальная длина векторного произведения не равна площади параллелограмма.

Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:

Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:

Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:

4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .

5) Вектор направлен так, что базис имеет правую ориентацию. Что это значит? Объяснять буду на пальцах вашей правой руки. Мысленно совместите указательный палец с вектором и средний палец с вектором , а безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет «смотреть» вверх. Это и есть правоориентированный базис (на рисунке именно он).
Теперь совместите указательный палец левой руки с тем же вектором , а средний – с вектором . При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис .
Говорят, что эти базисы ориентируют пространство в разные стороны, и это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало: если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом», ибо «лево» и «право» поменяются местами. Проверьте на собственном отражении!

Итак, определение разобрано и осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой, и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180 градусов равен нулю, а значит, и площадь нулевая

Таким образом, если , то с очевидной длиной . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.

Справедливо и обратное: если , то – и этот факт используют для проверки векторов на коллинеарность.

Частный случай – векторное произведение вектора на самого себя:

Ну что же, разжигаем огонь практики:

Задача 46

а) Найти длину векторного произведения векторов и , если .

б) Найти площадь параллелограмма, построенного на векторах и , если .

Нет, это не опечатка! – исходные данные в пунктах условия я намеренно сделал одинаковыми. Чтобы подчеркнуть отличие в решениях:

а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:

Для нахождения значений синуса удобно использовать соответствующую Тригонометрическую таблицу (см. Приложение Тригонометрия).

Ответ:

Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.

б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:

Ответ:

Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.

Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формируем чёткий ответ! В противном случае задание с высокой вероятностью вернётся на доработку, но это ещё не самое плохое. У рецензента может сложиться впечатление, что человек плохо разобрался в теме и его бы надо допросить с пристрастием :). Об этом нужно помнить, решая любую задачу по высшей математике, да и по другим предметам тоже.

Типовая задача для самостоятельного решения:

Задача 47

Найти площадь треугольника, построенного на векторах , если

Формула нахождения площади треугольника дана в комментариях к определению векторного произведения (см. выше). Решение и ответ в конце книги.

Для решения других задач нам понадобятся:

1.9.2. Свойства векторного произведения

1.8.4. Базис и система координат пространства

| Оглавление |

Автор: Aлeксaндр Eмeлин

04.

13. Векторное произведение векторов

Векторное произведение векторов

Так же, как и скалярное произведение, векторное произведение своим появлением обязано необходимости решения физических задач. Рассмотрим одну из таких – задачу о вычислении момента силы.

Принято считать моментом силы , приложенной в точке А относительно точки О, вектор , имеющий модуль, равный произведению модуля силы на кратчайшее расстояние (плечо силы) от этой точки до линий действия силы (рис 3.33). Если вектор связывает точку О с началом вектора , а – угол между векторами И , то .

Поэтому .

Вектор перпендикулярен плоскости, в которой лежат сила и точка О, и ориентирован в ту сторону, откуда вращение тела вокруг точки О видно как вращение, происходящее против часовой стрелки. Таким образом, двум векторным величинам И Ставится в соответствие тоже векторная величина. Это новый тип соответствия отличен от уже введенного скалярного произведения. Существуют разнообразные физические процессы, в которых соответствие между векторами осуществляется подобным образом. Вот почему в математике вводится еще одно действие умножения векторов – векторное произведение.

Рис. 3.33. Момент силы относительно точки О.

ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ вектора на вектор называется вектор , обозначаемый , обладающий следующими свойствами (рис. 3.34):

1. Его модуль равен произведению модулей данных векторов на синус угла между ними.

2. Он перпендикулярен плоскости, в которой располагаются данные векторы.

Рис. 3.34. Векторное произведение
векторов.

3. Его ориентация такова, что векторы , и образуют правую координатную тройку (то есть из конца вектора поворот от вектора до совмещения с вектором на кратчайший угол виден как поворот, осуществляемый против часовой стрелки).

По определению имеем:

Справедливо ли утверждение ?

Геометрически это означает, что равняется площади параллелограмма, построенного на векторах и как на сторонах.

Возвращаясь к задаче о вычислении момента силы, можно заключить, что

и .

Очевидно, что векторное произведение обращается в нуль , если векторы коллинеарны или же какой-нибудь из них нулевой.

Рассмотрим алгебраические свойства векторного произведения. Не все они сохраняются в том же виде, что и для скалярного произведения.

1. – антипереместительный закон.

Объясните физический смысл антипереместительного закона

Действительно, векторы и перпендикулярны одной и той же плоскости, в которой располагаются векторы и , но ориентированы в противоположные стороны, так как, если векторы , , образуют правую тройку, то векторы , , будут образовывать уже левую тройку векторов, что и доказывает данный закон.

2. – распределительный закон. Приведем его без доказательства.

3. – сочетательный закон относительно скалярного множителя.

Найти

Действительно, векторы и (рис. 3.35) имеют одинаковые модули. Их ориентация совпадает с ориентацией вектора , если , и противоположны ему при .

Рис. 3.35. Сочетательный закон для векторного
произведения векторов относительно скалярного
Множителя.

Очевидно, что векторный квадрат вектора равен нулю:

Получим формулы векторного произведения в координатном виде. Пусть даны векторы:

Поэтому

Векторные квадраты координатных ортов равны нулю:

А произведения определяются следующим образом:

Тогда

Эта запись может быть представлена в компактной форме с помощью определителя третьего порядка.

Определителем третьего порядка, составленного из таблицы девяти элементов

Называется выражение

Произведения элементов определителя, которые берутся со знаком плюс, символично для запоминания могут быть представлены следующей схемой:

Последние три слагаемых определителя, имеющие знак минус, получаются по другой схеме:

В курсе алгебры при решении систем линейных уравнений рассматриваются определители различных порядков, элементами которого чаще всего являются числа, а потому и определитель есть число.

Легко проверить справедливость формулы:

В заключение получим интересную формулу, связывающую скалярное и векторное произведения.

Так как

То очевидно соотношение:

Отсюда можно получить два полезных неравенства:

< Предыдущая		Следующая >

Векторное произведения. Векторное произведение — определения, свойства, формулы, примеры и решения

На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)

Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах

Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!

В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .

Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.

И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:

Результатом скалярного произведения векторов является ЧИСЛО:

Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .

Определение векторного произведения

Сначала будет определение с картинкой, затем комментарии.

Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:

Разбираем определение по косточкам, тут много интересного!

Итак, можно выделить следующие существенные моменты:

1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.

2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .

3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.

Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.

Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:

5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)

…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)

Векторное произведение коллинеарных векторов

Определение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая

Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.

Частный случай – векторное произведение вектора на самого себя:

С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.

Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.

Ну что же, разжигаем огонь:

Пример 1

а) Найти длину векторного произведения векторов , если

б) Найти площадь параллелограмма, построенного на векторах , если

Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!

а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:

Ответ :

Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.

Ответ :

Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.

Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.

Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.

Популярный пример для самостоятельного решения:

Пример 2

Найти площадь треугольника, построенного на векторах , если

Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.

На практике задача действительно очень распространена, треугольниками вообще могут замучить.

Для решения других задач нам понадобятся:

Свойства векторного произведения векторов

Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.

Для произвольных векторов и произвольного числа справедливы следующие свойства:

1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.

2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.

3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?

4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.

В качестве демонстрации рассмотрим коротенький пример:

Пример 3

Найти , если

Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:

(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.

(3) Дальнейшее понятно.

Ответ :

Пора подбросить дров в огонь:

Пример 4

Вычислить площадь треугольника, построенного на векторах , если

Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:

1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!

(1) Подставляем выражения векторов .

(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.

(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.

(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:

(5) Приводим подобные слагаемые.

В результате вектор оказался выражен через вектор, чего и требовалось достичь:

2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:

3) Найдём площадь искомого треугольника:

Этапы 2-3 решения можно было оформить и одной строкой.

Ответ :

Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:

Пример 5

Найти , если

Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)

Векторное произведение векторов в координатах , заданных в ортонормированном базисе , выражается формулой :

Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:

Пример 10

Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)

Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .

а) Найдём векторное произведение:

Таким образом, векторы не коллинеарны.

б) Найдём векторное произведение:

Ответ : а) не коллинеарны, б)

Вот, пожалуй, и все основные сведения о векторном произведении векторов.

Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.

Смешанное произведение векторов – это произведение трёх векторов :

Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.

Сначала опять определение и картинка:

Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.

Выполним рисунок. Невидимые нам линии прочерчены пунктиром:

Погружаемся в определение:

2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.

3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».

По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.

Примечание : чертёж является схематическим.

4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .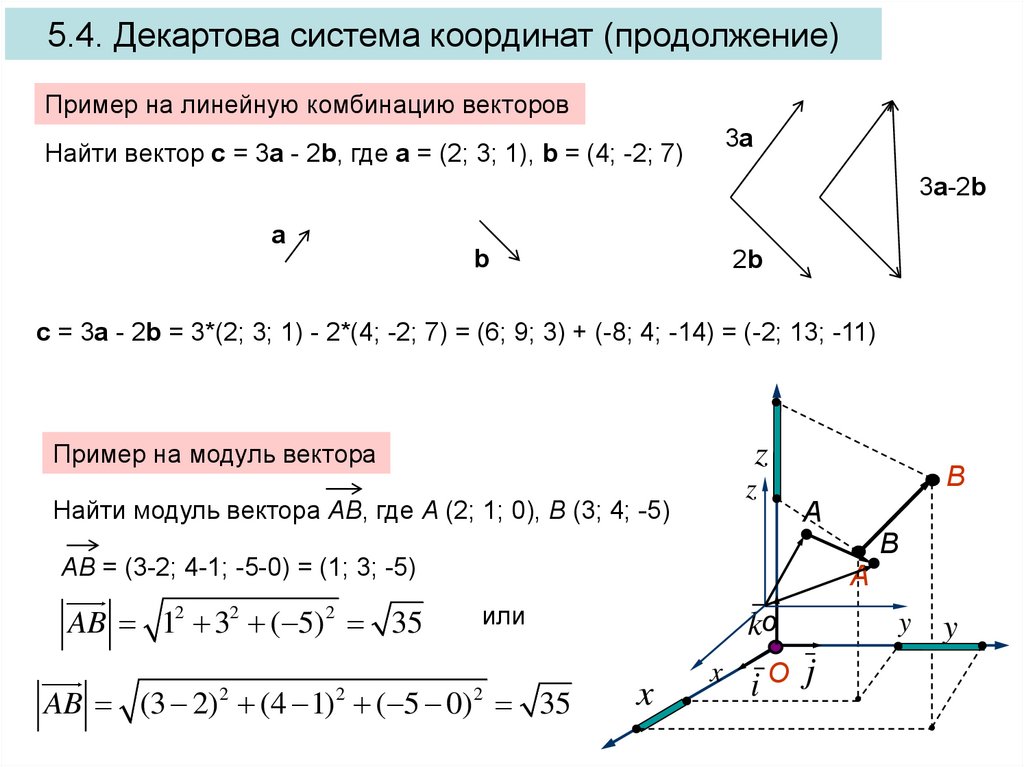

Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .

Yandex.RTB R-A-339285-1

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.

Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой , если по часовой стрелке – левой .

Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Определение 1

Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы a → и b → коллинеарны, он будет нулевым;
он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .

Координаты векторного произведения

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) называют вектор c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , где i → , j → , k → являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k →

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

антикоммутативность a → × b → = — b → × a → ;
дистрибутивность a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
ассоциативность λ · a → × b → = λ · a → × b → или a → × (λ · b →) = λ · a → × b → , где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = — i → j → k → b x b y b z a x a y a z = — b → × a → , что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

Пример 1

Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

Решение

С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Ответ: 15 2 2 .

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a → = (2 ; 1 ; — 3) , b → = (0 ; — 1 ; 1) . Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → = = (1 · 1 — (- 3) · (- 1)) · i → + ((- 3) · 0 — 2 · 1) · j → + (2 · (- 1) — 1 · 0) · k → = = — 2 i → — 2 j → — 2 k → .

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k → .

Ответ: a → × b → = — 2 i → — 2 j → — 2 k → .

Пример 3

Найдите длину векторного произведения векторов i → — j → и i → + j → + k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i → — j → × i → + j → + k → в данной прямоугольной системе координат.

Известно, что векторы i → — j → и i → + j → + k → имеют координаты (1 ; — 1 ; 0) и (1 ; 1 ; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → .

Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты (- 1 ; — 1 ; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6 .

Ответ: i → — j → × i → + j → + k → = 6 . .

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A (1 , 0 , 1) , B (0 , 2 , 3) , C (1 , 4 , 2) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.

Решение

Векторы A B → и A C → имеют следующие координаты (- 1 ; 2 ; 2) и (0 ; 4 ; 1) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи. Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .

Ответ: — 6 i → + j → — 4 k → . — один из перпендикулярных векторов.

Пример 5

Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → .

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b →

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b →

Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b → = — 6 · a → × b → — b → × a → . .

Из антикоммутативности векторного произведения следует — 6 · a → × b → — b → × a → = — 6 · a → × b → — (- 1) · a → × b → = — 5 · a → × b → . .

Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → — b → × a → — 2 · b → = = — 5 · a → × b → .

По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → — b → × a → — 2 · b → = — 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Ответ: 3 · a → — b → × a → — 2 · b → = 60 .

Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

Определение 3

Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

В этой статье мы подробно остановимся на понятии векторного произведения двух векторов. Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.

Навигация по странице.

Определение векторного произведения.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов в трехмерном пространстве.

Отложим векторы от одной точки. В зависимости от направления вектора тройка может быть правой или левой. Посмотрим с конца вектора на то, как происходит кратчайший поворот от вектора к . Если кратчайший поворот происходит против часовой стрелки, то тройка векторов называется правой , в противном случае – левой .

Теперь возьмем два не коллинеарных вектора и . Отложим от точки А векторы и . Построим некоторый вектор , перпендикулярный одновременно и и . Очевидно, что при построении вектора мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

В зависимости от направления вектора упорядоченная тройка векторов может быть правой или левой.

Так мы вплотную подошли к определению векторного произведения. Оно дается для двух векторов, заданных в прямоугольной системе координат трехмерного пространства.

Определение.

Векторным произведением двух векторов и , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор , что

Векторное произведение векторов и обозначается как .

Координаты векторного произведения.

Сейчас дадим второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов и.

Определение.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор , где — координатные векторы.

Это определение дает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора , а в третьей – координаты вектора в заданной прямоугольной системе координат:

Если разложить этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах (при необходимости обращайтесь к статье ):

Следует отметить, что координатная форма векторного произведения полностью согласуется с определением, данным в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.

Свойства векторного произведения.

Так как векторное произведение в координатах представимо в виде определителя матрицы , то на основании легко обосновываются следующие свойства векторного произведения :

Для примера докажем свойство антикоммутативности векторного произведения.

По определению и . Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому, , что доказывает свойство антикоммутативности векторного произведения.

Векторное произведение – примеры и решения.

В основном встречаются три типа задач.

В задачах первого типа заданы длины двух векторов и угол между ними, а требуется найти длину векторного произведения. В этом случае используется формула .

Пример.

Найдите длину векторного произведения векторов и , если известно .

Решение.

Мы знаем из определения, что длина векторного произведения векторов и равна произведению длин векторов и на синус угла между ними, поэтому, .

Ответ:

Задачи второго типа связаны с координатами векторов, в них векторное произведение, его длина или что-либо еще ищется через координаты заданных векторов и .

Здесь возможна масса различных вариантов. К примеру, могут быть заданы не координаты векторов и , а их разложения по координатным векторам вида и , или векторы и могут быть заданы координатами точек их начала и конца.

Рассмотрим характерные примеры.

Пример.

В прямоугольной системе координат заданы два вектора . Найдите их векторное произведение.

Решение.

По второму определению векторное произведение двух векторов в координатах записывается как:

К такому же результату мы бы пришли, если бы векторное произведение записали через определитель

Ответ:

Пример.

Найдите длину векторного произведения векторов и , где — орты прямоугольной декартовой системы координат.

Решение.

Сначала найдем координаты векторного произведения в заданной прямоугольной системе координат.

Так как векторы и имеют координаты и соответственно (при необходимости смотрите статью координаты вектора в прямоугольной системе координат), то по второму определению векторного произведения имеем

То есть, векторное произведение имеет координаты в заданной системе координат.

Длину векторного произведения находим как корень квадратный из суммы квадратов его координат (эту формулу длины вектора мы получили в разделе нахождение длины вектора):

Ответ:

Пример.

В прямоугольной декартовой системе координат заданы координаты трех точек . Найдите какой-нибудь вектор, перпендикулярный и одновременно.

Решение.

Векторы и имеют координаты и соответственно (смотрите статью нахождение координат вектора через координаты точек). Если найти векторное произведение векторов и , то оно по определению является вектором, перпендикулярным и к и к , то есть, является решением нашей задачи. Найдем его

Ответ:

— один из перпендикулярных векторов.

В задачах третьего типа проверяется навык использования свойств векторного произведения векторов. После применения свойств, применяются соответствующие формулы.

Пример.

Векторы и перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения .

Решение.

По свойству дистрибутивности векторного произведения мы можем записать

В силу сочетательного свойства вынесем числовые коэффициенты за знак векторных произведений в последнем выражении:

Векторные произведения и равны нулю, так как и , тогда .

Так как векторное произведение антикоммутативно, то .

Итак, с помощью свойств векторного произведения мы пришли к равенству .

По условию векторы и перпендикулярны, то есть угол между ними равен . То есть, у нас есть все данные для нахождения требуемой длины

Ответ:

Геометрический смысл векторного произведения.

По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки. Другими словами, длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.

Определение. Векторным произведением вектора а (множимое) на не коллинеарный ему вектор (множитель) называется третий вектор с (произведение), который строится следующим образом:

1) его модуль численно равен площади параллелограмма на рис. 155), построенного на векторах т. е. он равен направление перпендикулярно плоскости упомянутого параллелограмма;

3) при этом направление вектора с выбирается (из двух возможных) так, чтобы векторы с составляли правую систему (§ 110).

Обозначение: или

Дополнение к определению. Если векторы коллинеарны, то фигуре считая ее (условно) параллелограммом, естественно приписать нулевую площадь. Поэтому векторное произведение коллинеарных векторов считается равным нуль-вектору.

Поскольку нуль-вектору можно приписать любое направление, это соглашение не противоречит пунктам 2 и 3 определения.

Замечание 1. В термине «векторное произведение» первое слово указывает на то, что результат действия есть вектор (в противоположность скалярному произведению; ср. § 104, замечание 1).

Пример 1. Найти векторное произведение где основные векторы правой системы координат (рис. 156).

1. Так как длины основных векторов равны единице масштаба, то площадь параллелограмма (квадрата) численно равна единице. Значит, модуль векторного произведения равен единице.

2. Так как перпендикуляр к плоскости есть ось то искомое векторное произведение есть вектор, коллинеарный вектору к; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.

3. Из этих двух возможных векторов надо выбрать первый, так как векторы к образуют правую систему (а векторы левую).

Пример 2. Найти векторное произведение

Решение. Как в примере 1, заключаем, что вектор равен либо k, либо -k. Но теперь надо выбрать -k, так как векторы образуют правую систему (а векторы левую). Итак,

Пример 3. Векторы имеют длины, соответственно равные 80 и 50 см, и образуют угол 30°. Приняв за единицу длины метр, найти длину векторного произведения а

Решение. Площадь параллелограмма, построенного на векторах равна Длина искомого векторного произведения равна

Пример 4. Найти длину векторного произведения тех же векторов, приняв за единицу длины сантиметр.

Решение. Так как площадь параллелограмма, построенного на векторах равна то длина векторного произведения равна 2000 см, т. е.

Из сравнения примеров 3 и 4 видно, что длина вектора зависит не только от длин сомножителей но также и от выбора единицы длины.

Физический смысл векторного произведения. Из многочисленных физических величин, изображаемых векторным произведением, рассмотрим только момент силы.

Пусть А есть точка приложения силы Моментом силы относителько точки О называется векторное произведение Так как модуль этого векторного произведения численно равен площади параллелограмма (рис. 157), то модуль момента равняется произведению основания на высоту т. е. силе, умноженной на расстояние от точки О до прямой, вдоль которой действует сила.

В механике доказывается, что для равновесия твердого тела необходимо, чтобы равнялась нулю не только сумма векторов , представляющих силы, приложенные к телу, но также и сумма моментов сил. В том случае, когда все силы параллельны одной плоскости, сложение векторов, представляющих моменты, можно заменить сложением и вычитанием их модулей. Но при произвольных направлениях сил такая замена невозможна. В соответствии с этим векторное произведение определяется именно как вектор, а не как число.

Единичный вектор — это вектор , абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а , то его единичным вектором будет вектор а е. Этот единичный вектор направлен туда же, куда направлен и сам вектор а , и его модуль равен единице, то есть а е = 1.

Очевидно, а = а·а е (а — модуль вектора а) . Это следует из правила, по которому выполняется операция умножения скаляра на вектор .

Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

Напомню, что декартовой системой координат в пространстве традиционно называется тройка взаимно перпендикулярных осей, пересекающихся в точке, которая называется началом координат. Координатные оси обычно обозначают буквами X , Y , Z и называют соответственно осью абсцисс, осью ординат и осью аппликат. Сам Декарт пользовался только одной осью, на которой откладывались абсциссы. Заслуга использования системы осей принадлежит его ученикам. Поэтому фраза декартова система координат исторически ошибочна. Лучше говорить прямоугольная система координат или ортогональная система координат . Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же.

Единичный вектор , направленный вдоль оси Х, обозначается i , единичный вектор , направленный вдоль оси Y , обозначается j , а единичный вектор , направленный вдоль оси Z, обозначается k . Векторы i , j , k называются ортами (рис. 12, слева), они имеют единичные модули, то есть
i = 1, j = 1, k = 1.

Оси и орты прямоугольной системы координат в некоторых случаях имеют другие названия и обозначения. Так, ось абсцисс X может называться касательной осью, а ее орт обозначается τ (греческая строчная буква тау), ось ординат — осью нормали, ее орт обозначается n , ось аппликат — осью бинормали, ее орт обозначается b . Зачем менять названия, если суть остается той же?

Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k .

Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i , а τ . Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности — к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль — это одно и то же). Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это — бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.

Векторное произведение векторов | это… Что такое Векторное произведение векторов?

Содержание

1 Правые и левые тройки векторов
2 Определение
3 Свойства
- 3. 1 Геометрические свойства векторного произведения
- 3.2 Алгебраические свойства векторного произведения
- 3.3 Выражение для векторного произведения в декартовых координатах
4 Обобщения
- 4.1 Кватернионы
- 4.2 Преобразование к матричной форме
- 4.3 Распространение на матрицы
- 4.4 Размерности, не равные трём
5 Алгебра Ли векторов
6 См. также
7 Ссылки
8 Литература

Правые и левые тройки векторов

Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.

Тройка некомпланарных векторов называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.

Определение

Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:

длина вектора равна произведению длин векторов и на синус угла ; между ними

вектор ортогонален каждому из векторов и
вектор направлен так, что тройка векторов является правой.

Обозначение:

В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.

Свойства

Геометрические свойства векторного произведения

Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Модуль векторного произведения равняется площади S параллелограмма, построенного на приведённых к общему началу векторах и
Если — единичный вектор, ортогональный векторам и , а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:

Если — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости π и ортогональный к , — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости π вектора справедлива формула

Алгебраические свойства векторного произведения

(свойство антикоммутативности)
(свойство ассоциативности относительно умножения на скаляр)
(свойство дистрибутивности по сложению)
(тождество Якоби)
(формула «БАЦ минус ЦАБ», тождество Лагранжа)
. Это частный случай мультипликативности нормы кватернионов
; значение этого выражения называют смешанным произведением векторов a, b, c и обозначают либо .

Выражение для векторного произведения в декартовых координатах

Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе

то их векторное произведение имеет вид

Для запоминания этой формулы удобно использовать определитель:

или

где — символ Леви-Чивиты.

Обобщения

Кватернионы

Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.

Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор как кватернион a₁i + a₂j + a₃k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.

Преобразование к матричной форме

Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:

где

Пусть равен векторному произведению:

тогда

Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.

С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).

Из общих свойств векторного произведения следует, что

а так как кососимметрична, то

В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).

Распространение на матрицы

В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда

Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, , — векторы):

После этого можно изменить форму записи для векторного произведения:

E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:

где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:

Размерности, не равные трём

Пусть D — размерность пространства.

Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерности 3.

Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как

Такое обобщение дает гиперплощадь размерности (D − 1).

Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:

Эта конструкция называется внешним произведением.

Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.

Алгебра Ли векторов

Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.

См. также

Произведения векторов

Косое произведение векторов (2D)
Скалярное произведение векторов (2D и 3D)
Смешанное произведение векторов (3D)
Векторно-векторное произведение векторов (3D)

Другое

Ротор

Ссылки

Многомерное векторное произведение

Литература

Кочин Н. Е. Введение в векторный и тензорный анализ.

Векторное произведение векторов с примерами решения

Содержание:

Переходим к понятию векторного произведения
Некоторые приложения к механике векторов

В векторной алгебре наряду с умножением вектора на скаляр и скалярным произведением двух векторов определяется также векторное произведение двух векторов, к описанию которого мы переходим.

Напомним что поверхность в пространстве ориентирована, если указано, какая ее сторона считается внешней, а какая — внутренней. Принято считать, что если эта поверхность незамкнутая (т.е. с краем), то ориентация поверхности порождает также ориентацпю ее контура, т.е.

направление его обхода. Обратно, если указывается направление обхода контура, это приводит к ориентации самой поверхности. Связь между ориентацией поверхности и ориентацией ее контура указана па рис. 134; если за основу системы координат взята правая тройка векторов (т. е. такая тройка, что, смотря с конца третьего вектора, мы видим кратчайший поворот от первого ко второму против часовой стрелки), то применяется правило правого винта, в противном случае — правило левого винта.

Например, правило правого винта можно сформулировать так: если правый винт (который обычно применяется в технике и обыденной жизни) вращать в направлении обхода контура, то винт должен пойти от внутренней стороны поверхности к наружной. Или, другими словами: если маленький человечек обходит по наружной стороне поверхности ее контур по указанному направлению обхода, то сама поверхность должна быть у него но левую руку*).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Переходим к понятию векторного произведения

Векторное произведение двух векторов и определению, представляет собой вектор площадки (см. § Х.4), которая получится, если и отнести к одному началу, затем построить на этих векторах параллелограмм и обходить его контур, начиная с первого вектора (т. е. см. рис. 135,

Где принято правило правого винта, которым мы всегда будем пользоваться, если не оговорено противное).

Таким образом, векторное произведение двух векторов и — это вектор, направленный перпендикулярно обоим векторам, по модулю равный построенного на и и образующий с этими векторами тройку такого же смысла (т. е. правую пли левую), как векторы Обозначается векторное произведение косым крестом или квадратными скобками Отметим наиболее важные свойства векторного произведения. Так, векторное произведение двух ненулевых векторов равно нуль-вектору в том и только том случае, если векторы параллельны: равносильно так как параллельность векторов означает вырождение параллелограмма в отрезок, площадь которого равна нулю. В частности, всегда

Векторное произведение «аитикоммутативно» **)

Действительно, при перемене порядка множителей параллелограмм не изменится, но контур его будет проходиться в противоположном направлении и потому вектор площадки заменится на противоположный.

Можно проверить, что скалярный множитель можно выносить за знак векторного произведения:

на что справедлив распределительный закон:

Раскрывая скобки в выражениях, включающих векторное произведение, надо тщательно следить за порядком множителей. Приведем пример:

Пусть векторы и даны своими разложениями в декартовых проекциях

Тогда, если воспользоваться равенствами (проверьте их!)

получим

(продумайте структуру последнего выражения!).

Этот результат очень просто запомнить, если записать его в виде определителя (см. формулу

Пусть, например, надо вычислить площадь параллелограмма, построенного на векторах Так как то вычисляем

Так как в этом примере векторы безразмерные, то и площадь получается, соответственно, безразмерной.

Иногда применяется также векторно-скалярное или, иначе, смешанное произведение трех векторов которое, по определению, равно скалярной величине Ее геометрический смысл виден из рис. 136:

т. е. смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах. На рис. 138 векторы

образуют правую тройку, и получился объем со знаком плюс. Для левой тройки угол между и был бы тупой; в этом случае (Предполагается, что за основу принято правило правого винта.) Векторно-скалярное произведение равно пулю тогда и только тогда, когда все три вектора параллельны одной плоскости, так как такая параллельность означает, что параллелограмм вырождается в часть плоскости, т. е. имеет нулевой объем.

Легко получить выражение для смешанного иризведенпя в случае, с ели даны разложения сомножителей в декартовой системе координат. Для этого нужно правую часть (2) помножить обычным способом скалярнп (по формуле (IX,5)) на вектор Это даст после перегруппировки слагаемых

Нам понадобится еще формула для векторно-векторного произведения трех векторов. Для ее вывода представим себе, что мы выбрали оси координат так, что ось пошла по вектору а ось лежит в плоскости векторов Тогда вектор будет иметь проекцию только на ось т. е. аналогично Пользуясь формулой (3), получаем

Этот результат неудобен тем, что «привязан» к специальному выбору осей координат. Поэтому преобразуем его (проверьте)):

Эта формула уже не содержит координатных проекций, а потому не зависит от специального выбора системы координат.

Возможно вам будут полезны данные страницы:

Производная примеры решения

Производная функции

Несобственный интеграл примеры решения

Несобственный интеграл первого рода

Примеры с решением

Пример 1.

Определим векторное произведение векторов и из примера 48.

Векторное произведение векторов равно

Пример 2.

Даны точки Определим площадь треугольника

Из геометрического смысла векторного произведения векторов следует, что площадь треугольника равна Найдем координаты векторов

Тогда векторное произведение векторов и равно Отсюда Поэтому площадь треугольника равна

Пример 3.

Вектор перпендикулярный векторам и образует с осью тупой угол. Модуль вектора равен Определим координаты вектора

Из свойств векторного произведения векторов получаем что векторное произведение перпендикулярно векторам Поэтому векторы и коллинеарны.

Тогда модуль векторного произведения равен

Так как векторы коллинеарны, то соответствующие координаты этих векторов пропорциональны.

Пусть коэффициент пропорциональности. Тогда координаты вектора

Так как вектор образует с осью тупой угол, то соответствующий направляющий косинус меньше нуля:

Тогда Модуль вектора равен Отсюда Поэтому

Тогда вектор

Некоторые приложения к механике векторов

Векторное произведение особенно удобно при описании вращательного движения и связанных с ним понятий. Рассмотрим вращение твердого тела вокруг некоторой оси (рис. 137) с угловой скоростью Такое вращение принято изображать вектором угловой скорости который расположен но оси вращения и направлен в соответствии с направлением вращения согласно выбранному правилу винта; например, на рис. 137 направление выбрано по правилу правого винта, как мы всегда будем делать. Где именно на оси берется вектор

— безразлично; такой вектор, который можно произвольно перемещать вдоль некоторой оси, но не в сторону от этой оси, называется скользящим*).

Будем ‘ считать, что начало координа выбрано в любой точке оси вращения, и найдем линейную скорость произвольной точки с радиусом-вектором (рис. 137). Очевидно, что вектор перпендикулярен обоим векторам и а потому перпендикулярен и всему параллелограмму построенному на последних векторах. Численное значение равно произведению на кратчайшее расстояние точки оси вращения, т. е. как раз площади указанного параллелограмма. Но этим условиям, сформулированным для вектора удовлетворяет векторное произведение Таким образом,

(проверьте, что векторное произведение надо брать именно в выписанном порядке п что правая часть (5) не зависит от конкретного выбора точки на оси вращения).

Удобство вектора угловой скорости видно, в частности, из следующего. Допустим, что тело испытывает одновременно два вращения с (вообще говоря, непараллельными) векторами угловой скорости и причем оси вращения пересекаются в точке Тогда в силу формулы (5) линейная скорость любой точки равна где обозначено Значит, тело вращается с угловой скоростью и мы приходим к выводу, что при сложении вращений векторы угловой скорости складываются по правилу параллелограмма. Именно поэтому и можно называть угловую скорость вектором!

С помощью векторного произведения вводится такое важное понятие, как момент произвольного вектора с началом в точке относительно любой точки по определению, этот момент равен где В механике наиболее часто рассматривают момент силы т. е. величину и момент количества движения

При вычислении момента вектора этот вектор можно считать скользящим. В самом деле, если вектор скользит сам по себе, то это значит, что к прибавляется где — какой-то скаляр. Однако т. е. от такого скольжения момент вектора не меняется (рис. 138).

Если же вектор относить в сторону относительно его направления, то момент изменяется.

Рассмотрим систему как-то связанных между собой материальных частиц, каждая из которых имеет постоянную массу и (вообще говоря, переменный) радиус-вектор Пусть на каждую из этих точек действуют различные силы; обозначим равнодействующую всех «внутренних» сил (т. е. сил взаимодействия между точками системы), приложенных к точке, через а равнодействующую всех «внешних» сил — через ). Характерная особенность внутренних сил состоит в том, что на основе третьего закона Ньютона («действие рагсно противодействию») для каждой внутренней силы имеется противоположная ей внутренняя сила, причем, что очень важно, расположенная на продолжении первой.

Поэтому сумма всех внутренних сил, а также сумма их моментов относительно любой точки равны нулю.

Основные уравнения движения системы частиц получаются, если записать второй закон Ньютона («сила равна произведению массы на ускорение

Если просуммировать эти равенства по всем частицам, получим

гак как сумма всех внутренних сил, как было сказано выше, равна пулю. Удобно ввести точку с радиусом-вектором

— общая масса системы; эта точка называется «центром масс» рассматриваемой системы. При таком обозначении уравнение (7) можно переписать в виде

Итак, центр масс движется гак, как будто он обладает полной массой системы и на него действует сила, равная сумме всех внешних сил. В частности, если внешние силы отсутствуют, то центр масс системы движется прямолинейно и равномерно,

Перейдем к моментам. Если обе части равенства (6) умножить слева векторпо на мы получим

Воспользуемся равенством

которое вытекает из общей формулы производной векторного произведения

эта формула выводится совершенно так же, как аналогичная формула для скалярного произведения. Отсюда равенство (8) можно переписать так

Суммируя эти равенства по всем получим

так как сумма моментов всех внутренних сил равна нулю. Сумма

моментов количества движения всех частиц, составляющих систему, называется кинетическим моментом (моментом вращения) этой системы относительно той же точки по отношению к которой берутся все . моменты. Сумма моментов всех внешних сил, действующих на систему, называется полным (главным) моментом внешних сил. Таким образом, формулу (9) можно переписать

т. е. скорость изменения кинетического момента системы равна полному моменту внешних сил, действующих на эту систему. В частном случае, если внешние силы отсутствуют или если их полный момент равен нулю, получаем, что кинетический момент системы остается постоянным.

Формула векторного произведения

Геометрическое определение векторного произведения хорош для понимания свойств перекрестного произведения. Однако геометрическое определение не так полезно для вычисления векторное произведение векторов. Для вычислений нам понадобится формула в члены компонентов векторов. Начнем с использования геометрического определение для вычисления векторного произведения стандартных единичных векторов.

Перекрестное произведение единичных векторов 93$. (Мы определяем векторное произведение только в трех измерениях.

Обратите внимание, что мы предполагаем правостороннюю систему координат.)

Загрузка апплета

Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях: $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный) представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.

Дополнительная информация об апплете.

Параллелограмм, натянутый на любые два из этих стандартных единичных векторов, равен единичный квадрат, площадь которого равна единице. Следовательно, по геометрическое определение, крест произведение должно быть единичным вектором. Поскольку перекрестное произведение должно быть перпендикулярно двум единичным векторам, он должен быть равен другому единичный вектор или противоположный этому единичному вектору. Глядя на выше график, вы можете использовать правило правой руки, чтобы определить следующее полученные результаты. \начать{выравнивать*} \vc{i} \times \vc{j} &= \vc{k}\\ \vc{j} \times \vc{k} &=\vc{i}\\ \vc{k} \times \vc{i} &= \vc{j} \конец{выравнивание*} Эта небольшая циклическая диаграмма поможет вам запомнить эти результаты.

Как насчет $\vc{i} \times \vc{k}$? По правилу правой руки должно быть $-\vc{j}$. Помня, что $\vc{b} \times \vc{a} = — \vc{a} \times \vc{b}$, можно сделать вывод, что \начать{выравнивать*} \vc{j} \times \vc{i} &= -\vc{k}\\ \vc{k} \times \vc{j} &= -\vc{i}\\ \vc{i} \times \vc{k} &= -\vc{j}. \конец{выравнивание*}

Наконец, векторное произведение любого вектора на самого себя равно нулю вектор ($\vc{a} \times \vc{a}=\vc{0}$). В частности, перекрестное произведение любого стандартный единичный вектор с самим собой является нулевым вектором.

Общие векторы

За исключением двух специальных свойств, упомянутых выше ($\vc{b} \times \vc{a} = -\vc{a} \times \vc{b}$, и $\vc{a} \times \vc{a} = \vc{0}$), мы просто утверждаем, что векторное произведение ведет себя как обычное умножение. Он подчиняется следующим свойствам:

$(y\vc{a}) \times \vc{b} = y(\vc{a} \times \vc{b}) = \vc{a} \раз (г\вк{б})$,
$\vc{a} \times (\vc{b}+\vc{c}) = \vc{a} \times \vc{b} + \vc{a} \times \vc{c}$, 93$ и $y$ скаляр. (Эти свойства означают, что векторное произведение является линейным.) Мы можем использовать эти свойства вместе с векторным произведением стандартных единичных векторов, чтобы написать формулу для креста продукт по компонентам.
Компоненты $\vc{a}$ и $\vc{b}$ запишем как: \начать{выравнивать*} \vc{a} = (a_1,a_2,a_3)= a_1 \vc{i} + a_2 \vc{j} + a_3 \vc{k}\\ \vc{b} = (b_1,b_2,b_3)= b_1 \vc{i} + b_2 \vc{j} + b_3 \vc{k} \конец{выравнивание*}
Сначала предположим, что $a_3=b_3=0$. (Затем манипуляции намного проще.) Рассчитываем: \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j}) \times (b_1 \vc{i} + b_2 \vc{j})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) \конец{выравнивание*} Поскольку мы знаем, что $\vc{i} \times \vc{i}= \vc{0}= \vc{j} \times \vc{j}$ и что $\vc{i} \times \vc{j} = \vc{k} = -\vc{j} \times \vc{i}$, это быстро упрощается до \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1b_2-a_2b_1) \vc{k}\\ &= \влево| \begin{массив}{cc} а_1 и а_2\\ б_1 и б_2 \конец{массив} \право| \vc{к}. \конец{выравнивание*} Запись результата в виде определитель, как мы это делали в последний шаг, это удобный способ запомнить результат.
Общий случай, когда $a_3$ и $b_3$ не равны нулю, немного сложнее. Однако это просто вопрос повторения тех же манипуляций, описанных выше, с использованием векторного произведения единичных векторов и свойств векторного произведения.
Мы начинаем с расширения продукта \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j} + a_3\vc{k}) \times (b_1 \vc{i} + b_2 \vc{j} + b_3\vc{k})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_1b_3(\vc{i} \times \vc{k})\\ &\ четырехъядерный + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) + a_2b_3 (\vc{j} \times \vc{k})\\ &\ четырехъядерный + a_3b_1 (\vc{k} \times \vc{i}) + a_3b_2 (\vc{k} \times \vc{j}) + a_3b_3 (\vc{k} \times \vc{k}) \конец{выравнивание*} а затем вычислить все перекрестные произведения единичных векторов \начать{выравнивать*} \vc{a} \times \vc{b} &= a_1b_2 \vc{k} — a_1b_3 \vc{j} — a_2b_1 \vc{k} + a_2b_3 \vc{i} + a_3b_1 \vc{j} — a_3b_2 \vc{i}\\ знак равно (a_2b_3-a_3b_2)\vc{i} — (a_1b_3-a_3b_1) \vc{j} +(a_1b_2-a_2b_1) \vc{k}. \конец{выравнивание*} Используя определители, мы можем записать результат как \начать{выравнивать*} \vc{a} \times \vc{b} &=\left| \begin{массив}{cc} а_2 и а_3\\ б_2 и б_3 \конец{массив} \право| \vc{я} — \влево| \begin{массив}{cc} а_1 и а_3\\ б_1 и б_3 \конец{массив} \право| \vc{j} + \влево| \begin{массив}{cc} а_1 и а_2\\ б_1 и б_2 \конец{массив} \право| \vc{к}. \конец{выравнивание*}
Глядя на формулу определителя $3 \times 3$, мы видим, что формула для перекрестный продукт очень похож на формулу для $3 \times 3$ определитель. Если мы позволим матрице иметь вектор $\vc{i}$, $\vc{j}$ и $\vc{k}$ в качестве записей (хорошо, может быть, это не имеет смысла, но это всего лишь инструмент для запоминания перекрестного произведения), $3 Определитель \times 3$ дает удобную мнемонику для запоминания креста товар: \начать{выравнивать*} \vc{a} \times \vc{b} = \влево| \begin{массив}{ccc} \vc{i} & \vc{j} & \vc{k}\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \конец{массив} \право|. \конец{выравнивание*} Это компактный способ запомнить, как вычислять векторное произведение.
Статика: перекрестные произведения
Ключевые вопросы
- Чем перекрестное произведение отличается от скалярного?
- Что такое определитель?
- Что определяет правую декартову систему координат?
- Как использовать круг векторных произведений, чтобы найти векторное произведение двух единичных векторов?
Векторное произведение вектора — это математическая операция, примененная к двум векторам, в результате которой получается третий взаимно перпендикулярный вектор. Иногда его называют векторное произведение , чтобы подчеркнуть это и отличить его от скалярного произведения, которое дает скалярное значение. Для обозначения этой операции используется символ $\times$.
Перекрестные произведения используются в механике для нахождения момента силы относительно точки.
Перекрестное произведение — это процесс векторного умножения, определенный параметром
.
\begin{уравнение} \vec{A} \times \vec{B}= A \; B \sin\тета\; \ шляпа {\ vec {u}} \ text {.} \ tag {2.8.1} \end{уравнение}
Результатом является вектор, взаимно перпендикулярный первым двум, направление которого определяется правилом правой руки. Если $\vec{A}$ и $\vec{B}$ лежат в плоскости $xy$, это
\begin{уравнение} \vec{A} \times \vec{B}=(A_y B_x — A_x B_y)\ \хат\текст{.}\tag{2.8.2} \end{уравнение}
Операция не коммутативна, на самом деле
\begin{уравнение*} \vec{A}\times \vec{B}= — \vec{B} \times \vec{A} \text{.} \end{уравнение*}
Величина векторного произведения является произведением перпендикулярной составляющей $\vec{A}$ на величину $\vec{B},$, которая также является площадью параллелограмма, образованного векторами \ (\vec{A}\) и $\vec{B}\text{.}$ Величина перекрестного произведения равна нулю, если $\vec{A}$ и $\vec{B}\ ) параллельны и максимальны, когда они перпендикулярны.
Обратите внимание, что все члены в уравнении векторного произведения аналогичны тем, что используются в скалярном произведении, за исключением того, что вместо \(\cos$ используется $\sin$, а произведение включает единичный вектор $\hat{ \vec{u}}$, превращая результат в вектор. Этот единичный вектор $\hat{\vec{u}}$ легко найти в двумерной задаче, так как он всегда будет перпендикулярен странице, но для трехмерных перекрестных произведений рекомендуется использовать вектор детерминантный метод, обсуждаемый здесь.
Подраздел 2.8.1 Перекрестное произведение произвольных векторов
Перекрестное произведение двух трехмерных векторов может быть вычислено путем вычисления определителя этой матрицы $3 \times 3$.
\begin{уравнение} \vec{A} \times \vec{B} = \begin{vmatrix} \ihat \amp \jhat \amp \khat \\ A_x \amp A_y \amp A_z \\ B_x \amp B_y \amp B_z \end{vmatrix} \tag{2.8.3} \end{уравнение}
Здесь первая строка — единичные векторы, вторая строка — компоненты $\vec{A}$ и третья строка — компоненты $\vec{B}\text{. }$
Вычисление определителя $3 x 3$ можно свести к вычислению трех определителей $2 x 2$ методом кофакторов следующим образом
\begin{уравнение} \vec{A} \times \vec{B} = +\begin{vmatrix} A_y \amp A_z \\ B_y \amp B_z \end{vmatrix} \ihat -\begin{vmatrix} A_x \amp A_z \\ B_x \amp B_z \end{vmatrix} \jhat +\begin{vmatrix} A_x \amp A_y \\ B_x \amp B_y \end{vmatrix} \хат\tag{2.8.4} \end{уравнение}
Наконец, определитель $2 \times 2$ можно вычислить по формуле
\begin{уравнение} \begin{vmatrix} a \amp b \\ c \amp d\end{vmatrix} = a d — b c\tag{2.8.5} \end{уравнение}
После упрощения получается формула трехмерного перекрестного произведения:
\begin{уравнение} \vec{A} \times \vec{B} = (A_y B_z — A_z B_y) \ihat — (A_x B_z — A_z B_x) \jhat + (A_x B_y — A_y B_x)\khat\tag{2.8.6} \end{уравнение}
На практике проще всего запомнить это уравнение, используя приведенный ниже расширенный определитель, где первые два столбца были скопированы и помещены после определителя. Затем вычисляется векторное произведение путем сложения произведения красных диагоналей и вычитания произведения синих диагоналей.
Рисунок 2.8.1. Дополненный определитель
Результат равен
\begin{уравнение} \vec{A} \times \vec{B} = (A_y B_z — A_z B_y) \ihat + ( A_z B_x -A_x B_z) \jhat + (A_x B_y — A_y B_x)\khat\text{,}\tag{ 2.8.7} \end{уравнение}
, что математически эквивалентно уравнению (2.8.6).
В двух измерениях векторы $\vec{A}$ и $\vec{B}$ не имеют компонентов $z$, поэтому (2.8.3) сводится к
\begin{уравнение} \vec{A} \times \vec{B} = \begin{vmatrix}\ihat \amp \jhat \amp \khat \\ A_x \amp A_y \amp 0 \\ B_x \amp B_y \amp 0 \end{vmatrix } = (A_x B_y — A_y B_x) \хат\текст{.}\тег{2.8.8} \end{уравнение} 92\; \хат \end{gather*}
Решение 1.
В этом решении мы применим уравнение (2.8.1).
\begin{выравнивание*} \vec{A} \times \vec{B} \amp = A \; B \ грех \ тета \; \ шляпа {\ vec {и}} \end{align*}
Направление векторного произведения определяется применением правила правой руки. Правой рукой, вращая $\vec{A}$ в направлении $\vec{B}$, мы обнаруживаем, что наш большой палец указывает в плоскость $xy$, поэтому направление $\hat{\ vec{u}}$ равно $-\khat\text{.}$
92\; \хат \end{выравнивание*}
Пример 2.8.3. Трехмерное перекрестное произведение.
Найдите векторное произведение $\vec{A} = \langle 2,4,-1 \rangle $ и $\vec{B} = \langle 10, 25, 20 \rangle\text{.}\ ) Компоненты \(\vec{A}$ выражены в метрах, а $\vec{B}$ — в ньютонах.
Ответ.
\начать{собирать*} \vec{A} \times \vec{B} = \Nm{\langle 105, -50, 10 \rangle} \end{gather*}
Решение 1.
Для решения подставьте расширенный определитель и оцените его, складывая диагонали слева направо и вычитая диагонали справа налево. (2.8.6).
\begin{выравнивание*} \vec{A} \times \vec{B} \amp= \begin{vmatrix} \ihat \amp \jhat \amp \khat \\ 2\ампер 4\ампер -1\ 10 \amp 25 \amp 20 \end{vmatrix} \begin{матрица} \ihat \усилитель \jhat\\ 2 \усилитель 4\\ 10\ампер 25 \конец{матрица}\\ \amp = (4)(20)\;\ihat + (-1)(10)\;\jhat + (2)(25) \;\khat — (4)(10) \;\khat -(- 1)(25) \;\ihat — (2)(20) \;\jhat\\ \amp = (80 + 25) \;\ihat + (-10 — 40) \;\jhat + (50 — 40) \;\khat\\ \amp = \Nm{\langle 105, -50, 10 \rangle} \end{align*}
Решение 2.
Вычисление трехмерных перекрестных произведений вручную утомительно и чревато ошибками. Всякий раз, когда вы можете, вы должны использовать технологии, чтобы сделать за вас тяжелую работу и сосредоточиться на значении результатов. В этом решении мы будем использовать встроенный калькулятор Sage для вычисления перекрестного произведения. Этот же калькулятор можно использовать и для решения других задач.
Дано:
\begin{align*} \vec{A} \amp = \m{\langle 2,4,-1 \rangle}\\ \vec{B} \amp = \N{\langle 10, 25, 20 \rangle}. \end{выравнивание*}
$\vec{A}$ и $\vec{B}$ определены в первых двух строках, а A.cross_product(B) — это вычисляемое выражение. Щелкните Оценить , чтобы увидеть результат. Вы должны будете разработать правильные единицы для себя.
Попробуйте изменить третью строку на B.cross_product(A) . Какие изменения?
Подраздел 2.8.2 Перекрестное произведение единичных векторов
Поскольку единичные векторы имеют модуль, равный единице, и перпендикулярны друг другу, модуль векторного произведения двух перпендикулярных единичных векторов будет равен единице (2. 8.1). Направление определяется по правилу правой руки. С другой стороны, всякий раз, когда вы пересекаете единичный вектор сам с собой, результат равен нулю, поскольку $\theta=0\text{.}$
Один из способов применить правило правой руки — держать правую руку горизонтально и указывать пальцами в направлении первого вектора, а затем сгибать их в направлении второго вектора. Когда вы это сделаете, ваш большой палец будет ориентирован в направлении векторного произведения.
Для иллюстрации представьте, что единичные векторы $\ihat$ и $\jhat$ нарисованы на белой доске с нормальной ориентацией — $\ihat$ направлены вправо, $\jhat$ направлены вверх. Сориентируйте правую руку так, чтобы пальцы указывали вправо вдоль $\ihat\text{,}$, затем согните их в направлении $\jhat$, а ваш большой палец укажет за пределы доски и установит, что направление $ \ihat \times \jhat=\khat\text{.}$ Теперь попробуйте скрестить $-\ihat$ с $\jhat$, и вы обнаружите, что ваш большой палец теперь указывает на доску.
Вы должны быть в состоянии убедить себя, что векторные произведения положительных единичных векторов равны
.
\начать{выровнять*} \ihat \times \ihat \amp =0 \amp \ihat \times \jhat \amp = \khat \amp \ihat \times \khat \amp = -\jhat\\ \jhat \times \ihat \amp = -\khat \amp \jhat \times \jhat \amp = 0 \amp \jhat \times \khat \amp = \ihat \\ \хат \times \ihat \amp = \jhat \amp \khat \times \jhat \amp =-\ihat \amp \khat \times \khat \amp =0 \конец{выравнивание*}
Альтернативный способ запомнить это — использовать показанный круг перекрестного произведения. Например, когда вы пересекаете $\ihat$ с $\jhat$, вы движетесь в положительном (против часовой стрелки) направлении вокруг синего внутреннего круга, и, таким образом, ответ будет $+\khat\text{.}$ Но когда вы пересекаете $\jhat$ в $\ihat$, вы идете в отрицательном (по часовой стрелке) направлении по кругу и таким образом получаете $-\khat\text{.}$ Помните, что порядок перекрестные произведения имеют значение. Если вы поместите векторы в неправильном порядке, вы внесете ошибку знака.
Если у вас есть какие-либо отрицательные единичные векторы, проще всего разделить отрицательные значения до тех пор, пока вы не возьмете векторное произведение, например,
\begin{equation*} -\jhat \times \ihat = (-1)\left ( \jhat \times \ihat \right )=(-1)(-\khat )=+\khat \text{.} \end{equation*}
Рисунок 2.8.4. Круг векторного произведения единичного вектора.
1.4: Перекрестное произведение — Mathematics LibreTexts
1. Последнее обновление
2. Сохранить как PDF
Идентификатор страницы
2215

Майкл Коррал
Колледж Скулкрафт

В разделе 1. 3 мы определили скалярное произведение, которое давало способ умножения двух векторов. Однако полученный продукт был скаляром, а не вектором. В этом разделе мы определим произведение двух векторов, которое дает другой вектор. Этот продукт под названием 9{3}\) определяется как:

\[\textbf{v} \times \textbf{w} = (v_{2}w_{3} — v_{3}w_{2}, v_{3}w_{ 1} — v_{1}w_{3}, v_{1}w_{2} — v_{2}w_{1})\]

Пример 1.7

Найти $\textbf{i} \times \textbf{j}$.

Решение

Поскольку $\textbf{i} = (1,0,0)$ и $\textbf{j} = (0,1,0)$, то
\begin{align *}
\textbf{i} \times \textbf{j} &= ((0)(0) — (0)(1),(0)(0) — (1)(0),(1)( 1) — (0)(0))\\[4pt]
&= (0,0,1)\\[4pt]
&= \textbf{k}
\end{align*}

Аналогично можно показать, что $\textbf{j} \times \textbf{k} = \textbf{i}$ и $\textbf{k} \times \textbf{ i} = \textbf{j}$.

В приведенном выше примере векторное произведение заданных векторов было перпендикулярно обоим этим векторам. Оказывается, так будет всегда.

Теорема 1.11

Если векторное произведение $\textbf{v} \times \textbf{w}$ двух ненулевых векторов $\textbf{v}$ и $\textbf{w}$ также ненулевой вектор, то он перпендикулярен как $\textbf{v}$, так и $\textbf{w}$.

Доказательство

Мы покажем, что $(\textbf{v} \times \textbf{w}) \cdot \textbf{v} = 0$:
\begin{align*}
(\textbf{v} \times \textbf{w}) \cdot \textbf{v} &= (v_{2}w_{3} — v_{3}w_{2}, v_{3}w_{1} — v_{1}w_ {3}, v_{1}w_{2} — v_{2}w_{1}) \cdot (v_{1}, v_{2}, v_{3})\\[4pt]
&= v_{ 2}w_{3}v_{1} — v_{3}w_{2}v_{1} +
v_{3}w_{1}v_{2} — v_{1}w_{3}v_{2} + v_{1}w_{2}v_{3} —
v_{2}w_{1}v_{3}\\[4pt]
&= v_{1}v_{2}w_{3} — v_{ 1}v_{2}w_{3} + w_{1}v_{2}v_{3} —
w_{1}v_{2}v_{3} + v_{1}w_{2}v_{3} — v_{1}w_{2}v_{3}\\[4pt]
&= 0 \text { , после перестановки термов.}
\end{align*}
$\следовательно \textbf{v} \times \textbf{w} \perp \textbf{v}$ по следствию 1.7. Доказательство того, что $\textbf{v} \times \textbf{w} \perp \textbf{w}$, аналогично.

$\квадрат$

Как следствие приведенной выше теоремы и теоремы 1.9 имеем следующее:

Следствие 1.12

Если векторное произведение $\textbf{v} \times \textbf{w}$ двух ненулевых векторов $\textbf{v}$ и $\textbf{w}$ также ненулевой вектор, то он перпендикулярен промежутку $\textbf{v}$ и $\textbf{w}$. 9{3}\) является плоскостью $P$, поэтому приведенное выше следствие показывает, что $\textbf{v} \times \textbf{w}$ перпендикулярно этой плоскости. Как показано на рис. 1.4.2, существует два возможных направления для $\textbf{v} \times \textbf{w}$, одно противоположно другому. Оказывается (см. Приложение Б), что направление $\textbf{v} \times \textbf{w}$ задается $\textit{правилом правой руки}$, то есть векторы $\textbf{v}, \textbf{w}$, $\textbf{v} \times \textbf{w}$ образуют правую систему. Напомним, что в разделе 1.1 это означает, что вы можете указывать большим пальцем вверх в направлении $\textbf{v} \times \textbf{w}$, вращая $\textbf{v}$ в направлении $\textbf {w}$ оставшимися четырьмя пальцами. 9{3}\), тогда

\[\norm{\textbf{v} \times \textbf{w}} = \norm{\textbf{v}}\,\norm{\textbf{w}}\, \sin\тета\]

Может показаться странным возиться с приведенной выше формулой, когда величину векторного произведения можно вычислить напрямую, как и для любого другого вектора. Формула более полезна для ее приложений в геометрии, как в следующем примере.

Пример 1.8

Пусть $\треугольник PQR$ и $PQRS$ — треугольник и параллелограмм соответственно, как показано на рис. 1.4.3. 9{3}\). Пусть $\theta$ будет углом между $\textbf{v}$ и $\textbf{w}$. Площадь $A_{PQR}$ треугольника $\треугольник PQR$ равна $\frac{1}{2} b h$, где $b$ — основание треугольника, а \(h\ ) — высота. Итак, мы видим, что

\[\nonumber b = \norm{\textbf{v}} \text{ и } h = \norm{\textbf{w}}\,\sin \theta \]

\[\ nonumber \begin{align} A_{PQR} &= \frac{1}{2}\,\norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin\theta \\ [4pt] \nonumber&= \frac{1}{2}\,\norm{\textbf{v} \times \textbf{w}} \\[4pt] \end{align}\] 9{3}\}} равно:
\[\nonumber A = \norm{\textbf{v} \times \textbf{w}}\]

На первый взгляд может показаться, что, поскольку формулы, полученные в примере 1. 8, относятся только к смежным сторонам $QP$ и $QR$, то более общие утверждения теоремы 1.13 о том, что формулы верны для $\textit {любые}$ смежные стороны не выравниваются. Мы получили бы другую $\textit{формула}$ для площади, если бы выбрали $PQ$ и $PR$ в качестве смежных сторон, но можно показать (см. упражнение 26), что разные формулы давали бы одно и то же значение, поэтому выбор смежных сторон действительно не имеет значения, и теорема 1.13 верна.

Теорема 1.13 упрощает вычисление площади треугольника в трехмерном пространстве, чем при использовании традиционных геометрических методов.

Пример 1.9

Вычислить площадь треугольника $\треугольник PQR$, где $P = (2,4,-7)$, $Q = (3,7,18)$ и $R=(-5,12,8)$.

Решение

Пусть $\textbf{v} = \overrightarrow{PQ}$ и $\textbf{w} = \overrightarrow{PR}$, как на рис. 1.4.4 . Тогда $\textbf{v} = (3,7,18) — (2,4,-7) = (1,3,25)$ и $\textbf{w} = (-5,12, 8) — (2,4,-7) = (-7,8,15)$, поэтому площадь $A$ треугольника $\треугольник PQR$ равна 92} = \frac{1}{2}\,\sqrt{60966}\\[4pt]
A &\ приблизительно 123,46
\end{align*}

Пример 1. {3}\), такое что $z$-координата всегда $ 0$. Таким образом, мы можем написать $\textbf{v} = (-3,-1,0)$ и $\textbf{w} = (1,2,0)$. Тогда площадь $A$ $PQRS$ равна 9{3}\), и скалярное $k$, имеем

$\textbf{v} \times \textbf{w} = -\textbf{w} \times \textbf{v}$ Антикоммутативный закон
\(\textbf{u} \times (\textbf{v} + \textbf{w}) = \textbf{u} \times \textbf{v} + \textbf{u} \times \textbf{w}\ ) Дистрибьюторское право
\((\textbf{u} + \textbf{v}) \times \textbf{w} = \textbf{u} \times \textbf{w} + \textbf{v} \times \textbf{w}\ ) Дистрибьюторское право
$(k\textbf{v}) \times \textbf{w} = \textbf{v} \times (k\textbf{w}) = k(\textbf{v} \times \textbf{w}) $ Ассоциативное право
$\textbf{v} \times \textbf{0} = \textbf{0} = \textbf{0} \times \textbf{v}$
$\textbf{v} \times \textbf{v} = \textbf{0}$
$\textbf{v} \times \textbf{w} = \textbf{0}$ тогда и только тогда, когда $\textbf{v} \parallel \textbf{w}$

Доказательство

Доказательства свойств (b)-(f) просты. Мы докажем части (а) и (ж), а остальное предоставим читателю в качестве упражнений.

(a) По определению перекрестного произведения и скалярного умножения мы имеем:
\begin{align*}
\textbf{v} \times \textbf{w} &= (v_{2}w_{3} — v_{3}w_{2},
v_{3}w_{1} — v_{1}w_{3}, v_{1}w_{2} — v_{2}w_{1})\\[ 4pt]
&= -(v_{3}w_{2} — v_{2}w_{3},
v_{1}w_{3} — v_{3}w_{1}, v_{2}w_{ 1} — v_{1}w_{2})\\[4pt]
&= -(w_{2}v_{3} — w_{3}v_{2},
w_{3}v_{1} — w_{1}v_{3}, w_{1}v_{2} — w_{2}v_{1})\\[4pt]
&= -\textbf{w} \times \textbf{v}
\ конец{выравнивание*}
Обратите внимание, что это говорит о том, что $\textbf{v} \times \textbf{w}$ и $\textbf{w} \times \textbf{v}$ имеют одинаковую величину, но противоположное направление (см. рис. 1.4). .6).

(g) Если $\textbf{v}$ или $\textbf{w}$ равно $\textbf{0}$, то $\textbf{v} \times \textbf {w} = \textbf{0}$ по части (e), и либо $\textbf{v} = \textbf{0} = 0\textbf{w}$, либо $\textbf{w} = \textbf{0} = 0\textbf{v}$, поэтому $\textbf{v}$ и $\textbf{w}$ кратны скаляру, т. е. параллельны. 9{\circ}\) тогда и только тогда, когда $\textbf{v} \parallel \textbf{w}$.

$\квадрат$

Пример 1.11

Добавляя к примеру 1.7, мы имеем

\[\nonumber \textbf{i} \times \textbf{j} = \textbf{k},\quad \textbf{j} \times \textbf{k } = \textbf{i},\quad \textbf{k} \times \textbf{i} = \textbf{j}\]
\[\nonumber \textbf{j} \times \textbf{i} = -\ textbf{k},\quad \textbf{k} \times \textbf{j} = -\textbf{i},\quad \textbf{i} \times \textbf{k} = -\textbf{j}\]
\[\nonumber \textbf{i} \times \textbf{i} = \textbf{j} \times \textbf{j} = \textbf{k} \times \textbf{k} = \textbf{0}\ ] 9{3}\) представляют смежные стороны параллелепипеда $P$, причем $\textbf{u}, \textbf{v}, \textbf{w}$ образуют правую систему, как на рис. 1.4. .7. Покажите, что объем $P$ равен $\textit{скалярному тройному произведению}$ $\textbf{u} \cdot (\textbf{v} \times \textbf{w})$.

Решение

Напомним, что объем $\text{vol}(P)$ параллелепипеда $P$ равен площади $A$ основание параллелограмма, умноженное на высоту $h$. По теореме 1.13 (b) площадь $A$ базового параллелограмма равна $\norm{\textbf{v} \times \textbf{w}}$. И мы можем видеть, что поскольку $\textbf{v} \times \textbf{w}$ перпендикулярно базовому параллелограмму, определяемому $\textbf{v}$ и $\textbf{w}$, тогда высота $h$ равна $\norm{\textbf{u}}\,\cos \theta$, где $\theta$ — угол между $\textbf{u}$ и $\textbf{v} \times \textbf{w}$. По теореме 1.6 мы знаем, что

\[\nonumber \begin{align} \cos \theta &= \dfrac{\textbf{u} \cdot (\textbf{v} \times \textbf{w})}{\norm{\textbf{u }} \, \norm{\textbf{v} \times \textbf{w}}}. \text{ Следовательно,} \\[4pt] \nonumber \text{vol}(P) &= A \, h \\[4pt] \nonumber&= \norm{\textbf{v} \times \textbf{w} } \, \dfrac{\norm{\textbf{u}} \, \textbf{u} \cdot (\textbf{v} \times \textbf{w})}{\norm{\textbf{u}} \ ,\norm{\textbf{v} \times \textbf{w}}} \\[4pt] \nonumber&= \textbf{u} \cdot (\textbf{v} \times \textbf{w}) \\[ 4pt] \end{выравнивание}\]

В примере 1.12 высота $h$ параллелепипеда равна $\norm{\textbf{u}}\,\cos \theta$, а не $-\norm{\textbf{u}}\ ,\cos \theta$, потому что вектор $\textbf{u}$ находится на той же стороне плоскости базового параллелограмма, что и вектор $\textbf{v} \times \textbf{w}$ ( так что $\cos\theta > 0$). Поскольку объем один и тот же независимо от используемой базы и высоты, повторение тех же шагов с использованием базы, определяемой $\textbf{u}$ и $\textbf{v}$ (поскольку $\textbf {w}$ находится по ту же сторону от основания 9{3}\),

\[\textbf{u} \times (\textbf{v} \times \textbf{w}) = (\textbf{u} \cdot \textbf{w})\textbf{v } — (\textbf{u} \cdot \textbf{v})\textbf{w}\label{Eq1.13}\]

Изучение формулы в теореме 1.16 дает некоторое представление о геометрии векторного тройного произведения. В правой части уравнения \ref{Eq1.13} мы видим, что $\textbf{u} \times (\textbf{v} \times \textbf{w})$ является скалярной комбинацией $\ textbf{v}$ и $\textbf{w}$, и, следовательно, лежит в плоскости, содержащей $\textbf{v}$ и $\textbf{w}$ (т.е. $\textbf{ u} \times (\textbf{v} \times \textbf{w})$, $\textbf{v}$ и $\textbf{w}$ являются $\textbf{копланарными}$ ). Это имеет смысл, поскольку по теореме 1.11 $\textbf{u} \times (\textbf{v} \times \textbf{w})$ перпендикулярно как $\textbf{u}$, так и $ \textbf{v} \times \textbf{w}$. В частности, перпендикулярность $\textbf{v} \times \textbf{w}$ означает, что $\textbf{u} \times (\textbf{v} \times \textbf{w})$ лежит в плоскости, содержащей $\textbf{v}$ и $\textbf{w}$, поскольку эта плоскость сама перпендикулярна $\textbf{v} \times \textbf{w}$. Но тогда как $\textbf{u} \times (\textbf{v} \times \textbf{w})$ также перпендикулярно $\textbf{u}$, который может быть любым вектором? Следующий пример может помочь увидеть, как это работает.

Пример 1.13

Найти $\textbf{u} \times (\textbf{v} \times \textbf{w})$ для $\textbf{u} = (1, 2, 4)$, $\textbf{v} = (2, 2, 0)$, $\textbf{w} = (1, 3, 0)$.

Решение

Так как $\textbf{u} \cdot \textbf{v} = 6$ и $\textbf{u} \cdot \textbf{w} = 7$, то

\ begin{align*}
\textbf{u} \times (\textbf{v} \times \textbf{w}) &= (\textbf{u} \cdot \textbf{w})\textbf{v} — ( \textbf{u} \cdot \textbf{v})\textbf{w}\\[4pt]
&= 7\,(2, 2, 0) — 6\, (1, 3, 0) = (14, 14, 0) — (6, 18, 0)\\[4pt]
&= (8 , -4, 0)
\end{align*}

Обратите внимание, что $\textbf{v}$ и $\textbf{w}$ лежат в $xy$-плоскости, и что \ (\textbf{u} \times (\textbf{v} \times \textbf{w})\) также лежит в этой плоскости. Кроме того, $\textbf{u} \times (\textbf{v} \times \textbf{w})$ перпендикулярно как $\textbf{u}$, так и $\textbf{v} \times \textbf{w} = (0, 0, 4)$ (см. рис. 1.4.8).

Для векторов $\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}$ и $\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k}$ в компонентной форме перекрестное произведение записывается как: $\textbf{v} \times \textbf{w} = (v_{2}w_{3} — v_{3}w_{2})\textbf{i} + (v_{3}w_{1} — v_{1}w_{3 })\textbf{j} + (v_{1}w_{2} — v_{2}w_{1})\textbf{k}$. Часто проще использовать компонентную форму для перекрестного произведения, потому что его можно представить как $\textit{детерминант}$. Мы не будем слишком углубляться в теорию детерминант; мы просто рассмотрим то, что необходимо для наших целей.

A 2 $\times$ 2 матрица } представляет собой массив из двух строк и двух столбцов скаляров, записанный как

\[\nonumber \begin{bmatrix}a & b\\[4pt]c & d\end{bmatrix} \text{or} \begin{pmatrix}a & b\\[4pt]c & d\end{ pmatrix}\]

, где $a, b, c, d$ — скаляры. $\textbf{определитель}$ такой матрицы, записанной как

\[\nonumber \begin{vmatrix}a & b\\[4pt]c & d\end{vmatrix} \text{or} \det \begin{bmatrix}a & b\\[4pt]c & d\ конец{bmatrix},\]

— это скаляр, определяемый следующей формулой:

\[\nonumber \begin{vmatrix}a & b\\[4pt]c & d\end{vmatrix}= ad — bc\]

Может быть полезно запомнить эту формулу как произведение скаляров по нисходящей диагонали минус произведение скаляров по восходящей диагонали.

Пример 1.14

\[\nonumber \begin{vmatrix}1 & 2\\[4pt]3 & 4\end{vmatrix} = (1)(4) — (2)(3) = 4 — 6 = — 2\]

A $3 \times 3$ матрица — это массив из трех строк и трех столбцов скаляров, записанный как

\[\nonumber \begin{bmatrix}a_{1} & a_{2} & a_{3}\\[4pt]
b_{1} & b_{2} & b_{3}\\[4pt]
c_{1} & c_{2} & c_{3}
\end{bmatrix}
\text{or}
\begin{pmatrix}a_{1} & a_{2} & a_{3}\\[4pt ]
b_{1} & b_{2} & b_{3}\\[4pt]
c_{1} & c_{2} & c_{3}
\end{pmatrix},$$
и его определитель задается формулой:
\[\begin{vmatrix}a_{1} & a_{2} & a_{3}\\[4pt]
b_{1} & b_{2} & b_{3}\\[4pt]
c_{1} & c_{2} & c_{3}
\end{vmatrix}
= a_{1} \begin{ vmatrix}b_{2} & b_{3} \\[4pt] c_{2} & c_{3} \end{vmatrix} \;-\;
a_{2} \begin{vmatrix} b_{1} & b_{3} \\[4pt] c_{1} & c_{3} \end{vmatrix} \;+\;
a_{3} \begin{vmatrix} b_{1} & b_{2} \\[4pt] c_{1} & c_{2} \end{vmatrix}\]

Один из способов запомнить приведенную выше формулу заключается в следующем: умножьте каждую скалярную величину в первой строке на определитель матрицы $2 x 2$, оставшейся после удаления строки и столбца, содержащих эту скалярную величину, затем просуммируйте эти произведения. вверх, ставя перед каждым попеременно знаки плюс и минус (начиная с плюса).

Пример 1.15

\[\nonumber \left|\begin{array}{rrr}1 & 0 & 2\\[4pt]4 & -1 & 3\\[4pt]1 & 0 & 2\end{array }\право|
= 1 \left|\begin{array}{rr} -1 & 3 \\[4pt] 0 & 2 \end{array}\right| \;-\;
0 \left|\begin{array}{rr} 4 и 3 \\[4pt] 1 и 2 \end{array}\right| \;+\;
2 \left|\begin{array}{rr} 4 & -1 \\[4pt] 1 & 0 \end{array}\right|
= 1(-2-0)-0(8-3)+2(0+1)=0\]

Мы определили определитель как скаляр, полученный из алгебраических операций над скалярными элементами в матрице. Однако, если мы поместим три $\textit{vectors}$ в первую строку матрицы $3 \times 3$, то определение по-прежнему имеет смысл, так как мы будем выполнять скалярное умножение этих трех векторов ( они будут умножены на $2 \times 2$ скалярные определители, как и раньше). Это дает нам определитель, который теперь является вектором, и позволяет нам написать перекрестное произведение $\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3 }\textbf{k}$ и $\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k}$ как определитель:

\begin{align*}
\nonumber \textbf{v} \times \textbf{w} =
\begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\[4pt ] v_{1} & v_{2} & v_{3} \\[4pt]
w_{1} & w_{2} & w_{3}
\end{vmatrix} &= \begin{vmatrix} v_{ 2} & v_{3} \\[4pt] w_{2} & w_{3} \end{vmatrix} \textbf{i} \;-\;
\begin{vmatrix} v_{1} & v_{3} \\[4pt] w_{1} & w_{3} \end{vmatrix} \textbf{j} \;+\;
\begin{vmatrix} v_{1} & v_{2} \\[4pt] w_{1} & w_{2} \end{vmatrix} \textbf{k}\\[4pt] \nonumber
&= (v_{2}w_{3} — v_{3}w_{2})\textbf{i} + (v_{3}w_{1} — v_{1}w_{3})\textbf{ j} +
(v_{1}w_{2} — v_{2}w_{1})\textbf{k}
\end{align*}

Пример 1. 16

Пусть $\textbf{v} = 4\,\textbf{i} — \textbf{j} + 3\,\textbf{k}$ и $\textbf{w} = \textbf {i} + 2\,\textbf{k}$. Затем

\[\nonumber \textbf{v} \times \textbf{w} =
\left|\begin{array}{rrr}
\textbf{i} & \textbf{j} & \textbf{k} \\[4pt]
4 & -1 & 3\\[4pt]
1 & 0 & 2
\конец{массив}\право|
= \left|\begin{массив}{rr} -1 и 3 \\[4pt] 0 и 2 \end{массив}\right| \textbf{i} \;-\;
\left|\begin{array}{rr} 4 и 3 \\[4pt] 1 и 2 \end{array}\right| \textbf{j} \;+\;
\left|\begin{array}{rr} 4 & -1 \\[4pt] 1 & 0 \end{array}\right| \textbf{k}
= -2\,\textbf{i} — 5\,\textbf{j} + \textbf{k}\]

Скалярное тройное произведение также можно записать в виде определителя. Фактически, согласно примеру 1.12, следующая теорема дает альтернативное определение определителя матрицы $3 \times 3$ как объема параллелепипеда, смежные стороны которого являются строками матрицы и образуют правую систему (левосторонняя система даст отрицательный объем). 9{3}\):
\[\textbf{u} \cdot (\textbf{v} \times \textbf{w}) =
\begin{vmatrix}u_{1} & u_{2} & u_{3 }\\[4pt]
v_{1} & v_{2} & v_{3}\\[4pt]
w_{1} & w_{2} & w_{3}
\end{vmatrix}\]

Пример 1.17

Найдите объем параллелепипеда с прилегающими сторонами $\textbf{u} = (2, 1, 3)$, $\textbf{v} = (-1, 3, 2)$ , $\textbf{w} = (1, 1, -2)$ (см. рис. 1.4.9).

Решение

По теореме 1.15 объем $\text{vol}(P)$ параллелепипеда $P$ есть модуль скалярной тройки Произведение трех соседних сторон (в любом порядке). По теореме 1.17,

\begin{align*}
\nonumber \textbf{u} \cdot (\textbf{v} \times \textbf{w}) &=
\left|\begin{array}{rrr}
2 & 1 & 3\\[4pt]
-1 & 3 & 2\\[4pt]
1 & 1 &-2
\end{массив}\right|\\[4pt] \nonumber
&= 2 \left|\ begin{массив}{rr} 3 и 2 \\[4pt] 1 и -2 \end{массив}\right| \;-\;
1 \left|\begin{array}{rr} -1 и 2 \\[4pt] 1 & -2 \end{array}\right| \;+\;
3 \left|\begin{array}{rr} -1 & 3 \\[4pt] 1 & 1 \end{array}\right|\\[4pt] \nonumber
&= 2(-8) — 1(0) + 3(-4) = -28 \text{,so}\\[4pt] \nonumber
\text{vol}(P) &= |-28| = 28.
\end{выравнивание*}

Перестановка точечных и перекрестных произведений может быть полезна при доказательстве идентичности векторов:

Пример 1.18

Докажите: $(\textbf{u} \times \textbf{v}) \cdot (\textbf{w} \times \textbf{z}) =
\begin{vmatrix}
\textbf{ u} \cdot \textbf{w} & \textbf{u} \cdot \textbf{z}\\[4pt]
\textbf{v} \cdot \textbf{w} & \textbf{v} \cdot \textbf {z}\end{vmatrix}$ для всех векторов $\textbf{u}, 9{3}$.

Решение

Пусть $\textbf{x} = \textbf{u} \times \textbf{v}$. Затем

\begin{align*}
(\textbf{u} \times \textbf{v}) \cdot (\textbf{w} \times \textbf{z}) &=
\textbf{x} \cdot (\textbf{w} \times \textbf{z})\\[4pt]
&= \textbf{w} \cdot (\textbf{z} \times \textbf{x}) \text{(по уравнению \ ref{Eq1.1.2})}\\[4pt]
&= \textbf{w} \cdot (\textbf{z} \times (\textbf{u} \times \textbf{v}))\\[4pt ]
&= \textbf{w} \cdot ((\textbf{z} \cdot \textbf{v})\textbf{u} —
(\textbf{z} \cdot \textbf{u})\textbf{v}) \text{(по теореме 1. 16)}\\[4pt]
&= (\textbf{z} \cdot \textbf{v })(\textbf{w} \cdot \textbf{u}) —
(\textbf{z} \cdot \textbf{u})(\textbf{w} \cdot \textbf{v})\\[4pt ]
&= (\textbf{u} \cdot \textbf{w})(\textbf{v} \cdot \textbf{z}) —
(\textbf{u} \cdot \textbf{z})(\ textbf{v} \cdot \textbf{w}) \text{(по коммутативности скалярного произведения).}\\[4pt]
&= \begin{vmatrix}
\textbf{u} \cdot \textbf{w } & \textbf{u} \cdot \textbf{z}\\[4pt]
\textbf{v} \cdot \textbf{w} & \textbf{v} \cdot \textbf{z}\end{vmatrix}
\end{align*}

Эта страница под заголовком 1.4: Cross Product распространяется в соответствии с лицензией GNU Free Documentation License 1.3, автором, ремиксом и/или куратором этой страницы является Майкл Коррал.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Майкл Коррал
Лицензия
ГНУ ФДЛ
Показать страницу Содержание
нет
Метки
1. перекрестное произведение
2. определитель

14.

Еще одна полезная операция: по двум векторам найти третий (ненулевой!) вектор перпендикулярно первым двум. Их конечно бесконечное множество таких векторов разной длины. Тем не менее, давайте найдем его. Предположим, что $\ds {\bf A}=\langle a_1,a_2,a_3\rangle$ и $\ds {\bf B}=\langle b_1,b_2,b_3\rangle$. Мы хотим найти вектор $\ds {\bf v} = \langle v_1,v_2,v_3\rangle$ с ${\bf v}\cdot{\bf A}={\bf v}\cdot{\bf B}=0$, или $$\выравнивание{ a_1v_1+a_2v_2+a_3v_3&=0,\кр b_1v_1+b_2v_2+b_3v_3&=0.\cr }$$ Умножьте первое уравнение на $\ds b_3$, а второе на $\ds a_3$ и вычесть, чтобы получить $$\выравнивание{ b_3a_1v_1+b_3a_2v_2+b_3a_3v_3&=0\кр a_3b_1v_1+a_3b_2v_2+a_3b_3v_3&=0\кр (a_1b_3-b_1a_3)v_1 + (a_2b_3-b_2a_3)v_2&=0\cr }$$ Конечно, это уравнение с двумя переменными имеет много решений; а особенно легко увидеть $\ds v_1=a_2b_3-b_2a_3$, $\ds v_2=b_1a_3-a_1b_3$. Замена обратно на любой из исходных уравнения и решение для $\ds v_3$ дает $\ds v_3=a_1b_2-b_1a_2$.

Этот конкретный ответ на проблему, оказывается, имеет некоторые хорошие свойства, и он удостоился имени: перекрестное произведение : $$ {\bf A}\times{\bf B} = \langle a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle. $$ Хотя в этом векторе есть хороший шаблон, он может быть немного сложно запомнить; вот удобная мнемоника. Определитель матрицы два на два равен $$\left|\matrix{a&b\cr c&d\cr}\right|=ad-cb.$$ Это распространяется на определитель матрицы три на три: $$\выравнивание{ \left|\matrix{x&y&z\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\right|&=x\left|\matrix{a_2&a_3\cr b_2&b_3\cr}\right|-y\left|\matrix{a_1&a_3\cr b_1&b_3\cr}\right|+z\left|\matrix{a_1&a_2\cr b_1&b_2\cr}\право|\cr &=x(a_2b_3-b_2a_3)-y(a_1b_3-b_1a_3)+z(a_1b_2-b_1a_2)\cr &=x(a_2b_3-b_2a_3)+y(b_1a_3-a_1b_3)+z(a_1b_2-b_1a_2).\cr} $$ Каждая из матриц два на два формируется удалением верхней строки и один столбец матрицы три на три; вычитание середины термин также необходимо запомнить. Здесь не место превозносить использование определителя; достаточно сказать, что детерминанты необычайно полезно и важно. Здесь мы хотим использовать его просто как мнемонический прием. Вы могли заметить, что три выражения в круглые скобки в последней строке — это в точности три координаты перекрестный продукт; замена $x$, $y$, $z$ на $\bf i$, $\bf j$, $\bf k$ дает нам $$\выравнивание{ \left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\право| &=(a_2b_3-b_2a_3){\bf i}-(a_1b_3-b_1a_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=(a_2b_3-b_2a_3){\bf i}+(b_1a_3-a_1b_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=\лангл a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle\cr &={\bf A}\times{\bf B}.\cr} $$

Пример 14.4.1 Предположим, что ${\bf A}=\langle 1,2,3\rangle$, ${\bf B}=\langle 4,5,6\угол$. затем $$\выравнивание{ {\bf A}\times{\bf B}&=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr 1&2&3\кр 4&5&6\cr}\право|\cr &=(2\cdot 6-5\cdot 3){\bf i}+(4\cdot 3-1\cdot 6){\bf j}+ (1\cdot 5-4\cdot 2){\bf k}\cr &=-3{\bf i}+6{\bf j}-3{\bf k}\cr &=\langle -3, 6, -3\rangle\cr }$$ Немного потренировавшись, вы обнаружите, что избавляться от промежуточные шаги, переходя непосредственно от матрицы $3\times3$ к обычная векторная форма. 2\theta\cr |{\bf A}\times{\bf B}|&=|{\bf A}||{\bf B}|\sin\theta\cr }$$ Таким образом, величина ${\bf A}\times{\bf B}$ очень похожа на точку товар. В частности, обратите внимание, что если $\bf A$ параллелен $\bf B$, угол между ними равен нулю, поэтому $\sin\theta=0$, поэтому $|{\bf A}\times{\bf B}|=0$, и аналогично, если они антипараллельны, $\sin\theta=0$ и $|{\bf A}\times{\bf B}|=0$. Наоборот, если $|{\bf A}\times{\bf B}|=0$ и $|{\bf A}|$ и $|{\bf B}|$ не равны нулю, должно быть так, что $\sin\theta=0$, поэтому $\bf A$ параллелен или антипараллелен $\bf B$.

Вот любопытный факт по этому поводу количество, которое впоследствии оказывается весьма полезным: Даны два векторы, мы можем сложить их хвост к хвосту и сформировать параллелограмм, как на рисунке 14.4.1. высота параллелограмма $h$ равна $|{\bf A}|\sin\theta$, а основание равно $|{\bf B}|$, поэтому площадь параллелограмм $|{\bf A}||{\bf B}|\sin\theta$, в точности равно величине $|{\bf A}\times{\bf B}|$.

Рисунок 14. 4.1. Параллелограмм.

А как насчет направления перекрестного произведения? Примечательно, что существует простое правило, описывающее направление. Давайте посмотрим на простой пример: пусть ${\bf A}=\langle a,0,0\rangle$, ${\bf B}=\langle б, в, 0\угол$. Если векторы поставить хвостами в начале координат, $\bf A$ лежит вдоль оси $x$, а $\bf B$ лежит в плоскости $x$-$y$, поэтому мы знаем, что перекрестный продукт будет указывать либо вверх, либо вниз. Крест продукт $$\выравнивание{ {\bf A}\times {\bf B}=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а&0&0\кр b&c&0\cr}\right| &=\лангл 0,0,ac\угол.\cr} $$ Как и было предсказано, это вектор, направленный вверх или вниз, в зависимости от знак $ac$. Предположим, что $a>0$, поэтому знак зависит только от $c$: если $c>0$, $ac>0$ и вектор направлен вверх; если $c0$, то вектор указывает вниз, а если $a0$ и $c>0$ или $a

Хотя с вычислительной точки зрения довольно сложно увидеть, как это работает для любых двух начальных векторов, правило, по сути, такой же. Расположите $\bf A$ и $\bf B$ хвост к хвосту. Плоскость, в которой $\bf A$ и $\bf B$ можно рассматривать с двух сторон; посмотреть на это со стороны для которого $\bf A$ должен вращаться против часовой стрелки, чтобы достичь $\bf B$; тогда вектор ${\bf A}\times{\bf B}$ указывает на вас.

Это правило обычно называют правило правой руки . Представьте, что вы помещаете пятку правой руки в точку, где находятся решки. соединены так, чтобы ваши слегка согнутые пальцы указывали направление вращение из $\bf A$ в $\bf B$. Затем ваш большой палец указывает на направление векторного произведения ${\bf A}\times{\bf B}$.

Одним из непосредственных следствий этих фактов является то, что ${\bf A}\times{\bf B}\not={\bf B}\times{\bf A}$, потому что два перекрестные произведения указывают в противоположном направлении. С другой стороны, поскольку $$ |{\bf A}\times{\bf B}|=|{\bf A}||{\bf B}|\sin\theta =|{\bf B}||{\bf A}|\sin\theta=|{\bf B}\times{\bf A}|, $$ длины двух перекрестных произведений равны, поэтому мы знаем, что ${\bf A}\times{\bf B}=-({\bf B}\times{\bf A})$.

Перекрестное произведение имеет некоторые знакомые свойства, которые будут пригодится позже, поэтому мы перечислим их здесь. Как и в случае скалярного произведения, они могут быть доказано выполнением соответствующих вычислений по координатам, после чего мы можем иногда избежать таких вычислений, используя характеристики.

Теорема 14.4.2. Если ${\bf u}$, ${\bf v}$ и ${\bf w}$ — векторы, а $a$ — вещественное число, затем

1. ${\bf u}\times({\bf v}+{\bf w}) = {\bf u}\times{\bf v}+{\bf u}\times{\bf w}$

2. $({\bf v}+{\bf w})\times{\bf u} = {\bf v}\times{\bf u}+{\bf w}\times{\bf u}$

3. $(a{\bf u})\times{\bf v}=a({\bf u}\times{\bf v}) = {\ bf и} \ раз (a {\ bf v}) $

4. ${\bf u}\cdot({\bf v}\times{\bf w}) = ({\bf u}\times{\bf v})\cdot{\bf w}$

5. ${\bf u}\times({\bf v}\times{\bf w}) = ({\ bf u} \ cdot {\ bf w}) {\ bf v} — ({\ bf u} \ cdot {\ bf v}) {\ bf w} $ $\qed$

Вы можете использовать Sage для вычисления перекрестных произведений.

Пример 14.4.1 Найдите векторное произведение $\langle 1,1,1\rangle$ и $\лэнгл 1,2,3\рангл$. (отвечать)

Пример 14.4.2 Найдите векторное произведение $\langle 1,0,2\rangle$ и $\лангле -1,-2,4\рангл$. (отвечать)

Пример 14.4.3 Найдите векторное произведение $\langle -2,1,3\rangle$ и $\лэнгл 5,2,-1\рангл$. (отвечать)

Пример 14.4.4 Найдите векторное произведение $\langle 1,0,0\rangle$ и $\лэнгл 0,0,1\рангл$. (отвечать)

Пример 14.4.5 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/6$, а $|{\bf u}|=2$ и $|{\bf v}|=3$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 14.4.6 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/4$, а $|{\bf u}|=3$ и $|{\bf v}|=7$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 14.4.7 Найдите площадь параллелограмма с вершинами $(0,0)$, $(1,2)$, $(3,7)$ и $(2,5)$. (отвечать)

Пример 14.4.8 Найдите площадь параллелограмма с вершинами $(0,-1)$, $(3,4)$, $(1,6)$ и $(-2,1)$. (отвечать)

Пример 14.4.9 Найдите площадь треугольника с вершинами $(2,0,0)$, $(1,3,4)$, и $(-2,-1,1)$. (отвечать)

Пример 14.4.10 Найдите площадь треугольника с вершинами $(2,-2,1)$, $(-3,2,3)$, и $(3,3,-2)$. (отвечать)

Пример 14.4.11 Найдите и объясните значение $({\bf i} \times {\bf j}) \times {\bf k}$ и $({\bf i} + {\bf j}) \times ({\bf i} — {\bf j})$.

Пример 14.4.12 Докажите, что для всех векторов ${\bf u}$ и ${\bf v}$ $({\bf u}\times{\bf v})\cdot{\bf v}=0$.

Пример 14.4.13 Докажите теорему 14.4.2.

Пример 14.4.14 Определим тройное произведение трех векторов ${\bf x}$, ${\bf y}$ и ${\bf z}$, чтобы быть скаляром ${\bf x} \cdot ({\bf y} \times {\bf z})$. Докажите, что три вектора лежат в одной плоскости тогда и только тогда, когда их тройное произведение равно нулю. Убедитесь, что $\langle 1, 5, -2 \rangle$, $\langle 4, 3, 0 \rangle$ и $\langle 6, 13, -4 \rangle$ копланарный.

Формула векторного перекрестного произведения | Примеры с шаблоном Excel

Формула векторного перекрестного произведения (оглавление)

Формула
Примеры

В векторной алгебре и математике термин «векторное перекрестное произведение» относится к бинарным операциям между векторами в трехмерной геометрии. Перекрестное произведение обозначается перекрестным знаком «x» между двумя векторами, а операция перекрестного произведения приводит к другому вектору, который перпендикулярен плоскости, содержащей исходные два вектора. Формула для векторного векторного произведения может быть получена путем умножения абсолютных значений двух векторов и синуса угла между двумя векторами. Математически предположим, что A и B — два вектора, такие как A = A ₁ I + A ₂ J + A ₂ J + A ₂ J + A ₂ J + A ₂ J + ₂ J + ₂ . ₁ I + B ₂ J + B ₃ K , затем Vector Cross Product представлен как,

A X 6 B | 464646460 = 46460 = 4641464146414414410 2 a x 6. |б| sin θ n

, где θ = угол между a и b

|a| = √(a ₁ ² + a ₂ ² + a ₃ ² )

|b| = √ (B ₁ ² + B ₂ ² + B ₃ ²)

N 9024 2 )

n 418618618618618618618618618618618618618618618618618618618618666666666666666666666666666666666666666666666666668. 2 ).0241

Кроме того, векторное векторное произведение также можно разложить на компоненты трехмерного вектора, т. е. i , j и k , которые все перпендикулярны друг другу. Формула векторного векторного произведения представлена как а ₁ б ₃ ) + к (а ₁ б ₂ – a ₂ b ₁ )

Примеры формулы векторного перекрестного произведения (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет векторного перекрестного произведения.

Вы можете скачать этот шаблон Excel с формулой векторного перекрестного произведения здесь. Шаблон Excel с формулой векторного перекрестного произведения.0856 b такие, что их скалярная величина равна |a| = 5 и |b| = 3, а угол между двумя векторами равен 30 градусов. Вычислите векторное перекрестное произведение двух векторов.

Решение:

Векторное перекрестное произведение двух векторов вычисляется по формуле, приведенной ниже: |б| sin θ n

a x б = 5 * 3 * sin30 п
a x b = 7,5 n

Следовательно, векторное произведение двух векторов равно 7,5.

Формула векторного произведения векторов – пример № 2

Рассмотрим пример двух векторов a (4, 2, -5) и b (2, -3, 7), таких, что a = 4i + 2j – 5k и b= 2i – 3j + 7k. Вычислите векторное перекрестное произведение двух векторов.

Решение:

Векторное перекрестное произведение двух векторов вычисляется по формуле, приведенной ниже j (a ₃ b ₁ – a ₁ b ₃ ) + k (a ₁ b ₂ – a ₂ b ₁ )

a x б = я {2 * 7 — (-5) * (-3)} + j {(-5) * 2 – 4 * 7} + k {4 * (-3) – 2 * 2}
a x b = -i + ( – 38 j ) + ( – 16 k 1 0 )

Следовательно, векторное перекрестное произведение двух векторов (4, 2, -5) и (2, -3, 7) равно (-1, -38, -16).

Формула векторного векторного произведения – Пример №3

Рассмотрим пример параллелограмма, смежные стороны которого определяются двумя векторами a (6, 3, 1) и b (3, -1, 5), такие что a = 6i + 3j + 1k и b = 3i – 1j + 5k. Вычислите площадь параллелограмма.

Solution:

Now, the vector cross product of the two vectors can be calculated using above formula as,

a x b = i (a ₂ b ₃ – a ₃ б ₂ ) + к (а ₃ б ₁ – а ₁ б ₃ ) + к (а ₁ B ₂-A ₂ B ₁)

A X B = I A X B = I A X B =
6. 1 * 3 – 6 * 5} + k {6 * (-1) – 3 * 3}
a x b = 16 i + ( – 27 j ) + ( – 15 k ) 3 3 3

Теперь площадь параллелограмма может быть получена путем вычисления величины векторного векторного произведения как,

|а х б| = √[(16) ² + (-27) ² + (-15) ² ]
|а х б| = 34,79

Следовательно, площадь параллелограмма равна 34,79.

Объяснение

Формулу векторного векторного произведения можно вывести, выполнив следующие шаги:

Шаг 1: Сначала определите первый вектор a и его векторные компоненты.

Шаг 2: Затем определите второй вектор b и его компоненты вектора.

Шаг 3: Далее определите угол между плоскостями двух векторов, который обозначается как θ .

Шаг 4: Наконец, формула векторного векторного произведения между векторами a и b может быть получена путем умножения абсолютных значений a и b , который затем умножается на синус угла (шаг 3) между двумя векторами, как показано ниже.

a x b = |a| |б| sin θ n

Актуальность и использование формулы векторного перекрестного произведения

Концепция векторного перекрестного произведения имеет различные применения в области инженерии, математики, вычислительной геометрии, физики, компьютерного программирования и т. д. Лежащая в основе концепция помогает нам в определении не только величины скалярной составляющей произведения двух векторов, но и дает направление равнодействующей. Кроме того, он также используется для определения угла между плоскостями двух векторов. Концепция векторных перекрестных произведений и их применение могут быть очень сложными и интересными.

Руководство по перекрестным продуктам

Дом
О
Страницы математики и статистики
R Программирование
Предметы Python

Этот пост будет о векторном произведении. Эту тему можно найти в курсе исчисления и векторов средней школы (который я знаю в Онтарио, Канада) или во вводном курсе линейной алгебры.

Здесь мы будем иметь дело с векторами в трехмерном пространстве. Кроме того, легче вычислять произведения, если знать, как вычислять (2 на 2) определители. При этом я предполагаю, что читатель знаком с детерминантами.

Содержание

Перекрестное произведение
Вспомогательные средства памяти
Свойства перекрестных произведений
Примеры
Практические задачи
Решения
Каталожные номера

Перекрестное произведение

Предположим, у нас есть два вектора $\mathbf{u} = (u_1, u_2, u_{3})$ и $\mathbf{v} = (v_1, v_2, v_{3})$ в трех измерениях. Перекрестное произведение $ ( ) $ двух векторов представляет собой (другой) вектор, перпендикулярный двум векторам.

Источник: https://upload. wikimedia.org/wikipedia/commons/thumb/b/b0/Cross_product_vector.svg/220px-Cross_product_vector.svg.png

Существует два способа вычисления перекрестных произведений. Первая формула не предполагает, что читатель знает определители. Эта формула задается следующим образом:

\[ \mathbf{u} \times \mathbf{v} = (u_{2}v_{3} — u_{3}v_{2}, u_{3}v_{ 1} — u_{1}v_{3}, u_{1}v_{2} — u_{2}v_{1} )\]

Вторая формула фактически аналогична приведенной выше, но в детерминантной записи . Эта формула:

Источник: http://quicklatex.com/cache3/c4/ql_926219b87045b16e28f37e299ca0d7c4_l3.png

Напомним, что определитель 2 на 2 равен \(ad — bc).

Вспомогательные средства для запоминания

Посмотрев на эти две формулы, вы, возможно, задаетесь вопросом, как я все это запоминаю!? При внимательном наблюдении вы можете обнаружить несколько закономерностей и придумать некоторые вспомогательные средства для запоминания.

В первой формуле все члены имеют формат $uv$. Если вы внимательно посмотрите на пронумерованные нижние индексы, то увидите, что числа зеркальны. В первой части имеем $u_{2}v_{3} — u_{3}v_{2}$. Первый нижний индекс — это 2, который идет с u, а второй нижний индекс — это 3 с v. После знака минус индексы зеркально отражены в порядке 3 и 2. Вторая часть имеет индексы 3,1,1, 3, а последняя часть имеет 1,2,2,1.

Для первой формулы одним из возможных вспомогательных средств памяти будут 2332, 3113 и 1221. Альтернативой могут быть 23, 31 и 12, поскольку у нас есть $u_{2}v_{3}$, представляющий 23, и $- u_ {3}v_{2}$, 31 для $u_{3}v_{1} — u_{1}v_{3}$ и 12 для $u_{1}v_{2} — u_{2 }v_{1}$.

Вторая формула предполагает, что читатель знаком с концепцией детерминантов в линейной алгебре. Обратите внимание, что верхняя строка в каждом определителе соответствует вектору $\textbf{u}$, а нижняя строка — вектору $\textbf{v}$. Одним из возможных вспомогательных средств для запоминания могут быть 23, -13 и 12, поскольку числа с индексами используются при переходе от крайнего левого столбца к крайнему правому столбцу. Отрицательное значение для -13 представляет собой отрицательный определитель.

Другой способ получить вторую формулу — использовать этот метод, состоящий из нескольких частей.

Сформируйте матрицу 2 на 3 в формате
Первую составляющую перекрестного произведения можно вычислить, удалив первый столбец приведенной выше матрицы и взяв полученный определитель 2 на 2.
Второй компонент состоит из удаления второго столбца матрицы 2 на 3 и взятия определителя
Последним и третьим компонентом перекрестного произведения $\textbf{u} \times \textbf{v}$ будет удаление последнего столбца матрицы и вычисление определителя
Результатом будет вторая формула, преобразованная в первую формулу.

Свойства перекрестных произведений

Как и с любой новой математической операцией, такой как перекрестное произведение, с ними связаны правила. В начальной школе были правила сложения, вычитания, умножения и деления.

Вот свойства перекрестного произведения для векторов $\textbf{u}$, $\textbf{v}$ и $\textbf{w}$ в трехмерном пространстве с $k $ как числовой скаляр. ($\textbf{0}$ здесь нулевой вектор в трехмерном пространстве)

\[ \textbf{u} \times \textbf{v} = — (\textbf{v} \times \textbf{u})\]
\[ \textbf{u} \times (\textbf{v} + \textbf{w}) = (\textbf{u} \times \textbf{v}) + (\textbf{u} \times \textbf {w}) \text{ (Умножение слева) }\]
\[(\textbf{u} + \textbf{v}) \times \textbf{w} = (\textbf{u} \times \textbf{w}) + (\textbf{v} \times \textbf {w}) \text{ (Умножение справа) }\]
\[k(\textbf{u} \times \textbf{v}) = (k \textbf{u}) \times \textbf{v} = \textbf{u} \times (k \textbf{v} ) \]
\[\textbf{u} \times \textbf{0} = \textbf{0} \times \textbf{u} \]
\[\textbf{u} \times \textbf{u} = \textbf{0} \]

Мы можем использовать формулу \[\textbf{u} \times \textbf{v} = (u_{2}v_{3} — u_{3}v_{2}, u_{3}v_{1} — u_{1}v_{3 }, u_{1}v_{2} — u_{2}v_{1} )\] или обозначение определителя формулы. Здесь будет использоваться детерминантная запись формулы.

Мы также вычисляем $\textbf{v} \times \textbf{u}$.

Вы также можете проверить свойство $\textbf{u} \times \textbf{v} = — (\textbf{v} \times \textbf{u})$. В этом случае $\textbf{u} \times \textbf{v} = (1, 10, 15 ) = — (-1, -10, -15) = — (\textbf{v} \times \textbf{ у})$. Пример 2 , -1)\). Найдите вектор, который перпендикулярен/ортогонален обоим векторам $\textbf{u}$ и $\textbf{v}$.

Векторное перекрестное произведение двух векторов представляет собой (третий) вектор, который перпендикулярен обоим двум векторам.

Найдем перекрестное произведение $\textbf{u} \times \textbf{v}$ следующим образом:

Вектор, перпендикулярный векторам $\textbf{u}$ и $\textbf{ v}$ равно $\textbf{u} \times \textbf{v} = (1, -3, 2)$.

определения, свойства, формулы, примеры и решения

Определение векторного произведения

Координаты векторного произведения

Свойства векторного произведения

Векторное произведение – примеры и решения

Геометрический смысл векторного произведения

Физический смысл векторного произведения

Векторное произведение векторов. Определение и его смысл

04.

Векторное произведение векторов

Векторное произведения. Векторное произведение — определения, свойства, формулы, примеры и решения

Координаты векторного произведения

Свойства векторного произведения

Векторное произведение – примеры и решения

Физический смысл векторного произведения

Определение векторного произведения.

Координаты векторного произведения.

Свойства векторного произведения.

Векторное произведение – примеры и решения.

Геометрический смысл векторного произведения.

Векторное произведение векторов | это… Что такое Векторное произведение векторов?

Содержание

Правые и левые тройки векторов

Определение

Свойства

Геометрические свойства векторного произведения

Алгебраические свойства векторного произведения

Выражение для векторного произведения в декартовых координатах

Обобщения

Кватернионы

Преобразование к матричной форме

Распространение на матрицы

Размерности, не равные трём

Алгебра Ли векторов

См. также

Ссылки

Литература

Векторное произведение векторов с примерами решения

Переходим к понятию векторного произведения

Примеры с решением

Пример 1.

Пример 2.

Пример 3.

Некоторые приложения к механике векторов

Формула векторного произведения

Перекрестное произведение единичных векторов 93$. (Мы определяем векторное произведение только в трех измерениях.

Загрузка апплета

Общие векторы

Статика: перекрестные произведения

Ключевые вопросы

Подраздел 2.8.1 Перекрестное произведение произвольных векторов

Пример 2.8.3. Трехмерное перекрестное произведение.

Подраздел 2.8.2 Перекрестное произведение единичных векторов

1.4: Перекрестное произведение — Mathematics LibreTexts

14.

Формула векторного перекрестного произведения | Примеры с шаблоном Excel

Формула векторного произведения векторов – пример № 2

Формула векторного векторного произведения – Пример №3

Объяснение

Актуальность и использование формулы векторного перекрестного произведения

Рекомендуемые статьи

Руководство по перекрестным продуктам

Добавить комментарий Отменить ответ