Как выражается медиана треугольника через три его стороны: Все формулы медианы треугольника

Свойство медианы треугольника

• Бугрышева Татьяна Николаевна, учитель математики

Разделы: Математика

---

Цели урока:

1. Обучающие — познакомить ребят с дополнительными соотношениями между элементами треугольника, повторить сопутствующий материал.
2. Развивающие — формирование умений анализировать, сравнивать , делать выводы, самостоятельно открывать блок новых знаний.
3. Воспитывающие — формирование навыков коммуникативности , умение быть внимательным, уметь представить свою работу.

Ход урока

1.

Оргмомент. Учитель приветствует ребят, настраивает на работу, приглашает к сотрудничеству и совместному творчеству.

2. Актуализация знаний.

Вопросы к классу:

1. Что называется параллелограммом?
2. Свойства, признаки параллелограмма.
3. О диагоналях параллелограмма.
4. Что называется медианой треугольника? Что вы знаете о медианах?
5. Какой треугольник называется равнобедренным?

3. Самостоятельная работа. (1 ученик работает на переносной доске, проектор на экране высвечивает таблицу возможных ответов)

Номер \ N	1	2	3	4
A	12	40	6	8 и 16
B	3	12	3	4 и 20
C	4	8	10	4 и 8
Оценка:

СР- медиана, СР=6 см, СО — ? .

ABCD – параллелограмм , АВ= 2 ВС= 4 Найти сумму квадратов длин диагоналей параллелограмма

ABCD – параллелограмм АВ = 2 АD = 3 A = 300 SABCD — ?

PABCD =24 см. AB — ? BC — ?

Проверка: на проекторе пошаговое открытие правильных ответов, работавший у доски представляет свое решение, класс обсуждает решение. Исправляются неточности и ошибки ( если они есть), отвечавший сразу получает оценку, при необходимости ему можно задать дополнительные вопросы. Ребята, работавшие на местах, ставят себе оценку сами.

Задание. Учитель обращает внимание класса на задачу:

Дано треугольник АВС АВ = 5 см ВС = 6 см АС = 4 см АМ = МС Найти : ВМ

Ребята начинают искать способы ее решения и высказывают мысль о том, что хорошо бы иметь формулу, дающую связь между длиной медианы треугольника и ее сторонами.

4. Постановка проблемы.

Учитель предлагает ребятам еще раз сформулировать возникшую у них проблему. Тема урока все еще не формулируется.

5. Открытие учениками новых знаний.

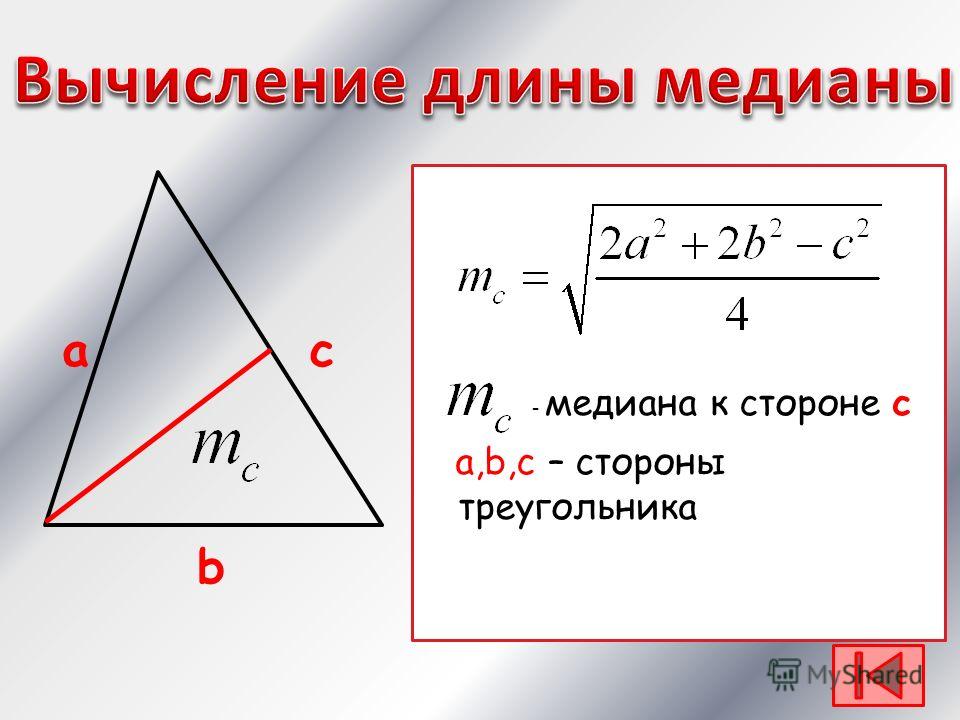
Учитель: давайте рассмотрим треугольник со сторонами a,b,c и медианой m _a, проведенной из вершины А.

1.) Продолжим медиану AD на расстояние DE=DA. 2.) Соединим т. В и т. Е, т.Е и т. С. Чем является полученный четырехугольник? Почему? 3.) Теперь используем теорему о том, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

АЕ² + ВС² = АВ² + ВЕ² + ЕС² + АС²

АЕ² +

АЕ²

АЕ =

m_a =

Ученики говорят о том, что нашли связь между длиной медианы треугольника и длинами его сторон.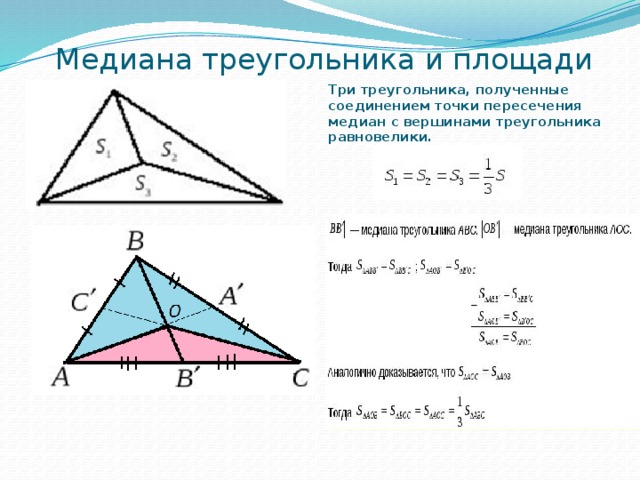

Формулируем теорему:

Длина медианы треугольника выражается формулой m_a=, где a, b, c –

длины сторон треугольника.

Учитель: Сможем ли мы теперь решить пропущенную задачу? Совместное решение.

Учитель: Давайте попробуем решить несколько заданий с помощью открытого нами свойства медианы треугольника. Можете ли вы, ребята, сейчас сформулировать тему нашего урока? Из предложенных вариантов выбирают самый удачный и записывают его.

6.Задача.

В равнобедренном треугольнике с боковой стороной, равной 4 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3 см.

Дано: теругольник АВС – равнобедренный АВ= ВС= 4 см AF=3 см Найти: АС

Выберите правильный рисунок.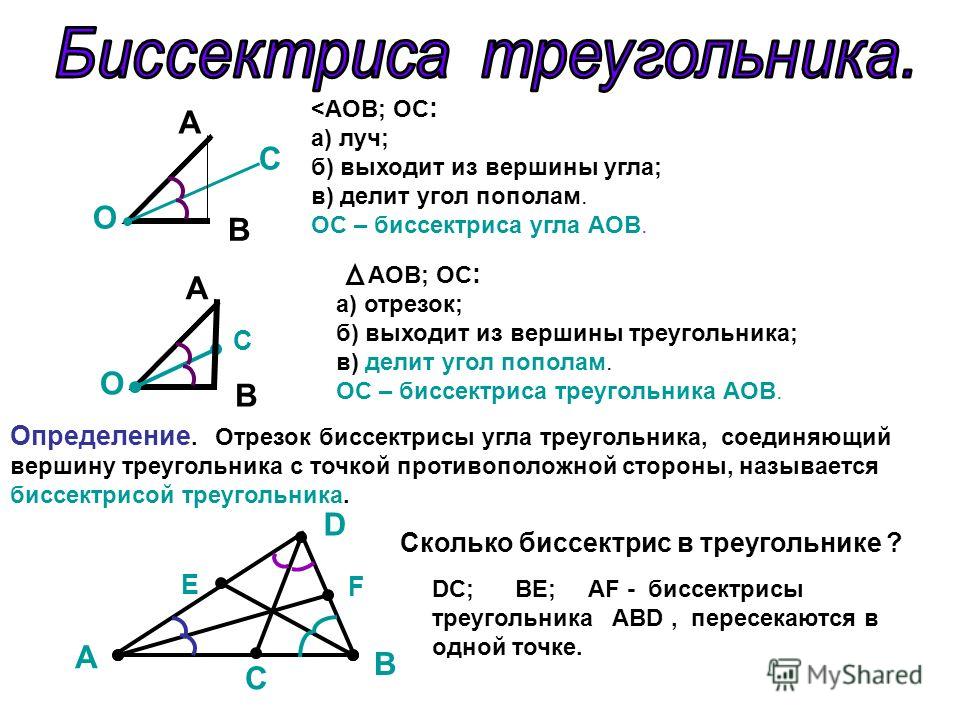

Решение: по свойству медианы треугольника AF =

АС= см.

Ответ: см.

7. Задача.

Основание равнобедренного треугольника равно 4 см, а медиана боковой стороны равна 5 см. Найти длину каждой из боковых сторон.

Дано: треугольник АВС – равнобедренный. АВ = ВС АС=4 см. AF=5 см Найти: АВ, ВС.

Решение: Пусть АВ = ВС= х (см) , тогда по свойству медианы треугольника имеем:

AF=, х=6.

Ответ: 6 см.

8. Итог урока.

Ребята, что нового вы узнали сегодня на уроке, все ли вам понятно? Можно поинтересоваться мнением учеников по структуре урока, какие моменты были особенно трудными.

9. Домашнее задание.

1. Записать теорему в тетрадь- памятку.

2. Придумать и решить задачу, где будут известны длины трех сторон треугольника, а найти надо его медиану.

Удачной работы! Спасибо за урок!

Список литературы:

1. Л.С. Атанасян, В.Ф. Бутузов, и др.”Геометрия 7-9” .
2. М.И.Сканави “Сборник задач по математике, для поступающих во ВТУЗы ”.

6.03.2008

Медиана треугольника. Теоремы связанные с медианами треугольника. Формулы для нахождения медиан — Студопедия.Нет

⇐ ПредыдущаяСтр 11 из 15Следующая ⇒

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

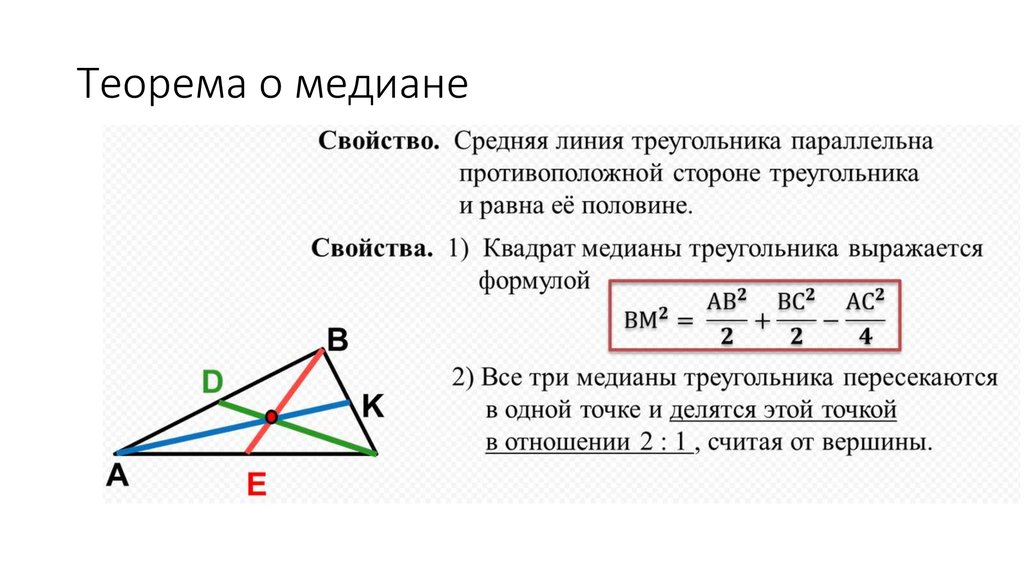
Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Длина медианы проведенной к стороне:  (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )

Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.   Дано: ∆ABC, СС₁, АА₁, ВВ

₁ — медианы
∆ABC. Доказать: и

. Д-во: Пусть М — точка пересечения медиан СС₁, АА₁ треугольника ABC. Отметим A₂ — середину отрезка AM и С₂ — середину отрезка СМ. Тогда A₂C₂ — средняя линия треугольника АМС. Значит,А₂ С₂ || АС

и A₂C₂ = 0,5*АС. С₁А₁ — средняя линия треугольника ABC. Значит, А₁С₁ || АС и А₁С₁ = 0,5*АС.

Четырехугольник А₂С₁А₁С₂ — параллелограмм, так как его противо­положные стороны А₁С₁ и А₂С₂ равны и параллельны. Следовательно, А₂М = МА

₁  и С₂М = МC₁. Это означает, что точки А₂ и M делят медиану АА₂ на три равные части, т. е. AM = 2МА₂ . Аналогично СМ = 2MC₁. Итак, точка М пересечения двух медиан АА₂ и CC₂ треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треу­гольника. Совершенно аналогично доказывается, что точка пересечения меди­ан АА₁ и BB₁ делит каждую из них в отношении 2:1, считая от вер­шин треугольника.

На медиане АА₁ такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА₁ иBB_1.

Таким образом, n

T2. Докажите, что отрезки, которые соединяют центроид с вер­шинами треугольника, делят его на три равновеликие части. Дано: ∆ABC ,  — его медианы.

Доказать:S_AMB =S_BMC =S_AMC. Доказательство.  и высота, проведенная из вершины В, у них общая. т.к. равны их основания  и высота, проведенная из вершины М, у них общая. Тогда

Аналогичным образом доказывается, чтоS_AMB = S_AMC. Таким образом,S_AMB = S_AMC = S_CMB .n

Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.

Свойства

1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

Вычисление длины биссектрисы

где:

l_c — длина биссектрисы, проведённой к стороне c,

a,b,c — стороны треугольника против вершин A,B,C соответственно,

p — полупериметр треугольника,

a_l,b_l — длины отрезков, на которые биссектриса l_c делит сторону c,

α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,

h_c — высота треугольника, опущенная на сторону c.

Метод площадей.

Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).

Можно выделить 2 направления этого метода:

1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур

2) Метод отношения S: основан на след опорных задачах:

 

 

Теорема Чевы

Пусть точки A’,B’,C’ лежат на прямых BC,CA,AB треугольника . Прямые AA’,BB’,CC’ пересекаются в одной точке тогда и только тогда, когда

Доказательство.

Обозначим через точку  пересечения отрезков   и . Опустим из точек С и А перпендикуляры на прямую ВВ₁ до пересечения с ней в точках Kи L соответственно (см. рисунок).

Поскольку треугольники  и  имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK :

Последнее равенство справедливо, так как прямоугольные треугольники и  подобны по острому углу.

Аналогично получаем и

Перемножим эти три равенства:

что и требовалось доказать.

Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.

Теорема (обратная теорема Чевы). Пусть точки A’,B’,C’ лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение

Тогда отрезки AA’,BB’,CC’ и пересекаются в одной точке.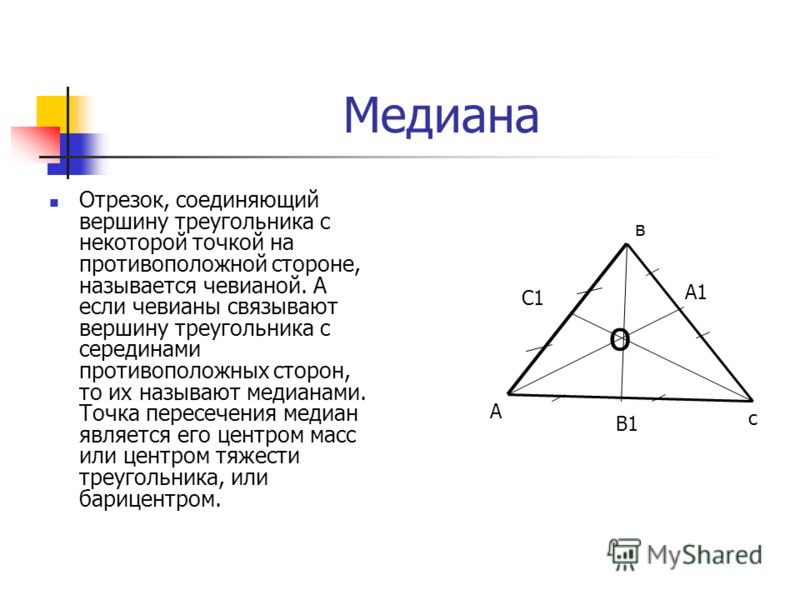

Теорема Менелая

Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C₁ – точка ее пересечения со стороной AB, A₁ – точка ее пересечения со стороной BC, и B₁ – точка ее пересечения с продолжением стороны AC. Тогда

Доказательство. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B₁C₁.

 

 

ТреугольникиAC₁B₁иCKB₁подобны (∟C₁AB₁= ∟KCB₁, ∟AC₁B₁= ∟CKB₁). Следовательно,

 

ТреугольникиBC₁A₁иCKA₁такжеподобны (∟BA₁C₁=∟KA₁C, ∟BC₁A₁=∟CKA₁). Значит,

Из каждого равенства выразим CK:

Откуда что и требовалось доказать.

Теорема (обратная теорема Менелая). Пусть дан треугольник ABC. Пусть точка C₁ лежит на стороне AB, точка A₁ – на стороне BC, а точка B₁ – на продолжении стороны AC, причем выполняется соотношение

Тогда точки A₁,B₁ и C₁ лежат на одной прямой.

---

Дата добавления: 2018-05-13; просмотров: 7951;

---

⇐ Предыдущая6789101112131415Следующая ⇒

---

Мы поможем в написании ваших работ!

Площадь треугольника по медианам

Площадь треугольника по медианам

По треугольнику ABC и его медианам AD, BE и CF постройте треугольник со сторонами AD, BE и CF.

а. Докажите, что треугольник единственный. Используйте GSP, чтобы связать строительство. То есть, если треугольник ABC изменить, то соответствующий изменяется и треугольник медиан.

б. Докажите, что площадь треугольника медиан равна трем четвертям. площади данного треугольника.

в. Докажите, что отношение периметра треугольника медианы периметра данного треугольника находятся между 0,75 и 1.0.

См. ЕМТ 668 Задание 6, пункты 1, 2 и 3.

---

 

Докажите, что медиана треугольника делит треугольник на две равные области.

  Подсказка:  Та же база, та же высота.

---

Докажите, что три медианы треугольника делят треугольник на шесть равных областей.

 

 

 

 

---

Докажите, что три медианы треугольника параллельны и каждая из них делится в отношении 2:1.

---

Даны три сегмента которые являются медианами треугольника, покажите построение треугольник.

---

Докажите, что площадь треугольника равна данный

 

, где u, v и w — длины медиан треугольника.

(Проблема 4651, Предложена Кием В. (Томас) Нго, Фолс-Черч, Вирджиния, школьная наука и математика, Том 98, номер 2, февраль 1998 г., с. 110.)

Полезный результат: Треугольник, образованный медианами данный треугольник будет иметь площадь, равную трем четвертям площади данный треугольник.

Если ABC — треугольник с медианами длин u, v и w и CGF представляет собой треугольник со сторонами той же длины, что и эти медианы. тогда отношение площади треугольника АВС к площади треугольника CGF равен 4 к 3. Треугольник CGF можно построить, сделав отрезок FG параллелен и конгруэнтен медиане BE, а сегмент CG параллелен и соответствует медиане AD. Отношение площадей можно доказать несколькими способами, но достаточно видеть, что площадь треугольника AFC составляет половину площади треугольника ABC треугольник CHF равен половине площади треугольника CGF, а треугольник AHF составляет одну четвертую площади треугольника AFC. Поэтому отношение площадей треугольника AFC и FHC составляет 4 к 3, поэтому отношение площади треугольника ABC в CGF составляет 4 к 3,

 

Следующий шаг. Используйте формулу Герона для площади треугольника со сторонами длиной u, v и w. Площадь треугольника с медианами длины u, v и w равна

.

 

 

Замена и упрощение приводят к результату.

No related posts.