Графики функций парабола: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

Графики функций парабола и кубическая парабола 7 класс | Методическая разработка по алгебре (7 класс) по теме:

Опубликовано 04.12.2014 — 21:32 — Бобовникова Ольга Геннадьевна

Графики функций парабола и кубическая парабола. Наглядные графики и таблица значений

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Функция y = и ее график.

Слайд 2

На основании определения функции каждому значению аргумента х из области определения R ( все действительные числа ) соответствует единственное значение функции y , равное Рассмотрим функцию заданную формулой y =

Слайд 3

а при х = –2 значение функции y = = 4 . y = Например при х = 3 значение функции y = = 9 ,

Слайд 4

х -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9 Изобразим график функции y = . Для этого присвоим аргументу х несколько значений, вычислим соответствующие значения функции y и внесем их в таблицу.

Слайд 5

Нанесем точки с вычисленными координатами (x ; y) на плоскость и соединим их плавной непрерывной кривой.

Слайд 6

и есть график исследуемой нами функции. Эта кривая, называющаяся параболой ,

Слайд 7

Функция y = и ее график.

Слайд 8

х -2 -1 0 1 2 y -8 — 1 0 1 8 Изобразим график функции y = . Для этого присвоим аргументу х несколько значений, вычислим соответствующие значения функции y и внесем их в таблицу.

Слайд 10

и есть график исследуемой нами функции. Эта кривая, называющаяся кубической параболой ,

По теме: методические разработки, презентации и конспекты

Рабочая программа элективного курса по математике «Построение графиков функций, уравнений и соответствий», 9 класс

Рабочая программа содержит пояснительную записку, цели и задачи элективного курса, требования к знаниям и умениям учащихся, формы и методы, используемые в преподавании, учебно-тематический план….

Урок «Построение графиков функций. Парабола» (8 кл)

Урок обобщения и систематизации знаний  по теме «Построение графиков функций&quot.. .

Графики функций, подготовка к ГИА, 9 класс

Тип урока: повторительно-обобщающее занятие.Формы работы учащихся на уроке: фронтальная, индивидуальная, элементы групповой деятельности.Основная технология, применяемая на уроке: технология уровневой…

График функции. Урок алгебры в 8 классе. (Урок математики в информационно-образовательной среде)

Разработка урока алгебры в 8 классе по теме «График функции» с применением УМК «Живая математика»…

Конспект урока с презентацией «Функции. Графики функции и их свойства» 10 класс

Конспект урока по теме  «Функции. Графики функции и их свойства» в 10 классе. Тип урока: Обобщение и систематизация знаний. К учебнику Алимова и др.Основная работа на уроке идет по презентации, т…

Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.

Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции….

Интерактивная презентация «Парабола и кубическая парабола» (7 класс)

         Интерактивная презентация «Парабола и кубическая парабола» (7 класс) составлена в программе MimioStudio. На страницах этой презентации даны только …

Поделиться:

 

01Математика — Профиль — Пересечение прямая/корень и парабола/парабола

По условию задачи рафики функций \(\displaystyle f\left(x\right)=a\sqrt{x} \) и \(\displaystyle g\left(x\right)=kx+b\) пересекаются в точке \(\displaystyle A{\small . }\) Самой точки \(\displaystyle A\) на рисунке не видно.

1. Найдем коэффициент \(\displaystyle a\) из уравнения функции \(\displaystyle f\left(x\right)=a\sqrt{x}{ \small .}\)

Заметим, что на графике функции \(\displaystyle f\left(x\right)=a\sqrt{x}\) отмечена точка с координатами \(\displaystyle (\color{blue}{4};\color{green}{5}){ \small .}\)

Значит, при подстановке её  координат \(\displaystyle x=\color{blue}4\) и \(\displaystyle y=\color{green}5\) в уравнение \(\displaystyle y=a \sqrt{x}\) получим верное равенство.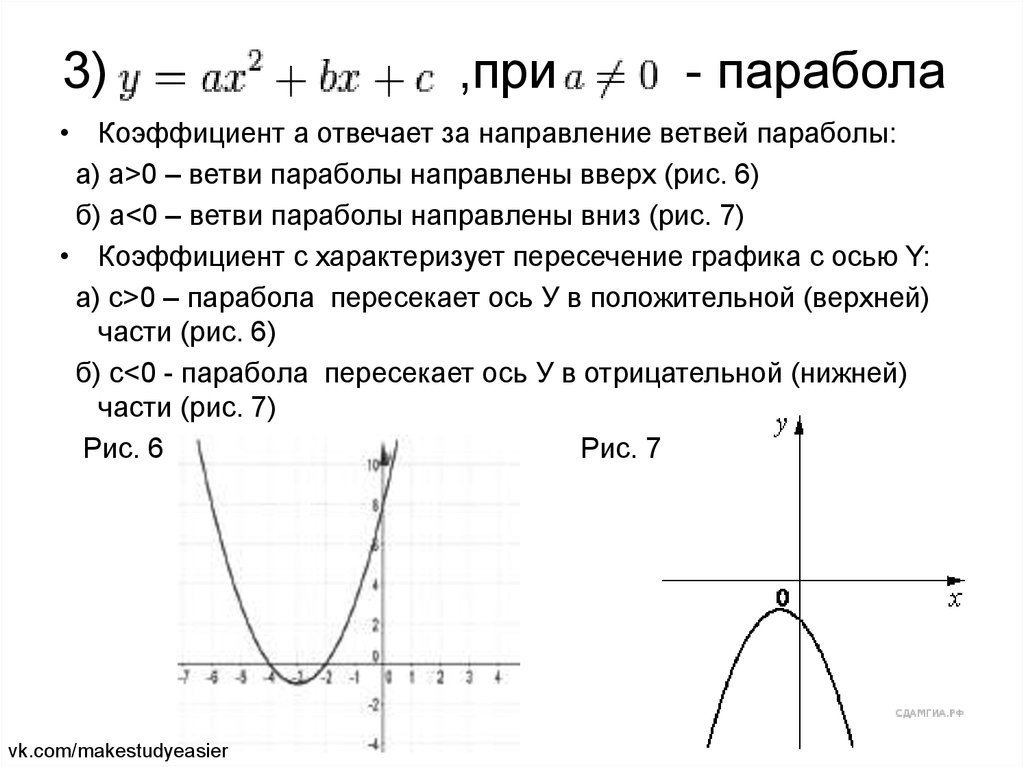

Подставляя, получаем уравнение:

\(\displaystyle \color{green}5=a\cdot \sqrt{\color{blue}4}{ \small ,} \)

\(\displaystyle 5=a \cdot 2{ \small ,} \)

откуда

\(\displaystyle a=2{,}5{ \small .}\)

Таким образом, исходная функция имеет вид:

\(\displaystyle f\left(x\right)=2{,}5\sqrt{x} \small.\)

2. Найдем коэффициенты \(\displaystyle k\) и \(\displaystyle b\) из уравнения прямой \(\displaystyle g\left(x\right)=kx+b{ \small .}\)

По рисунку видим, что точки \(\displaystyle С\) c координатами \(\displaystyle (2;-2)\) и \(\displaystyle D\) c координатами \(\displaystyle (4;-1)\) принадлежат графику функции \(\displaystyle g\left(x\right)=kx+b{ \small .}\)

 

Подставим координаты точек \(\displaystyle C(2;\,-2)\) и \(\displaystyle D(4;-1)\) в уравнение прямой \(\displaystyle y=kx+b\,{\small . } \)

Точка \(\displaystyle C(\color{blue}{ 2};\color{green}{-2}) \) имеет координаты \(\displaystyle x=\color{blue}{ 2}\) и \(\displaystyle y=\color{green}{ -2}{\small , }\) поэтому

\(\displaystyle \color{green}{-2}=k\cdot \color{blue}{ 2}+b \)
или, что то же самое,
\(\displaystyle 2k+b=-2{\small . }\)

Точка \(\displaystyle D(\color{blue}{ 4};\color{green}{ -1}) \) имеет координаты \(\displaystyle x=\color{blue}{ 4}\) и \(\displaystyle y=\color{green}{ -1}{\small , }\) поэтому

\(\displaystyle \color{green}{ -1}=k\cdot \color{blue}{ 4}+b {\small , }\)
или, что то же самое,
\(\displaystyle 4 k+b=-1{\small . } \)

Мы получили два уравнения для коэффициентов \(\displaystyle k \) и \(\displaystyle b {\small . }\) Запишем систему уравнений:

\(\displaystyle \left\{\begin{aligned}2k+b&=-2{\small , }\\4k+b&=-1{\small . }\end{aligned}\right.\)

Решим эту систему.

Решение системы

Таким образом, \(\displaystyle k=0{,}5 \) и \(\displaystyle b=-3{\small . } \)

Подставляя найденные значения для \(\displaystyle k \) и \(\displaystyle b \) в уравнение прямой \(\displaystyle y=kx+b{\small , } \) получаем:

\(\displaystyle y=0{,}5x-3{\small . } \)

3. Найдем абсциссу точки \(\displaystyle A{ \small .}\)

Точка \(\displaystyle A\) – это точка пересечения графиков функций \(\displaystyle f\left(x\right)=2{,}5\sqrt{x}\) и \(\displaystyle g\left(x\right)=0{,}5x-3{\small . 2-37x+36=0{\small.}\)

Корень \(\displaystyle x=1\) не удовлетворяет неравенству \(\displaystyle x\ge6{ \small .}\)

Корень \(\displaystyle x=36\) удовлетворяет неравенству \(\displaystyle x\ge6{ \small .}\)

Значит, решением иррационального уравнения \(\displaystyle 5\sqrt{x}=x-6\) является  \(\displaystyle x=36{ \small .}\)

Таким образом, абсцисса точки \(\displaystyle A\) равна \(\displaystyle 36{\small.}\)

Ответ: \(\displaystyle 36{\small.}\)

Объяснение урока: Построение графика квадратичных функций

В этом объяснении мы узнаем, как построить график любой квадратичной функции, заданной в ее стандартная, вершинная или факторизованная форма с использованием ключевых особенностей графика функции.

Напомним, что квадратичная функция — это полиномиальная функция, наибольшая порядок одной из переменных равен 2. Он также принимает вид в определении приведен ниже.

Определение: квадратичная функция

Квадратичная функция — это функция, которую можно описать как 𝑓(𝑥)=𝑎𝑥+𝑏𝑥+𝑐, где 𝑎, 𝑏 и 𝑐∈ℝ и 𝑎≠0.

График квадратичной функции мы называем параболой , так как это форму он принимает.

В зависимости от того, находится ли 𝑎 в 𝑓(𝑥)=𝑎𝑥+𝑏𝑥+𝑐 положительно или отрицательный, парабола открывается вверх или вниз, как показано на рисунках ниже.

Существуют различные подходы к построению графиков квадратичных функций. Первый использует таблица значений. Это означает, что при выборе или при задании значений для 𝑥, затем мы генерируем значения для 𝑦, подставляя их в квадратичную функцию мы пытаемся построить график. Как только мы это сделали, мы можем использовать упорядоченные пары для нанесите координаты на набор осей, а затем нарисуйте график квадратичная функция, используя эти координаты и наши знания о форме квадратичной функции.

Мы изучим, как набросать график квадратичной функции в нашем первом уроке. пример.

Пример 1. Нахождение графика квадратичной функции с помощью Таблица значений

Какой из следующих графиков представляет уравнение 𝑦=𝑥+3?

Ответ

Чтобы найти график, представляющий функцию 𝑦=𝑥+3 мы можем использовать таблицу значений. Для этого нам нужно выбрать некоторые значения для 𝑥, которые мы подставим, чтобы найти их соответствующие 𝑦-значения, которые затем составляют координаты, которые мы можно использовать для наброска графика.

Так как квадратичная функция является параболой, полезно использовать не менее 5 координаты для начала, чтобы набросать график, а затем больше, если это непонятно какой формы. Неважно, какие 𝑥-значения вы обычно выбирать, но значения, близкие к нулю, легче вычислить. Поэтому мы выберем −2, −1, 0, 1 и 2 в качестве наших 𝑥-значений для начала с, как видно из таблицы значений ниже.

𝑥	−2	−1	0	1	2
𝑦

9003 9000 3 9004-1 9000. 9004 до расчета. 𝑥-значение выше в функцию 𝑦=𝑥+3. При этом получаем следующее.

Когда 𝑥=−2, 𝑦=(−2)+3𝑦=7.

Когда 𝑥=−1, 𝑦=(−1)+3𝑦=4.

Когда 𝑥=0, 𝑦=(0)+3𝑦=3.

Когда 𝑥=1, 𝑦=1+3𝑦=4.

Когда 𝑥=2, 𝑦=2+3𝑦=7.

Рассчитав значения 𝑦, теперь мы можем поместить их в наша таблица значений.

𝑥	−2	−1	0	1	2
𝑦	7	4	3	4	7

This means что наша функция проходит через точки (−2,7), (−1,4), (0,3), (1,4), и (2,7). Если мы нанесем их на набор осей, мы получим следующий.

Глядя на график, мы видим, что он имеет форму обращенной вверх парабола, что и следовало ожидать в качестве коэффициента 𝑥-член положительный. Также представляется, что переломный момент квадратичная функция находится в точке (0,3).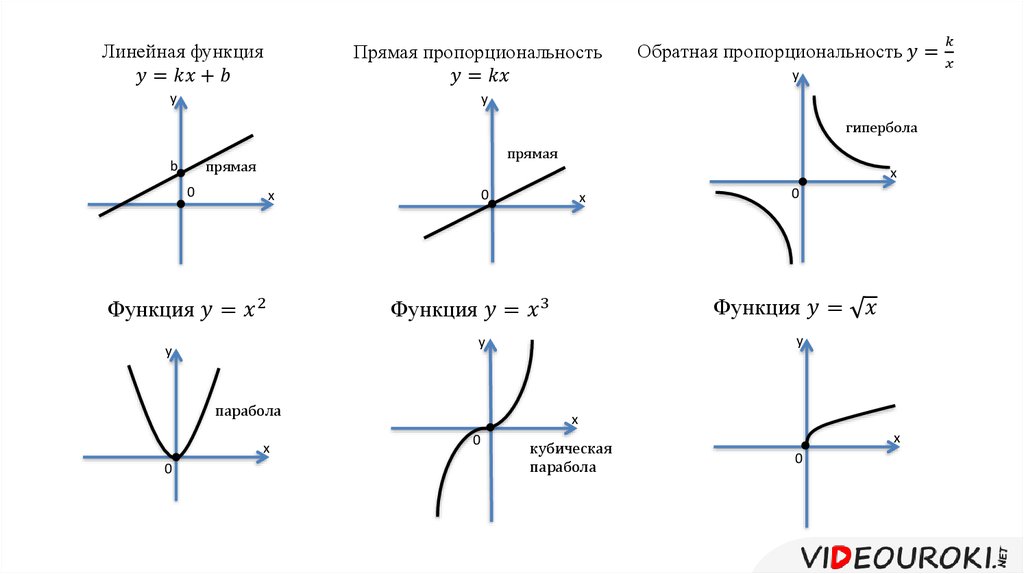 Если мы нарисуем график функции, проходящей через точки, получаем следующее.

Если сравнить этот график с приведенными вариантами, то видно, что только вариант E имеет ту же точку поворота, что и наш график. Мы также можем видеть, что график в варианте Е проходит через те же точки, что и наш график; следовательно, ответ должен быть вариантом E.

Из предыдущего примера видно, что использование таблицы значений — это один из методов. нахождения графика квадратичной функции. Однако мы также можем найти ключевые особенности графика и использовать их для построения графика функций.

В первом примере функция была задана в стандартной форме . Это когда квадратичная функция записывается в виде 𝑦=𝑎𝑥+𝑏𝑥+𝑐,𝑎≠0.

Когда функция записана в такой форме, мы можем легко найти 𝑦-перехват из функции. Мы также можем найти поворот точка, называемая вершина и 𝑥-перехваты для построения графика функция.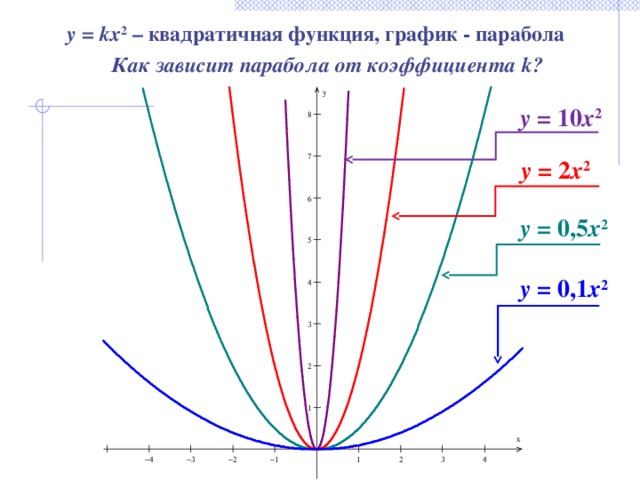

Сначала мы обсудим, как найти 𝑦-координату квадратичная функция в стандартной форме. Теперь, чтобы найти 𝑦-перехват любой функции воспользуемся тем, что 𝑥-координата равна нулю, и подставим 𝑥=0 в функцию. Делая это с квадратичной функцией в стандартной форме дает нам 𝑦=𝑎(0)+𝑏(0)+𝑐𝑦=𝑐.

Следовательно, 𝑦-перехват (0,𝑐) квадратичной функции в стандартная форма — 𝑐, постоянный член.

Во-вторых, мы обсудим, как найти 𝑥-перехваты квадратичной функции в стандартной форме. Как и раньше, чтобы найти 𝑥-перехват любой функции, воспользуемся тем, что 𝑦-координата равна нулю, и подставим 𝑦=0 в функцию. Делая это с квадратичной функцией в стандартная форма дает нам 0=𝑎𝑥+𝑏𝑥+𝑐.

Напомним, что для решения квадратного уравнения, равного нулю, у нас есть три ключа алгебраические методы: разложение на множители, завершение квадрата и квадратичная формула. Поскольку некоторые квадратичные числа неразложимы, мы можем использовать либо завершение квадрат или квадратичная формула. Обычно мы будем использовать квадратичную формулу в случаях, когда функция находится в стандартной форме. Вспомним квадратное формула.

Определение: Квадратная формула

Чтобы решить квадратное уравнение в форме 𝑎𝑥+𝑏𝑥+𝑐=0, 𝑎≠0, с переменной 𝑥 и константы 𝑎, 𝑏 и 𝑐, мы можем использовать квадратичную формулу для решения 𝑥, когда 𝑏−4𝑎𝑐 больше или равно нулю. 𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎.

Следовательно, используя приведенную выше формулу, когда они существуют, 𝑥-перехваты квадратичной функции в стандартной форме −𝑏−√𝑏−4𝑎𝑐2𝑎,0 и −𝑏+√𝑏−4𝑎𝑐2𝑎,0.

В-третьих, мы обсудим, как найти вершину квадратичной функции в стандартная форма. Поскольку квадратичные функции симметричны относительно вершины, то линия симметрии проходит через вершину вертикально. Это также означает, что линия симметрии проходит через середину 𝑥-перехваты. Используя этот факт, мы можем вывести формулу для нахождения 𝑥-координата вершины.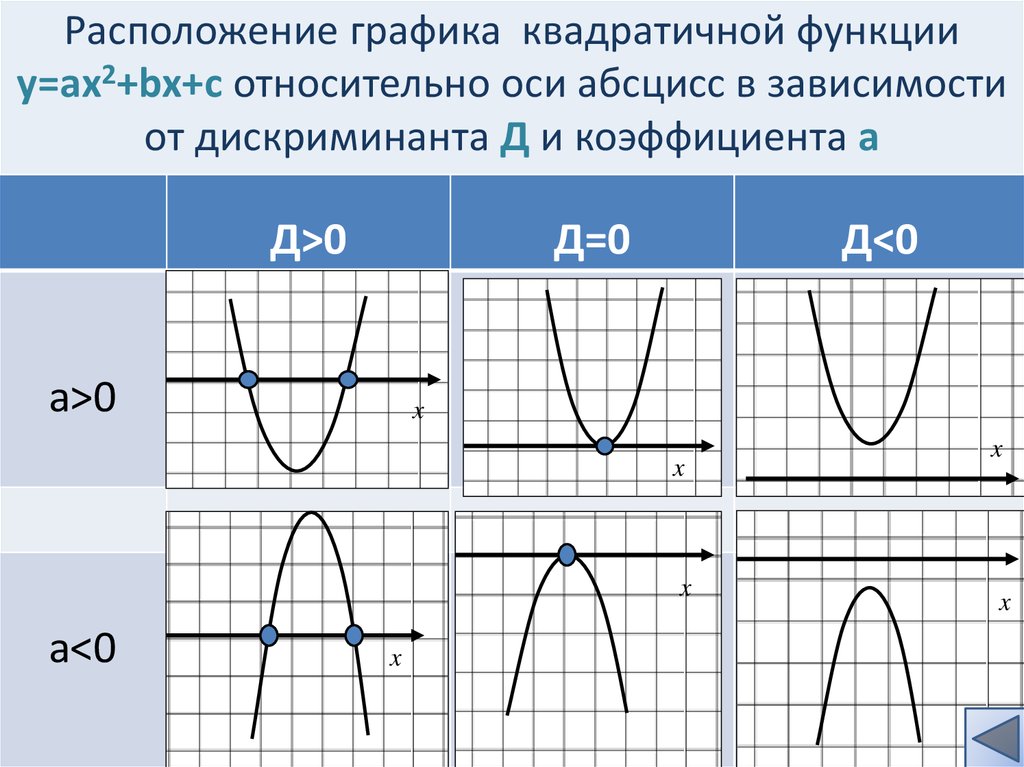

Так как 𝑥-координата вершины является серединой 𝑥-перехватов, то из средней точки получаем формула: 𝑥=𝑥+𝑥2=+2.√√

Теперь, с −√𝐎𝑏−4𝑊 и +√𝑏−4𝑎𝑐 сократим, получим 𝑥=+2=−𝑏2𝑎.

Следовательно, чтобы найти 𝑥-координату вершины квадратичной функции в стандартной форме, воспользуемся формулой 𝑥=−𝑏2𝑎.

Чтобы найти 𝑦-координату вершины, подставим 𝑥-координата обратно в квадратичную функцию. Мы можем использовать ту же формулу для вершины даже в том случае, когда мы не имеют двух 𝑥-перехватов.

Как только мы нашли 𝑦-координату, 𝑥-координаты и вершина, мы можем использовать эти функции для наброска график квадратичной функции. Мы также можем проверить, является ли коэффициент положительного или отрицательного члена 𝑥, чтобы определить, является ли парабола открывается вверх или вниз, соответственно, чтобы помочь нам нарисовать график. Давайте обобщим это в руководстве ниже.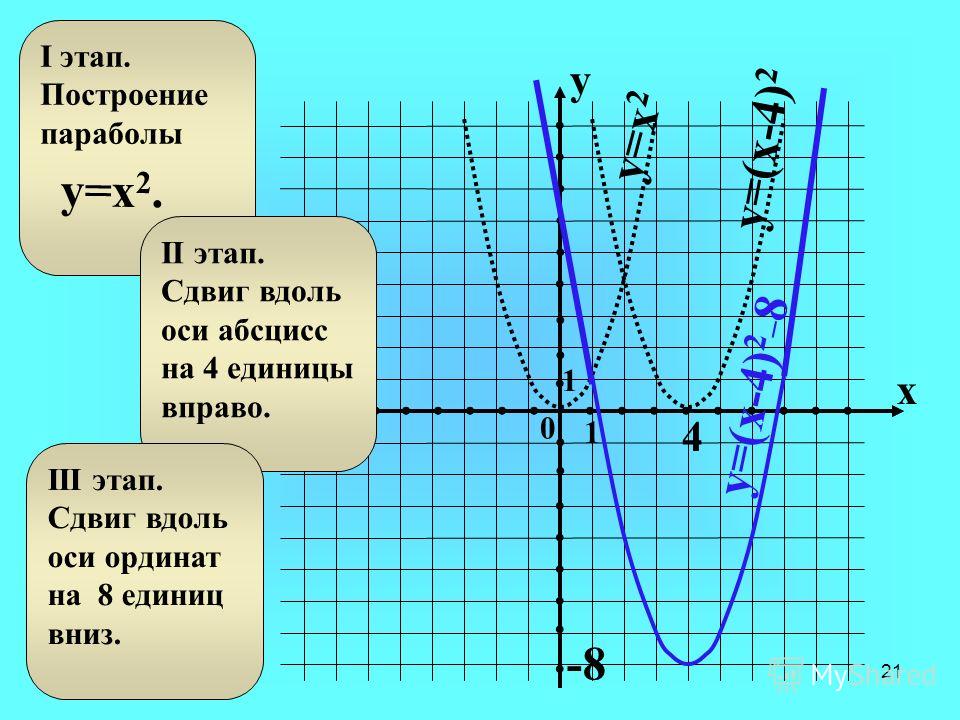

Практическое руководство. Поиск основных признаков графика квадратичной функции в Стандартная форма

Для квадратичной функции в стандартной форме 𝑦=𝑎𝑥+𝑏𝑥+𝑐, 𝑎≠0, мы можем нарисовать его график, найдя ключ особенности и направление, в котором он открывается с помощью следующих шагов.

Шаг 1: Нахождение 𝒚 -перехват

𝑦-перехват равен (0,𝑐).

Шаг 2: Нахождение 𝒙 -перехватов

Когда они существуют, 𝑥-перехваты −𝑏−√𝑏−4𝑎𝑐2𝑎,0 и −𝑏+√𝑏−4𝑎𝑐2𝑎,0, которые находятся по квадратичной формуле (или иным образом).

Шаг 3: Нахождение вершины

𝑥-координата вершины 𝑥=−𝑏2𝑎, а 𝑦-координата находится подстановкой 𝑥-координата в функцию.

Шаг 4. Определение направления графика вверх или вниз

График открывается вверх, если 𝑎>0, и вниз если 𝑎0.

Далее найдем график квадратичной функции в стандартной форме, используя шаги, которые мы обсуждали выше.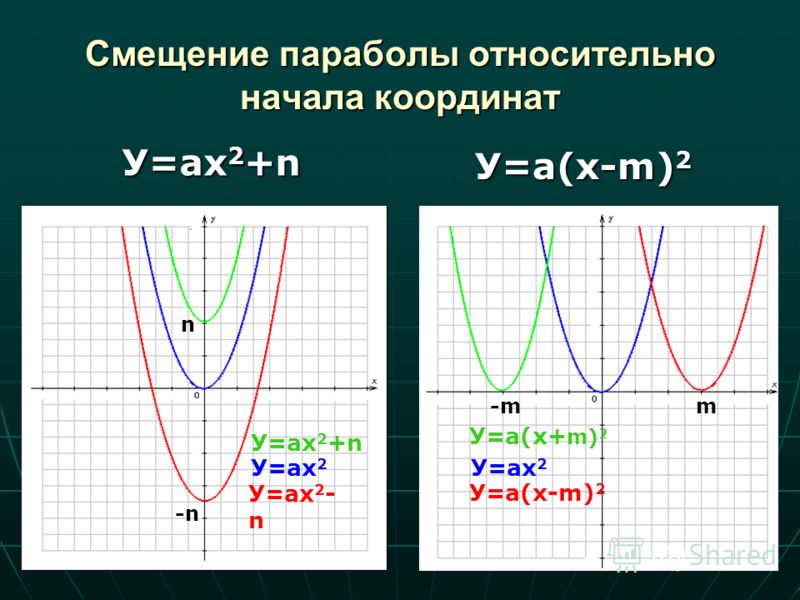

Пример 2. Нахождение графика квадратичной функции в Стандартная форма

Какой из следующих графиков представляет уравнение 𝑦=−5𝑥−10𝑥+6?

Ответ

Чтобы найти график функции 𝑦=−5𝑥−10𝑥+6, мы можем сначала найти его ключевые особенности, а затем использовать их для построения графика.

Мы видим, что квадратичная функция находится в стандартной форме или в форме 𝑦=𝑎𝑥+𝑏𝑥+𝑐,𝑎≠0.

Когда квадратичная функция находится в этой форме, мы используем определенные методы для найти 𝑦-перехват, 𝑥-перехват и вершину график.

Мы знаем, что 𝑦-перехват происходит, когда 𝑥-координата равна нулю. Таким образом, мы получаем 𝑦-координата 𝑐, которая в случае 𝑦=−5𝑥−10𝑥+6 равно 6. Итак, 𝑦-перехват равен (0,6).

Точно так же мы знаем, что 𝑥-перехват происходит, когда 𝑦-координата равна нулю. Это дает нам 0=−5𝑥−10𝑥+6, которое является квадратным уравнением.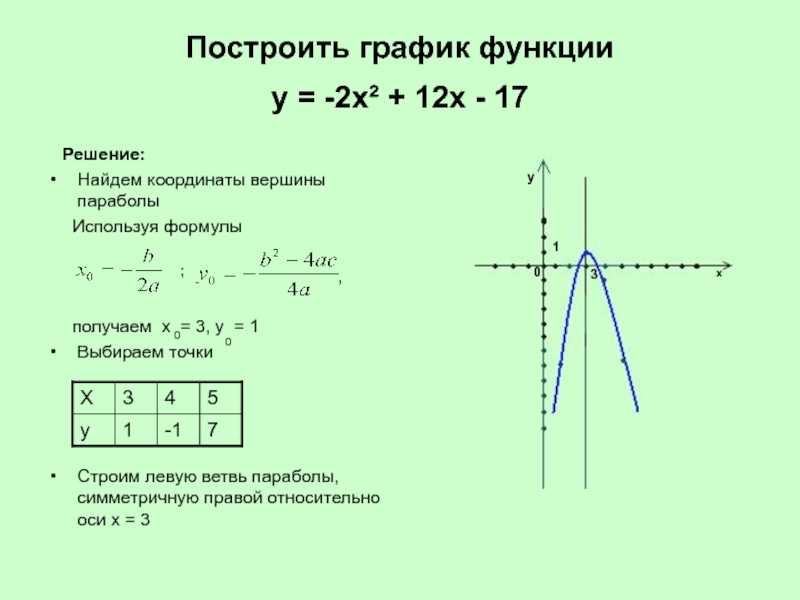 Напомним, что для решения квадратного уравнения можно использовать разложение на множители, завершение квадрата или квадратичная формула. Так как это не появляется легко разложить на множители, и, поскольку заполнить квадрат не так просто без дробей, мы будем использовать квадратную формулу.

Квадратичная формула утверждает, что для решения уравнения в форме 0=𝑎𝑥+𝑏𝑥+𝑐, 𝑎≠0, то имеем 𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎.

Для уравнения 𝑦=−5𝑥−10𝑥+6, где 𝑎=−5, 𝑏=−10 и 𝑐=6, это дает нам 𝑥=-(-10)±(-10)-4(-5)(6)2(-5)=10±√220-10=5±√55-5𝑥=-2,48…𝑥=0,48…. или

Следовательно, 𝑥-перехваты (−2,48,0) и (0,48,0), исправить до 2 знаков после запятой.

Чтобы найти 𝑥-координату вершины в стандартной форме, мы можно найти середину 𝑥-перехватов, что дает нас 𝑥=-2,48+0,482=-1.

Чтобы найти 𝑦-координату вершины, подставляем 𝑥-координата, −1, в функцию 𝑦=−5(−1)−10(−1)+6=−5+10+6=11. 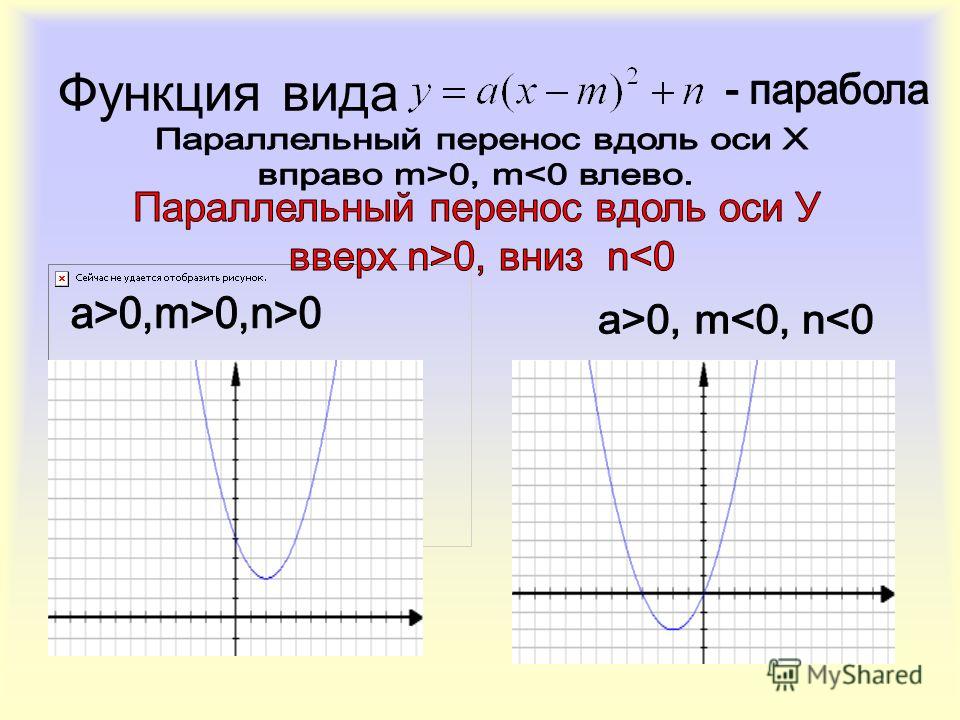

Следовательно, координаты вершины равны (−1,11).

Теперь, когда мы нашли точки пересечения и вершины, мы можем нарисовать график функция. Разложив эту информацию по набору осей, получим следующее.

Используя эту информацию, мы можем нарисовать график. Кроме того, мы также можем использовать коэффициент 𝑥-члена, который для 𝑦=−5𝑥−10𝑥+6 отрицательно, чтобы сказать нам, что функция открывается вниз. Набросав график, мы получим следующее.

Сравнивая это с различными опциями, мы видим, что открываются только опции D и E вниз, так что это должен быть один из этих вариантов. Мы можем видеть с вершины что вариант D имеет ту же вершину, что и наш граф. Следовательно, ответ должна быть опция D.

Рассмотрев, как набросать график, где функция находится в стандартной форме, теперь мы обсудим, как набросать график, где функция находится в форма вершины .

Под формой вершин мы подразумеваем форму, позволяющую легко считывать координаты вершины из функции. Здесь функция имеет вид 𝑦=𝑎(𝑥−ℎ)+𝑘,𝑎≠0,

Когда функция находится в этой форме, координаты вершины (ℎ,𝑘).

Чтобы набросать граф в виде вершин, полезно найти ключевые особенности граф, 𝑥-перехваты, 𝑦-перехват, и вершина (так же, как мы сделали для стандартной формы).

Как и прежде, для нахождения координат 𝑦-перехвата положим 𝑥=0 и найти 𝑦. Аналогично, чтобы найти координаты 𝑥-перехваты, мы устанавливаем 𝑦=0 и решаем для 𝑥. Поскольку форма вершин аналогична той, что мы получаем при заполнении квадрата, то это обычно лучший метод для решения квадратного уравнения.

Чтобы расшифровать, открывается ли график вверх или вниз, мы используем 𝑎 как и прежде, и является ли он положительным или отрицательным, чтобы определить, открывается ли график вверх или вниз соответственно.

Со всеми найденными ключевыми функциями мы можем использовать их для построения графика квадратичного функция в вершинной форме. Это кратко изложено в руководстве ниже.

Практическое руководство. Поиск основных признаков графика квадратичной функции в Форма вершины

Для квадратичной функции в форме вершины 𝑦=𝑎(𝑥−ℎ)+𝑘, 𝑎≠0 , мы можем нарисовать его график, найдя его ключевые особенности и направление, в котором он открывается, выполнив следующие действия.

Шаг 1. Нахождение вершины

Вершина (ℎ,𝑘).

Шаг 2: Нахождение 𝒚 -Пересечение

𝑦-пересечение происходит, когда 𝑥=0. Чтобы найти его, подставьте 𝑥=0 в функцию и найдите 𝑦.

Шаг 3: Нахождение 𝒙 -перехватов

Когда они существуют, 𝑥-перехваты имеют место, когда 𝑦=0. Чтобы найти их, подставьте 𝑦=0 в функцию и найдите 𝑥, заполнив квадрат, или иным образом.

Шаг 4. Определение направления графика вверх или вниз

График открывается вверх, если 𝑎>0, и вниз если 𝑎0.

В следующем примере мы рассмотрим, как найти график квадратичного функция в вершинной форме путем нахождения признаков графа.

Пример 3. Нахождение графика квадратичной функции в Vertex Form

Какой из следующих графиков представляет уравнение 𝑦=2(𝑥+3)−2?

Ответ

Нас просят найти график функции 𝑦=2(𝑥+3)−2. Мы видим, что квадратичный функция находится в вершинной форме, которая обычно 𝑦=𝑎(𝑥−ℎ)+𝑘,𝑎≠0.

Чтобы нарисовать функцию в виде вершины, мы можем использовать особенности графика чтобы помочь нам.

Первая функция, которую мы можем найти, как следует из названия, это вершина. Как правило, это (ℎ,𝑘) для 𝑦=𝑎(𝑥−ℎ)+𝑘. Следовательно, для функции 𝑦=2(𝑥+3)−2, вершина находится в (−3,−2). Обратите внимание, что на данный момент только два из наших вариантов имеют одинаковые значения.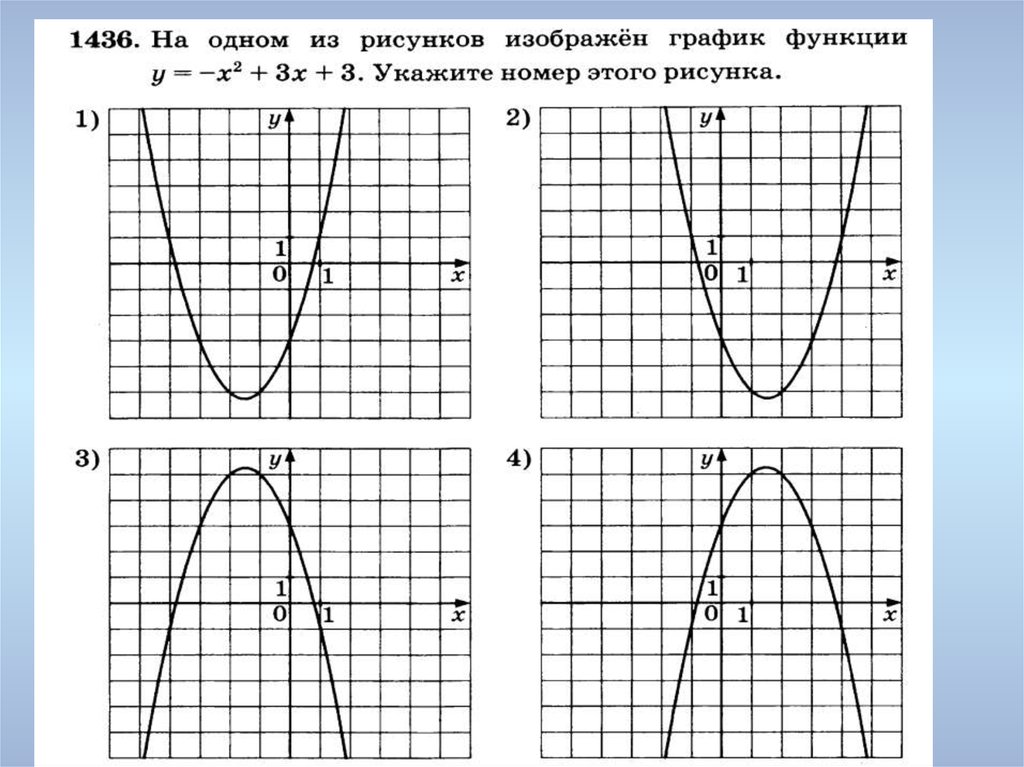 вершина, и мы можем сделать вывод, какой это вариант, посмотрев, является ли 𝑎 положительный или отрицательный, но мы рассмотрим, как график функции, как если бы мы не могли расшифровать это.

Во-вторых, мы можем найти 𝑦-перехват. Для всех функций, 𝑦-перехват — это когда 𝑥=0, поэтому мы можем найти значение 𝑦 подставив 𝑥=0 в 𝑦=2(𝑥+3)−2. Это дает нам 𝑦=2(0+3)−2=2(9)−2=16.

Следовательно, 𝑦-перехват (0,16).

В-третьих, мы можем найти 𝑥-перехваты. Как и раньше, мы знаем, что для всех функций 𝑥-перехваты происходят, когда 𝑦=0, поэтому мы можем найти 𝑥-перехваты по подставляя 𝑦=0 в функцию и решая для 𝑥. Это дает нам 0=2(𝑥+3)−2,

Так как это квадратное уравнение, нам нужно использовать либо разложение на множители, завершая квадрат или квадратичная формула, чтобы решить это. Так как это уже частично решается методом дополняя квадрат, мы склонны использовать этот метод для решения уравнений в вершинная форма.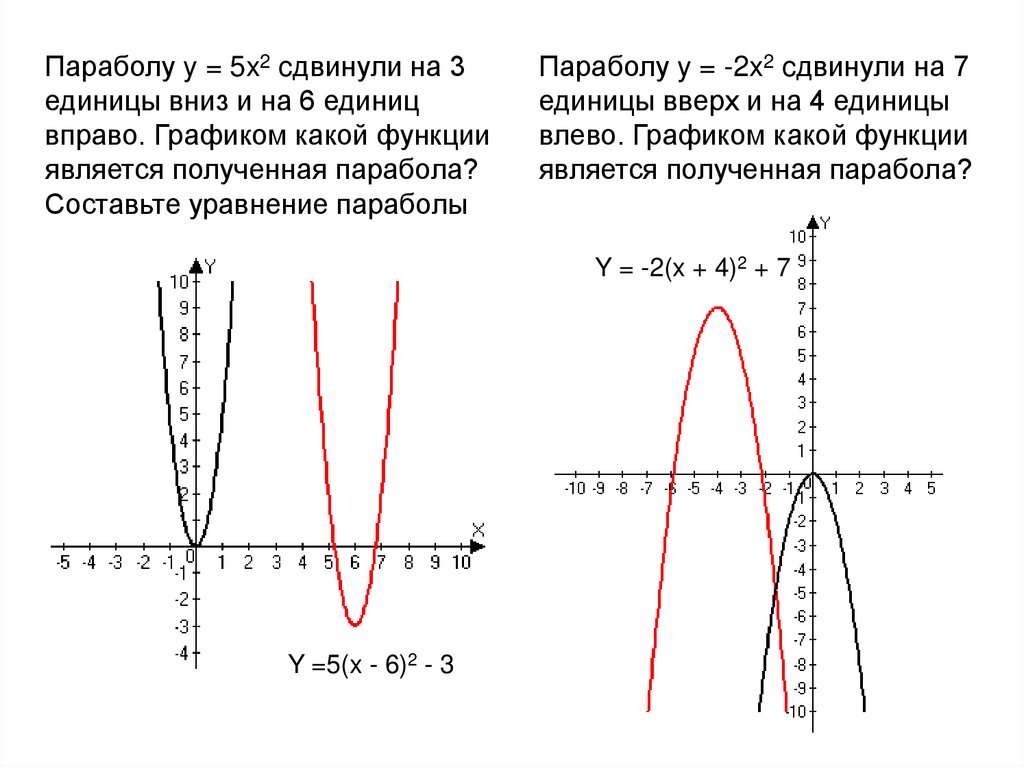 Это дает нам 0=2(𝑥+3)−22(𝑥+3)=2(𝑥+3)=1𝑥+3=±√1𝑥=−3±1𝑥=−4𝑥=−2.или

Следовательно, 𝑥-перехваты (−4,0) и (−2,0).

Найдя вершину, 𝑦-перехват и 𝑥-перехваты, теперь мы можем построить их на некоторых осях чтобы помочь построить график функции, как показано ниже.

Используя эту информацию, мы можем нарисовать график. Далее мы можем использовать является ли 𝑎 положительным или отрицательным, чтобы определить, открывается ли график вверх или вниз. Так как 𝑎=2, что положительно, то график открывается вверх. Набросав график, мы получим следующее.

Из приведенных вариантов мы видим, что варианты B, C и D открываются вверх, поэтому наш график должен быть одним из них. Мы видим, что вариант D имеет то же самое 𝑥-перехваты и вершина; следовательно, ответ должен быть вариант Д.

Рассказав, как построить график функции в стандартных и вершинных формы, мы теперь обсудим, как набросать график функции в факторизованных форма . Факторная форма — это когда квадратичная функция записывается как произведение его факторы или 𝑦=𝑎(𝑥−𝑝)(𝑥−𝑞),𝑎≠0.

Как и в случае с другими формами, мы можем найти ключевые особенности графика, которые помогут нам график функции.

В таком виде легко расшифровать 𝑥-перехваты функция. Мы можем определить 𝑥-перехваты, полагая 𝑦=0 и найти 𝑥. Это дает нам 0=𝑎(𝑥−𝑝)(𝑥−𝑞), а так как один из множителей должен быть равен нулю, то 𝑥=𝑝𝑥=𝑞.или

Таким образом, 𝑥-перехваты равны (𝑝,0) и (𝑞,0).

Чтобы найти 𝑦-перехваты, мы просто подставляем 𝑥=0 в функцию и найти 𝑦.

Чтобы найти координаты вершины, воспользуемся симметрией графа относительно вершина; мы знаем, что вершина является серединой 𝑥-перехваты, означающие, что 𝑥-координата вершина находится на полпути между 𝑥-перехватами. С использованием формула средней точки дает нам 𝑥=𝑥+𝑥2𝑥=𝑝+𝑞2.

Следовательно, 𝑥-координата вершины равна 𝑥=𝑝+𝑞2.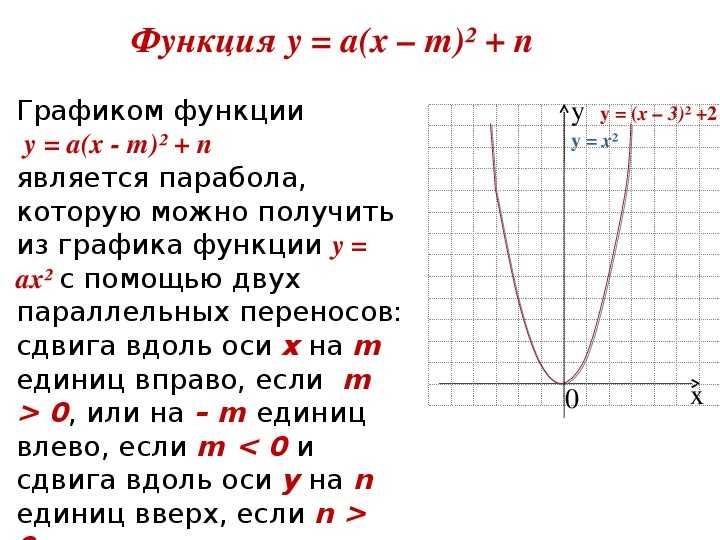 Чтобы найти 𝑦-координату, мы подставляем ее обратно в функцию и решить для 𝑦.

Чтобы расшифровать, открывается ли график вверх или вниз, мы используем 𝑎 как и раньше, и является ли он положительным или отрицательным, чтобы определить если график открывается вверх или вниз соответственно.

Давайте обобщим эти пункты в руководстве ниже.

Практическое руководство. Нахождение признаков графика квадратичной функции в факторизованной форме

Для квадратичной функции в факторизованной форме 𝑦=𝑎(𝑥−𝑝)(𝑥−𝑞), 𝑎≠0, мы можем нарисовать его график, найдя его ключевые особенности и направление, в котором он открывается, используя следующие шаги.

Шаг 1: Нахождение 𝒙 -Перехватов

𝑥-перехватов (𝑝,0) и (𝑞,0).

Шаг 2: Нахождение 𝒚 -Пересечение

𝑦-пересечение происходит, когда 𝑥=0. Чтобы найти его, подставьте 𝑥=0 в функцию и найти 𝑦.

Шаг 3: Нахождение вершины

𝑥-координата вершины 𝑥=𝑝+𝑞2. Чтобы найти 𝑦-координату, подставьте ее в функцию и решить для 𝑦.

Шаг 4. Определение направления графика вверх или вниз

График открывается вверх, если 𝑎>0, и вниз, если 𝑎0.

В следующем примере мы рассмотрим, как найти график квадратичного функции в факторизованной форме путем нахождения признаков графика.

Пример 4. Нахождение графика квадратичной функции в Factored Form

Какой из следующих графиков представляет уравнение 𝑦=(𝑥+4)(𝑥−2)?

Ответ

Чтобы найти график квадратичной функции 𝑦=(𝑥+4)(𝑥−2), мы можем найти особенности графика и использовать их для наброска графика. Мы найдем пересечения и вершины для построения графика функции.

Поскольку функция находится в факторизованной форме, как в 𝑦=𝑎(𝑥−𝑝)(𝑥−𝑞),𝑎≠0, то легко сначала найти его 𝑥-перехваты, как это (𝑝, 0) и (𝑞,0).

Итак, для квадратичной функции 𝑦=(𝑥+4)(𝑥−2), 𝑥-перехваты (−4,0) и (2,0). Обратите внимание, что на этом этапе мы можем сделать вывод, какой из вариантов верно, но для полноты картины рассмотрим, как построить график функции с помощью все особенности.

Далее мы можем найти координаты 𝑦-перехвата по подставляя 𝑥=0. Это дает нам 𝑦=(0+4)(0−2)𝑦=−8.

Следовательно, координаты 𝑦-перехвата равны (0,−8).

Чтобы найти координаты вершины, мы можем использовать симметрию граф о вершине. Поскольку 𝑥-координата вершина находится на полпути между 𝑥-перехватами, то, вообще говоря, для функции в факторизованной форме 𝑥-координата вершина 𝑥=𝑝+𝑞2.

Для нашей функции 𝑝=−4 и 𝑞=2, поэтому 𝑥-координата вершины 𝑥=−4+22𝑥=−1.

Затем мы берем 𝑥-координату вершины и подставляем ее обратно в функцию, чтобы найти 𝑦-координату. Это дает нам 𝑦=(−1+4)(−1−2)𝑦=−9.

Следовательно, координаты вершины равны (−1,−9).

Теперь мы нашли 𝑥-перехваты, 𝑦-перехват, и вершина, мы можем построить эти координаты на набор осей, чтобы помочь нам построить график функции.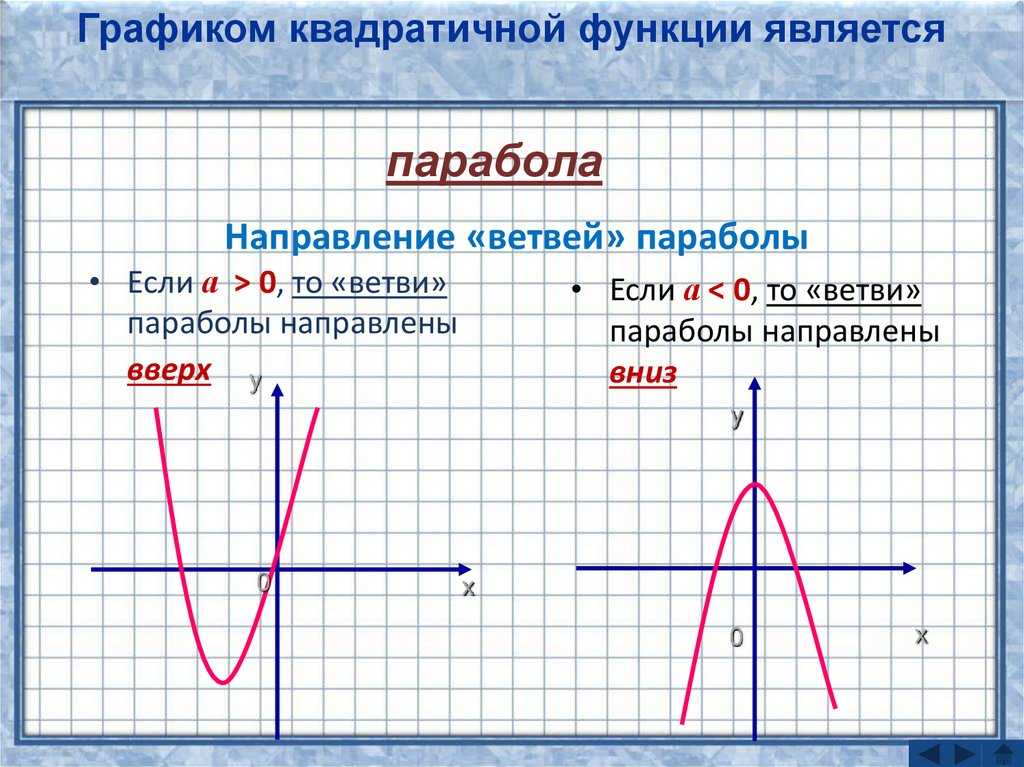 Это дает нам следующий.

Используя эту информацию, мы можем нарисовать график. Далее мы можем использовать является ли 𝑎 положительным или отрицательным, чтобы определить, открывается ли график вверх или вниз. Так как 𝑎=1, что положительно, то график открывается вверх. Набросав график, мы получим следующее.

Из приведенных вариантов мы видим, что только вариант E имеет то же самое 𝑥-перехваты, 𝑦-перехваты и вершины; следовательно, ответ должен быть вариантом E.

До сих пор мы рассматривали, как найти график функции, зная ее уравнение. Далее мы обсудим, как найти уравнение функции учитывая его график. Как правило, мы рассматриваем, какие признаки графа даны и в какой форме мы хотим, чтобы наше уравнение было, чтобы помочь нам определить подход.

В последнем примере мы обсудим, как найти уравнение функции в форма вершины по заданному графу.

Пример 5. Нахождение уравнения функции в форме вершины учитывая его график

Какое из следующих уравнений является уравнением функции, нарисованной на графике?

1. 𝑦=14(𝑥+2)−5
2. 𝑦=−14(𝑥+2)+5
3. 𝑦=14(𝑥+2)+5
4. 𝑦=−14 2)+5
5. 𝑦=−14(𝑥+2)−5

Ответ

Чтобы определить, какая функция соответствует приведенному графику, полезно использовать ключевые особенности графика.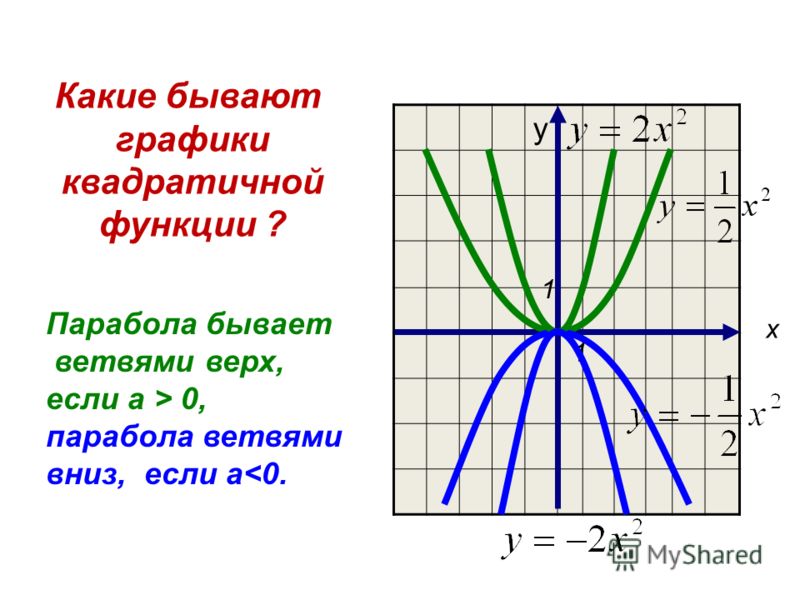 Поскольку все приведенные функции имеют вершинную форму, который 𝑦=𝑎(𝑥−ℎ)+𝑘,𝑎≠0, то мы знаем, что для функции в этом виде координаты точки вершина (ℎ,𝑘).

Из графика видно, что координаты вершины равны (−2,5), на что указывает точка на графике ниже.

Это означает, что ℎ=−2 и 𝑘=5, что дает нам уравнение 𝑦=𝑎(𝑥−(−2))+5𝑦=𝑎(𝑥+2)+5.

Чтобы найти 𝑎, нужно подставить в уравнение точку на графике. Обычно для этого проще всего использовать один из перехватов.

Из графика видно, что неясно, какие точные значения 𝑥-перехваты есть, но мы можем определить точное значение 𝑦-перехват. Поэтому воспользуемся этим моментом.

Глядя на график, мы видим, что 𝑦-перехват (0,4), что показано точкой на графике ниже.

Это означает, что когда 𝑥=0, то 𝑦=4. Подставляя это в 𝑦=𝑎(𝑥+2)+5 и решая для 𝑎, мы получаем 4=𝑎(0+2)+54=4𝑎+5−1=4𝑎𝑎=−14.

Мы видим, что если график открывается вниз, то 𝑎 должно быть отрицательным, что здесь имеет место.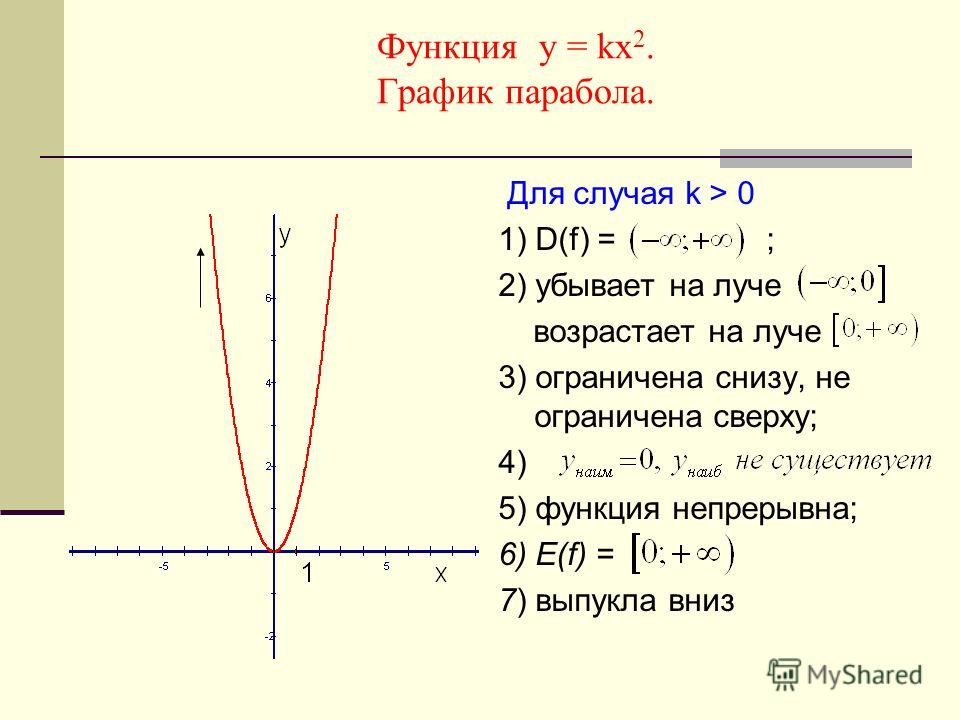

Замена 𝑎 на 𝑦=𝑎(𝑥+2)+5, мы можем затем определите функцию графика, которая 𝑦=−14(𝑥+2)+5,

Это означает, что ответ — вариант B.

В этом объяснении мы научились строить графики квадратичных функций, используя разные подходы, когда они находятся в разных формах. Мы также научились найти уравнение функции по ее графику. Напомним ключевые моменты.

Ключевые моменты

• Одним из методов построения графика квадратичной функции является использование таблицы значений. Мы делаем это, выбирая не менее 5 точек для 𝑥 и подставляя их в функция, чтобы найти 𝑦. Затем мы можем использовать точки для построения графика.
• Для квадратичной функции в стандартной форме 𝑦=𝑎𝑥+𝑏𝑥+𝑐, 𝑎≠0, мы используем следующие функции, чтобы помочь построить график функция:
  • 𝑦-перехват (0,𝑐),
  • 𝑥-перехват путем замены 𝑦=0 и по формуле квадрата, или, иначе, найти 𝑥-координаты, или существуют ли они,
  • вершины по формуле 𝑥=−𝑏2𝑎 для 𝑥-координата, а затем подстановка, чтобы найти 𝑦-координата,
  • , является ли 𝑎 положительным или отрицательным, чтобы определить, является ли график открывается вверх или вниз.
• Для квадратичной функции в вершинной форме 𝑦=𝑎(𝑥−ℎ)+𝑘, 𝑎≠0 используем следующие функции, помогающие построить график функции:
  • вершина (ℎ, 𝑘),
  • 𝑦-перехват, подставив 𝑥=0 и решив для 𝑦,
  • 𝑥-перехватывает, заменяя 𝑦=0 и с помощью заполнения квадрата или, иначе, найти 𝑥-координаты, или существуют ли они,
  • , является ли 𝑎 положительным или отрицательным, чтобы определить, график открывается вверх или вниз.
• Для квадратичной функции в факторизованной форме 𝑦=𝑎(𝑥−𝑝)(𝑥−𝑞), 𝑎≠0, мы используем следующие функции, чтобы помочь построить график функции:
  • 𝑥-перехваты (𝑝,0) и (𝑞,0),
  • 𝑦-перехват путем замены 𝑥=0 и решения для 𝑦,
  • вершина по формуле 𝑥=𝑝+𝑞2 для 𝑥-координаты, а затем подставляя, чтобы найти 𝑦-координату,
  • , является ли 𝑎 положительным или отрицательным, чтобы определить, является ли график открывается вверх или вниз.
• Чтобы найти уравнение квадратичной функции по ее графику, мы идентифицируем ее ключевые особенности и использовать их, чтобы найти уравнение в требуемой форме.

Математика Земли

Дом / Обзор Темы

Квадратичный функция имеет вид f(x) = ax ² + bx + c , где a, b, и c – константы с действительными числами, а – 0.  домен — все действительные числа. Константы a, b и c называются коэффициенты квадратичной функции. График квадратичного функция является параболой, раскрывающейся, если старший коэффициент a > 0 или открытие вниз, если a < 0. 

простейшие квадратичные функции: y = x ² и y = -x ² . Графики показаны ниже.

у = х ² y = -x ²

Чтобы увидеть, насколько разные значения коэффициенты влияют на график, поэкспериментируйте со следующим интерактивным пример.

Пример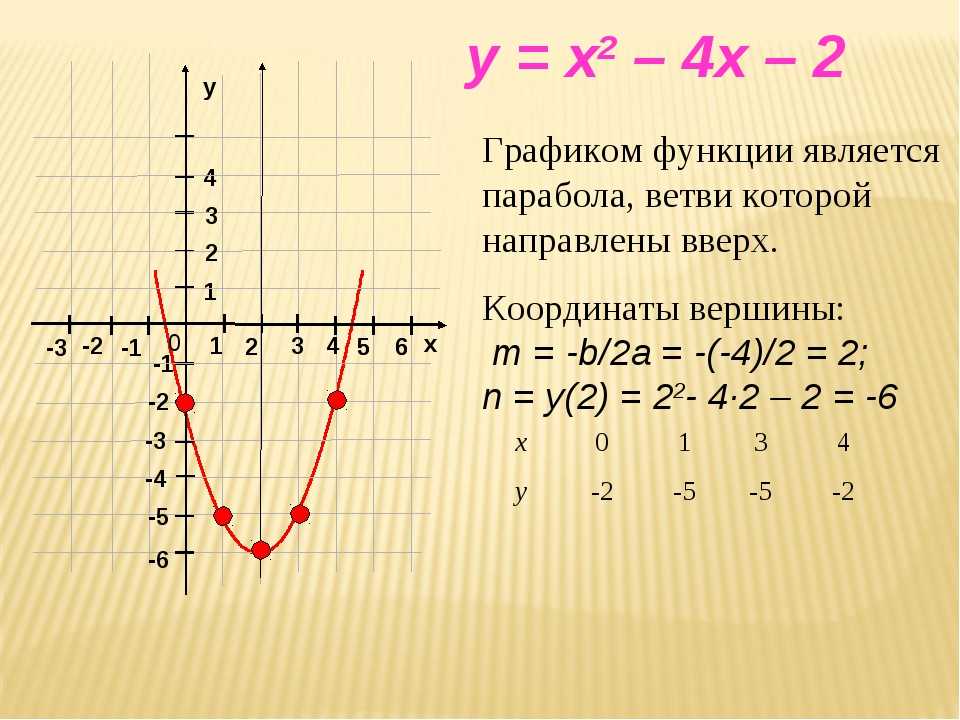

функция H(t) = -16t ²   + 45t + 200 описывает высоту в футах от мяча через t секунд после того, как он был брошен сверху вверх здания высотой 200 футов. На графике ниже показано, что мяч попадает земля вскоре после 5 секунд и достигает максимальной высоты примерно 230 футов примерно через 1,5 секунды. мы научимся рассчитать эти точные значения позже.

Перехватчики

график квадратичной функции всегда будет иметь одну точку пересечения с осью y и может иметь до двух пересечений по оси x (напомним, что пересечения — это точки где график пересекает ось). Y-перехват — это точка где график пересекает ось Y, поэтому это будет значение функция при x = 0. Поскольку f(0) = c, точка пересечения с осью y является точкой (0,с).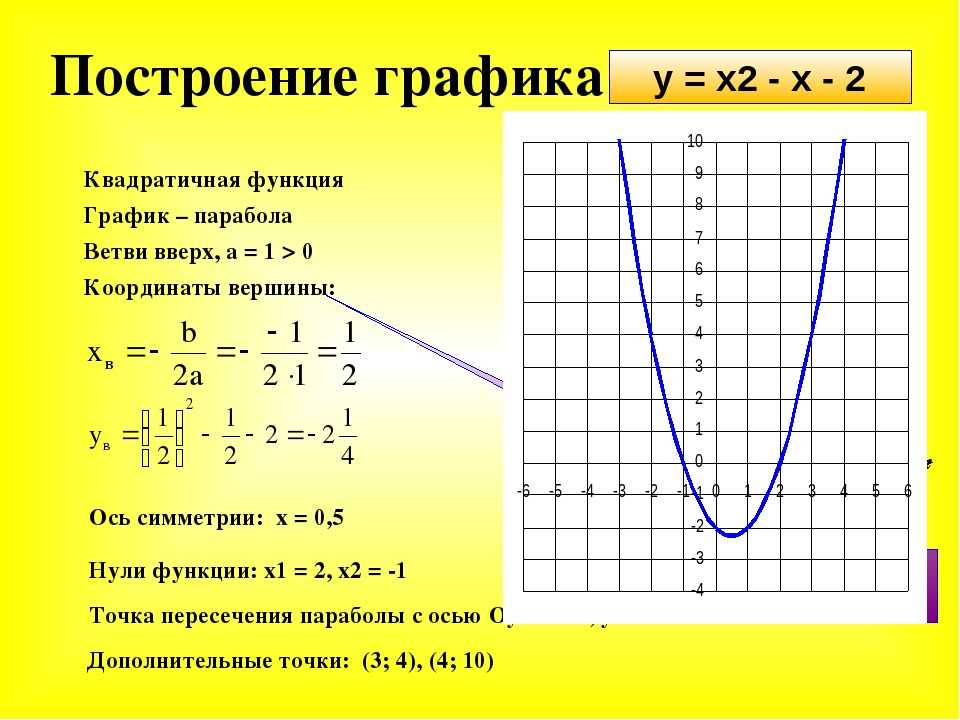 Х-пересечения, если они есть, являются точками где график пересекает ось x. Их можно найти, заменив y с 0 и решение полученного квадратного уравнения  для х. Это уравнение имеет одно, два или не имеет решений. Когда она имеет одно решение, будет один x-перехват; когда есть два решения, будет быть двумя x-перехватами, и когда уравнение не имеет решения, график не будет иметь x-перехватов. Чтобы увидеть примеры, изучите интерактивный пример ниже.

Пример

Найти точки пересечения x и y квадратичной функции

f(x) = 1,5x ² — 3,2x — 9,6.

Раствор

Y-пересечение находится путем замены x на 0:

f(0) = 1,5(0) ² — 3,2(0) — 9,6 = -9,6.

Таким образом, точка пересечения с осью y является точкой (0, -9,6).

Х-пересечения находятся путем замены y или f (x) на 0 и решение для x:

0 = 1,5 х ² — 3,2х — 9,6.

По формуле квадрата получаем

решения (округленные до двух знаков после запятой) равны x = 3,81 и x = -1,68. Х-пересечения приблизительно соответствуют точкам (3,81, 0) и (-1,68, 0). График показан ниже.

турецкая лира ЭТИ ЗАДАЧИ

Решите, каждая ли парабола открывается вверх или вниз и определяет координаты точек пересечения x и y.

1. у = 0,02x ² — 63,1x + 27

2. P(t) = -3t ² + 27,5t + 13,1

Вершина

А парабола, которая раскрывается, имеет самую низкую точку, а парабола, которая раскрывается вниз имеет наивысшую точку.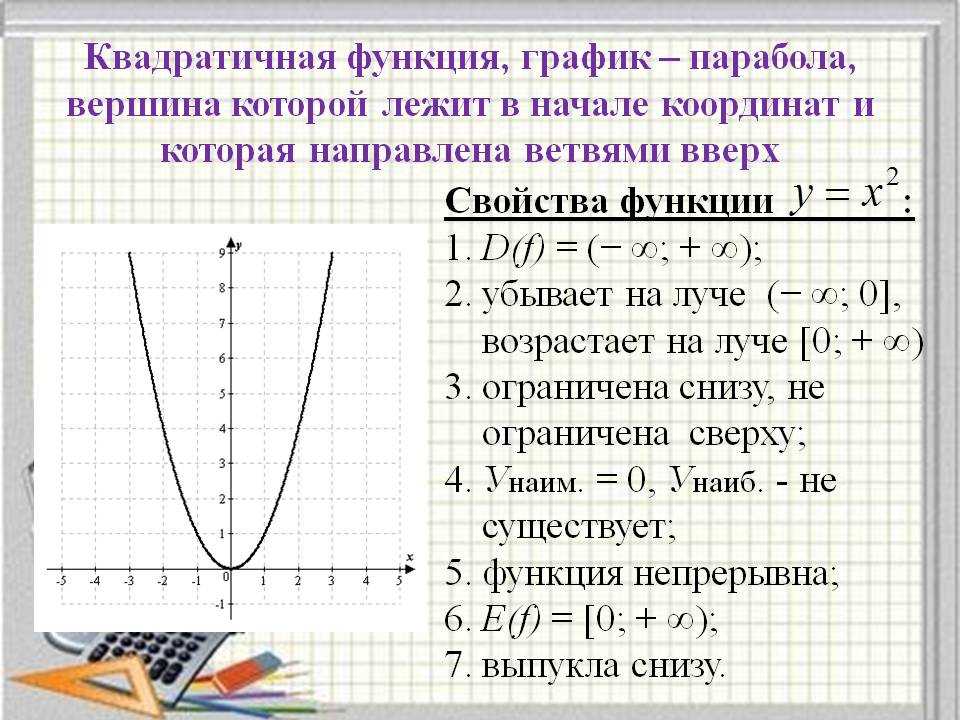 Самая высокая или самая низкая точка параболы называется вершиной . Парабола симметрична относительно вертикальная линия, проходящая через его вершину, называемая ось симметрии . На рисунке ниже показана раскрывающаяся парабола с вершиной (0,75, 0,875). и ось симметрии x = 0,75.

Вершина Форма квадратичной функции

Для нахождения вершины параболы напишем функцию по форме

. В качестве примера рассмотрим функцию . Сначала дорисовываем квадрат с правой стороны:

f(x) = 2(x ² — 4x) + 7 (вычтите 2 из слагаемых 2x ² — 8x)

= 2(х ² — 4х + 4) + 7 — 8       (заполните квадрат x ² — 4 шт.)

= 2(х — 2) ² — 1 (фактор идеальный квадрат и упростить. )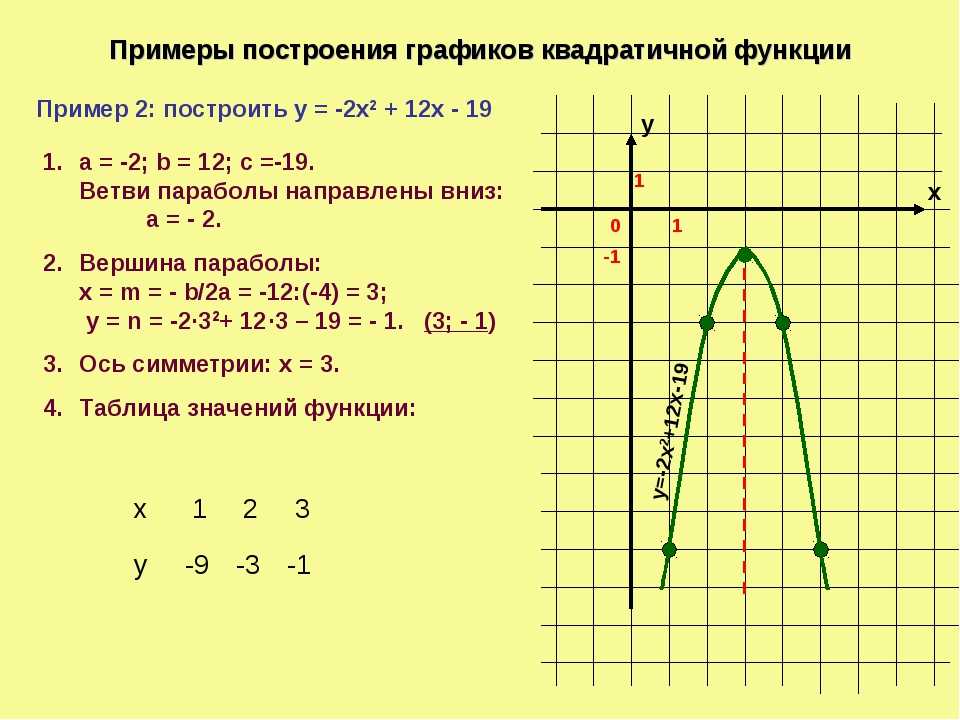

Уведомление что для всех значений x. Таким образом, f(x) = 2(x — 2) ² — 1 -1 для всех значений x и минимальное значение функции равно -1, когда x = 2. Точка (2, -1) является самой нижней точкой на графике, поэтому она является вершиной параболы. Вертикальная линия x = 2 является осью симметрии. См. график ниже.

В общем случае  называется вершинной формой квадратичного функция. Когда квадратичная функция записывается в вершинной форме, мы можем легко определить вершину (h, k). Если коэффициент a > 0 , то парабола раскрывается вверх и вершина самая нижняя точка параболы. Мы говорим, что к это минимум значение квадратичной функции. С другой стороны, если коэффициент a < 0 , то парабола раскрывается вниз и вершина высшая точка параболы. В данном случае к это максимум значение квадратичной функции. Изучите роль каждого коэффициента в следующем интерактивном примере.

Пример

Запись квадратичная функция в вершинной форме. Определить вершину и максимум или минимальное значение функции.

Решение

Заполним квадрат до запишите функцию в вершинной форме:

Форма вершины , поэтому вершина (3, -11) . Так как а < 0, парабола открывается вниз и вершина – самая высокая точка. Функция имеет максимальное значение 11. Его график показан ниже.

Зная вершину параболы, мы можем определить диапазон квадратичной функции. Рассмотрим функцию . Ранее мы определили, что парабола имеет минимальное значение -1, возникающее при x = 2. Таким образом, диапазон квадратичная функция равна {y y -1}. В качестве другого примера, давайте вернуться к функции в приведенном выше примере. График этой функции — парабола, развернутая вниз, и максимальное значение функции равно 11. Следовательно, диапазон квадратичной функции равен

Нахождение вершина Алгебраически

вершина квадратичной функции также может быть определена алгебраически. Мы первые предположим, что квадратичная функция имеет две точки пересечения по оси x. Затем график представляет собой параболу, пересекающую ось x в двух различных точках. Так как парабола симметрична относительно вертикали, проходящей через его вершина (ось симметрии) x-координата вершины равна всегда на полпути между двумя x-перехватами.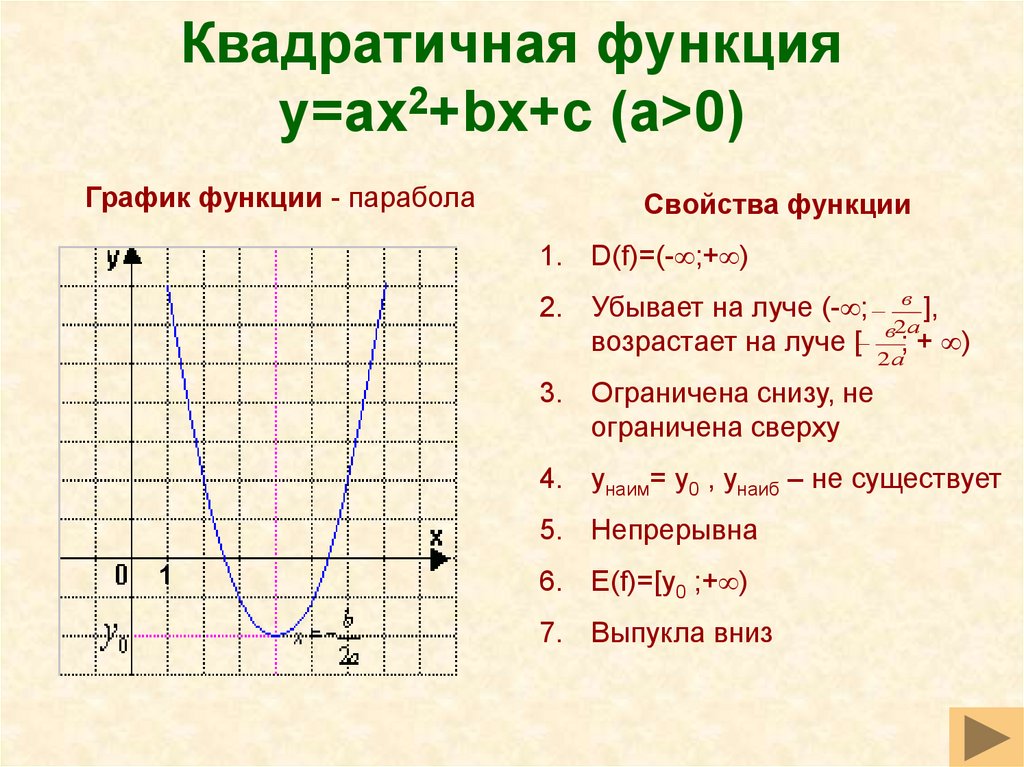 По квадратичной формуле два x-перехвата равны

Обратите внимание, что одно и то же число прибавляется и вычитается из . Отсюда следует, что число  находится посередине между  Это означает, что x-координата вершины это . Затем мы можем найти y-координату вершины путем вычисления  Хотя мы предполагали, что квадратичная функция имел два x-пересечения, когда мы выводили нашу вершинную формулу, она также верна в двух других случаях, когда парабола имеет одну точку пересечения с абсциссой или вообще не имеет ее.

Пример

Найти вершина квадратичной функции . Используйте вершину, чтобы определить максимум или минимум значение функции и найти ее диапазон.

Решение

Вершина формула дает  Чтобы найти вторую координату вершины, мы оцениваем Вершина параболы (3, 53). С г. < 0 , парабола открывается вниз и вершина является самой высокой точка. Это дает максимальное значение 53 и диапазон функции  Ниже показан график функции.

Вызов функция , описывающая высоту в футов мяча через t секунд после того, как он был брошен вверх с вершины здание высотой 200 футов. Теперь мы можем определить, когда мяч попадает земли и максимальной высоты, на которую он достигает, а также время, когда он достигает этой максимальной высоты. Когда мяч коснется земли, его высота над землей будет равна нулю. Это дает квадратное уравнение . Используя квадратичную формулу, находим, что решения

и  

(округленные до два десятичных знака). Поскольку время не может быть отрицательным, мы видим, что мяч ударяется о землю через 5,21 секунды.