Таблица факториалов
Таблица факториалов| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5 040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
| 13! | 6 227 020 800 |
| 14! | 87 178 291 200 |
| 15! | 1 307 674 368 000 |
| 16! | 20 922 789 888 000 |
| 17! | 355 687 428 096 000 |
| 18! | 6 402 373 705 728 000 |
| 19! | 121 645 100 408 832 000 |
| 20! | 2 432 902 008 176 640 000 |
| 51 090 942 171 709 440 000 | |
| 22! | 1 124 000 727 777 607 680 000 |
| 23! | 25 852 016 738 884 976 640 000 |
| 24! | 620 448 401 733 239 439 360 000 |
| 25! | 15 511 210 043 330 985 984 000 000 |
| 26! | 403 291 461 126 605 635 584 000 000 |
| 27! | 10 888 869 450 418 352 160 768 000 000 |
| 28! | 304 888 344 611 713 860 501 504 000 000 |
| 29! | 8 841 761 993 739 701 954 543 616 000 000 |
| 30! | 265 252 859 812 191 058 636 308 480 000 000 |
— версия для печати
- Определение (что такое факториал)
- Факториал числа — результат последовательного умножения числа на все натуральные числа меньшие данного числа и большие единицы.
 Обозначается факториал восклицательным знаком после числа — «n!».
Обозначается факториал восклицательным знаком после числа — «n!».
- Факториал натурального числа n можно также определить как рекуррентную функцию F (n). Определяется она следующим образом: F (0) = F (1) = 1; F (n) = n * F (n-1).
- Пример:
- 7! = 7×6×5×4×3×2×1 = 5040
- Не стоит забывать
- По общепринятой договоренности 0! = 1 (факториал нуля равен единице). Этот факт важен, к примеру, для вычисления биномиальных коэффициентов.
- Полезный факт
- Факториал числа, функцию от натурального аргумента можно продолжить на все действительные числа с помощью т.н. Гамма-функции (важно отметить, что для этого требуется определенный математический аппарат). В таком случае, мы сможем посчитать факториал любого действительного числа. Например, факториал (или, Гамма-функция, что математически правильнее)
 28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Интерактивный учебник языка Python
1. Функции
Напомним, что в математике факториал числа n определяется как n! = 1 ⋅ 2 ⋅ … ⋅ n. Например, 5! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120. Ясно, что факториал можно легко посчитать, воспользовавшись циклом for. Представим, что нам нужно в нашей программе вычислять факториал разных чисел несколько раз (или в разных местах кода). Конечно, можно написать вычисление факториала один раз, а затем используя Copy-Paste вставить его везде, где это будет нужно.
# вычислим 3!
res = 1
for i in range(1, 4):
res *= i
print(res)
# вычислим 5!
res = 1
for i in range(1, 6):
res *= i
print(res)Однако, если мы ошибёмся один раз в начальном коде, то потом эта ошибка попадёт в код во все места, куда мы скопировали вычисление факториала. Да и вообще, код занимает больше места, чем мог бы. Чтобы избежать повторного написания одной и той же логики, в языках программирования существуют функции.
Да и вообще, код занимает больше места, чем мог бы. Чтобы избежать повторного написания одной и той же логики, в языках программирования существуют функции.
Функции — это такие участки кода, которые изолированы от остальный программы и выполняются только тогда, когда вызываются. Вы уже встречались с функциями sqrt(), len() и print(). Они все обладают общим свойством: они могут принимать параметры (ноль, один или несколько), и они могут возвращать значение (хотя могут и не возвращать). Например, функция sqrt() принимает один параметр и возвращает значение (корень числа). Функция print() принимает переменное число параметров и ничего не возвращает.
Покажем, как написать функцию factorial(), которая принимает один параметр — число, и возвращает значение — факториал этого числа.
def factorial(n):
res = 1
for i in range(1, n + 1):
res *= i
return res
print(factorial(3))
print(factorial(5))Дадим несколько объяснений. Во-первых, код функции должен размещаться в начале программы, вернее, до того места, где мы захотим воспользоваться функцией factorial(). Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция. Список состоит из перечисленных через запятую идентификаторов параметров. В нашем случае список состоит из одной величины n. В конце строки ставится двоеточие.
Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция. Список состоит из перечисленных через запятую идентификаторов параметров. В нашем случае список состоит из одной величины n. В конце строки ставится двоеточие.
Далее идет тело функции, оформленное в виде блока, то есть с отступом. Внутри функции вычисляется значение факториала числа n и оно сохраняется в переменной res. Функция завершается инструкцией return res, которая завершает работу функции и возвращает значение переменной res.
Инструкция return может встречаться в произвольном месте функции, ее исполнение завершает работу функции и возвращает указанное значение в место вызова. Если функция не возвращает значения, то инструкция return используется без возвращаемого значения. В функциях, которым не нужно возвращать значения, инструкция return может отсутствовать.
Приведём ещё один пример. Напишем функцию max(), которая принимает два числа и возвращает максимальное из них (на самом деле, такая функция уже встроена в Питон).
10 20
def max(a, b):
if a > b:
return a
else:
return b
print(max(3, 5))
print(max(5, 3))
print(max(int(input()), int(input())))Теперь можно написать функцию max3(), которая принимает три числа и возвращает максимальное их них.
def max(a, b):
if a > b:
return a
else:
return b
def max3(a, b, c):
return max(max(a, b), c)
print(max3(3, 5, 4))Встроенная функция max() в Питоне может принимать переменное число аргументов и возвращать максимум из них. Приведём пример того, как такая функция может быть написана.
def max(*a):
res = a[0]
for val in a[1:]:
if val > res:
res = val
return res
print(max(3, 5, 4))Все переданные в эту функцию параметры соберутся в один кортеж с именем a, на что указывает звёздочка в строке объявления функции.
2. Локальные и глобальные переменные
Внутри функции можно использовать переменные, объявленные вне этой функции
def f():
print(a)
a = 1
f()Здесь переменной a присваивается значение 1, и функция f() печатает это значение, несмотря на то, что до объявления функции f эта переменная
не инициализируется. В момент вызова функции f() переменной a уже присвоено значение, поэтому функция f() может вывести его на экран.
Такие переменные (объявленные вне функции, но доступные внутри функции) называются глобальными.
Но если инициализировать какую-то переменную внутри функции, использовать эту переменную вне функции не удастся. Например:
def f():
a = 1
f()
print(a)Получим ошибку NameError: name 'a' is not defined. Такие переменные, объявленные внутри функции,
называются локальными. Эти переменные становятся недоступными после выхода из функции.
Эти переменные становятся недоступными после выхода из функции.
Интересным получится результат, если попробовать изменить значение глобальной переменной внутри функции:
def f():
a = 1
print(a)
a = 0
f()
print(a)Будут выведены числа 1 и 0. Несмотря на то, что значение переменной a изменилось внутри функции, вне функции оно осталось прежним! Это сделано в целях
“защиты” глобальных переменных от случайного изменения из функции.
Например, если функция будет вызвана из цикла по переменной i, а в этой функции
будет использована переменная i также для организации цикла, то эти переменные должны
быть различными. Если вы не поняли последнее предложение, то посмотрите на следующий код и подумайте, как бы он работал,
если бы внутри функции изменялась переменная i.
def factorial(n):
res = 1
for i in range(1, n + 1):
res *= i
return res
for i in range(1, 6):
print(i, '! = ', factorial(i), sep='')Если бы глобальная переменная i изменялась внутри функции, то мы бы получили вот что:5! = 1 5! = 2 5! = 6 5! = 24 5! = 120Итак, если внутри функции модифицируется значение некоторой переменной, то переменная с таким именем становится локальной переменной, и ее модификация не приведет к изменению глобальной переменной с таким же именем.
Более формально: интерпретатор Питон считает переменную локальной для данной функции, если в её коде
есть хотя бы одна инструкция, модифицирующая значение переменной, то эта переменная считается локальной
и не может быть использована до инициализации. Инструкция, модифицирующая значение переменной — это операторы +=, а также использование переменной в качестве параметра цикла for.
При этом даже если инструкция,
модицифицирующая переменную никогда не будет выполнена, интерпретатор это проверить
не может, и переменная все равно считается локальной. Пример:
def f():
print(a)
if False:
a = 0
a = 1
f()Возникает ошибка: UnboundLocalError: local variable 'a' referenced before assignment.
А именно, в функции f() идентификатор a становится локальной переменной,
т.к. в функции есть команда, модифицирующая переменную a, пусть даже никогда и
не выполняющийся (но интерпретатор не может это отследить). Поэтому вывод переменной
Поэтому вывод переменной a приводит к обращению к неинициализированной локальной переменной.
Чтобы функция могла изменить значение глобальной переменной, необходимо объявить эту переменную
внутри функции, как глобальную, при помощи ключевого слова global:
def f():
global a
a = 1
print(a)
a = 0
f()
print(a)В этом примере на экран будет выведено 1 1, так как переменная a объявлена, как глобальная,
и ее изменение внутри функции приводит к тому, что и вне функции переменная
будет доступна.
Тем не менее, лучше не изменять значения глобальных переменных внутри функции. Если ваша функция должна поменять какую-то переменную, пусть лучше она вернёт это значением, и вы сами при вызове функции явно присвоите в переменную это значение. Если следовать этим правилам, то функции получаются независимыми от кода, и их можно легко копировать из одной программы в другую.
Например, пусть ваша программа должна посчитать факториал вводимого числа, который вы потом захотите сохранить в переменной f. Вот как это не стоит делать:
Вот как это не стоит делать:
5
def factorial(n):
global f
res = 1
for i in range(2, n + 1):
res *= i
f = res
n = int(input())
factorial(n)
# дальше всякие действия с переменной fЭтот код написан плохо, потому что его трудно использовать ещё один раз. Если вам завтра понадобится в другой программе использовать функцию «факториал», то вы не сможете просто скопировать эту функцию отсюда и вставить в вашу новую программу. Вам придётся поменять то, как она возвращает посчитанное значение.
Гораздо лучше переписать этот пример так:
5
# начало куска кода, который можно копировать из программы в программу
def factorial(n):
res = 1
for i in range(2, n + 1):
res *= i
return res
# конец куска кода
n = int(input())
f = factorial(n)
# дальше всякие действия с переменной fЕсли нужно, чтобы функция вернула не одно значение, а два или более, то для этого функция может вернуть список из двух или нескольких значений:
Тогда результат вызова функции можно будет использовать во множественном присваивании:
3.
 Рекурсия
Рекурсияdef short_story():
print("У попа была собака, он ее любил.")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
short_story()Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя! Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что 0!=1, 1!=1. А как вычислить величину n! для большого n? Если бы мы могли вычислить величину (n-1)!, то тогда мы легко вычислим n!, поскольку n!=n⋅(n-1)!. Но как вычислить (n-1)!? Если бы мы вычислили (n-2)!, то мы сможем вычисли и (n-1)!=(n-1)⋅(n-2)!. А как вычислить (n-2)!? Если бы… В конце концов, мы дойдем до величины 0!, которая равна 1. Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа. Это можно сделать и в программе на Питоне:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
print(factorial(5))Подобный прием (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны. Также часто использование рекурсии приводит к ошибкам. Наиболее распространенная из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведен в эпиграфе к этому разделу. Две наиболее распространенные причины для бесконечной рекурсии:
- Неправильное оформление выхода из рекурсии. Например, если мы в программе вычисления факториала
забудем поставить проверку
if n == 0, тоfactorial(0)вызоветfactorial(-1), тот вызоветfactorial(-2)и т. д. - Рекурсивный вызов с неправильными параметрами. Например, если функция
factorial(n)будет вызыватьfactorial(n), то также получится бесконечная цепочка.
Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии
и думать, почему рекурсия когда-либо завершит работу.
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
Как обозначается факториал в паскале
Факториал – произведение натуральных чисел от единицы до заданного числа. Имеет условное обозначение в виде восклицательного знака. n!=1*2*3*. *n (Например: 3!=1*2*3=6).
В Turbo Pascal факториал находится, как правило, двумя способами: с помощью цикла или с помощью рекурсии.
Вычисление факториала в pascal с помощью цикла
Данный способ нахождения факториала исключительно прост. В цикле от 1 до n умножается число само на себя. При этом необходимо учитывать условие, что 0!=1. Ниже представлена реализация программы с помощью цикла for. Аналогично используются repeat и while.
if (n=0) then writeln(‘0!=1’) else
if x=0 then fact:=1
Факториал числа – Вычисление с помощью цикла (1 способ)
Факториал – Нахождение факториала в паскале с помощью рекурсии (2 способ)
Задача
Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа включительно. Например, факториал числа 7 выглядит так:
Например, факториал числа 7 выглядит так:
1 * 2 * 3 * 4 * 5 * 6 * 7
Факториал числа обозначается как само число после которого следует восклицательный знак. Например, 7!. Таким образом:
7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
С увеличением числа его факториал быстро возрастает. Так если 3! = 6, то уже 10! = 3628800. Поэтому для натуральных чисел больше 12-ти в языке программирования Паскаль просто так факториал вычислить нельзя.
Допустим, требуется определить факториал числа, которое ввел пользователь.
Решение
Переменной factorial сначала присваивается значение 1.
0! = 1 и 1! = 1.
Если пользователь ввел число больше единицы, то выполняется цикл, в теле которого на каждой итерации значение переменной factorial умножается на следующее натуральное число (переменную i ).
Обучение программированию идёт по пути от простого к сложному. Освоив типы данных и операторы языка, переходят к циклическим конструкциям. Задач на циклы существует бесчисленное количество: начиная от вывода цифр в столбик до подсчёта сумм по сложным формулам. Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Реализовать задачу можно как минимум тремя способами. Отличаются они используемыми операторами.
Математические сведения
Перед тем как перейти к построению алгоритмов и написанию программ, следует изучить теорию. В математике факториалом называют произведение целого числа, для которого вычисляется выражение, на целые положительные числа меньше его.
Понять определение поможет пример. Пусть требуется выполнить нахождение факториала для числа 3. Решение: 3! = 3 * 2 * 1 = 6.
Обозначается действие восклицательным знаком, который ставится после числа. Важное замечание: факториал определён только для целых положительных чисел. Вместе с тем, введено понятия для нуля: 0! = 1.
Считать выражение для больших значений вручную – занятие долгое. Чтобы убыстрить процесс вычислений, используют компьютерные программы. Далее рассмотрены способы, как найти факториал в «Паскале».
Первый способ
Код ниже показывает вариант программы.
В примере используют составную конструкцию с условием, которое записывается перед телом цикла. Синтаксис записи:
Выполняется код следующим образом: программа проверяет истинность выражения , в случае положительной проверки переходит на .
Возвращаясь к программе, нужно обратить внимание на следующие строки:
- 2 – задаётся число n, для которого будет выполнен расчёт;
- 6 – заголовок цикла;
- 7 – начало цикла;
- 8 – вычисление переменной fact, которая хранит значение факториала числа n;
- 9 – увеличение переменной-счётчика на единицу;
- 10 – конец цикла.
Второй способ
Следующий предлагает вычислить факториал в «Паскале» с помощью оператора repeat.
Конструкция цикла: repeat until <условие>;
Чтобы понять, как работает программа, рассмотрим её построчно:
- 2 – константе n назначается число, для которого выполняется вычисление;
- 7 – начало цикла;
- 8, 9 – расчёт факториала и увеличения счётчика i;
- 10 – конец тела цикла;
- 11 – проверка условия, поскольку условие располагается после последовательности операторов, повтор действий будет выполнен как минимум один раз.

Третий способ
Последняя программа также дает возможность вычислить факториал в «Паскале» и является самой компактной по размеру. Причина – используемый оператор for, для которого увеличение счётчика i задаётся в параметрах цикла.
Работает код следующим образом (цифрами указаны строки листинга):
- 2 – константе n присваивают значение числа, для которого вычисляется факториал;
- 6 – задаются параметры цикла – начальное и конечное значения;
- 7 – начало цикла;
- 8 – вычисление переменной fact;
- 9 – конец цикла.
Замечание
Даже для чисел из первой десятки факториал имеет значение больше, чем допускает тип данных integer. Поэтому программа в «Паскале» покажет сообщение об ошибке. Исправить её просто – нужно заменить тип данных для переменной-результата на longint или использовать типы для хранения вещественных значений.
swift — В Swift 3, как рассчитать факториал, когда результат становится слишком высоким?
Я написал эту функцию, чтобы вернуть факториал данного числа
func factorial(_ n: Int) -> Int {
if n == 0 {
return 1
}
else {
return n * factorial(n - 1)
}
}
print( factorial(20) ) // 2432902008176640000
Работает как надо, пока данное число не превышает 20, потому что тогда результат становится слишком высоким!
Как я могу обойти этот предел и таким образом вычислить факториал больших чисел?
Я искал вокруг и нашел несколько библиотек bignum для Swift. Я делаю это, чтобы изучить и быть знакомым со Swift, поэтому я хочу понять это самостоятельно.
Я делаю это, чтобы изучить и быть знакомым со Swift, поэтому я хочу понять это самостоятельно.
6
Jon 7 Май 2017 в 13:00
2 ответа
Лучший ответ
Вот подход, который позволит вам найти очень большие факториалы.
Представлять большие числа в виде массива цифр. Например, 987 будет [9, 8, 7]. Умножение этого числа на целое число n потребует двух шагов.
- Умножьте каждое значение в этом массиве на
n. - Выполните операцию переноса, чтобы получить результат, состоящий из одной цифры.
Например, 987 * 2:
let arr = [9, 8, 7]
let arr2 = arr.map { $0 * 2 }
print(arr2) // [18, 16, 14]
Теперь выполните операцию переноса. Начиная с цифры, 14 слишком велик, поэтому оставьте 4 и несите 1. Добавьте
Добавьте 1 в 16, чтобы получить 17.
[18, 17, 4]
Повторите с десятым местом:
[19, 7, 4]
А потом с сотней место:
[1, 9, 7, 4]
Наконец, для печати вы можете преобразовать это обратно в строку:
let arr = [1, 9, 7, 4]
print(arr.map(String.init).joined())
1974
Применяя эту технику, здесь есть carryAll функция, которая выполняет операцию переноса, и factorial, которая использует ее для вычисления очень больших факториалов:
func carryAll(_ arr: [Int]) -> [Int] {
var result = [Int]()
var carry = 0
for val in arr.reversed() {
let total = val + carry
let digit = total % 10
carry = total / 10
result.append(digit)
}
while carry > 0 {
let digit = carry % 10
carry = carry / 10
result. append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
4023872600770937735437024339230039857193748642107146325437999104299385123986290205920442084869694048004799886101971960586316668729948085589013238296699445909974245040870737599188236277271887325197795059509952761208749754624970436014182780946464962910563938874378864873371191810458257836478499770124766328898359557354325131853239584630755574091142624174743493475534286465766116677973966688202912073791438537195882498081268678383745597317461360853795345242215865932019280908782973084313928444032812315586110369768013573042161687476096758713483120254785893207671691324484262361314125087802080002616831510273418279777047846358681701643650241536913982812648102130927612448963599287051149649754199093422215668325720808213331861168115536158365469840467089756029009505376164758477284218896796462449451607653534081989013854424879849599533191017233555566021394503997362807501378376153071277619268490343526252000158885351473316117021039681759215109077880193931781141945452572238655414610628921879602238389714760 8850627686296714667469756291123408243920816015378088989396451826324367161676217916890977991190375403127462228998800519544441428201218736174599264295658174662830295557029902432415318161721046583203678690611726015878352075151628422554026517048330422614397428693306169089796848259012545832716822645806652676995865268227280707578139185817888965220816434834482599326604336766017699961283186078838615027946595513115655203609398818061213855860030143569452722420634463179746059468257310379008402443243846565724501440282188525247093519062092902313649327349756551395872055965422874977401141334696271542284586237738753823048386568897646192738381490014076731044664025989949022222176590433990188601856652648506179970235619389701786004081188972991831102117122984590164192106888438712185564612496079872290851929681937238864261483965738229112312502418664935314397013742853192664987533721894069428143411852015801412334482801505139969429015348307764456909907315243327828826986460278986432113908350621709500259738986355 4277196742822248757586765752344220207573630569498825087968928162753848863396909959826280956121450994871701244516461260379029309120889086942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560855903700624271243416909004153690105933983835777939410970027753472000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
17
vacawama 8 Июн 2018 в 10:37
Вы можете использовать эту библиотеку: BigInt
Установите его с помощью CocoaPods:
pod 'BigInt'
Тогда вы можете использовать это так:
import BigInt
func factorial(_ n: Int) -> BigInt {
if n == 0 {
return 1
}
else {
return BigInt(n) * factorial(n - 1)
}
}
print( factorial(50) ) // 30414093201713378043612608166064768844377641568960512000000000000
1
Anton Novoselov 7 Май 2017 в 10:18
Функция ФАКТР — Служба поддержки Office
Предположим, что у вас шесть колоколов с разными тонами и вы хотите найти количество уникальных последовательностей, в которых каждый колокол может запускаться один раз. В этом примере вычисляются факториал из шести. В общем, с помощью факториала можно подсчитать количество способов у организовать группу отдельных элементов (перемитации). Чтобы вычислить факториал числа, используйте функцию ФАКТС.
В этом примере вычисляются факториал из шести. В общем, с помощью факториала можно подсчитать количество способов у организовать группу отдельных элементов (перемитации). Чтобы вычислить факториал числа, используйте функцию ФАКТС.
В этой статье описаны синтаксис формулы и использование функции ФАКТР в Microsoft Excel.
Описание
Возвращает факториал числа. Факториал числа — это значение, равное 1*2*3*…* число.
Синтаксис
ФАКТР(число)
Аргументы функции ФАКТР описаны ниже.
-
Число — обязательный аргумент. Неотрицательное число, для которого вычисляется факториал. Если число не является целым, оно усекается.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=ФАКТР(5) |
Факториал числа 5 или 1*2*3*4*5 |
120 |
|
=ФАКТР(1,9) |
Факториал целой части числа 1,9 |
1 |
|
=ФАКТР(0) |
Факториал числа 0 |
1 |
|
=ФАКТР(-1) |
Факториал отрицательного числа возвращает значение ошибки |
#ЧИСЛО! |
|
=ФАКТР(1) |
Факториал числа 1 |
1 |
Python алгоритмы: Вычисление факториала
Мне кажется, что это самый классический алгоритм из существующих.
 С примером реализации вы наверняка сталкивались и не раз, но для полноты картины, я просто обязан его описать. :))
С примером реализации вы наверняка сталкивались и не раз, но для полноты картины, я просто обязан его описать. :))Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:*-Нравится статья? Кликни по рекламе! 🙂По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
- .
Комбинаторная интерпретация
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Рекуррентная формула
Итак это был тот минимум, который, как я считаю, должен знать любой уважающий себя. и всех тех кто его окружает, человек.
Теперь о реализации алгоритма. Как всегда средств много, от чего мы познакомимся с несколькими из них.

2 классических я возьму с сайта http://younglinux.info/algorithm/factorial
С использованием цикла
def fac(n):
fac = 1
i = 0
while i < n:
i += 1
fac = fac * i
return facС использованием рекурсии
def fac(n):
if n == 0:
return 1
return fac(n-1) * nИ на закуску, высокоинтеллектуальный пример с Вики :))
def factorial(x):
return 1 if x==0 else reduce(lambda x,y:x*y,xrange(1,x+1))
Ну и теперь самое вкусное и интересное, тестирование!
По их результатам я пришел к выводу, что скорость роста данных алгоритмов приблизительно равна. И по сему результат вычисления 70000! следующий:
- алгоритм с использованием цикла 4 function calls in 11.872 seconds
- алгоритм рекурсивный выбыл, подробнее читать тут
- зверский алгоритм с вики 70004 function calls in 13.211 seconds
- встроенный модуль math.factorial 4 function calls in 8.
 377 CPU seconds
377 CPU seconds
Просто получается многовато вызовов лямбда функций, ведь каждый вызов — это потери, хотим мы этого или нет.
Проблемы, возникшие с рекурсией: по умолчанию, максимальная глубина рекурсии равна 1000. Это ограничение предотвращает переполнение стека при бесконечных рекурсиях.
Я установил при помощи sys.setrecursionlimit(70000) новую глубину, но python падает через пару секунд, все таки нужно помнить, что рекурсия не самая хорошая штука для таких вычислений :((
Почему встроенная функция сильнее, лучше и быстрее? Могу предположить что написание на чистом С ему придает бодрости)))
Вычисление времени выполнения
Для примера разберем рекурсивный вариант. Мы должны с каждой рекурсивной процедурой связать временную функцию T(n), где n определяет объём аргументов процедуры. Затем получить рекуррентное соотношение для T(n). Естественной мерой объёма входных данных для функции fac, является значение n. Обозначим, через T(n) — время выполнения программы.
Обозначим, через T(n) — время выполнения программы.
Время сравнения if имеет порядок роста О(1), а для последней строки О(1)+T(n-1), где О(1)-умножение на n, а T(n-1)-факториала с меньшим входным аргументом. Таким образом для некоторых констант c и d имеем,
UPD:На сайте http://www.iso.ru/journal/articles/199.html
нашел интересный пример, который, как там и пишут считается скорее шуткой или поводом выиграть спор(на пыво))) у своих друзей:
f = lambda n: n-1 +abs(n-1) and f(n-1)*n or 1Этот «рецепт» реализует рекурсивное определение функции факториала в виде lambda формы. Поскольку lambda формы должны быть выражениями, это несколько мудрено. Директива if/else не допускается внутри выражения. Все же, закороченная форма идиомы Python для «условного (трехместного) оператора» справляется с этим (другие способы моделирования трехместного оператора, как закороченного, так и нет, см.
 в «Моделирование трехместного оператора» в «Справочном руководстве по Python»).
в «Моделирование трехместного оператора» в «Справочном руководстве по Python»).Реальная проблема, разумеется, состоит в том, что раз сильная сторона lambda в создании безымянных функций, то, как же мы выполняем рекурсию?
Подсчет числа размещений с использованием функции вычисления факториала — Процедуры и функции
[ЗВУК] [ЗВУК] [ЗВУК] Рассмотрим пример того, как может использоваться функция. Напишем постановку задачи, а также программу с использованием подпрограммы для вычисления значения по следующей формуле. Эта формула носит название «число размещений». Мы с вами видим, что в этой формуле дважды встречается факториал, то есть для вычисления факториала удобно будет сделать отдельную подпрограмму. Мы с вами видим, что результатом вычисления факториала является ровно одно число. Следовательно, мы можем сделать функцию. Например, если параметры для вычисления числа размещений равны 3 и 8, то по нашей формуле получается 336. Кстати говоря, это количество способов, которыми могут занять 3 первых места соревнующиеся 8 команд. Теперь вспомним, каково определение факториала. В школьном учебнике математики определение факториала звучит так: факториал есть произведение натуральных чисел от 1 до заданного числа. Это не совсем точное определение, потому что, строго говоря, факториал нуля тоже определен, и он равен 1, это во-первых. А во-вторых, мы с вами понимаем, что в математике произведение включает в себя как минимум два числа, а для единицы у нас получится произведение из одного числа, что как-то странно. Рассмотрим другое определение факториала. n факториал мы с вами будем вычислять по формуле, которая включает в себя два случая: n! = 1, когда n = 0, и вычисляется как факториал числа на единицу меньшего, умноженного на само это число, если n — это натуральное число. И рассмотрим постановку задачи. Нам с вами даны два целых числа, n и k. Результатом является A — число размещений. n должно быть положительным или равным нулю. k должно быть больше или равно n, и оба эти числа должны принадлежать множеству целых чисел.
Теперь вспомним, каково определение факториала. В школьном учебнике математики определение факториала звучит так: факториал есть произведение натуральных чисел от 1 до заданного числа. Это не совсем точное определение, потому что, строго говоря, факториал нуля тоже определен, и он равен 1, это во-первых. А во-вторых, мы с вами понимаем, что в математике произведение включает в себя как минимум два числа, а для единицы у нас получится произведение из одного числа, что как-то странно. Рассмотрим другое определение факториала. n факториал мы с вами будем вычислять по формуле, которая включает в себя два случая: n! = 1, когда n = 0, и вычисляется как факториал числа на единицу меньшего, умноженного на само это число, если n — это натуральное число. И рассмотрим постановку задачи. Нам с вами даны два целых числа, n и k. Результатом является A — число размещений. n должно быть положительным или равным нулю. k должно быть больше или равно n, и оба эти числа должны принадлежать множеству целых чисел. Мы с вами проверим при вводе, что это действительно так. Связью в данном случае является наша формула. И теперь рассмотрим программу, которая решает нашу задачу. Здесь у нас две переменных целого типа, это n и k. Кроме того, у нас есть три переменных вещественного типа: это n1 и k1, которые мы будем использовать для организации надежного ввода данных, и переменная a, которая является результатом. Так как результатом является частное, то переменная a, конечно же, имеет вещественный тип. Далее рассмотрим функцию, которая называется f. На входе у нее целое число, а на выходе — значение вещественного типа, причем эта функция будет рекурсивной, так как эта функция будет вычислять значение по второй формуле, где значение факториала вычисляется через факториал числа, на единицу меньшего. И посмотрите, как интересно. Наши исходные данные имеют целый тип, а результат — вещественный, хотя вроде бы у нас результатом является произведение целых чисел. Почему же мы выбрали вещественный тип для результата? Дело в том, что у целого типа гораздо более узкий диапазон, чем у вещественного.
Мы с вами проверим при вводе, что это действительно так. Связью в данном случае является наша формула. И теперь рассмотрим программу, которая решает нашу задачу. Здесь у нас две переменных целого типа, это n и k. Кроме того, у нас есть три переменных вещественного типа: это n1 и k1, которые мы будем использовать для организации надежного ввода данных, и переменная a, которая является результатом. Так как результатом является частное, то переменная a, конечно же, имеет вещественный тип. Далее рассмотрим функцию, которая называется f. На входе у нее целое число, а на выходе — значение вещественного типа, причем эта функция будет рекурсивной, так как эта функция будет вычислять значение по второй формуле, где значение факториала вычисляется через факториал числа, на единицу меньшего. И посмотрите, как интересно. Наши исходные данные имеют целый тип, а результат — вещественный, хотя вроде бы у нас результатом является произведение целых чисел. Почему же мы выбрали вещественный тип для результата? Дело в том, что у целого типа гораздо более узкий диапазон, чем у вещественного. То есть мы выбрали вещественный тип для результата, чтобы просто можно было вычислять значения факториалов больших чисел. И теперь записываем тело функции, используя вторую формулу. Если n = 0, то результатом будет 1, а в противном случае мы делаем рекурсивный вызов нашей функции, то есть вычисляем факториал числа, на единицу меньшего, и домножаем его на очередное n. Далее рассмотрим основную программу. Мы вводим два целых числа, на которые накладываются ограничения, соответствующие пункту три в постановке задачи. При этом, чтобы при вводе нецелых чисел наша программа не завершалась аварийно, мы используем переменные n1 и k1 вещественного типа, читаем в них значения, и будем повторять наш ввод до тех пор, пока n1 не будет больше или равно нулю, k1 не будет больше или равно n1, и, кроме того, на переменную k1 еще наложено ограничение сверху, то есть ее значение не может превышать числа 170. Это самое большое число, факториал которого мы сможем вычислить. И кроме того, n1 и k1 должны быть целого типа, то есть результат округления равен самому этому числу, как для первого, так и для второго числа.
То есть мы выбрали вещественный тип для результата, чтобы просто можно было вычислять значения факториалов больших чисел. И теперь записываем тело функции, используя вторую формулу. Если n = 0, то результатом будет 1, а в противном случае мы делаем рекурсивный вызов нашей функции, то есть вычисляем факториал числа, на единицу меньшего, и домножаем его на очередное n. Далее рассмотрим основную программу. Мы вводим два целых числа, на которые накладываются ограничения, соответствующие пункту три в постановке задачи. При этом, чтобы при вводе нецелых чисел наша программа не завершалась аварийно, мы используем переменные n1 и k1 вещественного типа, читаем в них значения, и будем повторять наш ввод до тех пор, пока n1 не будет больше или равно нулю, k1 не будет больше или равно n1, и, кроме того, на переменную k1 еще наложено ограничение сверху, то есть ее значение не может превышать числа 170. Это самое большое число, факториал которого мы сможем вычислить. И кроме того, n1 и k1 должны быть целого типа, то есть результат округления равен самому этому числу, как для первого, так и для второго числа.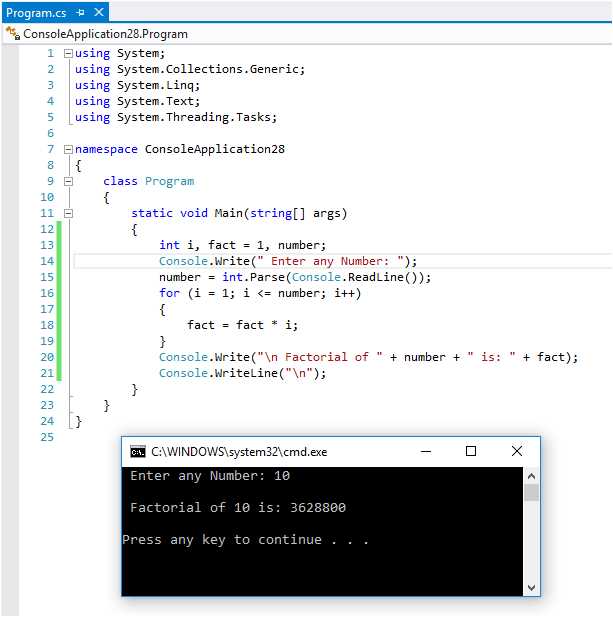 Затем мы, для того чтобы передать наше значение в функцию, чтобы оно приобрело целый тип, мы переменной n присваиваем результат округления n1 до целого, а переменной k — результат округления k1 до целого. Вычисляем значения переменной a, вызывая нашу функцию два раза, и выводим на экран полученный результат. Затем наша программа завершается. Рассмотрим программу с использованием рекурсивной функции для вычисления количества размещений по заданной формуле. Вначале у нас объявлены все глобальные переменные: это n и k — два значения, для которых мы будем считать количество размещений; это две переменных n1 и k1 типа real, для того чтобы проверить правильность ввода исходных данных; и это величина a, которая является результатом. Так как по формуле значение a является частным, то есть одна величина делится на другую, здесь нужно использовать переменную типа real, несмотря на то, что результат будет целым числом. Далее у нас следует тело функции, которое использует рекурсивную формулу.
Затем мы, для того чтобы передать наше значение в функцию, чтобы оно приобрело целый тип, мы переменной n присваиваем результат округления n1 до целого, а переменной k — результат округления k1 до целого. Вычисляем значения переменной a, вызывая нашу функцию два раза, и выводим на экран полученный результат. Затем наша программа завершается. Рассмотрим программу с использованием рекурсивной функции для вычисления количества размещений по заданной формуле. Вначале у нас объявлены все глобальные переменные: это n и k — два значения, для которых мы будем считать количество размещений; это две переменных n1 и k1 типа real, для того чтобы проверить правильность ввода исходных данных; и это величина a, которая является результатом. Так как по формуле значение a является частным, то есть одна величина делится на другую, здесь нужно использовать переменную типа real, несмотря на то, что результат будет целым числом. Далее у нас следует тело функции, которое использует рекурсивную формулу. При n = 0, результат будет равен 1, а во всех остальных случаях он будет считаться по формуле: факториал предыдущего числа, умноженный на текущее число. Далее мы рассматриваем основную программу, которая всегда располагается после всех процедур и функций. В основной программе вводятся значения n и k, причем пользователю сообщается, какие ограничения наложены на эти значения. У нас n должно быть больше или равно нулю, k должно быть больше или равно n, и оба значения должны быть целыми числами. Мы читаем данные в переменной n1 и k1, для того чтобы можно было проверить, что эти данные принадлежат к целому типу. Если это не так, то есть какое-нибудь из чисел не равно своей целой части, то будет повторный ввод данных. Далее, мы с вами приводим n и k к целому типу, чтобы можно было передать их в качестве аргументов в функцию, потому что параметр, который мы передаем в функцию, имеет целый тип. Дальше мы считаем значение a, вызывая функцию два раза, и выводим на экран полученный результат.
При n = 0, результат будет равен 1, а во всех остальных случаях он будет считаться по формуле: факториал предыдущего числа, умноженный на текущее число. Далее мы рассматриваем основную программу, которая всегда располагается после всех процедур и функций. В основной программе вводятся значения n и k, причем пользователю сообщается, какие ограничения наложены на эти значения. У нас n должно быть больше или равно нулю, k должно быть больше или равно n, и оба значения должны быть целыми числами. Мы читаем данные в переменной n1 и k1, для того чтобы можно было проверить, что эти данные принадлежат к целому типу. Если это не так, то есть какое-нибудь из чисел не равно своей целой части, то будет повторный ввод данных. Далее, мы с вами приводим n и k к целому типу, чтобы можно было передать их в качестве аргументов в функцию, потому что параметр, который мы передаем в функцию, имеет целый тип. Дальше мы считаем значение a, вызывая функцию два раза, и выводим на экран полученный результат. Давайте попробуем запустить программу и введем исходные данные. Если я дам, например, значения, равные 3 и 8, то я получу результат, который мы с вами получали, когда рассматривали саму формулу. Теперь попробуем, что будет, если я введу данные, например, наоборот. Программа не восприняла эти данные, нужно вести их заново, допустим, то есть первым должно стоять число, которое меньше. Теперь посмотрим, что будет получаться, если я введу, например, нецелые числа. [БЕЗ_ЗВУКА] В данном случае результат у нас не достигнут, данные не введены, и нам нужно повторить ввод. Если я ввожу числа в правильном порядке, то я получаю правильный результат. Обращаю ваше внимание, что если я ошибусь второй раз, то есть задам сначала большее число, а потом меньшее, то снова будет повторный ввод, как в данном случае. Если я даю правильную пару, то получаю результат. То же самое происходит, если я ввожу не только нецелые числа, но и, например, отрицательные. − 1,5 и 4,3 — это неправильная пара значений.
Давайте попробуем запустить программу и введем исходные данные. Если я дам, например, значения, равные 3 и 8, то я получу результат, который мы с вами получали, когда рассматривали саму формулу. Теперь попробуем, что будет, если я введу данные, например, наоборот. Программа не восприняла эти данные, нужно вести их заново, допустим, то есть первым должно стоять число, которое меньше. Теперь посмотрим, что будет получаться, если я введу, например, нецелые числа. [БЕЗ_ЗВУКА] В данном случае результат у нас не достигнут, данные не введены, и нам нужно повторить ввод. Если я ввожу числа в правильном порядке, то я получаю правильный результат. Обращаю ваше внимание, что если я ошибусь второй раз, то есть задам сначала большее число, а потом меньшее, то снова будет повторный ввод, как в данном случае. Если я даю правильную пару, то получаю результат. То же самое происходит, если я ввожу не только нецелые числа, но и, например, отрицательные. − 1,5 и 4,3 — это неправильная пара значений. Если я введу правильную пару, первое число должно быть меньше, а второе — больше, и оба должны быть целыми, то тогда получается результат. Таким образом, эта программа работает правильно и проверяет исходные данные на допустимость, то есть проверяет, что числа у нас принадлежат к расширенному натуральному ряду. Они являются либо натуральным числом, либо допустимо значение, равное нулю. И также проверяется, что у нас с вами k больше или равно n. При вводе неправильных данных происходит повторный ввод, и так, пока пользователь не даст нам правильную пару чисел. Только в этом случае мы с вами получим результат. [ЗВУК] [ЗВУК] [ЗВУК]
Если я введу правильную пару, первое число должно быть меньше, а второе — больше, и оба должны быть целыми, то тогда получается результат. Таким образом, эта программа работает правильно и проверяет исходные данные на допустимость, то есть проверяет, что числа у нас принадлежат к расширенному натуральному ряду. Они являются либо натуральным числом, либо допустимо значение, равное нулю. И также проверяется, что у нас с вами k больше или равно n. При вводе неправильных данных происходит повторный ввод, и так, пока пользователь не даст нам правильную пару чисел. Только в этом случае мы с вами получим результат. [ЗВУК] [ЗВУК] [ЗВУК]
C Программа для печати факториала заданного числа
Это программа на языке C для печати факториала заданного числа.
Описание проблемы
Эта программа на C печатает факториал заданного числа.
Решение проблемы
Факториал — это произведение всех чисел от 1 до n, где n — это число, указанное пользователем. Эта программа находит произведение всех чисел от 1 до указанного пользователем числа.
Эта программа находит произведение всех чисел от 1 до указанного пользователем числа.
Программа / исходный код
Вот исходный код программы C для вывода факториала заданного числа.Программа на C успешно скомпилирована и запускается в системе Linux. Вывод программы также показан ниже.
/ * * Программа на C для поиска факториала заданного числа * / #includeпустая функция() { int i, fact = 1, num; printf ("Введите число \ n"); scanf ("% d", & num); если (число <= 0) факт = 1; еще { для (я = 1; я <= число; я ++) { факт = факт * я; } } printf ("Факториал% d =% 5d \ n", число, факт); }
Описание программы
В этой программе на C мы читаем целое число с помощью целочисленной переменной num.Факториал - это произведение всех чисел от 1 до n, где n - это число, указанное пользователем.
Реклама: Присоединяйтесь к Sanfoundry @ Linkedin
Если для проверки используется оператор условия, значение переменной «num» меньше или равно 0. Если условие истинно, оно выполнит оператор и присвоит значение переменной «fact» как единицу. В противном случае, если условие ложно, выполняется инструкция else. Используя цикл for, умножьте все числа от 1 до n и отобразите факториал данного числа в качестве вывода.
Если условие истинно, оно выполнит оператор и присвоит значение переменной «fact» как единицу. В противном случае, если условие ложно, выполняется инструкция else. Используя цикл for, умножьте все числа от 1 до n и отобразите факториал данного числа в качестве вывода.
Случаи тестирования
$ cc pgm79.c $ a.out Введите номер 10 Факториал 10 = 3628800
Sanfoundry Global Education & Learning Series - Программы 1000 C.
Вот список лучших справочников по программированию, структурам данных и алгоритмам на C
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!Факториал
на языке программирования C - Newtum
Factorial в языке программирования C в основном используется для демонстрации применения цикла While Loop, For Loop и Recursion.На самом деле факторный ряд имеет много практических применений и используется для решения задач перестановок и комбинаций.
В этой статье мы пытаемся понять, что такое факторный ряд. Как используются факториальные ряды и как писать факториальные программы на языке программирования C
В этом блоге мы поймем, как написать факторную логику, используя 3 различных метода
- Факториальная программа с использованием цикла While
- Факториальная программа на языке C с использованием цикла For
- Рекурсивная функция для вычисления факториального значения
Сначала разберитесь, что такое факторный ряд и что он использует
Что такое факторный ряд? Факториальная серия обозначается восклицательным знаком (!) Вот так.Факториальный ряд - это умножение любого натурального числа на все меньшее, чем это число. Таким образом, математическое представление факторного ряда будет таким:
n! = n * (n-1) * (n-2) * (n-3) * ……… .. * 3 * 2 * 1
Факториальный ряд используется для решения многих математических задач, таких как перестановка и комбинация.
Эта перестановка и комбинация в дальнейшем используются в сложном аналитическом программировании, таком как искусственный интеллект и отчетность.
Можно сказать, что факторный ряд используется для решения многих других сложных рядов и операций.
Как программист, нам нужно написать много программ для решения многих сложных проблем. Например, мы пишем программы для проектирования машин, расчета стресса или прогнозирования рынка акций.
Эта логика расчета стресса, прогнозирования рынка акций или прогнозирования поведения пользователей написана каким-то великим математиком.
Разработчик программного обеспечения или программист реализует эту логику математика или ученого на компьютере. Эта логика имеет множество вариантов использования факториалов.
Итак, если вы хотите работать в очень большой компании, которая использует много аналитики и занимается основным программированием, вы должны знать, как написать факториальную программу на любом языке программирования.
Написание факторной программы с использованием цикла while
Цикл в то время как цикл очень важен для каждого языка программирования. Помимо цикла while вам нужно знать переменные, printf и scanf.Если вы не знаете, что такое программирование на C или инструкции printf и scanf. Затем вам нужно вернуться к книгам и обратиться к онлайн-курсу.
Если вы находитесь в США, вы можете посмотреть курс программирования C на Amazon Prime или также можете посмотреть серию программ C в Великобритании. Серия Amazon Prime C Programming - лучшая, бесплатная (для участников Amazon Prime) и очень простая для понимания.
Если вы находитесь за пределами США и Великобритании, вам следует подписаться на курс программирования на языке C в Newtum.
Подробное объяснение этой факториальной программы, использующей цикл While, приведено внизу в разделе how to этого блога.
Написание факториала в программировании на C с использованием цикла For
For Loop очень важен для каждого языка программирования. Он используется для написания сложных и вложенных циклов. Если вы не понимаете цикл for, вам следует изучить его в нашем другом блоге или на курсах.
Он используется для написания сложных и вложенных циклов. Если вы не понимаете цикл for, вам следует изучить его в нашем другом блоге или на курсах.
Если вы находитесь в США, вы можете посмотреть курс программирования C на Amazon Prime или также можете посмотреть серию программ C в Великобритании. Серия Amazon Prime C Programming - лучшая, бесплатная (для участников Amazon Prime) и очень простая для понимания.
Если вы находитесь за пределами США и Великобритании, вам следует подписаться на курс программирования на языке C в Newtum.
Подробное объяснение этой факторной программы, использующей цикл For, приведено внизу в разделе how to этого блога.
Запись факториала в программировании на C с использованием рекурсивной функции
Функция - бесполезная тема, и она не входит в рамки этого блога. Вы всегда можете обратиться к нашему курсу программирования на C, если хотите более подробно разобраться в функциях
Раздел «Как сделать» подробно объясняет каждую программу из перечисленных выше программ на языке C
Необходимое время: 10 часов.
Как написать факториальную программу C тремя разными способами
- Использование цикла while
1. Объявите 3 переменные «n» для входного числа, «i» для счетчика и «f» для хранения окончательных результатов.
2. Введите число, используя операторы scanf и выше, которые записывают оператор printf, чтобы пользователь понял.
3. Инициализируйте переменные i и f равными 1, это необходимо, поскольку факториал включает умножение и значение не может быть нулевым.
4. Напишите цикл while с условием i <= n, чтобы наш цикл выполнялся n раз
5.Внутри цикла while записываем логику умножения f = n * i, чтобы каждый раз, когда значение i увеличивалось, умножение выполнялось.
6. Увеличивайте значение i каждый раз, когда цикл выполняется с помощью оператора увеличения
7. После цикла while выведите значение переменной «f». - Использование для цикла
1. Сначала мы объявим 3 переменных «n» для входного числа, «i» для счетчика и «f» для хранения окончательных результатов.

2. Мы попросим пользователя ввести число с помощью оператора printf и оператора scanf.
3. Инициализировать переменную «f» значением 1
3. Записать цикл for с i = 1 и условием i <= n
4. Внутри цикла записать логику умножения f = n * i, чтобы каждый раз значение i увеличивается умножение будет выполнено.
5. После цикла for выведите значение переменной «f». - Факториальная программа на C с использованием рекурсивной функции
1. Сначала мы объявим 3 переменных «n» для входного числа, «i» для счетчика и «f» для хранения окончательных результатов.
2. Мы попросим пользователя ввести число с помощью оператора printf и оператора scanf.
3. Инициализировать переменную «f» значением 1
3. Вызвать функцию factorial, передав значение «n»
4. После цикла for выведите значение переменной «f».
5. Объявите функцию factorial в функции, принимающей ввод в переменной «x».
6. Внутри функции factorial объявите переменную temp.
7. Напишите оператор if и else для x> 1, а внутри условия напишите необходимое выражение, как показано в коде, и верните значение.Здесь мы снова вызываем ту же функцию, пока не будет выполнено условие. Это рекурсия.
8. В условии else напишите return 1.
(Посещали 165 раз, 1 посещали сегодня)
Программа на C ++ для определения суммы факторного ряда 1! + 2! + 3! + 4! ...
Программа на C ++ для определения суммы факторного ряда 1! + 2! + 3! + 4!…
В этом руководстве мы узнаем, как найти сумму факториалов ряда до определенной длины.Наша программа получит от пользователя значение n и найдет сумму . Например, если значение n равно 2 , будет найдено 1! + 2! , это 5 , найдет 1! + 2! +… 5! и т. Д.
Из этого поста вы узнаете, как получить вводимые пользователем данные и как найти факториал в C ++.
Программа C ++:
#include
используя пространство имен std;
интервал findFact (интервал n)
{
вернуть n == 1? 1: n * findFact (n - 1);
}
int main ()
{
int n, сумма = 0;
cout << "Введите значение n:" << endl;
cin >> n;
для (int i = 1; i <= n; i ++)
{
сумма + = findFact (i);
}
cout << "Sum:" << sum << endl;
} Explanation:
- findFact Метод используется для определения факториала числа.

- В основной функции у нас есть две переменные типа int n и сумма .
- Значение n принимается как вводимое пользователем. Используя цикл для , мы находим факториал всех чисел от 1 до n и складываем все значения для вычисления итоговой суммы результата.
Пример вывода:
Введите значение n:
4
Сумма: 33
Введите значение n:
10
Сумма: 4037913 Метод 2: Используя текущее значение факториала:
Мы также можем сохранить текущее значение факториала в переменной и умножить его на следующее число, чтобы получить следующее значение.
факториал 1: 1
факториал 2: факториал 1 * 2
факториал 3: факториал 2 * 3
факториал 4: факториал 3 * 4 Ниже приведена программа на C ++:
#include
используя пространство имен std;
int main ()
{
int n, сумма = 0, currentFact = 1;
cout << "Введите значение n:" << endl;
cin >> n;
для (int i = 1; i <= n; i ++)
{
currentFact * = i;
сумма + = currentFact;
}
cout << "Sum:" << sum << endl;
} Здесь мы сохраняем факториал в переменной currentFact .

 Обозначается факториал восклицательным знаком после числа — «n!».
Обозначается факториал восклицательным знаком после числа — «n!». 28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
 append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
 377 CPU seconds
377 CPU seconds
