Равенства на кругах эйлера – описание, примеры, для дошкольников, для школьников

Содержание

Множества и операции над ними. Решение задач с помощью кругов Эйлера

Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его элементом. Например, если множество – дни недели, то понедельник элемент этого множества.

Блок 1. Множества и операции над ними.

Презентация. (Слайд 2) Вопросы к слайду 2:

Перечислите элементы множеств:
а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
б) натуральных чисел; (1; 2; 3; 4;…)
в) целых чисел (…-2; -1; 0; 1; 2;…).
Как называется множество цветов, стоящих в вазе? (букет).
Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).

Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
Приведите примеры множеств, элементами которого являются геометрические фигуры.
Какие названия применяют для обозначения множеств животных? (млекопитающие, земноводные, хладнокровные и т.п.).
Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).

Задайте сами множество описанием.

(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

I – множество иррациональных чисел;

R – множество действительных чисел.

(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри фигурных скобок {,}.

Например, цифры десятичной системы счисления задаются множеством

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.

Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.

Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.

{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.

Чтобы задать конечное множество, можно просто перечислить все его элементы.

Например, запись А = {2; 3; 5; 7; 11; 13} означает, что множество А состоит из первых шести простых чисел.

Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.

Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а множество всех чисел, которые больше 5 и меньше 12 записать {х | 5< х <12} или (5; 12). В примерах использован оборот “ … и так далее” и символ “ | ” внутри фигурных скобок заменяющий комбинацию слов “ … таких, что …”. (Множество всех х таких, что 5< х <12).

Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных случаях множество называют пустым и обозначают символом O, в фигурные скобки его не ставят, так как никакого перечисления элементов пустого множества не происходит.

(Слайд 5) Задание 1. [3]

1) Задайте множество цифр, с помощью которых записывается число:

а) 3254; б) 8797; в) 11000; г) 555555.

2) Задайте множество А описанием:

а) А = {1, 3, 5, 7, 9}; б) А = {– 2, – 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д) А = {1/2, 2/3, 3/4, 4/5, … }.

3) Задание с выбором ответа. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7},

S = {4, 6}. Какое из утверждений неверно?

а) М = Р. б) Р S. в) М Т. г) Р = Т.

(Слайд 6) Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.

В математике эти выражения кратко записывают так: х А, где – знак принадлежности.

Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.

(Слайд 7) Задание 2. [3; 1]

1. Запишите на символическом языке следующее утверждение:

а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое.

2. Верно ли, что:

а) – 5 N; б) -5 Z; в) 2,(45) Q?

3. Верно ли, что:

а) 0,7 {х | х² – 1 < 0}; б) – 7 {х | х² + 16х ? – 64}?

(Слайд 8) Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.

Знак “” называют знаком включения.

Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).

Рис. 1

Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).

(Слайд 9) Задание 3. [3; 1]

1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.

Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в) С…А; г) С…В.

2. Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.

Верно ли, что: а) А В; б) В С; в) С А; г) С В?

(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:

1) Пересечением множества А и В называют множество, состоящие из всех общих 11элементов множеств А и В, т. е. из всех элементов, которые принадлежат и множеству А, и множеству В (рис. 2). Пересечение множеств А и В обозначают так: АВ. Это определение можно записать и так: АВ = {х | х А и х В}. Иными словами, пересечение двух множеств – это их общая часть. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100} и В = {6; 12; 18;…}, то АВ = {30; 60; 90}. Можно рассматривать пересечение не только двух, но трех, четырех и т. д. множеств. Пересечение множеств В, С и D обозначают так: ВСD.

Рис. 2

(Слайд 11) Задание 4. [3; 1]

1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.

Найдите: а) АВ; б) АС; в) СВ.

2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.

Найдите АВ.

3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.

Найдите (АВ) С.

(Слайд 12)

2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.
Рис. 3
Это определение можно записать и так: АUВ = {х | х А или х В}. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.

(Слайд 13) Задание 5. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АUВ)UС.
3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].
Найдите (АUВ)UС.
Продолжение статьи
Приложение
Презентация
urok.1sept.ru
Круги Эйлера: примеры и возможности
Математика по своей сути наука абстрактная, если отойти от элементарных понятий. Так, на паре-тройке яблок можно наглядно изобразить основные операции, что лежат в основе математики, но, как только плоскость деятельности расширяется, этих объектов становится недостаточно. Кто-нибудь пробовал изобразить на яблоках операции над бесконечными множествами? В том-то и дело, что нет. Чем сложнее становились понятия, которыми оперирует математика в своих суждениях, тем проблематичнее казалось их наглядное выражение, которое было бы призвано облегчить понимание. Однако, на счастье как современных студентов, так и науки в целом, были выведены круги Эйлера, примеры и возможности которых мы рассмотрим ниже.
Немного истории
17 апреля 1707 года мир подарил науке Леонарда Эйлера — замечательного ученого, чей вклад в математику, физику, кораблестроение и даже теорию музыки не переоценить.
Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.
В чем же суть?
На практике круги Эйлера, схема которых изображена ниже, могут применяться не только в математике, так как понятия «множества» присущи не только данной дисциплине. Так, они с успехом применяются и в менеджменте.
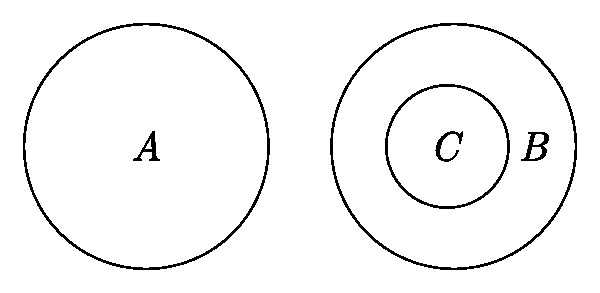
Схема выше показывает отношения множеств А (иррациональные числа), В (рациональные числа) и С (натуральные числа). Круги показывают, что множество С включено в множество В, тогда как множество А с ними никак не пересекается. Пример простейший, но наглядно объясняет специфику «взаимоотношений множеств», которые слишком абстрактны для реального сравнения хотя бы в силу их бесконечности.
Алгебра логики
Данная область математической логики оперирует высказываниями, которые могут носить как истинный, так и ложный характер. Например, из элементарного: число 625 делится нацело на 25, число 625 делится нацело на 5, число 625 является простым. Первое и второе утверждения – истина, тогда как последнее – ложь. Конечно, на практике все сложнее, но суть показана ясно. И, конечно же, в решении опять участвуют круги Эйлера, примеры с их использованием слишком удобны и наглядны, чтобы их игнорировать.
Немного теории:
Пусть множества А и В существуют и не являются пустыми, тогда для них определены следующие операции пересечения, объединения и отрицания.
Пересечение множеств А и В состоит из элементов, что принадлежат одновременно как множеству А, так и множеству В.
Объединение множеств А и В состоит из элементов, что принадлежат множеству А или множеству В.
Отрицание множества А — это множество, что состоит из элементов, которые не принадлежат множеству А.
Все это изображают опять же круги Эйлера в логике, так как с их помощью каждая задача, вне зависимости от степени сложности, становится очевидной и наглядной.
Аксиомы алгебры логики
Положим, что 1 и 0 существуют и определены во множестве А, тогда:
отрицание отрицания множества А есть множество А;
объединение множества А с не_А есть 1;
объединение множества А с 1 есть 1;
объединение множества А с самим собой есть множество А;
объединение множества А с 0 есть множество А;
пересечение множества А с не_А есть 0;
пересечение множества А с самим собой есть множество А;
пересечение множества А с 0 есть 0;
пересечение множества А с 1 есть множество А.
Основные свойства алгебры логики
Пусть множества А и В существуют и не являются пустыми, тогда:
для пересечения и объединения множеств А и В действует переместительный закон;
для пересечения и объединения множеств А и В действует сочетательный закон;
для пересечения и объединения множеств А и В действует распределительный закон;
отрицание пересечения множеств А и В есть пересечение отрицаний множеств А и В;
отрицание объединения множеств А и В есть объединение отрицаний множеств А и В.
Ниже показаны круги Эйлера, примеры пересечения и объединения множеств А, В и С.
Перспективы
Работы Леонарда Эйлера обоснованно считаются базой современной математики, однако сейчас их с успехом применяют в областях человеческой деятельности, что появились относительно недавно, взять хотя бы корпоративное управление: круги Эйлера, примеры и графики описывают механизмы моделей развития, будь то российская или англо-американская версия.
fb.ru
Отношение между понятиями. Круги Эйлера.

Понятие – это форма мысли, отображающая предметы в их наиболее общих и существенных признаках.
Понятие – это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.
По содержанию между понятиями могут быть два основных вида отношений: сравнимость и несравнимость.
Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»).
В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»).
Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ.
Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).
ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ) Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма.
1) А – Аристотель В – основатель логики 2) А – квадрат В – равносторонний прямоугольник
ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ) Объём одного понятия полностью входит в объём другого, но не исчерпывает его.
1) А – человек В – студент 2) А – животное В – слон
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ) Объёмы двух понятий частично совпадают. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них.
1) А – юрист В – депутат 2) А – студент В – спортсмен
СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ) Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия.
1) А – животное В – кот; С – собака; D – мышь 2) А – драгоценный металл В – золото; С – серебро; D — платина
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ) Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный.
1) А – белый кот; В – рыжий кот (коты бывают и чёрными и серыми) 2) А – горячий чай; холодный чай (чай может быть и тёплым) Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ) Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое – их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими.
1) А – высокий дом В – невысокий дом 2) А – выигрышный билет В – невыигрышный билет Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.
studfiles.net
Круги Эйлера — Википедия
Пример кругов Эйлера. Буквами обозначены, например, свойства: — живое существо, — человек, — неживая вещь
Круги́ Э́йлера^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[2]
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовались и немецкие математики Алекс ван Сивцео и Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.
↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
Логика
Формальная
Логические операции с понятиями
Изменение содержания понятия: отрицание • ограничение • обобщение • деление
Изменение объёма понятия: сложение • умножение • вычитание
Типы: Многозначная логика • Бинарная логика
Логическая константа
Законы: Закон обратного отношения между содержанием и объёмом понятия
Математическая
(теоретическая,
символическая)
Логические связки (операции) над высказываниями
Высказывание — построение над множеством {B, , , , 0, 1}
В — непустое множество, над элементами которого определены три базовые операции: конъюнкция ( или &,бинарная) • дизъюнкция (,бинарная) • отрицание (,унарная)
2 константы: 0 • 1
См. также импликация () • Круги Эйлера/Диаграмма Венна • Теория множеств
www.wiki-wiki.ru
No related posts.