Какова вероятность того что: Какова вероятность того, что случайно выбранное… — Задание 4 ЕГЭ по математике (теория вероятностей)

Теория вероятности (18 задач)

1 вариант.

1.  Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?

Решение

В нашем случае элементарным исходом является выбор одного числа от до

— пространство элементарных исходов.

— количество всех элементарных исходов.

Итак,  все элементарные исходы равновозможны, т. к. натуральное число выбирается наудачу и пространство элементарных исходов конечно, следовательно, эксперимент, описанный в задаче, удовлетворяет классическому определению вероятности.

— выбранное число является делителем

— множество благоприятствующих исходов.

— количество всех благоприятствующих исходов.

— искомая вероятность.

Ответ:

2.  В урне три белых и пять черных шаров. Наудачу вынимают два шара. Какова вероятность того, что эти шары разных цветов?

Решение

Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 8 шаров вынуть два, т.

е. числу сочетаний из 8 элементов по 2:

Число благоприятствующих исходов (числу способов, которыми можно из 3 белых шаров вынуть один и из 5 чёрных шаровы вынуть один):

Следовательно, искомая вероятность

Ответ:

3.  Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. Для второго станка эта вероятность равна 0,8. На первом станке изготовлены всего 2 детали, на втором – 3. Найти вероятность того, что все детали первосортные.

Решение

Так как изготовление деталей на станках независимые события. То, по теореме умножения вероятностей независимых событий, искомая вероятность равна

Ответ:

4.  В тире имеется 5 винтовок, вероятности попадания в цель из которых равны соответственно 0.5, 0.6, 0,7, 0,8 и 0,9. Определить вероятность попадания из взятой наугад винтовки.

Решение

Определим гипотезы:

Hi = {выбрана i-тая винтовка} i = 1, 2, 3, 4, 5.

A={попадание в мишень с одного выстрела}

A|Hi ={попадание в мишень из i-той винтовки}

Тогда их вероятности, по условию,

По формуле полной вероятности

Ответ:

5.   30% изделий некоторого предприятия – продукция высшего сорта. Приобретено 4 изделия этого предприятия. Какова вероятность того, что 2 из них высшего сорта?

Решение

Используем схему Бернулли. Здесь n= 4, m=2, p = 0,3, q =1-0,3= 0,7. Тогда по формуле

Вероятность того, что 2 изделия из 4 будут высшего сорта:

Ответ:

6.  Пусть n – число независимых испытаний, р – вероятность появления события А в отдельном испытании, k – число наступлений события А за n испытаний:

А) , . Найти

Б) Найти , если ,

Решение

а) Так как n = 600 – велико, то в данном случае применяем локальную формулу Лапласа:

, где .

По условию задачи , , , .

Вычислим .

По таблице находим .

Теперь вычислим искомую вероятность

.

б) Вероятность того, что отклонение частости события от вероятности при n независимых испытаниях не превышает заданного , находится по формуле

Тогда, по условию

Имеем

Используем таблицу значений функции Лапласа

Отвте: ,

7.   Случайная величина Х распределена по закону Коши: . Найьти коэффициент а, функцию распределения , вероятность попадания с. в. Х на интервал . Существует ли для с. в. Х числовые характеристики МХ и ДХ?

Решение

Найдём значение параметра а:

Тогда

Найдём функцию распределения

Найдём вероятность попадания с. в. Х на интервал

Посчитаем математическое ожидание и дисперсию:

Следовательно, для данной случайной величины не существуют ни М(Х) ни Д(Х)

8.  Изделия испытываются на надёжность. Вероятность выхода из строя за время испытания для каждого изделия равна 0,9. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Найти математическое ожидание числа испытаний.

Решение

— число испытаний.

— вероятность того, что изделие выдержало испытание.

Тогда получим ряд распределения

Это геометрическое распределение

Найдём — математическое ожидание случайной величины , имеющей геометрическое распределение

= (сходится так как )

В нашем случае р=0,9, следовательно

Ответ:

9.   Найти коэффициент корреляции двумерной случайной величины (Х, Y), заданной матрицей:

X\y	1	2
-1	0.15	0.1
0	0.15	0.05
1	0.32	0.23

Решение

События (X=xi, Y=yj) образуют полную группу событий, поэтому сумма всех вероятностей pij(i=1,2…,n, j=1,2..,m), указанных в таблице, равна 1.

1. Зависимость случайных величин X и Y.

Находим ряды распределения X и Y.

Пользуясь формулой ∑P(xi, yj) = pi (j=1..n), находим ряд распределения X.

X	-1	0	1
P	0.25	0.2	0.55	∑Pi = 1

Математическое ожидание M[X].

M[x] = (-1)*0.25 + 0*0.2 + 1*0.55 = 0.3

Дисперсия D[X]. D[X] = 12*0.25 + 02*0.2 + 12*0.55 — 0.32 = 0.71

Среднее квадратическое отклонение σ(x).

Пользуясь формулой ∑P(xi, yj) = qj (i=1..m), находим ряд распределения Y.

Y	1	2
P	0.62	0.38	∑Pi = 1

Математическое ожидание M[Y]. M[y] = 1*0.62 + 2*0.38 = 1.38

Дисперсия D[Y]. D[Y] = 12*0.62 + 22*0.38 — 1.382 = 0.24

Среднее квадратическое отклонение σ(y).

Поскольку, P(X=-1,Y=1) = 0.15≠0.25•0.62, то случайные величины X и Y зависимы.

Ковариация. cov(X, Y) = M[X•Y] — M[X]•M[Y]

Cov(X, Y)=1•(-1)•0.15+2•(-1)•0.1+1•0•0.15+2•0•0.05+1•1•0.32+2•1•0.23-0.3•1.38=0.016

Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X, Y) ≠ 0.

Коэффициент корреляции.

,

Ответ:

1.  Брошены 3 монеты. Найти вероятность того, что выпадут 2 «герба».

Решение

В нашем случае элементарным исходом является выпадение одной из возможных комбинаций. Обозначим «г»-выпадение герба на монете, «р» — выпадение решки на монете. Тогда возможны ситуации:

Ггг, ргг, грг, ррг, ррр, ргр, ггр, грр

— пространство элементарных исходов.

N=8 — количество всех элементарных исходов.

Итак,  все элементарные исходы равновозможны, следовательно эксперимент, описанный в задаче, удовлетворяет классическому определению вероятности.

— выпало 2 герба

— множество благоприятствующих исходов.

— количество всех благоприятствующих исходов.

— искомая вероятность.

Ответ:

2.  Из 10 карточек с буквами А, Д, А, Б, А, Д, В, Г, Д, А наудачу выбираются 3. Какова вероятность того, что из этих карточек можно сложить слово «два»?

Решение

Число всевозможных исходов-количество способов вытянуть 3 карточки из 10.

A = {из отобранных карточек можно составить слово «два»}

Число благоприятных исходов-количество способов вытянуть 3 буквы из которых можно составить слово «раз»:

M=3*1*4=12 – по теореме умножения вероятностей независимых событий.

Используем формулу классического определения вероятности:

Ответ:

3.  Стрелок стреляет 3 раза по удаляющейся цели. Вероятность попадания при первом выстреле – 0,8, при втором – 0,7 и при третьем – 0,6. Какова вероятность хотя бы одного попадания?

Решение

Вероятность не попасть при первом выстреле 1-0,8=0,2, вероятность не попасть при втором выстреле 1-0,7=0,3, вероятность не попасть при третьем выстреле 1-0,6=0,4.

По теореме об умножении вероятностей независимых событий, вероятность не попасть при трёх выстрелах 0,2*0,3*0,4=0,024.

Значит вероятность хотя бы одного попадания (противоположное событие): 1-0,024=0,976.

Ответ: 0,976.

4.  60% школьников – девочки. 80% девочек и 75% мальчиков имеют билеты в театр. В учительскую принесли потерянный кем-то билет. Какова вероятность того, что этот билет принадлежит девочке?

Решение

Определим гипотезы:

h2 = билет потеряла девочки

h3 = билет потерял мальчик

,

A={билет был потерян}

A|h2 ={был потерян билет, и он принадлежал девочке}

A|h3 ={был потерян билет, и он принадлежал мальчику}

Тогда их вероятности, по условию,

По формуле Байеса

Ответ:

5.  Изделия некоторого предприятия содержат 5% брака. Найти вероятность того, что среди 5 взятых наудачу изделий будут 2 бракованных.

Решение

Используем схему Бернулли.

Здесь n=5, m=2, p=0,05, q=1-0,05=0,95. Тогда по формуле

Вероятность того, что 2 изделия из 5 будут бракованные:

Ответ:

6.  Пусть n – число независимых испытаний, р – вероятность появления события А в отдельном испытании, k – число наступлений события А за n испытаний:

А) , . Найти

Б) Найти , если ,

Решение

а) Так как n = 600 – велико, то в данном случае применяем интегральную формулу Лапласа:

= Ф(х´´) – Ф(х´), где х´ = ; х´´ = ,

т. к. , , , , имеем

Х´ = ; х´´ = .

По таблицам найдем значения Ф(-1)=-Ф(1)=-0,34134

Тогда искомая вероятность будет

= Ф(1) – Ф(-1) =2Ф(1)= 2*0,34134=0,68268

б) Вероятность того, что отклонение частости события от вероятности при n независимых испытаниях не превышает заданного , находится по формуле

Тогда, по условию

Имеем

Используем таблицу значений функции Лапласа

Ответ: =0,68268,

7. Производятся 20 независимых испытаний, в каждом из которых вероятность появления успеха равна 0,2. Найти дисперсию числа появлений успеха в этих испытаниях.

Решение

Случайная величина X — число появлений успеха при 20 независимых испытаниях.
n = 20 — количество независимых испытаний

P = 0.2 — вероятность успеха при одном испытании

Q = 1 — p = 1 — 0.2 = 0.8

Случайная величина X имеет распределение Бернулли с параметрами

N = 20 и p = 0.2

D(X) = npq = 20*(0.2)*(0.8) = 3.2

Ответ: D(X)=3.2

8. Случайная величина Х равномерно распределена на . Построить графики и . Найти , если с. в.

Решение

Так как случайная величина распределена равномерно, то

, то есть

Построим график

Известно, что F(x)=

Поэтому,

Если х<-1, то F(x)==0;

Если -1≤х≤1, то

Если х>1, то F(x)= 1

Таким образом,

Построим график

Как известно, дисперсия равномерно распределённой случайной величины равна . Тогда в нашем случае

Используя свойства дисперсии

Тогда . Следовательно

9.  Найти коэффициент корреляции двумерной случайной величины (Х, Y), заданной матрицей:

X\y	1	3	4
1	0.4	0.1	0.1
3	0.2	0.1	0.1

Решение

События (X=xi, Y=yj) образуют полную группу событий, поэтому сумма всех вероятностей pij(i=1,2.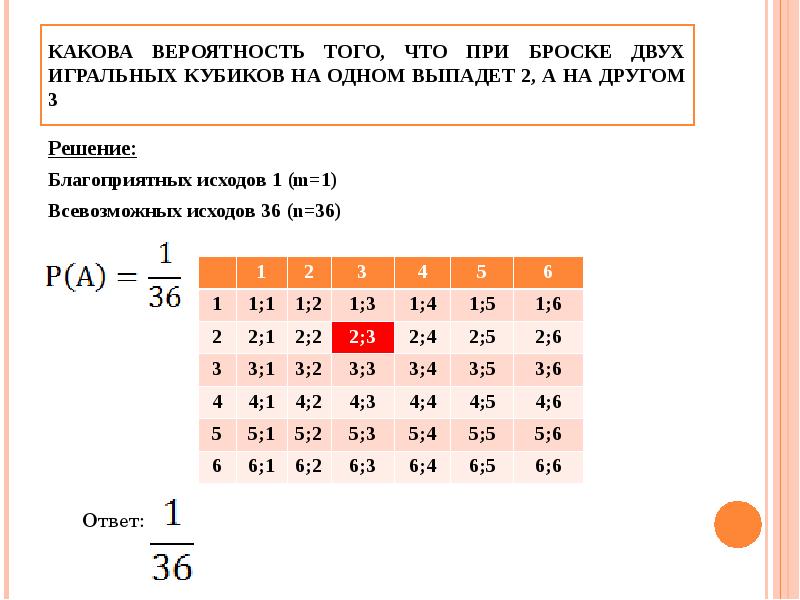 ..,n, j=1,2..,m), указанных в таблице, равна 1.

1. Зависимость случайных величин X и Y.

Находим ряды распределения X и Y.

Пользуясь формулой ∑P(xi, yj) = pi (j=1..n), находим ряд распределения X.

X	1	3
P	0.6	0.4	∑Pi = 1

Математическое ожидание M[X]. M[x] = 1*0.6 + 3*0.4 = 1.8

Дисперсия D[X]. D[X] = 12*0.6 + 32*0.4 — 1.82 = 0.96

Среднее квадратическое отклонение σ(x).

Пользуясь формулой ∑P(xi, yj) = qj (i=1..m), находим ряд распределения Y.

Y	1	3	4
P	0.6	0.2	0.2	∑Pi = 1

Математическое ожидание M[Y]. M[y] = 1*0.6 + 3*0.2 + 4*0.2 = 2

Дисперсия D[Y]. D[Y] = 12*0.6 + 32*0.2 + 42*0.2 — 22 = 1.6

Среднее квадратическое отклонение σ(y).

Поскольку, P(X=1,Y=1) = 0.4≠0.6•0.6, то случайные величины X и Y зависимы.

Ковариация. cov(X, Y) = M[X•Y] — M[X]•M[Y]

Cov(X, Y)=1•1•0.4+3•1•0.1+4•1•0.1+1•3•0.2+3•3•0.1+4•3•0.1-1.8 • 2=0.2

Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X, Y) ≠ 0.

Коэффициент корреляции.

,

Ответ:

< Предыдущая		Следующая >

Контрольная по теории вероятностей 1

Ответы к контрольной работе по теории вероятности помогут студентам первых курсов, изучающих математические дисциплины. Задания охватывают много теоретического материала, а обоснование их решения пригодится каждому студенту.

Задача 1. Куб все грани которого закрашены, распилен на 1000 кубиков одинаковых размеров. Определить вероятность того что кубик вытянутый наугад будет иметь:

• а) одну закрашеную грань;
• б) две закрашеные грани.

Вычисления: Если куб распилить на кубики одинакового размера то все грани будут поделены на 100 квадратов. (Примерно как на рисунке)
Дальше по условию кубик должен иметь одну закрашенную грань — это значит что кубики должны принадлежать внешней поверхности но не лежать на ребрах куба (2 закрашеные поверхности) и не на углах — имеют три закрашеные поверхности.
Следовательно, искомое количество равно произведению 6 граней на количество кубиков в квадрате размером 8*8.
6*8*8=384 – кубики с 1 закрашеной поверхностью.
Вероятность равна количеству благоприятных событий к общему их количеству P=384/1000=0,384.
б) Две закрашеные грани имеют кубики по ребрам без самих вершин куба. На одном ребре будет 8 таких кубиков. Всего в кубе 12 ребер, поэтому две закрашенные грани имеют
8*12=96 кубиков.
А вероятность вытянуть их среди 1000 всех равная
P=96/1000=0,096.
На этом задание решено и переходим к следующему.

Задача 2. На одинаковых карточках написаны буквы А, А, А, Н, Н, С. Какова вероятность того, что случайно разместив карточки в ряд, получим слово АНАНАС?
Вычисления: Нужно рассуждать всегда от того, что известно. Дано 3 буквы А, 2-Н, и 1 — С, всего их 6. Начнем выбирать буквы для слова «ананас». Первой идет буква А, которую мы можем выбрать 3 способами из 6, потому что есть 3 буквы А среди 6 известных. Поэтому вероятность вытянуть первой А равна
P₁=3/6=1/2.
Вторая буква Н, но не следует забывать, что после того как вытащили А остается 5 букв для выбора. Поэтому вероятность вытянуть под 2 номером Н равна
P₂=2/5.
Следующую А вероятность вытянуть среди 4, что осталось
P₃=2/4.
Далее Н можно извлечь из вероятностью
P₄=1/3.
Чем ближе к концу тем больше вероятность, и уже А можем извлечь при
P₅=1/2.
После этого остается одна карточка С, поэтому вероятность ее вытащить равна 100 процентам или
P₆=1.
Вероятность составить слово АНАНАС равна произведению вероятностей
P=3/6*2/5*2/4*1/3*1/2*1=1/60=0,016(6).
На этом и базируются подобные задачи по теории вероятностей.

Задача 3. Из партии изделий товаровед наугад выбирает образцы. Вероятность того что наугад взятое изделие окажется высшего сорта равна 0,8. Найти вероятность того, что среди 3 отобранных изделий будет два изделия высшего сорта?
Вычисления: Данный пример на применение формулы Бернулли.
p=0,8; q=1-0,8=0,2.
Вероятность вычисляем по формуле

Если объяснять не на языке формул, то нужно составить комбинации из трех событий, два из которых благоприятны, а одно нет. Это можно записать суммой произведений

Оба варианта являются равносильными, только первый можем применить во всех задачах, а второй в подобных к рассмотреной.

Задача 4. Из пяти стрелков двое попадают в цель с вероятностью 0,6 и трое с вероятностью 0,4. Что вероятнее: наугад выбранный стрелок попадает в цель или нет?
Вычисления: По формуле полной вероятности определяем вероятность, что стрелок попадет.
P=2/5*0,6+3/5*0,4=0,24+0,24=0,48.
Вероятность меньше P<0,5, следовательно вероятнее что наугад выбранный стрелок не попадет в цель.
Вероятность не попадания составляет

или
P=2/5*(1-0,6)+3/5*(1-0,4)=0,16+0,36=0,52.

Задача 5. C 20 студентов, пришедших на экзамен, 10 подготовлены отлично (знают все вопросы), 7 хорошо (знают по 35 вопросов), а 3 плохо (10 вопросов). В программе 40 вопросов. Наугад вызванный студент ответил на три вопроса билета. Какова вероятность того, что он подготовлен на

• а) отлично;
• б) плохо.

Вычисления: Суть задачи заключается в том что студент ответил на три вопроса билета, то есть на все что были заданы, а вот какова вероятность их вытянуть мы сейчас вычислим.
Найдем вероятность что студент ответил на три вопроса правильно. Это будет отношение количества студентов ко всей группе умноженное на вероятность вытянуть билеты которые они знают среди всех возможных

Теперь найдем вероятность что студент принадлежит группе которая подготовлена «на отлично». Это равносильно доле первого слагаемого предварительной вероятности, к самой вероятности

Вероятность, что студент принадлежит группе которая плохо подготовилась достаточно мала и равна 0,00216.

На этом задание выполнено. Хорошо его разберите и запомните как вычислять, поскольку на контрольных и тестах оно распространено.

Задача 6. Монету бросают 5 раз. Найти вероятность того что герб выпадет менее 3 раз?
Вычисления: Вероятность вытянуть герб или решку равносильна и равна 0,5. Менее 3 раз означает, что герб может выпасть либо 0, либо 1, либо 2 раза. «Или» всегда в вероятности в операциях сказывается добавлением.
Вероятности находим по формуле Бернулли

Поскольку p=q=0,5, то вероятность равна

Вероятность равна 0,5.

Задача 7. При штамповке металлических клемм получается в среднем 90% стандартных. Найти вероятность того что среди 900 клемм стандартными будут не менее 790 и не более 820 клемм.

Вычисления: Вычисления необходимо проводить по интегральной теореме Муавра-Лапласа.
Записываем известные величины
n=900; p=0,9; q=1-0,9=0,1; k1=790; k2=820.
Вероятность находим по формуле

где интегральная функция Лапласа

Значение x₁, x₂ вычисляем по формуле


Далее находим вероятность что среди 900 клемм стандартными будут не менее 790 и не более 820

Если объясните подобные задачи так как здесь написано то за контрольную по вероятности получите оценку «отлично».

Вероятность

Как вероятно что-то должно произойти.

Многие события невозможно предсказать с полной уверенностью. Лучшее, что мы можем сказать, это насколько вероятно они должны произойти, используя идею вероятности.

Подбрасывание монеты

При подбрасывании монеты возможны два исхода:

Головки (H) или хвостовики
(T)

Также:

• вероятность выпадения монеты H равно ½
• вероятность выпадения монеты T равна ½

 

Бросание игральных костей

При бросании одной кости возможны шесть исходов: 1, 2, 3, 4, 5, 6 .

Вероятность любого из них равна 1 6

Вероятность

В целом:

Вероятность события = Количество способов, которыми это может произойти Общее количество исходов

 

Пример: вероятность выпадения «4» кубиком

Количество возможных вариантов: 1 (есть только 1 грань с «4»)

Общее количество исходов: 6 (всего 6 граней)

Таким образом, вероятность = 1 6

Пример: в мешке 5 шариков: 4 синих и 1 красный. Какова вероятность того, что будет выбран синий шарик?

Количество возможных вариантов: 4 (есть 4 синих)

Общее количество исходов: 5 (всего 5 шариков)

Таким образом, вероятность = 4 5 = 0,8

Линия вероятности

Мы можем показать вероятность на линии вероятности:

Вероятность всегда между 0 и 1

Вероятность — это всего лишь ориентир

Вероятность не говорит нам точно, что произойдет, это всего лишь ориентир

Пример: подбросьте монету 100 раз, сколько выпадет орла?

Вероятность говорит о том, что орёл имеет ½ шанса, поэтому мы можем ожидать 50 орлов .

Но когда мы попытаемся это сделать, мы можем получить 48 или 55 орлов… или вообще что угодно, но в большинстве случаев это будет число около 50.

Узнайте больше в индексе вероятности.

слов

Некоторые слова имеют особое значение в Вероятности:

Эксперимент : повторяемая процедура с набором возможных результатов.

Пример: Бросание игральных костей

Мы можем бросать кости снова и снова, так что это повторяется.

Набор возможных результатов любого одиночного броска: {1, 2, 3, 4, 5, 6}

Результат: Возможный результат.

Пример: «6» — это один из результатов броска игральной кости.

 

Испытание: Одиночное выполнение эксперимента.

Пример: Я провел эксперимент с подбрасыванием монеты. После 4 попыток я получил следующие результаты:

Результат	Испытание	Испытание	Испытание	Пробная
Головка	✔	✔		✔
Хвост			✔

Три испытания имели исход «Голова», а одно испытание — «Хвост».

Sample Space: все возможные результаты эксперимента.

Пример: выбор карты из колоды

В колоде 52 карты (не считая джокеров)

Таким образом, Пространство выборки — это все 52 возможные карты : {Туз червей, 2 червей и т. д. .. }

 

Пространство выборки состоит из точек выборки:

Точка выборки: только один из возможных результатов

Пример: Колода карт

• 5 треф является точкой отсчета
• Король Червей является пробной точкой

«Король» не является точкой отбора. Есть 4 короля, то есть 4 различных точек выборки.

Пример: бросание игральных костей

В этой области выборки имеется 6 различных точек выборки.

 

Событие: одно или более результаты эксперимента

Пример событий:

Событие может иметь только один исход:

• Выпадение решки при подбрасывании монеты
• Роллинг «5»

Событие может включать более одного исхода:

• Выбор «Короля» из колоды карт (любого из 4 Королей)
• Выпадение «четного числа» (2, 4 или 6)

 

Эй, давайте использовать эти слова, чтобы вы привыкли к ним:

Пример: Алекс хочет узнать, сколько раз выпадет «дубль» при бросании двух костей.

Пространство выборки все возможно Результаты (36 точек выборки):

{1,1} {1,2} {1,3} {1,4} …
…
. .. {6,3} {6,4} {6,5} {6,6}

 

Событие , которое ищет Алекс, — это «двойное число», когда оба кубика имеют одинаковое число. Он состоит из этих 6 точек выборки :

{1,1} {2,2} {3,3} {4,4} {5,5} и {6,6}

 

Эти результаты Алекса:

Пробная версия	Это двойник?
{3,4}	№
{5,1}	№
{2,2}	Да
{6,3}	№
…	…

 После 100 испытаний , у Алекса 19 «двойных» События … это близко к тому, что вы ожидаете?

 

700, 701, 702, 1475, 1476, 1477, 2175, 2176, 2177, 2178

Эксперимент с кубиком
Эксперимент с кубиком

Вероятность: типы событий

Жизнь полна случайностей!

Чтобы они были умными и успешными, их нужно «пощупать».

Подбрасывание монеты, бросание игральной кости и розыгрыш лотереи — все это примеры случайных событий.

События

«Событие» может быть одним или несколькими исходами.

Примеры:

Событие может быть одним исходом:

• Выпадение решки при подбрасывании монеты является событием
• Выпадение «5» — это событие.

Событие может включать несколько исходов:

• Выбор «Короля» из колоды карт (любой из 4 Королей) также событие
• Выпадение «четного числа» (2, 4 или 6) является событием

События могут быть:

• Независимый (каждое событие не зависит от других событий),
• Зависимый (также называемый «условным», когда событие зависит от других событий)
• Взаимоисключающий (события не могут происходить одновременно)

Давайте рассмотрим каждый из этих типов.

Независимые события

События могут быть «независимыми», то есть каждое событие равно не влияет на никакими другими событиями.

Это важная идея! Монета не «знает», что раньше она выпадала орлом… каждый бросок монеты — это совершенная изолированная вещь.

Пример: Вы подбрасываете монету три раза, и каждый раз выпадает «орел»… какова вероятность того, что при следующем подбрасывании тоже выпадет «орел»?

Шанс просто 1/2, или 50%,
точно так же, как ЛЮБОЙ ДРУГОЙ подбрасывание монеты.

То, что он сделал в прошлом, не повлияет на текущий бросок!

Некоторые люди думают, что «решка уже настала», но на самом деле действительно следующий бросок монеты совершенно не зависит от любых предыдущих бросков.

Высказывание «Выпадение хвоста» или «Еще одна попытка, моя удача неизбежна» называется Заблуждение игрока

Узнайте больше на независимых мероприятиях.

Зависимые события

Но некоторые события могут быть «зависимыми». .. это значит, что на них могут влиять предыдущие события .

Пример: Взять 2 карты из колоды

После взятия одной карты из колоды доступно на карты меньше , поэтому вероятности меняются!

 

Давайте посмотрим на шансы получить короля.

Для 1-й карты шанс вытянуть короля 4 из 52

Но для 2-й карты:

• Если 1-й картой был король, то 2-й картой будет минус шансов быть королем , так как из оставшейся 51 карты только 3 короля.
• Если 1-я карта была , а не королем, то 2-я карта немного больше , вероятно, будет королем, так как 4 из 51 оставшейся карты являются королями.

Это потому, что мы удаляем карты из колоды.

Замена: Когда мы кладем каждую карту обратно после ее взятия, шансы не меняются, так как события независимы .

Без замены: шансы изменятся, а событий зависимый .

Вы можете узнать больше в Зависимые события: условная вероятность

Древовидные диаграммы

Когда у нас есть зависимые события, это помогает сделать «древовидную диаграмму»

Пример: футбольный матч

Вы собираетесь играть в футбол и любите быть вратарем, но это зависит от того, кто сегодня является тренером:

• с тренером Сэмом вероятность того, что вы станете вратарем, равна 0,5
• с тренером Алексом ваша вероятность быть вратарем равна 0,3

Сэм тренирует чаще .