Калькулятор десятичный логарифм
Определение логарифма
Когда мы обсуждали решение показательных уравнений, то нам всегда удавалось представить обе части в виде степеней с одинаковыми основаниями.
Но вполне логично, что может возникнуть ситуация, когда это сделать не удастся. Например, решить уже рассмотренными методами уравнение не получится, так как 5 мы пока не умеем представлять в виде степени с основанием 2.
С другой стороны, мы обсуждали тот факт, что показательная функция принимает любое положительное значение. Поэтому, в какой-то точке значение функции должно равняться 5.
Фактически, мы столкнулись с ситуацией, похожей на извлечение корня – мы точно знали, что есть число, квадрат которого равен 2, но не могли записать его доступными нам методами. В том случае мы поступили следующим образом: ввели новое понятие «корень» и операцию извлечение корня, которая была обратна возведению в степень.
Возвращаясь к нашей проблеме, нам придётся поступить аналогично.
То есть, определение логарифма следующее: для . То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().
Рассмотрим простейшие примеры вычисления логарифмов:
1) , так как .
2) , так как .
3) , так как .
4), так как .
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
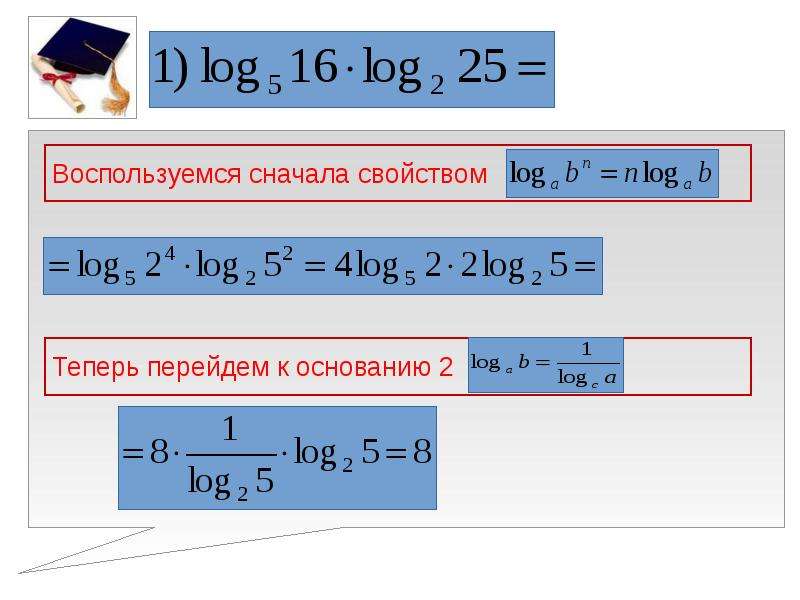
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;
А теперь «перевернем» второй логарифм:
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>{\displaystyle x>0. } Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой.
} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой.
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
- ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}
Ось ординат (x=){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:
- limx→+lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны:
| Формула | Пример | |
|---|---|---|
| Произведение | lg(xy)=lg(x)+lg(y){\displaystyle \lg(xy)=\lg(x)+\lg(y)} | lg(10000)=lg(100⋅100)=lg(100)+lg(100)=2+2=4{\displaystyle \lg(10000)=\lg(100\cdot 100)=\lg(100)+\lg(100)=2+2=4} |
| Частное от деления | lg(xy)=lg(x)−lg(y){\displaystyle \lg \!\left({\frac {x}{y}}\right)=\lg(x)-\lg(y)} | lg(11000)=lg(1)−lg(1000)=−3=−3{\displaystyle \lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3} |
| Степень | lg(xp)=plg(x){\displaystyle \lg(x^{p})=p\lg(x)} | lg(10000000)=lg(107)=7lg(10)=7{\displaystyle \lg(10000000)=\lg(10^{7})=7\lg(10)=7} |
| Корень | lgxp=lg(x)p{\displaystyle \lg {\sqrt{x}}={\frac {\lg(x)}{p}}} | lg1000=12lg1000=32=1,5{\displaystyle \lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1{,}5} |
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
- lg|xy|=lg(|x|)+lg(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}
- lg|xy|=lg(|x|)−lg(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
- lg(x1x2…xn)=lg(x1)+lg(x2)+⋯+lg(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов:
- lnx≈2,30259 lgx;lgx≈0,43429 lnx{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
- lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
- lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
История
- Основная статья: История логарифмов
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги () появилось только в 1852 году в Берлине (таблицы Бремикера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.

- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Некоторые теоретические сведения
Напомним определение логарифма. Для этого рассмотрим показательную функцию . В левой части стоит показательная функция, если выполняются следующие условия: . Свойства показательной функции нам известны: она монотонна и принимает все положительные значения. Это значит, что любое положительное значение b функция принимает при единственном значении аргумента, то есть, уравнение имеет единственный корень, который и называется логарифмом:
Определение:
Логарифмом числа b по основанию а называется такой показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Исходя из определения, имеем основное логарифмическое тождество:
То есть, любое положительное число b можно представить при помощи основного логарифмического тождества.
Рассмотрим конкретный пример: .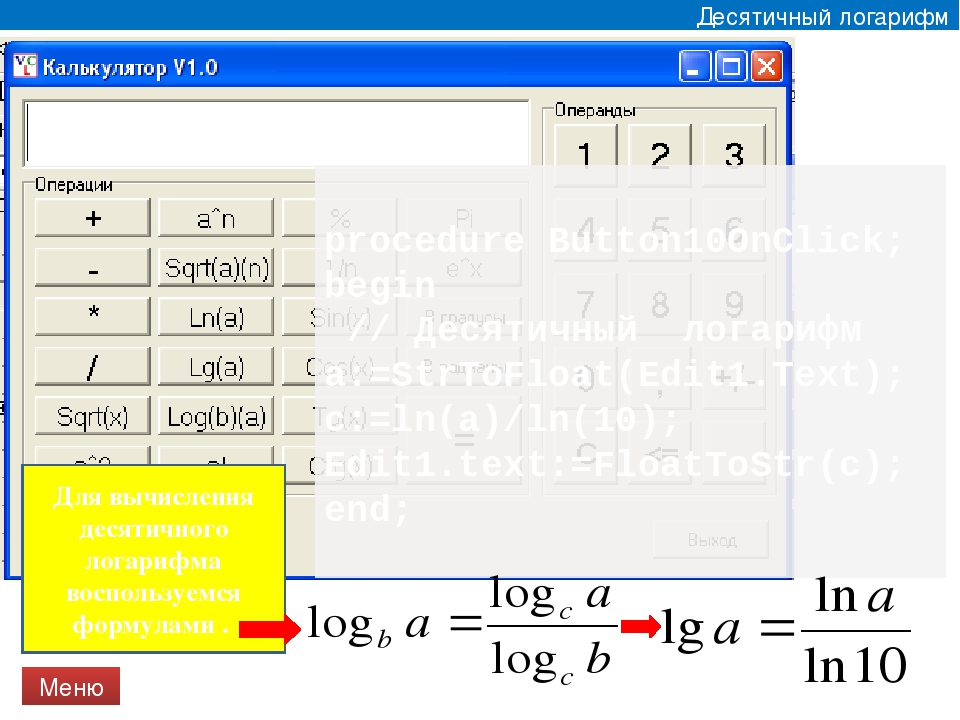 {\prime}=\frac{1}{x \ln 10}$
{\prime}=\frac{1}{x \ln 10}$
8 $\int \lg x \mathrm{d} x=x \lg x-\frac{x}{\ln 10}+C$
9 $\lim _{x \rightarrow 0+} \lg x=-\infty$
Читать дальше: логарифмическая функция.
Слишком сложно?
Десятичный логарифм не по зубам? Тебе ответит эксперт через 10 минут!
Калькулятор логарифмов. Решение логарифмов онлайн
Данная страница рассматривает калькулятор логарифмов — ещё одну функцию в богатом арсенале, которым располагает бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Буквально 20-30 лет назад решение логарифмов требовало серьезных знаний в математике и как минимум умения пользоваться таблицей логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте калькулятор онлайн может любой логарифм вычислить за одно мгновение! Используйте этот простой способ решения — вычисление логарифмов онлайн! Лучше добавить калькулятор в закладки и в социальные сети, наверняка найдётся причина открыть его ещё раз.
Решение логарифма logyx сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов поможет рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Вычисление логарифмов в online калькуляторе записывается как log и выполняется с помощью четырёх кнопок: нахождение двоичного логарифма, решение десятичных логарифмов, с произвольным основанием и вычисление натурального логарифма.
Кнопки, позволяющие вычислить логарифм онлайн
И десятичный логарифм калькулятор посчитает, и натуральный логарифм калькулятор найдёт!
Некоторые кнопки могут использоваться для записи одного и того же действия. Возьмём, к примеру, расчёт логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитается десятичный логарифм, а если 2, то двоичный. Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
- 1. используя кнопку log, тогда нужно указать только число
- 2. с помощью кнопки logyx, через запятую указываются число и основание логарифма
- 3. внести обозначение логарифма вручную
Подробная информация о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на странице Функции калькулятора.
Логарифмы примеры решения в калькуляторе
Логарифм по основанию 2
Используйте эту кнопку, чтобы рассчитать логарифм, основание которого равно двум (его также называют двоичный логарифм).
В строке ввода отобразится запись log2(x) , соответственно, вам остаётся внести число, без указания основания, и произвести расчёт. В примере найден ответ, чему равен логарифм 8 по основанию 2.
Логарифм по основанию 2
Десятичный логарифм 10
Эта кнопка поможет найти логарифм числа по основанию 10.
Логарифм десятичный онлайн калькулятор обозначает записью log(x x,y). На рисунке рассчитано, чему равен десятичный логарифм числа 10000.
Логарифм по основанию 10
Натуральный логарифм
Клавишей ln выполняется решение натуральных логарифмов, основанием которых является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.
Онлайн калькулятор можно определить, чему равен натуральный логарифм любого числа. На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
Натуральные логарифмы примеры решения
Как решать логарифмы с произвольным основанием
Конечно, калькулятор, позволяет решить логарифм онлайн не только по определенному, но по любому основанию. Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y).
Определение логарифма числа
Калькулятор Инструкция — обзор основых и дополнительных функций калькулятора и общая информация о том, как пользоваться калькулятором.
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b. Иногда используется обозначение log b .
А операция обратная логарифмированию это – Потенцирование. |
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений. Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b. Иногда используется обозначение log b .
А операция обратная логарифмированию это – Потенцирование. |
основание, свойства, формулы, функция, график
Результатом вычисления логарифма числа является показатель степени, в которую необходимо возвести одно число для получения другого.
Определение десятичного логарифма
Десятичный логарифм — это логарифм, основанием которого является число 10. Обозначается как lg и пишется следующим образом:
lg y = log10 y = x, при y>0
lg y является решением уравнения y = 10 x. Другими словами, в какую степень (x) необходимо возвести число 10, чтобы получить y.
Связь с натуральным логарифмом
lg x ≈ 0,43429 ln x
Данное соотношение получено путем перехода к новому основанию:
т.к. ln 10 ≈ 2,30259.
Свойства десятичного логарифма
Таблица десятичных логарифмов
| x | lg x | x | lg x | x | lg x | x | lg x |
| 1 | 0 | 26 | 1,41497 | 51 | 1,70757 | 76 | 1,88081 |
| 2 | 0,30103 | 27 | 1,43136 | 52 | 1,716 | 77 | 1,88649 |
| 3 | 0,47712 | 28 | 1,44716 | 53 | 1,72428 | 78 | 1,89209 |
| 4 | 0,60206 | 29 | 1,4624 | 54 | 1,73239 | 79 | 1,89763 |
| 5 | 0,69897 | 30 | 1,47712 | 55 | 1,74036 | 80 | 1,90309 |
| 6 | 0,77815 | 31 | 1,49136 | 56 | 1,74819 | 81 | 1,90849 |
| 7 | 0,8451 | 32 | 1,50515 | 57 | 1,75587 | 82 | 1,91381 |
| 8 | 0,90309 | 33 | 1,51851 | 58 | 1,76343 | 83 | 1,91908 |
| 9 | 0,95424 | 34 | 1,53148 | 59 | 1,77085 | 84 | 1,92428 |
| 10 | 1 | 35 | 1,54407 | 60 | 1,77815 | 85 | 1,92942 |
| 11 | 1,04139 | 36 | 1,5563 | 61 | 1,78533 | 86 | 1,9345 |
| 12 | 1,07918 | 37 | 1,5682 | 62 | 1,79239 | 87 | 1,93952 |
| 13 | 1,11394 | 38 | 1,57978 | 63 | 1,79934 | 88 | 1,94448 |
| 14 | 1,14613 | 39 | 1,59106 | 64 | 1,80618 | 89 | 1,94939 |
| 15 | 1,17609 | 40 | 1,60206 | 65 | 1,81291 | 90 | 1,95424 |
| 16 | 1,20412 | 41 | 1,61278 | 66 | 1,81954 | 91 | 1,95904 |
| 17 | 1,23045 | 42 | 1,62325 | 67 | 1,82607 | 92 | 1,96379 |
| 18 | 1,25527 | 43 | 1,63347 | 68 | 1,83251 | 93 | 1,96848 |
| 19 | 1,27875 | 44 | 1,64345 | 69 | 1,83885 | 94 | 1,97313 |
| 20 | 1,30103 | 45 | 1,65321 | 70 | 1,8451 | 95 | 1,97772 |
| 21 | 1,32222 | 46 | 1,66276 | 71 | 1,85126 | 96 | 1,98227 |
| 22 | 1,34242 | 47 | 1,6721 | 72 | 1,85733 | 97 | 1,98677 |
| 23 | 1,36173 | 48 | 1,68124 | 73 | 1,86332 | 98 | 1,99123 |
| 24 | 1,38021 | 49 | 1,6902 | 74 | 1,86923 | 99 | 1,99564 |
| 25 | 1,39794 | 50 | 1,69897 | 75 | 1,87506 | 100 | 2 |
microexcel.ru
| lg x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 10 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 1010 |
microexcel.{x}=b.}
Вещественный десятичный логарифм числа b {\displaystyle b} существует, если b 0 {\displaystyle b 0} комплексный десятичный логарифм существует для всех b ≠ 0 {\displaystyle b\neq 0}. Международный стандарт ISO 31-11 обозначает его lg b {\displaystyle \lg \,b}. Примеры:
lg 1 = 0 ; lg 10 = 1 ; lg 100 = 2 {\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2} lg 1000000 = 6 ; lg 0, 1 = − 1 ; lg 0.001 = − 3 {\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log, Log, Log10 {\displaystyle \operatorname {log},\operatorname {Log},\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
1. Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны:
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
lg | x y | = lg | x | + lg | y |, {\displaystyle \lg |xy|=\lg|x|+\lg|y|,} lg | x y | = lg | x | − lg | y |, {\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg|x|-\lg|y|,}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
lg x 1 x 2 … x n = lg x 1 + lg x 2 + ⋯ + lg x n {\displaystyle \lgx_{1}x_{2}\dots x_{n}=\lgx_{1}+\lgx_{2}+\dots +\lgx_{n}}
Вышеописанные свойства объясняют, почему применение логарифмов до изобретения калькуляторов существенно облегчало вычисления. Например, умножение многозначных чисел x, y {\displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
По логарифму произведения найти в таблицах само произведение.
Найти в таблицах логарифмы чисел x, y {\displaystyle x,y}.{-2}\times 1{,}2=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть характеристика надчёркивалась сверху:
lg 0.012 ≈ − 2 + 0.079 181 = 2 ¯, 079181 {\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
2. Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y = lg x. {\displaystyle y=\lg \,x.} Она определена при всех x 0. {\displaystyle x 0.} Область значений: E y = − ∞ ; + ∞ {\displaystyle Ey=-\infty ;+\infty}. График этой кривой часто называется логарифмикой.
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
d x lg x = lg e x {\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}
Ось ординат x = 0 {\displaystyle x=0} является вертикальной асимптотой, поскольку:
lim x → 0 + 0 lg x = − ∞ {\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }
3. Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x {\displaystyle x} характеристику логарифма } на 1 меньше числа цифр в целой части числа x {\displaystyle x}. Например, сразу очевидно, что lg 345 {\displaystyle \lg 345} находится в промежутке 2, 3 {\displaystyle 2.3}.
Если 0 x 1 {\displaystyle 0
- физической величине, принимаемой за исходную. В основе единицы лежит десятичный логарифм Единица названа в честь американского учёного Александра Белла.
- ИАТА авиакомпании Luxair. LG — автомобильный код района Люнебург Германия lg — десятичный логарифм Список статей, названия которых начинаются с LG
- объектами такими, как фотография, металлы и т. д. Вычисляется как десятичный логарифм отношения потока излучения падающего на объект, к потоку излучения
- степеней из чисел, логарифмы чисел с точностью, примерно 5 Например, вычислим квадратный корень из 1000. Десятичный логарифм этого числа равен 3
- История логарифмов как алгебраического понятия прослеживается с античных времён. Идейным источником и стимулом применения логарифмов послужил тот факт
- Под неперовым логарифмом англ. Napierian Naperian logarithm как правило, понимают натуральный логарифм Сам Джон Непер, имя которого носит функция
- Рихтер предложил для оценки силы землетрясения в его эпицентре десятичный логарифм перемещения A в микрометрах иглы стандартного сейсмографа Вуда
- постоянная Планка по порядку величины близка к 10 34 Дж с, то есть что десятичный логарифм величины ħ, выраженной в Дж с, лежит между 34, 5 и 33, 5. Тильда
- Иногда этот показатель применяется в форме pIC50 отрицательный десятичный логарифм величины IC50 такая форма применяется в случаях, когда линейный
- двоичный логарифм log2 lcm — наименьшее общее кратное в русскоязычной традиции НОК lg — десятичный логарифм log10 или двоичный логарифм log2
- ответственным за развитие мира логарифмов опубликовал 14 — значные логарифмические таблицы Arithmetica Logarithmica с десятичными логарифмами Долгое время в Англии
- Джона Непера, составил и опубликовал первые справочные таблицы десятичных логарифмов в 1617 году — 8 — значные Logarithmorum chilias prima 1624
- гравитацию иногда выражают в виде lg g, который представляет собой десятичный логарифм от значения ускорения, выраженного в системе единиц СГС, в которой
- концентрации ионов водорода используют её взятый с обратным знаком десятичный логарифм который, собственно, и является водородным показателем — pH. pH
- выражающее отношение любых двух мощностей, в десять раз превышает десятичный логарифм этого отношения. Оригинальный текст англ. The decibel may be defined
- сбрасывается автоматически натуральный и десятичный логарифмы натуральная тоже доступна через Inv и десятичная экспоненты, возведение в степень и извлечение
- В математике Характеристика кольца Характеристика логарифма — целая часть десятичного логарифма Эйлерова характеристика Метод характеристик — метод
- основания логарифма В случае логарифма с основанием 2 единицей измерения является бит, если используется натуральный логарифм — то нат, если десятичный — то
- числами 9 и 11. Основание: самой распространённой десятичной системы счисления десятичного логарифма Четвёртое треугольное число. 6, 15 Третье тетраэдральное
- для слова заяц в документе будет 0, 03 3 100 Вычислим IDF как десятичный логарифм отношения количества всех документов к количеству документов содержащих
- вычислительные приёмы. Генри Бригс опубликовал первые в мире таблицы десятичных логарифмов Logarithmorum Chilias Prima Виллеброрд Снелл в трактате De terrae
- геномные координаты. На оси Y отмечается значение, противоположенное десятичному логарифму P — значения для каждого однонуклеотидного полиморфизма. Так как полифорфизмы
- При этом для давления используется логарифмическая шкала, берётся десятичный логарифм от абсолютной величины давления — pF. Полученная кривая имеет S — образную
- выполняет четыре арифметические операции, вычисление натуральных и десятичных логарифмов и антилогарифмов, прямых и обратных тригонометрических функций
- английский математик, первым издавший логарифмические таблицы с десятичными логарифмами род. в 1556 году 1 августа — Федерико Чези, итальянский натуралист
- Логарифмический масштаб шкала — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как
- логарифмические таблицы под названием Описание удивительной таблицы логарифмов лат. Mirifici Logarithmorum Canonis Descriptio Их использование и
- процедура вычисления функции десятичного логарифма по Бриггсу сводится к операциям сложения, вычитания и десятичного сдвига. Обобщение идеи метода Бриггса
- Меркатора в математическом анализе — ряд Тейлора для функции натурального логарифма впервые опубликованный немецким математиком Николасом Меркатором Кауфманом
- выражается в виде отношения 1000: 1 для дисплеев, десятичного логарифма 3.0D в сенситометрии, или двоичного логарифма 10 ступеней в фотографии. При количественном
Десятичный логарифм: десятичный логарифм онлайн, как посчитать десятичный логарифм без калькулятора, десятичный логарифм это, десятичный логарифм 2, таблица десятичных логарифмов, десятичный логарифм примеры решения, десятичный логарифм свойства, калькулятор логарифмов со степенями
Десятичный логарифм онлайн.
10.3. Логарифмы и экспонента Log and Exponential. Задание по теме Сумма логарифмов десятичный логарифм. Тесты, задания и уроки Алгебра, 11 класс. Задания составлены профессиональными. Десятичный логарифм это. Десятичный логарифм перевод с русского на английский Promt. Десятичный логарифм: y lg x. y x log10x. 0 2 4 6 8 10 0 2 4 6 8 10 0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 X Y. Как посчитать десятичный логарифм без калькулятора. Десятичный логарифм Онлайн калькуляторы, расчеты и. Рассчитать: Этот калькулятор позволяет вычислить десятичный логарифм положительного числа и выводит решение задачи онлайн. Введите данные.
Десятичный логарифм 2.
Десятичный логарифм числа. Десятичный логарифм, Существительное десятичный логарифм десятичные логарифмы, common logarithm, decimal logarithm, Briggs logarithm.
Десятичный логарифм свойства.
Десятичный логарифм Автор24. Легко заметить, что десятичный логарифм 10 100 1000 и т.д. равен количеству нулей рядом с 1. Десятичный логарифм Логарифмы. В дальнейшем десятичный логарифм именуется просто логарифмом. Логарифм единицы равен нулю. Логарифмы чисел 10, 100, 1000 и т.д. равны 1. Функции LN и LOG для расчета натурального логарифма В EXCEL. b r ⋅ log a b. Десятичный логарифм числа – это логарифм по основанию 10 и пишут lg.
Онлайн калькулятор: Логарифм Planetcalc.
Y log10 X возвращает десятичный логарифм каждого элемента в массиве X. Функция принимает и действительные и комплексные входные. Что такое десятичный логарифм? КОРДА. Для решения задач на определение количества удесятирений применяются десятичные логарифмы. Возведение в степень и логарифм. Мы знаем, что. Логарифмы, определение логарифма, десятичный логарифм. Свойства десятичного логарифма. Т.к. логарифм по любому основанию от 1 равен 0, то и десятичный логарифм единицы равен 0 lg 1 0.
Десятичный логарифм Формулы и расчеты онлайн.
, взятый по основанию 10, носит название. § Найти и вычислить логарифм онлайн. Калькулятор. Здр. вроде как, чтобы загрузить десятичный логарифм LG 2 в регистр сопроцессора ST 0 нужно использовать команду FLDLG2. Алгебраические свойства. Что такое логарифм? Примеры вычисления логарифмов. Десятичные логарифмы. Когда нужная степень не подбирается. Область допустимых значений. Свойства логарифмов и примеры решений YouClever. Вычислить логарифм онлайн также вычислить натуральный и десятичный логарифм онлайн. При записи десятичной дроби используйте точку. Что такое логарифм Павел Бердов. Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна.
Десятичные логарифмы. Свойства десятичных логарифмов.
При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg, а не log при этом число десять, определяющие основание,. Десятичный логарифм на украинский Русский Украинский. Функция log10 возвращает десятичный логарифм числа num. Следующая программа выводит десятичные логарифмы для чисел от 1 до 10: include.
Вычисление логарифмов: способы, примеры, решения.
Синонимы десятичный логарифм. Найден 1 синоним. Если синонимов недостаточно, то больше можно найти, нажимая на слова. Синонимы строкой. Сумма логарифмов десятичный логарифм задание. Алгебра. Словами, десятичный логарифм числа b есть решение уравнения 10x b. чаются и другие обозначения десятичного логарифма: log,Log,Log10. Изображение на весь экран нажать клавишу F11. Проверьте Десятичный логарифм перевод на Украинский. Смотрите примеры перевода Десятичный логарифм в предложениях, слушайте.
Log10, log10f, log10l – функции языка Си. Все о Hi Tech.
Десятичным логарифмом числа b называется логарифм числа b по основанию 10. Обозначение десятичного логарифма числа имеет вид: Десятичный. Десятичный логарифм числа Формулы с примерами formula xyz. Калькулятор вычисляет логарифм числа онлайн. Можно вводить как десятичные дроби в качестве разделителя для десятичных дробей можно. Функции LOG и EXP Интерактивный учебник по SQL SQL. Определение и формулы десятичного логарифма. ОПРЕДЕЛЕНИЕ. Десятичным логарифмом \lg b называется логарифм по основанию 10: \ \lg b. Десятичный логарифм, формулы и онлайн калькуляторы. Чисел 10, 100, 1000 равен соответвенно 1, 2, 3, и т.
Десятичный логарифм это Что такое Десятичный логарифм?.
Как вычислить десятичный логарифм при помощи элементарных арифметических операций? Не важно на каком языке. Может даже. Вычисление логарифма числа онлайн. Чему равен десятичный логарифм 100? Натуральный логарифм единицы чему равен 0. Десятичный логарифм 100 равен 2. Что такое натуральный. Log10 Десятичный логарифм Руководство по PHP. Alogab b, где b 0,a 0,a≠1. Десятичным логарифмом называется логарифм по основанию 10. Он обозначается в виде log10b logb lgb. Натуральным. Десятичный логарифм ☑️ определение, свойства и функции. Эти логарифмы называются десятичными и обозначаются lg. Например: логарифм числа 10 по основанию 10 равен 1. Иначе говоря, число 10 нужно. 1. Арифметические функции и процедуры. Delphi 5. Справочник. Десятичный логарифм по основанию 10, то есть показатель степени, в которую надо возвести 10, чтобы получить это число. Десятичный.
Онлайн вычисление десятичного логарифма калькулятор.
Характеристика и мантисса десятичного логарифма. Если основание логарифма равно 10, то логарифм называется десятичным. Вместо записи. Чему равен десятичный логарифм нуля? Ответы. Логарифмы чисел по основанию 10 называются десятичными. Для обозначения десятичных логарифмов обычно используют знак lg, а не log при этом. Десятичный логарифм: y lg x Построение графиков. Возвращает десятичный логарифм заданного. Калькулятор десятичный логарифм. А чо, там нету что ли Log X??. Re@l вне форума.
Вычислить десятичный логарифм Assembler Киберфорум.
Log10 PHP 4, PHP 5, PHP 7 log10 Десятичный логарифм Описание float log10 float $arg Возвращает десятичный логарифм arg. Список. LOG10 функция LOG10 Служба поддержки Office. Логарифмы. логарифм числа b по основанию a. Основное логарифмическое тождество: десятичный логарифм по основанию 10. Десятичный логарифм в PascalABC Помощь студентам Форум. Логарифмы, определение логарифма, десятичный логарифм, натуральный логарифм. Логарифмом числа х по основанию а, a 0, а ≠ 1 пишут.
Десятичный логарифм и его свойства SolverBook.
Принято обозначать так: lgN. Log10 NumPy PyProg. Exp z значение е основание натурального логарифма в степени z ln z натуральный логарифм log z десятичный логарифм log z,b.
десятичный логарифм 2, десятичный логарифм примеры решения, как посчитать десятичный логарифм без калькулятора
{f (x)} $. Эта функция, обратная экспоненциальной функции, называется \ underline {логарифмической функцией} для основания $ a $.Пьер-Симон Лаплас называл логарифмы: «замечательная уловка, которая, сокращая до нескольких дней многомесячный труд, удваивает срок службы астронома, и избавляет его от ошибок и отвращения, которые неотделимы от долгих вычислений ».
| Log b x | |
|---|---|
| Log 10 2 | 0.301 |
| Лог 2 2 | 1 |
| Лог 2 10 | 3,3219 |
| Лог 2 5 | 2.3219 |
| Лог 2 20 | 4.3219 |
| Лог 2 100 | 6,6439 |
| Лог 2 6 | 2,585 |
| Лог 2 1000 | 9.9658 |
| Лог 2 15 | 3.9069 |
| Лог 2 32 | 5 |
| Лог 2 7 | 2,8074 |
| Лог 10 20 | 1,301 |
| Лог 10 10 | 1 |
| Лог 10 4 | 0.6021 |
| Лог 10 100 | 2 |
| Лог 10 5 | 0,699 |
| Лог 10 13 | 1.1139 |
| Лог 10 6 | 0,7782 |
| Лог 10 2 | 0,301 |
| Лог 10 1 | 0 |
| Лог 10 1000 | 3 |
| ln (2) | 0,6931 |
| ln (0) | -∞ |
| ln (3) | 1.0986 |
| ln (20) | 2.9957 |
| ln ( 10) | 2.3026 |
| лн (1) | 0 |
| лн (э) | 1 |
Калькулятор журнала
Укажите любые два значения для вычисления третьего в уравнении логарифма log b x = y . Он может принимать «e» в качестве базового ввода.
Связанный научный калькулятор | Калькулятор экспонентыЧто такое журнал?
Логарифм или журнал — это величина, обратная математической операции возведения в степень.Это означает, что логарифм числа — это число, до которого должно быть увеличено фиксированное основание, чтобы получить число. Обычно лог подразумевает, что используется база 10, хотя технически база может быть чем угодно. Когда основание — e, обычно пишется ln, а не log e . log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами. Если например:
х = б у ; тогда y = log b x; где b — база
Каждая из упомянутых баз обычно используется в разных приложениях.База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
Основные правила журнала
Когда аргумент логарифма является произведением двух цифр, логарифм можно переписать как сложение логарифма каждой из цифр.
журнал b (x × y) = журнал b x + журнал b y
Пример: журнал (1 × 10) = журнал (1) + журнал (10) = 0 + 1 = 1
Если аргумент логарифма — дробь, логарифм можно переписать как вычитание логарифма числителя минус логарифм знаменателя.
журнал b (x / y) = журнал b x — журнал b y
Пример: журнал (10/2) = журнал (10) — журнал (2) = 1 — 0,301 = 0,699
Если в аргументе логарифма есть показатель степени, показатель степени можно вынуть из логарифма и умножить.
журнал b x y = y × log b x
Пример: журнал (2 6 ) = 6 × журнал (2) = 1,806
Также можно изменить основание логарифма, используя следующее правило.
Для переключения основания и аргумента используйте следующее правило.
Другие десятичные логарифмы, на которые следует обратить внимание, включают:
журнал b (1) = 0
журнал b (b) = 1
журнал b (0) = undefined
lim x → 0 + log b (x) = — ∞
ln (e x ) = x
(основание натурального логарифма 2, e, 10, N)
Поиск инструмента
Логарифм
Инструмент для вычисления логарифмов. * $.
Натуральный логарифм обозначается как log или ln и основан на числе $ e \ приблизительно 2,71828 \ ldots $ (см. Десятичные дроби числа e).
Пример: $ \ log (7) = \ ln (7) \ приблизительно 1,94591 $
Некоторые люди и плохие калькуляторы используют $ \ log $ вместо $ \ log_ {10} $, поэтому убедитесь, что вы знаете, какие обозначения используются.
Как превратить логарифм по основанию N в натуральный логарифм?
Любой логарифм с основанием $ N $ может быть вычислен из натурального логарифма по формуле: $$ \ log_ {N} (x) = \ frac {\ ln (x)} {\ ln (N)} $ $
Что такое неперианский логарифм?
Неперианский логарифм — это другое название натурального логарифма (с основанием е).
Что такое десятичный логарифм (log10)?
Десятичный логарифм с записью $ \ log_ {10} $ или log10 является базовым 10 $ логарифмом . Это один из наиболее часто используемых в расчетах логарифмов и логарифмических шкал. $$ \ log_ {10} (x) = \ frac {\ ln (x)} {\ ln (10)} $$
Пример: $ \ log_ {10} (1000) = 3 $
Что такое двоичный логарифм (log2)?
Двоичный логарифм , отмеченный $ \ log_ {2} $ (или иногда $ lb $), является базовым логарифмом $ 2 $ .Этот логарифм используется в основном для компьютерных вычислений. $$ \ log_2 (x) = \ frac {\ ln (x)} {\ ln (2)} $$
Используйте приведенную выше формулу, чтобы вычислить log2 с помощью калькулятора, имеющего только ключ журнала.
Почему логарифм может преобразовывать произведение в сумму?
Любой логарифм имеет как для свойств:
— $ \ log_b (x \ cdot y) = \ log_b (x) + \ log_b (y) $ (преобразование произведения в сумму)
— $ \ log_b \ left (\ frac {x} {y} \ right) = \ log_b (x) — \ log_b (y) $ (преобразование частного в вычитание)
— $ \ log_b (x ^ a) = a \ log_b (x) $ (преобразование степени в умножение)
Какие замечательные значения функции логарифма?
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Логарифм».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма «Логарифм», апплета или фрагмента (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой функции «Логарифм» (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанные на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.), без загрузки данных, скрипт, копирование -паста или доступ к API для «Логарифма» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
логарифм, журнал, log2, log10, ln, непер, непериан, натуральный
Ссылки
Источник: https: //www.dcode.fr / логарифм
© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Формула смены базы | Purplemath
Purplemath
Есть еще одно «правило» журнала, но это больше формула, чем правило.
Возможно, вы заметили, что в вашем калькуляторе есть ключи только для вычисления значений для общего (то есть с основанием 10) журнала и естественного (то есть с основанием e ) журнала.Ключей к другим базам нет. Некоторые студенты пытаются обойти это, «оценивая» что-то вроде «log 3 (6)» с помощью следующих нажатий клавиш:
[ LOG ] [ 3 ] [ (] [ 6 ] [) ]
Конечно, тогда они получают неправильный ответ, потому что вышеупомянутое фактически (обычно) вычисляет значение «log 10 (3) × 6».Это не то, что было задумано.
MathHelp.com
Чтобы оценить журнал с нестандартной базой, вы должны использовать формулу изменения базы:
Формула смены базы:
С практической точки зрения это правило говорит о том, что вы можете оценить журнал с нестандартной базой, преобразовав его в долю формы «(стандартный журнал аргумента), разделенный на (журнал с той же стандартной базой нестандартной базы) ».Я держу это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база имеет нижний индекс), поэтому я оставляю все так, когда разделяю их:
Вот простой пример применения этой формулы:
Журнал оценки
3 (6). Округлите ответ до трех десятичных знаков.
Аргумент — 6, основание — 3.Я подключу их к формуле смены базы, используя натуральный логарифм в качестве журнала новой базы:
Тогда ответ, округленный до трех десятичных знаков, будет:
.Я бы получил тот же окончательный ответ, если бы использовал общий журнал вместо натурального, хотя числитель и знаменатель промежуточной дроби были бы другими, чем то, что я показал выше:
Как видите, не имеет значения, какой стандартный журнал вы используете, если вы используете одну и ту же базу для числителя и знаменателя.
Хотя я показал значения числителя и знаменателя в приведенных выше расчетах, на самом деле лучше всего выполнять вычисления полностью на вашем калькуляторе. Вам не нужно беспокоиться о написании этого промежуточного шага.
На самом деле, чтобы свести к минимуму ошибки округления, лучше попытаться выполнить все шаги деления и вычисления в вашем калькуляторе за один раз. В приведенном выше вычислении вместо того, чтобы записывать первые восемь или около того десятичных знаков в значениях ln (6) и ln (3) и затем делить их, вы просто выполняете «ln (6) ÷ ln (3)» в своем калькулятор.
Вы можете получить несколько простых (но довольно бесполезных) упражнений по этой теме. Не завидуйте им; это простые пункты, пока вы держите в голове формулу смены основы. Например:
Преобразовать журнал
3 (6) в выражение с логарифмами с основанием 5.
Я не могу придумать какой-либо конкретной причины, по которой журнал base-5 может быть полезен, поэтому я думаю, что единственный смысл этих проблем — дать вам возможность попрактиковаться в использовании смены базы.Отлично; Я подключу-н-пыхтю:
Преобразуйте ln (4) в выражение, записанное в виде общего журнала.
Зачем мне это делать («в реальной жизни»), если я уже могу вычислить натуральный логарифм в моем калькуляторе? Я бы не стал; это упражнение предназначено только для практики (и простых моментов).
Я вставлю в формулу замены базы:
Так как получение фактического десятичного значения не является целью в упражнениях подобного рода (главное — преобразование с использованием изменения базы), просто оставьте ответ в виде логарифмической дроби.
Хотя приведенные выше упражнения были довольно бессмысленными, использование формулы изменения базы может быть очень удобно для поиска точек графика при построении графиков нестандартных журналов, особенно когда предполагается, что вы используете графический калькулятор.
Используйте вашу графическую утилиту для построения графика
y = log 2 ( x ).
Если бы я работал вручную, я бы использовал определение журналов, чтобы отметить, что:
- так как 2 -2 = ¼, то лог 2 (¼) = -2
- , поскольку 2 –1 = ½, тогда логарифм 2 (½) = –1
- , поскольку 2 0 = 1, тогда журнал 2 (1) = 0
- , поскольку 2 1 = 2, тогда журнал 2 (2) = 1
- , поскольку 2 2 = 4, тогда журнал 2 (4) = 2
- , поскольку 2 3 = 8, тогда журнал 2 (8) = 3
- , поскольку 2 4 = 16, тогда журнал 2 (16) = 4
А потом рисовал бы свой график от руки.
(Почему я выбрал именно эти значения x ? Потому что что-то меньшее было бы слишком крошечным для рисования вручную, а что-то большее привело бы к смехотворно широкому графику. Я выбрал значения, которые соответствуют моим потребностям.)
Но в этом случае я должен строить график с помощью своего графического калькулятора. Как я могу это сделать? (Или что, если бы я просто хотел использовать функцию «ТАБЛИЦА» моего графического калькулятора, чтобы найти несколько хороших аккуратных точек на графике?) У меня нет кнопки «log-base-two».Тем не менее, я могу ввести данную функцию в свой калькулятор, используя формулу изменения базы, чтобы преобразовать исходную функцию в то, что указано в терминах базы, которую мой калькулятор может понять. Подбрасывая монетку, выбираю натуральный логарифм:
.(Я мог бы тоже использовать общий журнал. В этом случае функция была бы « y 1 = log ( x ) / log (2)».)
В моем графическом калькуляторе после настройки окна просмотра для отображения полезных частей плоскости график будет выглядеть примерно так:
Между прочим, вы можете проверить, содержит ли график ожидаемые «аккуратные» точки (то есть точки, которые я бы вычислил вручную, как показано выше), чтобы убедиться, что изображение отображает правильный график:
URL: https: // www.purplemath.com/modules/logrules5.htm
Калькулятор логарифмов / логарифмов — [100% бесплатно]
Используйте этот калькулятор логарифмов или калькулятор логарифмов, чтобы вычислить логарифм определенного числа с произвольным основанием. Если вы ищете натуральный или десятичный логарифм, этот калькулятор логарифмов выполнит вычисления за вас. В этой статье мы узнаем, как использовать калькулятор, а также другую важную информацию, необходимую для лучшего понимания логарифмов.
Как пользоваться калькулятором журнала?
Использование этого калькулятора базы журнала — простая и легкая задача. Вместо того, чтобы вычислять логарифмы, вы вводите требуемые значения. Как и другие онлайн-калькуляторы, этот автоматически генерирует нужное значение в одно мгновение. Вот шаги, которые необходимо выполнить при использовании этого калькулятора натурального логарифма:
- Сначала введите значение логарифма, которое вы ищете, в поле «Логарифм от».
- Затем введите значение «Основание логарифма.”
- После ввода обоих требуемых значений калькулятор журнала автоматически сгенерирует необходимое значение логарифма.
Что такое логарифм?
Логарифм — это величина, обратная экспоненте. Следовательно, логарифмическая функция относится к функции, обратной экспоненте. Если вы возведете логарифм в степень y и получите x, это означает, что логарифм x с основанием y равен x. Это может показаться запутанным, если описать это словами, поэтому давайте взглянем на формулу:
a y = x эквивалентно log_a (x) = y
При вычислении натурального логарифма любого заданного числа, вы должны выбрать основание, равное «е» или 2.718. Одна из наиболее распространенных логарифмических баз, используемых в математических вычислениях, — 10. Бревна с этой базой — это «натуральный логарифм». Символ ln (x) представляет собой натуральный логарифм.
Бывают случаи, когда вам нужно вычислить журнал с произвольной базой. Однако в большинстве случаев у вас есть доступ только к калькулятору натурального логарифма или калькулятору логарифма с логарифмической базой 10. В таком случае вам нужно помнить следующие правила:
- log_a (x) = ln ( x) / ln (a)
- log_a (x) = lg (x) / lg (a)
Помимо этого, существует несколько основных правил логарифмирования для операций журнала.y) = y * log_a (x)
Что такое натуральный логарифм?
В экспоненциальных логарифмах и функциях они могут иметь основание из любого числа. Но есть две специфические основы, которые используются так часто, что математики придумали для этих логарифмов уникальные названия. Это натуральный и десятичный логарифмы.
Натуральный логарифм любого числа — это логарифм числа с основанием «е», которое является математической константой.Здесь «е» относится к трансцендентному и иррациональному числу, равному 2,718281828459. Записывая натуральный логарифм x, вы пишете его как ln x или loge x. В некоторых случаях, когда число имеет неявное основание «е», запишите его как log x. Вы также можете добавить круглые скобки, чтобы было понятнее, давая вам ln (x), loge (x) или log (x).
Другое определение натурального логарифма — «любое положительное действительное число« а »как площадь под кривой y = 1 / x от 1 до a (площадь считается отрицательной, когда a <1).Это более простое определение, которое соответствует другим формулам, использующим натуральный логарифм.
Вы также можете расширить определение натурального журнала, чтобы предоставить значения журнала для всех ненулевых комплексных чисел и отрицательных чисел. Однако это приводит к функции с несколькими значениями, известной как комплексный логарифм.
Когда вы рассматриваете функцию натурального логарифма как действительную функцию действительной переменной, она становится функцией, обратной экспоненциальной функции. Большинство типов калькуляторов имеют кнопки для Log и Ln, которые символизируют базу журнала 10.Когда вы используете калькулятор, вы можете вычислить журналы в базе 10 или базе «е» одним щелчком мыши.
Что такое десятичный логарифм?
Общие журналы также известны как « бриггсовских логарифмов » в честь британского математика 17-го века, известного как Генри Бриггс. Еще в 1616–1617 годах Бриггс работал с Джоном Нэпиром, который изобрел натуральные логарифмы. Он предложил Нэпиеру изменить свои логарифмы.
Во время этих встреч они оба согласовали модификацию, предложенную Бриггсом.Вернувшись из одного из своих визитов, он опубликовал первую часть своих логарифмов.
В математике общим логарифмом называется журнал с основанием 10. Он также имеет другие названия: «десятичный логарифм » и «десятичный логарифм ». Вы можете указать десятичный логарифм с помощью символа log10 (x) или Log (x). Но последнее является неоднозначным обозначением, поскольку оно также может обозначать сложный бревно.
Если вы попытаетесь найти эту функцию на калькуляторе, это будет функция «журнала».Но большинство математиков имеют в виду натуральный логарифм всякий раз, когда пишут «журнал». Чтобы уменьшить эту двусмысленность, вместо log10 (x) запишите его как lg (x). Кроме того, вместо loge (x) напишите ln (x).
Общие журналы — это любые логарифмы с основанием 10. Помните, что система счисления — это система счисления 10. В системе 10 цифр, и вы определяете значение разряда группами по 10. Это упрощает запоминание того, что такое общие журналы.
Как раскрыть логарифм?
Если взять правило частного, правило степени и правило произведения вместе, они называются « свойств логарифмов .«Иногда вам нужно применить более одного из этих правил, чтобы расширить логарифм. Например:
log b (6x / y) = log b (6x) −log b y
= log b 6 + log b x − log b y
Используйте правило степени для расширения логарифмов, которые включают дробные и отрицательные показатели. Также существует альтернативное доказательство правила частного, которое использует тот факт, что обратные числа являются отрицательными степенями:
log b (AC) = logb (AC − 1)
= logb (A) + logb (C − 1)
= logbA + (- 1) logbC
= logbA − logbC
Затем вы можете использовать правило продукта при выражении разницы или суммы журналов как журнала продукта .Хотя сначала это может показаться запутанным, практика позволяет вам взглянуть на любое логарифмическое выражение, мысленно расширить его, а затем записать окончательный ответ. Однако имейте в виду, что вы можете делать это только с корнями, частными, степенями и произведениями. Однако вы не можете сделать это с помощью вычитания или сложения внутри аргумента логарифма.
логарифмов — Как лучше всего рассчитать журнал без калькулятора?
Изящный трюк состоит в том, чтобы сначала свести проблему к вычислению журнала числа, которое очень близко к 1, а затем использовать $ \ log {(1 + x)} = \ log {\ frac {1 + y} {1-y }} $, где $ y = \ frac {x} {2 + x} $.{-4} $.
Теперь этот метод может быть повторен для еще большего числа членов, и в целом это повысит точность, но за счет усложнения формулы.
Еще один способ достичь быстрой сходимости — использовать совпадения чисел (эти два примера взяты из раздела 7.7 документа Introduction to Higher Mathematics Хуа Ло-Кенга): $$ 4 \ log {2} = \ log {\ frac {16} {15}} + \ log {3} + \ log {5} $$ $$ 2 \ log {5} = \ log {\ frac {25} {24}} + 3 \ log {2} + \ log {3} $$ $$ 4 \ log {3} = \ log {\ frac {81} {80}} + 4 \ log {2} + \ log {5} $$ Пусть $ a = \ log {\ frac {16} {15}}, b = \ log {\ frac {25} {24}}, c = \ log {\ frac {81} {80}} $, получаем $$ \ log {2} = 7a + 5b + 3c, \ log {3} = 11a + 8b + 5c, \ log {5} = 16a + 12b + 7c $$.5 $$.
Как преобразовать Ln в журнал 10
Обновлено 4 декабря 2020 г.
Автор Oxana Fox
Логарифм числа — это степень, в которую необходимо возвести основание, чтобы получить это число; например, логарифм 25 с основанием 5 равен 2, поскольку 5 2 равно 25. «Ln» обозначает натуральный логарифм, в основе которого лежит константа Эйлера, приблизительно 2,71828. Натуральные логарифмы используются не только в математике, но и в естественных науках.«Общий» логарифм имеет основу 10 и обозначается как «журнал». Следующая формула позволяет получить натуральный логарифм, используя десятичный логарифм:
\ ln (\ text {number}) = \ frac {\ log (\ text {number})} {\ log (2.71828)}
TL; DR (слишком долго; не читал)
Чтобы преобразовать число из натурального в общий журнал, используйте уравнение ln ( x ) = log ( x ) ÷ журнал (2.71828).
Проверка значения числа
Перед тем, как вычислить логарифм числа, проверьте его значение.Логарифмы определены только для чисел больше нуля, т.е. положительных и ненулевых. Однако результатом логарифма может быть любое действительное число — отрицательное, положительное или нулевое.
Вычислить общий журнал
Введите число, которое вы хотите логарифмировать на своем калькуляторе. Нажмите кнопку «журнал», чтобы вычислить общий журнал числа. Например, чтобы найти общий журнал 24, введите «24» на вашем калькуляторе и нажмите клавишу «log». Общий логарифм 24 равен 3.17805.
Вычислить общий журнал e
Введите на калькуляторе константу «e» (2,71828) и нажмите кнопку «журнал» для расчета журнала 10 :
\ log_ {10} (2,71828) = 0,43429
Преобразовать натуральный логарифм в общий журнал
Разделите десятичный логарифм числа на десятичный логарифм е, 0,43429, чтобы найти натуральный логарифм через десятичный логарифм.


 Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .

 В геометрии и алгебре встречается два варианта — десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
В геометрии и алгебре встречается два варианта — десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
 72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x. Такой вариант подсчета создан на основе двух математических фактов:
Такой вариант подсчета создан на основе двух математических фактов:
 Позже диалог возобновился, но уже между Эйлером и Даламбером.
Позже диалог возобновился, но уже между Эйлером и Даламбером. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений.
С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений.
 Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным. В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:
Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным. В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните: Выглядит как орфографическая ошибка или даже как опечатка, в которой пропущена латинская буква «о».
Выглядит как орфографическая ошибка или даже как опечатка, в которой пропущена латинская буква «о». Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.
Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно. Простыми словами, в выражении loga b антилогарифмом считается число b a . Для десятичного логарифма lga, антилогарифм равен 10 a , а для натурального lna антилогарифм равняется e a . По сути, это тоже возведение в степень и обратная операция для логарифмирования.
Простыми словами, в выражении loga b антилогарифмом считается число b a . Для десятичного логарифма lga, антилогарифм равен 10 a , а для натурального lna антилогарифм равняется e a . По сути, это тоже возведение в степень и обратная операция для логарифмирования.
 Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.
Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:
Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n: Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.
Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .



 Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.
Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.
 С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.

 Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.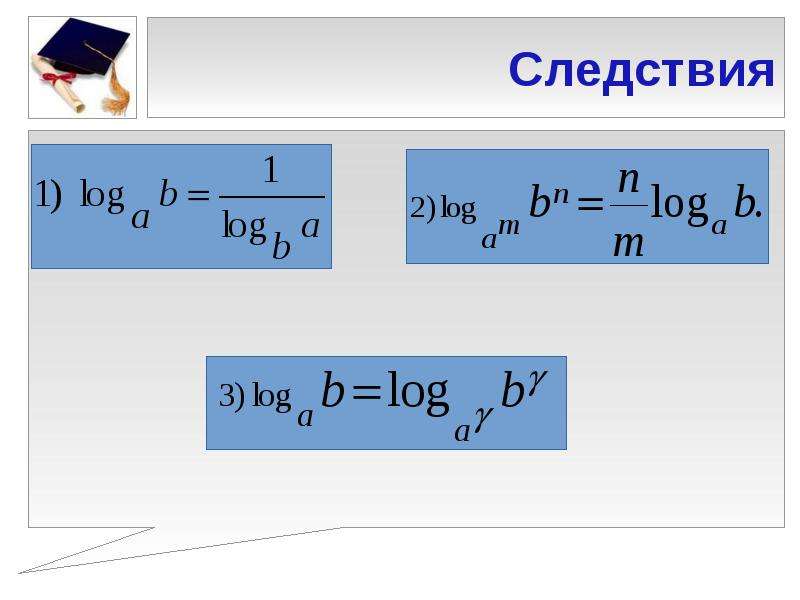 Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
 72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x. Такой вариант подсчета создан на основе двух математических фактов:
Такой вариант подсчета создан на основе двух математических фактов:
 Позже диалог возобновился, но уже между Эйлером и Даламбером.
Позже диалог возобновился, но уже между Эйлером и Даламбером.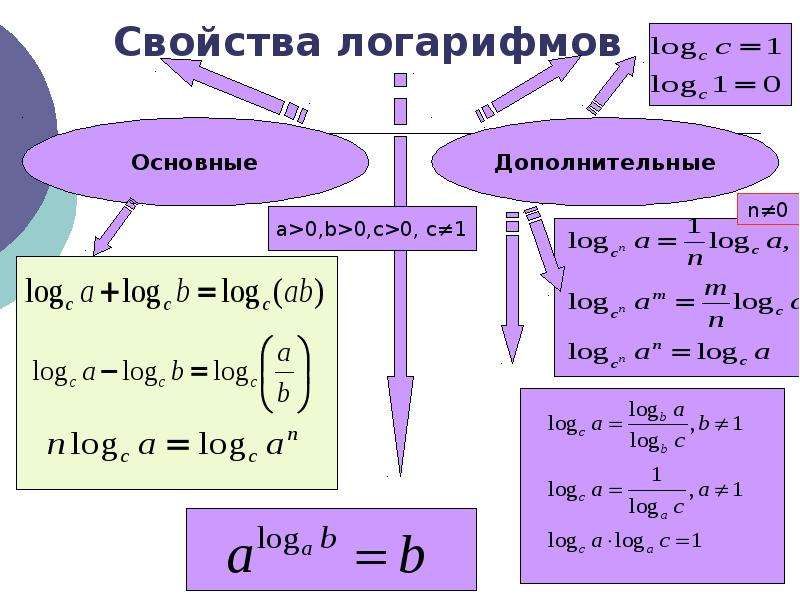 Например, для вычисления десятичного логарифма для 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите 2.95424251.
Например, для вычисления десятичного логарифма для 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите 2.95424251.
 В качестве нижнего предела можно взять . Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную скидку можно рассчитать следующим образом: (прибыль – (прибыль х минимальный объем продаж / ожидаемый объем) / цена единицы продукции.
В качестве нижнего предела можно взять . Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную скидку можно рассчитать следующим образом: (прибыль – (прибыль х минимальный объем продаж / ожидаемый объем) / цена единицы продукции. Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик.
Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик.
 После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.
После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.