Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»
Цель урока:
- Закрепить навыки решения простейших тригонометрических уравнений.
- Сформировать понятие решения тригонометрических уравнений сводящихся к квадратным.
- Развивать умения сравнивать, выявлять закономерности, обобщать.
- Воспитывать ответственное отношение к труду.
Оборудование:
- Карточки для повторения формул решения простейших тригонометрических уравнений.
- Плакат с алгоритмом решения тригонометрических уравнений (большой на доску и каждому на стол).
Литература: Учебник Колмагорова “Алгебра и начала анализа, 10-11 класс”.
Ход урока.
I. Повторение
1. sin x = a, cos x = a, tg x = a
При каких значениях а эти уравнения имеют решения?
[sin x и cos x при /а/ 1 tg x при любом a]
2. Повторить формулы решения простейших тригонометрических уравнений (на карточках):
sin x = а х = (-1)к arc sin a+
к, к z
sin x = 0
sin x = 1
sin x = -1
cos x = a x=± arc cos a + 2 , n z
cos x = 0
cos x = 1
cos x = -1
tg x = a x = arc tg a + n, n z
arc sin (-а) = — arc sin а
arc cos (-а) = — arc cos а
arc tg а (-а) = — arc tg а
II. Проверка домашнего задания.
Игра “Поле чудес”. Правила игры несколько изменены, а название оставлено.
Правила игры.
- Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же примеров или задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.
- Каждому ученику учитель дает карточку с заданиями и ученик сразу начинает решать.
- На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.
- Ниже записаны числа по порядку (по количеству букв в высказывании).
- Ученик, выполнявший задание, называет номер своей карточки и букву, под которой записан ответ.
- Учитель под числом (…) ставит букву (…). И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.
- За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь более чем число.
Ум хорошо, а два лучше
12 3 45 67 8 9 10 11 12 13 14 15 1 6 17
| в | д | |
| n z | , к z | , n z |
| е | л | м |
| , n z | , n z | , n z |
| о | р | у |
| , n z | , n z | , n z |
| x | ч | ш |
| , n z | , n z | , n z |
Уравнение:
| , n z | у | |
| cos x = -1 | х = +2 n, n z | м |
| , n z | x | |
| , n z | o | |
| , n z | p | |
| , n z | o | |
| , n z | ш | |
| , n z | o | |
| , n z | a | |
| , n z | д | |
| , k z | в | |
| , n x | a | |
| , n z | л | |
| , n z | у | |
| , n z | ч | |
| , n z | ш | |
| , n z | е |
Дополнительные уравнения
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , k z | |
| , n z | |
| , n z |
III. Объяснение нового.
1.
- В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a
- К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.
- Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.
- На доске записаны уравнения:
а) 3х-8=х+6 (линейное уравнение)
б) х2+2х-15=0 (квадратное уравнение)
в) х4-5х2+4=0 (квадратное уравнение
относительно х2).
г) 2 cos2x-cosx-1=0 (квадратное уравнение
относительно cosx)
- Какие из них являются квадратными?
- Общий вид квадратного уравнения:
ax2+bx+c=0
,
Корни квадратного уравнения, приведенного, т.е. х2+рх+q=0 можно находить по теореме Виета:
Х1+х2=-р; х1х2=q
- х4-5х2+4=0 – квадратное уравнение относительно х2. Это уравнение назвали биквадратным. Общий вид ах4+вх2+с=0, где а± 0.
- Его легко решить методом введения новой переменной, т.е. х2=а и уравнение принимает вид: а2-5а+4=0
3. Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у2-у-1=0. Получили квадратное уравнение.
Д=1+8=9;
Следовательно:
а) cosx=1 б) cosx=
х=2p n, n z , n z
, n n
Ответ: 2 n, n z; , n z
4. Решим уравнение:
Надо привести уравнение к одной функции. Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:
Пусть xinx=у, тогда 2у2+5у-3=0
Получили квадратное уравнение
Д=25+24=49
;
Следовательно:
а) б) xinx=-3 – решение не имеет
, к z
Ответ: , к z
5.
tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgx через tgx.
пусть tgx=у, то у2+у-2=0 (дальше, как в предыдущем случае).
6. Для закрепления
4 xin2x- cosx-1=0
Заменим xin2x на 1- cos2x. Получим
4(1- cos2x)- cosx-1=0
4-4 cos2x- cosx-1=0
-4 cos2x- cosx+3=0
4 cos2x+ cosx-3=0
пусть cosx=у, то
4у2+у-3=0
Д=1-48=49 ;
Следовательно,
а) cosx=-1 б)
х= +2 n, n z , n z
Ответ: +2 n; , n z
7. №164 (в) — cамостоятельно
2 xin2x- xinx-1=0
пусть xinx=у, то
2у2-у-1=0
Д=1+8=9;
Следовательно,
а) xinx=1 б), n z , n z
,к z.
Ответ: , n z
, к z
№ 165(б)
2 xin2x+3 cosx=0
Заменим xin2x на 1- cos2x получим
2(1- cos2x)+3 cosx=0
2-2 cos2x+3 cosx=0
-2 cos2x+3 cosx+2=0, т.е.
2 cos2x-3 cosx-2=0
пусть cosx=у, то
2у2-3у=0
Д=9+16=25
;
Следовательно,
а) cosx=2 б)
решение не имеет , n z
, n z
, n z
Ответ: , n z
8.
Итог урока
Алгоритм решения тригонометрических уравнений.
- Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.
- Ввести новую переменную.
- Записать данное уравнение, используя эту переменную.
- Найти корни полученного квадратного уравнения.
- Перейти от новой переменной к первоначальной.
- Решить простейшие тригонометрические уравнения.
- Записать ответ.
urok.1sept.ru
Решение простейших тригонометрических уравнений
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок изучения новой темы.
Класс: 10 класс.
Продолжительность урока: 2 часа (130 минут).
Цели урока:
- дидактические: усвоить навык решения простейших тригонометрических уравнений и их частные случаи;
- развивающие: развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;
- воспитательные: формировать эстетические навыки при оформлении записей в тетради и самостоятельность мышления у учащихся.
Организационный этап.
Девиз:
“Не делай никогда того, чего не знаешь, но научись всему, что следует знать”. (Пифагор)
Сегодня на уроке мы научимся решать с вами простейшие тригонометрические уравнения.
1. Актуализация опорных знаний (устная работа).
В результате выполнения задания мы повторим определения арккосинуса, арксинуса, арктангенса и арккотангенса.
1. Сформулировать определение арксинуса числа.
2. Сформулировать определение арккосинуса числа.
3. Сформулировать определение арктангенса числа.
4. Сформулировать определение арккотангенса числа.
5. С помощью тригонометрической окружности найти все значения из промежутка [-2 которые соответствуют числам , , , , arcsin 0, arcsin (Приложение 1)
6. Проверить, верно ли равенство:
7. Имеет ли смысл выражение:
2. Объяснение новой темы. Простейшие тригонометрические уравнения.
Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.
1. Пусть дано простейшее уравнение cos t = a.
Данное уравнение:
a) при -1< t < 1 имеет две серии корней
t1 = arсcos a + 2k, k Z
t 2 = — arсcos a + 2m, m Z.
Эти серии можно записать так
t = ± arсcos a + 2n, n Z ;
б) при а = 1 имеет одну серию решений
t = 2n, n Z ;
в) при а = -1 имеет одну серию решений
t = + 2n, n Z ;
г) при а = 0 имеет две серии корней
t1 = + 2k, k Z
t 2 = — + 2m, m Z. Обе серии можно записать в одну серию
t= + n, n Z.
д) при а > 1 и a < -1 уравнение не имеет корней.
Задание 1. Решить уравнения:
1) cos х = ;
2) cos х = — ;
3) cos 4x = 1
4x = 2n, n Z
.
4)
,
.
5)
,
,
.
6) Решите уравнение ; укажите корни, принадлежащие промежутку [-; -2].
а)
б) сделаем выборку корней, принадлежащих промежутку [-2; -].
1) с помощью окружности
2) с помощью графика функции
Ответ: а) ; б) .
Задание 2. Найти корни уравнения:
1) a) cos x =1 б) cos x = — 1 в) cos x = 0 г) cos x =1,2 д) cos x = 0,2
2) а) б) в) г)
2. Пусть дано простейшее уравнение sin t = a.
Данное уравнение :
a) при -1< t < 1 имеет две серии корней
t1 = arсsin a + 2n, n Z
t 2 = — arсcsin a + 2n, n Z.
Эти серии можно записать так
t = ( -1)karсsin a + k, k Z ;
б) при а = 1 имеет одну серию решений
t= + 2n, n Z
в) при а = -1 имеет одну серию решений
t = — + 2n, n Z;
г) при а = 0 имеет две серии корней
t1 = 2k, k Z,
t2 = + 2m, m Z.
Обе серии можно записать в одну серию
t = n, n Z ;
д) при а > 1 и a < -1 уравнение не имеет корней.
Задание 3. Решить уравнения:
1) sin х = ;
, ; , ; , .Запишем ответ в виде одной серии x= ( -1)k+ k, k Z .
2) sin х = -;
, ; , ; , .Запишем ответ в виде одной серии x= ( -1)k ( — + k, k Z или x= ( -1)k+1+ k, k Z .
Задание 3. Найти корни уравнения :
1) a) sin x =1 б) sin x = — 1 в) sin x = 0 г) sin x =1,2 д) sin x = 0,7
2) а) б) в) г)
3. Пусть дано простейшее уравнение tg t = a.
Данное уравнение при любом а R имеет одну серию решений
х = аrctg a + n, n Z.
1) tg х =
х = аrctg + n, n Z.
x = + n, n Z.
2) tg х = ,
х = аrctg + n, n Z,
x = + n, n Z.
4. Пусть дано простейшее уравнение ctg t = a.
Данное уравнение при любом а R имеет одну серию решений
х = аrcctg a + n, n Z.
1) ctg x = 1
х = аrcctg 1 + n, n Z,
х = + n, n Z.
2) ctg x = — 1
х = аrcctg ( -1) + n, n Z,
х = — аrcctg 1 + n, n Z
х = + n, n Z.
5. Итог урока
Продолжите фразу :
- Сегодня на уроке я повторил …
- Сегодня на уроке я узнал …
- Сегодня на уроке я научился …
Вы молодцы! Каждый из вас “научись тому, что следует знать”. Формулы для решения тригонометрических уравнений записаны на карточке — информаторе. (Приложение 2)
6. Домашнее задание: п.9, пример 1-9, № 137, 139, 141, 142.
Спасибо за урок!
Литература.
- А.Н.Колмогоров Алгебра и начала анализа. 10–11 классы
- С.М. Никольский, М.К. Потапов и др “Алгебра и начала анализа 10”
urok.1sept.ru
Методическая разработка (алгебра, 10 класс) на тему: Примеры решения тригонометрических уравнений
Фамилия, имя, отчество | Морозова Елена Николаевна |
Место работы | МОУ «Ильинская средняя общеобразовательная школа» Судогодского района |
Должность | Учитель математики |
Предмет | Математика |
Тема урока | Примеры решения тригонометрических уравнений |
Номер урока в теме | 7-8 |
Базовый учебник | Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П., Ивлев Б.М., Шварцбурд С.И. Алгебра и начала математического анализа. 10-11: Учебник для общеобразовательных учреждений. — М.:Просвещение, 2011 |
Цель урока | Создать условия для формирования умений решать уравнения разных типов |
Задачи урока | Обучающие: -проверить умения находить значения аркфункций и решать простейшие тригонометрические уравнения; -провести классификацию предложенных тригонометрических уравнений и найти способы их решения |
Развивающие: -создать условия для самореализации возможностей учащихся по формированию умений и навыков решения уравнений |
Воспитательные: -формирование у учащихся познавательных, информационных, коммуникативных компетенций, навыков самооценки |
Тип урока | комбинированный |
Формы работы учащихся | Фронтальная, в парах, индивидуальная |
Необходимое техническое оборудование | Мультимедийный проектор, компьютер, карточки |
1. Организационный момент. (Презентация. Слайды 1 – 2. )
Слайд 1.
Французский писатель Анатоль Франс (1844 – 1924) однажды заметил: «Учиться можно только весело…Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.
Сегодня у нас урок по теме «Примеры решения тригонометрических уравнений».
Давайте выясним, что мы уже знаем и умеем?
Предполагаемые ответы:
— знаем определения аркфункций
— умеем находить значения аркфункций
— умеем решать простейшие тригонометрические уравнения
Чему же будет посвящен сегодняшний урок?
1. проверим умения находить значения аркфункций
и умения решать простейшие тригонометрические уравнения
2. рассмотрим решения некоторых более сложных тригонометрических уравнений.
2.Проверочная работа и проверка результатов
(Презентация. Слайды 3, 4, 5.)
Индивидуальная работа по выполению заданий. Уч-ся выдается карточка. В заданиях 1-6 найти значения аркфункций, в заданиях 7-15 решить уравнения и записать ответ
№ п/п | Задание | Ответ |
Слайд 3
Самопроверка результатов:
Слайд 4
Самооценка по критериям
Критерии оценки: за каждый правильный ответ – 1 балл 14-15 баллов «5» 12-13 баллов «4» 9-11 баллов «3» 0-8 баллов «2» |
Слайд 5
3.Этап усвоения новых знаний
(Презентация. Слайды 6-10 . )
Групповая работа
Учащимся предлагаются карточки, на каждой одно из 8 уравнений. Необходимо провести их классификацию, объяснив критерий отбора, привести принцип их решения (там, где это возможно)
2sin2x + sin x – 1= 0 sin2x — 3sin x cos x +2cos2 x =0 cos 5x – cos 3x = 0 6cos2x + cos x – 1 = 0 sin x — 2cos x = 0 sin x + √3cos x = 0 2sin2x -sin x cos x = cos2x sin 5x – sin x = 0 |
Слайд 6
Предполагаемый результат:
№ группы | Уравнения | Критерий отбора | Способ решения |
1 | 2sin2x + sin x – 1= 0 6cos2x + cos x – 1 = 0 | Сводящиеся к квадратному | Введение новой переменной |
2 | sin 5x – sin x = 0 cos 5x – cos 3x = 0 | Разность (сумма) одноименных функций | Разложение на множители |
3 | sin x — 2cos x = 0 sin x + √3cos x = 0 | Вида Аsin x + Вcos x = 0 (Однородные 1 степ) | ? |
4 | sin2x — 3sin x cos x +2cos2 x =0 2sin2x -sin x cos x = cos2x | Аsin2x +Вsin xcos x + +Сcos2x=0 (однородные 2 степени) | ? |
Слайд7
Вы не смогли предложить способы решения уравнений 3 и 4 групп. Попробуем найти их в учебнике (Работа с текстом п.11 учебника)
Предполагаемый результат: уч-ся делают ссылку на примеры 4-5 для решения уравнений 4 группы (в таблицу вносится запись)
№ группы | Уравнения | Критерий отбора | Способ решения |
1 | 2sin2x + sin x – 1= 0 6cos2x + cos x – 1 = 0 | Сводящиеся к квадратному | Введение новой переменной |
2 | sin 5x – sin x = 0 cos 5x – cos 3x = 0 | Разность (сумма) одноименных функций | Разложение на множители |
3 | sin x — 2cos x = 0 sin x + √3cos x = 0 | Вида Аsin x + Вcos x = 0 (Однородные 1 степ) | ? |
4 | sin2x — 3sin x cos x +2cos2 x =0 2sin2x -sin x cos x = cos2x | Аsin2x +Вsin xcos x + +Сcos2x=0 (однородные 2 степени) | Обе части уравнения делим на cos2 x, получаем уравнение вида Аtg2x +Вtg x + +С=0 |
Слайд 8
Давайте подумаем: нельзя ли этот прием применить к решению ур-ий 3 группы?
(в таблицу вносится запись)
№ группы | Уравнения | Критерий отбора | Способ решения |
1 | 2sin2x + sin x – 1= 0 6cos2x + cos x – 1 = 0 | Сводящиеся к квадратному | Введение новой переменной |
2 | sin 5x – sin x = 0 cos 5x – cos 3x = 0 | Разность (сумма) одноименных функций | Разложение на множители |
3 | sin x — 2cos x = 0 sin x + √3cos x = 0 | Вида Аsin x + Вcos x = 0 (Однородные 1 степ) | Обе части уравнения делим на cos x, получаем уравнение вида Аtgx +В=0 |
4 | sin2x — 3sin x cos x +2cos2 x =0 2sin2x -sin x cos x = cos2x | Аsin2x +Вsin xcos x + +Сcos2x=0 (однородные 2 степени) | Обе части уравнения делим на cos2 x, получаем уравнение вида Аtg2x +Вtg x + +С=0 |
Слайд 9
Всем учащимся выдается полученная таблица в качестве справочной
К какой группе вы отнесете следующие уравнения:
5sin2x +6cosx – 6= 0 cos 2x + cos2x + sin x cos x = 0 cos x = sin x |
Слайд 10
4. Этап закрепления
Учащимся предлагается решить уравнения из таблицы (Слайд 10). При этом они работают в парах. Каждая пара решает по 1 уравнению из каждой группы, 1 ученик – одно, второй – другое, договариваясь между собой кто какое будет решать, возможна взаимопомощь.
5. Подведение итогов
Подведем итоги. Какой багаж знаний вы унесете с собой с сегодняшнего урока? Дайте самооценку своей деятельности и достигнутых результатов на уроке.
(Выставляются оценки в журнал)
6. Домашнее задание (Слайд 11)
п.11, №166(а), 170(а,б),173(а), подобрать уравнения других типов
Структура и ход урока:
Этап урока | Содержание | Деятельность учащихся | Деятельность учителя | Какие компетенции формируются |
Организационный | Слайды 1-2 | Комментарии к слайдам | Р.Д.:Владение навыками организации и участия в коллективной деятельности |
Проверочная работа и проверка результатов | Слайд 3-5 | -выполнение работы -самопроверка -самооценка | Хронометраж времени | Р.Д.: объективное оценивание своих учебных достижений |
Этап усвоения новых знаний | Слайды 6-10 | -Проводят классификацию предложенных уравнений — ищут способы их решения | Направляет действия учащихся | П.Д.:самостоятельный выбор критериев для сравнения, сопоставления, оценки и классификации объектов И-К.Д.:Поиск и извлечение необходимой информации в источниках различного типа |
Этап закрепления | Слайд 9 | Самостоятельно решают предложенные уравнения | Проверяет работы учащихся в режиме он-лайн, при необходимости оказывает помощь | П.Д.: умение самостоятельно и мотивированно организовывать свою деятельность; самостоятельное создание алгоритмов для решения поставленных задач |
Подведение итогов | — | Отвечают на вопросы учителя | Задает вопросы | Р.Д.: Формулирование полученных результатов, объективное оценивание своих учебных достижений, учет мнения других людей при самооценке |
Домашнее задание | Слайд11 | Записывают в дневник | Комментирует задание |
nsportal.ru
7 методов решения тригонометрических уравнений. | Математика и геометрия
7 методов решения тригонометрических уравнений.
Первый вопрос.Как привести к простейшим тригонометрическим уравнениям?
1) Нужно выразить тригонометрическую функцию, так чтобы можно было выполнить задание 2.
2) Найти аргумент функции по формулам.
3) Нахождение неизвестной переменной.
Пример решения уравнения:
Решение:
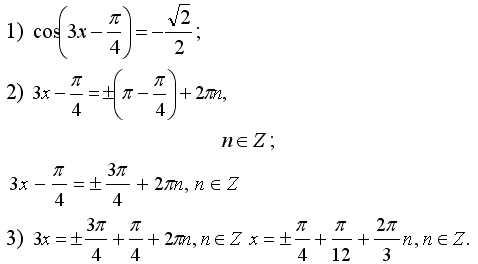
Ответ:
Вопрос второй.
Как применяется метод замены переменной?
1) Нужно привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.
2) Выразить переменную через какую то неизвестную.
3) После того как мы выразили переменную, нужно решить алгебраическое уравнение.
4) Сделать обратную замену.
5) Решить уже простое тригонометрическое уравнение.
Пример решения уравнения:
Решение:
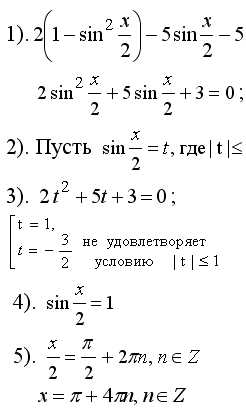
Ответ:
Третий вопрос.
Как применить метод понижения порядка тригонометрического уравнения?
1) Используя формулы понижения степени, нужно заменить данное уравнение на линейное:
2) Решить полученное уравнение так как мы решали в 1 и во 2 примерах.
Пример решения уравнения:
Решение:
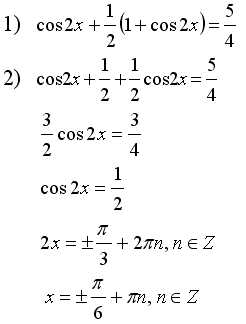
Ответ:
Вопрос четвертый:
Как использовать однородные уравнения?
1) Привести уравнение к виду:
2) Разделить обе части уравнения на
и получить уравнение относительно
3)Решить полученное уравнение известными способами.
Пример решения уравнения:
Решение:
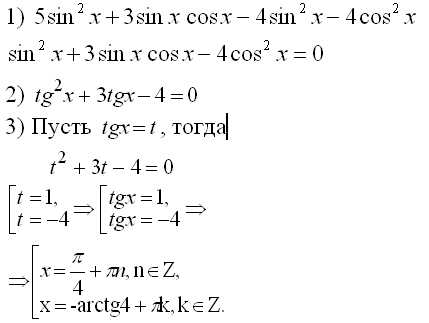
Ответ:
Пятый метод решения.
Использование метода преобразования уравнения с помощью тригонометрических формул.
1) Используя тригонометрические формулы, нужно привести уравнение к виду для решения способами 1, 2, 3, 4.
2) Решить полученное уравнение известными методами.
Пример решения уравнения:
Решение:
Ответ:
Шестой вопрос.
Как разложить на множители тригонометрические уравнение?
Пример решения уравнения:
Решение:
Перенесём все члены уравнения влево:
преобразуем и разложим на множители выражение в левой части уравнения:
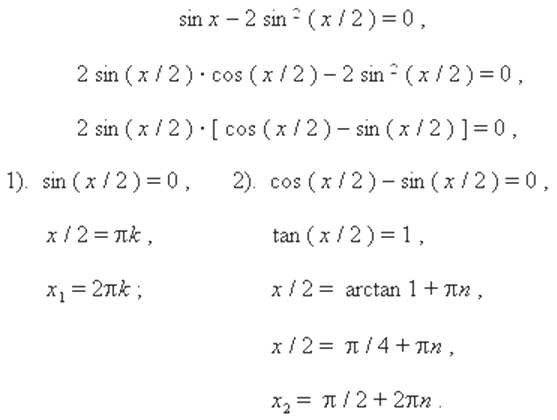
Вопрос седьмой.
Как применить преобразование произведения в сумму?
Пример решения уравнения:
Порядок вывода комментариев: По умолчаниюСначала новыеСначала старые
testent.ru
План-конспект урока по алгебре (10 класс) на тему: Примеры решения тригонометрических уравнений
Тема урока: «Примеры решения тригонометрических уравнений».
Цели и задачи урока.
Образовательные: 1. сформировать у учащихся умения решать однородные тригонометрические уравнения;
2. отработать навыки решения других видов тригонометрических уравнений.
Развивающие: 1. развивать и совершенствовать умение применять имеющиеся у учащихся знания в измененной ситуации;
2.развивать логическое мышление, умение делать выводы и обобщения.
Воспитательные: Воспитывать у учащихся аккуратность, культуру поведения, чувство ответственности.
Формы:
Индивидуальная, парная, фронтальная.
Методы:
Словесные, наглядные, информационно – коммуникативные.
Приемы:
Постепенное сокращение объяснений по мере усвоения алгоритма решения, правильная последовательность задач, контрольные упражнения как средство проверки.
Ход урока:
- Проверка д/з.
- Проверочная работа (проводится по вариантам). Условие записано на интерактивной доске.
I вариант | II вариант |
1) Сформулируйте определение: | |
а) арксинуса числа б) арккотангенса числа | а) арккосинуса числа б) арктангенса |
2) Для каких чисел определен | |
арккосинус | арксинус |
3) Записать общий вид корней уравнения | |
sin x = a | сos x = a |
4) Записать формулу корней уравнения tg x = a | 4) При каких значениях а уравнения sin x = a, сos x = a имеют решения? |
- Фронтальный опрос.
Назвать решения частных случаев простейших тригонометрических уравнений. Условия записаны на интерактивной доске, решения проверяются с помощью гиперссылок.
sin x = 0 | cos x = 1 |
sin x = 1 | tg x = 0 |
cos x = 0 | ctg x = 1 |
sin x = -1 | cos x = -1 |
ctg x = 0 | tg x = -1. |
- Рассмотрим некоторые методы решения тригонометрических уравнений.
а) Метод замены переменных
Пример1. Решите уравнение 2sin2x + cosx – 1=0.
Решение: Запишем уравнение в виде 2(1 – cos2x) + cosx – 1=0, откуда 2cos2x – cosx – 1 = 0.
Заметим, что данное уравнение представляет собой квадратное уравнение относительно cosx. Обозначим t = cos x, получим уравнение
2t2 — t — 1 =0, корни которого t1 = 1 и t2 = —.
Получаем два случая:
- cosx = 1, откуда x=2πk, k
- cosx = — 0,5, откуда x=
+2πn, n
.
Ответ: 2πk, +2πn, где n,k
.
- Закрепление изученного материала.
Решите уравнение:
а) 2sin2x + 5cosx + 1 =0
б)cos2x + 3sinx + 1 =0
б) Однородные тригонометрические уравнения
Методом замены можно решать так называемые «однородные тригонометрические» уравнения.
Тригонометрическое уравнение называют однородным, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени.
Пример 2 Решите уравнение 5sin2x – 8sinx cosx — cos2x = — 2.
Решение: Перепишем уравнение в виде
7sin2x – 8sinx cosx + cos2x = 0.
Получили уравнение, однородное относительно sinx и cosx.
Рассмотрим два случая:
- cosx = 0, тогда 7sin2x – 8sinxּ0 + 02 =0, откуда sinx = 0, что невозможно, поскольку sin2x + cos2x =1; в этом случае корней нет.
- cosx
≠ 0, тогда разделим обе части уравнения на cos2x:
7tg2x – 8 tgx + 1 =0.
Пусть y=tgx. Получим: 7y2-8y +1=0, откуда y1 = 1, y2=.
Осталось решить уравнения tgx = 1 и tgx = .
Ответ: + πm, arctg
+ πm, где m.
6) Закрепление изученного материала.
Решите уравнение:
2sin23x – 5sin3x cos3x + 3cos23x = 0.
в) Универсальная тригонометрическая подстановка
При решении тригонометрических уравнений можно использовать так называемую универсальную тригонометрическую подстановку на основе формул:
sinx =, cos x =, tg x =
.
Если теперь ввести обозначение t = tg, то sin x = ,
cos x = , tg x =
.
Пример 3 (учащиеся самостоятельно пробуют ввести новую переменную и решить уравнение, затем вызывается к доске один из учащихся для проверки).
Решить уравнение cos x + tg = 1.
Сделаем универсальную подстановку t=tg , тогда
+ t = 1 ⬄ t3 – 2t2 + t = 0 ⬄ t1 = 0, t2 =1.
Таким образом:
а) tg = 0, откуда x = 2πk, k
;
б) tg = 1, откуда x =
.
Ответ: 2πk, .
- Задания появляются на интерактивной доске. Также каждому учащемуся раздаются карточки с таким же заданием.
Задание заключается в следующем: среди уравнений на карточке (доске) выберите те, которые решаются
а) методом замены переменных;
б) как однородные тригонометрические уравнения;
в) с помощью универсальной тригонометрической подстановки:
- 2sin
x + cos
x = 5sin x cos x;
- cosx sin 7x = cos 3x sin5x
cosx – sin x = 0
- sin x – sin2x+sin3x – sin4x = 0
- 2cosx+3sinx+2cosx = 0
- cos
x + 3sin2x + 2
sinx cosx = 3
- sin2x —
sin2x = cos2x
- sin x + cos x = 1
- sin2x + cos22x +sin23x = 1,5
10)sin2x -2sin x -3 = 0
11)sin x + sin 3x = sin 5x – sin x
Учащиеся помечают на карточке уравнения видов а, б и в.
Результат проверяется с помощью фронтального опроса.
8. Домашнее задание: повторить конспект урока, решить отмеченные уравнения с карточки.
nsportal.ru
