калькулятор дисперсии — найти случайную дисперсию онлайн
Онлайн-калькулятор дисперсии поможет вам определить дисперсию, сумму квадратов и коэффициент дисперсии для определенного набора данных. Кроме того, этот калькулятор также отображает среднее значение и стандартное отклонение путем пошагового расчет дисперсии онлайн. Прочтите, чтобы узнать, как найти дисперсию онлайн и стандартное отклонение, используя формулу выборочной дисперсии.
Что такое дисперсия?Дисперсия группы или набора чисел – это число, которое представляет «разброс» набора. Формально это квадрат отклонения набора от среднего и квадрат стандартного отклонения.
Другими словами, небольшая дисперсия означает, что точки данных имеют тенденцию быть близкими к среднему и очень близко друг к другу. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения и друг от друга. Дисперсия – это среднее значение квадрата расстояния от каждой точки до среднего.
Типы дисперсии:Вариация выборки: дисперсия выборки не охватывает всю возможную выборку (случайная выборка людей).
{2n − 1}
Эти формулы запоминать не нужно. Чтобы вам было удобно, наш примерный калькулятор дисперсии выполняет все расчет дисперсии онлайн, связанные с дисперсией, автоматически, используя их.
Тем не менее, Калькулятор диапазона среднего среднего значения режима поможет вам рассчитать средний средний режим и диапазон для введенного набора данных.
Пример расчета
Давайте посчитаем дисперсию оценок пяти студентов на экзамене: 50, 75, 89, 93, 93. Выполните следующие действия:
- Найдите среднее
Чтобы найти среднее значение (x), разделите сумму всех этих значений на количество точек данных:
х = (50 + 75 + 89 + 93 + 93) / 5
х̄ = 80
- Вычислите разницу между средним значением и квадратом отличий от среднего. Следовательно, среднее значение равно 80, мы используем формулу для вычисления разницы от среднего:
xi – x̄
Первая точка – 50, поэтому разница от среднего составляет 50 – 80 = -30.
Квадрат отклонения от среднего – это квадрат предыдущего шага:
(xi – x̄) 2
Итак, квадрат отклонения равен:
(50 – 80) 2 = (-30) 2 = 900
В приведенной ниже таблице квадрат отклонения рассчитан на основе среднего значения всех результатов испытаний. Столбец «Среднее отклонение» – это результат минус 30, а столбец «Стандартное отклонение» – это столбец перед квадратом.
| Счет | Отклонение от среднего | Квадратное отклонение |
| 50 | -30 | 900 |
| 75 | -5 | 25 |
| 89 | 9 | 81 |
| 93 | 13 | 169 |
| 93 | 13 | 169 |
- Рассчитайте стандартное отклонение и дисперсию
Затем используйте квадраты отклонений от среднего:
σ2 = ∑ (xi – x̄) 2 / N
σ2 = (900 + 25 + 81 + 169 + 169) / 5
σ2 = 268,5
дисперсия случайной величины онлайн результатов экзамена составила 268,8.
Онлайн-калькулятор дисперсии совокупности вычисляет дисперсию для заданных наборов данных. Вы можете просмотреть работу, проделанную для расчет дисперсии онлайн из набора данных, следуя этим инструкциям:
Вход:- Сначала введите значения набора данных через запятую.
- Затем выберите дисперсию для выборки или совокупности.
- Нажмите кнопку «Рассчитать», чтобы получить результаты.
- Калькулятор дисперсии выборки отображает дисперсию, стандартное отклонение, количество, сумму, среднее значение, коэффициент дисперсии и сумму квадратов.
- Этот калькулятор также обеспечивает пошаговые вычисления дисперсии, коэффициента дисперсии и стандартного отклонения.
Дисперсия – это квадрат отклонения от среднего, а стандартное отклонение – это квадратный корень из числа.
Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).
Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией обычно выгодны для агрессивных инвесторов с меньшим неприятием риска, в то время как акции с низкой дисперсией обычно выгодны для консервативных инвесторов с более низкой толерантностью к риску.
Каков диапазон отклонений?Диапазон – это разница между высоким и низким значением. Поскольку используются только крайние значения, потому что эти значения будут сильно на него влиять. Чтобы найти диапазон отклонения, возьмите максимальное значение и вычтите минимальное значение.
Заключение:Воспользуйтесь этим онлайн-калькулятором дисперсии, который работает как с выборкой, так и с наборами данных о генеральной совокупности, используя формулу генеральной и выборочной дисперсии.
Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.
Other Languages: Variance Calculator, Varyans Hesaplama, Calculadora De Variancia, Kalkulator Varians, Kalkulator Wariancji, Výpočet Rozptylu, 分散 計算.
Калькулятор бассейна — калькуляторы статистики
инструкции
: Этот калькулятор вычисляет объединенную дисперсию и стандартное отклонение для двух приведенных стандартных отклонений образца \(s_1\) и \(s_2\), с соответствующими размерами образцов \(n_1\) и \(n_2\).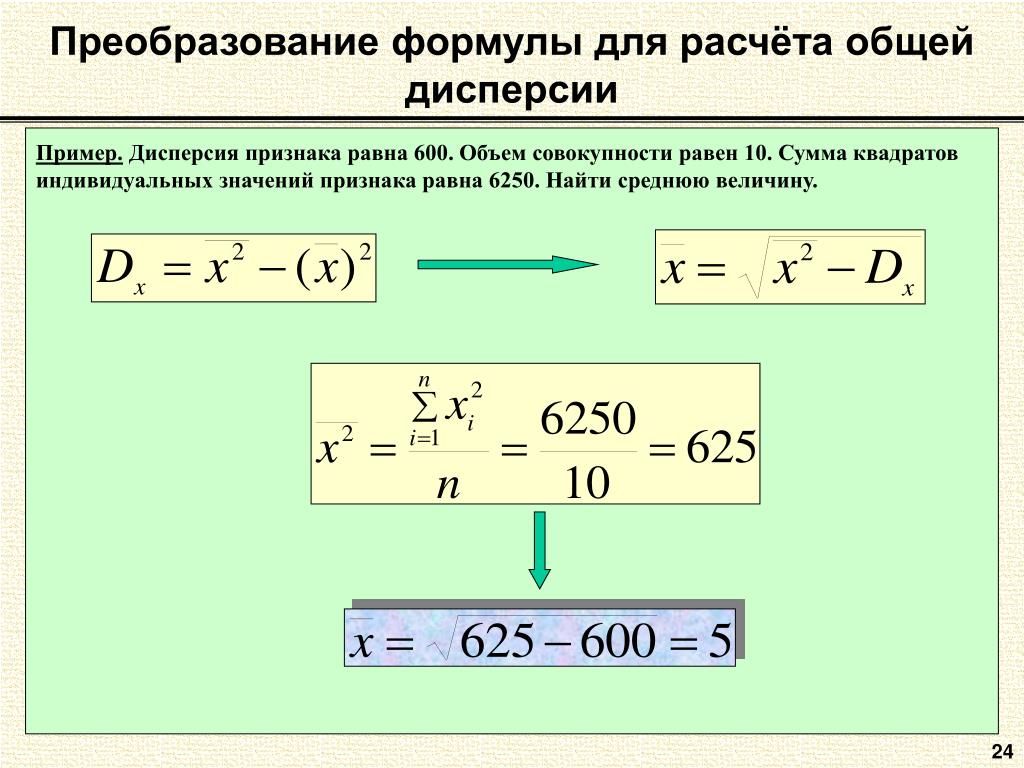
Образец Стдева.Образец 1 (_ xyz_a__) = Размер образца 1 (\(n_1\)) =
Образец Св.Образец 2 (\(s_2\)) =
Размер образца 2 (\(n_2\)) =
Объединенная дисперсия представляет собой оценку дисперсии населения, полученную из двух вариантов образца, когда предполагается, что два образца происходят от населения с тем же стандартным отклонением населения.В этой ситуации ни одна из вариантов образцов не является лучшей оценкой, чем другие, и два приведенных образца «объединены» вместе, в рода средневзвешенном средневзвешении, для вычисления объединенной дисперсии.
Формула для объединенной дисперсии, учитывая два варианта образца:
\[ s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2} \]
С другой стороны, объединенное стандартное отклонение:
\[s_p = \sqrt{ \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}}\]
На прохладный способ выражения вышеуказанных формул основан на идее
Сумма площадей
(__Xxyz_a__).
2}{n_1+n_2-2} = \frac{ SS_1 + SS_2}{df_1+df_2}\]
Идея объединенных вариантов требует предположения, что отклонения населения равны.Для случая неравных вариантов населения вы должны использовать это Перехлаждающие варианты калькулятора Отказ
Используется один контекст, в котором используется идея объединенных вариантов, предназначена для T-тестирования для двух независимых отклонений.Для калькулятора T-теста (где используется идея объединенных вариантов), Проверье это здесь.
Основная статистика
Расчет описательной статистики
Управляемая дисперсия калькулятора
Статистические средства Solver.
Калькулятор дисперсии — пошаговый расчет
Образец
Население
Введите значения для расчета дисперсии (разделенные запятыми) 3, 8, 10, 17, 24, 27
Как пользоваться этим калькулятором дисперсии?
Чтобы использовать этот калькулятор отклонений, выполните шаги, указанные ниже.
- Введите значения через запятую в поле ввода.
- Выберите, для каких данных вы хотите рассчитать дисперсию, т.е. ( образец или население )
- Нажмите кнопку » вычислить «, чтобы получить результат справа.
Этот поисковик дисперсии даст вам количество выборок, среднее значение, стандартное отклонение и дисперсию одним щелчком мыши. Используя этот калькулятор, вы получите пошаговые результаты стандартного отклонения, среднего значения и дисперсии.
Стандартное отклонение —
Сумма квадратов (SS) —
Расчет среднего:
Расчет дисперсии:
Расчетное стандартное отклонение:
Оставьте свой отзыв!
Худший Бедный Средний Хороший Супер
Содержание
| 1 | Что такое дисперсия? |
| 2 | Формула дисперсии: |
| 3 | Разница между генеральной совокупностью и выборкой: |
| 4 | Как найти дисперсию? |
Этот искатель дисперсии даст вам количество выборок, среднее значение, стандартное отклонение и дисперсию одним щелчком мыши.
Используя этот калькулятор дисперсии с шагами, вы получите пошаговые результаты стандартного отклонения, среднего значения и дисперсии.
Калькулятор дисперсии — это бесплатный онлайн-инструмент для расчета вариации каждого числа в наборе данных на основе среднего значения этого набора данных. Вы можете использовать этот инструмент, чтобы понять и решить сложные и длительные проблемы с отклонениями.
Что такое дисперсия?
В статистике дисперсией случайной величины является среднее значение квадрата расстояния от среднего. Он показывает распределение случайной величины по среднему значению.
Небольшая дисперсия указывает на то, что распределение случайной величины близко к среднему значению. Если дисперсия больше, это показывает, что случайная величина далека от среднего значения. 92 = s2=N−11i=1∑n(xi-xˉ)2
В этом уравнении s 2 – выборочная дисперсия x 90 102 i – набор выборочных данных x̄ – среднее значение выборочного набора значений, а N относится к размеру выборочного набора данных.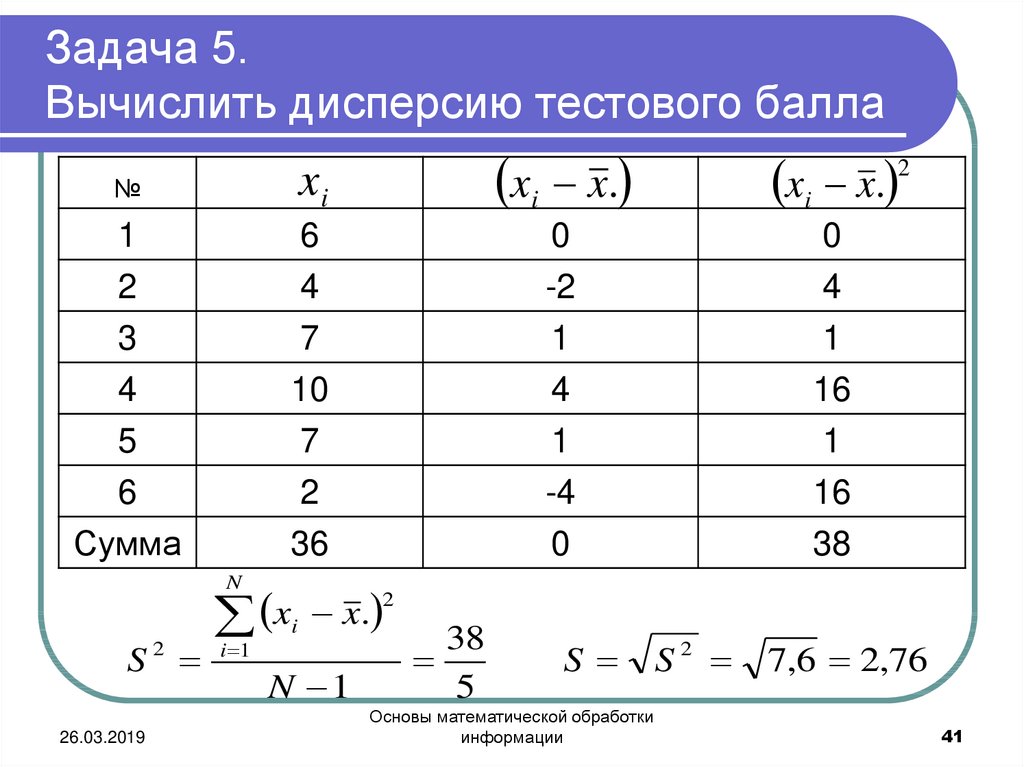
Разница между популяцией и выборкой:
Термин «популяция» относится ко всему количеству соответствующих наблюдений. Анализ возраста жителей Токио, например, будет включать возраст каждого жителя Токио в населении.
Выборка данных — это набор данных из совокупности в статистике. Совокупность обычно очень велика, что делает невозможным перечисление всех значений в совокупности.
Решение состоит в том, чтобы собрать выборку населения и выполнить статистику по этим выборкам. Затем эти выборки отражают всю совокупность.
Как найти дисперсию?
Расчет дисперсии вручную — утомительная задача. Вам понадобится среднее значение набора данных, арифметическая разность и множество сложений и вычитаний, чтобы найти дисперсию.
Вы также можете использовать приведенный выше калькулятор дисперсии генеральной совокупности, чтобы рассчитать дисперсию для вашего набора данных. Первый пример — дисперсии генеральной совокупности , а второй пример — выборочной дисперсии .
Предположим, что в гостинице ровно пять номеров. Каждая комната рассчитана на следующее количество человек:
x 1 = 6, x 2 = 5, x 3 = 6, x 4 = 7 и x 5 = 4
Найдите дисперсию.
Решение:
Воспользуемся приведенной выше формулой для дисперсии генеральной совокупности.
Выполните следующие действия, чтобы измерить дисперсию для заданного набора данных с помощью этой формулы.
Шаг 1: Найдите среднее значение набора данных
Среднее (= m = ∑ xn = (6+5+6+7+4) 5 = 285 = 5,6 (= \: m \: = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = \:\frac{\sum \:x}{n}\:=\:\frac{\left(6\:+\:5\:+\:6\:+\:7\:+\:4 \right)}{5}\:=\:\frac{28}{5}\:=\:5.6(=M=n∑x=5(6+5+6+7+4)=528 = 5,6
Шаг 2: Вычтите среднее значение из каждого числа в наборе данных, чтобы найти арифметическую разность .
x1-µ=6-5,6=0,4x_1 — \mu = 6 — 5,6 = 0,4×1-µ=6-5,6=0,4
x2-µ=5-5,6=-0,6x_2 — \mu = 5 — 5,6 = -0,6×2-µ=5-5,6=-0,6
x3-µ=6-5,6=0,4x_3 — \mu = 6 — 5,6 = 0,4×3-µ=6-5,6=0,4
x4- μ=7−5,6=1,4x_4 — \mu = 7 — 5,6 = 1,4×4-μ=7−5,6=1,4
x5−μ=4−5,6=-1,6x_5 — \mu = 4 — 5,6 = -1,6 x5−μ=4−5,6=−1,6
Шаг 3: 92 = \Big\{\dfrac{0,16 + 0,36 + 0,16 + 1,96 + 2,56}{5}\Big\} = \dfrac{5,2}{5} = 1,04σ2 = {50,16+0,36+0,16+1,96+2,56 }=55,2=1,04
Пример № 2:Владелец магазина продавал такое количество яблок каждый день в течение семи дней: 42,48,30,36,46,53,62,42, 48, 30, 36, 46. , 53, 62,42,48,30,36,46,53,62.. Используйте эти данные выборки, чтобы вычислить выборочную дисперсию для количества яблок, проданных в день владельцем магазина.
Решение:
Шаг 1: Напишите формулу выборочной дисперсии.
Используйте следующую формулу для расчета выборочной дисперсии при работе с выборочными наборами данных.
Шаг 2: Вычислить среднее значение для данных выборки \sum x}{n} = \dfrac{42 + 48 + 30 + 36 + 46 + 53 + 62}{7} = \dfrac{317}{7} = 45,28xˉ=n∑x=742+48+ 30+36+46+53+62=7317=45,28
Шаг 3: Вычесть среднее значение из каждого числа в наборе данных
Вычислить xi−xˉx_i — \bar{x}xi−xˉ, где х i представляет значения в наборе данных.
x1-xˉ=42-45,28=-3,8x_1 — \bar{x} = 42 — 45,28 = -3,8×1-xˉ=42-45,28=-3,8 \bar{x} = 48 — 45,28 = 2,72×2-xˉ=48-45,28=2,72
x3-xˉ=30-45,28=-15,8x_3 — \bar{x} = 30 — 45,28 = -15,8×3- xˉ=30-45,28=-15,8
x4-xˉ=36-45,28=-9,28x_4 — \bar{x} = 36 — 45,28 = -9,28×4-xˉ=36-45,28=-9,28
x5-xˉ =46−45,28=0,72x_5 — \bar{x} = 46 — 45,28 = 0,72×5−xˉ=46−45,28=0,72
x6−xˉ=53−45,28=7,72x_6 — \bar{x} = 53 — 45,28 = 7,72×6−xˉ=53−45,28=7,72 92= \dfrac{697,27}{7 — 1} = 116,21=s2=7−1697,27=116,21
Ссылки:
Бхандари, П. (2020, 12 октября). Понимание и расчет дисперсии | Scribbr
Как рассчитать дисперсию | wikiHow
В чем разница между генеральной совокупностью и выборкой | Статистические решения
Другие языки
Рейтинги пользователей
- Всего отзывов 0
- Общий рейтинг 0/5
- Звезды
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Еще нет обзора
Пожалуйста, заполните хотя бы 1 строку
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
Калькулятор дисперсии | Justfreetools
Калькулятор дисперсии и как его рассчитать.
Калькулятор дисперсии генеральной совокупности и выборочной дисперсии
Введите значения
Тип данных Данные всего населенияВыборочные данные
Дисперсия
Стандартное отклонение
Иметь в виду
Калькулятор дискретной дисперсии случайной величины
Введите вероятность или вес и количество данных в каждой строке:
Расчет дисперсии всей популяции
Среднее значение популяции:
Дисперсия популяции:
Расчет дисперсии отбора данных
.
среднее значение переменной:
дисперсия случайной переменной:
В настоящее время у нас есть около 5613 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация пароля или калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 15 Инструменты Онлайн-инструменты
- Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Бесплатные онлайн-калькуляторы и инструменты для электротехники
- Бесплатные онлайн финансовые калькуляторы и инструменты
- Бесплатные онлайн калькуляторы оценок и инструменты
- Бесплатные онлайн калькуляторы и инструменты для освещения
- Бесплатные онлайн математические калькуляторы и инструменты
- Бесплатные онлайн калькуляторы и инструменты для проводов
- Бесплатные онлайн детские калькуляторы и инструменты
- Бесплатные онлайн-калькуляторы тела и инструменты
- Калькулятор преобразования переменного тока в постоянный
- Сложение дробей бесплатный онлайн-калькулятор
- Сложение бесплатный онлайн-калькулятор
- Antilog бесплатный онлайн-калькулятор
- Arccos бесплатный онлайн-калькулятор
- Arcsin бесплатный онлайн-калькулятор
- Arctan бесплатный онлайн-калькулятор
- Average бесплатный онлайн-калькулятор
- Base бесплатный онлайн-калькулятор
- Binary бесплатный онлайн-калькулятор 5 19 09 19 09 бесплатно 90 Калькулятор косинуса
- Деление дробей онлайн калькулятор
- Деление бесплатно онлайн калькулятор
- Формула экспоненциального роста/убывания онлайн калькулятор бесплатно
- Экспоненты бесплатный онлайн калькулятор
- Факториал бесплатный онлайн калькулятор
- Дроби бесплатный онлайн калькулятор
- Наибольший общий множитель бесплатный онлайн калькулятор
- Наименьшее общее кратное бесплатный онлайн калькулятор
- Логарифм бесплатный онлайн калькулятор онлайн калькулятор
- Умножение дробей бесплатный онлайн калькулятор
- Натуральный логарифм бесплатный онлайн калькулятор
- Процентный безошибочный онлайн калькулятор
- Процентный калькулятор бесплатный онлайн
- Процентный бесплатный онлайн калькулятор
- Процентный калькулятор онлайн бесплатный калькулятор
- Бесплатный онлайн генератор случайных чисел
- Генератор случайных чисел 0-1
- Генератор случайных чисел 0-10
- Генератор случайных чисел 0-100
- Генератор случайных чисел 0-9
- Генератор случайных чисел 0-99
- Генератор случайных чисел 1-10
- Генератор случайных чисел 1-100
- 1-5 90 Генератор случайных чисел Генератор случайных чисел 1-20
- Генератор случайных чисел 1-3
- Генератор случайных чисел 1-4
- Генератор случайных чисел 1-5
- Генератор случайных чисел 1-6
- Бесплатный онлайн калькулятор коэффициентов
- Функционал онлайн калькулятор
- Упрощение дробей онлайн калькулятор
- Синус онлайн калькулятор
- Квадратный корень онлайн бесплатно
- Стандартное отклонение бесплатно онлайн калькулятор
- Вычитание дробей бесплатный онлайн калькулятор
- Вычитание бесплатный онлайн калькулятор
- 6 90 бесплатно онлайн калькулятор
- Тригонометрия бесплатный онлайн калькулятор
- Дисперсия бесплатный онлайн калькулятор
- Средневзвешенный бесплатный онлайн-калькулятор
И мы все еще разрабатываем больше.