Решение линейных неравенств — презентация онлайн
Похожие презентации:
Решение линейных неравенств
Решение линейных неравенств
Неравенства. Линейные неравенства. Квадратные неравенства
Решение линейных неравенств
Линейные неравенства. 8 класс
Линейные неравенства
Линейные неравенства. Квадратные неравенства
Решение линейных неравенств. 8 класс
Решение линейных неравенств
Решение неравенств с одной переменной
(Электронное пособие)
(с) Кочагин Вадим Витальевич, 2005 год
Данная работа является началом пути в
создании электронной версии учебника по
математике.
Материал данной презентации может
использоваться как на уроках объяснения
нового материала, так и на уроках
обобщающего повторения.
Выберите необходимый раздел
Простейшими среди неравенств с одной
переменной являются линейные неравенства, т.е.
неравенства вида ax<b (>b, b, b).
При решении линейных неравенств слагаемые с
известные слагаемые в другую часть. Затем
выражают неизвестную переменную, т.е. делят на
коэффициент при этой переменной ( если он не
равен нулю).
Если коэффициент равен нулю, то …(см. далее
справочный материал).
Особые случаи (коэффициент при х равен 0):
0x<0
0x 0
0x< a
(a>0)
0x< a
(a<0)
0x a
(a>0)
0x a
(a<0)
Ответ.
Решений нет
Ответ.
Ответ.
Ответ.
(- ;+ )
(- ;+ )
Ответ.
Решений нет.
(- ;+ )
Ответ.
Решений нет.
0x>0
0x 0
0x> a
(a>0)
0x> a
(a<0)
0x a
(a>0)
0x a
(a<0)
Ответ.
Решений нет
Ответ.
Ответ.
Решений нет.
Ответ.
Ответ.
Решений нет.
Ответ.
(- ;+ )
(- ;+ )
(- ;+ )
Если делим обе части неравенства на
отрицательное число, то знак неравенства
меняется на противоположный .
Например: -2х>4.
Делим на (-2). Получим: х<-2.
Если делим обе части неравенства на
положительное число, то знак неравенства
не меняется.
Например: 3х< 12.
Делим на 3. Получим: х<4.
Выберете номер задания
Задание 1. Решите неравенство 5х-3>3x-7.
Задание 2. Решите неравенство
12 11x
3 2x
2
Задание 3. Решите систему неравенств
( x 5) 2 ( x 1) 2
23x 5 22 x 13
В ответе укажите наибольшее целое решение.
Задание 1. Решите неравенство 5х-3>3x-7.
Перенесем неизвестные слагаемые в левую часть неравенства,
а известные в правую.
5х-3х>-7+3
Приведем подобные слагаемые в левой части
и упростим правую часть.
2х>-4
Выразим переменную х,
т.е. разделим обе части неравенства на 2.
х>-2
Ответ запишем в виде промежутка.
Ответ: (-2;+ )
Задание
2. Решите неравенство
3 2.x
2
Умножим обе части неравенства на 2.
12-11x>6-4x
Перенесем неизвестные слагаемые в левую часть, а
известные в правую
-11x+4х>6-12
Приведем подобные слагаемые
-7х>-6
Выразим переменную х.
Знак неравенства изменится на противоположный.x
Ответ.
6
7
6
;
7
Если делим обе части неравенства на
отрицательное число, то знак неравенства меняется
на противоположный .
Например: -2х>4. Делим на (-2). Получим: х<-2.
Если делим обе части неравенства на
положительное число, то знак неравенства не
меняется.
Например: 3х< 12. Делим на 3. Получим: х<4.
Вернуться к решению Задания 2
Задание 2. Решите неравенство
12 11x
3 2 x
2
Умножим обе части неравенства на 2.
12-11x>6-4x
Перенесем неизвестные слагаемые в левую часть, а
известные в правую
-11x+4х>6-12
Приведем подобные слагаемые
-7х>-6
Выразим переменную х. Знак неравенства изменится на противоположный.
x
Ответ.
6
7
6
;
7
•Задание 3. Решите систему неравенств
( x 5) 2 ( x 1) 2
23x 5 22 x 13
В ответе укажите наибольшее целое решение.
Чтобы решить систему неравенств, необходимо сначала решить каждое
неравенство в отдельности.
Решением первого неравенства является промежуток
-2
Решение второго неравенства промежуток
( ; 2)
13;
-13
Решением системы неравенств является пересечение промежутков
-13
-2
Наибольшим целым решением является (-3)
Ответ: -3.
13; 2
Сейчас Вам предстоит решить
различные линейные неравенства .
Если Вы укажете номер правильного
ответа, то Вам откроется часть
красивой фотографии.
лото.
Задание 1.
Решением неравенства 6x – 5 < 4x +19
является промежуток
Задание 2.
3 2x
Решением неравенства 5 x
3
является промежуток
1) ( ; 12)
1) ( ; 12)
2) ( ;12)
2) ( ;12)
3) (12; )
3) (12; )
4) ( 12; )
4) ( 12; )
Задание 3.
Задание 4.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
1) ( ; 12)
Решите неравенство
0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет
15.
Ваш выбор неверен. Подумайте еще.Вернуться к решению Задания 1Задание 2.
Решением неравенства
5 x
3 2x
3
является промежуток
1) ( ; 12)
2) ( ;12)
3) (12; )
4) ( 12; )
Задание 3.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
1) ( ; 12)
Задание 4.
Решите неравенство 0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет
17. Ваш выбор неверен. Подумайте еще.
Вернуться к решению Задания 21) ( ; 12)
Задание 3.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
Задание 4.
Решите неравенство 0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет
19. Ваш выбор неверен. Подумайте еще.
Вернуться к решению Задания 31) ( ; 12)
Задание 4.
Решите неравенство 0х> 2005
1) ( ; 12)
1) ;
2) ;0
3) 0;
4) Решений нет
21.
Ваш выбор неверен. Подумайте еще. Вернуться к решению Задания 41) ( ; 12)
1) ( ; 12)
English Русский Правила
Система линейных неравенств онлайн калькулятор. Системы линейных неравенств и выпуклые множества точек
Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.
Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств :
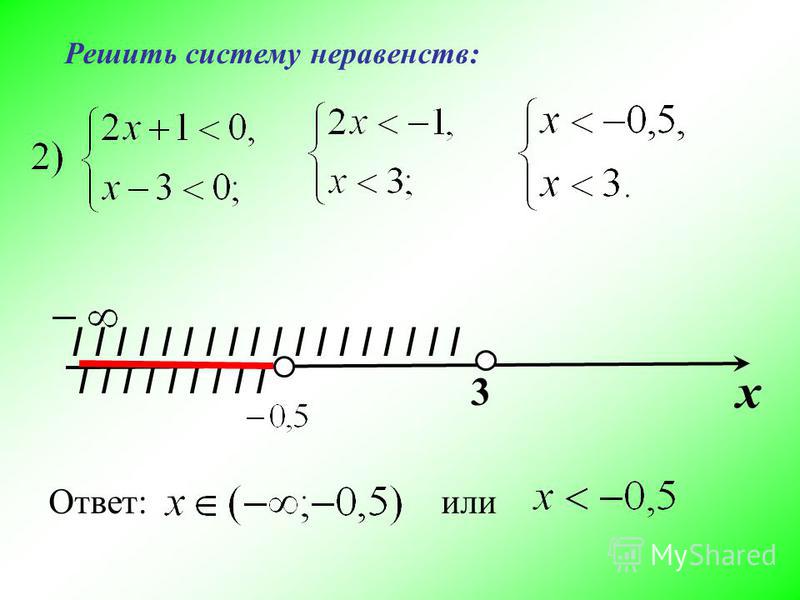
Решить систему неравенств
— означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x , при которых первое неравенств о (x > 1) становиться верным, а на нижней—величину х , которые являются решением второго неравенства (х > 4).
Сопоставив данные на числовых прямых , отметим, что решением для обоих неравенств
Пример 2.
Вычисляя первое неравенство получаем -3х x > 2, второе —х > -8, или х х , при которых реализуется первое неравенство системы , а на нижнюю числовую прямую, все те значения х , при которых реализуется второе неравенство системы.
Сопоставив данные, получаем, что оба неравенства будут реализовываться при всех значениях х , размещенных от 2 до 8. Множеств значений х обозначаем двойным неравенством 2 х
Пример 3. Найдем
Неравенство — это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств),
Неравенство является линейным при тех же условиях, что и
уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту полуплоскость, а в случае системы линейных неравенств — часть плоскости, ограниченную несколькими прямыми, требуется найти на чертеже.
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования , в которых требуется найти максимум или минимум функции.
Решение систем линейных неравенств с любым числом неизвестных
Сначала разберём линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и :
,
где — коэффициенты при переменных (некоторые числа), — свободный член (также некоторое число).
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет
бесчисленное множество решений.
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1). Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу после этого теретического экскурса.
Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :
Подставляя значение в первое уравнение, получаем
Откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:
,
следовательно, координаты точки B : .
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две части, лежащие справа и слева (выше и ниже) от этой прямой.
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств , то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение.
Начертим прямую
Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A (3; 0) , B (0; 2) . Через эти точки проведём прямую (опять рисунок 1).
Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0) :
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость.
Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений.
Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае — может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2.
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую , и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1,
тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым
в данной системе.
Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC . Это означает, что множество точек плоскости, составляющих открытый угол ABC , является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы. Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).
Полуплоскости решений, соответствующие неравенствам данной системы,
заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на
рисунке, в виде четырёхугольника ABCE .
Получили, что
многоугольник решений системы линейных неравенств с двумя переменными является
четырёхугольником ABCE .
Всё описанное выше о системах линейных неравенств с двумя неизвестными относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением неравенства с n неизвестными будет совокупность n чисел (), удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость n -мерного пространства. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.
На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств. Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.
Тема : Рацион альные неравенства и их системы
Урок: Основн ые понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства , и квадратные и рациональные.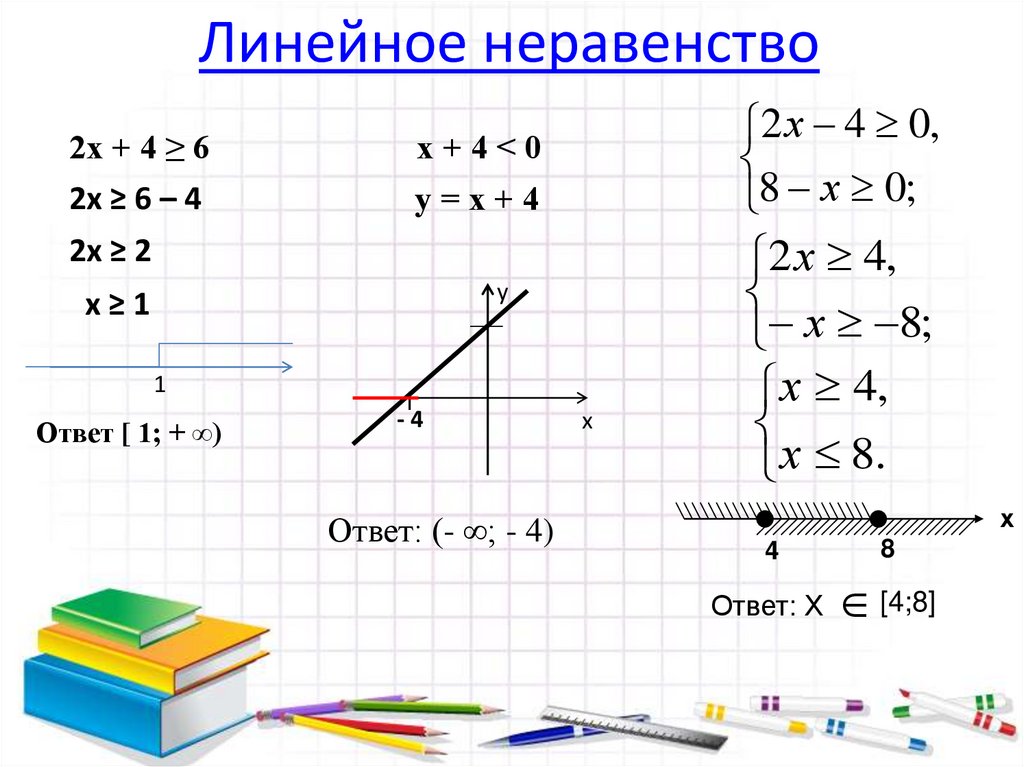
Теперь перейдем к решению систем неравенств — сначала линейных систем . Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратних корня, т.е.
Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.
Изобразим на оси ox множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение.
Такой метод изображения решения системы неравенств иногда называют методом крыш.
Решением системы является пересечение двух множеств.
Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.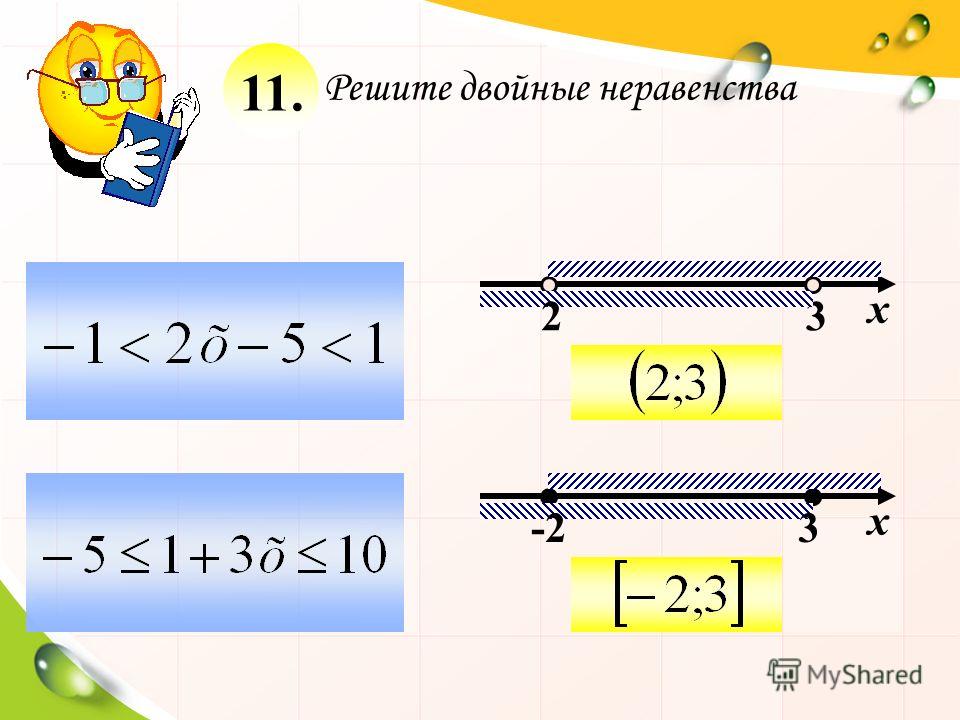
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.
Решить систему неравенств:
Ответ: (7; 10].
4. Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
Ответ: система противоречива.
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.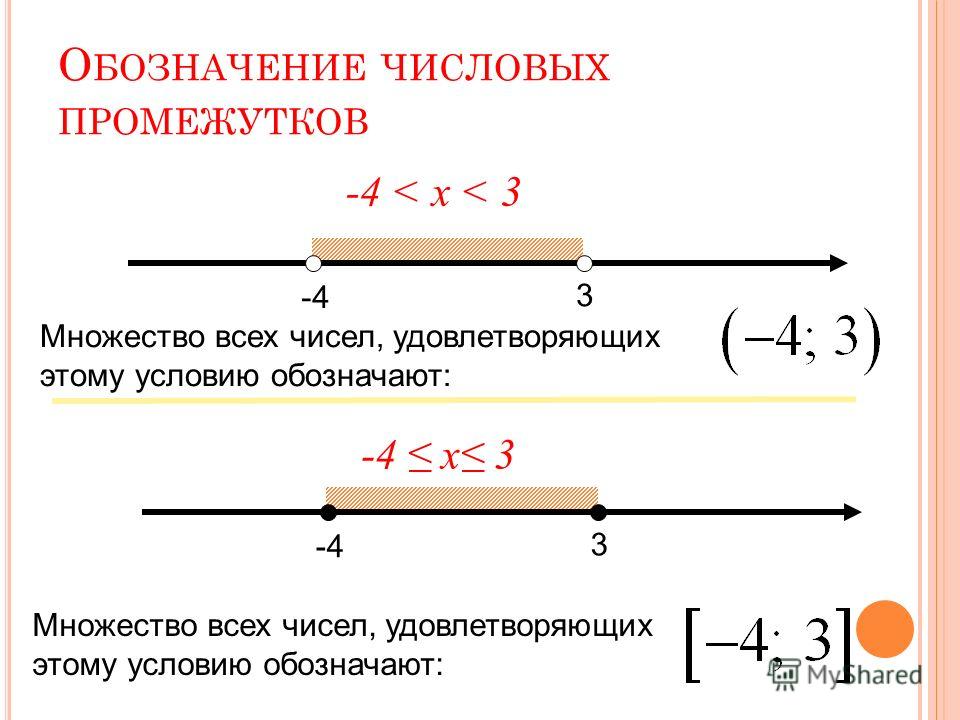
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр.
— М.: 2010.-223 с.: ил.
1. Портал Естественных Наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Центр образования «Технология обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.
В этой статье собрана начальная информация о системах неравенств. Здесь дано определение системы неравенств и определение решения системы неравенств. А также перечислены основные виды систем, с которыми наиболее часто приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по странице.
Что такое система неравенств?
Системы неравенств удобно определить аналогично тому, как мы вводили определение системы уравнений , то есть, по виду записи и смыслу, вложенному в нее.
Определение.
Система неравенств – это запись, представляющая собой некоторое число записанных друг под другом неравенств, объединенных слева фигурной скобкой, и обозначающая множество всех решений, являющихся одновременно решениями каждого неравенства системы.
Приведем пример системы неравенств. Возьмем два произвольных , например, 2·x−3>0
и 5−x≥4·x−11
, запишем их одно под другим
2·x−3>0
,
5−x≥4·x−11
и объединим знаком системы – фигурной скобкой, в результате получим систему неравенств такого вида:
Аналогично дается представление о системах неравенств в школьных учебниках. Стоит отметить, что в них определения даются более узко: для неравенств с одной переменной или с двумя переменными .
Основные виды систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не заблудиться в этом многообразии, их целесообразно рассматривать по группам, имеющим свои отличительные признаки.
Все системы неравенств можно разбить на группы по следующим критериям:
- по числу неравенств в системе;
- по числу переменных, участвующих в записи;
- по виду самих неравенств.
По числу неравенств, входящих в запись, различают системы двух, трех, четырех и т.д. неравенств. В предыдущем пункте мы привели пример системы , которая является системой двух неравенств. Покажем еще пример системы четырех неравенств .
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в этом случае по сути речь идет о самом неравенстве, а не о системе.
Если смотреть на число переменных, то имеют место системы неравенств с одной, двумя, тремя и т.д. переменными (или, как еще говорят, неизвестными). Посмотрите на последнюю систему неравенств, записанную двумя абзацами выше. Это система с тремя переменными x
, y
и z
. Обратите внимание, что ее два первых неравенства содержат не все три переменные, а лишь по одной из них. В контексте этой системы их стоит понимать как неравенства с тремя переменными вида x+0·y+0·z≥−2
и 0·x+y+0·z≤5
соответственно.
Заметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обговорить, какие виды неравенств участвуют в записи систем. В школе в основном рассматривают системы двух неравенств (реже – трех, еще реже — четырех и более) с одной или двумя переменными, причем сами неравенства обычно являются целыми неравенствами первой или второй степени (реже – более высоких степеней или дробно рациональными). Но не удивляйтесь, если в материалах по подготовке к ОГЭ столкнетесь с системами неравенств, содержащими иррациональные, логарифмические, показательные и другие неравенства. В качестве примера приведем систему неравенств , она взята из .
Что называется решением системы неравенств?
Введем еще одно определение, связанное с системами неравенств, — определение решения системы неравенств :
Определение.
Решением системы неравенств с одной переменной называется такое значение переменной, обращающее каждое из неравенств системы в верное , другими словами, являющееся решением каждого неравенства системы.
Поясним на примере. Возьмем систему двух неравенств с одной переменной . Возьмем значение переменной x , равное 8 , оно является решением нашей системы неравенств по определению, так как его подстановка в неравенства системы дает два верных числовых неравенства 8>7 и 2−3·8≤0 . Напротив, единица не является решением системы, так как при ее подстановке вместо переменной x первое неравенство обратится в неверное числовое неравенство 1>7 .
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т.д. переменными называется пара, тройка и т.д. значений этих переменных, которая одновременно является решением каждого неравенства системы, то есть, обращает каждое неравенство системы в верное числовое неравенство.
К примеру, пара значений x=1 , y=2 или в другой записи (1, 2) является решением системы неравенств с двумя переменными , так как 1+2
Системы неравенств могут не иметь решений, могут иметь конечное число решений, а могут иметь и бесконечно много решений.
Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича . Под частным решением системы неравенств понимают ее одно отдельно взятое решение. В свою очередь общее решение системы неравенств — это все ее частные решения. Однако в этих терминах есть смысл лишь тогда, когда требуется особо подчеркнуть, о каком решении идет речь, но обычно это и так понятно из контекста, поэтому намного чаще говорят просто «решение системы неравенств».
Из введенных в этой статье определений системы неравенств и ее решений следует, что решение системы неравенств представляет собой пересечение множеств решений всех неравенств этой системы.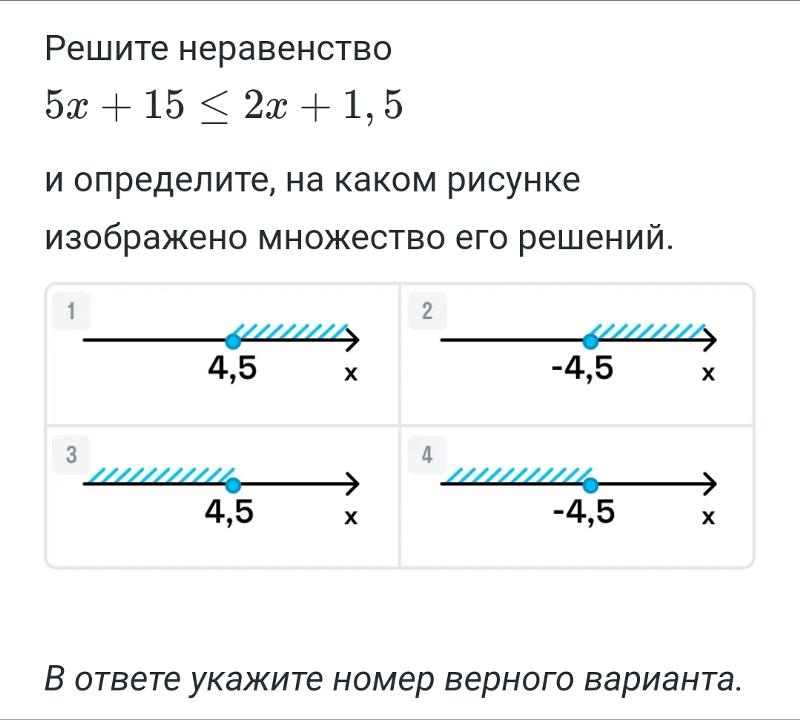
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.
: ил. ISBN 978-5-346-01027-2. - ЕГЭ -2013. Математика: типовые экзаменационные варианты: 30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство «Национальное образование», 2012. – 192 с. – (ЕГЭ-2013. ФИПИ – школе).
: ил. ISBN 978-5-346-01027-2.Рассмотрим на примерах, как решить систему линейных неравенств.
4x + 29 \end{array} \right.\]» title=»Rendered by QuickLaTeX.com»>
Чтобы решить систему, нужно каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их фигурной скобкой.
В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:
Title=»Rendered by QuickLaTeX.
com»>
Решение неравенств отмечаем на числовых прямых:
В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.
Ответ: x∈[-2;1).
В первом неравенстве избавимся от дроби. Для этого обе части умножим почленно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не изменяется.
Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разности двух выражений.
Title=»Rendered by QuickLaTeX.com»>
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком и упрощаем:
Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:
Title=»Rendered by QuickLaTeX.
com»>
Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом « «. Меньшим является 1, следовательно, система сводится к неравенству
Отмечаем его решение на числовой прямой:
Ответ: x∈(-∞;1].
Раскрываем скобки. В первом неравенстве — . Оно равно сумме кубов этих выражений.
Во втором — произведение суммы и разности двух выражений, что равно разности квадратов. Поскольку здесь перед скобками стоит знак «минус», лучше их раскрытие провести в два этапа: сначала воспользоваться формулой, а уже потом раскрывать скобки, меняя знак каждого слагаемого на противоположный.
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
Оба знака «больше». Используя правило «больше большего», сводим систему неравенств к одному неравенству.
Большее из двух чисел 5, следоветельно,
Title=»Rendered by QuickLaTeX.com»>
Решение неравенства отмечаем на числовой прямой и записываем ответ:
Ответ: x∈(5;∞).
Поскольку в алгебре системы линейных неравенств встречается не только в качестве самостоятельных заданий, но и в ходе решения разного рода уравнений, неравенств и т.д., важно вовремя усвоить эту тему.
В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений либо его решением является любое число.
Рубрика: |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
jpg»> 
Я изо всех сил пытался понять алгебру, но ничего не добился. Я попросил друзей о помощи, но свет просто не включался. Я перестал спрашивать, потому что чувствовал себя глупо. Но с вашим программным обеспечением все это было там. Пошаговые инструкции помогали мне в каждом вопросе, пока, наконец, я не увидел закономерности и не понял их. Я также мог бы учиться в уединении моего дома. 
Я действительно впечатлен удобной для пользователя настройкой и возможностями вашей системы. Спасибо еще раз! 
Наших пользователей: Ваша программа спасла мою оценку в этом семестре. Это было очень полезно. Математика не может быть проще с Algebrator. Спасибо! Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные 30.10.2010:
|
Это не только помогло мне с домашним заданием, но и научило решать проблемы. 
алгебра Ферстера и тригонометрия Companiton web