Онлайн сокращение дробей с буквами и степенями. Сокращение дробей, определение и формула
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют сокращением дроби .
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \(\frac{3}{4} \) означает три четвёртых доли единицы.
Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными .
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.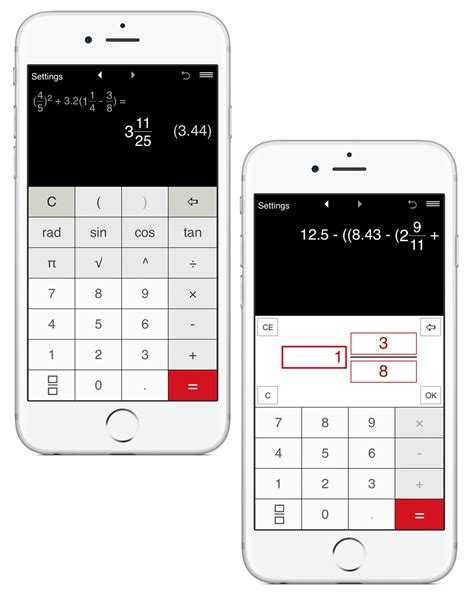
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \). Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \).
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби.
Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \). Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 .
Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.
Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3.
В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.
К этому же ответу можем прийти другим путем.
И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.
И еще один вариант решения.
В следующий раз рассмотрим примеры сокращения дробей.
Калькулятора онлайн выполняет сокращение алгебраических дробей в соответствии с правилом сокращения дробей: замена исходной дроби равной дробью, но с меньшими числителем и знаменателем, т.е. одновременное деление числителя и знаменателя дроби на их общий наибольший общий делитель (НОД). Также калькулятор выводит подробное решение, которое поможет понять последовательность выполнения сокращения.
Дано:
Решение:
Выполнение сокращения дробей
проверка возможности выполнения сокращения алгебраической дроби
1) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби
определение наибольшего общего делителя (НОД) числителя и знаменателя алгебраической дроби
2) Сокращение числителя и знаменателя дроби
сокращение числителя и знаменателя алгебраической дроби
3) Выделение целой части дроби
выделение целой части алгебраической дроби
4) Перевод алгебраической дроби в десятичную дробь
перевод алгебраической дроби в десятичную дробь
Помощь на развитие проекта сайт
Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Порядок действий при сокращении алгебраической дроби калькулятором онлайн:
- Чтобы выполнить сокращение алгебраической дроби введите в соответствующие поля значения числителя, знаменателя дроби. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
- Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
- В зависимости от задаваемой алгебраической дроби автоматически выполняется следующая последовательность действий:
- определение наибольшего общего делителя (НОД) числителя и знаменателя дроби ;
- сокращение числителя и знаменателя дроби на НОД ;
- выделение целой части дроби , если числитель итоговой дроби больше знаменателя.
- перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.
II. Для справки:
Дробь — число, состоящее из одной или нескольких частей (долей) единицы. Обыкновенная дробь (простая дробь) записывается в виде двух чисел (числитель дроби и знаменатель дроби), разделенных горизонтальной чертой (дробной чертой), обозначающей знак деления.
числитель дроби — число, стоящее над дробной чертой. Числитель показывает, сколько долей взяли у целого.
знаменатель дроби — число, стоящее под дробной чертой. Знаменатель показывает, на сколько равных долей разделено целое.
простая дробь — дробь, не имеющая целой части. Простая дробь может быть правильной или неправильной.
правильная дробь — дробь, у которой числитель меньше знаменателя, поэтому правильная дробь всегда меньше единицы. Пример правильных дроби: 8/7, 11/19, 16/17.
неправильная дробь — дробь, у которой числитель больше или равен знаменателю, поэтому неправильная дробь всегда больше единицы или равна ей.
Пример неправильных дроби: 7/6, 8/7, 13/13.
смешанная дробь — число, в состав которого входит целое число и правильная дробь, и обозначает сумму этого целого числа и правильной дроби. Любая смешанная дробь может быть преобразована в неправильную простую дробь. Пример смешанных дробей: 1¼, 2½, 4¾.
III. Примечание:
- Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
- Для сложения, вычитания, умножения и деления обыкновенных или смешанных дробей воспользуйтесь онлайн калькулятором дробей с подробным решением.
Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.
Сокращение дробей, определение и формула.
Что такое сокращение дробей? Что значит сократить дробь?
Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице.
В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно .
Формула сокращения дробей основного свойства рациональных чисел.
\(\frac{p \times n}{q \times n}=\frac{p}{q}\)
Рассмотрим пример:
Сократите дробь \(\frac{9}{15}\)
Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.
\(\frac{9}{15}=\frac{3 \times 3}{5 \times 3}=\frac{3}{5} \times \color{red} {\frac{3}{3}}=\frac{3}{5} \times 1=\frac{3}{5}\)
Ответ: после сокращения получили дробь \(\frac{3}{5}\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.
\(\frac{9}{15}=\frac{3}{5}\)
Как сокращать дроби? Сокращение дроби до несократимого вида.
Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.
Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.
Получите несократимую дробь \(\frac{48}{136}\).
Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6
\(\frac{48}{136}=\frac{\color{red} {2 \times 2 \times 2} \times 2 \times 3}{\color{red} {2 \times 2 \times 2} \times 17}=\frac{\color{red} {6} \times 2 \times 3}{\color{red} {6} \times 17}=\frac{2 \times 3}{17}=\frac{6}{17}\)
Правило сокращения дроби до несократимого вида.
- Нужно найти наибольший общий делитель для числители и знаменателя.
- Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.
Пример:
Сократите дробь \(\frac{152}{168}\).
Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6
\(\frac{152}{168}=\frac{\color{red} {6} \times 19}{\color{red} {6} \times 21}=\frac{19}{21}\)
Ответ: \(\frac{19}{21}\) несократимая дробь.
Сокращение неправильной дроби.
Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.
Рассмотрим пример:
Сократите неправильную дробь \(\frac{44}{32}\).
Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.
\(\frac{44}{32}=\frac{\color{red} {2 \times 2 } \times 11}{\color{red} {2 \times 2 } \times 2 \times 2 \times 2}=\frac{11}{2 \times 2 \times 2}=\frac{11}{8}\)
Сокращение смешанных дробей.
Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.
Рассмотрим пример:
Сократите смешанную дробь \(2\frac{30}{45}\).
Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.
\(2\frac{30}{45}=2\frac{2 \times \color{red} {5 \times 3}}{3 \times \color{red} {5 \times 3}}=2\frac{2}{3}\)
Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.
\(2\frac{30}{45}=\frac{45 \times 2 + 30}{45}=\frac{120}{45}=\frac{2 \times \color{red} {5 \times 3} \times 2 \times 2}{3 \times \color{red} {3 \times 5}}=\frac{2 \times 2 \times 2}{3}=\frac{8}{3}=2\frac{2}{3}\)
Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:
Вычислите выражение \(\frac{50+20-10}{20}\) .
Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.
\(\frac{50+\color{red} {20}-10}{\color{red} {20}}=\frac{60}{20}=\frac{3 \times 20}{20}=\frac{3}{1}=3\)
На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя.
Например, дробь \(\frac{100}{150}\).
Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50
\(\frac{100}{150}=\frac{2 \times 50}{3 \times 50}=\frac{2}{3}\)
Получили несократимую дробь \(\frac{2}{3}\).
Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac{100}{150}\) на 2.
\(\frac{100}{150}=\frac{2 \times 50}{2 \times 75}=\frac{50}{75}\)
Получили сократимую дробь \(\frac{50}{75}\).
Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac{4}{8}\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.
Пример:
Сравните две дроби \(\frac{2}{3}\) и \(\frac{8}{12}\).
Эти две дроби равны. Рассмотрим подробно дробь \(\frac{8}{12}\):
\(\frac{8}{12}=\frac{2 \times 4}{3 \times 4}=\frac{2}{3} \times \frac{4}{4}=\frac{2}{3} \times 1=\frac{2}{3}\)
Отсюда получаем, \(\frac{8}{12}=\frac{2}{3}\)
Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.
Пример:
Сократите если возможно следующие дроби: а) \(\frac{90}{65}\) б) \(\frac{27}{63}\) в) \(\frac{17}{100}\) г) \(\frac{100}{250}\)
Решение:
а) \(\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}\)
б) \(\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}\)
в) \(\frac{17}{100}\) несократимая дробь
г) \(\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}\)
Без знания того, как сократить дробь, и наличия устойчивого навыка в решении подобных примеров очень непросто изучать в школе алгебру.
Чем дальше, тем больше на базовые знания о сокращении обыкновенных дробей накладывается новой информации. Сначала появляются степени, потом множители, которые позже становятся многочленами.
Как тут не запутаться? Основательно закреплять умения в предыдущих темах и постепенно готовиться к знаниям о том, как сократить дробь, усложняющуюся год от года.
Базовые знания
Без них не удастся справиться с заданиями любого уровня. Чтобы понять, нужно уяснить два простых момента. Первый: сокращать можно только множители. Этот нюанс оказывается очень важным при появлении многочленов в числителе или знаменателе. Тогда нужно четко различать, где находится множитель, а где стоит слагаемое.
Второй момент говорит о том, что любое число можно представить в виде множителей. Причем результатом сокращения является такая дробь, числитель и знаменатель которых уже невозможно сократить.
Правила сокращения обыкновенных дробей
Для начала стоит проверить, делится ли числитель на знаменатель или наоборот.
Тогда именно на это число нужно провести сокращение. Это самый простой вариант.
Вторым является анализ внешнего вида чисел. Если оба заканчиваются на один или несколько нолей, то их можно сократить на 10, 100 или тысячу. Здесь же можно заметить, являются ли числа четными. Если да, то смело можно сокращать на два.
Третьим правилом того, как сократить дробь, становится разложение на простые множители числителя и знаменателя. В это время нужно активно использовать все знания о признаках делимости чисел. После такого разложения остается только найти все повторяющиеся, перемножить их и произвести сокращение на получившееся число.
Как быть, если в дроби стоит алгебраическое выражение?
Здесь появляются первые трудности. Потому что именно здесь появляются слагаемые, которые могут быть идентичны множителям. Их очень хочется сократить, а нельзя. До того как сократить алгебраическую дробь, ее нужно преобразовать так, чтобы она имела множители.
Для этого потребуется выполнить несколько действий.
Возможно, потребуется пройти их все, а может, уже первое даст подходящий вариант.
Проверить, не отличаются ли числитель и знаменатель или какое-либо выражение в них на знак. В этом случае необходимо просто вынести за скобки минус единицу. Так получаются одинаковые множители, которые можно сократить.
Посмотреть, можно ли вынести из многочлена за скобки общий множитель. Возможно, так получится скобка, которую также можно сократить, или это будет вынесенный одночлен.
Попробовать провести группировку одночленов с тем, чтобы потом в них вынести общий множитель. После этого может оказаться, что появятся множители, которые можно сократить, или снова повторить вынесение за скобки общих элементов.
Попытаться рассмотреть в записи формулы сокращенного умножения. С их помощью легко удастся преобразовать многочлен в множители.
Последовательность действий с дробями со степенями
Для того чтобы без проблем разобраться в вопросе о том, как сократить дробь со степенями, необходимо твердо запомнить основные действия с ними.
Первое из них связано с умножением степеней. В этом случае, если основания одинаковые, показатели необходимо сложить.
Второе — деление. Опять же у тех, которые имеют одинаковые основания, показатели потребуется вычесть. Причем вычитать нужно из того числа, которое стоит в делимом, а не наоборот.
Третье — возведение в степень степени. В этой ситуации показатели перемножаются.
Для успешного сокращения потребуется также умение приводить степени к одинаковым основаниям. То есть видеть, что четыре — это два в квадрате. Или 27 — куб трех. Потому что сократить 9 в квадрате и 3 в кубе сложно. Но если преобразовать первое выражение как (3 2) 2 , то сокращение пройдет успешно.
Приведение алгебраических дробей к общему знаменателю
Приведение алгебраических дробей к общему знаменателю выполняется по тем же правилам, что и приведение обыкновенных дробей к общему знаменателю. Следовательно, чтобы привести алгебраические дроби к общему знаменателю, нужно:
- найти общий знаменатель для данных дробей;
- найти дополнительный множитель для каждой дроби;
- умножить числитель каждой дроби на её дополнительный множитель;
- записать дроби с найденными новыми числителями и общим знаменателем.
Чтобы найти наименьший общий знаменатель для дробей, надо разложить знаменатель каждой дроби на множители и взять каждый множитель в наибольшей встречающейся степени.
Пример 1. Привести дроби к общему знаменателю:
| 2b | , | c | и | a | . |
| 3a2 | 2b | 6ab |
Решение: Разложим знаменатели дробей на множители:
3a2 = 3 · a2;
2b = 2 · b;
6ab = 2 · 3 · a · b.
Выпишем множители первого знаменателя и добавим к ним недостающие множители из второго и третьего знаменателя:
3 · a2 · 2 · b = 6a2b.
Мы нашли наименьший общий знаменатель для данных дробей. Теперь, чтобы привести дроби к общему знаменателю, нам надо найти для каждой дроби дополнительный множитель.
Для этого нужно разделить общий знаменатель на знаменатель каждой дроби:
6a2b : 3a2 = 2b;
6a2b : 2b = 3a2;
6a2b : 6ab = a.
Умножаем числитель каждой дроби на её дополнительный множитель:
2b · 2b = 4b2;
c · 3a2 = 3a2c;
a · a = a2.
Осталось записать дроби с найденными новыми числителями и их общим знаменателем:
| 4b2 | , | 3a2c | и | a2 | . |
| 6a2b | 6a2b | 6a2b |
Пример 2. Привести дроби к общему знаменателю:
| 3a | и | 4 | . |
| a — 2 | a2 — 4 |
Решение: Разложим на множители знаменатель второй дроби, используя формулу разности квадратов:
a2 — 4 = a2 — 22 = (a + 2)(a — 2).
Получившееся произведение и будет общим знаменателем для данных дробей. Значит, для приведения дробей к общему знаменателю, нам нужно только умножить числитель первой дроби на сумму чисел (a + 2).
3a · (a + 2) = 3a2 + 6a.
В результате у нас получилось:
| 3a2 + 6a | и | 4 | . |
| (a + 2)(a — 2) | (a + 2)(a — 2) |
Произведение суммы и разности чисел a и 2 можно обратно свернуть в квадрат разности для более краткой записи дробей:
| 3a2 + 6a | и | 4 | . |
| a2 — 4 | a2 — 4 |
Бесплатный онлайн-калькулятор алгебраических дробей
- Выражение
- Уравнение
- Неравенство
- Свяжитесь с нами
- Упростить
- Коэффициент 900 04
- Expand
- GCF
- LCM
- Решить
- График
- Система
- Решение
- График
- Система
- Математический решатель на вашем сайте
Наших пользователей:
Мне действительно нужен был способ получить помощь с домашним заданием, когда я не мог поговорить со своим учителем. Алгебратор действительно решил мою проблему 🙂
Брайан Клэпман, Висконсин
Один из моих студентов принес программу под названием «Алгебратор». Сначала я думал, что это будет отличный инструмент, чтобы помочь всем моим ученикам, которые боролись.
Когда я исследовал дальше, я понял, что это также помогает мне подготовить урок в два раза быстрее.
Южная Каролина, Коннектикут
Окончив среднюю школу, я был одним из лучших учеников по математике в классе. Поступление в колледж было унизительным, потому что внезапно я стал едва ли средним. Итак, мои родители помогли мне выбрать Алгебратор, и через несколько недель я снова вернулся. Ваша программа не только отлично подходит для начинающих, как мои младшие братья в старшей школе, но и помогла мне, как новому студенту колледжа!
ПК, Калифорния
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Поисковые фразы, использованные 11 января 2013 г.:
- трюки для запоминания перестановок и комбинаций
- алгебраизатор
- распечатки вопросов по математике
- макдугал литтел алгебра 2 четные ответы
- программное обеспечение для решения математических уравнений
- онлайн научный калькулятор (корень в 3 степени
- предварительная алгебра 2004 калифорнийское издание
- решатель квадратного корня 9Лист деления 0003 образец 3 класс
- калькулятор нелинейных систем уравнений клен
- перевести дроби в десятичные знаменатели 10 и 100, смешанные числа
- добавление радикальных уравнений
- изменить номер смеси на десятичный
- бесплатных печатных листа по математике для колледжа с ключом к ответу на промежуточную алгебру
- тесты математических комбинаций
- сложный рациональный
- замена алгебры
- Бумаги с вопросами о способностях CAT
- компьютеров выражение радикального
- как проверить задачу по алгебре
- Наибольший общий знаменатель
- калькулятор рациональных выражений онлайн
- ответа на алгебру Холта 1
- комбинированный метод для линейных систем
- упрощение экспоненциальных выражений
- matlab «нелинейные уравнения»
- сколько стоит мирна холт математика ответ
- бесплатных образца рабочих листов из больших квадратов
- вероятностные игры для 3-х классов
- делаем корень третьей степени на калькуляторе
- Клен квадратный 12
- как поставить корни на калькуляторе ти-83
- Приложение словаря ti 89
- может ли быть более одного ответа на квадратный корень
- как найти наклон линии на ТИ-83
- как решать задачи, связанные с алгеброй наклонов
- ой тест на базовые способности
- Рабочий лист сложения и вычитания положительных и отрицательных чисел
- ti интерактивная бесплатная пробная версия скачать
- калькулятор упрощения квадратного корня
- применение геометрической прогрессии в повседневной жизни
- 3x-6 лет
- вопрос о способностях с ответами
- найти ЖК-печать
- как найти диапазон в уравнении
- Алгебра Решатель
- алгебра 1 7. 6 рабочий лист ответы
- добавление целочисленных печатных форм
- учебник геометрии ответы
- решения сложных рациональных выражений
- умножить на 2 рабочих листа
- Упростите калькулятор рациональных выражений онлайн
- САМЫЙ ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯ СТЕПЕНЕЙ
- упростить подкоренное выражение
- как упростить корень
- программное обеспечение для обучения алгебре
- подготовка к экзамену по теории электрика, альберта, канада
- предварительные алгебраические комбинации перестановок практические задачи
- сложение и вычитание числа шесть для печати
- полиномиальный рабочий лист
- Бесплатные ответы по математике Решение задач
- Канадский математический уклон девятого класса
- учить алгебру онлайн бесплатно
- Техасский третий класс математики
- упростить показатель степени
- Холт Математика ответы
- онлайн-тест по математике KS3 (9 класс)
- пример математических стихов
- Калькулятор радикальных выражений и уравнений
- Лист размерного анализа для 7-го класса
- контрольных вопросов с часами для 5-х классов
- Программное обеспечение Linear Equations для решения стихотворного ритма
- Рабочий лист математического неравенства
- проблемы с исчислением читы
- самая сложная математическая задача в мире
- эффективно решать уравнения, упрощая
- как вычислить подкоренные выражения без калькулятора
- Флорида элементарная матричная алгебра
- бесплатный онлайн калькулятор уравнений
- Как складывать, вычитать, умножать и делить целые числа
- алгебра — функциональные машины бесплатные рабочие листы
6 рабочий лист ответы| Предыдущий | Далее |
Калькулятор дробных неравенств
Наши пользователи: Одно лишь наблюдение за тем, как мои студенты, один за другим, легко усваивают эти высшие математические концепции и действительно, по-настоящему понимают, что они делают, делает Алгебратор достойным платы за вход. Спасибо создателям программы. Контекстно-зависимая помощь по любой теме алгебры помогла мне прояснить основы математики. Очень очень полезный инструмент.. Мне нужно было пройти тест по алгебре, чтобы соответствовать требованиям для поступления в школу. Алгебратор спас меня. Спасибо! Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, используемые на 2015-04-12:
|
Кроме того, для прибыли цена чрезвычайно недорогая! 
com
коричневый