Треугольники подобны по двум углам: Признаки подобия треугольников — урок. Геометрия, 8 класс.

Три признака подобия треугольников

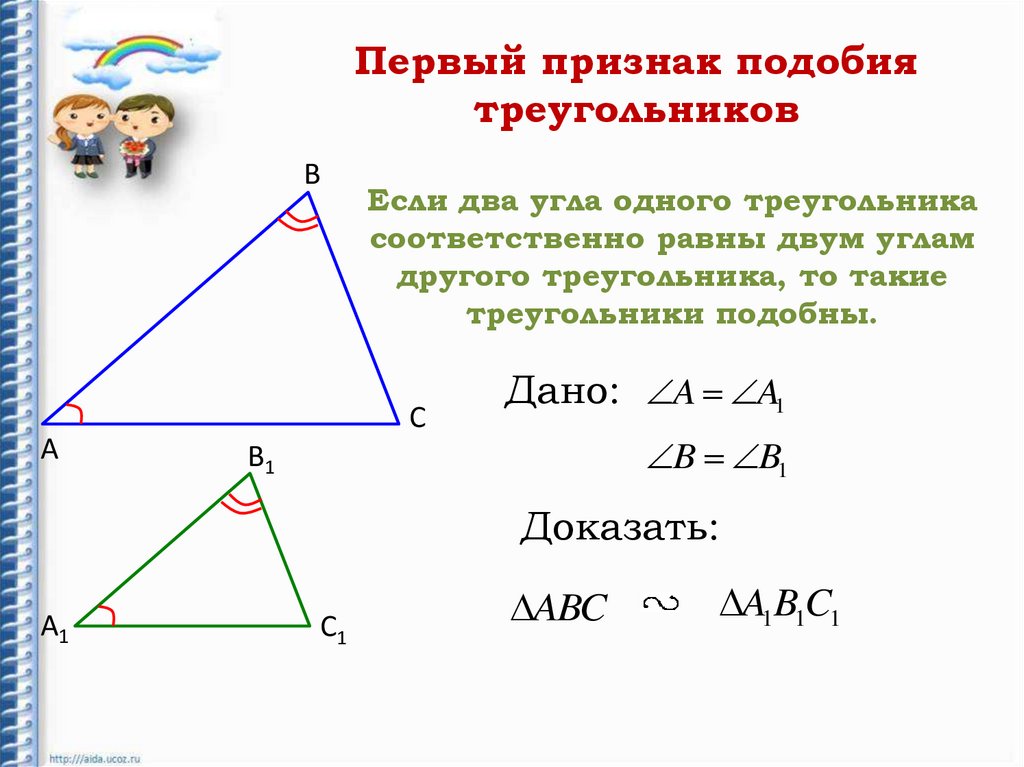
Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).

Доказать, что \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С (рис. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.

Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).

Если \(\Delta\)MBN \(\sim\) \(\Delta\)AВС, то \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABC. Эта теорема выражает 1-й признак подобия треугольников.

Следствия. 1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Теорема 2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\) и ∠В = ∠В’

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’ (рис. 368).

Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.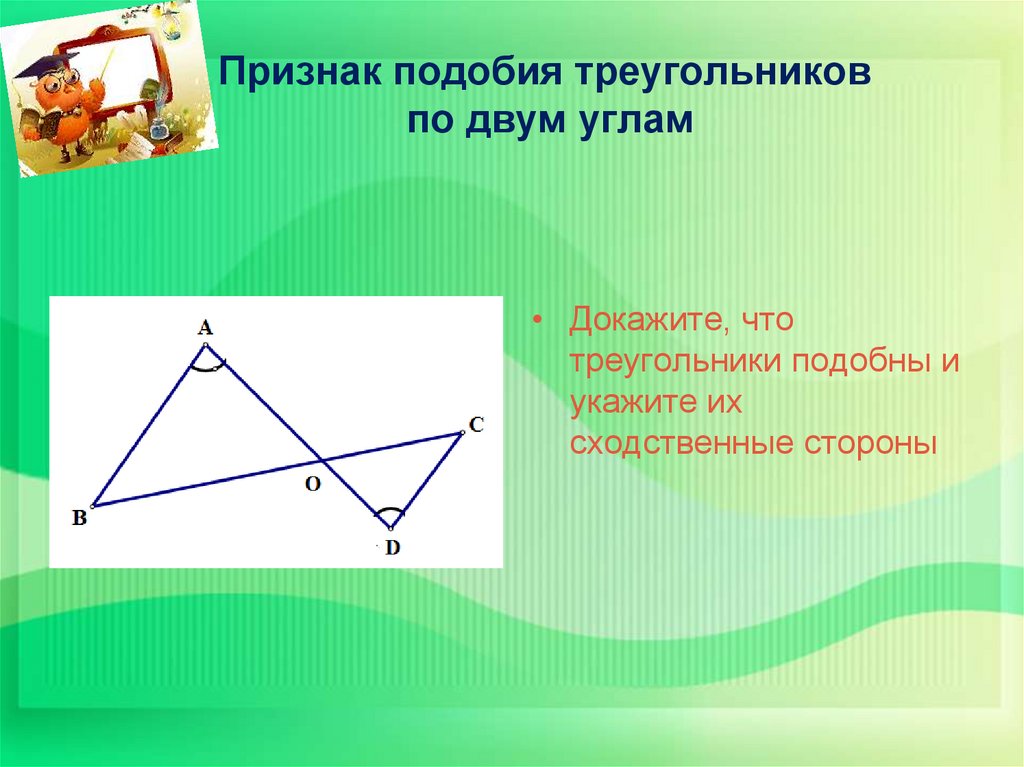

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию ^AB/_MB = ^BC/_BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,

т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.

Так как \(\Delta\)MBN \(\sim\) \(\Delta\)А’В’С’, то, следовательно, и \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABС.

Эта теорема выражает 2-й признак подобия треугольников.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

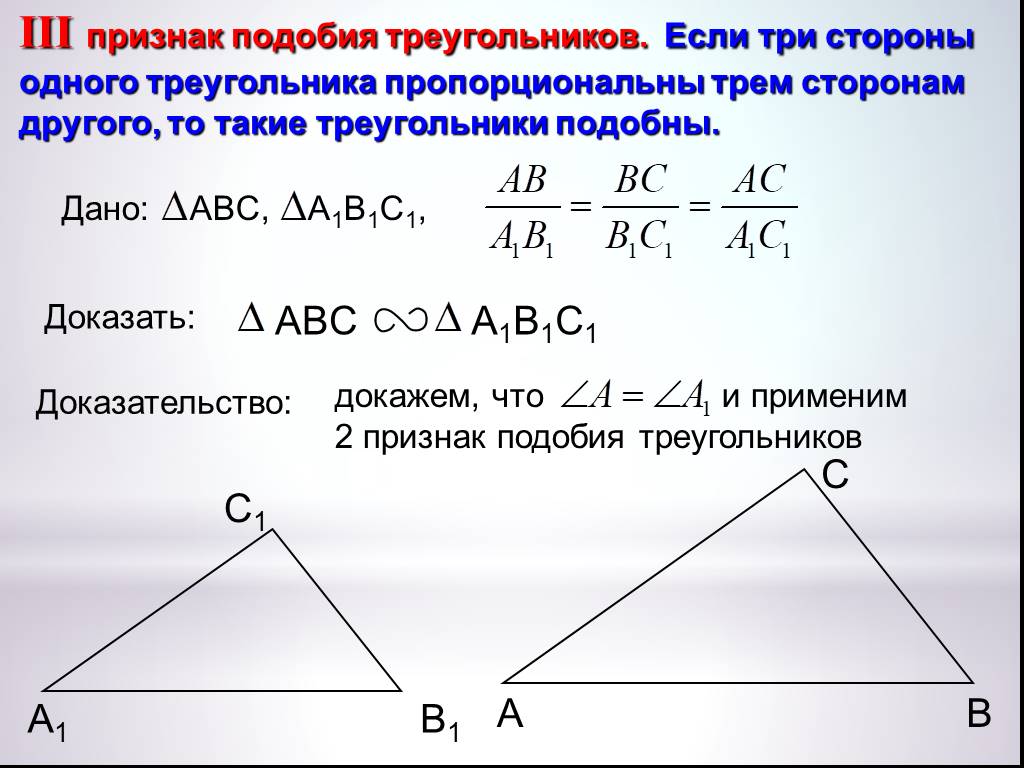
Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.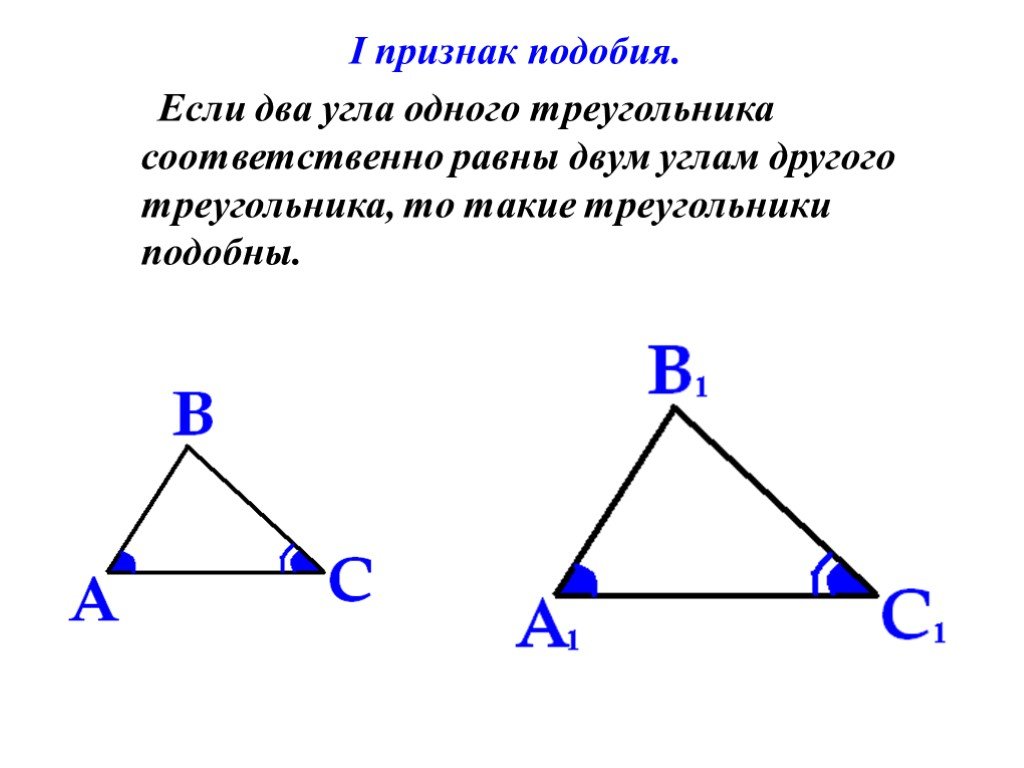

Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’} = \frac{AC}{A’C’}\) (рис. 369).

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’

Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, \(\frac{AB}{MB} = \frac{BC}{BN} = \frac{AC}{MN}\).

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. Для доказательства сравним две пропорции

\(\frac{AB}{MB} = \frac{BC}{NB}\) и \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.

Сравним ещё две пропорции: \(\frac{AB}{MB} = \frac{AC}{MN}\) и \(\frac{AB}{A’B’} = \frac{AC}{A’C’}\) . В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.

Оказалось, что три стороны \(\Delta\)BMN равны трём сторонам \(\Delta\)А’В’С’, а именно:

MB = А’В’, BN = В’С’ и MN = А’С’.

Следовательно, \(\Delta\)MBN = \(\Delta\)А’В’С’, а \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’.

Эта теорема выражает 3-й признак подобия треугольников.

Первый признак подобия треугольников 8 класс онлайн-подготовка на Ростелеком Лицей

Тема 3: Подобные треугольники

• Видео
• Тренажер
• Теория

Заметили ошибку?

 Первый признак подобия треугольников.

Докажем подобие треугольников по двум углам.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

 

 

Дано: ΔABC, ΔA₁B₁C₁,

∠A = ∠A₁, ∠B = ∠B₁,

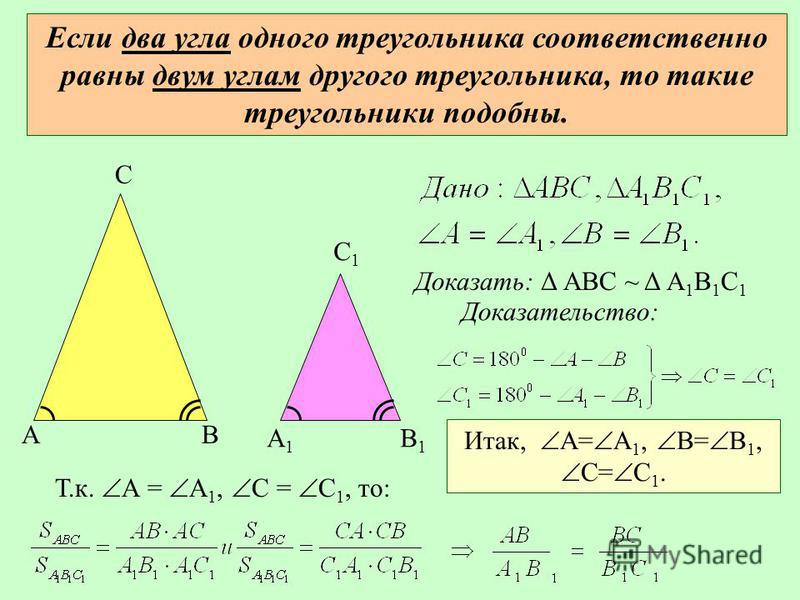
Доказать: ΔABC∼ΔA₁B₁C₁

Доказательство:

1. По теореме о сумме углов треугольника

   ∠C = 180°-(∠A+∠B), ∠C₁ = 180°-(∠A₁+∠B₁).

   Так как ∠A = ∠A_{1и ∠B = ∠B1}

   , то и ∠C = ∠C₁.

    

    

2. Пусть AB<A₁B₁. На луче A₁B₁ отложим отрезок A₁B₂ такой, что A₁B₂ = AB.

3. Через точку B₂ проведем прямую B₂C₂, параллельную прямой B₁C₁.

4. ∠A₁B₂C₂ = ∠A₁B₁C₁ (как соответственные при B₂C_{2∥ B1C1 и секущей A1B1).}

   Значит, ∠A₁B₂C₂ = ∠B.

5. В треугольниках A₁B₂C_{2и ABC:}

   ∠A₁ = ∠A,

   ∠A₁B₂C₂ = ∠B,

   A₁B₂ = AB.

   Значит, ΔA₁B₂C_{2= ΔABC (по стороне и двум прилежащим к ней углам).}

   Из равенства треугольников следует равенство соответствующих сторон: A₁C₂ = AC.

6. По теореме о пропорциональных отрезках А₁С₂:А₁С₁ = А₁В₂:А₁В₁.

   Так как A₁B_{2= AB и A1C2 = AC, то АС:А1С1 = АВ:А1В1.}

7. Аналогично доказывается, что АВ:А₁В₁ = ВС:В₁С₁.

8. Таким образом, в треугольниках ABC и A₁B₁C₁:

   ∠A = ∠A₁, ∠B = ∠B

   1, ∠C = ∠C₁,

   АВ:А₁В₁ = ВС:В₁С₁ = АС:А₁С₁.

   Значит, ΔABC∼ΔA₁B₁C₁ по определению подобных треугольников, что и требовалось доказать.

При решении задач чаще других используется именно 1-й признак подобия треугольников.

Задача 1. Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.

Решение. Пусть даны равнобедренные треугольники ABC и A₁B₁C₁ с ∠A = ∠A₁ (углы А и А₁ лежат против оснований ВС и В₁С₁ соответственно). Так как треугольник ABC равнобедренный, то ∠B = ∠C = (180−∠A):2. Так как треугольник A₁B₁

C₁ равнобедренный, то ∠B₁ = ∠C₁ = (180−A₁):2 = (180−∠A):2 = ∠B = ∠C.

То есть ∠B = ∠B₁, ∠C = ∠C₁. По первому признаку подобия получаем, что треугольники ABC и A₁B₁C₁ подобны.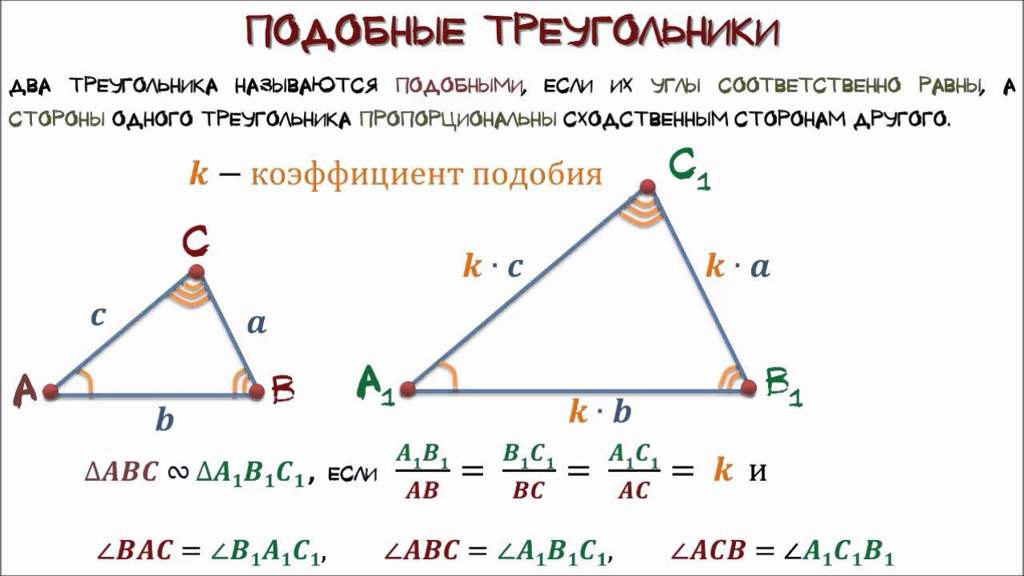

Задача 2.

 

 

Дано:

∠А = ∠В

СО:DO = 7:2

AC = 21 см

Найти: ВD

Решение: рассмотрим ∆АОС и ∆ВОD.

Так как ∠А = ∠В (по условию задачи), ∠АОС = ∠ВОD (как вертикальные углы), то по первому признаку подобия треугольников ∆АОС ~ ∆ВОD.

Следовательно, сходственные стороны треугольников пропорциональны:

АО:ВО = АС:BD = CO:DO

Подставив данные, получим 21:BD = 7:2

Ответ: BD = 6см.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Подобные треугольники. Как доказать, определить и теоремы (Видео) Пол Маццола

Подобные треугольники (определение, доказательство, & теоремы)

Сходство в математике не означает то же самое, что и сходство в повседневной жизни. Подобные треугольники — это треугольники с одинаковой формой, но разными размерами сторон.

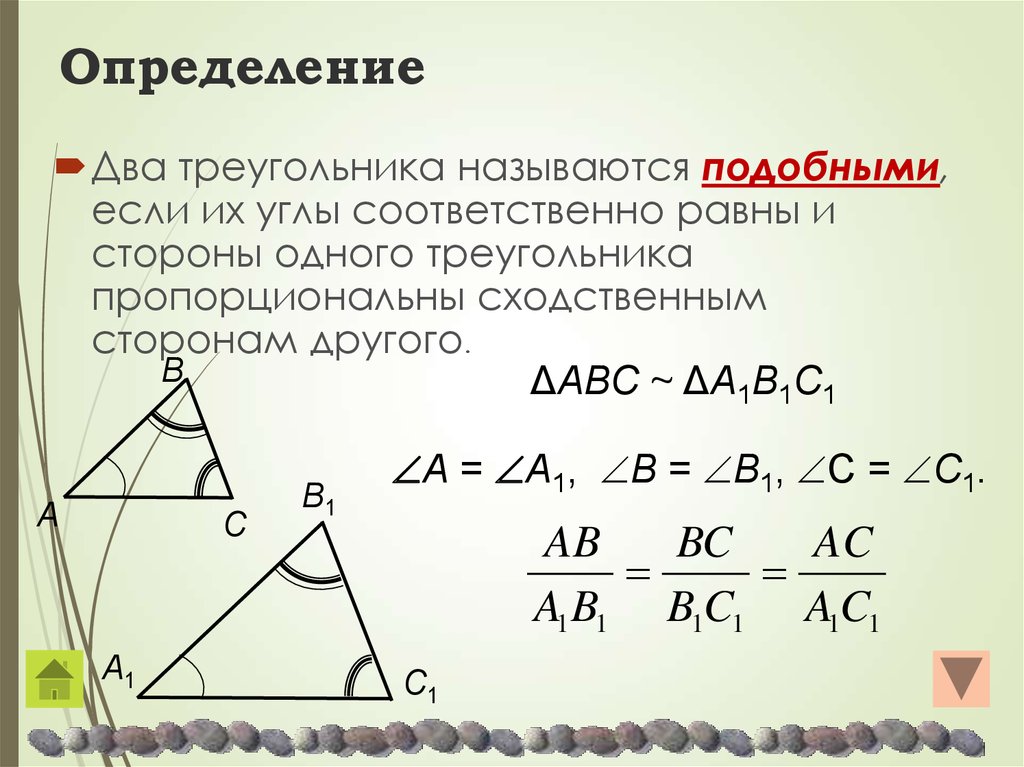
Определение подобных треугольников

Мятное мороженое с шоколадной крошкой и мороженое с шоколадной крошкой похожи, но не одно и то же. Это повседневное использование слова «подобный», но не так, как мы используем его в математике.

В геометрии две фигуры похожи  если они имеют одинаковую форму, но разные размеры. У вас может быть квадрат со сторонами 21 см и квадрат со сторонами 14 см ; они были бы похожи. Равносторонний треугольник со сторонами 21 см и квадрат со сторонами 14 см не будут похожи, потому что они разной формы.

Подобные треугольники  легко определить, поскольку к треугольникам можно применить три теоремы. Эти три теоремы, известные как Угол-Угол (AA) , Сторона-Угол-Сторона (SAS) и Сторона-Сторона-Сторона (SSS) , являются надежными методами определения сходства в треугольниках.

1. Угол-угол (AA)

2. Сторона-угол-бок (SAS)

3. Сторона-сторона-сторона (SSS)

Соответствующие углы

В геометрии соответствие  означает, что конкретная часть одного многоугольника точно относится к аналогично расположенной части другого. Даже если два треугольника ориентированы по-разному, если вы можете повернуть их, чтобы сориентировать одинаково, и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.

Три теоремы подобия треугольников зависят от соответствующих частей. Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом другого треугольника.

Подобные треугольники Соответствующие углы

Пропорция

Подобие связано с пропорцией. Треугольники легко оценить по пропорциональным изменениям, которые делают их похожими. Их сравнительные стороны пропорциональны друг другу; их соответствующие углы равны.

Вы можете установить соотношения для сравнения длин сторон двух треугольников. Если отношения конгруэнтны, соответствующие стороны подобны друг другу.

Угол в комплекте

включенный угол  относится к углу между двумя парами соответствующих сторон. Вы не можете сравнить две стороны двух треугольников, а затем перепрыгнуть на угол, который не находится между этими двумя сторонами.

Доказательство подобия треугольников

Вот два конгруэнтных треугольника. Чтобы облегчить вам жизнь, мы сделали их равносторонними треугольниками.

Доказательство похожих треугольников

△FOX  сравнивается с △HEN . Обратите внимание, что ∠O на △FOX соответствует ∠E  на  △HEN . Оба ∠O и ∠E представляют собой включенные углы между сторонами FO и OX на △FOX , и стороны HE и EN на △HEN .

Сторона  FO  соответствует стороне  HE ; сторона OX равна стороне EN , а ∠O и ∠E являются вложенными конгруэнтными углами.

Два равносторонних треугольника одинаковы, за исключением букв. Они одного размера, поэтому их 9.0023 одинаковые треугольники . Если бы они оба были равносторонними треугольниками, но сторона EN была вдвое длиннее стороны HE , то они были бы подобными треугольниками .

Теоремы подобия треугольников

Теоремы подобия треугольников

Теорема об угле-угле (AA)

Угол-угол (AA) говорит, что два треугольника подобны, если они имеют две пары соответствующих углов, которые конгруэнтны. Два треугольника могут быть на 90 099 больше, чем на 90 100, чем похожи; они могут быть идентичными. Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.

Пробуем угол-угол

Вот два разносторонних треугольника  △JAM  и  △OUT . Мы уже отметили два внутренних угла каждого треугольника с помощью геометрического обозначения конгруэнтности: маленьких косых черт.

Одинарная косая черта для внутреннего ∠A и такая же одиночная косая черта для внутреннего ∠U  означают, что они совпадают. Обратите внимание, что ∠M соответствует ∠T , потому что у каждого из них есть две косые черты.

Поскольку ∠A сравнимо с ∠U , а ∠M сравнимо с ∠T , теперь у нас есть две пары конгруэнтных углов, поэтому AA Теорема говорит, что два треугольника подобны.

Подобие треугольника. Теорема AA (угол-угол)

Хитрости мастерства

Следите за хитростями из учебников, онлайн-задач и учителей математики. Иногда треугольники не ориентированы одинаково, когда вы смотрите на них. Возможно, вам придется повернуть один треугольник, чтобы увидеть, сможете ли вы найти две пары соответствующих углов.

Еще одна задача: на одном треугольнике измерены и определены два угла, а на другом измерены и определены два разных угла.

Поскольку каждый треугольник имеет только три внутренних угла, каждый из идентифицированных углов должен быть конгруэнтным. Вычитая измеренные, идентифицированные углы каждого треугольника из 180°, вы можете узнать меру недостающего угла. Затем вы можете сравнить любые два соответствующих угла на конгруэнтность.

Теорема сторона-угол-сторона (SAS)

Вторая теорема требует точного порядка: сторона, затем прилежащий угол, затем следующая сторона. Теорема Сторона-Угол-Сторона (SAS) утверждает, что если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, а их соответствующие углы равны, то два треугольника подобны.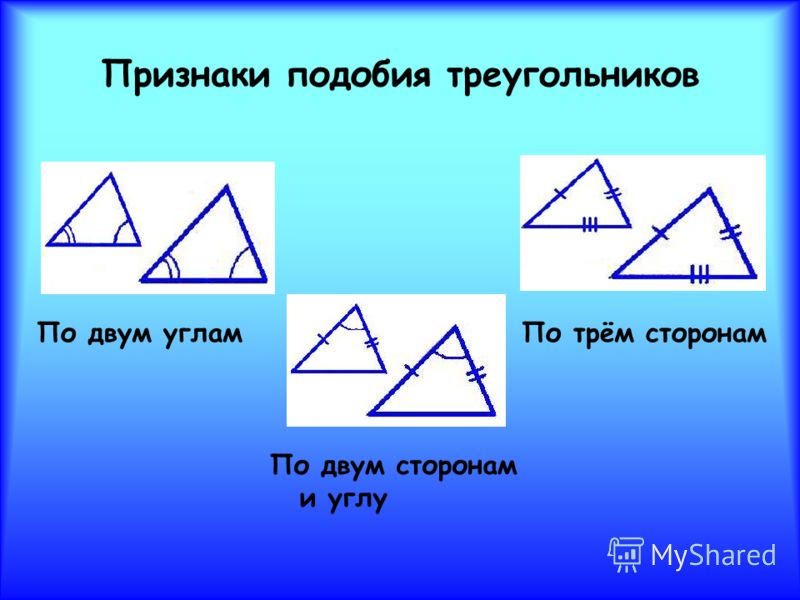

Пробуем сторона-угол-сторона

Вот два треугольника, расположенных рядом и ориентированных одинаково. △RAP  и  △EMO  идентифицированы стороны размером 37 дюймов на △RAP и 111 дюймов на △EMO , а также стороны 17 на △RAP и 51 дюйм на △EMO . Обратите внимание, что угол между идентифицированными и измеренными сторонами в обоих треугольниках одинаков:  47° .

Подобие треугольника — теорема SAS (сторона, угол, сторона)

Является ли отношение 37111\frac{37}{111}11137​ таким же, как отношение 1751\frac{17}{51}5117​? Да; два соотношения пропорциональны, поскольку каждое из них упрощается до 13\frac{1}{3}31​. При одинаковом углу между ними эти два треугольника подобны.

Теорема Side-Side-Side (SSS)

Последняя теорема  Side-Side-Side, или SSS . Эта теорема утверждает, что если два треугольника имеют пропорциональные стороны, то они подобны. Это может показаться большим скачком, который игнорирует их углы, но подумайте об этом: единственный способ построить треугольник со сторонами, пропорциональными сторонам другого треугольника, — это скопировать углы.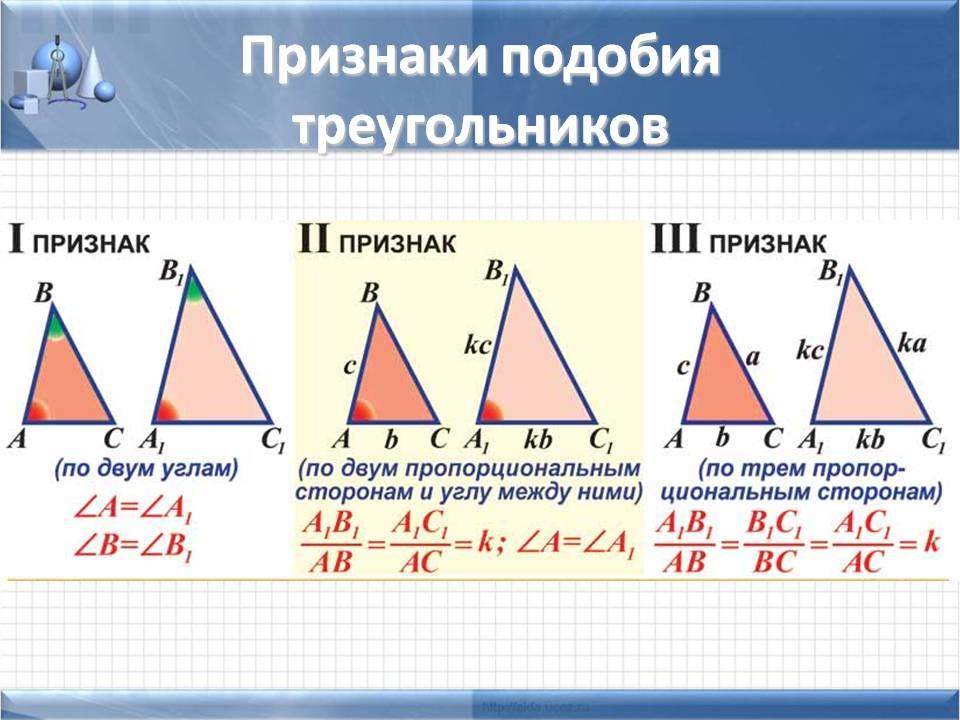

Пробуем бок-бок-бок

Вот два треугольника: △FLO и △HIT . Обратите внимание, что мы не определили внутренние углы. Стороны △FLO  измерить 15 , 20 и 25 см в длину. Стороны △HIT имеют длину 30 , 40 и 50 см .

Сходство треугольников — Теорема SSS (Side Side Side)

Вам необходимо установить отношения соответствующих сторон и оценить их:

Все они представляют собой одно и то же отношение, если упростить. Все они 12\frac{1}{2}21​. Таким образом, даже не зная внутренних углов, мы знаем, что эти два треугольника подобны, потому что их стороны пропорциональны друг другу.

Итоги урока

Теперь, когда вы изучили этот урок, вы можете определять и идентифицировать подобные фигуры, а также можете описать требования, чтобы треугольники были подобными (у них должны быть либо две конгруэнтные пары соответствующих углов, либо два пропорциональных соответствующих угла).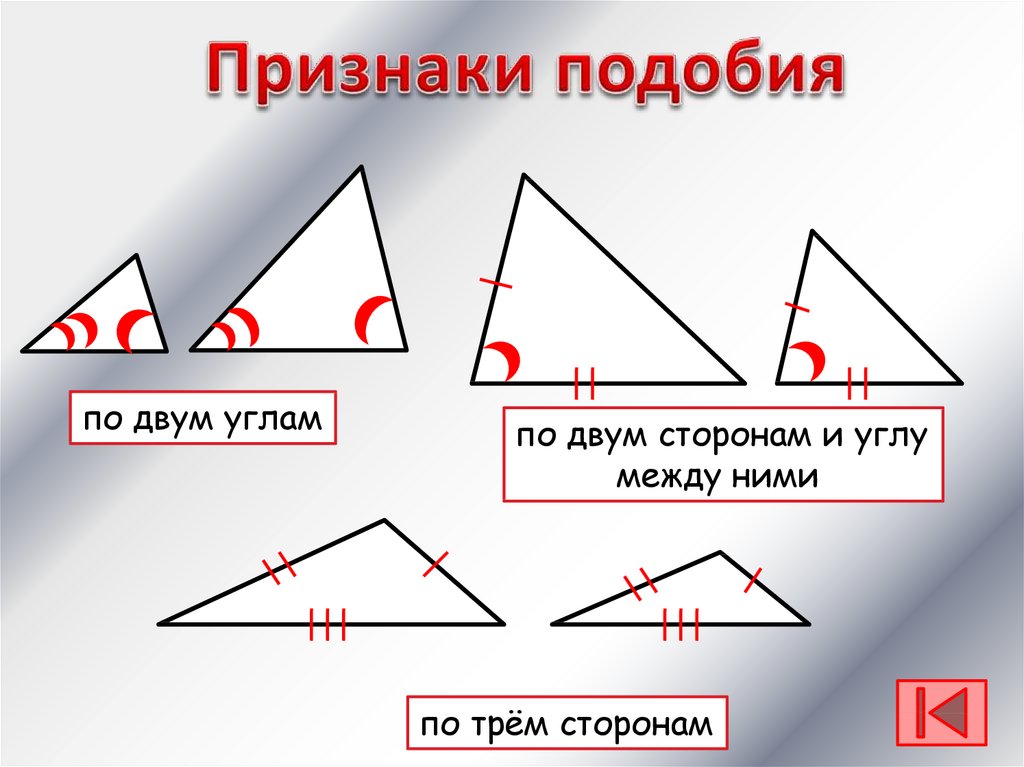 стороны с включенным соответствующим углом конгруэнтны или все соответствующие стороны пропорциональны).

Вы также можете применить три теоремы подобия треугольников, известные как угол-угол (AA), сторона-угол-сторона (SAS) или сторона-сторона-сторона (SSS), чтобы определить, подобны ли два треугольника.

Теоремы для доказательства подобия треугольников — Криста Кинг Математика

Подобные фигуры имеют одинаковую форму, но могут быть разных размеров

В этом уроке мы рассмотрим, как доказать, что треугольники подобны друг другу.

В математике слово «подобие» имеет очень конкретное значение.

Вне математики, когда мы говорим, что две вещи похожи, мы просто имеем в виду, что они в целом похожи друг на друга.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Но в математике сказать, что две фигуры похожи, означает, что они имеют одинаковую форму, но разные размеры. Вот примеры подобных квадратов, подобных пятиугольников и подобных треугольников:

Подобные треугольники

Подобные треугольники имеют одинаковую форму, но разные размеры. Помните, что если два треугольника имеют одинаковую форму и одинаковый размер, то они идентичны, и мы говорим, что они «конгруэнтны».

В паре  подобных треугольников все три соответствующие пары углов конгруэнтны, а соответствующие пары сторон пропорциональны. Символом подобия является ???\sim???, поэтому, если мы хотим сказать, что треугольники ???A??? и ???Б??? похожи друг на друга, то мы можем записать это как ???A\sim B???.

Треугольники ниже подобны, потому что соответствующие внутренние углы конгруэнтны, а длины сторон пропорциональны следующим образом:

???\frac{a}{t}=\frac{b}{u}=\frac {резюме}???

Мы рассмотрим три теоремы, позволяющие доказать, что треугольники подобны.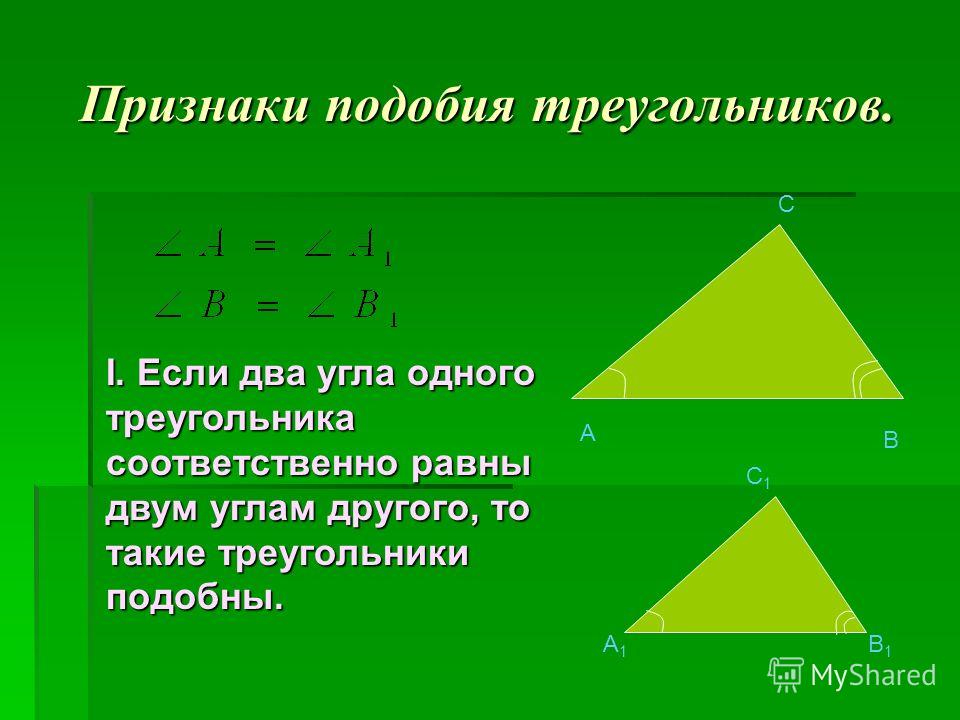 \circ???.

Сторона Сторона Сторона (SSS)

Если пара треугольников имеет три пропорциональные соответствующие стороны, то мы можем доказать, что треугольники подобны. Причина в том, что если все соответствующие длины сторон пропорциональны, то это заставит соответствующие меры внутренних углов быть конгруэнтными, что означает, что треугольники будут подобны.

???\frac{a}{d}=\frac{b}{e}=\frac{c}{f}???

Side Angle Side (SAS)

Если пара треугольников имеет одну пару соответствующих конгруэнтных углов, зажатую между двумя парами пропорциональных сторон, то мы можем доказать, что треугольники подобны.

???\frac{a}{d}=\frac{b}{e}???

Теоремы для доказательства подобия двух треугольников

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.

\circ???. Итак, у нас есть пара конгруэнтных углов, и нам нужно посмотреть, есть ли у нас пропорциональные длины сторон.

???\frac{\overline{ZY}}{\overline{AC}}=\frac{18}{3}=6???

???\frac{\overline{ZX}}{\overline{AB}}=\frac{54}{9}=6???

У нас такое же соотношение между соответствующими длинами сторон.

Собрав все это вместе, мы можем сказать, что треугольники подобны по стороне, углу, стороне (SAS). Когда мы сопоставляем соответствующие части, выражение подобия будет ???\треугольник ABC\sim \треугольник ZXY???.

В паре подобных треугольников 9\ круг???. У нас также есть пара вертикальных углов ???Y???, и помните, что вертикальные углы конгруэнтны друг другу.

Сложив все это вместе, мы можем сказать, что треугольники подобны по углу угла (АА). Когда мы сопоставляем соответствующие части, выражение подобия будет ???\треугольник WXY\sim \треугольник VZY???.