Калькулятор онлайн сокращение дробей со степенями: Онлайн калькулятор для сокращения дробей

Сокращение дробей. Что значит сократить дробь? Выражение со степенью

Основано на их основном свойстве: если числитель и знаменатель дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Сокращать можно только множители!

Члены многочленов сокращать нельзя!

Чтобы сократить алгебраическую дробь, многочлены, стоящие в числителе и знаменателе, нужно предварительно разложить на множители.

Рассмотрим примеры сокращения дробей.

В числителе и знаменателе дроби стоят одночлены. Они представляют собой произведение (чисел, переменных и их степеней), множители сокращать можем.

Числа сокращаем на их наибольший общий делитель, то есть на наибольшее число, на которое делится каждое из данных чисел. Для 24 и 36 это — 12. После сокращения от 24 остается 2, от 36 — 3.

Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а показатели вычитаем.

a² и a⁷ сокращаем на a². При этом в числителе от a² остается единица (1 пишем только в том случае, когда кроме нее после сокращения других множителей не осталось. От 24 осталась 2, поэтому 1, оставшуюся от a², не пишем). От a⁷ после сокращения остается a⁵.

b и b сокращаем на b, полученные в результате единицы не пишем.

c³º и с⁵ сокращаем на с⁵. От c³º остается c²⁵, от с⁵ — единица (ее не пишем). Таким образом,

Числитель и знаменатель данной алгебраической дроби — многочлены. Сокращать члены многочленов нельзя! (нельзя сократить, к примеру, 8x² и 2x!). Чтобы сократить эту дробь, надо . В числителе есть общий множитель 4x. Выносим его за скобки:

И в числителе, и в знаменателе есть одинаковый множитель (2x-3). Сокращаем дробь на этот множитель. В числителе получили 4x, в знаменателе — 1. По 1 свойству алгебраических дробей, дробь равна 4x.

Сокращать можно только множители (сократить данную дробь на 25x² нельзя!). Поэтому многочлены, стоящие в числителе и знаменателе дроби, нужно разложить на множители.

В числителе — полный квадрат суммы, в знаменателе — разность квадратов. После разложения по формулам сокращенного умножения получаем:

Сокращаем дробь на (5x+1) (для этого в числителе зачеркнем двойку в показатель степени, от (5x+1)² при этом останется (5x+1)):

В числителе есть общий множитель 2, вынесем его за скобки. В знаменателе — формула разности кубов:

В результате разложения в числителе и знаменателе получили одинаковый множитель (9+3a+a²). Сокращаем дробь на него:

Многочлен в числителе состоит из 4 слагаемых. первое слагаемое со вторым, третье — с четвертым и выносим из первых скобок общий множитель x². Знаменатель раскладываем по формуле суммы кубов:

В числителе вынесем за скобки общий множитель (x+2):

Сокращаем дробь на (x+2):

Калькулятора онлайн выполняет сокращение алгебраических дробей в соответствии с правилом сокращения дробей: замена исходной дроби равной дробью, но с меньшими числителем и знаменателем, т. е. одновременное деление числителя и знаменателя дроби на их общий наибольший общий делитель (НОД). Также калькулятор выводит подробное решение, которое поможет понять последовательность выполнения сокращения.

Дано:

Решение:

Выполнение сокращения дробей

проверка возможности выполнения сокращения алгебраической дроби

1) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби

определение наибольшего общего делителя (НОД) числителя и знаменателя алгебраической дроби

2) Сокращение числителя и знаменателя дроби

сокращение числителя и знаменателя алгебраической дроби

3) Выделение целой части дроби

выделение целой части алгебраической дроби

4) Перевод алгебраической дроби в десятичную дробь

перевод алгебраической дроби в десятичную дробь

Помощь на развитие проекта сайт

Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при сокращении алгебраической дроби калькулятором онлайн:

1. Чтобы выполнить сокращение алгебраической дроби введите в соответствующие поля значения числителя, знаменателя дроби. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
2. Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
3. В зависимости от задаваемой алгебраической дроби автоматически выполняется следующая последовательность действий:

• определение наибольшего общего делителя (НОД) числителя и знаменателя дроби ;
• сокращение числителя и знаменателя дроби на НОД ;
• выделение целой части дроби , если числитель итоговой дроби больше знаменателя.
• перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.

В результате сокращения может получиться неправильная дробь. В этом случае у итоговой неправильной дроби будет выделена целая часть и итоговая дробь будет переведена в правильную дробь.

II. Для справки:

Дробь — число, состоящее из одной или нескольких частей (долей) единицы. Обыкновенная дробь (простая дробь) записывается в виде двух чисел (числитель дроби и знаменатель дроби), разделенных горизонтальной чертой (дробной чертой), обозначающей знак деления. числитель дроби — число, стоящее над дробной чертой. Числитель показывает, сколько долей взяли у целого. знаменатель дроби — число, стоящее под дробной чертой. Знаменатель показывает, на сколько равных долей разделено целое. простая дробь — дробь, не имеющая целой части. Простая дробь может быть правильной или неправильной. правильная дробь — дробь, у которой числитель меньше знаменателя, поэтому правильная дробь всегда меньше единицы. Пример правильных дроби: 8/7, 11/19, 16/17. неправильная дробь — дробь, у которой числитель больше или равен знаменателю, поэтому неправильная дробь всегда больше единицы или равна ей. Пример неправильных дроби: 7/6, 8/7, 13/13. смешанная дробь — число, в состав которого входит целое число и правильная дробь, и обозначает сумму этого целого числа и правильной дроби. Любая смешанная дробь может быть преобразована в неправильную простую дробь. Пример смешанных дробей: 1¼, 2½, 4¾.

III. Примечание:

1. Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
2. Для сложения, вычитания, умножения и деления обыкновенных или смешанных дробей воспользуйтесь онлайн калькулятором дробей с подробным решением.

Деление и числителя и знаменателя дроби на их общий делитель , отличный от единицы, называют сокращением дроби .

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.

Это число является наибольшим общим делителем числителя и знаменателя данной дроби.

Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.

Учащийся вправе выбрать любую форму записи.

Примеры. Упростить дроби.

Сократим дробь на 3 (делим числитель на 3;

делим знаменатель на 3).

Сокращаем дробь на 7.

Выполняем указанные действия в числителе и знаменателе дроби.

Полученную дробь сокращаем на 5.

Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.

Разложим числитель и знаменатель этой дроби на простые множители.

Получаем: 756=2²·3³·7 и 1176=2³·3·7² .

Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5) .

Это произведение общих множителей, взятых с наименьшими показателями.

НОД(756; 1176)=2²·3·7 .

Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14 .

А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14 .

И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2 . Сокращаем дробь на 2

. Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2 . Сокращаем дробь на 2 . Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на 3 .

(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3 . Сокращаем дробь на 3 . Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7 . Сокращаем дробь на 7 и получаем несократимую дробь 9/14 .

На этом уроке мы изучим основное свойство дроби, узнаем, какие дроби являются равными друг другу. Научимся сокращать дроби, определять, является ли дробь сократимой или нет, попрактикуемся в сокращении дробей и узнаем, когда стоит использовать сокращение, а когда нет.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Основное свойство дроби

Представьте себе такую ситуацию.

За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по \(\mathbf{\frac{5}{3}}\) яблока.

А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по \(\mathbf{\frac{5}{3}}\)

При этом всего 10 яблок и 6 человек. Каждому по \(\mathbf{\frac{10}{6}}\)

Но это одно и то же.

\(\mathbf{\frac{5}{3} = \frac{10}{6}}\)

Эти дроби эквивалентны.

Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.

В математике это формулируется так:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной .

Это свойство иногда называют «основным свойством дроби ».

$$\mathbf{\frac{a}{b} = \frac{a\cdot c}{b\cdot c} = \frac{a:d}{b:d}}$$

Например, Путь от города до деревни- 14 км.

Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя шесть столбиков, шесть километров, мы понимаем, что прошли \(\mathbf{\frac{6}{14}}\) пути.

Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 40 штук на каждый километр. То есть всего 560 на всем пути. Шесть километров- \(\mathbf{6\cdot40 = 240}\) столбов. То есть мы прошли 240 из 560 столбов- \(\mathbf{\frac{240}{560}}\)

\(\mathbf{\frac{6}{14} = \frac{240}{560}}\)

Пример 1

Отметьте точку с координатами (5; 7 ) на координатной плоскости XО Y . Она будет соответствовать дроби \(\mathbf{\frac{5}{7}}\)

Соедини начало координат с получившейся точкой. Построй другую точку, которая имеет координаты в два раза больших предыдущих. Какую дробь ты получил? Будут ли они равны?

Решение

Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь \(\mathbf{\frac{5}{7}}\), отметим точку с координатой 5 по оси Y и 7 по оси X . Проведем прямую из начала координат через нашу точку.

На этой же прямой будет лежать и точка, соответствующая дроби \(\mathbf{\frac{10}{14}}\)

Они являются эквивалентными: \(\mathbf{\frac{5}{7} = \frac{10}{14}}\)

Работая с дробями, многие ученики допускают одни и те же ошибки. А все потому, что они забывают элементарные правила арифметики . Сегодня мы повторим эти правила на конкретных задачах, которые я даю на своих занятиях.

Вот задача, которую я предлагаю каждому, кто готовится к ЕГЭ по математике:

Задача. Морская свинья ест 150 грамм корма в день. Но она выросла и стала есть на 20% больше. Сколько грамм корма теперь ест свинья?

Неправильное решение. Это задача на проценты, которая сводится к уравнению:

Многие (очень многие) сокращают число 100 в числителе и знаменателе дроби:

Вот такую ошибку допустила моя ученица прямо в день написания этой статьи.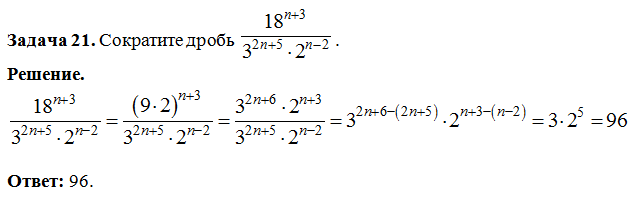 Красным отмечены числа, которые были сокращены.

Излишне говорить, что ответ получился неправильный. Судите сами: свинья ела 150 грамм, а стала есть 3150 грамм. Увеличение не на 20%, а в 21 раз, т.е. на 2000%.

Чтобы не допускать подобных недоразумений, помните основное правило:

Сокращать можно только множители. Слагаемые сокращать нельзя!

Таким образом, правильное решение предыдущей задачи выглядит так:

Красным отмечены цифры, которые сокращаются в числителе и знаменателе. Как видите, в числителе стоит произведение, знаменателе — обыкновенное число. Поэтому сокращение вполне законно.

Работа с пропорциями

Еще одно проблемное место — пропорции . Особенно когда переменная стоит с обеих сторон. Например:

Задача. Решите уравнение:

Неправильное решение — у некоторых буквально руки чешутся сократить все на m :

Сокращаемые переменные показаны красным. Получается выражение 1/4 = 1/5 — полный бред, эти числа никогда не равны.

А теперь — правильное решение. По существу, это обыкновенное линейное уравнение . Решается либо переносом всех элементов в одну сторону, либо по основному свойству пропорции:

Многие читатели возразят: «Где ошибка в первом решении?» Что ж, давайте разбираться. Вспомним правило работы с уравнениями:

Любое уравнение можно делить и умножать на любое число, отличное от нуля .

Просекли фишку? Можно делить только на числа, отличные от нуля . В частности, можно делить на переменную m , только если m != 0. А что делать, если все-таки m = 0? Подставим и проверим:

Получили верное числовое равенство, т.е. m = 0 — корень уравнения. Для остальных m != 0 получаем выражение вида 1/4 = 1/5, что, естественно, неверно. Таким образом, не существует корней, отличных от нуля.

Выводы: собираем все вместе

Итак, для решения дробно-рациональных уравнений помните три правила:

1. Сокращать можно только множители. Слагаемые — нельзя. Поэтому учитесь раскладывать числитель и знаменатель на множители;
2. Основное свойство пропорции: произведение крайних элементов равно произведению средних;
3. Уравнения можно умножать и делить только на числа k , отличные от нуля. Случай k = 0 надо проверять отдельно.

Помните эти правила и не допускайте ошибок.

Как делать сокращение дробей. Правила сокращения дробей с примерами

Калькулятора онлайн выполняет сокращение алгебраических дробей в соответствии с правилом сокращения дробей: замена исходной дроби равной дробью, но с меньшими числителем и знаменателем, т.е. одновременное деление числителя и знаменателя дроби на их общий наибольший общий делитель (НОД). Также калькулятор выводит подробное решение, которое поможет понять последовательность выполнения сокращения.

Дано:

Решение:

Выполнение сокращения дробей

проверка возможности выполнения сокращения алгебраической дроби

1) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби

определение наибольшего общего делителя (НОД) числителя и знаменателя алгебраической дроби

2) Сокращение числителя и знаменателя дроби

сокращение числителя и знаменателя алгебраической дроби

3) Выделение целой части дроби

выделение целой части алгебраической дроби

4) Перевод алгебраической дроби в десятичную дробь

перевод алгебраической дроби в десятичную дробь

Помощь на развитие проекта сайт

Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при сокращении алгебраической дроби калькулятором онлайн:

1. Чтобы выполнить сокращение алгебраической дроби введите в соответствующие поля значения числителя, знаменателя дроби. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
2. Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
3. В зависимости от задаваемой алгебраической дроби автоматически выполняется следующая последовательность действий:

• определение наибольшего общего делителя (НОД) числителя и знаменателя дроби ;
• сокращение числителя и знаменателя дроби на НОД ;
• выделение целой части дроби , если числитель итоговой дроби больше знаменателя.
• перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.

В результате сокращения может получиться неправильная дробь. В этом случае у итоговой неправильной дроби будет выделена целая часть и итоговая дробь будет переведена в правильную дробь.

II. Для справки:

Дробь — число, состоящее из одной или нескольких частей (долей) единицы. Обыкновенная дробь (простая дробь) записывается в виде двух чисел (числитель дроби и знаменатель дроби), разделенных горизонтальной чертой (дробной чертой), обозначающей знак деления. числитель дроби — число, стоящее над дробной чертой. Числитель показывает, сколько долей взяли у целого. знаменатель дроби — число, стоящее под дробной чертой. Знаменатель показывает, на сколько равных долей разделено целое. простая дробь — дробь, не имеющая целой части. Простая дробь может быть правильной или неправильной. правильная дробь — дробь, у которой числитель меньше знаменателя, поэтому правильная дробь всегда меньше единицы. Пример правильных дроби: 8/7, 11/19, 16/17. неправильная дробь — дробь, у которой числитель больше или равен знаменателю, поэтому неправильная дробь всегда больше единицы или равна ей. Пример неправильных дроби: 7/6, 8/7, 13/13. смешанная дробь — число, в состав которого входит целое число и правильная дробь, и обозначает сумму этого целого числа и правильной дроби. Любая смешанная дробь может быть преобразована в неправильную простую дробь. Пример смешанных дробей: 1¼, 2½, 4¾.

III. Примечание:

1. Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
2. Для сложения, вычитания, умножения и деления обыкновенных или смешанных дробей воспользуйтесь онлайн калькулятором дробей с подробным решением.

В прошлый раз мы составили план, следуя которому, можно научиться быстро сокращать дроби. Теперь рассмотрим конкретные примеры сокращения дробей.

Примеры .

Проверяем, а не делится ли бо́льшее число на меньшее (числитель на знаменатель или знаменатель на числитель)? Да, во всех трех этих примерах бо́льшее число делится на меньшее. Таким образом, каждую дробь сокращаем на меньшее из чисел (на числитель либо на знаменатель). Имеем:

Проверяем, а не делится ли бо́льшее число на меньшее? Нет, не делится.

Тогда переходим к проверке следующего пункта: а не оканчивается ли запись и числителя, и знаменателя одним, двумя или несколькими нулями? В первом примере запись числителя и знаменателя оканчивается нулем, во втором — двумя нулями, в третьем — тремя нулями. Значит, первую дробь сокращаем на 10, вторую — на 100, третью — на 1000:

Получили несократимые дроби.

Бо́льшее число на меньшее не делится, запись чисел нулями не оканчивается.

Теперь проверяем, а не стоят ли числитель и знаменатель в одном столбце в таблице умножения? 36 и 81 оба делятся на 9, 28 и 63 — на 7, а 32 и 40 — на 8 (они делятся еще и на 4, но если есть возможность выбора, всегда сокращать будем на бо́льшее). Таким образом, приходим к ответам:

Все полученные числа являются несократимыми дробями.

Бо́льшее число на меньшее не делится. А вот запись и числителя, и знаменателя оканчивается нулем. Значит, сокращаем дробь на 10:

Эту дробь еще можно сократить. Проверяем по таблице умножения: и 48, и 72 делятся на 8. Сокращаем дробь на 8:

Полученную дробь еще можем сократить на 3:

Эта дробь — несократимая.

Бо́льшее из чисел на меньшее не делится. Запись числителя и знаменателя оканчивается на нуль.Значит, сокращаем дробь на 10.

Полученные в числителе и знаменателе числа проверяем на и . Так как сумма цифр и 27, и 531 делятся на 3 и на 9, то эту дробь можно сократить как на 3, так и на 9. Выбираем большее и сокращаем на 9. Полученный результат — несократимая дробь.

Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.

Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.

К этому же ответу можем прийти другим путем.

И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.

И еще один вариант решения.

В следующий раз рассмотрим примеры сокращения дробей.

На этом уроке мы изучим основное свойство дроби, узнаем, какие дроби являются равными друг другу. Научимся сокращать дроби, определять, является ли дробь сократимой или нет, попрактикуемся в сокращении дробей и узнаем, когда стоит использовать сокращение, а когда нет.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Основное свойство дроби

Представьте себе такую ситуацию.

За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по \(\mathbf{\frac{5}{3}}\) яблока.

А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по \(\mathbf{\frac{5}{3}}\)

При этом всего 10 яблок и 6 человек. Каждому по \(\mathbf{\frac{10}{6}}\)

Но это одно и то же.

\(\mathbf{\frac{5}{3} = \frac{10}{6}}\)

Эти дроби эквивалентны.

Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.

В математике это формулируется так:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной .

Это свойство иногда называют «основным свойством дроби ».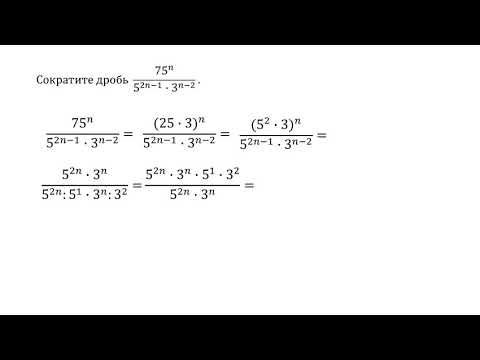

$$\mathbf{\frac{a}{b} = \frac{a\cdot c}{b\cdot c} = \frac{a:d}{b:d}}$$

Например, Путь от города до деревни- 14 км.

Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя шесть столбиков, шесть километров, мы понимаем, что прошли \(\mathbf{\frac{6}{14}}\) пути.

Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 40 штук на каждый километр. То есть всего 560 на всем пути. Шесть километров- \(\mathbf{6\cdot40 = 240}\) столбов. То есть мы прошли 240 из 560 столбов- \(\mathbf{\frac{240}{560}}\)

\(\mathbf{\frac{6}{14} = \frac{240}{560}}\)

Пример 1

Отметьте точку с координатами (5; 7 ) на координатной плоскости XО Y . Она будет соответствовать дроби \(\mathbf{\frac{5}{7}}\)

Соедини начало координат с получившейся точкой. Построй другую точку, которая имеет координаты в два раза больших предыдущих. Какую дробь ты получил? Будут ли они равны?

Решение

Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь \(\mathbf{\frac{5}{7}}\), отметим точку с координатой 5 по оси Y и 7 по оси X . Проведем прямую из начала координат через нашу точку.

На этой же прямой будет лежать и точка, соответствующая дроби \(\mathbf{\frac{10}{14}}\)

Они являются эквивалентными: \(\mathbf{\frac{5}{7} = \frac{10}{14}}\)

Дроби и их сокращение — еще одна тема, которая начинается в 5 классе. Здесь формируется база этого действия, а потом эти умения тянутся ниточкой в высшую математику. Если ученик не усвоил, то у него могут возникнуть проблемы в алгебре. Поэтому лучше уяснить несколько правил раз и навсегда. А еще запомнить один запрет и никогда его не нарушать.

Дробь и ее сокращение

Что это такое, знает каждый ученик. Любые две цифры расположенные между горизонтальной чертой сразу воспринимаются, как дробь. Однако не все понимают, что ею может стать любое число. Если оно целое, то его всегда можно разделить на единицу, тогда получится неправильная дробь. Но об этом позже.

Начало всегда простое. Сначала нужно выяснить, как сократить правильную дробь. То есть такую, у которой числитель меньше, чем знаменатель. Для этого потребуется вспомнить основное свойство дроби. Оно утверждает, что при умножении (так же, как и делении) одновременно ее числителя и знаменателя на одинаковое число получается, равноценная исходной дробь.

Действия деления, которые выполняются в этом свойстве и приводят к сокращению. То есть максимальному ее упрощению. Дробь можно сокращать до тех пор, пока над чертой и под ней есть общие множители. Когда их уже не будет, то сокращение невозможно. И говорят, что эта дробь несократимая.

Два способа

1. Пошаговое сокращение. В нем используется метод прикидки, когда оба числа делятся на минимальный общий множитель, который заметил ученик. Если после первого сокращения видно, что это не конец, то деление продолжается. Пока дробь не станет несократимой.

2. Нахождение наибольшего общего делителя у числителя и знаменателя. Это самый рациональный способ того, как сокращать дроби. Он подразумевает разложение числителя и знаменателя на простые множители. Среди них потом нужно выбрать все одинаковые. Их произведение даст наибольший общий множитель, на который сокращается дробь.

Оба эти способа равноценны. Ученику предлагается освоить их и пользоваться тем, который больше понравился.

Что делать, если есть буквы и действия сложения и вычитания?

С первой частью вопроса все более-менее понятно. Буквы можно сокращать так же как и числа. Главное, чтобы они выступали в роли множителей. А вот со второй у многих возникают проблемы.

Важно запомнить! Сокращать можно только числа, которые являются множителями. Если они слагаемые — нельзя.

Для того чтобы понять, как сокращать дроби, имеющие вид алгебраического выражения, нужно усвоить правило. Сначала представить числитель и знаменатель в виде произведения. Потом можно сокращать, если появились общие множители. Для представления в виде множителей пригодятся такие приемы:

• группировка;
• вынесение за скобку;
• применение тождеств сокращенного умножения.

Причем последний способ дает возможность сразу получить слагаемые в виде множителей. Поэтому его необходимо использовать всегда, если видна известная закономерность.

Но это еще не страшно, потом появляются задания со степенями и корнями. Вот тогда требуется набраться смелости и усвоить пару новых правил.

Выражение со степенью

Дробь. В числителе и знаменателе произведение. Есть буквы и числа. А они еще и возведены в степень, которая тоже состоит из слагаемых или множителей. Есть чего испугаться.

Для того чтобы разобраться в том, как сокращать дроби со степенями, потребуется выучить два момента:

• если в показателе степени стоит сумма, то ее можно разложить на множители, степенями которых будут исходные слагаемые;
• если разность, то на делимое и делитель, у первого в степени будет уменьшаемое, у второго — вычитаемое.

После выполнения этих действий становятся видны общие множители. В таких примерах нет необходимости вычислять все степени. Достаточно просто сократить степени с одинаковыми показателями и основаниями.

Для того чтобы окончательно усвоить то, как сокращать дроби со степенями, нужно много практиковаться. После нескольких однотипных примеров действия будут выполняться уже автоматически.

А если в выражении стоит корень?

Его тоже можно сократить. Только опять же, соблюдая правила. Причем верны все те, которые были описаны выше. В общем, если стоит вопрос о том, как сократить дробь с корнями, то нужно делить.

На иррациональные выражения тоже можно разделить. То есть если в числителе и знаменателе стоят одинаковые множители, заключенные под знак корня, то их можно смело сокращать. Это приведет к упрощению выражения и выполнению задания.

Если после сокращения под чертой дроби осталась иррациональность, то от нее нужно избавиться. Другими словами, умножить на нее числитель и знаменатель. Если после этой операции появились общие множители, то их снова нужно будет сократить.

Вот, пожалуй, и все о том, как сокращать дроби. Правил немного, а запрет один. Никогда не сокращать слагаемые!

Калькулятор

футов и дюймов в метрические единицы • Общие калькуляторы • Онлайн-конвертеры единиц измерения

Определения и формулы

Преобразование неправильных дробей в смешанные числа

Сокращение дробей и наибольший общий множитель

Сложение, вычитание, умножение и деление значений длины в футы и дюймы

Расчеты и перевод британских единиц в метрические и наоборот

Измерение расстояний

Контактные дальномерные устройства

Бесконтактные дальномеры

Измерение расстояний в астрономии

Определения и формулы

Для этого калькулятора мы ограничим его использование следующим:

• Положительные дроби.
• Дроби крупнее 1/64.

При выполнении вычислений необходимо решить следующие задачи:

• Преобразование неправильных дробей в смешанные числа
• Сложение, вычитание, умножение и деление футов и дюймов
• Преобразование имперских единиц в метрические и наоборот

Преобразование неправильных дробей в смешанные числа

Положительная дробь называется правильной, если ее числитель меньше знаменателя. Его значение всегда меньше 1. Примерами правильных дробей являются 2/3 и 5/30. Вторую дробь можно уменьшить до 1/6.

Дробь называется неправильной, если ее числитель больше знаменателя. Его значение, если оно положительное, всегда больше или равно 1. Неправильную дробь можно представить как целое число плюс правильную дробь. Пример неправильной дроби: 30/29., что может быть выражено как 1 1/29.

Смешанное число — это целое число, за которым следует правильная дробь. Например, 2 2/3.

Чтобы преобразовать неправильную дробь в смешанное число, необходимо сделать следующее:

• Найти наибольший общий делитель (НОД).
• Сократите дробь, разделив числитель и знаменатель на наибольший общий множитель.
• Разделите числитель на знаменатель.
• Запишите целую часть коэффициента.
• Дробная часть смешанного числа будет состоять из остатка над знаменателем.

Например, превратим неправильную дробь 30/8 в смешанное число.

• Сокращение дроби путем деления числителя и знаменателя на наибольший общий делитель 2:

• Деление числителя на знаменатель: 15 : 4 = 3 с остатком 3.
• Целая часть результата деления 3.
• Записав смешанное число в виде целой части и остатка над знаменателем: 3 3/4.

Сокращение дробей и наибольший общий делитель

Числитель и знаменатель дроби можно разделить на одно и то же ненулевое число, чтобы получить эквивалентную дробь. Эта новая дробь называется сокращенной дробью. Иногда новую дробь можно еще уменьшить, чтобы получить дробь с меньшим числителем и меньшим знаменателем. Чтобы получить эквивалентную дробь с наименьшими числителем и знаменателем, необходимо определить наибольший общий множитель. Если и числитель, и знаменатель делятся только на 1, то говорят, что эта дробь несократима. Например, 3/4 из приведенного выше примера — несократимая дробь, и ее нельзя сокращать дальше.

Сложение, вычитание, умножение и деление значений длины в футах и ​​дюймах

Перед сложением, вычитанием, умножением и делением необходимо преобразовать все измерения в одну общую единицу длины. Наш калькулятор сначала преобразует дюймовые дроби в десятичные, затем преобразует футы в дюймы, умножая количество футов на 12, потому что 1 фут содержит 12 дюймов, а затем выполняет необходимые арифметические операции.

Расчеты и преобразование имперских единиц в метрические и наоборот

Калькулятор работает со смешанными числами в футах, дюймах и дюймовых долях и возвращает результаты вычислений в виде смешанного дробного числа (если есть) и десятичных дробей. Если вам нужно преобразовать другие единицы длины и расстояния, попробуйте наш конвертер длины и расстояния.

Измерение расстояний

В этой длинной статье мы просто перечислим различные способы измерения расстояний. От очень старых инструментов, таких как линейка или измерительная цепь, до новейших лазерных и радарных дальномеров. В таблице ниже показан диапазон расстояний, которые люди научились измерять.

Table 1. The Scale of Distance in Meters

10 -12	10 -9	10 -6	10 -3	10 0	10 3	10 6	10 9	10 12	10 16	10 19	10 21
Distances between atoms	Расстояния между ячейками		Межличностные расстояния		Расстояния на Земле		Расстояния Солнечной системы		Расстояния до ближайших звезд	Расстояния между галрактами

. пожалуй, самые древние измерительные приборы, которые изобрел и использовал человек. Люди могут измерять расстояния от размера атома до расстояния до других галактик. Мы перечислим эти инструменты в порядке величины расстояния.

Контактные устройства для измерения расстояния

Микрометр, изготовленный в 1937 году

Как следует из названия, измерительное устройство должно касаться поверхностей во время измерения. Примеры контактных измерительных приборов приведены ниже:

Микрометр

Микрометр — прибор, предназначенный для высокоточного измерения наружных линейных размеров, имеющий в своем составе калиброванный измерительный винт с С-образным корпусом. Результаты измерений можно считывать по шкалам на гильзе и наперстке или на цифровом дисплее.

Штангенциркуль

Цифровой штангенциркуль; порт данных закрыт крышкой в ​​правом верхнем углу пластикового корпуса

Штангенциркуль – инструмент для точного измерения малых расстояний между двумя противоположными сторонами объекта или внутреннего размера объекта, а также глубины отверстий . Чтение можно производить с нониусной шкалы, циферблата или цифрового дисплея с возможностью в расширенных инструментах загружать данные на персональный компьютер.

Щуп

Щуп — это инструмент для измерения небольших зазоров между двумя деталями. Инструмент обычно состоит из нескольких небольших гибких стальных полос разной толщины, закрепленных на шарнире.

Мерный брусок

Мерный брусок представляет собой стандартный металлический или керамический брусок в форме прямоугольного параллелепипеда с прецизионной длиной от 0,5 до 1000 мм и с двумя противоположными сторонами, отшлифованными точно плоско и параллельно. У них нет шкалы и системы из таких блоков используются для калибровки измерительного оборудования.

Опизометр (курвиметр, картомер, картометр)

Опизометр — это прибор для измерения длины произвольных кривых линий, например, на картах. Измерение может быть считано с циферблата или цифрового дисплея.

Ультразвуковой толщиномер

Ультразвуковой толщиномер — это прибор для неразрушающего измерения толщины материала с использованием ультразвуковых волн. Такие устройства могут измерять толщину различных материалов, включая пластик, стекло, металл, керамику и другие материалы. Они также могут измерять толщину покрытий. В отличие от других контактных измерительных устройств, они требуют доступа только к одной стороне образца.

50-сантиметровая линейка, используемая в металлообработке

Линейка

Линейка — это инструмент для измерения длин и расстояний и рисования прямых линий. Это очень старый инструмент; самый старый сохранившийся правитель датируется ок. 2650 г. до н.э.

Масштабная линейка

Масштабная линейка — это специальная линейка с двумя или более шкалами для измерения длин и расстояний с фиксированным соотношением длин. На таких линейках часто отмечается соотношение в виде, например, 1:1/1:10 или 1:100/1:300.

Логарифмическая линейка

Логарифмическая линейка (логарифмическая линейка) — это механический аналоговый компьютер, используемый в основном для умножения, деления и таких функций, как тригонометрия, экспоненты и логарифмы. Некоторые логарифмические линейки также можно использовать в качестве простых линеек для измерения длины или рисования прямых линий.

Логарифмическая линейка

Карман с пружинным возвратом и брелок Рулетки с четвертью для сравнения

Измерительная линейка

Измерительная линейка (или аршин) представляет собой измерительный инструмент в виде длинной линейки, которая может складываться, использоваться для рисования линий и измерения небольших расстояний до двух метров. В США их длина обычно составляет один ярд.

Рулетка мерная

Рулетка измерительная или рулетка — измерительный инструмент в виде гибкой или полугибкой линейки со шкалой в метрических и (или) традиционных единицах измерения.

Пластиковая гибкая рулетка, используемая портными; до изобретения пластмасс такие ленты делали из клеенки

Цепь Гюнтера

Цепь Гюнтера — измерительный инструмент, используемый для измерения относительно больших расстояний при геодезических работах. Он содержит 100 звеньев по 0,66 фута каждое.

Геодезическое колесо

Геодезическое колесо — это измерительный инструмент, используемый при геодезических работах, строительстве, благоустройстве и железнодорожных работах для измерения расстояния по прямым и кривым линиям. Точность колеса не так хороша, как у измерительной ленты; однако он может дать хорошую оценку расстояния или длины, например, для прокладки кабеля.

Цифровой одометр Honda Civic 2012

Одометр

Одометр — измерительный прибор, устанавливаемый на транспортном средстве и используемый для измерения пройденного транспортным средством расстояния. Такие устройства были изобретены очень давно и существовали в Древнем Китае, Древней Греции и Древнем Риме. ὁδός в переводе с древнегреческого означает «путь».

Зонд

Зонд представляет собой прибор для измерения глубины воды в виде тонкой веревки с прикрепленным к концу свинцовым грузом. Это очень старый инструмент, и древнегреческие и римские моряки использовали его для измерения глубины воды. Зондирующая линия по-прежнему используется в качестве резервной, когда имеется эхолот.

Бесконтактные устройства для измерения расстояния

Сканирующий электронный микроскоп

Сканирующий электронный микроскоп

Как и оптические микроскопы, сканирующие электронные микроскопы также могут использоваться для измерения длины. Для их калибровки доступны различные калибровочные образцы, а также калибровочные стандарты. Калибровочный эталон представляет собой сетку, выполненную на различных материалах, например сетку из линий хрома, нанесенных на плоскую кремниевую подложку.

Интерферометр

Интерферометр — это научный прибор, работа которого основана на явлении интерференции. Используется для высокоточных измерений. Интерферометры являются самыми высокоточными из существующих приборов для измерения длины. Например, в технике интерферометр можно использовать для проверки оптических поверхностей на плоскостность на завершающих стадиях их полировки. Существует много типов интерферометров.

Микрометры предметного столика микроскопа (калибровочные предметные стекла)

Микроскоп

При использовании составного микроскопа измерения длины можно производить с помощью сетки окуляра (кусок стекла с выгравированной на нем линейкой, установленный в окуляре). Перед измерением с помощью сетки окуляра микроскоп необходимо откалибровать с помощью предметного микрометра (предметное стекло с выгравированной на нем линейкой).

Измерительный микроскоп

Измерительный микроскоп представляет собой высокоточный измерительный оптический прибор со вспомогательным программным обеспечением, способный измерять длину малых или больших образцов с субмикронной точностью. Они используются для анализа поверхности и измерений в микроэлектронике, оптоэлектронике, телекоммуникациях и других отраслях промышленности.

Медицинские устройства визуализации

Все медицинские устройства визуализации, такие как флюороскопы, проекционные рентгенограммы (рентгеновские аппараты), сканеры магнитно-резонансной томографии (МРТ), сканеры позитронно-эмиссионной томографии (ПЭТ), устройства ультразвуковой визуализации могут измерять размеры внутренних органов с помощью большая точность.

Сонар

Сонар — это устройство, которое можно использовать во многих приложениях, основанных на распространении звука под водой. Его можно использовать для эхолота, подводной навигации, связи, обнаружения объектов, измерения глубины для определения расстояния до дна океана. Сонары могут быть активными или пассивными. Активные гидролокаторы излучают звуковые импульсы и слушают их эхо. Пассивные гидролокаторы прислушиваются к звукам, издаваемым судами и их оборудованием, и анализируют их. Их можно использовать для обнаружения целей в воде.

Ультразвуковой дальномер

Ультразвуковой дальномер — это устройство для измерения расстояния, работающее по тому же принципу, что и гидролокатор, только в воздухе. Он определяет расстояние до объекта, излучая ультразвуковой импульс, принимая отражающий сигнал и измеряя время, необходимое звуковому импульсу для возвращения к приемнику дальномера. Они могут измерять расстояние от нескольких миллиметров до нескольких десятков метров.

Ростомер

Ростомер — это оптический прибор для измерения расстояния, аналогичный секстанту, используемый для оценки расстояния до объекта известной высоты. Он измеряет угол между верхом и низом объекта при наблюдении с ростомера.

Окно фокусного расстояния объектива 24–105 мм, показывающее расстояние в метрах и футах

Устройства автофокусировки камеры

Оптическая система автофокусировки (AF) камеры используется не только для фокусировки на автоматически или вручную выбранной точке или объекте, но и также как устройство для измерения расстояния с отображением расстояния в окне дистанции фокусировки.

Бинокль или оптический прицел

Бинокль с визирной сеткой и оптический прицел измеряют расстояния с помощью метода, называемого стадиометрическим дальномером. Они используют тот же принцип, что и ростомер, описанный выше. Для измерения угла к удаленному объекту известной высоты у них есть сетка с отметками известного углового расстояния для оценки угла к объекту известной высоты, например, человеку или танку.

Фотоаппарат Plaubel Makina IIs с дальномером

Оптический (стереоскопический и совпадений) дальномер

Оптические дальномеры используют сравнение двух изображений, полученных от двух разных оптических систем, расположенных на разных устройствах от нескольких сантиметров (дальномерные камеры) до нескольких метров (военно-морские дальномеры) ). Оператор вращает оптические призмы, чтобы добиться совпадения изображений, и считывает расстояние с циферблата.

Лазерный дальномер

Лазерный дальномер — оптоэлектронный прибор для измерения расстояния от наблюдателя до объекта. Он измеряет время пути лазерного луча от наблюдателя до объекта и обратно после отражения от объекта. Ручные лазерные дальномеры могут измерять расстояния до 25 км. Лазеры с оптическими телескопами использовались для измерения расстояния между Землей и Луной. Этот метод также используется в лазерных высотомерах.

Лидар

Лидар — это инструмент, используемый для съемки. Он измеряет расстояние до объекта, освещая его лазерным лучом и измеряя время, которое требуется лучу, чтобы добраться до объекта и вернуться к датчику. Название лидар является аббревиатурой термина LI ght D etection A nd R anging . Лидары используются для создания карт и управления автономными автомобилями.

Щелевые антенны морских РЛС

РЛС измерения высоты и дальности

Как и в лазерных дальномерах, радарные высотомеры и дальномеры излучают короткий импульс и измеряют время его прохождения до попадания в целевой объект или поверхность, отражения от него и возврата обратно. Эти устройства также могут измерять скорость.

Радионавигационная система (LORAN, TACAN, РСДН-20 и другие системы)

AN/UPN-12 (XN-2) Loran A Receiver Set

Радионавигационные системы используют радиочастоты для определения местоположения судна или самолет на Земле. Это включает, конечно, измерение расстояния от приемника до передатчика наземной станции. Радионавигационные системы также измеряют угловые направления и скорости посредством измерения доплеровского сдвига радиоволн. Примерами радионавигационных систем являются ЛОРАН, ЛОРАН-С, Декка, Альфа (РСДН-20). Технология GPS сделала большинство таких систем устаревшими.

Дальномерное оборудование (DME)

DME — это радионавигационное оборудование, используемое гражданскими воздушными судами для измерения расстояния (наклонной дальности) между воздушным судном и наземной станцией DME. Измерение достигается за счет синхронизации задержки распространения радиосигналов между самолетом и наземной станцией. Бортовой запросчик посылает сигнал на наземную станцию, которая отвечает своим сигналом. Этот сигнал принимается бортовым запросчиком, и расстояние рассчитывается по известной временной задержке и скорости света. Наземное оборудование DME обычно сочетается с Оборудование всенаправленного диапазона очень высокой частоты (VOR) , которое используется воздушным судном для определения его местоположения.

Инерциальные навигационные системы

Инерциальные навигационные системы используют аналоговые или цифровые компьютеры, акселерометры (датчики линейного ускорения) и гироскопы (датчики угловой скорости) для непрерывного определения положения, ориентации и направления движения и скорости корабля, подводной лодки , самолет, ракета или космический корабль без необходимости использования внешних ссылок. Конечно, такие системы также могут измерять расстояние.

Эти системы называются инерционными, потому что они работают путем измерения и интегрирования сил инерции, то есть сил, возникающих за счет ускорения системы отсчета, например, космического корабля. В более старых инерциальных навигационных системах использовались гиростабилизированные платформы с множеством точных механических движущихся частей, которые могли изнашиваться и были уязвимы для блокировки карданного подвеса.

В более новых системах не используются механические движущиеся части, а их датчики жестко закреплены на конструкции движущегося объекта. Вместо механических вращающихся гироскопов используются кольцевые лазерные гироскопы. В отличие от навигационных систем, основанных на радиоволнах наземных станций или спутников, инерциальные навигационные системы невосприимчивы к помехам и обману.

Например, в 2016–2017 годах у Кремля начали странно работать GPS-навигаторы, показывая пользователям, что они находятся в центре аэропорта Внуково, примерно в 20 милях к юго-западу от Кремля. Скорее всего, это произошло из-за того, что правительство хотело убрать из этого района беспилотники. В конце концов, многие из них запрограммированы на прекращение работы вблизи крупных аэропортов. Если бы смартфоны и дроны были оснащены инерциальными навигационными системами вместо спутниковых приемников, смартфоны показывали бы правильное местоположение, а дроны летали бы.

Подробнее о дронах, их датчиках и навигации.

В 2015 году автор этой статьи впервые в жизни наблюдал полную блокировку сигналов спутниковой навигации возле Ливадийского дворца в Крыму (Россия) во время визита туда президента Путина.

DA40 Diamond Star с авионикой стеклянной кабины на базе GPS Garmin G1000

Спутниковые навигационные системы (GPS, ГЛОНАСС и т. д.)

Спутниковая навигационная система использует спутники для определения местоположения движущегося транспортного средства, оснащенного приемником. Как и все другие навигационные системы, спутниковые навигационные системы могут измерять расстояние с большой точностью. Покрытие этих систем может быть региональным или глобальным, последнее может быть достигнуто за счет использования спутниковой группировки из 18–30 спутников на средней околоземной орбите (19000 до 23 000 км). Как и все радионавигационные системы, спутниковая навигация также уязвима, и даже небольшое карманное устройство может легко блокировать очень слабые сигналы со спутников. Защищенные военные зашифрованные системы GPS невосприимчивы к спуфингу. Однако они не застрахованы от помех, потому что сигналы со спутников очень слабые.

Измерение расстояний в астрономии

Измерить огромные расстояния в астрономии непросто. Астрономы не могут измерять расстояния линейкой или рулеткой — они используют разные методы для определения расстояний до объектов во Вселенной. Конкретные методы, которые они используют, зависят от расстояния до интересующих их объектов. Все эти методы представляют собой комбинации устройств, способных принимать все виды электромагнитного излучения, с математикой и программным обеспечением. Ниже приведен список нескольких методов, используемых астрономами:

Радары

Радары используются для измерения расстояний в нашей Солнечной системе. Метод основан на том, что электромагнитное излучение распространяется с известной скоростью 300 000 км/с. Следовательно, если мы измерим время, мы сможем вычислить расстояние. Дополнительную информацию о радарах вы найдете в наших Калькуляторе максимальной дальности РЛС, Калькуляторе максимальной однозначной дальности РЛС и частоты повторения импульсов, а также Калькуляторе дальности прямой видимости радиотелескопа

Радиотелескоп РТ-70, 13 км от Евпатории, Крым, Россия. Он может измерять расстояние до Венеры с точностью до 700 м.

Звездный параллакс

Параллакс используется для измерения расстояний до ближайших звезд. В методе используется геометрия орбиты Земли вокруг Солнца. Пока Земля движется вокруг Солнца, астрономы могут наблюдать за близлежащими звездами из разных мест. Эти местоположения лишь немного отличаются по сравнению с расстояниями до звезд. Звезда, до которой измеряется расстояние, кажется, движется относительно более удаленных объектов на небе. Если мы знаем диаметр земной орбиты и угол между двумя линиями обзора звезды, наблюдаемый, когда Земля находится на противоположных сторонах от Солнца на своей орбите, мы можем рассчитать расстояние до звезды. Этот метод не работает для далеких звезд, потому что углы параллакса становятся слишком малыми и не могут быть измерены с необходимой точностью.

Цефеиды

Цефеиды используются для измерения расстояний в нашей Галактике и внегалактических расстояний. Цефеиды — это звезды, которые пульсируют и вызывают изменения светимости. Период и амплитуда их пульсаций хорошо определены. Это соотношение можно использовать для измерения расстояний до ближайших галактик. Однако мы не можем видеть отдельные звезды в далеких галактиках, и этот метод для них не работает.

Сверхновые

Сверхновые используются для измерения расстояний до далеких галактик. Сверхновая — это звезда, которая взрывается. Такие звезды внезапно появляются в галактике и могут светить в течение короткого периода в несколько недель или месяцев так же ярко, как целая галактика. Астрономы используют измеренную наблюдаемую яркость для измерения очень больших расстояний, примерно до 1 миллиарда световых лет.

Красное смещение

Красное смещение используется для измерения расстояний до объектов, которые невозможно измерить описанными выше методами. Красное смещение является примером эффекта Доплера в видимом спектре. Если звезда движется к нам, частота световых волн выше (свет смещается в синюю часть спектра), а если она движется от нас, то частота ниже (свет смещается в красную часть спектра). спектр). Красное смещение измеряется астрономами с помощью спектроскопии. Согласно закону Хаббла, существует связь между расстояниями до галактик и их красными смещениями.

Подробнее об измерении расстояний в астрономии.

Эта статья была написана Анатолием Золотковым

Калькулятор объема выборки и полное руководство в 2022 г. %2%3%4%5%6%7%8%9%10%

Идеальный размер выборки:

Какую долю целевой группы вам необходимо опросить, чтобы получить результаты, репрезентативные для целевой группы с уровень доверия, который вы готовы принять?

Введение в размер выборки

Как можно рассчитать размер выборки, уменьшить погрешность и проводить обследования со статистически значимыми результатами? В этом кратком руководстве мы объясним, как вы можете улучшить свои опросы, и продемонстрируем некоторые инструменты и ресурсы, которые вы можете использовать в процессе.

Но сначала, когда дело доходит до исследования рынка, сколько людей вам нужно опросить, чтобы получить результаты, представляющие целевую группу населения, с уровнем уверенности, который вы готовы принять?

Однако, если все это кажется вам новым, давайте начнем с размера выборки.

Что такое размер выборки?

Размер выборки — это термин, используемый в исследованиях рынка для определения количества субъектов, включенных в опрос, исследование или эксперимент. В опросах с большим населением размер выборки невероятно важен. Причина этого в том, что нереально получить ответы или результаты от всех — вместо этого вы можете взять случайную выборку людей, представляющих население в целом.

Например, мы можем захотеть сравнить результаты бегунов на длинные дистанции, которые едят Weetabix на завтрак, и тех, кто этого не делает. Поскольку невозможно отследить диетические привычки каждого бегуна на длинные дистанции по всему миру, нам придется сосредоточиться на сегменте опрошенных. Это может означать выбор 1000 бегунов для исследования.

Бесплатная электронная книга : Руководство по определению размера выборки

Как размер выборки может повлиять на результаты?

Тем не менее, независимо от того, насколько усердно мы относимся к нашему выбору, в результатах исследования всегда будет некоторая погрешность (также называемая доверительным интервалом), потому что мы не можем говорить с каждым бегуном на длинные дистанции или быть уверенным в том, как Weetabix влияет (во всех возможных сценариях) на результаты бегунов на длинные дистанции. Это известно как «ошибка выборки».

Большие размеры выборки помогут уменьшить погрешность, что поможет получить более статистически значимые и значимые результаты. Другими словами, более точная картина того, как употребление Weetabix может повлиять на результаты бегунов на длинные дистанции.

Итак, что вам нужно знать при расчете минимального размера выборки, необходимого для исследовательского проекта?

Что нужно знать для расчета размера выборки обследования

Доверительный интервал (или погрешность)

Доверительный интервал — это положительное или отрицательное число, которое представляет точность сообщения. Рассмотрим следующий пример:

Канадская национальная выборка показала, «на кого канадцы тратят свои деньги в День матери». 82% канадцев рассчитывают купить подарки для своей мамы, по сравнению с 20% для жены и 15% для свекрови. Что касается расходов, то канадцы рассчитывают потратить 93 доллара на свою жену в этот День матери против 58 долларов на мать. Национальные данные точны, плюс-минус 2,75 процента, 19раз из 20.

Например, если вы используете доверительный интервал 2,75 и 82% процентов вашей выборки указывают, что они «купят подарок для мамы», вы можете быть «уверены (95% или 99%)», что если вы задали вопрос ВСЕМ КАНАДЦАМ, где-то между 79,25% (82%-2,75%) и 84,75% (82%+2,75%) выбрали бы этот ответ.

Доверительный интервал также называют «пределом погрешности». Вам нужно понять, как соотносятся эти два расчета?

Попробуйте наш калькулятор погрешности

Уровень достоверности

Уровень достоверности показывает, насколько вы уверены в этом результате. Он выражается в процентах случаев, когда разные выборки (если были взяты повторные выборки) давали бы этот результат. Доверительный уровень 95% означает, что в 19 случаях из двадцати результаты попадут в этот — + интервал доверительного интервала. Наиболее часто используется уровень достоверности 95%.

Если сложить вместе доверительный интервал и доверительный интервал, можно сказать, что вам 9 лет. 5% (19 из 20) уверены, что истинный процент населения, которое «купит подарок маме», составляет от 79,25% до 84,75%.

Более широкие доверительные интервалы повышают уверенность в том, что истинный ответ находится в указанном диапазоне. Эти более широкие доверительные интервалы исходят из меньших размеров выборки. Когда цена ошибки чрезвычайно высока (на карту поставлено многомиллионное решение), доверительный интервал должен оставаться небольшим. Это можно сделать, увеличив размер выборки.

Численность населения

Численность населения — это общее количество людей в группе, которую вы пытаетесь изучить. Если бы вы брали случайную выборку людей по всей Великобритании, то численность вашего населения составила бы чуть более 68 миллионов человек (по состоянию на 9 августа 2021 года).

Стандартное отклонение

Это относится к тому, насколько отдельные ответы будут отличаться друг от друга и среднего значения. При низком стандартном отклонении баллы будут сгруппированы около среднего значения с минимальными отклонениями. Более высокое стандартное отклонение означает, что при отображении на графике ответы будут более разбросанными.

Стандартное отклонение выражается в виде десятичной дроби, и 0,5 считается «хорошим» стандартным отклонением, которое необходимо установить, чтобы обеспечить размер выборки, который представляет генеральную совокупность.

Как рассчитать размер выборки?

После того, как вы рассмотрели четыре вышеуказанные переменные, у вас должно быть все необходимое для расчета размера выборки.

Однако, если вы не знаете размер своей совокупности, вы все равно можете рассчитать размер выборки. Для этого вам нужны две части информации: z-показатель и формула размера выборки.

Что такое z-оценка?

Z-оценка — это просто числовое представление желаемого уровня достоверности. Он сообщает вам, сколько стандартных отклонений от среднего составляет ваш результат.

Наиболее распространенные проценты: 90%, 95% и 99%.

z = (x – μ) / σ

Как показывает формула, z-значение представляет собой просто необработанный показатель минус среднее значение генеральной совокупности и деленное на стандартное отклонение генеральной совокупности.

Использование расчета объема выборки

Получив z-значение, вы можете ввести формулу размера выборки, а именно:

Есть ли более простой способ расчета размера выборки?

Если вам нужен более простой вариант, Qualtrics предлагает онлайн-калькулятор размера выборки, который поможет вам определить идеальный размер выборки для опроса за считанные секунды. Просто введите уровень достоверности, размер совокупности, погрешность, и идеальный размер выборки будет рассчитан для вас.

Практические советы по размеру выборки

При формировании выборки определенного размера необходимо учитывать множество переменных. Тем не менее, есть несколько практических советов (или правил), которые помогут вам получить наилучшие возможные результаты:

1) Сбалансировать стоимость и уровень достоверности

Чтобы повысить уровень достоверности или уменьшить погрешность, необходимо увеличить размер выборки. Большие размеры почти всегда приводят к более высоким затратам. Потратьте время на то, чтобы подумать, какие результаты вы хотите получить от своих опросов и какую роль они играют в ваших кампаниях в целом.

2) Вам не всегда нужны статистически значимые результаты

В зависимости от вашей целевой аудитории вы не сможете получить достаточное количество ответов (или достаточно большой размер выборки) для достижения «статистически значимых» результатов.

Если это для вашего собственного исследования, а не для более широкого исследования, это может быть не такой уж большой проблемой, но помните, что любая обратная связь, которую вы получаете от своих опросов, важна. Это может быть статистически незначимым, но может помочь вашей деятельности в будущем.

В конечном счете, вы должны рассматривать это в индивидуальном порядке. Выборки опросов по-прежнему могут дать вам ценные ответы, не имея размеров выборки, которые представляют генеральную совокупность.
Но подробнее об этом в разделе ниже.

3) Задавайте открытые вопросы

Да и никакие вопросы дают уверенность, но открытые вопросы дают информацию, которую вы иначе не получили бы. Чтобы получить наилучшие результаты, стоит сочетать закрытые и открытые вопросы.
Для более подробного ознакомления с типами вопросов опроса ознакомьтесь с нашим справочником.

Различные типы опросов

Существует множество различных опросов, от исследования рынка до оценки удовлетворенности клиентов, которые вы можете провести, чтобы получить необходимую вам информацию, соответствующую размеру вашей выборки.

Самое замечательное в том, что мы делаем в Qualtrics, это то, что мы предлагаем полную коллекцию готовых шаблонов опросов клиентов, продуктов, сотрудников и брендов. Сюда входят опросы Net Promoter Score (NPS), опросы менеджеров, опросы по обслуживанию клиентов и многое другое.

Лучшая часть? Вы можете получить доступ ко всем этим шаблонам бесплатно. Каждый из них разработан нашей специализированной командой экспертов и исследователей в предметной области, поэтому вы можете быть уверены, что наш выбор вопросов, основанный на передовом опыте, и четкий дизайн приведут к большему участию и более качественным данным.