свойство, теорема и доказательство, формула
Содержание:
-
Касательная к окружности
- Свойство №1
- Свойство №2
- Свойство №3
- Свойство №4
- Теоремы и доказательства
Содержание
-
Касательная к окружности
- Свойство №1
- Свойство №2
- Свойство №3
- Свойство №4
- Теоремы и доказательства
Касательная к окружности
Определение
Касательная к окружности — в геометрии это прямая, которая имеет с окружностью одну общую точку.
Такая точка называется точкой касания.
У этой прямой есть ряд свойств.
Свойство №1
Отрезки линий касательных, проведенных из одной точки, равны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На чертеже это выглядит таким образом:
Свойство №2
Касательная линия перпендикулярна радиусу, проведенному в точку касания.
При этом, если провести отрезок из центра окружности до начальной точки прямых (OM), мы получим два равных прямоугольных треугольника (OAM=OBM).
Свойство №3
Соотношение между касательной и секущей.
Графическое изображение этого утверждения выглядит так:
Это утверждение о касательной и секущей, которые проходят через общую точку (M). Секущая дает нам два отрезка: BC (внутренний отрезок, хорда) и CM (внешняя часть секущей).
\circ\), так как \(OВ\perp АВ\), \(ОС\perp АС\) согласно теореме о свойстве касательной, поэтому \(\triangle ABO\) и \(\triangle ACO\) — прямоугольные. OB и OC — радиусы, OB=OC, AO — общая сторона. Значит, \(\triangle ABO = \triangle ACO\) по гипотенузе и катету. Следовательно, уравнения AB=AC и \(\angle3=\angle4\) верны (по равенству треугольников). Ч.Т.Д.
Теорема №2
Касательная перпендикулярна радиусу, проведенному в точку касания.
Доказательство
Дано: a — касательная к кругу с центром O. Она пересекает круг в точке H.
Доказать: \(OH\perp a\).
Доказательство: воспользуемся методом от противного. Предположим, что OH не перпендикулярна a. В этом случае радиус OH — наклонная к прямой a. Перпендикуляр, проведенный из точки O к a, меньше наклонной OH. Тогда расстояние от центра O до прямой a меньше радиуса. Значит, у прямой a и окружности есть две общие точки, что противоречит условию, в котором прямая a — касательная.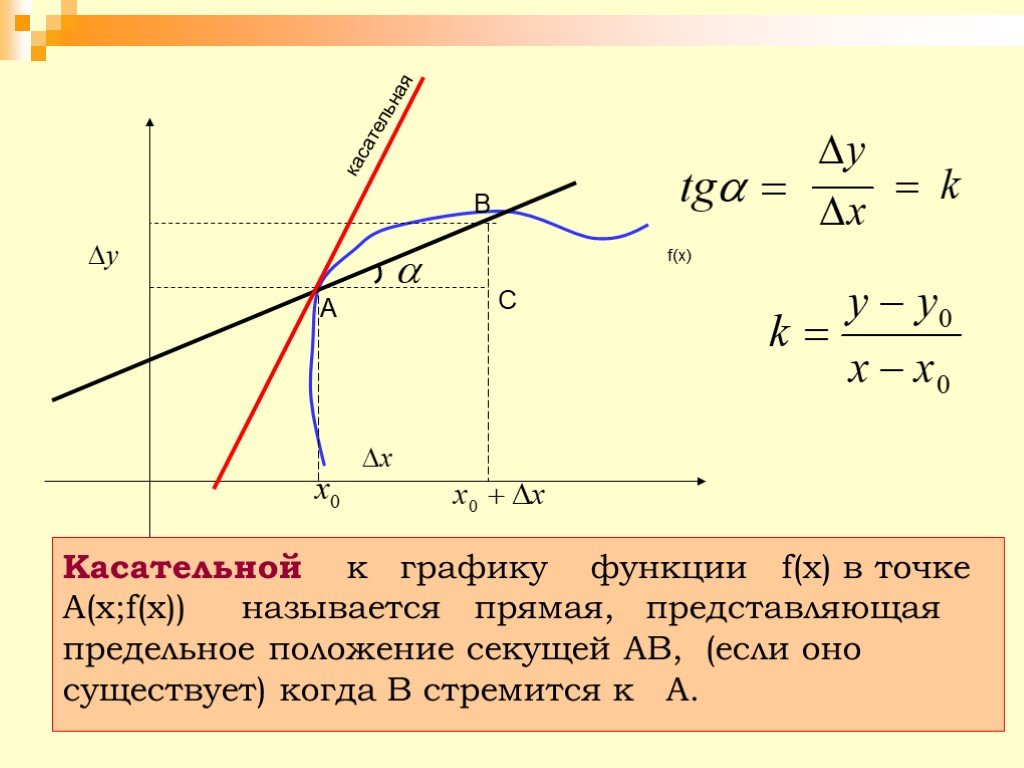
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Касательная к окружности и свойства отрезков касательных
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Расскажем подробнее, что такое касательная и секущая.
Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках.
Такую прямую называют секущей.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.
Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.
Теорема 1.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
На рисунке радиус OA перпендикулярен прямой m.
Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Доказательство:
Дана окружность с центром O.
Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и
Проведем радиусы OB и OC в точки касания.
По свойству касательной, и .
В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и
Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство:
Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.
Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Угол ACМ на рисунке равен половине угловой величины дуги AC.
Доказательство теоремы здесь.
Теорема 5, о секущей и касательной.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
Доказательство теоремы смотрите здесь.
Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.
Задача 1.
Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла.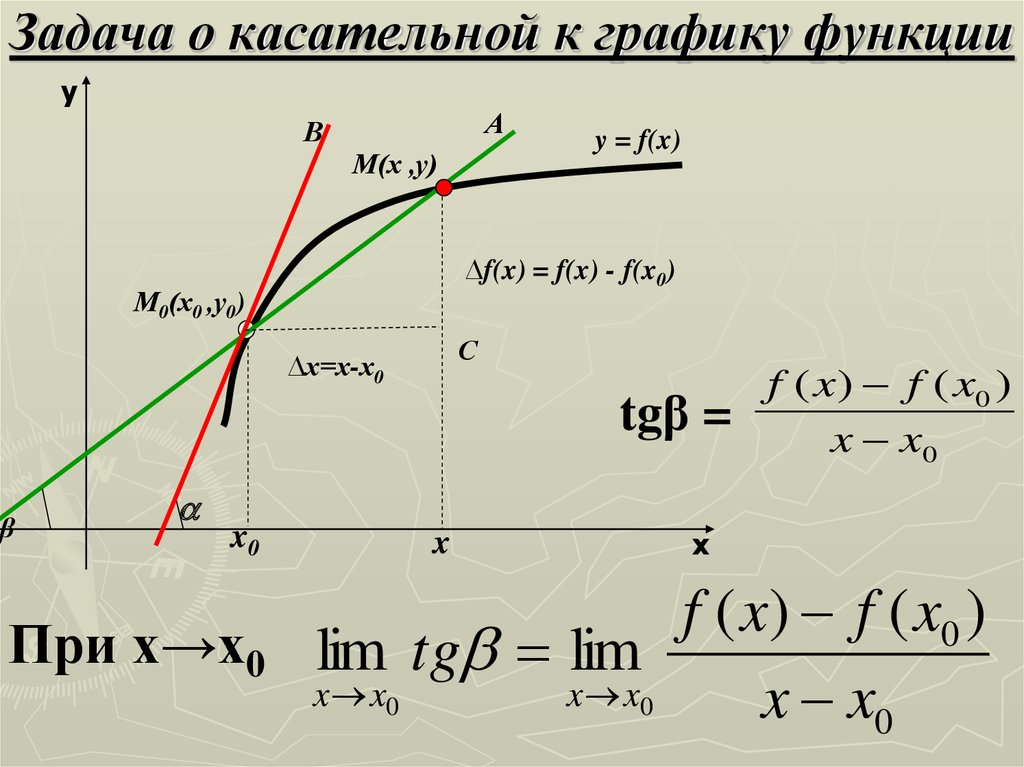
Ответ дайте в градусах.
Решение:
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.
Ответ: 62.
Задача 2.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Решение:
Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен
Ответ: 26.
Задача 3.
Хорда AB стягивает дугу окружности в Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B.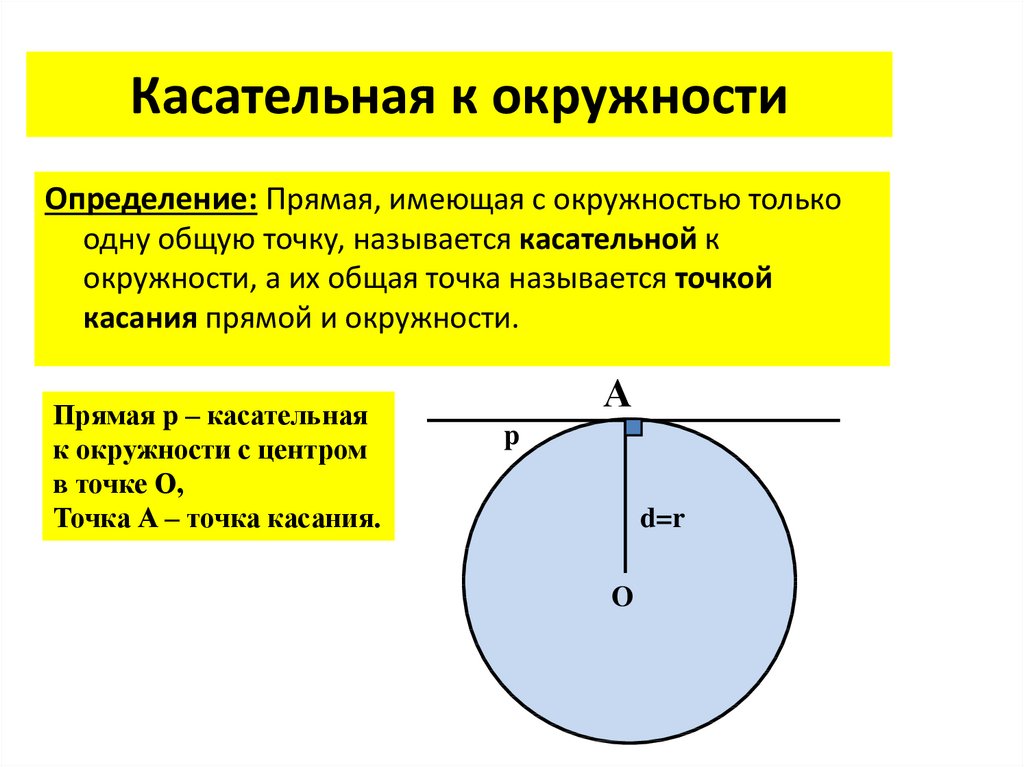
Ответ дайте в градусах.
Решение:
Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.
Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Задача 4.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Решение:
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности.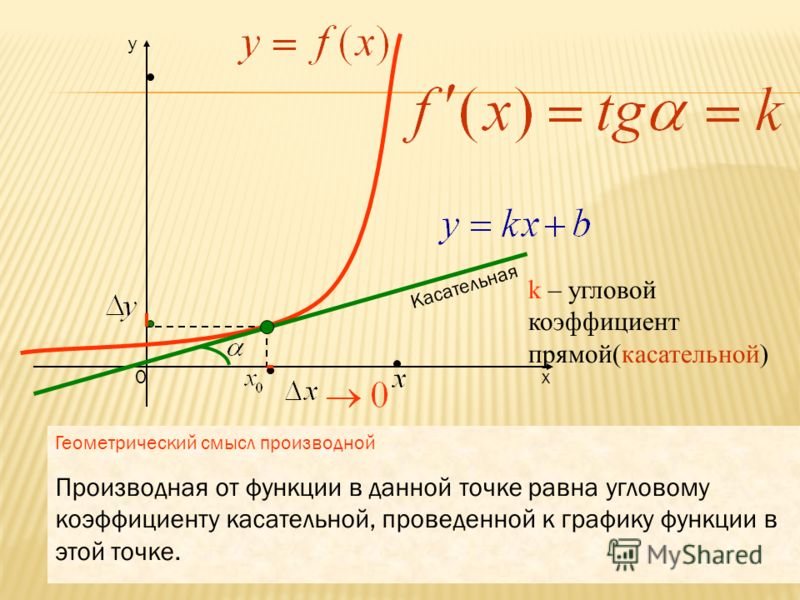
Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.
Ответ: 24.
Вот более сложная задача из вариантов ЕГЭ:
Задача 5.
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Решение:
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.
Очевидно, что площадь многоугольника
Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.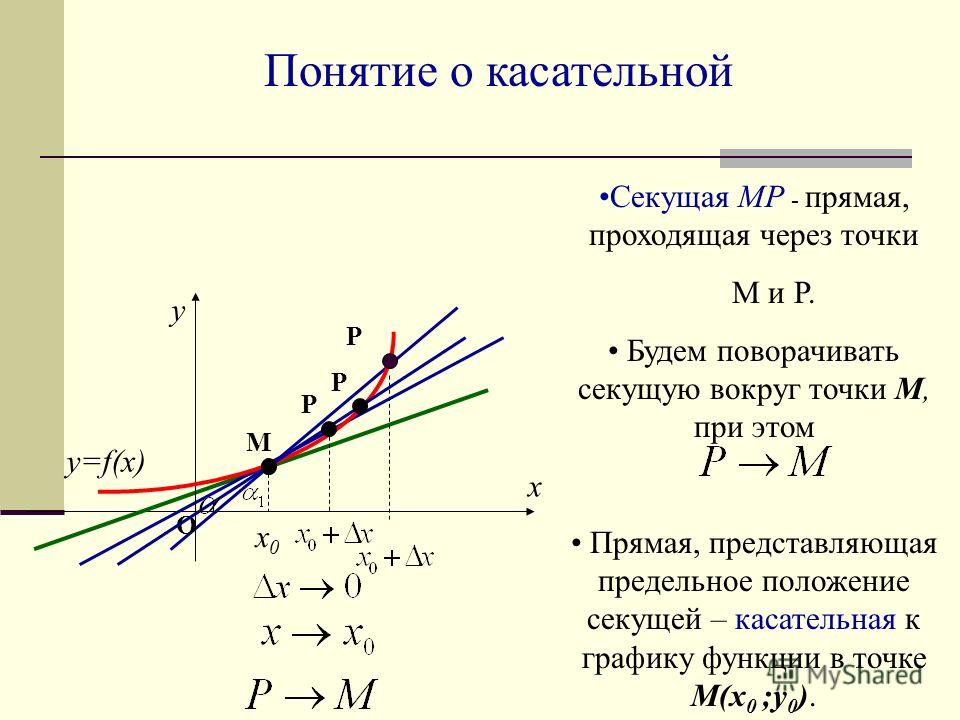
где p — полупериметр многоугольника.
По условию, P = 10, S = 5, тогда
Ответ: 1
Задачи ЕГЭ
1. Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.
Решение:
По условию, CA — касательная, A — точка касания.
. Треугольник ACO — прямоугольный, .
Угол — центральный, и он равен угловой величине дуги AB, на которую опирается. Значит, градусная мера дуги AB равна . Это меньшая дуга AB, а большая — с другой стороны от точек A и B, и она больше 180 градусов.
Ответ: 63.
2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна . Найдите угол ACB. Ответ дайте в градусах.
Решение:
Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть
AC и BC — касательные, поэтому , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.
Сумма углов четырехугольника ACBO равна
Ответ: 122.
3. Хорда AB стягивает дугу окружности в . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Решение:
Применим теорему об угле между касательной и хордой.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Значит, угол ABC равен .
Ответ: 46.
4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен . Найдите угол AOB. Ответ дайте в градусах.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Поэтому меньшая дуга AB окружности равна . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен .
Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.
Ответ: 64.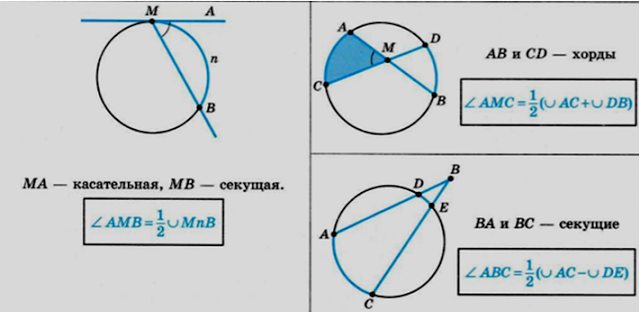
5. Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:
Ответ: 118.
6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Решение:
По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна . На эту дугу опирается центральный угол AOB, он равен . Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.
Ответ: 26.
Задачи ОГЭ по теме: Касательная к окружности
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Решение:
Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:
Ответ: 5.
2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный . Найдите величину угла OMK. Ответ дайте в градусах.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой. Тогда Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому
Ответ: 7.
3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:
Ответ: 10.
4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10.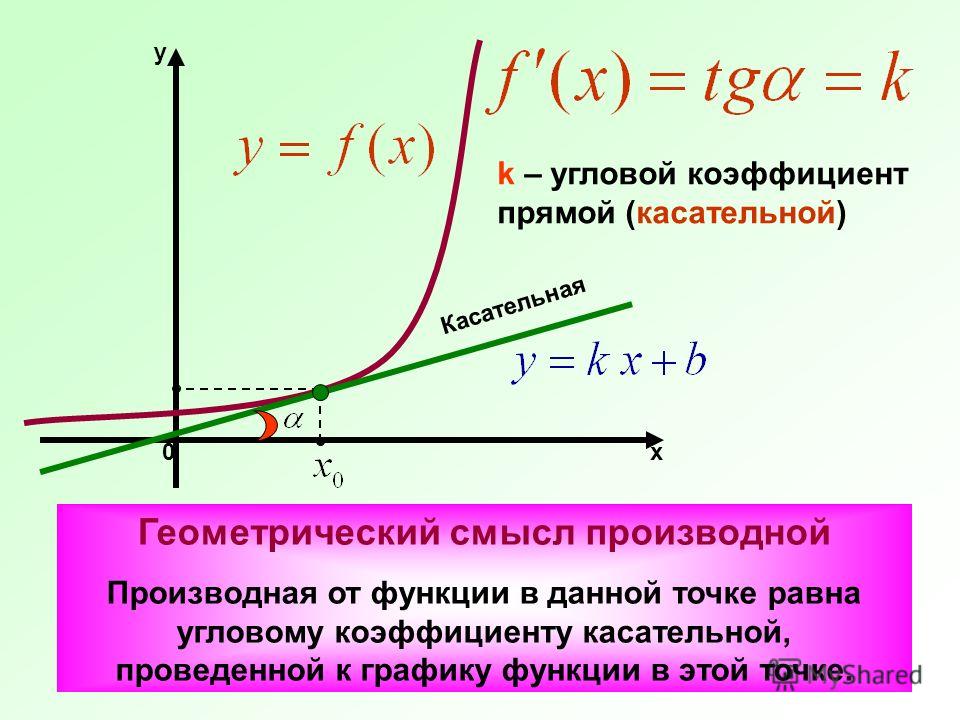
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Решение:
Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:
Ответ: 40.
5. Касательные в точках A и B к окружности с центром O пересекаются под углом . Найдите угол ABO. Ответ дайте в градусах.
Решение:
Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна . Угол AOB — центральный, он равен дуге, на которую опирается, то есть . Треугольник AOB равнобедренный,
Ответ: 36.
6. Из точки A проведены две касательные к окружности с центром в точке О.
Найдите радиус окружности, если угол между касательными равен , а расстояние от точки A до точки O равно 8.
Решение:
Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.
OB — OC как радиусы окружности, гипотенуза общая. Значит,
Из треугольника AOB найдём OB, то есть радиус окружности.
Ответ: 4.
7. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.
Решение:
По теореме о секущей и касательной,
Ответ: 4.
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
Ответ: 36.
Касательная окружности: уравнения, примеры и формулы
Касательная — это линия, которая совпадает с чем-либо в одной точке. Таким образом, касательная окружности — это линия, которая совпадает с окружностью в одной точке.
Например, является касательной к окружности
, потому что она касается окружности один раз в точке (3, 0).
Касательная к окружности
Касательная отличается от секущей тем, что секанс — это линия, пересекающая окружности в двух местах.
Как найти уравнение касательной окружности
Многие вопросы связаны с нахождением уравнения касательной окружности. Чтобы найти уравнение касательной окружности, нужно понять, как тангенс относится к радиусу окружности. Тангенс относится к радиусу между внешней точкой (точкой на окружности) и центром окружности. Внешняя точка действует как точка пересечения радиуса окружности и касательной.
Нахождение градиента радиуса между центром окружности и внешней точкой
Первым шагом для нахождения уравнения касательной окружности в конкретной точке является нахождение градиента радиуса окружности.
Вам нужен радиус между центром окружности и внешней точкой, потому что он будет перпендикулярен касательной. Это потому, что этот радиус окружности действует как нормаль к касательной.
Чтобы найти градиент радиуса круга, вы подставляете точки в центре круга и внешней точке в формулу градиента:
Окружность с уравнением касается касательной в точке (3, 0). Чему равен градиент радиуса окружности, перпендикулярной данной касательной?
:
Вы находите уравнение линии (радиуса), соединяющей центр окружности и внешнюю точку окружности (между синей и зеленой точками).
Следовательно, градиент радиуса окружности равен 0.
Нахождение градиента касательной окружности
Одна из наших теорем о кругах — уравнение биссектрисы. Здесь касательная окружности перпендикулярно пересекается с радиусом окружности. Следовательно, чтобы найти градиент касательной, вам нужно сделать отрицательную обратную величину градиента радиуса окружности.
Если градиент радиуса равен м, то градиент касательной равен.
Каков градиент касательной к окружности, если градиент радиуса той же окружности имеет градиент ?
- Отрицательная обратная величина касательной (¼) равна
Следовательно, градиент касательной окружности равен -4.
Нахождение уравнения касательной окружности
Когда у нас есть внешняя точка и градиент касательной, мы можем использовать формулу уравнения, чтобы найти уравнение касательной.
Есть три формулы, которые помогут составить уравнения касательной к окружности:
Первые два намного проще в использовании, чем третий. Поэтому, если вас попросят поместить ваш окончательный ответ в третью форму, используйте первую или вторую формулу, а затем переставьте ее в эту форму.
Касательная касается окружности A в точке (5, 6). Каково уравнение касательной окружности А, если градиент радиуса равен ?
- Чтобы найти градиент касательной, вы делаете отрицательное обратное выражение, поэтому
- Используя , вы можете подставить (5, 6) и градиент (5), а затем переставить
- или, используя и (5, 6)
Это те же уравнения:
Следовательно, уравнение о касании может быть написано на и.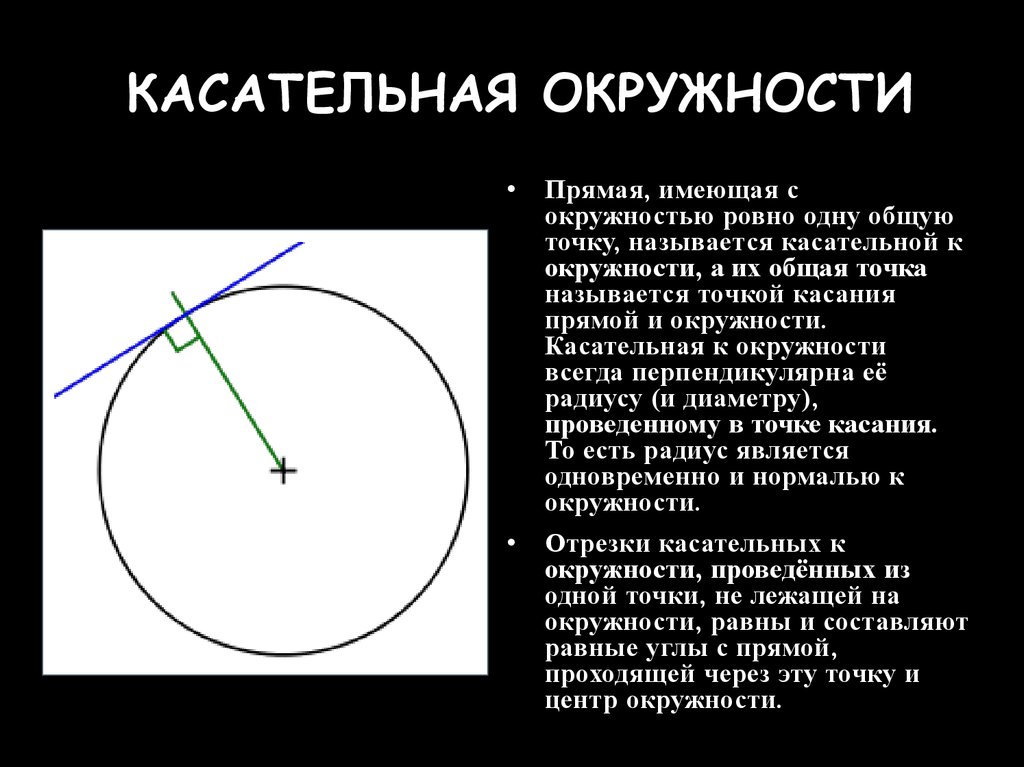
Рабочий пример для создания уравнения касательной окружности
Вопрос: Круг 1 имеет уравнение . Касательная выравнивается с окружностью 1 в точке (4, -3). Каково уравнение этой окружности?
Шаг 1: Найдите градиент радиуса окружности
- Поскольку к переменным x и y не привязаны константы, можно сделать вывод, что центр окружности равен (0,0).
- Чтобы найти градиент радиуса круга, вы подставляете свои координаты в формулу градиента.
.
- Следовательно, градиент окружности в точке (4, -3) равен .
Шаг 2: Найдите градиент касательной окружности
- Чтобы найти градиент касательной окружности, вы делаете обратную обратную величину градиента радиуса окружности.
- Следовательно, градиент касательной окружности равен
Шаг 3: Найдите уравнение касательной окружности
- Я буду использовать формулу, подставив градиент касательной к окружности ( ) и внешнюю точку (4, -3).
- Графически это можно представить следующим образом:
Касательная окружности — основные выводы линейное уравнение.
TAN Функция Excel (формула, примеры)
Функция TAN Excel — это встроенная в Excel тригонометрическая функция, используемая для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла. Здесь угол — это число в Excel.
Эта функция принимает только один аргумент, который представляет собой введенное число.Например, чтобы получить значение TAN 80 градусов в ячейке A1, мы можем использовать одну из следующих формул:
=TAN(RADIANS(A1))
= 5,671282.
Использование функций TAN и PI:
=TAN((A1*(PI()/180)))
=5,67.
Функция TAN Excel — это встроенная функция, классифицируемая как функция Math/Trig, которая возвращает тангенс угла. Формула для TAN всегда возвращает числовое значение.
В тригонометрии тангенс угла равен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона/соседняя сторона
Следовательно, TAN Θ = a/b
Содержание
- Функция TAN Excel
- Формула TAN в Excel
- Как использовать TAN в Excel?
- Тангенс в Excel, пример №1
- Тангенс в Excel, пример №2
- Тангенс в Excel, пример №3
- Тангенс, пример функции №4
- Рекомендуемые статьи
Ниже приведена формула 8 TAN1 в Excel 90 для ТАН в Excel.
Здесь число — это аргумент, передаваемый функции в радианах.
Угол, указанный нами в качестве входных данных, распознается функцией TAN, только если он определен в радианах.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математической зависимости.
Радиан = угол, градус * (π/180)
π в Excel представлен функцией PI()
Следовательно, радиан = градус *(PI()/180) Функции TAN и RADIANS:
Расчет значения TAN с использованием функций TAN и PI:
Функция TAN имеет множество практических применений. Он широко используется в архитектуре для вычисления высоты и длины геометрических фигур. Функция TAN используется в навигационных системах, GPS и аэронавтике.
Например, если самолет летит на высоте 3000 м и образует с наблюдателем на земле угол 26°, мы хотим найти расстояние от самолета до наблюдателя.
Поскольку мы знаем, что TAN Θ = противоположная сторона/соседняя сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А примыкающая сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.
Итак, используя формулу для TAN, мы имеем:
TAN(26°) = 3000/x
Следовательно, x = 3000/(TAN(26°))
В Excel, взяв относительную ссылку Относительная ссылкаВ Excel, относительные ссылки — это тип ссылки на ячейку, которая изменяется, когда одна и та же формула копируется в разные ячейки или рабочие листы. Допустим, у нас есть =B1+C1 в ячейке A1, и мы копируем эту формулу в ячейку B2, и она становится C2+D2.Читать больше значений, у нас есть,
X =B2/(TAN(B3*(PI()/180)))
X= 6150,91 метра
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять работу формулы для TAN в Excel на нескольких примерах.
Вы можете скачать этот шаблон Excel для функции TAN здесь — Шаблон Excel для функции TAN
Касательная в Excel, пример №1
Человек ростом 6 футов находится в 55 метрах от дерева.
Он делает угол 47° для зрения параллельно земле. Мы хотим вычислить высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию касательной.
Высота дерева будет равна:
Высота человека + расстояние человека от дерева * TAN(47°)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра)
Подставив все относительные значения в Excel, формула для высоты дерева будет:
=(0,3*B2)+(B3*TAN((B4*(PI()/180)) ))
TAN Вывод Excel:
Высота дерева 60,78 метра.
Касательная в Excel Пример #2
Предположим, у нас есть пять прямоугольных треугольников, учитывая углы и длину одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов треугольника равна 180.° Следовательно, мы можем легко вычислить третий угол.
Мы знаем, что Sin Θ = противоположность/гипотенуза.
Значит, длина противоположной стороны будет Sin Θ * Гипотенуза .
В Excel длина противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN:
=E2*SIN(C2*(PI()/180))
Применение формулы TAN для пяти треугольников, мы можем получить длины перпендикуляров треугольников.
Теперь у нас есть две стороны треугольника, гипотенуза и перпендикуляр. Используя TAN в Excel, мы можем легко вычислить третью сторону (основание).
Мы знаем, что TAN Θ = Противоположная сторона/Смежная сторона.
Значит, длина смежной стороны будет Противоположная сторона / TAN Θ.
В Excel формула TAN рассчитает длину прилегающей стороны (основания).
=F2/(TAN(РАДИАНЫ(C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.
TAN в Excel Вывод:
Тангенс в Excel Пример №3
Самолет выполняет разворот радиусом 160 м и летит с постоянным углом крена 87°.
Затем в идеальных условиях (отсутствие колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Формула дает радиус поворота.
Радиус поворота = V2/ g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена равен 87°, g — ускорение свободного падения, значение которого равно 9,8 м/с 2 , поэтому путевая скорость будет:
V = (Радиус поворота * (g * TAN Θ)) 1/2
Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN:
=КОРЕНЬ(B2*(9,8*(TAN(РАДИАНЫ(B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в Excel Вывод:
Итак, путевая скорость самолета составляет 172,97 м/с.
Пример функции тангенса #4
У нас есть формула для TAN, обозначенная как f(x) = 2c*TAN2Θ, где c — постоянное значение, равное 0,9.88. Значением варианта является значение Θ, а формула для TAN зависит от значения Θ.
Во-первых, нам нужно построить график данной касательной функции.
Используя функцию Excel TAN, мы затем рассчитаем значения функции, поэтому, взяв эталонные значения в качестве входных данных, мы получим формулу TAN:
= 2 * 0,988 * (TAN (РАДИАНЫ (2 * B3)) )
Применяя формулу TAN к другим ячейкам, мы имеем:
TAN в выходных данных Excel:
График функции касательной:
Рекомендуемые статьи
Эта статья представляет собой руководство по функции TAN Excel. Здесь мы обсуждаем формулу TAN в Excel и способы использования функции TAN, а также примеры Excel и загружаемые шаблоны Excel. Вы также можете посмотреть на эти полезные функции в Excel: –
- Функция EVEN в Excel
- Функция LOG в Excel
- Функция Excel
- RIGHT
- PI в ExcelPI В ExcelExcel есть встроенная функция PI() которая хранит точное значение до 15 знаков после запятой, эта функция используется в других формулах для дальнейшего расчета.
