А 1 а матрица: Обратная матрица онлайн

1.3.3. Обратная матрица

Пусть А – квадратная матрица порядка П. Матрица А-1 называется Обратной к матрице А, если

АА-1 = А-1А = Е.

Из того, что матрица А-1 может быть умножена на А как справа, так и слева, вытекает, что А-1 – тоже квадратная матрица порядка П.

Упражнение 1. Доказать, что (А-1)-1 = А.

Решение.

Пусть В = А-1. Тогда, поскольку по определению обратной матрицы

АВ = ВА = Е, матрица А является обратной для матрицы В, то есть

(А-1)-1 = А.

Из теоремы 3.1 следует, что |A||A-1| = |E| = 1. Таким образом, если у матрицы А существует обратная, то |A| ≠ 0 (такие матрицы называются Невырожден-ными) и

|A-1| = |A|-1.

Теорема 3.2 (о фальшивом разложении).

Для любой квадратной матрицы А = ||Aij|| Порядка п справедливы равенства

Доказательство.

В случае I = J эти формулы вытекают из формул (5) темы «Определители». Докажем равенство (1) при I ≠ J. Пусть для определенности I < J. Рассмотрим определитель матрицы, которая получена из А заменой J-ой строки на I-ую. По следствию 2.1 определитель такой матрицы равен нулю. Тем не менее напишем его разложение по J-ой строке:

Остается заметить, что алгебраические дополнения Bjk совпадают с Ajk. Аналогично доказывается равенство (2) при I ≠ J (здесь вместо строк надо рассматривать столбцы и разлагать нулевой определитель по столбцу).

Для квадратной матрицы А = ||Aij|| порядка П присоединенной называется матрица

Пример 2. Найдем для матрицы

Присоединенную. Имеем

Из теоремы 3.2 непосредственно вытекает

Следствие 3.1.

Теорема 3.3 (об обратной матрице). Для любой невырожденной матрицы А обратная матрица единственна и имеет вид

Доказательство.

В силу следствия 3.1 имеем:

Тем самым матрица, определенная равенством (3.3), действительно является обратной. Докажем единственность обратной матрицы. Предположим, что нашлись две обратные матрицы А1-1 и А2-1. Тогда, умножив равенство

АА1-1 = Е

Слева на А2-1, получим:

Отсюда, в силу того, что А2-1А = Е, вытекает равенство

А1-1 = А2-1.

Пример 3. Найдем обратную матрицу для

Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения:

Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце),

Поскольку |A| = 1· A11 + 0· A12 + 1· A13 = — 9, получаем:

Упражнение 2. Найти обратную матрицу для

Решение.

Проверим невырожденность матрицы А:

Следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:

Построим присоединенную матрицу:

Используя теорему 3.3, находим обратную матрицу:

Упражнение 3. Доказать, что (АВ)-1 = В-1А-1.

Решение.

Пусть С = В-1А-1. Тогда, применяя свойство 1 произведения матриц, понятие единичной матрицы (лекция 1) и определение обратной матрицы, получим:

Следовательно, матрица С = В-1А-1 удовлетворяет определению обратной матрицы для матрицы АВ. Значит, (АВ)-1 = В-1А-1.

< Предыдущая		Следующая >

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ — Студопедия

Поделись  

Обратная матрица

Пусть А – квадратная матрица порядка п.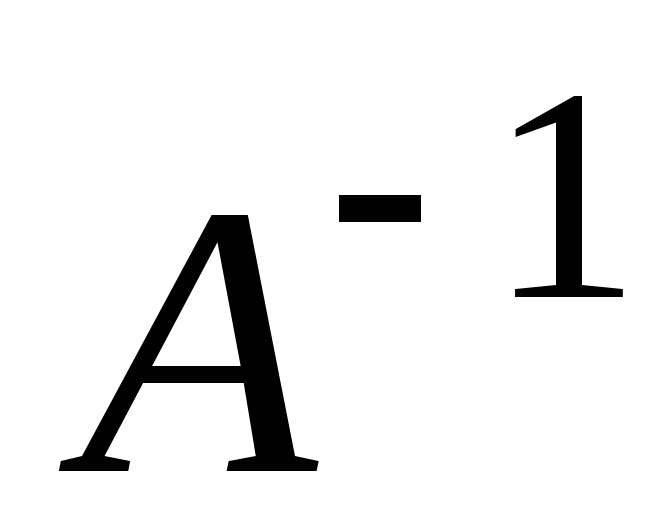 Матрица А^-1 называется обратной к матрице А, если

АА-1 = А-1А = Е.

 

Из того, что матрица А^-1 может быть умножена на А как справа, так и слева, вытекает, что А^-1 – тоже квадратная матрица порядка п.

 

Упражнение 1. Доказать, что (

А^-1)^-1 = А.

Решение.

Пусть В = А^-1. Тогда, поскольку по определению обратной матрицы

АВ = ВА = Е, матрица А является обратной для матрицы В, то есть

(А^-1)^-1 = А.

 

Из теоремы 3.1 следует, что |A||A^-1| = |E| = 1. Таким образом, если у матрицы А существует обратная, то |A| ≠ 0 (такие матрицы называются невырожден-ными) и

|A^-1| = |A|^-1.

 

 

Для квадратной матрицы А = ||a_ij|| порядка п присоединенной называется матрица

Пример 2. Найдем для матрицы

присоединенную. Имеем

 

 

Теорема об обратной матрице.Для любой невырожденной матрицы А обратная матрица единственна и имеет вид

 

 

Пример 3.Найдем обратную матрицу для

Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения:

Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце),

Поскольку |A| = 1· A₁₁ + 0· A₁₂ + 1· A₁₃ = — 9, получаем:

 

Упражнение 2. Найти обратную матрицу для

Решение.

Проверим невырожденность матрицы А:

следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:

Построим присоединенную матрицу:

Используя теорему 3.3, находим обратную матрицу:

 

 

Упражнение 3. Доказать, что (АВ)^-1 = В^-1А^-1.

 

Решение.

Пусть С = В^-1А^-1. Тогда, применяя свойство 1 произведения матриц, понятие единичной матрицы (лекция 1) и определение обратной матрицы, получим:

Следовательно, матрица С = В^-1А^-1 удовлетворяет определению обратной матрицы для матрицы АВ. Значит, (АВ)^-1 = В^-1А^-1.

 

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ

«Обратная матрица»

 

Задача 1.

Найти обратную матрицу для матрицы

и проверить выполнение условий ­А А^-1 = А^-1А = Е.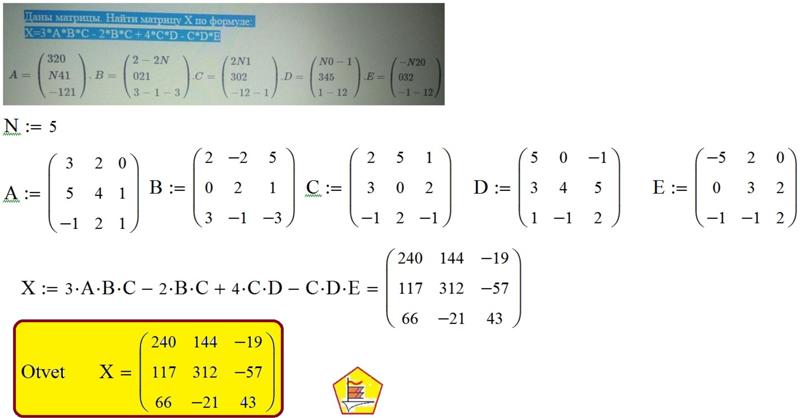

 

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

 

Решение

 

Убедимся, что матрица А – невырожденная. Δ_А = 1·4 — 2·(-1) ≠ 0, следовательно, А^-1 существует.

Вычислим алгебраические дополнения к элементам А:

Применим способ вычисления обратной матрицы:

.

 

Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам транспонированной матрицы!

 

Найдем произведения ­А А^-1 и А^-1А:

Таким образом, найденная матрица А^-1 отвечает определению обратной матрицы.

Ответ: .

 

Задача 2.

Найти обратную матрицу для матрицы

.

 

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.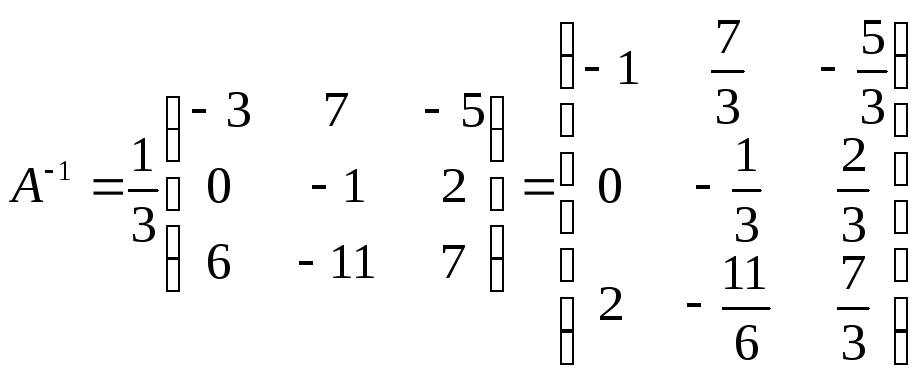

 

Решение

Следовательно, матрица А невырожденная, и обратная матрица существует.

Вычислим алгебраические дополнения к элементам матрицы А:

Обратная матрица имеет вид:

 

Ответ: .

 

Задача 3.

Найти обратную матрицу для матрицы

.

 

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

 

Решение

 

Вычислим определитель матрицы А разложением по первому столбцу:

.

Следовательно, обратная матрица для матрицы А существует.

Найдем алгебраические дополнения к элементам матрицы

А:

Значит,

.

Ответ: .

 

Задача 4.

Найти обратную матрицу для матрицы

.

 

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

 

Решение

 

.

 

 

Ответ:

 



Минор матрицы – формула, определение, примеры

Минор матрицы относится к каждому элементу матрицы и равен части матрицы, оставшейся после исключения строки и столбца, содержащего этот конкретный элемент. Новая матрица, образованная минорами каждого элемента данной матрицы, называется минором матрицы.

Минор матрицы широко используется при нахождении ее определителя, сопряженной и обратной матрицы. Давайте узнаем больше о миноре матрицы в приведенном ниже содержании.

1.	Что такое минор матрицы?
2.	Как найти минор матрицы?
3.	Применение минора матрицы
4.	Решенные примеры на миноре матрицы
5.	Практические вопросы
6.	Часто задаваемые вопросы о миноре матрицы

Что такое минор матрицы?

Минор матрицы для определенного элемента в матрице определяется как матрица, полученная после удаления строки и столбца матрицы, в которой находится этот конкретный элемент. Здесь минор элемента \(a_{ij}\) обозначается как \(M_{ij}\). Например, для данной матрицы A минор \(a_{12}\) является частью матрицы после исключения первой строки и второго столбца матрицы. \(A = \left[\begin{массив}{ccc}
а_{11} и а_{12} и а_{13} \\
а_{21} и а_{22} и а_{23} \\
а_{31} и а_{32} и а_{33}
\end{array}\right] \)

Минор элемента \(a_{12}\) выглядит следующим образом.

\(M_{12} = \left[\begin{array}{ccc} a_{21} & a_{23} \\
а_{31} и а_{33}
\end{array}\right] \)

Аналогично, мы можем взять миноры матрицы и сформировать минорную матрицу M данной матрицы A как:

\(M = \left[\begin{массив}{ccc}
М_{11} и М_{12} и М_{13} \\
М_{21} и М_{22} и М_{23} \\
М_{31} и М_{32} и М_{33}
\конец{массив}\справа] \)

Как найти минор матрицы?

Есть три простых шага, чтобы найти минор матрицы.

• Сначала идентифицируйте и исключите строку и столбец, содержащие определенный элемент в матрице.
• В качестве второго шага сформируйте новую меньшую матрицу из оставшихся элементов, чтобы представить минор определенного элемента матрицы.
• Наконец, найдите определитель минора каждого элемента матрицы и сформируйте новую матрицу, содержащую минорные значения соответствующих элементов.

Создает минор матрицы.

\(A =\begin{bmatrix}a_{11} & a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{ 33}\end{bmatrix}\)

Младший из \(a_{11} = M_{11} =\left|\begin{array}{ll}
а_{22} и а_{23} \\
а_{32} и а_{33}
\конец{массив}\право| = a_{22}.a_{33} — a_{23}.a_{32}\)

Младший из \(a_{23} = M_{23} =\left|\begin{array}{ll}
а_{11} и а_{12} \\
а_{31} и а_{32}
\конец{массив}\право| = a_{11}.a_{32} — a_{12}.a_{31}\)

Младший из \(a_{32} = M_{23} =\left|\begin{array}{ll}
а_{11} и а_{13} \\
а_{21} и а_{23}
\конец{массив}\право| = a_{11}.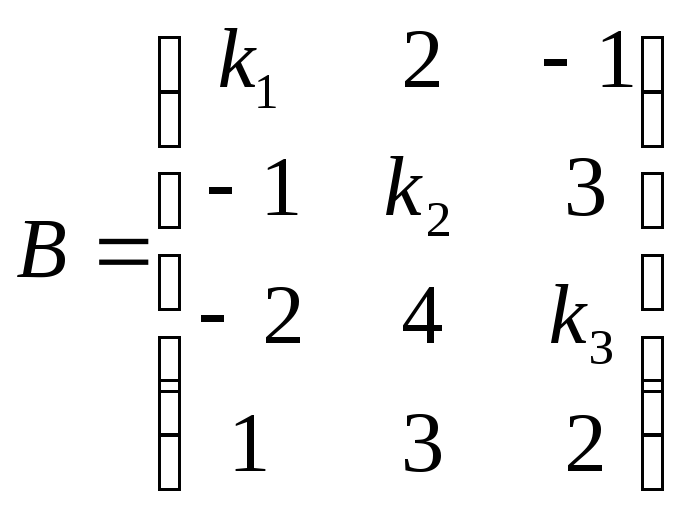 a_{23} — a_{13}.a_{21}\)

Аналогично можно найти минор каждого элемента матрицы A. Далее можно образовать минор матрицы A, записав минор каждого элемента в матричном массиве.

Минор матрицы A = \(\begin{bmatrix}M_{11} & M_{12}&M_{13}\\M_{21}&M_{22}&M_{23}\\M_{31}&M_{32 }&M_{33}\end{bmatrix}\)

Применение минора матрицы

Минор матрицы полезен для нахождения кофакторов элементов матрицы, что полезно для нахождения сопряженной матрицы и обратной матрицы. Также минор матрицы используется при вычислении определителя матрицы. Попробуем теперь понять следующие важные применения минора матрицы. 9{i+j}) M_{ij}\)

Матрица образована из кофакторов элементов матрицы и называется кофакторной матрицей.

Матрица кофакторов = \(\left[\begin{array}{ccc}
С_{11} и С_{12} и С_{13} \\
С_{21} и С_{22} и С_{23} \\
C_{31} и C_{32} и C_{33}
\end{array}\right] \)

Эта матрица сомножителей относится к приведенной ниже матрице A.

Определитель матрицы

Определитель матрицы представляет собой суммарное значение и рассчитывается с использованием матрица. Определитель матрицы равен сумме произведений элементов определенной строки или столбца с их соответствующими кофакторами. Скажем, рассмотрим матрицу A. 9{1 + 3} \left|\begin{matrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{matrix}\right|\)

Примыкание к матрице

сопряженную матрицу 3 x 3 можно получить, выполнив два простых шага. Сначала нам нужно найти матрицу кофакторов данной матрицы, а затем транспонировать матрицу этой матрицы кофакторов, чтобы получить сопряженную матрицу. Рассмотрим следующую матрицу A.

\(A = \begin{bmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31 }&a_{32}&a_{33}\end{bmatrix}\)

Кофакторная матрица \(A = \begin{bmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32} &A_{33}\end{bmatrix}\).

Adj A = транспонирование матрицы кофакторов = транспонирование \(\begin{bmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31 }&A_{32}&A_{33}\end{bmatrix}\) =\(\begin{bmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32} \\A_{13}&A_{23}&A_{33}\end{bmatrix}\)

Обратная матрица 9{1 + 3} \left|\begin{matrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{matrix}\right|\)

Adj A = транспонирование матрицы кофакторов = Транспонирование \(\begin{bmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33} \end{bmatrix}\) =\(\begin{bmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23 }&A_{33}\end{bmatrix}\)

A ^-1 = \(\dfrac{1}{|A|}\). \(\begin{bmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\end{ bматрица}\)

Связанные темы

Следующие связанные темы помогут лучше понять концепцию минора матрицы.

• Квадратная матрица
• Типы матриц
• Матричная формула
• Транспонирование матрицы

Часто задаваемые вопросы о миноре матрицы

Что такое минор матрицы?

Минор матрицы относится к каждому элементу матрицы и равен части матрицы, оставшейся после исключения строки и столбца, содержащего этот элемент. Минор матрицы определен только для квадратной матрицы. Минор элемента ‘a’ в матрице A = \(\begin{bmatrix}a & b\\c&d\end{bmatrix}\) равен d.

Как найти миноры матрицы?

Есть два простых шага, чтобы найти минор матрицы. Сначала идентифицируйте и исключите строку и столбец, который содержит конкретный элемент в матрице. Затем сформируйте новую меньшую матрицу из оставшихся элементов, чтобы представить минор конкретного элемента матрицы.

Минор элемента ‘e’ в матрице A = \(\begin{bmatrix}a&b & c\\d&e&f\\g&h&i\end{bmatrix}\) равен M = \(\begin{bmatrix}a & c\\g&i\end{bmatrix}\).

Как найти миноры матрицы 2 × 2?

Для матрицы порядка 2 × 2 вида A = \(\begin{pmatrix}a & b\\c&d\end{pmatrix}\) минор матрицы A = \(\begin{pmatrix}d & c\\b&a\end{pmatrix}\). Минор определенного элемента в матрице равен оставшемуся элементу после исключения строки и столбца, содержащего этот конкретный элемент.

В чем разница между минорами матрицы и кофактором матрицы?

Минор элемента \(a_{ij}\) обозначается как \(M_{ij}\). Кофактор матрицы получается из минора матрицы и равен произведению (-1) 9{i+j}) M_{ij}\).

Для чего используются миноры матрицы?

Минор матрицы полезен для нахождения кофакторов элементов матрицы. Миноры матрицы используются для нахождения значения определителя матрицы. Кроме того, эти миноры и кофакторы матрицы можно использовать для нахождения определителя матрицы, сопряженного к матрице и обратного к матрице.

Определение обратной матрицы

Предполагая, что у нас есть квадратная матрица A , которое невырожденно (т.е. det ( A ) не равно нулю), то существует n × n матрица A ^-1

обратная к A такая, что:
AA ^-1 = A ^-1 A = I , где I 90,223 — единичная матрица

Обратная матрица 2×2
Возьмем, к примеру, произвольную матрицу 2×2 9.0220 A , определитель которого (ad − bc) не равен нулю.

где a , b , c и d — числа.

Обратное:

Обратная матрица n × n A может быть найдена с помощью следующего уравнения.

где adj ( A ) обозначает сопряжение матрицы. Его можно рассчитать следующим методом:
Для матрицы A n × n определим B = b _ij как матрицу, коэффициенты которой находятся, взяв определитель -1) матрица , полученная удалением строки i ^th и столбца j ^th A .

Термины B (т.е. B = b _ij ) известны как кофакторы А .
Задайте матрицу C , где c _ij = (−1) ^i+j b _ij .

Транспонирование C (т.е. C ^T ) называется сопряженным к матрице A .

Пример 1:  . Найдите прил. A .
Решение :
Расчет прил А :
Кофактор 1 = a ₁₁ = — 4
Кофактор 3 = a ₁₂ = -1
Кофактор 7 = a ₁₃ = 6
Кофактор 4 = a ₂₁ = 11
Кофактор 2 = a ₂₂ = -6
Кофактор 3 = a ₂₃ = 1
Кофактор 1 = a ₃₁ = -5
Кофактор 2 = a ₃₂ =-25
Кофактор 1 = a ₃₃ = -10
Следовательно, мы имеем:

Пример 2: Найдите обратное число

Решение :
Следующий метод поиска обратного применим только для 2 × 2 матриц.

1. Замена ведущих диагональных элементов:
-7 → 2; 2 → -7

2. Измените знаки двух других элементов:
-3 → 3; 4 → -4

3. Найдите определитель | А |

4. Умножить результат [2] на 1/ | А |
 
 
Пример 3: Найти обратное число

Решение 3 : 3 : Матрица кофакторов для A может быть рассчитана следующим образом:
Кофактор 1 = a ₁₁ = 24
Кофактор 2 = a ₁₂ = 5
Кофактор 3 = a ₁₃ = -4
Кофактор 0 = a ₂₁ = -12
Сомножитель 4 = а ₂₂ = 3
Кофактор 5 = a ₂₃ = 2
Кофактор 1 = a ₃₁ = -2
Кофактор 0 = a ₃₂ = -5
Кофактор 6 = a ₃₃ = 4
Итак, кофактор
Следовательно, примыкание к .

И, наконец, число, обратное A , равно

Пример 4: Вычисление обратной величины

Решение : Матрица кофакторов для A 90 может быть рассчитана2 следующим образом: Сомножитель 3: а ₁₁ = 12
Сомножитель 2: а ₁₂ = 6
Кофактор -1: a ₁₃ = -16
Кофактор 1: a ₂₁ = 4
Сомножитель 6: a ₂₂ = 2
Кофактор 3: а ₂₃ = 16
Сомножитель 2: а ₃₁ = 12
Кофактор -4: a ₃₂ = -10
Сомножитель 0: a ₃₃ = 16

Таким образом, сомножитель
Поэтому сопряжение .