Свойства функции по ее графику. Основные элементарные функции и их свойства
Нули функции
Нулём функции называется то значение х , при котором функция обращается в 0, то есть f(x)=0.
Нули – это точки пересечения графика функции с осью Ох.
Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)
Четная функция симметрична относительно оси Оу
Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).
Нечетная функция симметрична относительно начала координат.
Функция которая не является ни чётной,ни нечётной называется функцией общего вида.
Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.
Убывание функции
Функция f(x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.
Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . Функция f(x) имеет 3 промежутка монотонности:
Находят промежутки монотонности с помощью сервиса Интервалы возрастания и убывания функции
Локальный максимум
Точка х 0 называется точкой локального максимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0) > f(x)
Локальный минимум
Точка х 0 называется точкой локального минимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0)
Точки локального максимума и точки локального минимума называются точками локального экстремума.
точки локального экстремума.
Периодичность функции
Функция f(x) называется периодичной, с периодом Т , если для любого х выполняется равенство f(x+T) = f(x) .
Промежутки знакопостоянства
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.
Непрерывность функции
Функция f(x) называется непрерывной в точке x 0 , если предел функции при x → x 0 равен значению функции в этой точке, т.е. .
Точки разрыва
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.
x 0 — точка разрыва.
Общая схема для построения графиков функций
1. Найти область определения функции D(y).
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график.
Пример: Исследовать функцию и построить ее график: y = x 3 – 3x
1) Функция определена на всей числовой оси, т. е. ее область определения D(y) = (-∞; +∞).
2) Найдем точки пересечения с осями координат:
с осью ОХ: решим уравнение x 3 – 3x = 0
с осью ОY: y(0) = 0 3 – 3*0 = 0
3) Выясним, не является ли функция четной или нечетной:
y(-x) = (-x) 3 – 3(-x) = -x 3 + 3x = — (x 3 – 3x) = -y(x)
Отсюда следует, что функция является нечетной.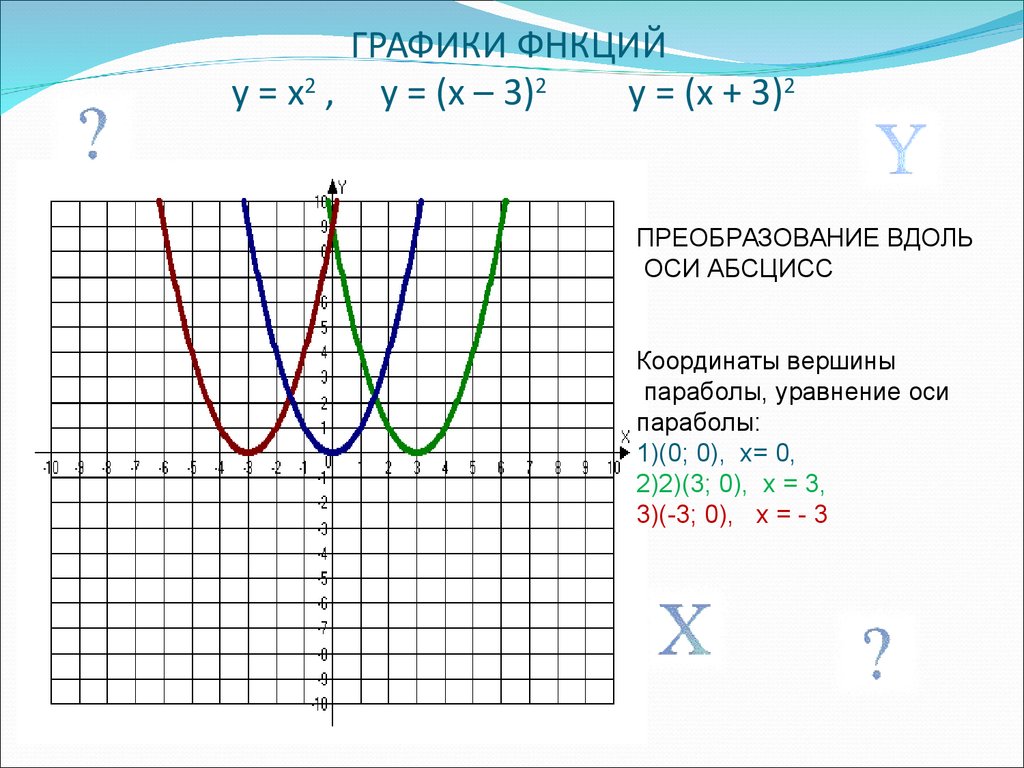
4) Функция непериодична.
5) Найдем промежутки монотонности и точки экстремума функции: y’ = 3x 2 — 3.
Критические точки: 3x 2 – 3 = 0, x 2 =1, x= ±1.
y(-1) = (-1) 3 – 3(-1) = 2
y(1) = 1 3 – 3*1 = -2
6) Найдем промежутки выпуклости и точки перегиба функции: y’’ = 6x
Критические точки: 6x = 0, x = 0.
y(0) = 0 3 – 3*0 = 0
7) Функция непрерывна, асимптот у нее нет.
8) По результатам исследования построим график функции.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.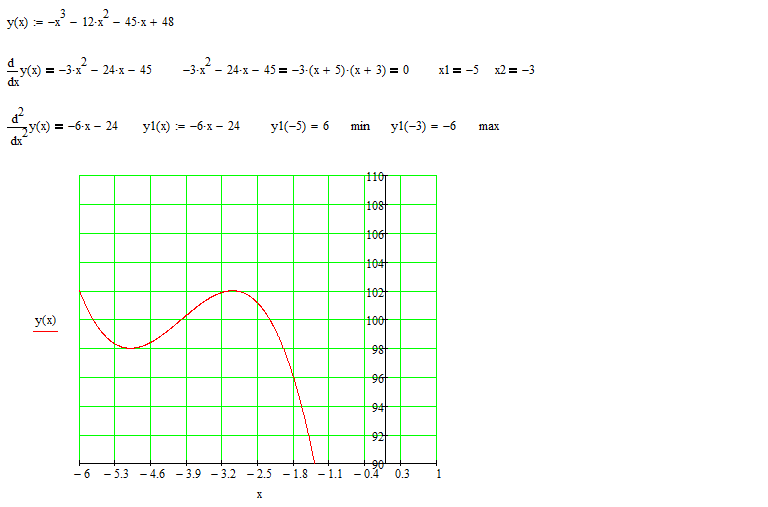
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.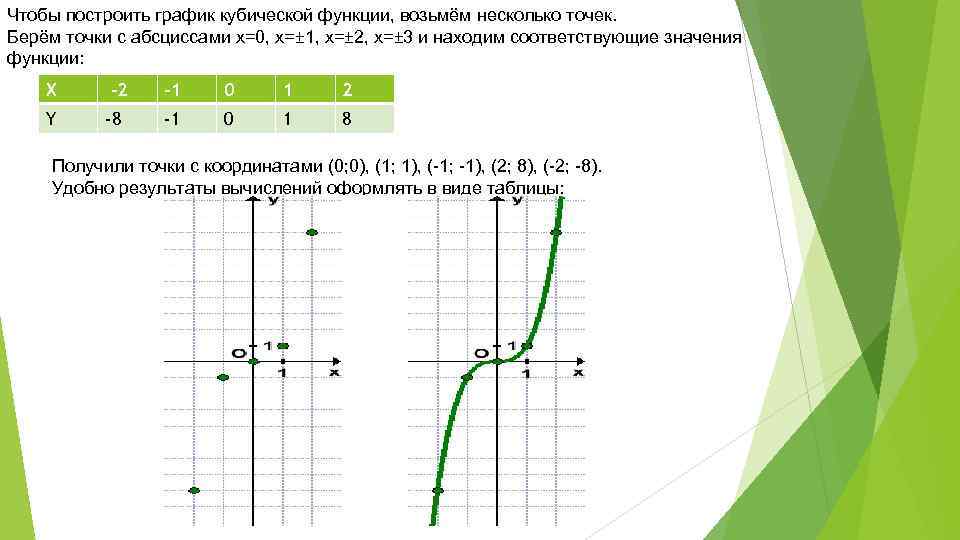
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Для понимая данной темы, рассмотрим функцию, изображенную на графике // Покажем, как график функции позволяет определить ее свойства.
Разбираем свойства функции на примере
Областью определения функции явл. промежуток [ 3,5; 5,5].
Областью значений функции явл. промежуток [ 1; 3].
1. При x = -3, x =- 1, x = 1,5, х=4,5 значение функции равно нулю.
Значение аргумента, при котором значение функции равно нулю, называют нулем функции.
//т.е. для данной функции числа -3;-1;1,5; 4,5 являются нулями.
2. На промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] график функции f расположен над осью абсцисс, а на промежутках (-3; -1) и (1,5; 4,5) под осью абсцисс, это объясняется так -на промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] функция принимает положительные значения, а на промежутках (-3; -1) и (1,5; 4,5) отрицательные.
Каждый из указанных промежутков (там где функция принимает значения одного и того же знака) называют промежутком знакопостоянства функции f.//т.е. например, если взять промежуток (0; 3), то он не является промежутком знакопостоянства данной функции.
В математике принято при поиске промежутков знакопостоянства функции указывать промежутки максимальной длины. //Т.е. промежуток (2; 3) является промежутком знакопостоянства функции f, но в ответ следует включить промежуток [ 4,5; 3), содержащий промежуток (2; 3).
3. Если перемещаться по оси абсцисс от 4,5 до 2, то можно заметить, что график функции идет вниз, то есть значения функции уменьшаются. //В математике принято говорить, что на промежутке [ 4,5; 2] функция убывает.
С увеличением x от 2 до 0 график функции идет вверх, т.е. значения функции увеличиваются. //В математике принято говорить, что на промежутке [ 2; 0] функция возрастает.
Функцию f называют , если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f (x2) > f (x1).
// или Функцию называют возрастающей на некотором промежутке
Функцию f называют убывающей на некотором промежутке , если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f(x2)убывающей на некотором промежутке, если для любых значений аргумента из этого промежутка большему значению аргумента соответствует меньшее значение функции. //т.е. чем больше х, тем меньше у.
Если функция возрастает на всей области определения, то ее называют возрастающей .
Если функция убывает на всей области определения, то ее называют убывающей .
Пример 1. график возрастающей и убывающей функций соотвественно.
Пример 2.
Определить явл. ли линейная функция f (x) = 3x + 5 возрастающей или убывающей?
Доказательство.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.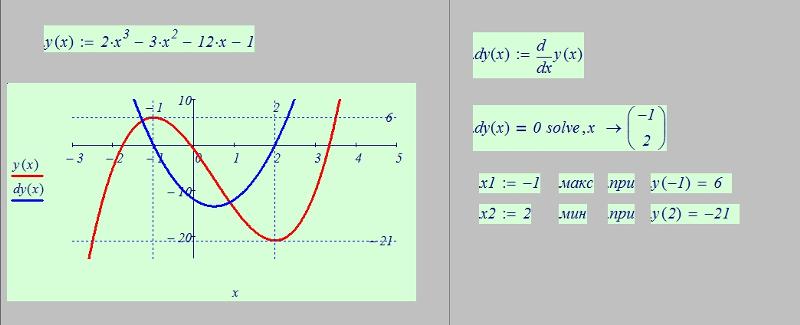
2} + 1\] 92} + 1 $, то $ (4,1) $ лежит на его обратном. Чтобы найти график прямой, достаточно координат двух точек, лежащих на прямой, но чтобы найти график кривой, нужно больше координат, чтобы наблюдать закономерность.
Недавно обновленные страницы
Если abc — это pthq-й и r-й термины GP, то left fraccb математика класса 11 JEE_Main
Если pthqth и rth термин GP — это abc соответственно математика класса 11 Ifc JEE_Main
любые четыре последовательные коэффициенты любого класса 11 математики JEE_Main
Если A1A2 являются двумя АП между двумя числами a и b, математика класса 11 JEE_Main
Если pthqthrth и sth члены AP находятся в GP, то p математика класса 11 JEE_Main
Один корень уравнения cos x x + frac12 0 лежит in class 11 maths JEE_Main
Если abc являются pthq и rth членами GP, то left fraccb class 11 maths JEE_Main
Если pthqth и rth члены GP равны abc соответственно, математика class 11 JEE_Main
Если abcda есть любые четыре последовательных коэффициента любой математики 11 класса JEE_Main
Если A1A2 являются двумя АП между двумя числами a и b, математика класса 11 JEE_Main
Если pthqthrth и sth члены AP находятся в GP, то p математика класса 11 JEE_Main
Один корень уравнения cos x x + frac12 0 лежит В классе 11 Maths Jee_main
Трендовые сомнения
Программное обеспечение
cdn.
kutasoftware.com › Рабочие листы › Alg1 › Наклон на графике
Рабочий лист от Kuta Software LLC. Программное обеспечение Kuta — Бесконечная алгебра 1 … Поиск наклона по графику. Найдите наклон каждой линии.
[PDF] Наклон из графика.pdf
www.cusd80.com › cms › lib6 › Centricity › Домен › Наклон от … Программное обеспечение Kuta — Бесконечная алгебра 1 … Поиск наклона по графику. Найдите наклон каждой линии.
[DOC] Модуль: Линейные уравнения
Teachers.henrico.k12.va.us › Math › Documents › studentnotesslope
ПОИСК НАКЛОНА НА ГРАФИКЕ ЛИНИИ: Пример 1: Объясните своими словами, как вы находите наклон линии, заданной на графике. Также объясните по-своему …
[PDF] Infinite Algebra 1 – 1.4 Нахождение наклона по графику
www.sd27j.org › cms › lib › Centricity › Domain › 1.4 Нахождение наклона …
Алгебра 1. 2017 ООО «Кута Софтвер». Α11 права защищены. 1.4 Нахождение наклона по графику.
Найдите наклон каждой линии.
Рабочие листы по уклону — Рабочие листы по математике для детей 4
www.mathworksheets4kids.com › уклон
Рабочие листы по уклону содержат идентифицирующие типы; нахождение склонов с использованием метода пропорций, двухточечной формулы, подсчета подъемов и пробегов и т. д.
Получение уклона из рабочего листа графика Форма и заполнение в… Подписывайте, отправляйте по факсу и распечатывайте с ПК, iPad, планшета или мобильного телефона с помощью pdfFiller ✓ Мгновенно. Попробуй сейчас!
Наклон из графиков Рабочий лист Учебные ресурсы | TPT
www.teacherspayteachers.com › Обзор › Search:sl…
Результаты 1 — 24 из 1300+ · Учащиеся найдут наклон 20 линейных функций по упорядоченным парам, таблице, графику или словесной ситуации .
[DOC] Форма пересечения наклона Рабочий лист
www.wsfcs.k12.nc.us › cms › lib › Centricity › Domain › Slope and …
Найдите наклон линии через каждую пару точек.