Пример расчета коэффициента корреляции Пирсона
Рассмотрим пример использования коэффициента корреляции Пирсона.
Например, нам необходимо определить взаимосвязь двух переменных агрессивности и IQ у школьников по полученным данным тестирования.
Данные сведем в одну таблицу:
| № | Данные по агрессивности () | Данные по IQ () |
| 1 | 24 | 100 |
| 2 | 27 | 115 |
| 3 | 26 | 117 |
| 4 | 21 | 119 |
| 5 | 20 | 134 |
| 6 | 31 | 94 |
| 7 | 26 | 105 |
| 8 | 22 | 103 |
| 9 | 20 | 111 |
| 10 | 18 | 124 |
| 11 | 30 | 122 |
| 12 | 29 | 109 |
| 13 | 24 | 110 |
| 14 | 26 | 86 |
1.
Вычисляем суму значений и
= 344
= 1549
2. Вычисляем среднее арифметическое для и
= 24,6
= 110,5
3. Вычисляем для каждого испытуемого отклонения от среднего арифметического для и
| № | ||
| 1 | 0,6 | 10,6 |
| 2 | -2,4 | -4,4 |
| 3 | -1,4 | -6,4 |
| 4 | 3,6 | -8,4 |
| 5 | 4,6 | -23,4 |
| 6 | -6,4 | 16,6 |
| 7 | -1,4 | 5,6 |
| 8 | 2,6 | 7,6 |
| 9 | 4,6 | -0,4 |
| 10 | 6,6 | -13,4 |
| 11 | -5,4 | -11,4 |
| 12 | -4,4 | 1,6 |
| 13 | 0,6 | 0,6 |
| 14 | -1,4 | 24,6 |
4.
Затем мы возводим в квадрат каждое отклонение:
| № | ||
| 1 | 0,36 | 112,36 |
| 2 | 5,76 | 19,36 |
| 3 | 1,96 | 40,96 |
| 4 | 12,96 | 70,56 |
| 5 | 21,16 | 547,56 |
| 6 | 40,96 | 275,56 |
| 7 | 1,96 | 31,36 |
| 8 | 6,76 | 57,79 |
| 9 | 21,16 | 0,16 |
| 10 | 43,56 | 179,56 |
| 11 | 29,16 | 129,96 |
| 12 | 19,36 | 2,56 |
| 13 | 0,36 | 0,36 |
| 14 | 1,96 | 605,16 |
5. Потом рассчитываем сумма квадратов отклонений: и
= 207,44
= 2073,24
6. Рассчитываем для каждого наблюдения произведение разности среднего арифметического и значения
| № | |
| 1 | 6,36 |
| 2 | 10,56 |
| 3 | 8,96 |
| 4 | -30,24 |
| 5 | -107,64 |
| 6 | -106,24 |
| 7 | -7,84 |
| 8 | 19,76 |
| 9 | -1,84 |
| 10 | -88,44 |
| 11 | 61,56 |
| 12 | -7,04 |
| 13 | 0,36 |
| 14 | -34,44 |
7.
Рассчитываем сумму
= -276,16
8. Подставляем полученные значения , , в формулу коэффициента корреляции Пирсона:
9. Вывод: В соответствии с таблицей значений величин коэффициента корреляции делаем вывод о том, что это слабая по силе отрицательная корреляция.
| Расчет коэффициента корреляции Пирсона | |
| Расчет коэффициента корреляции Пирсона в SPSS | Пример расчета коэффициента корреляции Пирсона в SPSS |
| Расчет коэффициента корреляции Пирсона в Excell | Пример расчета коэффициента корреляции Пирсона в Excell |
| Коэффициент корреляции Пирсона | |
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
Функция КОРРЕЛ в Excel используется для расчета коэффициента корреляции между для двух исследуемых массивов данных и возвращает соответствующее числовое значение.
Примеры использования функции КОРРЕЛ в Excel
Пример 1. В таблице Excel содержатся данные о курсе доллара и средней зарплате сотрудников фирмы на протяжении нескольких лет. Определить взаимосвязь между курсом валюты и средней зарплатой.
Таблица данных:
Формула для расчета:
Описание аргументов:
- B3:B13 – диапазон ячеек, в которых хранятся данные о среднем курсе доллара;
- C3:C13 – диапазон ячеек со значениями средней зарплаты.
Результат расчетов:
Полученный результат близок к 1 и свидетельствует о сильной прямой взаимосвязи между исследуемыми величинами. Однако прямо пропорциональной зависимости между ними нет, то есть на увеличение средней зарплаты оказывали влияние и прочие факторы.
Определение коэффициента корреляции влияния действий на результат
Пример 2. Два сильных кандидата на руководящий пост воспользовались услугами двух различных пиар-агентств для запуска предвыборной компании, которая длилась 15 дней.
Ежедневно проводился соцопрос независимыми исследователями, которые определяли процент поддержки одного и второго кандидата. Респонденты могли отдавать предпочтение первому, второму кандидату или выступать против обоих. Определить, насколько влияла каждая предвыборная кампания на степень поддержки кандидатов, какая из них оказалась более эффективной?
Исходные данные:
Произведем расчет коэффициентов корреляции с помощью формул:
=КОРРЕЛ(A3:A17;B3:B17)
=КОРРЕЛ(A3:A17;C3:C17)
Описание аргументов:
- A3:A17 – массив ячеек, содержащий номера дней предвыборной кампании;
- B3:B17 и C3:C17 – диапазон ячеек, содержащие данные о проценте поддержки первого и второго кандидатов соответственно.
Полученные результаты:
Как видно, уровень поддержки первого кандидата увеличивался с каждым днем кампании, поэтому коэффициент корреляции в первом случае стремится к единице. На старте кампании второй кандидат имел больший процент поддержки, и это значение на протяжении первых пяти дней демонстрировало положительную динамику изменений.
Анализ популярности контента по корреляции просмотров и репостов видео
Пример 3. Владелец канала YouTube использует социальную сеть для рекламы своих роликов. Он заметил, что между числом просмотров и количеством репостов в социальной сети существует некоторая взаимосвязь. Можно ли спрогнозировать виральность контента канала в Excel? Определить целесообразность использования уравнения линейной регрессии для предсказания количества просмотров роликов в зависимости от числа репостов.
Исходные данные:
Определим наличие взаимосвязи между двумя параметрами по формуле:
Если модуль коэффициента корреляции больше 0,7, считается рациональным использование функции линейной регрессии (y=ax+b) для описания связи между двумя величинами.
В данном случае:
Построим график зависимости числа просмотров от количества репостов, отобразим линию тренда и ее уравнение:
Используем данное уравнение для определения количества просмотров при 200, 500 и 1000 репостов:
=9,2937*D4-206,12
Полученные результаты:
Аналогичное уравнение использует функция ПРЕДСКАЗ. То есть, чтобы найти количество просмотров в случае, если было сделано, например, 250 репостов, можно использовать формулу:
Полученный результат:
Коэффициент корреляции – один из множества статистических критериев определения наличия взаимосвязи между двумя рядами значений. Для построения точных статистических моделей рекомендуется использовать дополнительные параметры, такие как коэффициент детерминации, стандартная ошибка и другие.
Особенности использования функции КОРРЕЛ в Excel
Функция КОРРЕЛ имеет следующий синтаксис:
=КОРРЕЛ(массив1;массив2)
Описание аргументов:
- массив1 – обязательный аргумент, содержащий диапазон ячеек или массив данных, которые характеризуют изменения свойства какого-либо объекта.
- массив2 – обязательный аргумент (диапазон ячеек либо массив), элементы которого характеризуют изменение свойств второго объекта.
Примечания 1:
- Функция КОРРЕЛ не учитывает в расчетах элементы массива или ячейки из выбранного диапазона, в которых содержатся данные текстового или логического типов. Пустые ячейки также игнорируются. Текстовые представления числовых значений учитываются.
- Если необходимо учесть логические ИСТИНА или ЛОЖЬ в качестве числовых значений 1 или 0 соответственно, можно выполнить явное преобразование данных используя двойное отрицание «—».
- Размерности массив1 и массив2 или количество ячеек, переданных в качестве этих двух аргументов, должны совпадать. Если аргументы содержат разное количество точек данных, например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом выполнения функции будет код ошибки #Н/Д.
- Если один из аргументов представляет собой пустой массив или массив нулевых значений, функция КОРРЕЛ вернет код ошибки #ДЕЛ/0!.
- Функция КОРРЕЛ производит расчет коэффициента корреляции по следующей формуле:
Примечание 2: Коэффициент корреляции представляет собой количественную характеристику степени взаимосвязи между двумя свойствами объектов. Этот коэффициент может принимать значения из диапазона от -1 до 1, при этом:
- Если значение коэффициента приближается к 1 или -1, между двумя исследуемыми свойствами существует сильная прямая или обратная взаимосвязи соответственно.
- Если значение коэффициента стремится к 0,5 или -0,5, два свойства слабо прямо или обратно взаимосвязаны друг с другом соответственно.
- Если коэффициент корреляции близок к 0 (нулю), между двумя исследуемыми свойствами отсутствует прямая либо обратная взаимосвязи.
Примечание 3: Для понимания смысла коэффициента корреляции можно привести два простых примера:
- При нагреве вещества количество теплоты, содержащееся в нем, будет увеличиваться. То есть, между температурой и количеством теплоты (физическая величина) существует прямая взаимосвязь.
- При увеличении стоимости продукции спрос на нее уменьшается. То есть, между ценой и покупательной способностью существует обратная взаимосвязь.
То есть, между температурой и количеством теплоты (физическая величина) существует прямая взаимосвязь.Помощь со статистикой Уравнения — Статистика Как
Справочник по статистике > Помощь со статистикой Уравнения
Нужна помощь со статистическими уравнениями? Вы найдете ответы здесь.
Нужна помощь по статистике? Если вы похожи на большинство людей, вам будет сложно разобраться с гигантскими статистическими уравнениями. Они занимают так много времени, и одна крошечная ошибка на этом пути сводит все на нет. Очень неприятно! Вот шесть способов получить помощь в решении статистических уравнений:
Помощь со статистическими уравнениями №1: онлайн-репетиторы.
Нужна помощь сейчас с конкретной домашней задачей или сложным вопросом подготовки к тесту? Посетите нашу страницу обучения.
Помощь со статистическими уравнениями № 2: Книга статистики практических обманов.
Это книга, которую ваш профессор не хочет, чтобы вы видели! Ушли в прошлое раздутые объяснения в вашей традиционной книге статистики. Вы получаете простые пошаговые решения задач, а также использование калькулятора TI-83 в классе. Нажмите здесь, чтобы узнать больше о справочнике по статистике практических махинаций.
Справочник по статистике практического мошенничества поможет вам с очень простыми пошаговыми инструкциями для каждой формулы статистики. Вот пример того, насколько это просто:
Страшная формула:
Простой ответ — шаг за шагом — из Справочника:
Зачем биться головой о стол, пытаетесь справиться с неприятными проблемами, когда можно пойти по легкому пути?
Книжный магазин колледжа Цена: $96 Распродажа Только $19,93
Хотите знать, что еще может сделать для вас Справочник по статистике практического мошенничества? Нажмите здесь, чтобы узнать больше!
Статистика Справка №3: Сотни статей с инструкциями.
Мы рассмотрели сотни тем с пошаговыми объяснениями на простом английском языке. Вот скриншот из одной из наших статей. Видишь, как легко?
Если вы хотите просмотреть такие категории, как доверительные интервалы или нормальное распределение, перейдите к основному указателю вероятностей и статистики. Вы найдете список основных разделов справки по статистике.
Если вы точно знаете, что ищете (например, «Как сделать гистограмму»), введите свой запрос в пользовательский поиск Google на боковой панели (или вверху страницы). Это выполнит поиск по сайту и даст вам именно ту статью, которая вам нужна.
Статистика Справка №4: Глоссарий статистики.
Вам нужны простые, понятные объяснения того, что означают статистические термины, такие как межквартильный размах, стандартное отклонение и дисперсия? Ознакомьтесь с нашими определениями статистики, в которых есть сотни объяснений всего, что вы хотели бы знать о вероятности и статистике.
Статистика Справка №5: Наш канал на YouTube.
На нашем канале YouTube можно найти десятки разделов статистики с простым объяснением. Подписывайтесь и следите за видео по мере их публикации. Вы найдете помощь по базовым понятиям, таким как межквартильный диапазон, и есть широкий выбор видеороликов Excel для статистики, которые помогут вам с анализом данных и графиками.
Статистика Справка №6: Онлайн-калькуляторы.
У нас есть множество бесплатных онлайн-калькуляторов статистики. Большинство из них не просто дадут вам ответ, они также покажут вам работу! Например, вот скриншот из нашего калькулятора дисперсии и стандартного отклонения. Обратите внимание на результат ниже:
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Помощь со статистическими уравнениями» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/practically-cheating-statistics-handbook/help-with-statistics-equations/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Линейная регрессия: простые шаги, видео. Уравнение поиска, коэффициент, наклон
Содержание:
Что такое простая линейная регрессия?
Как найти уравнение линейной регрессии:
- Как найти уравнение линейной регрессии вручную .
- Найдите уравнение линейной регрессии в Excel .
- TI83 Линейная регрессия.
- ТИ 89 Линейная регрессия
Поиск связанных элементов:
- Как найти коэффициент регрессии.
- Найдите наклон линейной регрессии.
- Найдите значение теста линейной регрессии.
Кредитное плечо:
- Кредитное плечо в линейной регрессии.
Наверх
Посмотрите видео с кратким введением в линейную регрессию:
Введение в линейную регрессию
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Если вы только начинаете изучать регрессионный анализ, простая линейная регрессия — это первый тип регрессии, с которым вы столкнетесь в классе статистики.
Линейная регрессия является наиболее широко используемым статистическим методом ; это способ моделирования связи между двумя наборами переменных. Результатом является уравнение линейной регрессии, которое можно использовать для прогнозирования данных.
Большинство программных пакетов и калькуляторов могут рассчитывать линейную регрессию. Например:
- ТИ-83.
- Эксель.
Вы также можете найти линейную регрессию вручную.
Перед тем, как приступить к вычислениям, вы всегда должны сделать точечный график, чтобы увидеть, соответствуют ли ваши данные примерно линии.
Почему? Потому что регрессия всегда даст вам уравнение, и оно может не иметь никакого смысла, если ваши данные следуют экспоненциальной модели. Если вы знаете, что взаимосвязь нелинейна, но не знаете точно, что это за взаимосвязь, одним из решений является использование моделей линейных базисных функций, которые популярны в машинном обучении.
Этимология
«Линейный» означает линию. Слово Регрессия произошло от ученого 19-го века, сэра Фрэнсиса Гальтона, который ввел термин «регрессия к посредственности» (на современном языке это регрессия к среднему). Он использовал этот термин для описания феномена того, как природа стремится к
Зачем использовать линейные отношения?
С линейными отношениями, т. е. с линиями, легче работать, и большинство явлений естественным образом линейно связаны. Если переменные не являются линейно связанными, тогда некоторая математика может преобразовать эту связь в линейную, чтобы исследователю (то есть вам) было легче ее понять.
Что такое простая линейная регрессия?
Вы, вероятно, знакомы с построением линейных графиков с одной осью X и одной осью Y. Переменную X иногда называют независимой переменной, а переменную Y — зависимой переменной. Простая линейная регрессия отображает одну независимую переменную X против одной зависимой переменной Y. Технически, в регрессионном анализе независимая переменная обычно называется переменной-предиктором, а зависимая переменная называется переменной-критерием. Однако многие люди просто называют их независимыми и зависимыми переменными. Более продвинутые методы регрессии (например, множественная регрессия) используют несколько независимых переменных.
Регрессионный анализ может дать линейных или нелинейных графиков. Линейная регрессия — это когда отношения между вашими переменными можно описать прямой линией. Нелинейные регрессии дают изогнутые линии.( ** )
Простая линейная регрессия для количества осадков за год.
Регрессионный анализ почти всегда выполняется с помощью компьютерной программы, поскольку вычисления уравнений вручную требуют очень много времени.
**Поскольку это вводная статья, я сделал ее простой. Но на самом деле между линейным и нелинейным существует важное техническое различие, которое станет еще более важным, если вы продолжите изучать регрессию. Подробнее см. в статье о нелинейной регрессии.
Вернуться к началу
Регрессионный анализ используется для поиска уравнений, соответствующих данным. Получив уравнение регрессии, мы можем использовать модель для прогнозирования. Одним из видов регрессионного анализа является линейный анализ. Когда коэффициент корреляции показывает, что данные, вероятно, могут предсказывать будущие результаты, а точечная диаграмма данных выглядит как прямая линия, вы можете использовать простую линейную регрессию, чтобы найти прогностическую функцию. Если вы помните из элементарной алгебры, уравнение прямой равно у = мх + б .
В этой статье показано, как брать данные, вычислять линейную регрессию и находить уравнение y’ = a + bx . Примечание : Если вы берете статистику AP, вы можете увидеть уравнение, написанное как b 0 + b 1 x, что то же самое (вы просто используете переменные b 0 + b 1 вместо a + b.0003
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Уравнение линейной регрессии
Линейная регрессия — это способ моделирования связи между двумя переменными. Вы также можете узнать это уравнение как формулу наклона . Уравнение имеет вид Y = a + bX, где Y — зависимая переменная (это переменная, которая идет по оси Y), X — независимая переменная (т. е. она отложена по оси X), b — наклон кривой линия и a — это точка пересечения с осью y.
Первым шагом в поиске уравнения линейной регрессии является определение наличия связи между двумя переменными.
Это часто является призывом к суждению для исследователя. Вам также понадобится список ваших данных в формате x-y (т. е. два столбца данных — независимые и зависимые переменные).
Предупреждения:
- То, что две переменные связаны, не означает, что одна вызывает другую. Например, хотя существует взаимосвязь между высокими баллами GRE и лучшей успеваемостью в аспирантуре, это не означает, что высокие баллы GRE равны 9.0018 причина хорошей успеваемости в аспирантуре.
- Если вы попытаетесь найти уравнение линейной регрессии для набора данных (особенно с помощью автоматизированной программы, такой как Excel или TI-83), вы найдете его, но это не обязательно означает, что уравнение является хорошим. подходит для ваших данных. Один из методов состоит в том, чтобы сначала построить точечный график, чтобы увидеть, соответствуют ли данные примерно линии до , когда вы пытаетесь найти уравнение линейной регрессии.
Как найти уравнение линейной регрессии: шаги
Шаг 1: Составьте диаграмму ваших данных, заполнив столбцы так же, как если бы вы находили коэффициент корреляции Пирсона.
| Субъект | Возраст x | Уровень глюкозы y | ху | х 2 | г 2 | 1 | 43 | 99 | 4257 | 1849 | 9801 |
|---|---|---|---|---|---|
| 2 | 21 | 65 | 1365 | 441 | 4225 | 3 | 25 | 79 | 1975 | 625 | 6241 |
| 4 | 42 | 75 | 3150 | 1764 | 5625 | 5 | 57 | 87 | 4959 | 3249 | 7569 |
| 6 | 59 | 81 | 4779 | 3481 | 6561 |
| Σ | 247 | 486 | 20485 | 11409 | 40022 |
Из приведенной выше таблицы Σx = 247, Σy = 486, Σxy = 20485, Σx2 = 11409, Σy2 = 40022.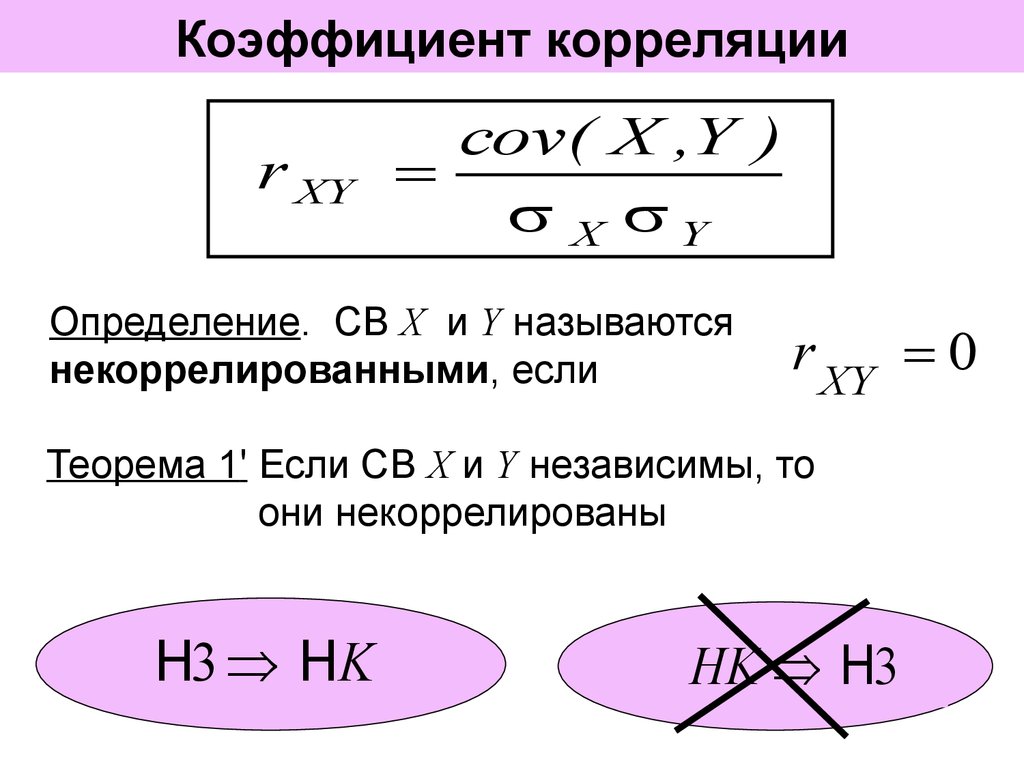
n — размер выборки (6 в нашем случае).
Шаг 2: Используйте следующие уравнения, чтобы найти a и b.
a = 65,1416
b = .385225
Щелкните здесь, если вам нужны простые пошаговые инструкции по решению этой формулы.
Найти :
- ((486 × 11 409) – ((247 × 20 485)) / 6 (11 409) – 247 2 )
- 484979 / 7445
- = 65,14
Найти b :
- (6(20,485) – (247 × 486)) / (6 (11409) – 247 2 )
- (122 910 – 120 042) / 68 454 – 247 2
- 2 868 / 7 445
- = .385225
Шаг 3: Вставьте значения в уравнение .
y’ = a + bx
y’ = 65,14 + 0,385225x
Вот как найти уравнение линейной регрессии вручную!
Нравится объяснение? Ознакомьтесь со Справочником по статистике практического мошенничества, в котором есть еще сотни пошаговых решений, таких как это!
* Обратите внимание, , что этот пример имеет низкий коэффициент корреляции и, следовательно, не слишком хорош для предсказания чего-либо.
Наверх
Посмотрите видео или прочитайте шаги ниже:
Как найти регрессию в Excel 2013
Посмотрите это видео на YouTube.
Уравнение линейной регрессии Microsoft Excel: Шаги
Шаг 1: Установите пакет инструментов анализа данных , если он еще не установлен. Инструкции по загрузке пакета инструментов анализа данных см. здесь.
Шаг 2: Введите данные в два столбца в Excel. Например, введите данные «x» в столбец A, а данные «y» — в столбец b. Не оставляйте пустых ячеек между вашими записями.
Шаг 3: Нажмите вкладку «Анализ данных» на панели инструментов Excel.
Шаг 4: Нажмите «регрессия» во всплывающем окне, а затем нажмите «ОК».
Всплывающее окно анализа данных имеет множество параметров, включая линейную регрессию.
Шаг 5: Выберите диапазон ввода Y. Вы можете сделать это двумя способами: либо выбрать данные на листе, либо ввести местоположение ваших данных в поле «Ввод диапазона Y».
Например, если ваши данные Y находятся в диапазоне от A2 до A10, введите «A2: A10» в поле «Входной диапазон Y».
Шаг 6: Выберите диапазон ввода X , выбрав данные на листе или введя местоположение ваших данных в поле «Диапазон ввода X».
Шаг 7: Выберите место, куда вы хотите отправить диапазон вывода, выбрав пустую область на листе или введя местоположение, куда вы хотите, чтобы ваши данные попали в поле «Диапазон вывода».
Шаг 8: Нажмите «ОК». Excel рассчитает линейную регрессию и заполнит лист результатами.
Совет. Информация об уравнении линейной регрессии содержится в последнем наборе выходных данных (столбец коэффициентов). Первая запись в строке «Пересечение» — «a» (пересечение по оси y), а первая запись в столбце «X» — «b» (наклон).
Вернуться к началу
Посмотрите видео с шагами:
TI83 Линейная регрессия
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
TI 83 Линейная регрессия: обзор
Линейная регрессия утомительна и подвержена ошибкам, когда выполняется вручную, но вы можете выполнить линейную регрессию за время, необходимое для ввода нескольких переменных в список. Линейная регрессия даст разумный результат только в том случае, если ваши данные выглядят как линия на точечной диаграмме, поэтому, прежде чем найти уравнение для линии линейной регрессии , вы можете сначала просмотреть данные на точечной диаграмме. См. эту статью, чтобы узнать, как сделать точечный график на TI 83.
TI 83 Линейная регрессия: шаги
Пример задачи: Найдите уравнение линейной регрессии (в форме y = ax + b) для значений x 1, 2, 3, 4, 5 и значений y 3, 9 , 27, 64 и 102.
Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы открыть экран списков. Если у вас уже есть данные в L1 или L2, очистите данные: переместите курсор на L1, нажмите CLEAR и затем ENTER.
Повторите для L2.
Шаг 2: Введите x-переменные по одной за раз. Следуйте за каждым числом, нажимая клавишу ENTER. Для нашего списка вы должны ввести:
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER
Шаг 3: С помощью клавиш со стрелками перейдите к следующему столбцу, L2.
Шаг 4: Введите переменные Y по одной за раз. Следуйте за каждым числом, нажимая клавишу ввода. Для нашего списка введите:
3 ENTER
9 ENTER
27 ENTER
64 ENTER
102 ENTER
Шаг 5: Нажмите кнопку STAT, затем с помощью клавиши прокрутки выделите «CALC».
Шаг 6: Нажмите 4, чтобы выбрать «LinReg(ax+b)». Нажмите ENTER, а затем снова ENTER. TI 83 вернет переменные, необходимые для уравнения. Просто вставьте заданные переменные (a, b) в уравнение линейной регрессии (y=ax+b). Для приведенных выше данных это y = 25,3x – 34,9 .
Вот как выполнить линейную регрессию TI 83!
Вернуться к началу
Помните из алгебры, что наклон — это «m» в формуле y = mx + b .
В формуле линейной регрессии наклон представляет собой a в уравнении у’ = b + ах .
По сути, это одно и то же. Поэтому, если вас попросят найти наклон линейной регрессии, все, что вам нужно сделать, это найти b так же, как вы нашли бы m .
Вычисление линейной регрессии вручную, мягко говоря, сложно. Есть лот суммирования (это символ Σ, что означает сложение). Основные шаги приведены ниже, или вы можете посмотреть видео в начале этой статьи. В видео более подробно рассказывается о том, как выполнять суммирование. Поиск уравнения также даст вам наклон. Если вы не хотите находить наклон вручную (или хотите проверить свою работу), вы также можете использовать Excel.
Как найти наклон линейной регрессии: Шаги
Шаг 1: Найдите следующие данные из предоставленной информации: Σx, Σy, Σxy, Σx 2 , Σy 2 .
Если вы не помните, как получить эти переменные из данных, см. эту статью о том, как найти коэффициент корреляции Пирсона. Следуйте указанным там шагам, чтобы создать таблицу и найти Σx, Σy, Σxy, Σx 2 и Σy 2 .
Шаг 2: Вставьте данные в b формула (нет необходимости находить a ).
Если вас пугают формулы, вы можете найти более подробные инструкции по работе с формулой здесь: Как найти уравнение линейной регрессии: обзор.
Как найти наклон регрессии в Excel 2013
Как найти регрессию в Excel 2013
Посмотрите это видео на YouTube.
Подпишитесь на наш канал Youtube, чтобы узнать больше советов и рекомендаций по статистике.
Вернуться к началу
Коэффициент регрессии — это то же самое, что и наклон линии уравнения регрессии . Уравнение для коэффициента регрессии, которое вы найдете в тесте AP Statistics, выглядит следующим образом: (х i – х) 2 ].
«у» в этом уравнении — это среднее значение у, а «х» — это среднее значение х.
Коэффициент регрессии можно найти вручную (как указано в разделе вверху этой страницы).
Однако вам не придется рассчитывать коэффициент регрессии вручную в тесте AP — вы будете использовать свой калькулятор TI-83. Почему? Вычисление линейной регрессии вручную требует очень много времени (выделите себе около 30 минут, чтобы выполнить расчеты и проверить их) и из-за огромное количество вычислений, которые вам нужно сделать, очень вероятно, что вы сделаете математические ошибки. Когда вы найдете уравнение линейной регрессии на TI83, вы получите коэффициент регрессии как часть ответа.
Пример задачи : Найдите коэффициент регрессии для следующего набора данных:
x: 1, 2, 3, 4, 5.
y: 3, 9, 27, 64, 102.
Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы войти в LISTS. Вам может потребоваться очистить данные, если у вас уже есть номера в L1 или L2.
Чтобы очистить данные: переместите курсор на L1, нажмите CLEAR и затем ENTER. Повторите для L2, если вам нужно.
Шаг 2: Введите x-данные в список. Нажимайте клавишу ENTER после каждого ввода.
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER
Шаг 3: Перейдите к следующему столбцу, L2, используя клавиши со стрелками в правом верхнем углу клавиатуры.
Шаг 4: Введите y-данные:
3 ВВЕДИТЕ
9 ВВЕДИТЕ
27 ВВЕДИТЕ
64 ВВЕДИТЕ
102 ВВЕДИТЕ
Шаг 5: Нажмите кнопку STAT, затем прокрутите до выделения «STAT». Нажмите ВВОД
Шаг 6: Нажмите 4, чтобы выбрать «LinReg(ax+b)». Нажмите Ввод. TI 83 вернет переменные, необходимые для уравнения линейной регрессии. Значение, которое вы ищете > коэффициент регрессии >, равно b, что составляет 25,3 для этого набора данных.
Вот и все!
Вернуться к началу
Две линии линейной регрессии.
Значения теста линейной регрессии используются в простой линейной регрессии точно так же, как значения теста (например, z-показатель или T-статистика) используются при проверке гипотез. Вместо работы с z-таблицей вы будете работать с t-таблицей распределения. Значение теста линейной регрессии сравнивается со статистикой теста, чтобы помочь вам подтвердить или отвергнуть нулевую гипотезу.
Значение теста линейной регрессии: Шаги
Пример вопроса : Учитывая набор данных с размером выборки 8 и r = 0,454, найдите значение теста линейной регрессии.
Примечание : r — коэффициент корреляции.
Шаг 1: Найдите r, коэффициент корреляции, , если он уже не был указан в вопросе. В этом случае задано значение r (r = 0,0454). Не знаете, как найти r? См. Коэффициент корреляции, чтобы узнать, как найти r.
Шаг 2: Используйте следующую формулу для вычисления контрольного значения ( n — размер выборки):
Как решить формулу:
- Замените переменные вашими числами:
T = . 454√((8 – 2)/(1-[.454] 2 )) - Вычесть 2 из n:
8 – 2 = 6 - Квадрат r:
.454 × .454 = .206116 - Вычесть шаг (3) из 1:
1 – .206116 = .793884 - Разделите шаг (2) на шаг (4):
6 / 0,793884 = 7,557779 - Извлеките квадратный корень из шага (5):
√7,557779 = 2,74914154 - Умножить r на шаг (6):
.454 × 2,74914154 = 1,24811026
- Вычесть 2 из n:
454√((8 – 2)/(1-[.454] 2 ))
Значение теста линейной регрессии, T = 1,24811026
Вот и все!
Нахождение статистики теста
Значение теста линейной регрессии бесполезно, если вам не с чем его сравнивать. Сравните свое значение с тестовой статистикой. Статистика теста также представляет собой t-показатель (t), определяемый следующим уравнением:
t = наклон линии выборочной регрессии / стандартная ошибка наклона.
См.: Как найти наклон линейной регрессии / Как найти стандартную ошибку наклона (TI-83).
Рабочий пример расчета значения теста линейной регрессии (с альфа-уровнем) можно найти здесь: Коэффициенты корреляции.
Вернуться к началу
Точки данных, имеющие рычаги, могут сместить линию линейной регрессии. Они склонны быть аутсайдерами. Выброс — это точка, которая является либо чрезвычайно высоким, либо чрезвычайно низким значением.
Влияющие точки
Если оценки параметров (выборочное стандартное отклонение, дисперсия и т. д.) значительно изменяются после удаления выброса, эта точка данных называется влиятельным наблюдением .
Чем больше точка данных отличается от среднего значения других x-значений, тем больше рычагов она имеет. Чем больше кредитное плечо у точки, тем выше вероятность того, что точка будет влиятельной (т.е. она может изменить оценки параметров).
Кредитное плечо в линейной регрессии: как оно влияет на графики
В линейной регрессии влиятельная точка (выброс) будет пытаться подтянуть линию линейной регрессии к себе.
На приведенном ниже графике показано, что происходит с линией линейной регрессии при включении выброса A:
Выбросы с экстремальными значениями X (значения, которые не находятся в диапазоне других точек данных) имеют большее значение в линейной регрессии, чем точки с менее экстремальными значениями x. Другими словами, 9Экстремальные выбросы x-значения 0018 сместят линию на больше, чем менее экстремальные значения.
На следующем графике показана точка данных за пределами диапазона других значений. Значения варьируются от 0 до примерно 70 000. Эта точка имеет значение x около 80 000, что выходит за пределы диапазона. Это влияет на линию регрессии намного больше, чем точка на первом изображении выше, которая находилась внутри диапазона других значений.
Выброс с высоким кредитным плечом. Точка сдвинула график больше, потому что она находится вне диапазона других значений.
Как правило, выбросы, значения которых близки к среднему значению x, будут иметь меньшее кредитное плечо, чем выбросы ближе к краям диапазона. Выбросы со значениями x за пределами диапазона будут иметь большее влияние. Экстремальные значения по оси Y (по сравнению с другими значениями) будут иметь большее влияние, чем значения, расположенные ближе к другим значениям Y.
Понравились видео? Подпишитесь на наш Youtube-канал.
Связь с аффинным преобразованием
Линейная регрессия бесконечно связана с аффинным преобразованием. Формула y′ = b + ax на самом деле не является линейной… это аффинная функция, которая определяется как линейная функция плюс преобразование. Так что это действительно следует называть аффинной регрессией, а не линейной!
Ссылки
Эдвардс, А. Л. Введение в линейную регрессию и корреляцию. Сан-Франциско, Калифорния: WH Freeman, 1976.
Эдвардс, А. Л. Множественная регрессия и анализ дисперсии и ковариации. Сан-Франциско, Калифорния: WH Freeman, 1979.