60 градусов это какой угол: 60 градусов это какой угол?

Углы 30, 45, 60, 90 градусов: наглядные, боевые, электрические

Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.

Содержание

1. Градусы наглядные: как их определить с помощью своей ладони
2. Градусы стихотворные и число «пи»
3. Градусы боевые: почему наши деды победили
4. Градусы электрические: отклонение между напряжением и током
5. Градусы драматические: косинус 90 градусов равен нулю
6. Градусы из радиоточки
7. Градусы музыкальные

Градусы наглядные: как их определить с помощью своей ладони

Рис. 1. Углы 0, 30, 45, 60 и 90 градусов.

Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!

Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…

Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.

А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.

Но не только об этом хотелось сказать, глядя на рисунок…

Градусы стихотворные и число «пи»

Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.

Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:

Кто и шутя, и скоро пожелаетъ
Пи узнать число  — ужъ знаетъ

Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».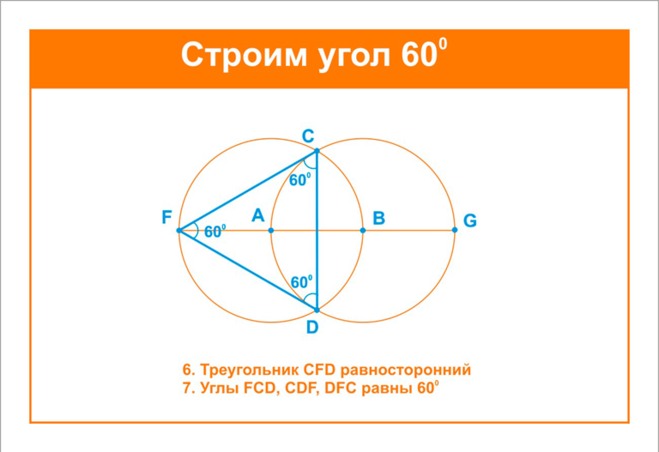

Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.

Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.

Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».

Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?

Градусы боевые: почему наши деды победили

Плывет боевой корабль. Вернее, идет боевой корабль, ибо корабли не плавают, а ходят. Штурман прокладывает курс на карте. И вдруг появляется супостат. Тревога!

Штурман откладывает карту в сторону. Достает маневренный планшет.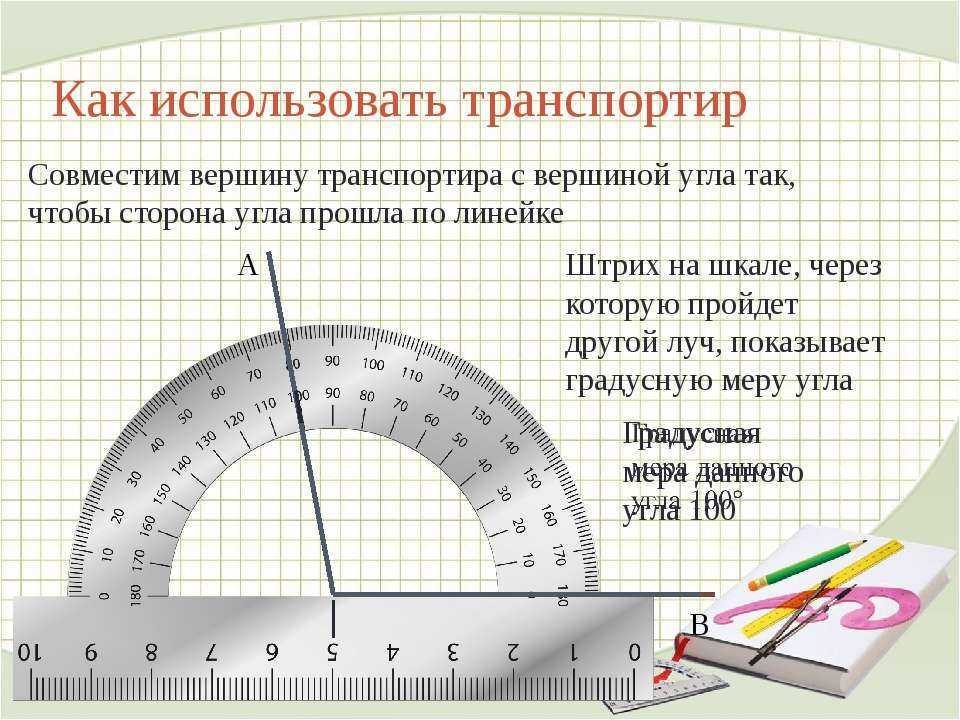 Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.

Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.

Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.

А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!

Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!

Градусы электрические: отклонение между напряжением и током

Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.

Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.

Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.

Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.

Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!

Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.

Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.

И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…

Градусы драматические: косинус 90 градусов равен нулю

А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!

Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.

Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.

Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.

Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.

Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.

Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…

Градусы из радиоточки

Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.

«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.

Пришло оно к нам из того самого электротехнического «косинуса фи».

Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…

Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.

Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «.., два тире один». Это про «наши» градусы, про «косинус фи»!

Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.

Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.

А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.

Градусы музыкальные

Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!

Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли:

Особые свойства треугольника с углом 60 градусов — NovaInfo 32

1. Баталаев А.В.

   Калмыцкий государственный университет

NovaInfo 32, скачать PDF
Опубликовано 13 марта 2015
Раздел: Физико-математические науки
Язык: Русский
Просмотров за месяц: 442
CC BY-NC

Аннотация

Треугольник с углом 60 градусов обладает необычными свойствами. Если этот треугольник не является правильным, то все три угла всегда образуют арифметическую прогрессию. Выполняется и обратное утверждение: Если сумма углов треугольника образует арифметическую прогрессию, то один из углов равен 60 градусам. Кроме того, между треугольниками с углами 45, 60, 75 и 30, 60, 90 градусов существует сложная взаимность.

Ключевые слова

ГЕОМЕТРИЯ, УГЛЫ, СВОЙСТВО ТРЕУГОЛЬНИКА, АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ, АЛГЕБРЫ, УГОЛ 60 ГРАДУСОВ, ВЗАИМНОСТЬ

Текст научной работы

Докажем свойство треугольника с углом 60 градусов.

Теорема. Если треугольник с углом 60 градусов не является правильным, то его углы составляют арифметическую прогрессию.

Рисунок 1.

Доказательство:

Пусть в треугольнике ABC угол B равен 60^о, а угол A=α (рис.1). Так как сумма углов треугольника равна 180^о, то ÐA+ÐC=120^o. Тогда, ÐС=120^o−α.

Таким образом, ÐA=α, ÐB=60^o=α+(60^o−α), ÐC=120^o−α=α+2(60^o−α) (1)

Из соотношения (1) видно, что углы треугольника составляют арифметическую прогрессию с разностью 60^o−α.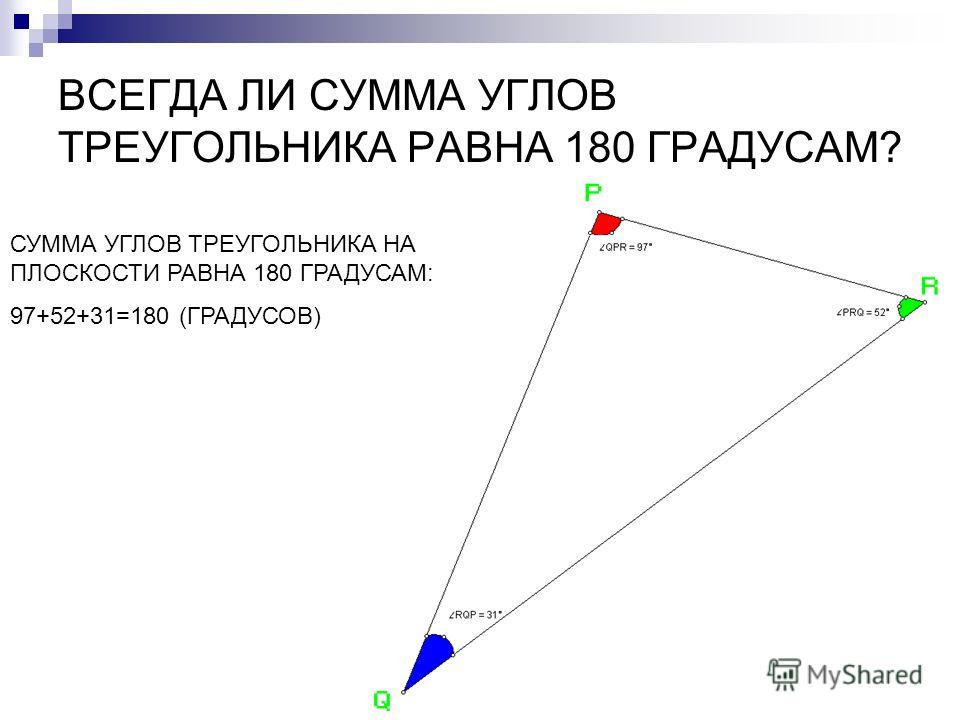 Теорема доказана.

Справедливо и обратное утверждение.

Теорема. Если углы треугольника составляют арифметическую прогрессию, то один из углов равен 60^о.

Рисунок 2.

Доказательство:

Пусть ÐA=α, ÐB=α+d, ÐC=α+2d (рис.2). Сумма углов треугольника равна 180^о, поэтому α+α+d+α+2d=180^o=>3α+3d=180^o=>α+d=60^o=>d=60^o−α.

Отсюда ÐB=α+60^o−α=60^o. Теорема доказана.

Существуют и другие необычные свойства треугольников с углами 60^о.

Для треугольника 45^о, 60^о, 75^о ортоцентрическим является треугольник с углами 30^о, 60^о, 90^о. Если продолжить высоты треугольника до их пересечения с описанной окружностью, то получим треугольник подобный высотному (рис.3).

Рисунок 3. Высотный треугольник и ему подобный

Назовём инцентрическим треугольник, образованный основаниями перпендикуляров опущенных из центра вписанной окружности на стороны. Для треугольника с углами 30^о, 60^о, 90^о инцентрическим будет треугольник с углами 45^о, 60^о, 75^о (рис.4).

Рисунок 4. Инцентрический треугольник

Читайте также

Список литературы

1. Алгебра. 9 класс : учеб. для общеобразоват. организаций [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова] ; под ред. С. А. Теляковского. – 21-е изд. – М.: Просвещение, 2014. – 271 с.: ил.
2. Геометрия: учеб. для 7-9 кл. сред. шк. /Л. С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1990. – 336 с.

Цитировать

Баталаев, А.В. Особые свойства треугольника с углом 60 градусов / А.В. Баталаев. — Текст : электронный // NovaInfo, 2015. — № 32. — URL: https://novainfo.ru/article/3266 (дата обращения: 28.11.2022).

Поделиться

Угол 60 градусов — Значение, конструкция, примеры

Угол 60 градусов является острым углом, так как углы меньше прямого угла (менее 90°) называются острыми углами. В случае геометрического угла дуга центрируется в вершине и ограничивается сторонами. В случае вращения дуга центрируется в центре вращения и ограничивается любой другой точкой и ее изображением при вращении. Давайте узнаем больше об углах 60 градусов, способах их построения и решим несколько примеров, чтобы лучше понять концепцию.

1.	Что такое угол 60 градусов?
2.	Значение угла 60 градусов
3.	Построение угла 60 градусов
4.	Углы 60 градусов в реальной жизни
5.	Часто задаваемые вопросы об угле 60 градусов

Что такое угол 60 градусов?

Угол 60 градусов является острым углом в геометрии и выражается как π/3 в радианах. Каждый угол равностороннего треугольника равен 60 градусам. Мы можем построить угол 60 градусов с помощью циркуля, транспортира и линейки и наблюдать этот угол в нашей повседневной жизни на различных объектах.

Значение угла 60 градусов

Мы знаем, что угол образуется, когда два луча встречаются в вершине. Если угол, образованный при вершине О, равен 60 градусам, мы называем его углом 60 градусов. Размер каждого угла равностороннего треугольника равен 60°. Поэтому его также называют треугольником с углом 60 градусов. Углы также могут быть представлены в радианах, т.е. пи (π) и пи (π) радиан = 180°. Следовательно, 60° можно выразить в радианах как π/3 радиан.

Построение угла 60 градусов

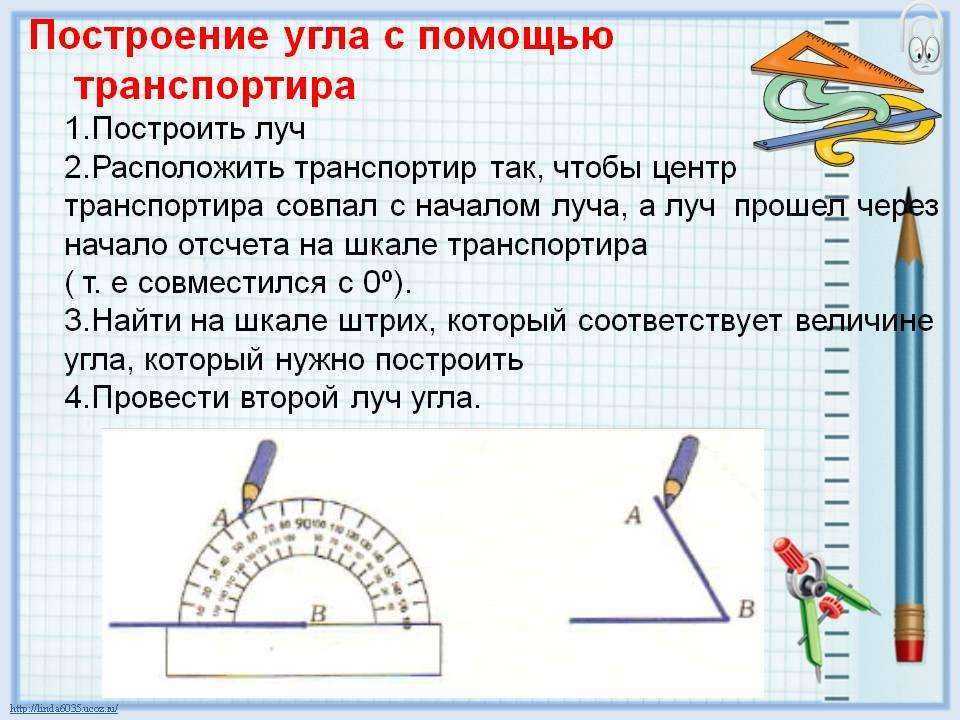
Построение угла 60 градусов является одним из самых основных построений, так как он формируется как строительный угол и для других измерений. Давайте рассмотрим, как построить угол 60 градусов с помощью транспортира. Выполните указанные шаги:

• Шаг 1: Нарисуйте отрезок OA
• Шаг 2: Поместите транспортир в точку O
• Шаг 3: Во внешнем круге транспортира найдите показание 60 градусов, карандашом отметьте точку и назовите ее C
• Шаг 4: Соедините O и C. Теперь ∠AOC=60°

Углы 60 градусов в реальной жизни

Углы окружают нас повсюду. Например, когда мы открываем рот, наши губы образуют угол. Когда минутная стрелка часов находится на 12, а часовая на 2, угол, образованный между двумя стрелками, составляет 60°. Некоторые дорожные знаки имеют форму равностороннего треугольника, а мера каждого угла равностороннего треугольника составляет 60°. Угол 60 градусов используется в архитектуре для создания дизайнерских домов, дверей и оконных решеток.

На изображении ниже показаны различные примеры ракурсов в нашем окружении. Обратите внимание, где вы можете видеть углы в 60 градусов в окружающих вас областях.

Важные замечания по углу 60 градусов

• Угол 60 градусов в геометрии является острым углом.
• Равносторонний треугольник называется треугольником с углом 60 градусов, так как мера каждого угла в нем равна 60 градусам.
• Мы можем построить угол 60 градусов, используя транспортир, циркуль и линейку.

Похожие статьи

• Угол 30 градусов
• Прямоугольный
• Угол 180 градусов
• Треугольники

 

Решенные примеры для угла 60 градусов

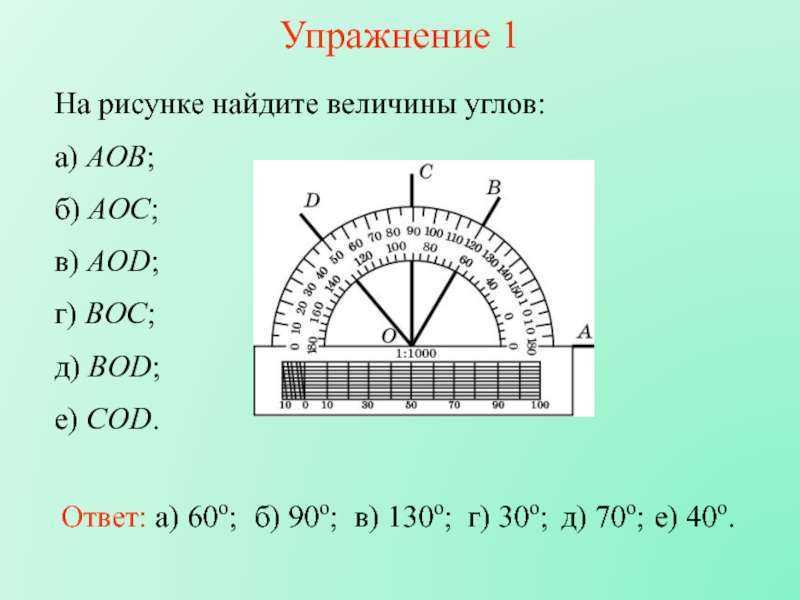
1. Пример 1: В ΔABC используйте транспортир для измерения ∠CAB.

   Решение: Поместите базовую линию транспортира вдоль линии AB и центр транспортира в вершине A. Обратите внимание на показания транспортира, которые перекрываются с линией AC.

   Ответ: Следовательно, ∠CAB = 60°

2. Пример 2: Помогите Джози построить угол 60°.

   Решение: Вот шаги, которые Джози может выполнить, чтобы построить угол 60°

   Шаг-1: Нарисуйте линию OP.

   Шаг 2:

   • Поместите транспортир на линию OP.
   • Поместите середину транспортира в точку O.

   Шаг-3:

   • На OP справа, начните отсчет с 0° в порядке возрастания, отметьте точку Q с помощью острого карандаша в точке, показывающей 60°.
   • Снимите транспортир и присоединитесь к OQ.
   • Получаем искомый угол ∠QOP = 60°.

   Ответ: Следовательно, ∠QOP = 60°

перейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по углу 60 градусов

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле 60 градусов

Что такое угол 60 градусов?

Угол в 60 градусов является острым, потому что он меньше 90 градусов. 60° в радианах равно π/3, а мера каждого угла равностороннего треугольника равна 60°. Поэтому его также называют треугольником с углом 60 градусов.

Как построить угол 60 градусов с помощью транспортира?

Чтобы построить угол в 60 градусов, необходимо 2 дуги, чтобы нарисовать угол в 60 градусов.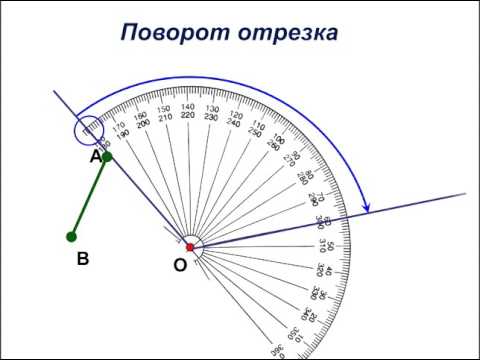 Вот шаги для построения угла в 60 градусов:

Шаг 1: Нарисуйте отрезок PQ
Шаг 2: Поместите транспортир в точку P
. Шаг 3: Во внешнем круге транспортира найдите показание 60°, отметьте карандашом точку и назовите ее R
. Шаг 4: Соедините P и R. Теперь ∠QPR=60°

Что вы называете углом в 60 градусов?

Угол, градусная мера которого больше 0°, но меньше 90°, называется острым углом. Углы 30°, 40°, 60° являются острыми углами. Поэтому угол в 60 градусов называется острым углом.

Как найти угол 60 градусов без транспортира?

Вот шаги, необходимые для построения угла 60 градусов без транспортира:

Шаг 1: Начертите отрезок (AB). Установив компас в точку A, проведите дугу через точку AB и вверх над указанной выше точкой A.

Шаг 2: Не изменяя ширину компаса, переместите компас в точку пересечения дуги AB и нарисуйте дугу, пересекающую первую.

Шаг 3: Соедините точку A с точкой пересечения двух дуг (точка C). ∠CAB = 60°

Сколько углов в 60 градусов нужно, чтобы сделать полный оборот?

Углы измеряются в градусах, и в одном полном обороте, который завершает один полный круг, содержится 360 градусов. Поскольку 60 × 6 = 360, значит, на один полный оборот приходится шесть углов по 60°.

Что такое угол 60 градусов в радианах?

Мы можем выразить угол 60 градусов в радианах, используя формулу: Угол в радианах = Угол в градусах × π/180. Итак, у нас есть 60 градусов в радианах = 60 × π/180 = π/3 радиан.

Скачать БЕСПЛАТНЫЕ учебные материалы

Угловые рабочие листы

Как построить угол 60 градусов — GCSE Maths

Введение

Как построить угол 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Как построить рабочий лист с углом 60 градусов

Как построить угол 30 градусов

Как построить угол 90 градусов

Как построить угол 45 градусов

Распространенные заблуждения

Похожие уроки

Попрактикуйтесь в составлении вопросов под углами 30, 60, 45, 90 градусов

Как построить углы 30, 60, 45, 90 градусов вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Как построить угол 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Как построить рабочий лист угла 60 градусов

Как построить угол 30 градусов

Как построить угол 90 градусов

Как построить угол 45 градусов

Распространенные заблуждения

Похожие уроки

Попрактикуйтесь в составлении вопросов под углами 30, 60, 45, 90 градусов

Как построить угол 30, 60, 45, 90 градусов вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы научимся строить углы в 30, 60, 45 и 90 градусов с помощью карандаша, линейки и циркуля.

Существуют также рабочие листы по конструированию на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что мы подразумеваем под углом 30, 60, 45, 90 градусов?

Построение 30, 60, 45, 9Угол 0 градусов точно строит эти углы без использования транспортира.

Для этого нам понадобится карандаш, линейка (линейка) и циркуль.

Угол 60 градусов можно построить, начертив равносторонний треугольник.
Тогда биссектриса угла образует угол в 30 градусов.

Угол 90 градусов можно построить с помощью биссектрисы.
Тогда биссектриса угла образует угол 45 градусов.

Что такое построение угла 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Чтобы построить угол 60 градусов:

1. Нарисуйте линию.
2. От одного конца линии проведите дугу.
3. От места пересечения дуги с линией нарисуйте еще одну дугу.
4. Соедините конечную точку линии с пересечением двух дуг.

Как построить угол 60 градусов

Как построить рабочий лист угла 60 градусов

Получите бесплатный рабочий лист Конструкции с более чем 20 вопросами и ответами, включая построение углов 30º, 60º, 90º без транспортира. Рассуждения и прикладные вопросы.

СКОРО

Икс

Как построить рабочий лист с углом 60 градусов

Получите бесплатный рабочий лист из 20+ вопросов и ответов, включая построение 30º, 60º, 9Углы 0º без транспортира. Рассуждения и прикладные вопросы.

СКОРО

Пример построения угла 60 градусов

Пример 1: построение угла 60 градусов

Построение угла 60 градусов

1. Нарисуйте линию.

Карандашом и линейкой проведите прямую линию

2 От одного конца линии проведите дугу.

Используйте циркуль с центром на одном конце линии, начертите дугу.

3 От места пересечения дуги с линией нарисуйте еще одну дугу.

Держите компасы в одном и том же положении. Новая дуга должна пересекать первую дугу.

4 Соедините конечную точку линии с пересечением двух дуг.

Используйте линейку, чтобы соединить конечную точку, использованную в шаге 2, с пересечением двух дуг.

Как построить угол 30 градусов

Чтобы построить угол 30 градусов:

1. Построить угол 60 градусов.
2. Построить биссектрису угла 60 градусов.

Как построить угол 30 градусов

Пример построения угла 30 градусов

Пример 2. Построение угла 30 градусов

Построение угла 30°

Построение угла 60 градусов.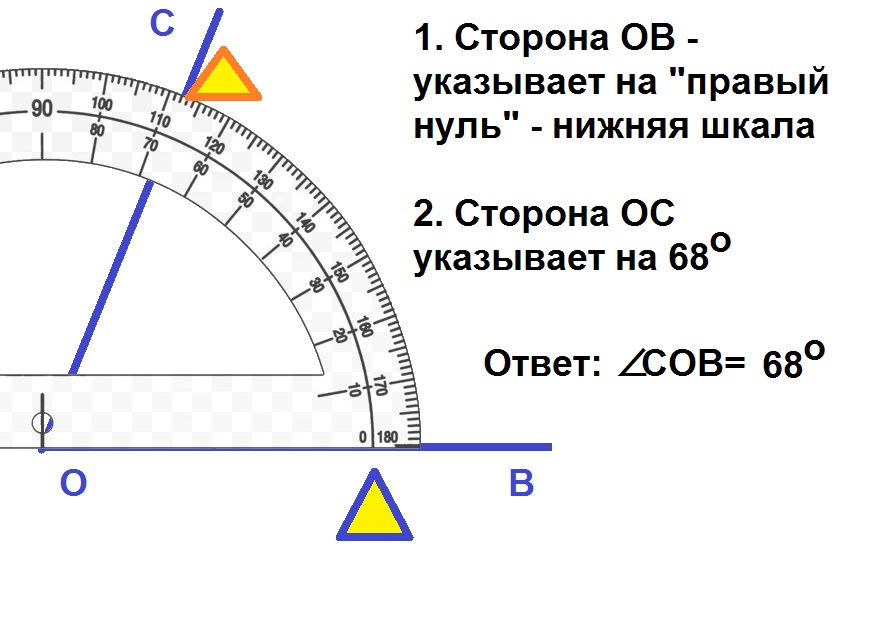

Выполните действия из примера 1, чтобы построить угол 60 градусов

Угол ABC равен 60°

Построить биссектрису угла 60 градусов.

Поместите острие компаса в точку А и начертите дугу. Держите циркуль в том же положении и повторите, поместив точку в C и нарисовав другую дугу. Используя линейку, соедините точку, где дуги пересекаются друг с другом, с вершиной B .

Угол в 60 градусов был разделен пополам на два равных угла по 30 градусов.

Как построить угол 90 градусов

Чтобы построить 9Угол 0 градусов:

1. Нарисуйте линию.
2. Построить серединный перпендикуляр.

Как построить угол 90 градусов

Пример построения угла 90 градусов

Пример 3: построение угла 90 градусов

Построение угла 90 градусов

Нарисуйте линию.

Построить серединный перпендикуляр.

Установите циркуль примерно на три четверти длины линии. Поместите острие циркуля на одну из конечных точек линии и нарисуйте дугу. Удерживая компасы в том же положении, нарисуйте еще одну дугу из другой конечной точки. Наконец, используйте линейку, чтобы соединить два пересечения дуг.

Новая линия является биссектрисой исходного сегмента линии.

Как построить угол 45 градусов

Чтобы построить угол 45 градусов:

1. Построить угол 90 градусов.
2. Постройте биссектрису угла 90 градусов.

Как построить угол 45 градусов

Пример построения угла 45 градусов

Пример 4: построить угол 45 градусов

построить угол 45°

построить угол 90 градусов.

Выполните действия из примера 3, чтобы построить угол 90 градусов

Постройте биссектрису угла 90 градусов.

Поместите острие циркуля в центр А и начертите дугу. Поместите острие циркуля в точку B и начертите дугу. Держите компасы в том же положении, поместите циркуль в точку С и начертите другую дугу, пересекая дугу, сделанную в точке В. Используя линейку, соедините точку, где дуги пересекаются друг с другом, с центром A.

Угол 90 градусов был разделен пополам на два равных угла по 45 градусов.

Распространенные заблуждения

• Карандаш должен быть острым

Острый карандаш поможет вашей диаграмме быть точной. Использование маленького карандаша в компасе также может быть полезным.

Как построить угол 30, 60, 45, 90 градусов – это часть нашей серии уроков, посвященных пересмотру конструкций. Возможно, вам будет полезно начать с урока по основным конструкциям, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя:

• Constructions
• Угол бисектор
• Как нарисовать шестигранник
• Конструирование треугольников
• между точками и линиями
• Perpendicular Bisector

Практика.