Задача №54. Расчёт коэффициента корреляции
Имеются данные о рейтинге авиакомпании и оценке ее безопасности. Вычислите линейный коэффициент корреляции.
| № п/п | Рейтинг авиакомпании, y | Оценка безопасности, х |
|---|---|---|
| 1 | 3,9 | 0,7 |
| 2 | 3,9 | 0,68 |
| 3 | 3,8 | 0,59 |
| 4 | 3,7 | 0,25 |
| 5 | 3,6 | 0,63 |
| 6 | 3,3 | 0,5 |
| 7 | 3,3 | 0,46 |
| 8 | 3,3 | 0,24 |
| 9 | 3,2 | 0,23 |
| 10 | 3,2 | 0,6 |
| 11 | 3,2 | 0,46 |
| 12 | 3,2 | 0,5 |
| 13 | 3,2 | 0,51 |
| 14 | 3,1 | 0,3 |
| 15 | 3,1 | 0,55 |
| 16 | 3,1 | 0,6 |
| 17 | 3,1 | 0,76 |
| 18 | 3,1 | 0,46 |
| 19 | 3,1 | 0,3 |
| 20 | 3 | 0,35 |
| 21 | 3 | 0,4 |
| 22 | 3 | 0,35 |
| 23 | 3 | 0,3 |
| 24 | 2,9 | 0,3 |
| 25 | 2,9 | 0,57 |
| 26 | 2,8 | 0,33 |
| 27 | 2,7 | 0,3 |
| 28 | 2,6 | 0,3 |
| 29 | 2,3 | 0,4 |
| 30 | 2,1 | 0,25 |
Решение:
Линейный коэффициент корреляции можно рассчитать по формуле:
Таблица 1 Расчетные данные для определения коэффициента корреляции
| № п/п | Рейтинг авиакомпании, y | Оценка безопасности, х | y2 | x2 | x*y |
|---|---|---|---|---|---|
| 1 | 3,9 | 0,7 | 15,21 | 0,49 | 2,73 |
| 2 | 3,9 | 0,68 | 15,21 | 0,4624 | 2,652 |
| 3 | 3,8 | 0,59 | 14,44 | 0,3481 | 2,242 |
| 4 | 3,7 | 0,25 | 13,69 | 0,0625 | 0,925 |
| 5 | 0,63 | 12,96 | 0,3969 | 2,268 | |
| 6 | 3,3 | 0,5 | 10,89 | 0,25 | 1,65 |
| 7 | 3,3 | 0,46 | 10,89 | 0,2116 | 1,518 |
| 8 | 3,3 | 0,24 | 10,89 | 0,0576 | 0,792 |
| 9 | 3,2 | 0,23 | 10,24 | 0,0529 | 0,736 |
| 10 | 3,2 | 0,6 | 10,24 | 0,36 | 1,92 |
| 11 | 3,2 | 0,46 | 10,24 | 0,2116 | 1,472 |
| 12 | 3,2 | 0,5 | 10,24 | 0,25 | 1,6 |
| 13 | 3,2 | 0,51 | 10,24 | 0,2601 | 1,632 |
| 14 | 3,1 | 0,3 | 9,61 | 0,09 | 0,93 |
| 15 | 3,1 | 0,55 | 9,61 | 0,3025 | 1,705 |
| 16 | 3,1 | 0,6 | 9,61 | 0,36 | 1,86 |
| 17 | 3,1 | 0,76 | 9,61 | 0,5776 | 2,356 |
| 18 | 3,1 | 0,46 | 9,61 | 0,2116 | 1,426 |
| 19 | 3,1 | 0,3 | 9,61 | 0,09 | 0,93 |
| 20 | 3 | 0,35 | 9 | 0,1225 | 1,05 |
| 21 | 3 | 0,4 | 9 | 0,16 | 1,2 |
| 22 | 3 | 0,35 | 9 | 0,1225 | 1,05 |
| 23 | 3 | 0,3 | 9 | 0,09 | 0,9 |
| 24 | 2,9 | 0,3 | 8,41 | 0,09 | 0,87 |
| 25 | 2,9 | 0,57 | 8,41 | 0,3249 | 1,653 |
| 26 | 2,8 | 0,33 | 7,84 | 0,1089 | 0,924 |
| 27 | 2,7 | 0,3 | 7,29 | 0,09 | 0,81 |
| 28 | 2,6 | 0,3 | 6,76 | 0,09 | 0,78 |
| 29 | 2,3 | 0,4 | 5,29 | 0,16 | 0,92 |
| 30 | 2,1 | 0,25 | 4,41 | 0,0625 | 0,525 |
| Итого | 93,7 | 13,17 | 297,45 | 6,4667 | 42,026 |
| Среднее | 3,123333333 | 0,439 | 9,915 | 0,215557 | 1,400867 |
Полученный коффициент означает, что связь между рейтингом авиакомпании и оценкой ее безопасности оценивается как прямая (так как значение коэффициента положительное, в противном случае связь оценивалась бы как обратная), умеренная (в соответствии со шкалой Чеддока, смотри задачу №47).
Коэффициент корреляции в Excel – как рассчитать, использовать корреляционный анализ, построить корреляционное поле или матрицу, примеры использования
Excel КомментироватьЗадать вопросНаписать пост
Коэффициент корреляции показывает наличие или отсутствие зависимости между различными факторами, выраженными в числовой форме. Этот показатель может принимать значения от -1 до +1. Чем ближе число по модулю к единице, тем сильнее зависимость. При значении коэффициента равном 0 зависимость между двумя величинами отсутствует.
Выявив корреляционную зависимость, можно прогнозировать поведение одного из показателей, проанализировав поведение другого.
Вычисление коэффициента посредством мастера функций
Предположим, что требуется установить связь между затратами на рекламу и объемом продаж какой-либо продукции. Для этого будем использовать коэффициент корреляции в Excel.
Порядок действий:
- Кликнуть по ячейке, в которой должен появиться результат.
- Нажать кнопку «Вставить формулу».
- В появившемся окне выбрать категорию «Полный алфавитный перечень».
- Найти и активировать функцию «КОРРЕЛ».
- Кликнуть «ОК».
- В открывшемся окне аргументов поставить курсор в поле «Массив 1», выделить первый столбец с данными.
- Поставить курсор в поле «Массив 2», выделить второй столбец из таблицы.
- Кликнуть «ОК».
В выделенной ячейке появляется результат вычислений корреляции в Excel.
Расчёт с помощью пакета анализа
Прежде чем воспользоваться инструментом корреляционного анализа, его нужно активировать. Для этого необходимо выполнить следующие действия:
- Выполнить действия « Файл» — «Сведения» — «Параметры».
- В появившемся окне перейти в раздел «Надстройки». В нижней части окна в выпадающем списке выбрать «Надстройки Excel». Нажать кнопку «Перейти».
- В открывшемся окне «Надстройки» следует отметить пункт «Пакет анализа» и нажать «ОК»
В нижней части окна в выпадающем списке выбрать «Надстройки Excel». Нажать кнопку «Перейти».Чтобы воспользоваться пакетом, следует:
- На панели задач активировать вкладку «Данные».
- Нажать кнопку «Анализ данных».
- В новом окне выделить строку «Корреляция» и нажать «ОК». Появится окно с параметрами.
- Для выбора входного интервала необходимо установить курсор в соответствующее поле и выделить сразу оба столбца.
- Параметр группировки следует отметить «по столбцам». Вывод результатов возможен в указанное место, на новый лист или в новую книгу.
- Следует отметить соответствующее поле.
После указание всех параметров следует нажать «ОК».
Значение получилось тем же, что и в первом случае.
Поле корреляции (диаграмма рассеяния)
Корреляционное поле — это графическое отображение исходных данных. По расположению точек можно определить наличие зависимости и ее характер.
В редакторе Excel построение выполняется с помощью инструмента «Диаграмма»:
- Выделить столбцы с данными.
- Кликнуть «Вставка» — «Точечная» — «Точечная с маркерами».
Результат построения корреляционной матрицы.
По расположению точек на диаграмме можно сделать вывод о том, что прослеживается сильная положительная корреляционная зависимость между величиной затрат на маркетинг и объемом продаж.
Для того, чтобы использовать диаграмму в практических целях, можно добавить линию тренда и уравнение. Для этого нужно выполнить следующие действия:
- Кликнуть правой кнопкой мыши на любой точке диаграммы.
- В контекстном меню выбрать «добавить линию тренда».
- Настроить параметры линии тренда (можно оставить по умолчанию).
- Нажать кнопку «закрыть».
Примеры использование корреляционного анализа
Как уже отмечалось выше, вычислить соотношение можно между любыми числовыми величинами. Обнаруженная высокая корреляция позволяет прогнозировать
В рассмотренном выше примере была установлена высокая положительная корреляция между затратами на рекламу и объемом продаж определенного вида продукции. Кроме того, была определена формула, связывающая эти два показателя. Это исследование позволяет руководителю предприятия грамотно спланировать затраты на рекламу, с учетом необходимого размера продаж.
Другие примеры использования коэффициента корреляции:
- зависимость средней заработной платы от величины областного бюджета;
- связь между числом репостов в социальных сетях и количеством просмотров видео на YouTube;
- связь коэффициента интеллекта и длины прыжка с места.
Редактор электронных таблиц Microsoft Excel является удобным инструментом для вычисления и наглядного представления результатов вычисления коэффициента корреляции.
На главную
Reader Interactions
Что это такое, что он говорит инвесторам
Что такое коэффициент корреляции?
Коэффициент корреляции является статистической мерой силы линейной связи между двумя переменными. Его значения могут находиться в диапазоне от -1 до 1. Коэффициент корреляции, равный -1, описывает полную отрицательную или обратную корреляцию, при которой значения в одном ряду возрастают, а значения в другом снижаются, и наоборот. Коэффициент 1 показывает идеальную положительную корреляцию или прямую связь. Коэффициент корреляции 0 означает отсутствие линейной зависимости.
Коэффициенты корреляции используются в науке и финансах для оценки степени связи между двумя переменными, факторами или наборами данных. Например, поскольку высокие цены на нефть благоприятны для производителей сырой нефти, можно предположить, что корреляция между ценами на нефть и форвардной доходностью акций нефтяных компаний строго положительна.
Расчет коэффициента корреляции для этих переменных на основе рыночных данных показывает умеренную и непостоянную корреляцию в течение длительных периодов времени.
Основные выводы
- Коэффициенты корреляции используются для оценки силы связи между переменными данных.
- Наиболее распространенный, называемый коэффициентом корреляции Пирсона, измеряет силу и направление линейной зависимости между двумя переменными.
- Значения всегда находятся в диапазоне от -1 для абсолютно обратной или отрицательной зависимости до 1 для абсолютно положительной корреляции. Значения, равные или близкие к нулю, указывают на отсутствие линейной зависимости или на очень слабую корреляцию.
- Значения коэффициентов, необходимые для сигнализации значимой ассоциации, зависят от приложения. Статистическую значимость корреляции можно рассчитать по коэффициенту корреляции и количеству точек данных в выборке, предполагая нормальное распределение генеральной совокупности.
Понимание коэффициента корреляции
Различные типы коэффициентов корреляции используются для оценки корреляции на основе свойств сравниваемых данных. Безусловно, наиболее распространенным является коэффициент Пирсона или 9 Пирсона.0023 r, , который измеряет силу и направление линейной зависимости между двумя переменными. Коэффициент Пирсона не может оценить нелинейные связи между переменными и не может различать зависимые и независимые переменные.
Коэффициент Пирсона использует формулу математической статистики для измерения того, насколько точно точки данных, объединяющие две переменные (со значениями одного ряда данных, нанесенными на ось x, и соответствующими значениями другого ряда на оси y), приближаются к линии наилучшего соответствия. Линия наилучшего соответствия может быть определена с помощью регрессионного анализа.
Чем дальше коэффициент от нуля, будь он положительным или отрицательным, тем лучше соответствие и больше корреляция.
Значения -1 (для отрицательной корреляции) и 1 (для положительной) описывают идеальное совпадение, при котором все точки данных выстраиваются по прямой линии, указывая на то, что переменные идеально коррелированы. Другими словами, взаимосвязь настолько предсказуема, что значение одной переменной может быть определено из совпадающего значения другой. Чем ближе коэффициент корреляции к нулю, тем слабее корреляция, пока при нуле не существует никакой линейной зависимости.
Оценки силы корреляции на основе значения коэффициента корреляции различаются в зависимости от приложения. В физике и химии коэффициент корреляции должен быть ниже -0,9 или выше 0,9, чтобы корреляция считалась значимой, в то время как в социальных науках порог может достигать -0,5 и всего 0,5.
Для коэффициентов корреляции, полученных в результате выборки, определение статистической значимости зависит от p-значения, которое рассчитывается на основе размера выборки данных, а также значения коэффициента.
Уравнение коэффициента корреляции
Чтобы вычислить корреляцию Пирсона, начните с определения стандартного отклонения каждой переменной, а также ковариации между ними. Коэффициент корреляции представляет собой ковариацию, деленную на произведение стандартных отклонений двух переменных.
р Икс у знак равно Ков ( Икс , у ) о Икс о у куда: р Икс у знак равно Коэффициент корреляции Пирсона продукт-момент Ков ( Икс , у ) знак равно ковариация переменных Икс а также у о Икс знак равно стандартное отклонение Икс о у знак равно стандартное отклонение у \begin{выровнено} &\rho_{xy} = \frac { \text{Cov} ( x, y ) }{ \sigma_x \sigma_y } \\ &\textbf{где:} \\ &\rho_{xy} = \text{Коэффициент корреляции Пирсона произведение-момент} \\ &\text{Cov} ( x, y ) = \text{ковариация переменных } x \text{ и } y \\ &\sigma_x = \text{стандартное отклонение } x \\ &\sigma_y = \text{стандартное отклонение} y \\ \end{выровнено} ρxy=σxσyCov(x,y)где: ρxy=коэффициент корреляции Пирсона произведение-момент Cov(x,y)=ковариация переменных x и yσx=стандартное отклонение xσy=стандартное отклонение y
Стандартное отклонение является мерой отклонения данных от их среднего значения.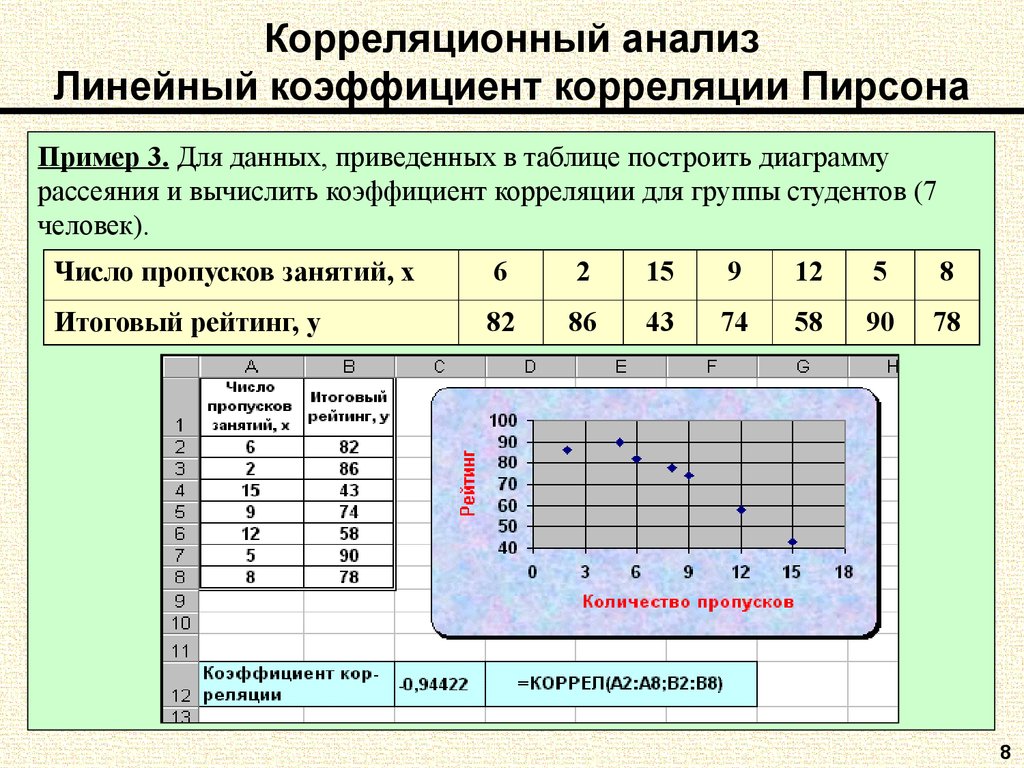
2 ) } } } \\&\textbf{где:}\\&r=\ text{Коэффициент корреляции}\\&n=\text{Количество наблюдений}\end{выровнено}
r=(n×∑(X2)−∑(X)2)×(n×∑(Y2)−∑(Y)2)n×(∑(X,Y)−(∑(X)×∑ (Y)))где:r=коэффициент корреляцииn=количество наблюдений
Корреляция Статистика и инвестиции
Коэффициент корреляции особенно полезен при оценке инвестиционных рисков и управлении ими. Например, современная портфельная теория предполагает, что диверсификация может снизить волатильность доходности портфеля, ограничивая риск. Коэффициент корреляции между исторической доходностью может указать, улучшит ли добавление инвестиций в портфель его диверсификацию.
Расчеты корреляции также являются одним из основных элементов факторного инвестирования, стратегии построения портфеля на основе факторов, связанных с избыточной доходностью. Между тем, количественные трейдеры используют исторические корреляции и коэффициенты корреляции, чтобы предвидеть краткосрочные изменения цен на ценные бумаги.
Ограничения коэффициента корреляции Пирсона
Как говорится, корреляция не подразумевает причинно-следственной связи, и коэффициент Пирсона не может определить, зависит ли одна из коррелирующих переменных от другой.
Коэффициент корреляции также не показывает, какая часть вариации зависимой переменной относится к независимой переменной. Это показано коэффициентом детерминации, также известным как R-квадрат, который представляет собой просто квадрат коэффициента корреляции.
Коэффициент корреляции не описывает наклон линии наилучшего соответствия; наклон можно определить методом наименьших квадратов в регрессионном анализе.
Коэффициент корреляции Пирсона нельзя использовать для оценки нелинейных ассоциаций или ассоциаций, возникающих из выборочных данных, не подпадающих под нормальное распределение. Он также может быть искажен выбросами — точками данных, находящимися далеко за пределами диаграммы рассеяния распределения. Эти отношения могут быть проанализированы с использованием непараметрических методов, таких как коэффициент корреляции Спирмена, коэффициент ранговой корреляции Кендалла или коэффициент полихорической корреляции.
Нахождение коэффициентов корреляции в Excel
Самый простой способ рассчитать корреляцию в Excel — ввести два ряда данных в соседние столбцы и использовать встроенную формулу корреляции:
Если вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль «Анализ данных» на вкладке «Данные» в разделе «Анализ».
Выберите таблицу возвратов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel знал, что их следует рассматривать как заголовки. Затем вы можете выбрать вывод на тот же лист или на новый лист.
Investopedia.comНажатие Enter создаст матрицу корреляции. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Investopedia.comЧто такое коэффициент корреляции?
Коэффициент корреляции описывает, как одна переменная движется по отношению к другой. Положительная корреляция указывает на то, что они движутся в одном направлении, а значение 1 означает идеальную положительную корреляцию.
Значение -1 показывает полную отрицательную или обратную корреляцию, а ноль означает отсутствие линейной корреляции.
Как рассчитать коэффициент корреляции?
Коэффициент корреляции рассчитывается путем определения ковариации переменных и деления этого числа на произведение стандартных отклонений этих переменных.
Как коэффициент корреляции используется в инвестировании?
Коэффициенты корреляции играют ключевую роль в оценке рисков портфеля и количественных торговых стратегиях. Например, некоторые управляющие портфелем будут контролировать коэффициенты корреляции своих активов, чтобы ограничить волатильность и риск портфеля. 92}}\)
Если x — это рост человека, измеренный в дюймах, а y — это вес человека, измеренный в фунтах, то единицами измерения числителя являются дюймы × фунты. Точно так же единицами измерения знаменателя являются дюймы × фунты. Поскольку они одинаковы, единицы в числителе и знаменателе компенсируют друг друга, что дает «безразмерную» меру.
Другая формула для r , которую вы можете встретить в литературе по регрессии, иллюстрирует, как коэффициент корреляции 92}}\times b_1\)
Из этой версии формулы легко увидеть, что:
- Расчетный наклон \(b_{1}\) линии регрессии и коэффициент корреляции r всегда разделяют один и тот же знак. Если вы не понимаете, почему это должно быть правдой, посмотрите видео.
- Коэффициент корреляции r является безразмерной мерой. Если вы не понимаете, почему это должно быть правдой, посмотрите видео.
- Если расчетный наклон \(b_{1}\) линии регрессии равен 0, то коэффициент корреляции равен r также должен быть 0.
