Пример расчета t-критерия Стьюдента для независимых выборок
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок | |
Пример расчета t-критерия Стьюдента для независимых выборок
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2.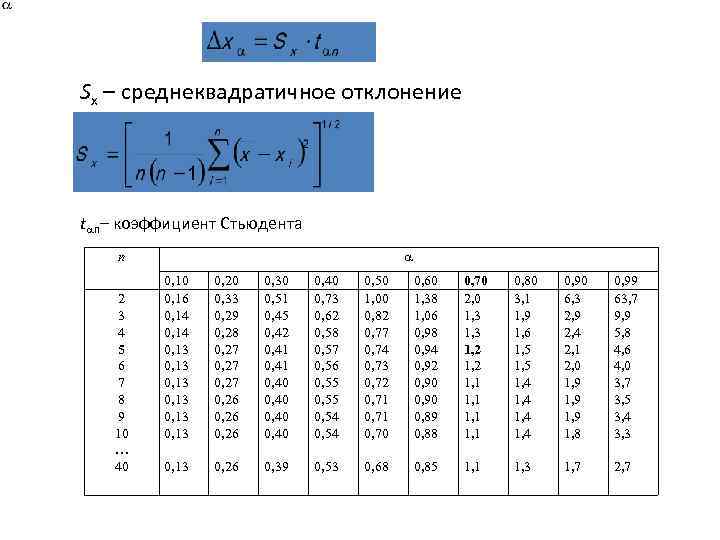 Проверить распределения на нормальность.
Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок | |
T Формула распределения | Вычислить распределение T студентов
Формула для расчета распределения T (которое также широко известно как распределение T Стьюдента) показана как вычитание среднего значения генеральной совокупности (среднее значение второй выборки) из среднего значения выборки (среднего значения первой выборки), которое составляет [ x̄ – μ ], которое затем делится на стандартное отклонение средних значений, которое изначально делится на квадратный корень из n, который представляет собой количество единиц в этой выборке [s ÷ √(n)].
Т-распределение — это вид распределения, который выглядит почти как кривая нормального распределения или кривая нормального распределения, но с немного более толстым и коротким хвостом. Если размер выборки мал, то это распределение будет использоваться вместо нормального распределения.
t = (x̄ – μ) / (s/√n)
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторствоКак указать авторство?Статья Ссылка на быть гиперссылкой
Например:
Источник: T Distribution Formula (wallstreetmojo.com)
Где
- x̄ — среднее значение выборки
- μ — среднее значение генеральной совокупности
- s — стандартное отклонение
- n — размер n данного образца
СОДЕРЖАНИЕ СОДЕРЖАНИЕ
- Формула. Для расчета распределения Стьюдента T
- Расчет распределения T
- Примеры
- Пример № 1
- Пример № 2
- Пример № 3
- Соглашение и использование

Расчет T-распределения
Расчет T-распределения Стьюдента довольно прост, но да, нужны значения. Например, нужно среднее значение генеральной совокупности, то есть среднее значение всей совокупности, которое представляет собой не что иное, как среднее значение генеральной совокупности, в то время как среднее значение выборки требуется для проверки подлинности среднего значения генеральной совокупности, действительно ли утверждение, заявленное на основе генеральной совокупности, верно и образец, если он будет взят, будет представлять одно и то же утверждение. Таким образом, формула распределения t здесь вычитает среднее значение выборки из среднего значения генеральной совокупности, а затем делит его на стандартное отклонение и умножает на квадратный корень. количество. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Кроме того, эта функция принимает один аргумент. Подробнее о размере выборки для стандартизации значения.
Однако, поскольку нет диапазона для расчета распределения t, значение может стать странным, и мы не сможем вычислить вероятность, так как распределение t студента имеет ограничения по получению значения и, следовательно, полезно только для небольших размер образца. Кроме того, чтобы рассчитать вероятность после получения оценки, необходимо найти ее значение из таблицы распределения t студента.
Примеры
Вы можете скачать этот шаблон Excel T Distribution здесь – Шаблон T Distribution Excel
Пример № 1
Рассмотрим следующие переменные:
- Среднее значение популяции = 310
- Стандартное отклонение = 50
- Размер выборки = 16
- 9009. = 290
Рассчитайте значение t-распределения.
Решение:
Используйте следующие данные для расчета T-распределения.
Итак, расчет Т распределения можно сделать следующим образом:
Здесь приведены все значения. Нам просто нужно включить значения.
Нам просто нужно включить значения.
Мы можем использовать формулу t распределения на уровне аналитика зарабатывают в среднем 500 долларов в час. Выбрана выборка из 30 сотрудников на уровне аналитиков, и их средний заработок в час составил 450 долларов США при отклонении выборки в 30 долларов США. И предполагая, что их утверждение верно, рассчитайте значение t-распределения, которое будет использоваться для нахождения вероятности для t-распределения.
Решение:
Используйте следующие данные для расчета T-распределения.
Итак, вычисление T распределения можно сделать следующим образом:
Здесь приведены все значения; нам просто нужно включить значения. Мы можем использовать формулу распределения t #3
Совет колледжей Universal провел тест на уровень IQ для 50 случайно выбранных профессоров. И результатом, который они получили, было то, что средний показатель уровня IQ составил 120 с дисперсией 121. Предположим, что показатель t равен 2,407. Каково среднее значение генеральной совокупности для этого теста, которое оправдывает значение t как 2,407?
Предположим, что показатель t равен 2,407. Каково среднее значение генеральной совокупности для этого теста, которое оправдывает значение t как 2,407?
Решение:
Используйте следующие данные для расчета T-распределения.
Здесь все значения даны вместе со значением t; на этот раз нам нужно вычислить среднее значение населения вместо значения t.
Опять же, мы будем использовать доступные данные и рассчитаем средние значения населения, вставив значения, указанные в формуле ниже.
Среднее значение выборки равно 120, средние значения генеральной совокупности неизвестны, стандартное отклонение выборки будет представлять собой квадратный корень из дисперсии, которая будет равна 11, а размер выборки равен 50.
Таким образом, вычисление среднего значения совокупности (μ ) можно сделать следующим образом:
Мы можем использовать формулу распределения t.
Значение t = (120 – μ ) / (11 / √50)
2,407 = (120 – μ ) / (11 / √50)
-μ = -2,407 * (11/√50)-120
Среднее значение населения (μ) будет –
μ = 116,26
4 9 Следовательно значение для среднего значения генеральной совокупности будет 116,26
Релевантность и использование
T-распределение (и связанные с ним значения t-показателей) используется при проверке гипотез Проверка гипотез Проверка гипотез — это статистический инструмент, который помогает измерить вероятность правильности результата гипотезы. полученный после выполнения гипотезы на выборочных данных. Он подтверждает правильность полученных результатов первичной гипотезы. Подробнее, когда нужно выяснить, следует ли отклонить или принять нулевую гипотезу.
полученный после выполнения гипотезы на выборочных данных. Он подтверждает правильность полученных результатов первичной гипотезы. Подробнее, когда нужно выяснить, следует ли отклонить или принять нулевую гипотезу.
На приведенном выше графике центральная область будет областью принятия, а хвостовая область будет областью отклонения. На этом графике, который представляет собой двусторонний тест, заштрихованная синим цветом будет область отклонения. Область в хвостовой области может быть описана либо с помощью t-показателей, либо с помощью z-показателей. Z-оценки. Z-оценка необработанных данных относится к оценке, полученной путем измерения того, сколько стандартных отклонений выше или ниже совокупности означает данные, что помогает проверить рассматриваемую гипотезу. Другими словами, это расстояние точки данных от среднего значения генеральной совокупности, которое выражается как кратное стандартному отклонению. Подробнее. Возьмите пример; на изображении слева будет изображена область в хвостах пяти процентов (что составляет 2,5% с обеих сторон). Z-оценка должна быть 1,96 (взяв значение из z-таблицы), которое должно представлять эти 1,96 стандартных отклонения от среднего или среднего значения. Нулевая гипотезаНулевая гипотезаНулевая гипотеза предполагает, что выборочные данные и данные о населении не имеют различий, или, говоря простыми словами, она предполагает, что утверждение, сделанное человеком в отношении данных или совокупности, является абсолютной истиной и всегда верно. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Подробнее можно отклонить, если значение z-показателя меньше значения -1,9.6, или значение показателя z больше 1,96.
Z-оценка должна быть 1,96 (взяв значение из z-таблицы), которое должно представлять эти 1,96 стандартных отклонения от среднего или среднего значения. Нулевая гипотезаНулевая гипотезаНулевая гипотеза предполагает, что выборочные данные и данные о населении не имеют различий, или, говоря простыми словами, она предполагает, что утверждение, сделанное человеком в отношении данных или совокупности, является абсолютной истиной и всегда верно. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Подробнее можно отклонить, если значение z-показателя меньше значения -1,9.6, или значение показателя z больше 1,96.
Как правило, это распределение должно использоваться, как описано выше, когда имеется меньший размер выборки (в основном менее 30) или если неизвестно, что такое дисперсия генеральной совокупности или стандартное отклонение генеральной совокупности. Для практических целей (то есть в реальном мире) это в основном всегда так. Если размер предоставленной выборки достаточно велик, то 2 распределения будут практически одинаковыми.
Если размер предоставленной выборки достаточно велик, то 2 распределения будут практически одинаковыми.
Рекомендуемые статьи
Это руководство по формуле распределения T. Здесь мы узнаем, как рассчитать значение распределения студентов T и среднее значение совокупности (μ), а также практические примеры в Excel и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:
- Вычислить размер выборкиВычислить размер выборкиФормула размера выборки отображает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности.Подробнее
- Формула кривой Белла Формула кривой Белла График кривой Белла изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол.
 читать дальше
читать дальше - Формула биномиального распределения
- Формула асимметрии
Таблица Стьюдента t (скачать бесплатно)
Опубликован в 29 апреля 2022 г. по Шон Терни. Отредактировано 17 октября 2022 г.
Таблица Стьюдента t является справочной таблицей, в которой перечислены критические значения
Критическое значение t определяет порог значимости для некоторых статистических тестов и верхнюю и нижнюю границы доверительных интервалов для некоторых оценок. Чаще всего используется, когда:
- Проверка значимости различий между двумя средними значениями (испытания с двумя выборками)
- Проверка значимости двух переменных (линейная регрессия или корреляция)
- Расчет доверительных интервалов (средних или коэффициентов регрессии)
Скачать таблицу t
Критические значения t рассчитываются по распределению Стьюдента t .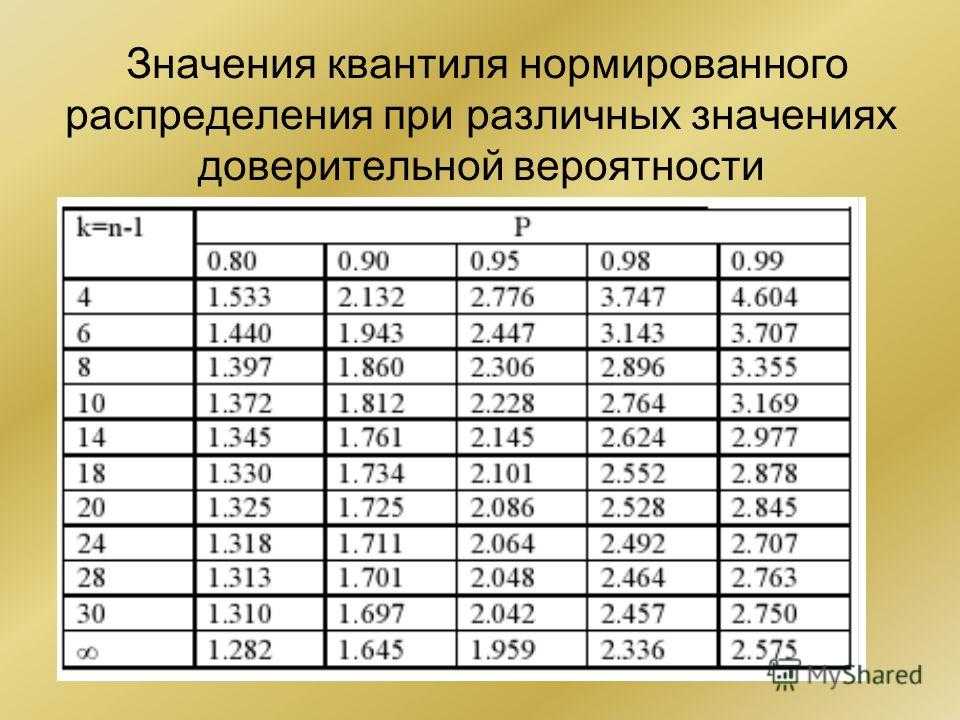
Содержание
- t-таблица Стьюдента для одно- и двусторонних тестов
- Как пользоваться t-таблицей
- Практические вопросы
- Часто задаваемые вопросы о t-таблице Стьюдента
Таблица Стьюдента
t для одно- и двусторонних тестовИспользуйте таблицы ниже, чтобы найти критические значения t или узнайте, как пользоваться столом t
- Критические значения t для двусторонних испытаний
- Критические значения t для односторонних испытаний
- Пошаговое руководство по использованию стола
Загрузить таблицу t
Как пользоваться столом
t Если вам нужно найти критическое значение t для выполнения статистического теста или расчета доверительного интервала, следуйте этому пошаговому руководству.
Чтобы выяснить, эффективен ли крем от прыщей, вы решаете сравнить среднее количество прыщей у участников экспериментальной и контрольной групп, используя независимых образцов t тест .
- Нулевая гипотеза: Участники экспериментальной и контрольной групп имеют одинаковое среднее число прыщей ().
- Альтернативная гипотеза: Участники группы лечения и контрольной группы различаются средним количеством прыщей.
Вы вычисляете значение t для выборки. Чтобы узнать, следует ли отклонить нулевую гипотезу, вам нужно сравнить это значение t с критическим значением т .
Шаг 1: Выберите двусторонний или односторонний
Двусторонние тесты используются, когда альтернативная гипотеза является ненаправленной .
- Ненаправленная гипотеза утверждает, что параметр генеральной совокупности (такой как среднее значение или коэффициент регрессии) не равен определенному значению (например, 0). Двусторонние тесты подходят для большинства исследований.
Односторонние тесты используются, когда альтернативная гипотеза направлена .
- Направленная гипотеза утверждает, что параметр совокупности больше или меньше определенного значения.
- Ваша альтернативная гипотеза является направленной, если она включает такие слова, как «больше», «меньше», «увеличивается», «уменьшается» или знак «<» или «>».
 Если он не включает эти (или подобные), он, вероятно, ненаправленный.
Если он не включает эти (или подобные), он, вероятно, ненаправленный.
- Альтернативная гипотеза: Участники группы лечения и контрольной группы различаются средним количеством прыщей.
Эта альтернативная гипотеза является ненаправленной. В нем не указано, больше или меньше среднее значение группы лечения, чем среднее значение контрольной группы, просто средние значения различаются.
Поскольку альтернативная гипотеза является ненаправленной, ее следует проверить с помощью двустороннего критерия.
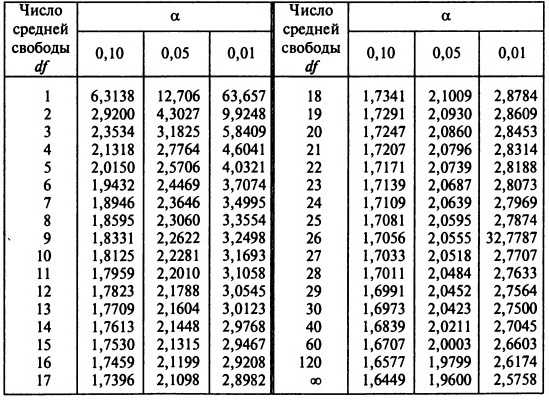
Шаг 2: Расчет степеней свободы
Степени свободы ( df ) статистики рассчитываются исходя из размера выборки ( n ). Уравнение, которое вам нужно использовать, зависит от того, какой тип теста или процедуры вы выполняете 90–200 .
| Тест или процедура | Степени свободы ( df ) уравнение |
|---|---|
| дф = n – 1 |
| df = n 1 + n 2 – 2 Где n 1 – размер выборки группы 1, а n 2 – размер выборки группы 2 |
| дф = н – 1 Где n количество пар |
| дф = n – 2 |
df = n 1 + n 2 – 2
Если вы провели экспериментальное исследование с 14 участниками в группе плацебо и 17 участниками в группе лечения, то
дф = 14 + 17 – 2
дф = 29
Шаг 3.
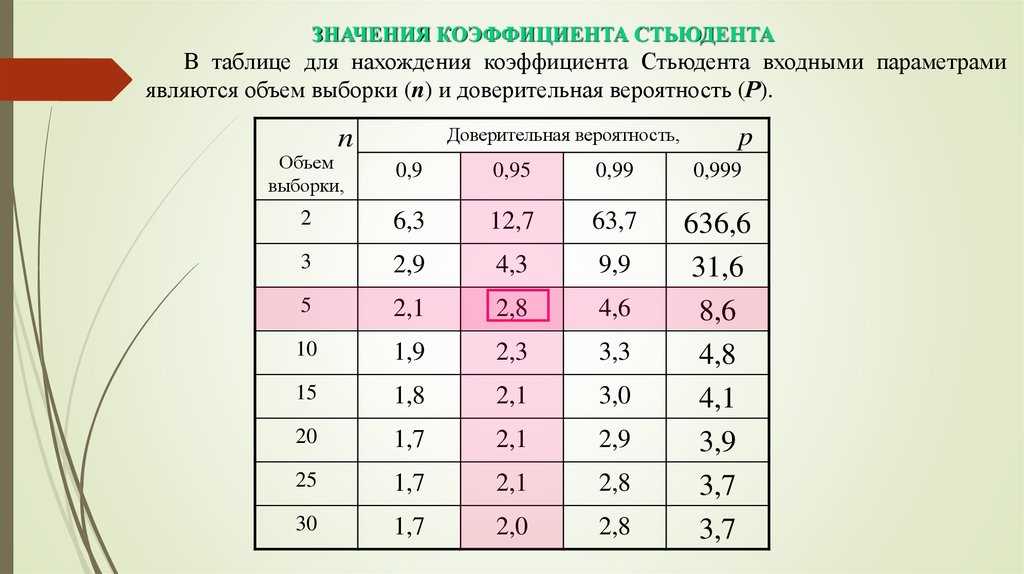 Выберите уровень значимости
Выберите уровень значимостиПо соглашению уровень значимости (α) почти всегда равен 0,05. Столбец α = 0,05 выделен в таблице, поскольку это наиболее часто используемый уровень значимости.
В определенных ситуациях вы можете уменьшить риск ошибки типа I, уменьшив α, или уменьшить риск ошибки типа II, увеличив α.
Если вы рассчитываете доверительный интервал, выберите уровень значимости на основе желаемого уровня достоверности:
α = 1 – уровень достоверности
Наиболее распространенный доверительный уровень составляет 95 % (или 0,95 при выражении в виде доли), что соответствует α = 0,05.
Пример: Выбор уровня значимости. Вы выбираете α = 0,05 для проверки своей гипотезы, так как этот уровень значимости используется большинством исследователей.Шаг 4: Найдите критическое значение
t в таблице t Теперь, когда вы знаете, является ли ваш критерий двусторонним или односторонним, степени свободы ( df ) и уровень значимости, у вас есть вся информация, необходимая для использования таблицы t .
- Если тест является двусторонним или если вы рассчитываете доверительный интервал, используйте первую таблицу. Если тест односторонний, используйте вторую таблицу.
- Степени свободы ( df ) перечислены в левой части таблицы. Найдите строку таблицы для df , которую вы вычислили на шаге 2. Если вам нужен df , которого нет в списке, округлите его до следующего наименьшего числа (например, используйте df = 40 вместо df ). = 46).
- Уровни значимости перечислены в верхней части таблицы. Найдите столбец для уровня значимости, который вы выбрали на шаге 3. В большинстве случаев вы будете использовать выделенный столбец (α = 0,05).
- Критическое значение t для вашего теста находится там, где встречаются строка и столбец.

Теперь вы можете сравнить это критическое значение t с t , рассчитанным для вашего образца. Это сравнение позволит вам решить, следует ли отклонить нулевую гипотезу.
Что может сделать корректура для вашей статьи?
Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в статье не было неясных выражений, избыточных слов и неудобных формулировок.
См. пример редактирования
Практические вопросы
на базе Typeform
Часто задаваемые вопросы о Столе студента
- Как найти критическое значение t в R?
Вы можете использовать функцию qt() , чтобы найти критическое значение t в R.
Пример: Расчет критического значения t в R Чтобы вычислить критическое значение t для двустороннего теста с df = 29 и α = 0,05: Функция дает критическое значение t для одностороннего теста. Если вам нужно критическое значение t для двустороннего теста, разделите уровень значимости на два.
Функция дает критическое значение t для одностороннего теста. Если вам нужно критическое значение t для двустороннего теста, разделите уровень значимости на два.кварта ( p = 0,025, df = 29)
- Как найти критическое значение t в Excel?
Вы можете использовать функцию T.ОБР() , чтобы найти критическое значение t для односторонних тестов в Excel, и вы можете использовать функцию T.ОБР.2T() для двусторонних тестов .
Пример: расчет критического значения t в Excel. Чтобы вычислить критическое значение t для двустороннего теста с df = 29 и α = 0,05, щелкните любую пустую ячейку и введите:
Чтобы вычислить критическое значение t для двустороннего теста с df = 29 и α = 0,05, щелкните любую пустую ячейку и введите:=Т.ОБР.2Т(0,05,29)
- Как проверить гипотезу, используя критическое значение t?
Чтобы проверить гипотезу, используя критическое значение t , выполните следующие четыре шага:
- Рассчитайте значение t для вашей выборки.
- Найдите критическое значение t в таблице t .
- Определите, превышает ли (абсолютное) значение t критическое значение t .
- Отклонить нулевую гипотезу, если значение выборки t больше критического значения t .
 В противном случае не отвергайте нулевую гипотезу.
В противном случае не отвергайте нулевую гипотезу.
- Как рассчитать доверительный интервал среднего, используя критическое значение t?
Чтобы вычислить доверительный интервал среднего значения, используя критическое значение t , выполните следующие четыре шага:
- Выберите уровень значимости на основе желаемого уровня достоверности. Наиболее распространенный уровень достоверности — 9.5%, что соответствует α = 0,05 в двусторонней таблице t .
- Найдите критическое значение t в двусторонней таблице t .
- Умножьте критическое значение t на s / √ n .
- Добавьте это значение к среднему, чтобы вычислить верхний предел доверительного интервала, и вычтите это значение из среднего, чтобы вычислить нижний предел.

Источники в этой статье
Мы настоятельно рекомендуем учащимся использовать источники в своей работе. Вы можете процитировать нашу статью (стиль APA) или глубоко погрузиться в статьи ниже.
Эта статья Scribbr
Терни, С. (17 октября 2022 г.). Студенческий стол (скачать бесплатно) | Руководство и примеры. Скриббр. Проверено 21 октября 2022 г., с https://www.scribbr.com/statistics/students-t-table/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса.


 читать дальше
читать дальше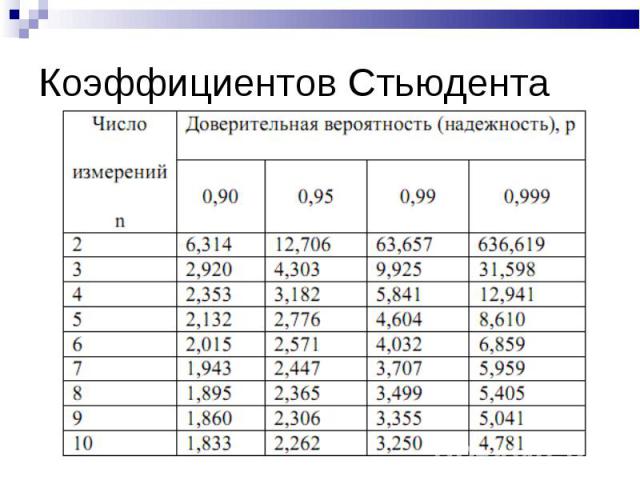 Если он не включает эти (или подобные), он, вероятно, ненаправленный.
Если он не включает эти (или подобные), он, вероятно, ненаправленный. Функция дает критическое значение t для одностороннего теста. Если вам нужно критическое значение t для двустороннего теста, разделите уровень значимости на два.
Функция дает критическое значение t для одностороннего теста. Если вам нужно критическое значение t для двустороннего теста, разделите уровень значимости на два. Чтобы вычислить критическое значение t для двустороннего теста с df = 29 и α = 0,05, щелкните любую пустую ячейку и введите:
Чтобы вычислить критическое значение t для двустороннего теста с df = 29 и α = 0,05, щелкните любую пустую ячейку и введите: В противном случае не отвергайте нулевую гипотезу.
В противном случае не отвергайте нулевую гипотезу.