Решение линейных уравнений и систем линейных уравнений, содержащих параметры (4 урока)
Урок 1. Решение линейных уравнений, содержащих параметры
Урок 2. Решение систем линейных уравнений, содержащих параметры
Урок 3. Решение линейных уравнений и систем линейных уравнений, содержащих параметры
Урок 4. Контрольная работа
Цели урока: формировать умение решать системы линейных уравнений, содержащих параметры; осуществить оперативный контроль и самоконтроль учащихся; развивать исследовательскую и познавательную деятельность школьников.
Тип урока: введение нового материала.
Ход урока
1. Проверка домашнего задания.
2. Введение нового материала.
Говорят, что дана система двух уравнений первой степени с двумя неизвестными x и y, если требуется найти пары чисел (x0; y0), являющиеся решениями одновременно и первого, и второго уравнения.
Если
то система имеет единственное решение.
Если
то система не имеет решений.
Если
то система имеет бесконечно много решений.
Пример 1. При каких значениях параметра a система
а) имеет бесконечное множество решений;
б) имеет единственное решение?
Решение.
Ответ: а) если a=4, то система имеет бесконечное множество решений; б) если то решение единственное.
Пример 2. Решите систему уравнений
Решение. система имеет единственное решение.
1–ym–y=n–2y , –ym+y=n–1;
исходная система решений не имеет.
система имеет бесконечно много решений.
Ответ: если m=1 и n1, то решений нет; если m = 1
и n = 1, то решений бесконечное множество, если m 1 и n – любое, тоПример 3. (Предложите ученикам выполнить это задание самостоятельно с последующей проверкой.) Решите систему уравнений
Решение.
Пример 4. Определите, при каком условии уравнение
а) имеет единственное решение;
б) имеет бесконечно много корней;
в) не имеет корней.
Решение.
– при этом условии уравнение корней не имеет.
– при этом условии решение исходного уравнения есть любое число из R.
Ответ:
б) если a = 0 или b = 0, то x – любое число;
в) если 2b = a, a 0, b 0, то корней нет.
Самостоятельная работа
Вариант 1
1. При каком значении k система имеет бесконечное множество решений?
2. Решите систему уравнений
Вариант 2
1. При каком значении d система не имеет решений?
2. Решите систему уравнений
Ответы
В-1. 1. k = 2,5. 2. Если b = 0, c = 0, то решений нет; если b = c, d 0, a – любое число, то решений нет; если a = 0, b, c, d – любые числа, то решений нет; если c 0, b 0, a 0, b c, d – любое число, то
если b = c, d = 0, то
1. k = 2,5. 2. Если b = 0, c = 0, то решений нет; если b = c, d 0, a – любое число, то решений нет; если a = 0, b, c, d – любые числа, то решений нет; если c 0, b 0, a 0, b c, d – любое число, то
если b = c, d = 0, то
В-2. 1. d = – 20. 2. Если b = 0, c = 0, то решений нет; если c = – b, то решений нет; если b 0 и c 0, c – b, то если c = – b и dbc = ac, то
Задание на дом
1. При каких значениях параметра b система уравнений
а) имеет бесконечное множество решений;
б) не имеет решений?
2. Графики функций y = ax + 3 и y = (2 – a)x + a пересекаются в точке с абсциссой – 1. Найдите ординату точки пересечения графиков.
3. Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.
а) Найдите b и k.
б) найдите координаты точки пересечения этих графиков.
4. Решите систему уравнений
Ответы: 1. а) b = 10; б) b 10. 2. 3. а) b = 6, k = – 4; б) (0; 6). 4. Если mn = – 1 и m 1, n – 1, то решений нет; если m = 1 и n = – 1, то x – любое число, y = 1 + mx; если mn 1 и n – 1, m 1, то
Урок по теме «Решение систем линейных уравнений, содержащих параметры»
Если в задаче меньше трех переменных, это не задача; если больше восьми – она неразрешима. Энон.
Задачи с параметрами встречаются во всех вариантах ЕГЭ, поскольку при их
решении наиболее ярко выявляется, насколько глубоки и неформальны знания
выпускника. Трудности, возникающие у учащихся при выполнении подобных заданий,
вызваны не только относительной их сложностью, но и тем, что в учебных пособиях
им уделяется недостаточно внимания.

Цели урока:
- систематизация знаний учащихся;
- выработка умений применять графические представления при решении систем уравнений;
- формирование умения решать системы линейных уравнений, содержащих параметры;
- осуществление оперативного контроля и самоконтроля учащихся;
- развитие исследовательской и познавательной деятельности школьников, умения оценивать полученные результаты.
Урок рассчитан на два учебных часа.
Ход урока
- Организационный момент
Сообщение темы, целей и задач урока.
- Актуализация опорных знаний учащихся
Проверка домашней работы. В качестве домашнего задания учащимся было предложено решить каждую из трех систем линейных уравнений
а) б) в)
графически и аналитически; сделать вывод о количестве полученных решений для каждого случая
Ответы:
Заслушиваются и анализируются выводы, сделанные учащимися. Результаты работы
под руководством учителя в краткой форме оформляются в тетрадях.
Результаты работы
под руководством учителя в краткой форме оформляются в тетрадях.
В общем виде систему двух линейных уравнений с двумя неизвестными можно представить в виде: .
Решить данную систему уравнений графически – значит найти координаты точек пересечения графиков данных уравнений или доказать, что таковых нет. Графиком каждого уравнения этой системы на плоскости является некоторая прямая.
Возможны три случая взаимного расположения двух прямых на плоскости:
- если (если хотя бы один из знаменателей равен нулю, последнее неравенство надо понимать как ), то прямые пересекаются в одной точке; в этом случае система имеет единственное решение
<Рисунок1>;
- если то прямые не имеют общих точек, т.е. не пересекаются; а значит, система решений не имеет
<Рисунок2>;
- если
то
прямые совпадают.
 В этом случае система имеет бесконечно много решений
В этом случае система имеет бесконечно много решений
<Рисунок3>.
К каждому случаю полезно выполнить рисунок.
- Изучение нового материала
Сегодня на уроке мы научимся решать системы линейных уравнений, содержащие параметры. Параметром будем называть независимую переменную, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству. Решить систему уравнений с параметром – значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество решений системы.
Решение задачи с параметром зависит от вопроса, поставленного в ней. Если
нужно просто решить систему уравнений при различных значениях параметра или
исследовать ее, то необходимо дать обоснованный ответ для любого значения
параметра или для значения параметра, принадлежащего заранее оговоренному в
задаче множеству.
Пример 1. Для каждого значения параметра решим систему уравнений
Решение.
- Система имеет единственное решение, если
В этом случае имеем
- Если а = 0, то система принимает вид
Система несовместна, т.е. решений не имеет.
- Если то система запишется в виде
Очевидно, что в этом случае система имеет бесконечно много решений вида x = t; где t-любое действительное число.
Ответ:
- при система имеет единственное решение
- при а = 0 — нет решений;
- при а = 3 — бесконечно много решений вида где t R
Пример 2. При каких значениях параметра a система уравнений
При каких значениях параметра a система уравнений
- имеет единственное решение;
- имеет множество решений;
- не имеет решений?
Решение.
- система имеет единственное решение, если
- подставим в пропорцию значение а = 1, получим , т.е. система имеет бесконечно много решений;
- при а = -1 пропорция примет вид: . В этом случае система не имеет решений.
Ответ:
- при система имеет единственное решение;
- при система имеет бесконечно много решений;
- при система не имеет решений.
Пример 3. Найдем сумму параметров a и b, при которых система
имеет бесчисленное множество решений.
Решение. Система имеет бесчисленное множество решений, если
То есть если a = 12, b = 36; a + b = 12 + 36 =48.
Ответ: 48.
- Закрепление изученного в ходе решения задач
- № 15.24(а) [1]. Для каждого значения параметра решите систему уравнений
- № 15.25(а) Для каждого значения параметра решите систему уравнений
- При каких значениях параметра a система уравнений
а) не имеет решений; б) имеет бесконечно много решений.
Ответ: при а = 2 решений нет, при а = -2 бесконечное множество решений
- Практическая работа в группах
Класс разбивается на группы по 4-5 человек. В каждую группу входят учащиеся с разным уровнем математической подготовки. Каждая группа получает карточку с заданием. Можно предложить всем группам решить одну систему уравнений, а решение оформить. Группа, первой верно выполнившая задание, представляет свое решение; остальные сдают решение учителю.
Карточка. Решите систему линейных уравнений
Решите систему линейных уравнений
при всех значениях параметра а.
Ответ: при система имеет единственное решение ; при нет решений; при а = -1бесконечно много решений вида , (t; 1- t) где t R
Если класс сильный, группам могут быть предложены разные системы уравнений, перечень которых находится в Приложении1. Тогда каждая группа представляет классу свое решение.
Отчет группы, первой верно выполнившей задание
Участники озвучивают и поясняют свой вариант решения и отвечают на вопросы, возникшие у представителей остальных групп.
- Самостоятельная работа
Вариант 1
- При каком значении k система имеет бесконечно много решений?
- При каком значении p система не имеет решений?
Вариант 2
- При каком значении k система имеет бесконечно много решений?
- При каком значении p система не имеет решений?
- Итоги урока
Решение систем линейных уравнений с параметрами можно сравнить с исследованием,
которое включает в себя три основных условия.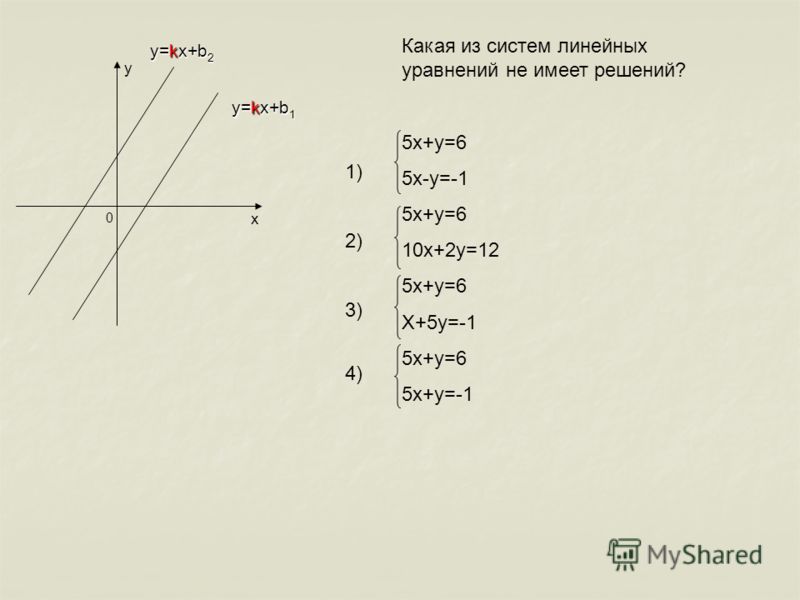 Учитель предлагает учащимся их
сформулировать.
Учитель предлагает учащимся их
сформулировать.
При решении следует помнить:
- для того, чтобы система имела единственное решение, нужно, чтобы прямые, отвечающие уравнению системы, пересекались, т.е. необходимо выполнение условия;
- чтобы не имела решений, нужно, чтобы прямые были параллельны, т.е. выполнялось условие,
- и, наконец, чтобы система имела бесконечно много решений, прямые должны совпадать, т.е. выполнялось условие.
Учитель оценивает работу на уроке класса в целом и выставляет отметки за урок отдельным учащимся. После проверки самостоятельной работы оценку за урок получит каждый ученик.
- Домашнее задание
При каких значениях параметра b система уравнений
- имеет бесконечно много решений;
- не имеет решений?
Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.
- Найдите b и k,
- найдите координаты точки пересечения этих графиков.
Решите систему уравнений при всех значениях m и n.
Решите систему линейных уравнений при всех значениях параметра а (любую на выбор).
Литература
- Алгебра и начала математического анализа: учеб. для 11 кл. общеобразоват. учреждений : базовый и профил. уровни / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин – М. : Просвещение, 2008.
- Математика : 9 класс : Подготовка к государственной итоговой аттестации / М. Н. Корчагина, В. В. Корчагин – М. : Эксмо, 2008.
- Готовимся в вуз. Математика. Часть 2. Учебное пособие для подготовки к ЕГЭ,
участию в централизованном тестировании и сдаче вступительных испытаний в КубГТУ
/ Кубан. гос. технол. ун-т; Ин-т совр. технол. и экон.; Сост.: С. Н. Горшкова,
Л. М. Данович, Н.
 А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар,
2006.
А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар,
2006. - Сборник задач по математике для подготовительных курсов ТУСУР: Учебное пособие / З. М. Гольдштейн, Г. А. Корниевская, Г. А. Коротченко, С.Н. Кудинова. – Томск: Томск. Гос. ун-т систем управления и радиоэлектроники, 1998.
- Математика: интенсивный курс подготовки к экзамену/ О. Ю. Черкасов, А.Г.Якушев. – М.: Рольф, Айрис-пресс, 1998.
Тема 1.2. Системы линейных уравнений.
Понятие систем линейных уравнений и методы их решения.
Матричный метод.
Правило Крамера.
Метод Гаусса.
Пунтк 1. Понятие систем линейных уравнений и методы их решения.
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n)
– некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс i
— обозначает
номер уравнения, а второй j – номер неизвестного, при котором стоит
этот коэффициент.
В обозначении коэффициентов aij первый индекс i
— обозначает
номер уравнения, а второй j – номер неизвестного, при котором стоит
этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.

Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Существует три основных метода решения систем линейных уравнений:
Матричный метод.
Правило Крамера.
Метод Гаусса.
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов
Найдем произведение
т. е.
в результате произведения мы получаем
левые части уравнений данной системы.
Тогда пользуясь определением равенства
матриц данную систему можно записать
в виде
е.
в результате произведения мы получаем
левые части уравнений данной системы.
Тогда пользуясь определением равенства
матриц данную систему можно записать
в виде
или короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Заметим,
что поскольку обратную матрицу можно
найти только для квадратных матриц, то
матричным методом можно решать только
те системы, в которых число
уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна
и в случае, когда число уравнений не
равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя
найти решение системы в виде X
= A-1B.
Однако, матричная запись системы возможна
и в случае, когда число уравнений не
равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя
найти решение системы в виде X
= A-1B.
Пример 10. Решить системы уравнений.
Найдем матрицу обратную матрице A.
,
Таким образом, x = 3, y = – 1.
Итак, х1=4,х2=3,х3=5.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А-1.
Проверка:
Р ешите матричное уравнение AX+B=C, где
Из
уравнения получаем .
Следовательно,
Определитель— Набор линейных уравнений не имеет решения, единственного решения или бесконечного решения?
Вероятно, самый простой метод (чтобы полностью различать различные возможности), который я видел, — это преобразование соответствующей расширенной матрицы в эшелонированную форму с уменьшенным числом строк. В этом случае вы должны начать с: $$\left[\begin{array}{ccc|c}1 & 3 & -1 & -4\\4 & -1 & 2 & 3\\2 & -1 & -3 & 1\end{array}\right]$$ Вычитая первую строку из второй, умноженную на $4$, и первую строку из третьей, умноженную на $2$, мы получим: $$\left[\begin{array}{ ccc|c}1 и 3 и -1 и -4\\0 и -13 и 6 и 19\\0 & -7 & -1 & 9\end{array}\right]$$ Вычитая $2$ из третьей строки, умноженной на вторую, мы имеем: $$\left[\begin{array}{ccc|c} 1 & 3 & -1 & -4\\0 & 1 & 8 & 1\\0 & -7 & -1 & 9\end{массив}\right]$$ Добавляя $7$ раз вторую строку к третьей, у нас есть: $$\left[\begin{array}{ccc|c}1 & 3 & -1 & -4\\0 & 1 & 12 & 1\\0 & 0 & 55 & 16\end{array} \right]$$
В этой точке у нас есть только нули ниже главной диагонали, но нет нулей на диагонали, поэтому существует единственное решение. Продолжая уменьшать до тех пор, пока часть расширенной матрицы размером $3\times 3$ не станет просто единичной матрицей размером $3\times 3$, мы получим $$\left[\begin{array}{ccc|c}1 & 0 & 0 & 3 /11\\0 & 1 & 0 & -73/55\\0 & 0 & 1 & 16/55\end{array}\right]$$ Это говорит нам, что $x=3/11,$ $y= -73/55,$ $z=16/55$ — единственное решение системы.
Продолжая уменьшать до тех пор, пока часть расширенной матрицы размером $3\times 3$ не станет просто единичной матрицей размером $3\times 3$, мы получим $$\left[\begin{array}{ccc|c}1 & 0 & 0 & 3 /11\\0 & 1 & 0 & -73/55\\0 & 0 & 1 & 16/55\end{array}\right]$$ Это говорит нам, что $x=3/11,$ $y= -73/55,$ $z=16/55$ — единственное решение системы.
Рассмотрим другую систему: $$\begin{cases}x+3y-z=4\\4x-y+2z=8\\2x-7y+4z=-3,\end{cases}$$, которая имеет соответствующую матрицу $$\left[\begin{array}{ccc|c}1 & 3 & -1 & 4\\4 & -1 & 2 & 8\\2 & -7 & 4 & -3\end{ array}\right].$$ Начав таким же образом, получим $$\left[\begin{array}{ccc|c}1 & 3 & -1 & 4\\0 & -13 & 6 & -8\ \0 & -13 & 6 & -11\end{array}\right],$$ и вычитание второй строки из третьей дает нам $$\left[\begin{array}{ccc|c}1 & 3 & -1 & 4\\0 & -13 & 6 & -8\\0 & 0 & 0 & -3\end{array}\right].$$ Теперь у нас есть только нули ниже главной диагонали, но у нас есть ноль на главной диагонали тоже. Это говорит нам о том, что либо решений нет, либо их бесконечно много. В обратном переводе на $x,y,z$ это эквивалентная система $$\begin{cases}x+3y+-z=4\\0x-13y+6z=-8\\0x+0y+0z=- 3,\end{cases}$$ или альтернативно $$\begin{cases}x=-\frac5{13}z+\frac{28}{13}\\y=\frac6{13}z+\frac8{13} \\0=3,\end{cases}$$, но у последнего уравнения нет решения, поэтому нет решения и у системы.
В обратном переводе на $x,y,z$ это эквивалентная система $$\begin{cases}x+3y+-z=4\\0x-13y+6z=-8\\0x+0y+0z=- 3,\end{cases}$$ или альтернативно $$\begin{cases}x=-\frac5{13}z+\frac{28}{13}\\y=\frac6{13}z+\frac8{13} \\0=3,\end{cases}$$, но у последнего уравнения нет решения, поэтому нет решения и у системы.
Результат : У нас не будет решений, когда мы получим одну или несколько строк всех $0$s , за исключением последнего столбца , поскольку мы уменьшаем расширенную матрицу.
Напротив, если бы мы начали с системы $$\begin{cases}x+3y-z=4\\4x-y+2z=8\\2x-7y+4z=0,\end{ case}$$, которому соответствует матрица $$\left[\begin{array}{ccc|c}1 & 3 & -1 & 4\\4 & -1 & 2 & 8\\2 & -7 & 4 & 0\end{array}\right],$$, тогда наш процесс сокращения даст нам $$\left[\begin{array}{ccc|c}1 & 3 & -1 & 4\\0 & -13 & 6 & -8\\0 & 0 & 0 & 0\end{массив}\right].$$ Опять же, у нас не должно быть решений или их должно быть бесконечно много. Продолжая сокращать количество строк, насколько это возможно, мы получаем $$\left[\begin{array}{ccc|c}1 & 0 & 5/13 & 28/13\\0 & 1 & -6/13 & 8 /13\\0 & 0 & 0 & 0\end{массив}\right]. $$ В обратном переводе на $x,y,z$ это эквивалентная система $$\begin{cases}x+0y+\ frac5{13}z=\frac{28}{13}\\0x+y-\frac6{13}z=\frac8{13}\\0=0.\end{cases}$$ Одно из этих уравнений всегда истинно, поэтому одна из наших переменных может принимать любое значение. С таким же успехом мы могли бы позволить $z$ принимать любое значение, после чего два других уравнения сообщат нам значения, которые должны принимать $x$ и $y$. Следовательно, у нас есть бесконечно много решений.
$$ В обратном переводе на $x,y,z$ это эквивалентная система $$\begin{cases}x+0y+\ frac5{13}z=\frac{28}{13}\\0x+y-\frac6{13}z=\frac8{13}\\0=0.\end{cases}$$ Одно из этих уравнений всегда истинно, поэтому одна из наших переменных может принимать любое значение. С таким же успехом мы могли бы позволить $z$ принимать любое значение, после чего два других уравнения сообщат нам значения, которые должны принимать $x$ и $y$. Следовательно, у нас есть бесконечно много решений.
Итог : у нас будет бесконечно много решений всякий раз, когда мы получим одну или несколько строк со всеми $0$ при уменьшении расширенной матрицы, пока у нас нет строк со всеми $0$, кроме в последней колонке.
Добавлено : Просто взять определитель нерасширенной матрицы системы — значение $$\begin{bmatrix}1 & 3 & -1\\4 & -1 & 2\\2 & -1 & -3\end{bmatrix}$$ в первом примере и $$\begin{bmatrix}1 & 3 & -1\\4 & -1 & 2\\2 & -7 & 4\end{bmatrix}$ $ в двух других примерах — даст нам часть ответа. Если определитель равен $0$ (как во втором и третьем примерах), то система либо не имеет решений, либо бесконечно много, но мы не можем (одним этим методом) сказать, какие именно. В противном случае система имеет единственное решение, но мы не можем (одним только этим методом) сказать, каким оно может быть. Вот почему я предпочитаю первый предложенный мной метод, по крайней мере, когда имеешь дело только с несколькими уравнениями и несколькими переменными: он рассказывает нам всю историю.
Если определитель равен $0$ (как во втором и третьем примерах), то система либо не имеет решений, либо бесконечно много, но мы не можем (одним этим методом) сказать, какие именно. В противном случае система имеет единственное решение, но мы не можем (одним только этим методом) сказать, каким оно может быть. Вот почему я предпочитаю первый предложенный мной метод, по крайней мере, когда имеешь дело только с несколькими уравнениями и несколькими переменными: он рассказывает нам всю историю.
Решения систем уравнений: объяснение, обзор и примеры
Решение — это слово, которое мы часто используем в математике, но оно может означать разные вещи в зависимости от контекста. Однако в целом решение представляет собой значение или набор значений, которые делают уравнения верными. Хотя идея истины может показаться чем-то более подходящим для таких дисциплин, как наука и философия, чем математика, мы ищем истину, когда ищем решения систем уравнений.
Что такое решение системы уравнений?
Чтобы понять, что такое решение системы уравнений, давайте начнем с рассмотрения некоторых уравнений и их решений.
| Equation | Solution |
| 5+4=s | s=9 |
| n+7=9 | n=2 |
What do the two общего между уравнениями и их решениями? Решения делают уравнения верными. Когда с=9, то 5+4=с. Когда n=2, то n+7=9.
Система уравнений включает два или более уравнений. Каждое из уравнений должно иметь как минимум две переменные, например, x и y.
Чтобы узнать, что такое система уравнений, ознакомьтесь с нашим постом: Написание систем уравнений .
набор решений системы уравнений будет координатами упорядоченной пары (пар), которые удовлетворяют всем уравнениям в системе. Другими словами, эти значения x и y сделают уравнения верными. Соответственно, при построении системы уравнений решением будут все точки пересечения графиков.
Соответственно, при построении системы уравнений решением будут все точки пересечения графиков.
Заинтересованы в лицензии школы Альберта?
Количество решений системы уравненийКоличество решений системы уравнений зависит от самих уравнений. Системы могут иметь одно решение, несколько решений, бесконечно много решений или даже не иметь решения.
Системы линейных уравнений классифицируются по количеству решений, которые они имеют. Существуют две основные категории систем уравнений:
- An несовместная система, не имеющая решений
- непротиворечивая система, имеющая одно или несколько решений
- Зависимая система , с бесконечным числом решений
Начните практиковать Алгебру 1 на Альберте прямо сейчас!
Системы уравнений без решения (пример)
Давайте начнем с рассмотрения несовместимых систем, как мы это называем, когда у систем уравнений нет решений. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, если наша система уравнений состоит из двух или более параллельных прямых, то не будет мест пересечения графиков прямых, а значит, не будет и решений.
Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, если наша система уравнений состоит из двух или более параллельных прямых, то не будет мест пересечения графиков прямых, а значит, не будет и решений.
Обзор параллельных линий см. в нашем обзорном руководстве Параллельные и перпендикулярные линии .
Прямые y=x+3 и y=x-2 параллельны. Их графики показаны справа.
Из графика видно, что линии никогда не пересекаются , а значит, у этой системы уравнений нет решений. Таким образом, хотя каждое линейное уравнение в системе имеет бесконечное число решений, система уравнений, состоящая из обоих этих линейных уравнений, не имеет решений. Мы можем классифицировать систему как несовместимую.
Системы нелинейных уравнений также могут не иметь решений. Ниже приведен график системы двух квадратных уравнений, которые никогда не пересекаются. Вместе эти уравнения составляют систему, не имеющую решений.
Как насчет систем с более чем двумя уравнениями? Решения должны удовлетворять всем уравнениям системы. Графически только точки пересечения всех графов в системе считаются решениями.
Графически только точки пересечения всех графов в системе считаются решениями.
Например, на приведенном ниже графике показана система из трех уравнений: две параллельные прямые и одна прямая, пересекающая параллельные прямые. Эта система уравнений не имеет решения, потому что нет места, где все три прямые пересекаются друг с другом одновременно.
Заинтересованы в лицензии школы Альберта?
Система уравнений с бесконечными решениями (пример)
Теперь давайте впадем в противоположную крайность и рассмотрим системы уравнений, которые являются одновременно непротиворечивыми и зависимыми, что происходит, когда существуют бесконечные решения систем уравнений. Графически мы ищем систему уравнений, которая пересекается в бесконечном числе точек. Как это может случиться? Это происходит всякий раз, когда два уравнения на самом деле являются одним и тем же уравнением.
Например, рассмотрим систему:
y=x+3
х=у-3
Хотя второе уравнение не записано в форме точки пересечения наклона, мы можем видеть, что уравнение имеет тот же наклон, 1, и ту же точку пересечения по оси y, 3, что и y=x+3.
Для краткого ознакомления с формами линейных уравнений ознакомьтесь с нашим сообщением в блоге Форма пересечения наклонов .
Тот факт, что два уравнения идентичны, станет очевидным, если мы перепишем x=y-3 в форме пересечения наклона:
х=у-3
x{\color{red}{-y}}=y-3{\color{red}{-y}}
х-у=-3
х-у {\ цвет {красный} {-x}} = -3 {\ цвет {красный} {-x}}
-у=-х+-3
{\ color {красный} {(-1)}} (-y) = {\ color {красный} {(-1)}} (-x + -3)
у=х+3
Таким образом, мы также можем записать эту систему как:
y=x+3
у=х+3
Графики этих двух уравнений показаны справа.
Как видно из графика, эти уравнения представляют собой одну и ту же прямую на координатной плоскости. Поскольку все точки на одной прямой находятся и на другой прямой, у этой системы существует бесконечное число решений.
Обратите внимание: это не означает, что каждый набор координат является решением этого уравнения. Например, координаты (0,5) не являются решением системы уравнений, так как эта точка не лежит на прямых. Однако, поскольку линия простирается до бесконечности в обоих направлениях, на каждой линии существует бесконечное количество точек и, следовательно, бесконечное количество решений системы уравнений.
Например, координаты (0,5) не являются решением системы уравнений, так как эта точка не лежит на прямых. Однако, поскольку линия простирается до бесконечности в обоих направлениях, на каждой линии существует бесконечное количество точек и, следовательно, бесконечное количество решений системы уравнений.
Другие системы уравнений, которые являются как непротиворечивыми, так и зависимыми, включают любые комбинации уравнений, такие как уравнения для окружностей, парабол и других фигур, где графики уравнений полностью перекрываются.
Начните практиковать Алгебру 1 на Альберте прямо сейчас!
Система уравнений с одним решением (пример)
Сколько существует решений систем уравнений для системы, которая одновременно независима и непротиворечива? Такая система имеет ровно одно решение, что означает, что она имеет один набор значений, который делает все уравнения в системе верными.
Линейные уравнения в приведенной ниже системе соответствуют этому описанию:
y=x+3
y=-x-1
Линии, представляющие эти уравнения на координатной плоскости, будут пересекаться ровно в одной точке, как показано ниже.
Поскольку эти прямые пересекаются в точке (-2,1), эта точка является единственным решением системы. Мы можем использовать алгебру, чтобы убедиться, что координаты (\color{red}{-2},\color{blue}{1}) превращают каждое уравнение в истинное утверждение.
Начнем с первого уравнения:
y=x+3
{\color{синий}{1}}={\color{красный}{-2}}+3
1=1
А теперь давайте проверим второе уравнение:
y=-x-3
{\color{синий}{1}}=-({\color{красный}{-2}})-1
1=2-1
1=1
Обратите внимание: мы могли бы определить, что эта система уравнений имеет одно решение, просто взглянув на сами уравнения, если бы заметили, что они имеют разные наклоны. Наклон y=x+3 равен 1, а наклон y=-x-1 равен -1. Линии с разным наклоном никогда не бывают параллельными, а прямые, лежащие в одной плоскости, но не параллельные, всегда пересекаются ровно в одной точке.
Заинтересованы в лицензии школы Альберта?
Как найти решение системы уравнений Существует несколько методов решения систем уравнений, в том числе: Такие инструменты, как Desmos и Geogebra, предлагают графические онлайн-калькуляторы, помогающие в этом процессе.
Каждый из этих методов может помочь нам найти не только количество решений систем уравнений, но и то, что это за решения.
Когда мы находим решение или решения системы уравнений, мы можем подставить значения обратно в уравнения, чтобы убедиться, что они верны.
Начни практиковать Алгебру 1 на Альберте прямо сейчас!
Решения систем уравнений: ключи для запоминания- Решение систем уравнений — это набор координат, который делает все уравнения в системе верными.
- Системы уравнений могут иметь любое количество решений от нуля до бесконечности.
- Мы можем классифицировать системы уравнений как несовместные, зависимые или независимые и непротиворечивые в зависимости от количества решений.
- Системы уравнений без решений несовместны, а системы с бесконечными решениями зависимы.
 Системы уравнений, имеющие ровно одно решение, называются независимыми и непротиворечивыми.
Системы уравнений, имеющие ровно одно решение, называются независимыми и непротиворечивыми. - Решения систем уравнений можно найти графически или алгебраически.
Заинтересованы в школьной лицензии?
Пригласите Альберта в свою школу и предоставьте всем учителям лучший в мире банк вопросов для:
➜ SAT® и ACT®
➜ AP®
➜ ELA, математика, естествознание и социальные науки
➜ Государственные оценки
Варианты для учителей, школы, районы.
УЗНАТЬ О ВАРИАНТАХ
Уникальное решение Нет решений Бесконечное количество решений
Рассмотрим следующую систему линейных уравнений, представленную в виде пересечения наклона.
Y = M 1 x + B 1
(Slope = M 1 и Y-Intercept = B 1 )
Y = M 2 x + B 2
( slope = m 2 and y-intercept = b 2 )
Unique Solution
y = m 1 x + b 1
y = m 2 x + b 2
Если приведенная выше система линейных уравнений имеет единственное решение или только одно решение, то она должна удовлетворять следующему условию.
м 1 ≠ м 2
То есть уклоны не должны быть равными.
Мы уже знаем, что график любого линейного уравнения будет линией.
Если две прямые имеют разные наклоны (m 1 ≠ m 2 ), то прямые пересекаются только в одной точке и система имеет единственное решение или только одно решение.
Пусть в системе уравнений с двумя переменными наклоны не равны (m 1 ≠ m 2 ).
Что делать, если есть тот же y-перехват, скажем, ‘b’?
В системе двух линейных уравнений, если наклоны не равны (m 1 ≠ m 2 ), то система имеет единственное решение или только одно решение. Неважно, есть ли один и тот же y-перехват или разные y-перехваты.
Если есть такая же точка пересечения с осью y, скажем, ‘b’, единственным решением будет
(0, b)
Нет решения
Если приведенная выше система линейных уравнений не имеет решения, то она должна удовлетворять условию следующие условия.
M 1 = M 2
B 1 ♠ B 2
Если две линии имеют одинаковый наклон (M 1 = M 2 ) и различные Y-Intercepts (B = M 2 ) и различные Y-Intercepts (B = M 2 ) и различные 1 ≠ b 2 ), то эти две прямые параллельны и никогда не пересекутся.
Итак, нет решения для системы линейных уравнений с одинаковым наклоном и разными точками пересечения по оси y.
Бесконечные решения
Два линейных уравнения в системе совершенно одинаковы, тогда система имеет бесконечно много решений.
Рассмотрим следующую систему уравнений.
3x — y + 5 = 0 —-(1)
15x — 5y + 25 = 0 —-(2)
Разделите обе части уравнения (2) на 5.
(2 ) ÷ 5 —-> 15x/5 — 5y/5 + 25/5 = 0/5
3x — y + 5 = 0
Если разделить уравнение (2) на 5, получится уравнение ( 1).
Таким образом, два уравнения, приведенные в приведенной выше системе, совершенно одинаковы. Следовательно, система имеет бесконечно много решений.
Следовательно, система имеет бесконечно много решений.
Другой способ проверить, имеет ли система линейных уравнений с двумя переменными бесконечное множество решений, — записать уравнения в форме пересечения наклона.
Рассмотрим следующую систему уравнений, представленную в форме пересечения наклона.
Y = M 1 x + B 1
(Slope = M 1 и Y-Intercept = B 1 )
Y = M 2 x + B 2
( наклон = m 2 и точка пересечения y = b 2 )
Если приведенная выше система уравнений имеет бесконечно много решений, то она должна удовлетворять следующим двум условиям.
м 1 = м 2
b 1 = b 2
Линии одинаковые и, следовательно, совпадают.
Поскольку прямые совпадают, они касаются друг друга во всех точках на обеих прямых, и система имеет бесконечно много решений.
Примечание:
Если система линейных уравнений дана в общей или стандартной форме, запишите их в форме пересечения наклона и действуйте, как описано выше.
Общая форма:
a 1 x + b 1 Y + C 1 = 0
A 2 X + B 2 Y + C 2 = 0
Стандартная форма:
A 1 X + B 1 903 c 1
a 2 x + b 2 y = c 2
Примеры 1-2: Определите, имеют ли следующие системы линейных уравнений единственное решение.
Пример 1:
y = 2x + 5
y = 3x — 2
Решение:
y = 2x + 5 —-> уклон m = 2
y = 3x — 2 —-> наклон m = 3
В приведенных выше двух линейных уравнениях наклоны различны.
Итак, прямые пересекаются только в одной точке.
Следовательно, система имеет единственное решение.
Пример 2:
y = -2x + 5
y = -2x + 3
Решение:
y = -2x + 5 —-> наклон m = -2
y = -2x + 1 —-> наклон m = -2
В приведенных выше двух линейных уравнениях наклоны равны.
Следовательно, система не имеет единственного решения.
Примеры 3-4: Определите, не имеют ли решения следующие системы линейных уравнений.
Пример 3:
y = 3x + 5
y = 3x — 2
Решение:
y = 3x + 5 —-> m = 3 и b = 5
y = 3x — 2 —> m = 3 и b = -2
В приведенных выше двух линейных уравнениях наклон одинаков, а точки пересечения y различны.
Итак, прямые параллельны и никогда не пересекаются.
Следовательно, система не имеет решения.
Пример 4 :
4x + 2y — 1 = 0
2x + y + 5 = 0
Решение :
Уравнения не в форме пересечения наклона.
Запишите их в форме пересечения наклона.
4x + 2y — 1 = 0 2y = -4x + 1 y = -2x + 1/2 | 2х + у + 5 = 0 у = -2х — 5 |
y = -2x + 1/2 —-> m = -2 и b = 1/2
y = -2x — 5 —-> m = -2 и b = -5
В данных двух линейных уравнениях наклон один и тот же, а точки пересечения у разные.
Итак, прямые параллельны и никогда не пересекаются.
Следовательно, система не имеет решения.
Примеры 5-7 : Определите, имеют ли следующие системы линейных уравнений бесконечное множество решений.
Пример 5:
y = 3x + 5
y = 3x + 5
Решение:
y = 3x + 5 —-> m = 3 и b = 5
y = — 3x + 5 —> m = 3 и b = 5
В приведенных выше двух линейных уравнениях наклоны и точки пересечения у равны.
Итак, прямые совпадают и касаются друг друга во всех точках на прямой.
Следовательно, система имеет бесконечно много решений.
Пример 6 :
4x + 2y — 1 = 0
2x + y — 0,5 = 0
Решение :
Уравнения не в форме пересечения наклона.
Запишите их в форме пересечения наклона.
4х + 2у — 1 = 0 2у = -4х + 1 у = -2х + 1/2 | 2x + y — 0,5 = 0 y = -2x + 0,5 y = -2x + 1/2 |
y = -2x + 1/2 —-> m = -2 и b = 1/2
y = -2x + 1/2 —-> m = -2 и b = 1 /2
В данных двух линейных уравнениях наклоны и точки пересечения с осью y одинаковы.
Итак, прямые совпадают и касаются друг друга во всех точках на прямой.
Следовательно, система имеет бесконечно много решений.
Пример 7 :
2x — y = 1
4x + y = 5
Решение :
Уравнения не в форме пересечения наклона.
Запишите их в форме пересечения наклона.
2x — y = 1 -y = -2x + 1 y = 2x — 1 —> m = 2 | 4x + y = 5 y = -4x + 5 —-> m = -4 |
В данных двух линейных уравнениях наклон различен.
Итак, строки не совпадают.
Следовательно, система не имеет бесконечного множества решений.
Пример 8 :
В следующей системе линейных уравнений k — константа, а x и y — переменные. При каком значении k система уравнений будет иметь единственное решение?
kx — y = 4
10x — 5y = 7
Решение:
Уравнения не в форме пересечения наклона.
Запишите их в форме пересечения наклона.
кх — у = 4 -у = -кх + 4 у = кх — 4 | 10x — 5y = 7 -5y = -10x + 7 5y = 10x — 7 y = 2x — 7/5 |
y = kx — 4/3 —-> наклон m = k
y = 2x — 7/5 —-> наклон m = 2
Если система имеет единственное решение, то наклоны не должны быть равны.
k ≠ 2
Когда k ≠ 2, система имеет единственное решение.
Пример 9 :
В следующей системе линейных уравнений k — константа, а x и y — переменные. При каком значении k система уравнений не будет иметь решения?
kx — 3y = 4
4x — 5y = 7
Решение :
Уравнения не в форме пересечения наклона.
Запишите их в форме пересечения наклона.
kx — 3y = 4 -3y = -kx + 4 3y = kx — 4 y = (k/3)x — 4/3 | 4x — 5y = 7 -5y = -4x + 7 5y = 4x — 7 y = (4/5)x — 7/5 |
y = (k/3)x — 4/3 —-> m = k/3 и b = -4/3
y = (4/5)x — 7/5 —-> m = 4/5 и b = -7/5
В данных двух линейных уравнениях точки пересечения y различны.
Если наклоны равны, то линии будут параллельны и никогда не пересекутся. Кроме того, система не будет иметь решения.
Дано, что система не имеет решений.
Итак, наклоны должны быть равными.
k/3 = 4/5
Умножьте обе части на 3.
k = 12/5
Когда k = 12/5, система не будет иметь решения.
Пример 10 :
В следующей системе линейных уравнений k — константа, а x и y — переменные. При каком значении k система уравнений будет иметь бесконечно много решений?
kx — 3y = 12
4x — 5y = 20
Решение:
Уравнения не имеют форму пересечения наклона.
Запишите их в форме пересечения наклона.
кх — 3у = 12 -3у = -кх + 12 3у = кх — 12 у = (к/3)х — 4 | 4x — 5y = 20 -5y = -4x + 20 5y = 4x — 20 y = (4/5)x — 4 |
y = (k/3)x — 4 —-> m = k/3 и b = -4
y = (4/5)x — 4 —-> m = 4/ 5 и b = -4
В данных двух линейных уравнениях точки пересечения у равны.

 В этом случае система имеет бесконечно много решений
В этом случае система имеет бесконечно много решений А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар,
2006.
А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар,
2006.
 Системы уравнений, имеющие ровно одно решение, называются независимыми и непротиворечивыми.
Системы уравнений, имеющие ровно одно решение, называются независимыми и непротиворечивыми.