Коллинеарность векторов, условия коллинеарности векторов.
Навигация по странице:
- Определение коллинеарности векторов
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- плоские задачи
- пространственные задачи
Смотрите также онлайн калькулятор для проверки коллинеарности векторов.
Онлайн упражнения на тему коллинеарность векторов на плоскости.
Онлайн упражнения на тему коллинеарность векторов в пространстве.
Определение.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b
Два вектора a и b
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
a × b =
ijkaxayazbxbybz = i (aybz — a zby) — j (axbz — azbx) + k (axby — aybx) =
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | . | |
| bx | by |
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
Вектора с и b не коллинеарны т. к. к. |
5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3.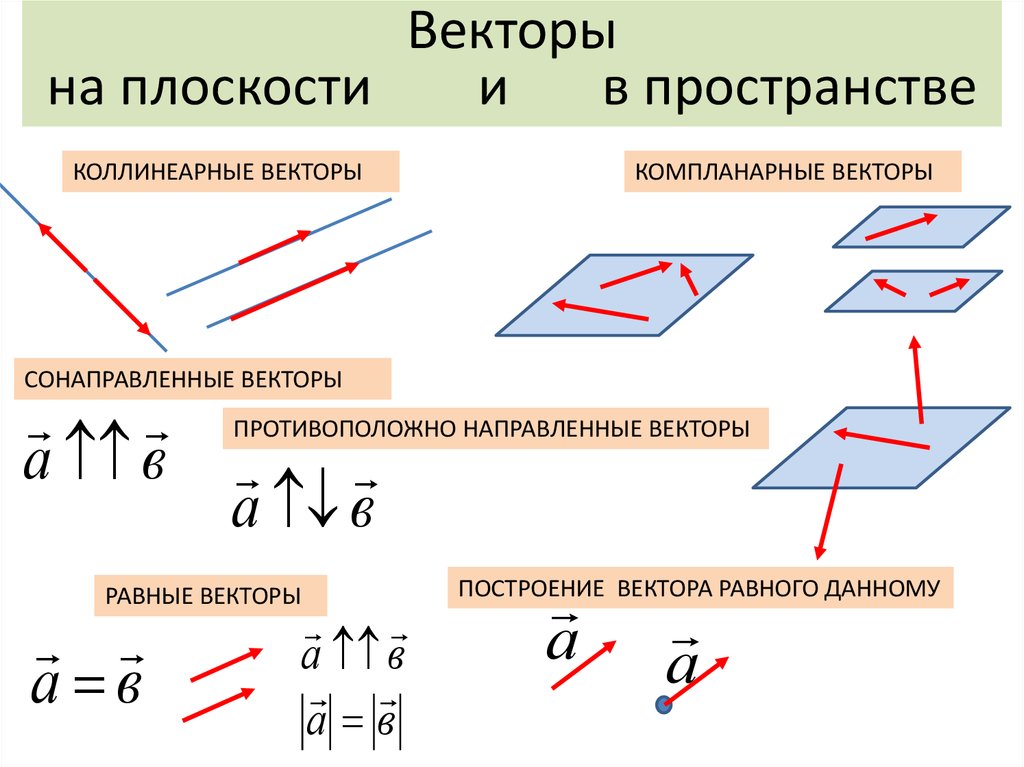 найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
Значит:
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Вектора a и b коллинеарны т.к. 14 = 28 = 312
Вектора a и с не коллинеарны т.к. 15 = 210 ≠ 312
Вектора с и b не коллинеарны т.к. 54 = 108 ≠ 1212
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.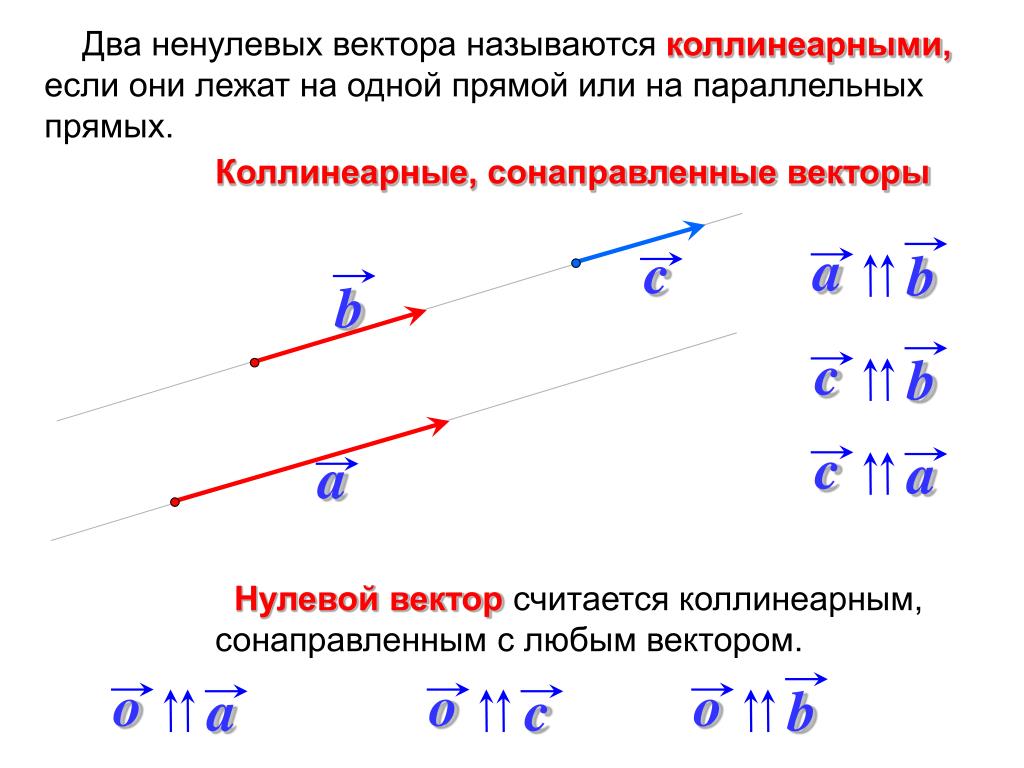
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.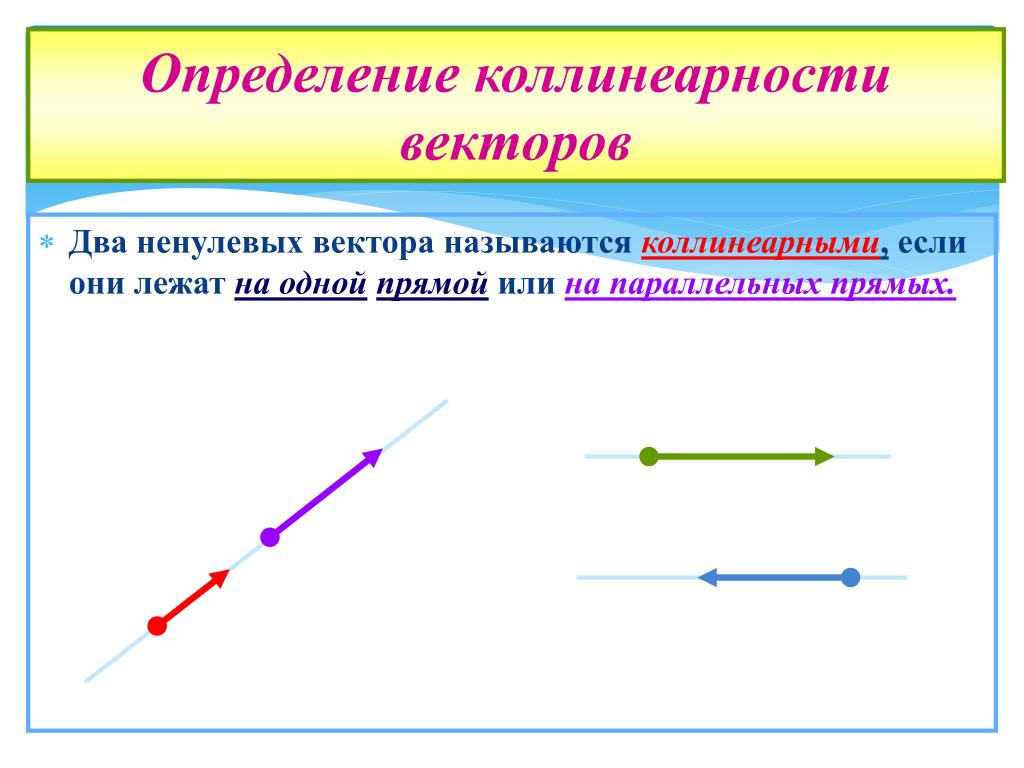
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В одном парке есть бамбук, который каждую ночь с незапамятных времён становит- ся выше на одну и ту же величину. Каждый день садовник отрезает от
Каждый день садовник отрезает от
Клетки таблицы 4*7 раскрашены в черный и белый цвета. Пар соседних клеток разного цвета всего 26, пар соседних клеток черного цвета всего 9. Сколько соседних клеток белого цвета.
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Зайчик находится в некоторой точке на некоторой прямой. По этой прямой он может прыгать вправо или влево, но только на расстояние, равное 840, 1785,
1.Вычислить f(2), если 25f(x/1580)+(3-√34) f(1580/x)=2017x. Ответ округлить до целого числа 2.Папа на машине вез сына на занятие в математическом
Кузнецов Л. А / Кузнецов решебник Аналитическая геометрия. Решены все варианты. / 20 / 20
Скачано с http://antigtu.ru
Задача Кузнецов Аналитическая геометрия
Условие задачи
Написать разложение вектора по векторам
Решение
Искомое разложение вектора имеет вид:
Или в виде системы:
Получаем: | Скачано | с |
К первой строке приб вим вторую умноженную на
К первой стро е прибавим третью умноженную на
1-20
antigtu:
:
:
Скачано | с | antigtu |
| ||
|
| |
Искомое разложение: |
|
|
Задача Кузнецов Аналитическая геометрия 2-20
Условие задачи
Коллинеарны ли векторы и , построенные по векторам и ?
Решение |
|
|
Векторы коллинеарны если существует такое число | такое, что | |
коллинеарны если их координаты пропорциональны. |
| |
Нетрудно заметить, что | для любых и . | |
Т.е. | , а значит векторы и — коллинеарны. | |
. Т.е. векторы
Задача Кузнецов Аналитическая геометрия 3-20
Условие задачи
Найти косинус угла между векторами | и . | antigtu | |
Решение |
|
| |
Найдем и : |
|
|
|
Находим косинус угла между векторами |
| и : | |
Скачано | с |
|
|
|
|
| |
Т.е. косинус угла: |
|
|
|
и следовательно угол
Задача Кузнецов Аналити еская геометрия 4-20
Условие з д чи
Вычислить площадь параллелограмма, построенного на векторах и .
Решение | . | ru |
Т.е. площадь параллелограмма, построенного на векторахantigtuи равна .
Площадь параллелограмма, построенного на векторах и , численно равна модулю их векторного произведения:
Вычисляем | , используя его свойства векторного произведения: |
Вычисляем площадь: | |
Задача Кузнецов Аналитическая геометрия 5-20
Так как | Скачано, то векторы , | и компланарны. |
Условие задачи | с | |
Компланарны ли векторы , и ? | ||
Решение
Для того чтобы три вектора были компланарны (лежали в одной плоскости или параллельных
плоскостях), необходимо и достаточно, чтобы их смешанное произведение | было равно |
нулю. |
|
Получаем:
Так как
Согласно геометрическому смыслу векторного произведения:
Задача Кузнецов Аналитическая геометрия 6-20 |
|
| ||||
Условие задачи |
|
|
|
|
| |
Вычислить объем тетраэдра с вершинами в точках | и его высоту, опущенную из | |||||
вершины | на грань | . |
|
| . | ru |
|
|
|
|
| ||
Решение |
|
|
|
|
|
|
Из вершины | проведем векторы: |
|
|
|
| |
В соответствии с геометрическим смыслом смешанного произведения имеем: |
| |||||
|
|
| с | antigtu |
|
|
Вычислим смешанное произведение: |
|
|
| |||
Скачано |
|
|
| |||
|
|
|
| |||
Вычислим векторное произведение:
Получаем: |
|
| antigtu |
|
|
| |
Тогда: |
|
|
|
Объем тетраэдра: |
|
| |
Высота: | Скачано |
| |
Задача Кузнецов Аналитическая ге метрияс | 7-20 | ||
Условие задачи |
|
| |
Найти расстояние от точки | до плоскости, проходящей через три точки | ||
Решение
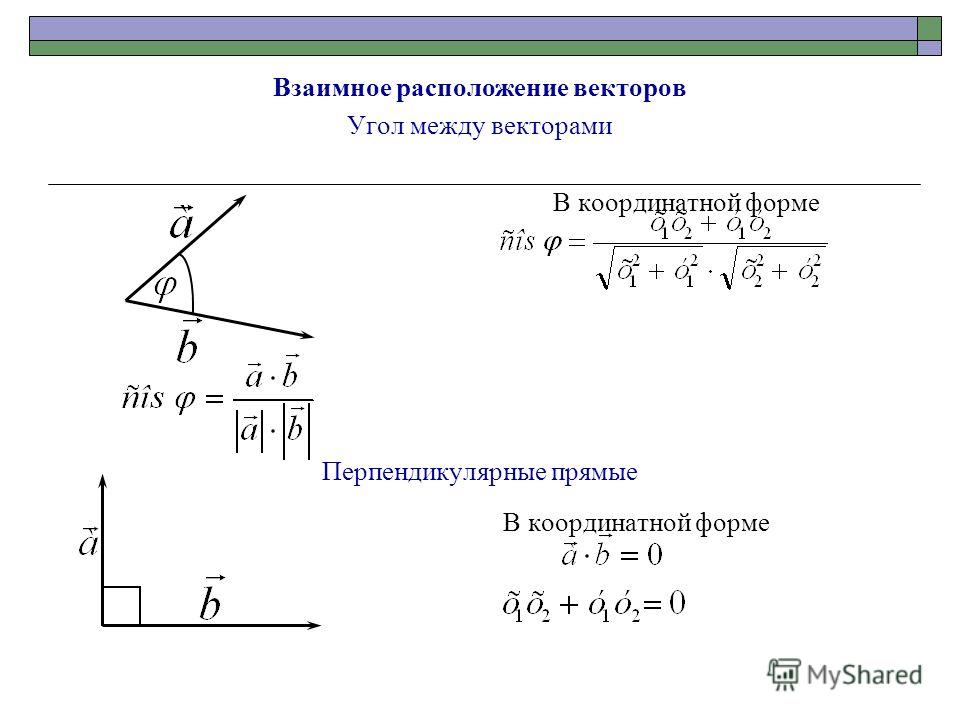
Находим уравнение плоскости, проходящей через три точки
Проведем преобразования:
.
:
|
|
|
| antigtu | . | ru |
|
Расстояние от точки |
|
|
|
| |||
до плоскости |
| : |
| ||||
Находим: |
|
| с |
|
|
|
|
|
|
|
|
|
|
| |
Задача Кузнецов Аналитическая геометрия 8-20 |
|
|
| ||||
| Скачано |
|
|
|
|
| |
Условие задачи |
|
|
|
|
|
| |
Написать уравнение плоскости, пр х дящей через точку перпендикулярно вектору | . | ||||||
Решение |
|
|
|
|
|
|
|
Найдем вектор | : |
|
|
|
|
| |
Так как ве тор | перпендикулярен искомой плоскости, то его можно взять в качестве вектора | ||||||
нормали. Поэтому уравнение плоскости будет иметь вид:
Задача Кузнецов Аналитическая геометрия 9-20
Условие задачи
Найти угол между плоскостями:
Решение | antigtu |
Двугранный угол между плоскостями равен углу между их нормальными векторы заданных плоскостей:
Угол между плоскостями определяется формулой:
| Скачано | с | ||
Задача Кузнецов Аналитическая ге метрия 10-20 | ||||
Условие задачи |
|
|
| |
Найти координаты точки |
| , рав оудале ой от точек и . | ||
Решение |
|
|
|
|
Найдем расстояние | и | : |
| |
Так как по условию задачи |
| , то | ||
векторами. Нормальные
|
| antigtu | . |
Таким образом | . |
| |
|
|
Задача Кузнецов Аналитическая геометрия 11-20
Условие задачи
Пусть — коэффициент преобразования подобия с центром в начале координат. точка принадлежит образу плоскости ?
Решение |
|
| с |
При преобразовании подобия с центром в начале координат плоскость | |||
| и коэффициентом переходит в плоскость | ||
| Скачано | . | Находим образ плоскости : |
|
| ||
Подставим координаты точки в урав е ие : | |||
Так как | , то то ка не принадлежит образу плоскости . | ||
Задача Кузнецов Ан литическая геометрия 12-20 | |||
Условие з д чи |
|
| |
Написать | аноничес ие уравнения прямой. | ||
ru
Верно ли, что
Решение |
|
|
| ru |
Канонические уравнения прямой: | antigtu | . |
| |
| , |
| ||
|
|
| ||
где | — координаты какой-либо точки прямой, а | — ее направляющий | ||
вектор.
Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей. Нормальные вектора плоскостей:
Найдем направляющий вектор :
Скачано | с | . Пусть , тогда |
Найдем какую-либо точку прям й |
|
коллинеарных векторов | Tutor Pace
Сегодня мы рассмотрим основные понятия и свойства линейной алгебры. Линейную алгебру также можно назвать векторной алгеброй, поскольку она изучает векторные пространства. Теперь вы можете задаться вопросом, что такое векторы. Ну, количества делятся на два типа, такие как скаляры и векторы. Скалярная величина – это величина, которая имеет только величину и не имеет направления. Величина, которая имеет как величину, так и направление, называется вектором.
Как сортировать и решать задачки на прошедшее время http://t. co/j3zGC5Q6m8 #алгебра #backtoschool #homeschool pic.twitter.com/dzdb9M73Rl
co/j3zGC5Q6m8 #алгебра #backtoschool #homeschool pic.twitter.com/dzdb9M73Rl
— Tutor Pace (@TutorPace) 4 августа 2015 г.
Давайте рассмотрим некоторые определения и свойства векторов, которые значительно упростят изучение векторных пространств.
Вектор положения: Вектор положения определяет положение любой заданной точки в трехмерной прямоугольной системе координат. Вспомним, что трехмерная прямоугольная координатная плоскость имеет оси x, y и z. Начальная точка для такой системы координат задается (0,0,0). Вектор положения или любая точка P в пространстве задается OP (x, y, z). Величина вектора |OP| может быть задан как √(x 2 + у 2 + я 2 ).
Итак, у нас есть |OP| = √(x 2 + y 2 + z 2 ).
Давайте рассмотрим один из таких вопросов.
Вопрос: Каков вектор положения точки (3, 4, 5). Найдите величину заданного вектора положения?
Вектор положения находится от начала координат (0, 0, 0) до точки P. Чтобы найти величину заданного вектора, выполните действия, указанные на диаграмме ниже:
Чтобы найти величину заданного вектора, выполните действия, указанные на диаграмме ниже:
Давайте теперь рассмотрим некоторые основные типы векторных пространств.
Нулевой вектор: Нулевой вектор также называют нулевым вектором. Помните, что начальная точка вектора называется начальной точкой, а конечная точка называется конечной точкой. Вектор, у которого и начальная точка, и конечная точка совпадают, называется нулевым вектором. Как следует из названия, величина нулевого вектора всегда равна нулю. Нулевые векторы записываются как PP, AA и так далее.
Единичный вектор: Величина вектора, равная 1, называется единичным вектором.
Нужен пример? Ну вот!
Найдите модуль вектора AB (0, 1, 0).
Применить формулу модуля вектора. Вот что вы получите:
Равный вектор: Как следует из названия, равные векторы — это векторы, одинаковые по величине и направлению. Если AB и CD два равных вектора, то они задаются как AB = CD.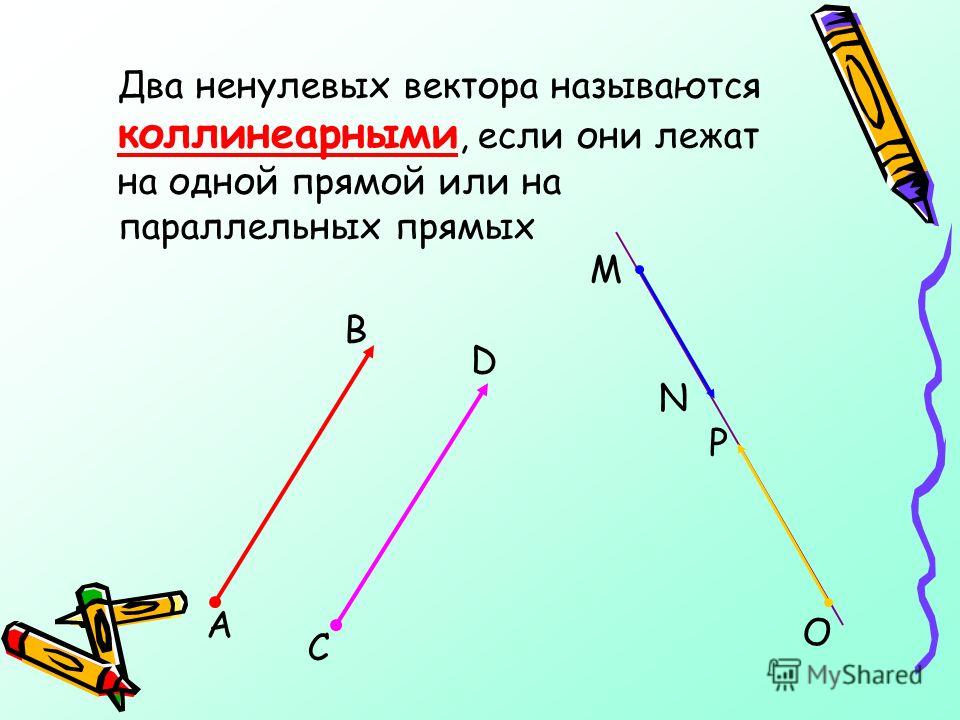
Отрицательный вектор: Опять же, как следует из названия, векторы, имеющие одинаковую величину и противоположные по направлению, называются отрицательными векторами. Если OP — вектор, то PO называется отрицательным вектором. Это можно представить как OP = – PO.
Здесь АВ = – ВА. Таким образом, BA является отрицательным вектором для вектора AB.
Совместно-начальные векторы: Любые данные два вектора называются ко-начальными векторами, если оба заданных вектора имеют одну и ту же начальную точку. Например, OA и OB — два ко-начальных вектора.
Коллинеарные векторы: Любые два заданных вектора называются коллинеарными, если оба вектора параллельны одной прямой.
На приведенной выше диаграмме AB и CD параллельны одной прямой, поэтому два вектора коллинеарны друг другу.
Сложение векторов: Большинство учащихся считают, что сложение векторов довольно запутанно. Проще говоря, вот как вы можете следовать этому:
Проще говоря, вот как вы можете следовать этому:
На приведенной выше диаграмме E является начальной точкой для вектора EF и конечной точкой для вектора DF. Итак, чтобы получить равнодействующую, мы начинаем от начальной точки одного вектора (DE) до конечной точки другого вектора (EF). Следовательно, результирующая векторов есть DF.
Это можно выразить как DF (результирующий вектор) = DE + EF.
Теперь, когда вы знаете о сложении векторов, давайте посмотрим на свойства сложения векторного пространства.
Как решить задачи по #алгебре за 5 шагов http://t.co/kg6CqctO6O #backtoschool #homeschooling pic.twitter.com/wApx3S0D5R
— Tutor Pace (@TutorPace) 4 августа 2015 г.
Коммутативное свойство: Сложение векторов коммутативно. Рассмотрим два вектора a и b, они могут быть выражены как: Ассоциативное свойство: Сложение векторов также ассоциативно.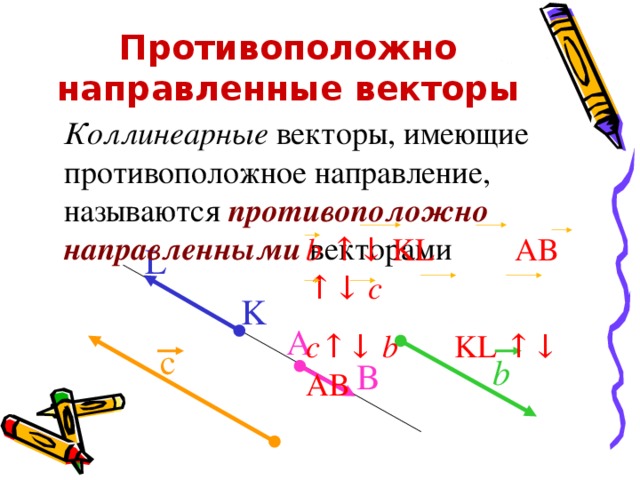 Как и ассоциативное свойство для чисел, нам нужно 3 вектора, чтобы выразить ассоциативное свойство для векторов. Свойство можно записать следующим образом: Скалярное умножение: Теперь давайте кратко рассмотрим умножение вектора на скалярную величину. Пусть есть скалярное число или константа k. Возьмем вектор а. Теперь мы можем получить новый вектор, умножив его на константу k. Это выражается как ka, всегда помните, что вектор, полученный после скалярного умножения, коллинеарен данному вектору. Итак, ka коллинеарно вектору a. Вектор имеет положительное или отрицательное направление в зависимости от знака k. Вот несколько примеров для лучшего понимания: На приведенной выше диаграмме есть вектор, который затем умножается на скаляр 2. Здесь 2 — положительное число, поэтому направление вектора 2a такое же, но величина вектора в два раза больше исходной. вектор а. На приведенной выше диаграмме вектор умножается на скалярное число -3. Поскольку скаляр является отрицательным числом, направление вектора обратно направлению вектора a.
Как и ассоциативное свойство для чисел, нам нужно 3 вектора, чтобы выразить ассоциативное свойство для векторов. Свойство можно записать следующим образом: Скалярное умножение: Теперь давайте кратко рассмотрим умножение вектора на скалярную величину. Пусть есть скалярное число или константа k. Возьмем вектор а. Теперь мы можем получить новый вектор, умножив его на константу k. Это выражается как ka, всегда помните, что вектор, полученный после скалярного умножения, коллинеарен данному вектору. Итак, ka коллинеарно вектору a. Вектор имеет положительное или отрицательное направление в зависимости от знака k. Вот несколько примеров для лучшего понимания: На приведенной выше диаграмме есть вектор, который затем умножается на скаляр 2. Здесь 2 — положительное число, поэтому направление вектора 2a такое же, но величина вектора в два раза больше исходной. вектор а. На приведенной выше диаграмме вектор умножается на скалярное число -3. Поскольку скаляр является отрицательным числом, направление вектора обратно направлению вектора a. Величина вектора будет в три раза больше величины вектора а. Теперь вы чувствуете, что лучше понимаете основы векторных пространств? Что ж, угадайте, что это только начало, и в линейной алгебре предстоит еще многому научиться и открыть для себя. Так что не забывайте, продолжайте практиковаться!
Величина вектора будет в три раза больше величины вектора а. Теперь вы чувствуете, что лучше понимаете основы векторных пространств? Что ж, угадайте, что это только начало, и в линейной алгебре предстоит еще многому научиться и открыть для себя. Так что не забывайте, продолжайте практиковаться!
Как подготовиться к тесту по математике, не сойдя с ума http://t.co/eZ7iCRSVvX pic.twitter.com/gtYneR2Bc2 — Tutor Pace (@TutorPace) 16 сентября 2015 г. самый простой способ получить решения сложных математических задач. Tutor Pace предлагает эффективное репетиторство по математике и помощь в выполнении заданий, которые персонализированы и адаптированы для удовлетворения потребностей учащихся на индивидуальных занятиях.
Как происходит вычитание векторов в физике. Правила сложения коллинеарных векторов 9Стандартное определение 0001
: «Вектор — это направленный отрезок прямой». Обычно это предел знаний выпускника о векторах. Кому нужны какие-то «направленные сегменты»?
А на самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, и направление ветра (откуда дует), и модуль (то есть абсолютная величина) его скорости.
«Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, и направление ветра (откуда дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярами. вес, работа, электрический заряд никуда не отправлены. Они характеризуются только числовым значением – «сколько килограммов» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «где». Например, ускорение свободного падения направлено к поверхности Земли, а его величина равна 9,8 м/с 2. Импульс, напряженность электрического поля, индукция магнитного поля также являются векторными величинами.
Вы помните, что физические величины обозначаются латинскими или греческими буквами. Стрелка над буквой указывает, что величина является вектором:
Вот еще один пример.
Автомобиль движется из А в Б. Конечным результатом является его движение из точки А в точку Б, т.е. движение по вектору.
Конечным результатом является его движение из точки А в точку Б, т.е. движение по вектору.
Теперь понятно, почему вектор является направленным отрезком. Обратите внимание, конец вектора там, где стрелка. Длина вектора называется длиной этого отрезка. Обозначение: или
До сих пор мы работали со скалярными величинами по правилам арифметики и элементарной алгебры. Векторы — это новая концепция. Это другой класс математических объектов. У них свои правила.
Когда-то мы даже не знали о числах. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число один и число ноль.
Теперь мы познакомимся с векторами.
Для векторов не существует понятий «больше» и «меньше» — ведь их направления могут быть разными. Сравнивать можно только длины векторов.
Но понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковую длину и одинаковое направление. Это означает, что вектор можно перемещать параллельно самому себе в любую точку плоскости.
Это означает, что вектор можно перемещать параллельно самому себе в любую точку плоскости.
single называется вектором, длина которого равна 1 . Ноль — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой мы рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты x и y, абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора — по x и по y.
Их легко найти: координата конца вектора минус координата его начала.
Если координаты вектора заданы, то его длина находится по формуле
Сложение векторов
Существует два способа сложения векторов.
один . правило параллелограмма. Чтобы сложить векторы и , мы поместим их начало в одну и ту же точку. Завершаем параллелограмм и проводим диагональ параллелограмма из той же точки. Это будет сумма векторов и .
Это будет сумма векторов и .
Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули телегу. Ведь векторная сумма сил, приложенных ими к тележке, была равна нулю.
2. Второй способ сложения векторов — правило треугольника. Возьмем одинаковые векторы и . Добавляем начало второго к концу первого вектора. Теперь соединим начало первой и конец второй. Это сумма векторов и .
По этому же правилу можно добавить несколько векторов. Прикрепляем их по очереди, а затем соединяем начало первой с концом последней.
Представьте, что вы едете из точки А в точку Б, из В в С, из С в D, затем в Е и потом в F. Конечным результатом этих действий является перемещение из А в F.
При сложении векторов и получаем:
Вычитание вектора
Вектор направлен противоположно вектору . Длины векторов и равны.
Теперь понятно, что такое вычитание векторов. Разность векторов и есть сумма вектора и вектора .
Умножение вектора на число
Умножение вектора на число k дает вектор, длина которого в k раз отличается от длины . Он сонаправлен вектору, если k выше нуля, и направлен в противоположную сторону, если k меньше нуля.
Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярное произведение векторов — это произведение длин векторов на косинус угла между ними.
Обратите внимание — мы перемножили два вектора, и получили скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот как скалярное произведение выражается через координаты векторов и:
Из формулы скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 профильного ЕГЭ по математике нужно найти угол между пересекающимися прямыми или между прямой и плоскостью. Задача 14 часто решается векторным методом в несколько раз быстрее, чем классическим.
Задача 14 часто решается векторным методом в несколько раз быстрее, чем классическим.
В школьной программе по математике изучается только скалярное произведение векторов.
Оказывается, помимо скаляра существует еще и векторное произведение, когда вектор получается в результате перемножения двух векторов. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. Формулы для нахождения этих сил включают именно векторные произведения.
Векторы — очень полезный математический инструмент. Вы убедитесь в этом на первом курсе.
Определение
Сложение векторов и осуществляется по правило треугольника .
сумма двумя векторами и называется такой третий вектор, начало которого совпадает с началом, а конец с концом при условии, что конец вектора и начало вектора совпадают (рис. 1).
Для добавления векторов Также применяется правило параллелограмма.
Определение
Правило параллелограмма — если два неколлинеарных вектора u ведут в общее начало, то вектор совпадает с диагональю параллелограмма, построенного на векторах u (рис. 2). При этом начало вектора совпадает с началом заданных векторов.
2). При этом начало вектора совпадает с началом заданных векторов.
Определение
Вектор называется противоположным вектору вектору, если он коллинеарен вектору , равному ему по длине, но направленному в противоположную вектору сторону.
Операция сложения векторов обладает следующими свойствами:
Определение
разность векторов и называется вектор такой, что выполняется условие: (рис. 3).
Умножить вектор на число
Определение
работа вектор на число называется вектором, удовлетворяющим условиям:
Свойства умножения вектора на число:
Здесь u — произвольные векторы, а — произвольные числа.
Евклидово пространство (также Евклидово пространство ) — в исходном смысле пространство, свойства которого описаны аксиомами евклидова геометрия . В этом случае предполагается, что пространство имеет размерность равна 3.
В современном понимании, в более общем смысле может обозначать один из подобных и тесно связанных объектов: конечномерный реальный векторное пространство с положительно определенным скалярным произведением или метрическое пространство , соответствующее такому векторному пространству. В данной статье первое определение будет принято за исходное.
Также часто используется размерное евклидово пространство (если из контекста ясно, что пространство имеет евклидову структуру).
Для определения евклидова пространства проще всего взять в качестве основного понятия скалярное произведение . Евклидово векторное пространство определяется как конечномерных векторное пространство выше поле действительных чисел , на векторах которых действительнозначная функция со следующими тремя свойствами:
аффинное пространство , соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством .
Примером евклидова пространства является координатное пространство, состоящее из всех возможных n -ок действительных чисел, скалярное произведение в котором определяется по формуле
Базис и координаты вектора
Основание ( др. греч. βασις, базис) — множество таких векторов в векторном пространстве , что любой вектор этого пространства может быть однозначно представлен в виде линейных комбинаций векторов из этого множества — базисных векторов .
В случае, когда базис бесконечен, необходимо уточнить понятие «линейная комбинация». Это приводит к двум основным типам определения:
базис Гамеля , определение которого рассматривает только конечные линейные комбинации. Базис Гамеля используется в основном в абстрактной алгебре (в частности, в линейной алгебре).
Базис Шаудера , определение которого также рассматривает бесконечные линейные комбинации, а именно разложение по занимает место . Это определение используется в основном в функциональном анализе, в частности для гильбертова пространства ,
Это определение используется в основном в функциональном анализе, в частности для гильбертова пространства ,
В конечномерных пространствах оба типа базиса совпадают.
Векторные координаты являются коэффициентами единственно возможной линейной комбинации базовый векторов в выбранной системе координат равны заданному вектору.
где координаты вектора.
Скалярное произведение.
операция над двумя векторами , результатом которой является число [при рассмотрении векторов числа часто называют скалярами ], которое не зависит от системы координат и характеризует длины фактор-векторов и впрыск между ними. Эта операция соответствует умножению длины вектора x на проекцию вектора y на вектор x . Эта операция обычно считается коммутативной и линейной для каждого фактора.
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
векторное произведение
Этот псевдовектор , перпендикулярная плоскость, построенная двумя факторами, являющаяся результатом бинарной операции «умножение векторов» на векторов в трехмерном евклидовом пространстве . Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативностью ) и, в отличие от скалярного произведения векторов , является вектором. Широко используется во многих технических и физических приложениях. Например, углового момента и силы Лоренца математически записываются как векторное произведение. Взаимное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны или антипараллельны.
Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативностью ) и, в отличие от скалярного произведения векторов , является вектором. Широко используется во многих технических и физических приложениях. Например, углового момента и силы Лоренца математически записываются как векторное произведение. Взаимное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны или антипараллельны.
смешанный продукт
Смешанный продукт векторов — скалярное произведение вектор на векторном продукте векторов и:
Иногда его называют тройным скалярным произведением векторов, видимо, из-за того, что результатом является скалярное (точнее — псевдоскалярное ).
Геометрический смысл: Модуль смешанного произведения численно равен объему параллелепипеда образованных векторов . смешанное произведение три вектора можно найти через определитель
Самолет в космосе
Самолет — алгебраическая поверхность первого порядка: в декартовой системе координат плоскости можно задать уравнение первой степени.
Некоторые характерные свойства самолета
Плоскость — поверхность , содержащая полностью каждую прямую , соединяющую любые точки ;
Две плоскости либо параллельны, либо пересекаются по прямой.
Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо лежит на плоскости.
Две прямые, перпендикулярные одной плоскости, параллельны друг другу.
Две плоскости, перпендикулярные одной прямой, параллельны друг другу.
Аналогично сегменту и интервалу плоскость, не включающая крайние точки, может называться плоскостью интервала или открытой плоскостью.
где и — константы, и при этом не равны нулю; в вектор форма:
где радиус-вектор точки, вектор перпендикулярный плоскости (вектор нормали). Направляющие косинусы вектор:
Вектор \(\overrightarrow(AB)\) можно рассматривать как перемещение точки из положения \(A\) (начало движения) в положение \(B\) (конец движения). То есть траектория движения в данном случае не важна, важны только начало и конец!
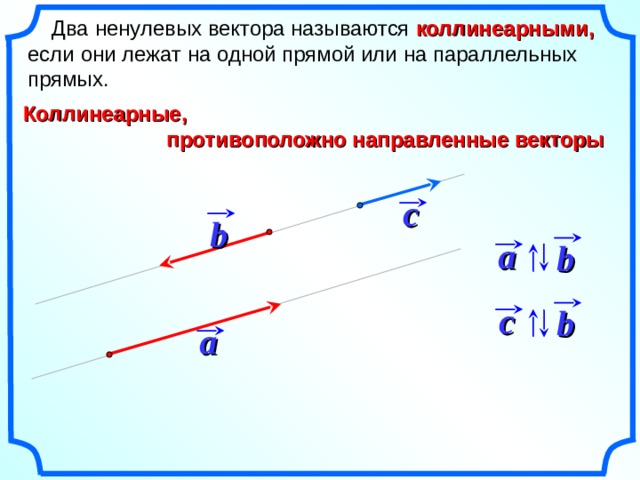
\(\blacktriangleright\) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.
\(\blacktriangleright\) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются разнонаправленными.
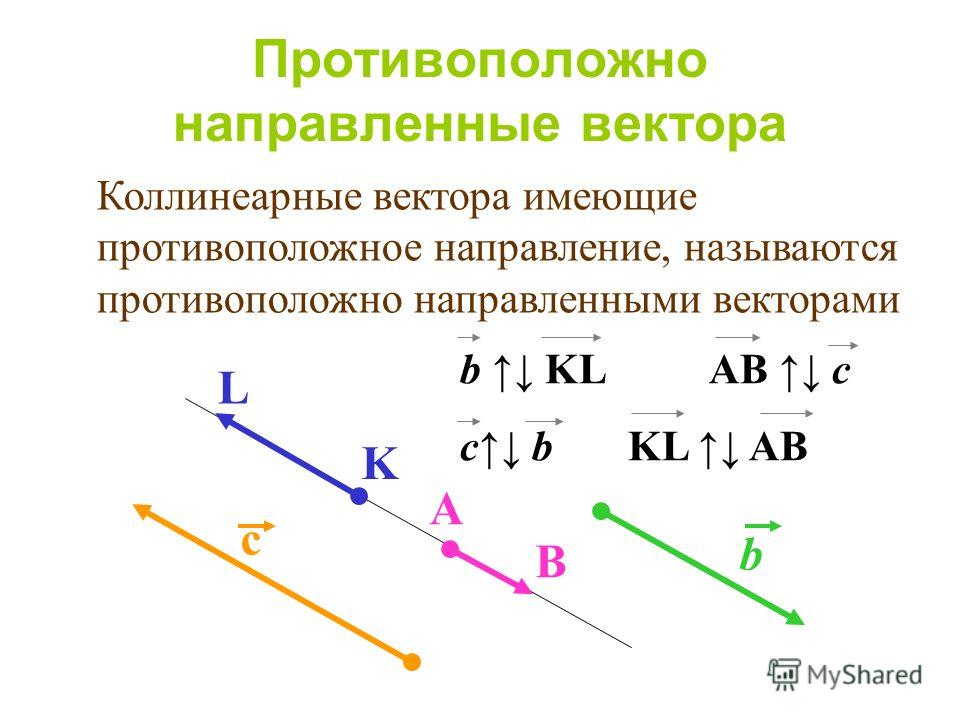
Правила сложения коллинеарных векторов:
сонаправленный конец первый. Тогда их сумма представляет собой вектор, начало которого совпадает с началом первого вектора, а конец совпадает с концом второго (рис. 1).
1).
\(\blacktriangleright\) Чтобы сложить два противоположных направления вектора, можно отложить второй вектор из начать первым. Тогда их сумма представляет собой вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением более длинного вектора (рис. 2).
Правила сложения неколлинеарных векторов \(\overrightarrow (a)\) и \(\overrightarrow(b)\) :
\(\blacktriangleright\) Правило треугольника (рис. 3).
Необходимо отложить вектор \(\overrightarrow (b)\) от конца вектора \(\overrightarrow (a)\) . Тогда сумма представляет собой вектор, начало которого совпадает с началом вектора \(\overrightarrow (a)\) , а конец совпадает с концом вектора \(\overrightarrow (b)\) .
\(\blacktriangleright\) Правило параллелограмма (рис. 4).
Необходимо отложить вектор \(\overrightarrow (b)\) от начала вектора \(\overrightarrow (a)\) . Тогда сумма \(\overrightarrow (a)+\overrightarrow (b)\) есть вектор, совпадающий с диагональю параллелограмма, построенного на векторах \(\overrightarrow (a)\) и \(\overrightarrow (b)\ ) (начало которого совпадает с началом обоих векторов).
\(\blacktriangleright\) Чтобы найти разность двух векторов \(\overrightarrow(a)-\overrightarrow(b)\), нужно найти сумму векторов \(\overrightarrow (a)\) и \(-\overrightarrow(b)\) : \(\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\)(рис. 5).
Задание 1 #2638
Уровень задания: Сложнее экзамена
Дан прямоугольный треугольник \(ABC\) с прямым углом \(A\), точка \(O\) является центром треугольника описанную окружность вокруг данного треугольника. Координаты вектора \(\overrightarrow(AB)=\(1;1\)\), \(\overrightarrow(AC)=\(-1;1\)\). Найдите сумму координат вектора \(\overrightarrow(OC)\) .
Так как треугольник \(ABC\) прямоугольный, то центр описанной окружности лежит в середине гипотенузы, т.е. \(O\) является серединой \(BC\) .
обратите внимание, что \(\overrightarrow(BC)=\overrightarrow(AC)-\overrightarrow(AB)\), следовательно, \(\overrightarrow(BC)=\(-1-1;1-1 \)=\(-2;0\)\).
Поскольку \(\overrightarrow(OC)=\dfrac12 \overrightarrow(BC)\), то \(\overrightarrow(OC)=\(-1;0\)\).
Следовательно, сумма координат вектора \(\overrightarrow(OC)\) равна \(-1+0=-1\) .
Ответ: -1
Задание 2 #674
Уровень задания: Сложнее экзамена
\(ABCD\) — четырехугольник, стороны которого содержат векторы \(\overrightarrow(AB)\) , \(\overrightarrow(BC)\) , \(\overrightarrow(CD)\) , \(\overrightarrow(DA ) \) . Найдите длину вектора \(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA)\).
\(\overrightarrow(AB) + \overrightarrow(BC) = \overrightarrow(AC)\), \(\overrightarrow(AC) + \overrightarrow(CD) = \overrightarrow(AD)\), затем
\(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \overrightarrow(AC) + \overrightarrow(CD) + \overrightarrow(DA)= \overrightarrow(AD) + \overrightarrow(DA) = \overrightarrow(AD) — \overrightarrow(AD) = \vec(0)\).
Длина нулевого вектора равна \(0\) .
Вектор можно рассматривать как смещение, затем \(\overrightarrow(AB) + \overrightarrow(BC)\)- перемещение из \(A\) в \(B\) , а затем из \(B\ ) в \(C\) — в конце концов, это ход из \(A\) в \(C\) .
При такой интерпретации становится ясно, что \(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \vec(0)\), поскольку в результате здесь мы переместились из точки \(А\) в точку \(А\) , то есть длина такого движения равна \(0\) , а значит, сам вектор такого движения равен \( \vec(0)\) .
Ответ: 0
Задание 3 #1805
Уровень задания: Сложнее экзамена
Дан параллелограмм \(ABCD\) . Диагонали \(AC\) и \(BD\) пересекаются в точке \(O\). Пусть тогда \(\overrightarrow(OA) = x\cdot\vec(a) + y\cdot\vec(b)\)
\[\overrightarrow(OA) = \frac(1)(2) \overrightarrow(CA) = \frac(1)(2)(\overrightarrow(CB) + \overrightarrow(BA)) = \frac(1)( 2)(\overrightarrow(DA) + \overrightarrow(BA)) = \frac(1)(2)(-\vec(b) — \vec(a)) = — \frac(1)(2)\vec (a) — \frac(1)(2)\vec(b )\]\(\Стрелка вправо\) \(x = — \frac(1)(2)\) , \(y = — \frac(1)(2)\) \(\Стрелка вправо\) \(x + у = — один\) .
Ответ: -1
Задание 4 #1806
Уровень задания: Сложнее экзамена
Дан параллелограмм \(ABCD\) . Точки \(K\) и \(L\) лежат на сторонах \(BC\) и \(CD\) соответственно, причем \(BK:KC = 3:1\) и \(L\) это середина \ (CD\) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(KL) = x\cdot\vec(a ) + y\cdot\vec(b)\), где \(x\) и \(y\) — некоторые числа. Найдите число, равное \(x + y\) .
Точки \(K\) и \(L\) лежат на сторонах \(BC\) и \(CD\) соответственно, причем \(BK:KC = 3:1\) и \(L\) это середина \ (CD\) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(KL) = x\cdot\vec(a ) + y\cdot\vec(b)\), где \(x\) и \(y\) — некоторые числа. Найдите число, равное \(x + y\) .
\[\overrightarrow(KL) = \overrightarrow(KC) + \overrightarrow(CL) = \frac(1)(4)\overrightarrow(BC) + \frac(1)(2)\overrightarrow(CD ) = \frac (1)(4)\overrightarrow(AD) + \frac(1)(2)\overrightarrow(BA) = \frac(1)(4)\vec(b) — \frac(1)( 2)\vec (a)\]\(\Стрелка вправо\) \(x = -\frac(1)(2)\) , \(y = \frac(1)(4)\) \(\Стрелка вправо\ ) \(х + у = -0 ,25\) .
Ответ: -0.25
Задание 5 #1807
Уровень задания: Сложнее экзамена
Дан параллелограмм \(ABCD\) . Точки \(M\) и \(N\) лежат на сторонах \(AD\) и \(BC\) соответственно, где \(AM:MD = 2:3\) и \(BN:NC = 3 ): один\) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(MN) = x\cdot\vec(a ) + у\cdot\vec(b)\)
\[\overrightarrow(MN) = \overrightarrow(MA) + \overrightarrow(AB) + \overrightarrow(BN) = \frac(2)(5)\overrightarrow(DA) + \overrightarrow(AB) + \frac(3 )(4)\overrightarrow(BC) = — \frac(2)(5)\overrightarrow(AD) + \overrightarrow(AB) + \frac(3)(4)\overrightarrow(BC) = — \frac(2 )(5)\vec(b) + \vec(a) + \frac(3)(4)\vec(b) = \vec(a) + \frac(7)(20)\vec (b)\ ]\(\Стрелка вправо\) \(x = 1\) , \(y = \frac(7)(20)\) \(\Стрелка вправо\) \(x\cdot y = 0,35\) .
Ответ: 0,35
Задание 6 #1808
Уровень задания: Сложнее экзамена
Дан параллелограмм \(ABCD\) . Точка \(P\) лежит на диагонали \(BD\) , точка \(Q\) лежит на стороне \(CD\) , где \(BP:PD = 4:1\) , и \( CQ:QD = 1:9 \) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(PQ) = x\cdot\vec(a ) + y\cdot\vec(b)\), где \(x\) и \(y\) — некоторые числа. Найдите число, равное \(x\cdot y\) .
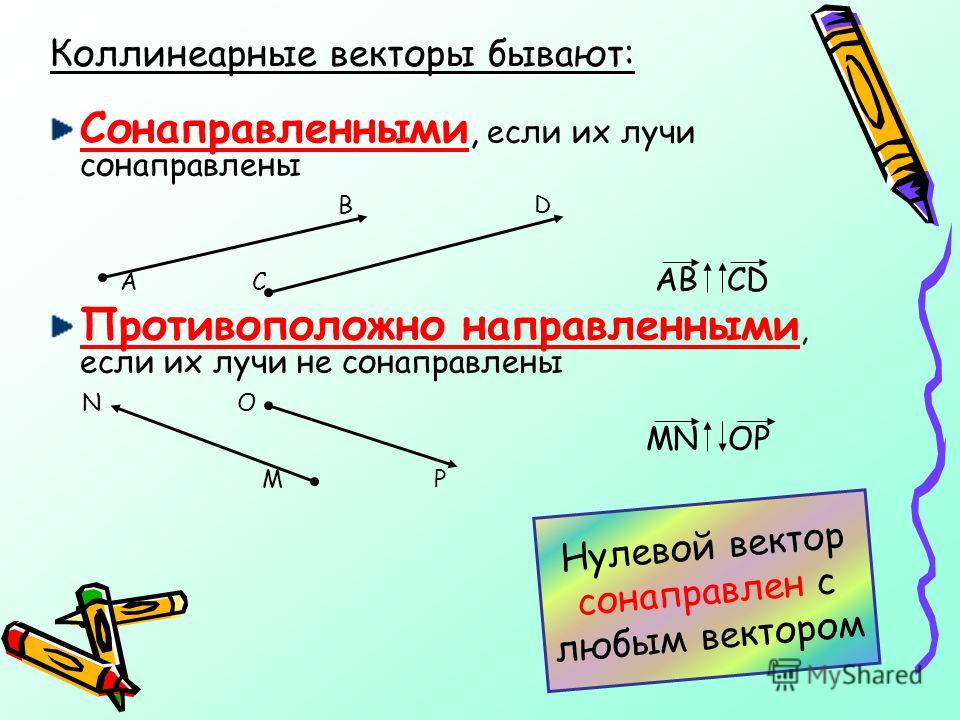
\[\begin(собраны) \overrightarrow(PQ) = \overrightarrow(PD) + \overrightarrow(DQ) = \frac(1)(5)\overrightarrow(BD) + \frac(9)(10)\overrightarrow( DC) = \frac(1)(5)(\overrightarrow(BC) + \overrightarrow(CD)) + \frac(9)(10)\overrightarrow(AB) =\\ = \ frac(1)(5) (\overrightarrow(AD) + \overrightarrow(BA)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)(\overrightarrow(AD) — \overrightarrow(AB)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)\overrightarrow(AD) + \frac(7)(10)\overrightarrow(AB) = \ frac(1)(5) \vec(b) + \frac(7)(10)\vec(a)\end(собранный)\]
\(\Rightarrow\) \(x = \frac(7) (10)\) , \(y = \frac(1)(5)\) \(\Стрелка вправо\) \(x\cdot y = 0, четырнадцать\) . и \(ABCO\) — параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow (AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\]\(\Rightarrow\) \(x = 1\) , \(y = 1\) \(\Rightarrow\) \(х + у = 2\) .
и \(ABCO\) — параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow (AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\]\(\Rightarrow\) \(x = 1\) , \(y = 1\) \(\Rightarrow\) \(х + у = 2\) .
Ответ: 2
Старшеклассникам, готовящимся к сдаче ЕГЭ по математике и при этом рассчитывающим на получение достойных баллов, необходимо обязательно повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, такие задания ежегодно входят в аттестационный тест. Если у выпускника возникают трудности с заданиями из раздела «Геометрия на плоскости», например, в которых требуется применять правила сложения и вычитания векторов, ему обязательно следует повторить или заново понять материал, чтобы успешно выполнить сдать экзамен.
Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационным испытаниям. Наш ресурс построен таким образом, чтобы студенты могли выделить для себя самые сложные разделы и восполнить пробелы в знаниях. Специалисты Школково подготовили и систематизировали весь необходимый материал для подготовки к сертификационному испытанию.
Наш ресурс построен таким образом, чтобы студенты могли выделить для себя самые сложные разделы и восполнить пробелы в знаниях. Специалисты Школково подготовили и систематизировали весь необходимый материал для подготовки к сертификационному испытанию.
Для того чтобы задания ЕГЭ, в которых необходимо применять правила сложения и вычитания двух векторов, не вызывали затруднений, рекомендуем прежде всего освежить в памяти основные понятия. Студенты могут найти этот материал в разделе «Теоретическая справка».
Если вы уже запомнили правило вычитания векторов и основные определения по данной теме, предлагаем вам закрепить свои знания, выполнив соответствующие упражнения, которые были подобраны экспертами образовательного портала «Школково». Для каждой задачи сайт представляет алгоритм решения и дает правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; после выполнения двух-трех относительно легких заданий учащиеся могут последовательно переходить к более сложным.
Оттачивать собственные навыки в таких задачах, например, как у школьников есть возможность онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому можно быстро найти интересующие примеры и обсудить с преподавателем алгоритмы поиска правильного ответа.
В математике и физике у студентов и школьников часто встречаются задачи на векторные величины и на выполнение над ними различных операций. Чем отличаются векторные величины от привычных нам скалярных величин, единственной характеристикой которых является числовое значение? Потому что у них есть направление.
Использование векторных величин наиболее ясно объясняется в физике. наиболее простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, так как помимо числовых значений они имеют еще и направление действия. Для сравнения возьмем примеров скаляров : это может быть расстояние между двумя точками или масса тела. Почему необходимо выполнять операции над векторными величинами, такие как сложение или вычитание? Это необходимо для того, чтобы можно было определить результат действия векторной системы, состоящей из 2-х и более элементов.
Почему необходимо выполнять операции над векторными величинами, такие как сложение или вычитание? Это необходимо для того, чтобы можно было определить результат действия векторной системы, состоящей из 2-х и более элементов.
Определения векторной математики
Введем основные определения, используемые при реализации линейных операций.
- Вектор — это направленный (имеющий начальную и конечную точки) отрезок.
- Длина (модуль) — длина направленного отрезка.
- Коллинеарные векторы — это два вектора, которые либо параллельны одной прямой, либо лежат на ней одновременно.
- Разнонаправленные векторы называются коллинеарными и при этом направлены в разные стороны. Если их направление совпадает, то они сонаправлены.
- Векторы равны, если они сонаправлены и имеют одинаковое абсолютное значение.
- Сумма двух векторов a и b есть такой вектор c , начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, где заканчивается и .

- Разность векторов a и b вызов суммы a и ( — б ) , где ( — б ) — напротив вектора b . Также определение разности двух векторов можно дать следующим образом: разностью c пару векторов a и b назовем этим c , который при сложении с вычитаемым b образует приведенный а.
Аналитический метод
Аналитический метод предполагает получение координат разности по формуле без построения. Возможен расчет для плоского (2D), объемного (3D) или n-мерного пространства.
Для двумерного пространства и векторных величин a { a₁; а₂ ) и б { б₁; б₂ } вычислений будут иметь следующий вид: c { c₁; c₂ } = { a₁ – b₁; а₂ – б₂ }.
В случае добавления третьей координаты расчет будет производиться аналогично, а для а { а₁; а₂ ; а₃ ) и б { б₁; б₂; b₃ ) координаты разности также получатся попарным вычитанием: c { c₁; с₂; с₃ } = { а₁ – б₁; а₂ – б₂; а₃–б₃ }.
Графическое вычисление разности
Для графического построения разности используйте правило треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Соедините их концы (т.е. постройте два равных заданным направленных отрезка, которые будут заканчиваться в одной точке).
- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вычитаемый вектор, и заканчиваться в начальной точке вычитаемого вектора.
Результат операции вычитания показан на рисунке ниже. .
Существует также способ построения разности, немного отличающийся от предыдущего. Суть его заключается в применении теоремы о разности векторов, которая формулируется следующим образом: чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с противоположным отрезком ко второму. Алгоритм построения будет выглядеть так:
Алгоритм построения будет выглядеть так:
- Построить начальные направленные сегменты.
- Тот, что вычитается, надо отразить, т. е. построить противоположно направленный и равный отрезок; затем совместите его начало с сокращенным.
- Постройте сумму: соедините начало первого отрезка с концом второго.
Результат этого решения показан на рисунке:
Решение задач
Для закрепления навыка разберем несколько задач, в которых требуется вычислить разницу аналитически или графически.
Задача 1 . На плоскости 4 точки: А (1;-3), В (0;4), С (5;8), D (-3;2). Определить координаты вектора q = AB — CD, а также вычислить его длину.
Решение . Сначала нужно найти координаты AB и CD . Для этого из координат конечных точек вычтем координаты начальных точек. Для АВ начало А (1;-3), а конец — Б (0; 4). Вычислить координаты направленного отрезка:
АВ {0 — 1; 4 — (- 3)} = {- 1; 7}
Аналогичный расчет выполняется для CD :
CD {- 3 — 5; 2 — 8} = {- 8; — 6}
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоской задачи обсуждалась ранее: c = a — b координаты имеют вид ( с₁; c₂ } = { a₁ – b₁; а₂ – б₂ ). Для конкретного случая можно написать:
Формула для аналитического решения плоской задачи обсуждалась ранее: c = a — b координаты имеют вид ( с₁; c₂ } = { a₁ – b₁; а₂ – б₂ ). Для конкретного случая можно написать:
q = {- 1 — 8; 7 — (- 6)} = { — 9; — 1}
Чтобы найти длину q , мы используем формулу | д | = √( q₁² + q ₂²) = √((- 9)² + (- 1)²) = √(81 + 1) = √82 ≈ 9,06.
Задача 2 . На рисунке показаны векторы m, n и p.
По ним необходимо построить разности: п — н; м — н; м -н — с. Определите, у какого из них наименьший модуль.
Решение . Задача требует трех построений. Рассмотрим каждую часть задачи более подробно.
Часть 1. Чтобы изобразить p -n, Воспользуемся правилом треугольника. Для этого с помощью параллельного переноса соединяем отрезки так, чтобы их конечная точка совпадала. Теперь давайте соединим начальные точки и определим направление. В нашем случае разностный вектор начинается там же, где и вычитаемый. с.п.
В нашем случае разностный вектор начинается там же, где и вычитаемый. с.п.
Часть 2. Изобразим м-н . Теперь для решения воспользуемся теоремой о разности векторов. Для этого постройте вектор напротив n, и затем найдите его сумму с m. Результат будет выглядеть так:
Часть 3 Чтобы найти разность m-n-p, разобьем выражение на два шага. Поскольку в векторной алгебре действуют законы, аналогичные законам арифметики, то возможны следующие варианты:
- m-(n+p) : в этом случае сначала строится сумма n+p , которая затем вычитается из m ;
- (m-n)-p : здесь сначала нужно найти m-n , а потом из этой разницы p вычесть ;
- (m-p)-n : первое действие определяется m-p , после чего из результата нужно вычесть n .
Так как в предыдущей части задачи мы уже нашли разницу m-n , мы можем только вычесть из него p . Построим разность двух заданных векторов с помощью разностной теоремы. Ответ показан на изображении ниже (красный цвет указывает на промежуточный результат, а зеленый — на окончательный).
Построим разность двух заданных векторов с помощью разностной теоремы. Ответ показан на изображении ниже (красный цвет указывает на промежуточный результат, а зеленый — на окончательный).
Осталось определить, какой из отрезков имеет наименьший модуль. Напомним, что понятия длины и модуля в векторной математике идентичны. Оцените визуально длины р — п, м -н и м -н -р . Очевидно, что ответ в последней части задачи самый короткий и имеет наименьший модуль, а именно m -n -p .
Сумма векторов. Длина вектора. Дорогие друзья, есть группа заданий с векторами в типах экзамена. Довольно широкий круг задач (важно знать теоретическую базу). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же есть множество задач, при решении которых необходимо производить действия с координатами векторов.
Теория векторов проста и должна быть хорошо понята. В этой статье мы разберем задачи, связанные с нахождением длины вектора, а также суммы (разности) векторов. Некоторые теоретические моменты:
В этой статье мы разберем задачи, связанные с нахождением длины вектора, а также суммы (разности) векторов. Некоторые теоретические моменты:
Концепция вектора
Вектор — это направленный отрезок прямой.
Все векторы, имеющие одинаковое направление и одинаковую длину, равны.
*Все четыре приведенных выше вектора равны!
То есть, если мы используем параллельный перенос для перемещения заданного нам вектора, мы всегда будем получать вектор, равный исходному. Таким образом, может быть бесконечное количество одинаковых векторов.
Векторное представление
Вектор можно обозначать латинскими прописными буквами, Например:
При такой форме записи сначала пишется буква, обозначающая начало вектора, затем буква, обозначающая конец вектора.
Другой вектор обозначается одной буквой латинского алфавита (заглавной):
Возможно также обозначение без стрелок:
Сумма двух векторов AB и BC будет вектором AC.
Записывается как AB+BC=AC.
Это правило называется — правило треугольника .
То есть, если у нас есть два вектора — назовем их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то сумма этих векторов будет — вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если у нас есть два вектора на плоскости, мы всегда можем найти их сумму. С помощью параллельного переноса можно переместить любой из этих векторов и соединить его начало с концом другого. Например:
Переместим вектор b , или по-другому — построим равные ему:
Как находится сумма нескольких векторов? По тому же принципу:
* * *
правило параллелограмма
Это правило является следствием предыдущего.
Для векторов с общим началом их сумма представлена диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет их суммой:
Еще немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, также обозначается, но имеет противоположный знак:
Эта информация чрезвычайно полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов — это одна и та же сумма в модифицированном виде.
Пусть даны два вектора, найдите их разность:
Построили вектор, противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из конечных координат вычесть соответствующие начальные координаты:
То есть координаты вектора представляют собой пару чисел.
Если
И координаты векторов выглядят так:
Тогда c 1 = a 1 + b 1 c 2 = a 2 + b 2
Если a
Тогда c 1 = a 1 — b 1 c 2 = a 2 — b 2
Модуль вектора
Модуль вектора – это его длина, определяемая по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Рассмотрим задачи:
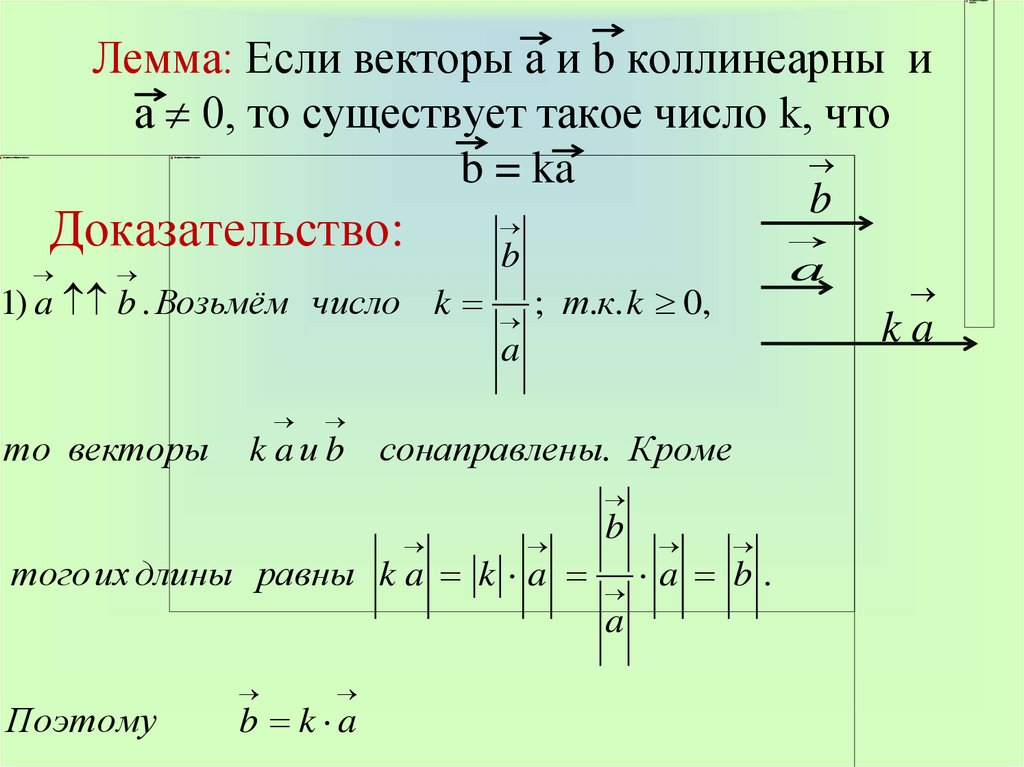
Две Стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO.
Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO.
Найдем вектор, который будет результатом АО — ВО:
АО -ВО = АО + (-ВО) = АВ
То есть разность между векторами АО и ВО будет вектор АВ. И длина его восемь.
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора AB +AD.
Найдем вектор, который будет суммой векторов AD и AB BC равным вектору AD. Таким образом, AB+AD=AB+BC=AC
AC — это длина диагонали ромба 9.0348 AC , равно 16.
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора AO + BO.
Найдем вектор, который будет суммой векторов AO и BO BO равен вектору OD,
AD длина стороны ромба. Задача состоит в том, чтобы найти гипотенузу прямоугольного треугольника AOD. Рассчитаем ноги:
По теореме Пифагора:
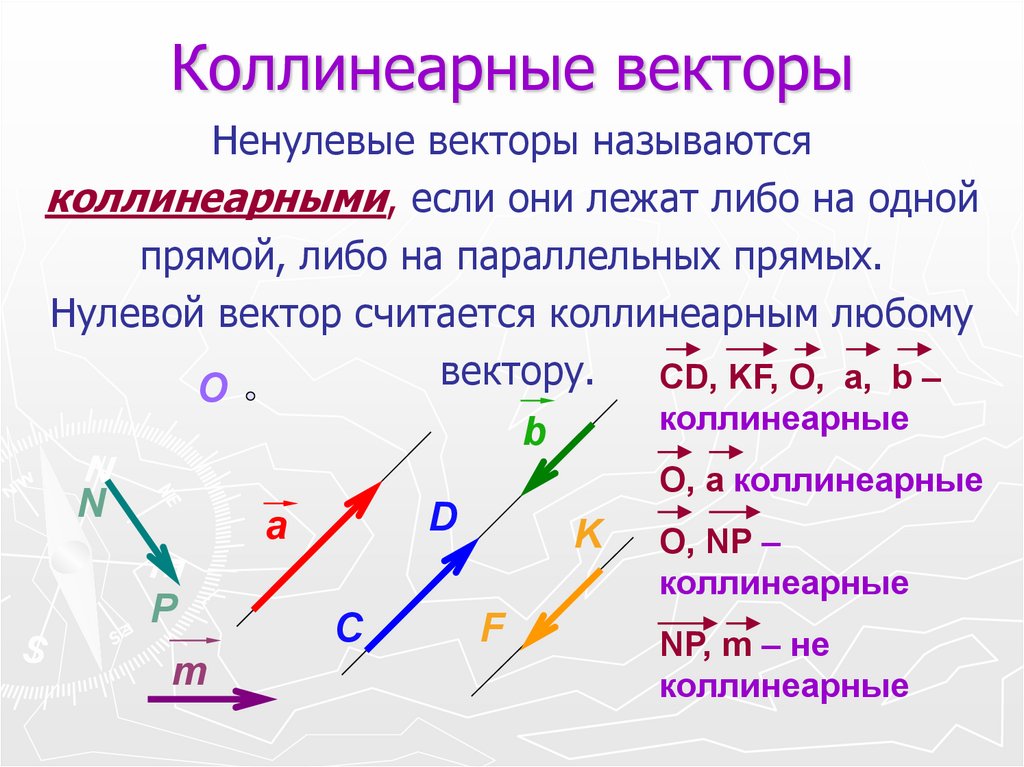
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора AO –BO.
Найдите длину вектора AO –BO.
Найдем вектор, который будет результатом АО — ВО:
АВ — длина стороны ромба. Задача сводится к нахождению гипотенузы АВ прямоугольного треугольника АОВ. посчитаем катеты:
По теореме Пифагора:
Стороны прямоугольного треугольника ABC равны 3.
Найдите длину вектора AB -AC.
Найдем результат разности векторов:
CB равно трем, так как условие гласит, что треугольник равносторонний и его стороны равны 3.
27663. Найдем длину вектора a (6; 8).
27664. Найдите квадрат длины вектора AB.
Векторная алгебра: типы векторов
что вы узнаете…
Обзор
Классификация векторов
» Классификация по величине
→ нулевой или нулевой вектор : величина 0″ 11
→ собственный вектор : величина не равна 0″ role=»presentation»>00
» По сходству двух векторов
→ равные векторы : все соответствующие компоненты равны
→ подобные векторы: одинаковые направления
→ разнонаправленные векторы : разные направления
→ ко-начальные векторы : одна и та же начальная точка
→ коллинеарные векторы : на одной прямой плоские векторы: не в одной плоскости
ноль
Слово «нуль» означает «ноль; ничего такого’.
Вектор с нулевой величиной является «нулевым или нулевым вектором».
Все следующие векторы имеют 0″ role=»presentation»>00 величина
0i+0j+0k» role=»презентация»>0i+0j+0k0i+0j+0k
0i+0j» role=»презентация»>0i+0j0i+0j
0″ role=»презентация»> 00
Нулевой вектор является не только вектором, но и скаляром
Нулевой вектор также называют неправильным вектором, так как он не имеет направления.
• Ноль или Нулевой вектор (величина 0″ role=»presentation»>00)
Нулевой вектор или нулевой вектор: Величина нулевой величины, заданная как 0→» role=»presentation»>→00→ или 0″ role=»presentation»>00. Для вычислений его можно использовать как 0i+0j+0k» role=»presentation»>0i+0j+0k0i+0j+0k.
Технически нулевой вектор не является вектором. Арифметические операции над векторами, такие как сложение, могут привести к в нулевом векторе.
0i» role=»presentation»>0i0i можно назвать одним из следующих:
нулевой вектор
неправильный вектор
нулевой вектор
скалярный 0″ role=»presentation»>00
правильный
Слово «правильный» означает «правильный тип или форма».
«Вектор с направлением» является «правильным вектором».
Собственный вектор: Вектор с ненулевой величиной.
Если вектор p→=ai+bj+ck» role=»presentation»>→p=ai+bj+ckp→=ai+bj+ck является правильным вектором, то a2+b2+c2≠0″ role=»презентация»>√a2+b2+c2≠0a2+b2+c2≠0
unit
Слово «единица» означает 1″ role=»presentation»>11
«Вектор, имеющий величину 1» role=»presentation»>11′, является «единичным вектором».
Единичный вектор: Вектор с величиной 1.
Если вектор p→=ai+bj+ck» role=»presentation»>→p=ai+bj+ckp→=ai+bj+ck единичный вектор, тогда
a2+b2+c2=1″ role=»presentation»>√a2+b2+c2=1a2+b2+c2=1
Is i+j-k» role=»presentation»>i+j− ki+j-k единичный вектор?
Величина не 1+1-1=1″ role=»presentation»>1+1−1=11+1-1=1
Величина 1+1+1≠1″ role=» представление»>√1+1+1≠11+1+1≠1
Таким образом, данный вектор не является единичным вектором.
равный
Слово «равный» означает «одинаковый по количеству или стоимости».
Два вектора «равны», когда и величина, и направление одинаковы.
Равные векторы: Два вектора p→=pxi+pyj+pzk» role=»presentation»>→p=pxi+pyj+pzkp→=pxi+pyj+pzk и q→=qxi+qyj+qzk» role=»presentation»>→q=qxi+qyj+qzkq→=qxi+qyj+qzk равны
p→=q→» role=»presentation»>→p=→qp→=q→
тогда и только тогда, когда
px=qx» role=»presentation»>px=qxpx=qx
py=qy» role=»presentation»>py=qypy =qy
pz=qz» role=»presentation»>pz=qzpz=qz
Два вектора p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ равны, то верно следующее
стр→|p|=q→|q|» role=»presentation»>→p|p|=→q|q|p→|p|=q→|q|
Направленные косинусы p→ ;» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ равны
|p|=|q|» role=»presentation»>|p|=|q||p|=|q|
похожий и непохожий
Слово «подобный» означает «имеющий такие же характеристики или свойства» .
Два вектора, называемые «подобными векторами», «когда векторы имеют одинаковое направление».
Like Vectors: Векторы одного направления.
Векторы p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ подобны векторам, если
p→|p|=q→|q|» role=»presentation»>→p|p|=→q|q|p→ |p|=q→|q|
В отличие от векторов: Векторы разного направления.
Векторы p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ являются разными векторами, если
p→|p|≠q→|q|» role=»presentation»>→p|p|≠→q|q|p→|p|≠q→|q|
Два вектора p& #x2192;» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ подобны векторам, то верно следующее
p→|p|=q→|q|» role=»presentation»>→p|p|=→q|q|p→|p|=q→|q|
направленные косинусы р→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ равны
углов, сделанных с осями x» role=»presentation»>xx, y» role=»presentation»>yy, z» role=»presentation»>zz осей p→» role=»presentation»>→pp→ равны q→» role=»presentation»>→qq→.
начальный
Слово «начальный» означает «начало или начало».
Приставка «со» в со-инициале означает «совместно; взаимно’.
Два вектора являются «совместно начальными» векторами «Когда векторы начинаются с одной и той же позиции».
Вектор можно расположить в любой точке без изменения величины и направления определяющих параметров. Когда векторы используются для представления форм или величин, положение вектора указывается дополнительно.
Соначальные векторы: Два вектора p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ являются ко-начальными векторами, когда они расположены в одной и той же начальной точке (x,y,z)» role=»presentation»>(x,y,z)(x,y,z) ).
Имеются два вектора, 2i+3j» role=»presentation»>2i+3j2i+3j и 4i+6j» role=»presentation»>4i+6j4i+6j, являются ли эти векторы взаимно начальными?
Ответ: «Невозможно определить по предоставленной информации». Начальное положение вектора должно быть указано отдельно, а если оно не указано, то векторы могут располагаться где угодно.
Начальное положение вектора должно быть указано отдельно, а если оно не указано, то векторы могут располагаться где угодно.
коллинеарность
Слово «коллинеарность» означает «нахождение на одной линии». «со» означает «вместе; совместно»; а «линейный» означает «линейный».
Два вектора называются «коллинеарными» векторами «Когда векторы лежат на одной линии».
Коллинеарные векторы: Два вектора p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ коллинеарные векторы, если p→=nq→» role=»presentation»>→p=n→qp→=nq→ где n∈ℝ» роль=»презентация»>n∈Rn∈ℝ.
Учитывая, что два вектора коллинеарны, означает ли это также, что данные векторы подобны векторам?
‘Нет’
Коллинеарные векторы могут быть как в одном, так и в противоположном направлении.
Кроме того, в коллинеарных векторах необходимо учитывать два параметра при сравнении их на предмет сходства с векторами.
1. направление — в том же направлении или в противоположном направлении.
2. положение — векторы могут располагаться в разных точках. Подобные векторы, имеющие одинаковое направление, могут не быть коллинеарными из-за положения.
копланарный
Слово «копланарный» означает «лежащий в одной плоскости».
Два вектора «компланарны» «Когда два вектора лежат в одной плоскости»
Копланарные векторы: Два вектора p→» role=»presentation»>→pp→ и q→» role=»presentation»>→qq→ компланарны, если они лежат в одной плоскости.
При условии, что положения векторов не указаны и векторы могут быть эквивалентно размещены в любом месте трехмерного пространства, любые два вектора будут компланарны.
Три вектора p→» role=»presentation»>→pp→, q→» role=»presentation»>→qq→, r→» role=»presentation»>→rr→ компланарны (при условии, что векторы эквивалентно расположены в любом месте трехмерного пространства), если
|pxpypzqxqyqzrxryrz |=0″ роль=»презентация»>∣∣
∣
∣∣pxpypzqxqyqzrxryrz∣∣
∣
∣∣=0|pxpypzqxqyqzrxryrz|=0
Свойство копланарности в терминах векторного произведения задается как p→⋅(q→×r→)=0″ role=» представление «>→p⋅(→q×→r)=0p→⋅(q→×r→)=0.
Некомпланарные векторы: Три вектора p→» role=»presentation»>→pp→, q→» role=»presentation»>→qq→, r→» role=»presentation»>→rr→ некомпланарны (при условии, что векторы эквивалентно расположены в любом месте трехмерного пространства), если
|pxpypzqxqyqzrxryrz|≠0″ role=»презентация»>∣∣
∣
∣∣pxpypzqxqyqzrxryrz∣∣
∣
∣∣≠0|pxpypzqxqyqzrxryrz|≠0
Свойство копланарности в терминах векторного произведения задается как p→⋅(q→×r→)≠0″ role=»презентация»>→p⋅(→q×→r)≠0p→⋅(q→× г→)≠0.
Являются ли 3i+4j» role=»presentation»>3i+4j3i+4j и 4i-2j» role=»presentation»>4i−2j4i-2j компланарными?
Ответ: «Да, они лежат в плоскости xy».
отрицательный
Слово «отрицательный» означает «противоположный»; задний ход’
Отрицательное значение p→=ai+bj» role=»presentation»>→p=ai+bjp→=ai+bj равно -p→=-ai-bj» role=»presentation»>− →p=−ai−bj-p→=-ai-bj
Отрицательное значение векторов: Для вектора p→=ai+bj+ck» role=»presentation»>→p=ai+bj+ckp→=ai+bj+ck отрицательное значение p&# х2192;» role=»презентация»>→pp→ is
-p→=-ai-bj-ck» role=»presentation»>-→p=-ai-bj-ck-p→=-ai-bj-ck
Что такое «минус» вектора p→=2i-j» role=»presentation»>→p=2i-jp→=2i-j?
Ответ: ‘-2i+j» role=»presentation»>−2i+j-2i+j’.
компонент
Слово «компонент» означает «составная часть большего целого».
Компоненты вектора — это «компоненты x, y и z по трем осям».
Компонентная форма вектора: Вектор p→» role=»presentation»>→pp→ задается в компонентной форме как
p→=pxi+pyj+pzk» role=»presentation» >→p=pxi+pyj+pzkp→=pxi+pyj+pzk,
, где px,py,pz» role=»presentation»>px,py,pzpx,py,pz — компоненты вдоль x,y,z» role=»presentation»>x,y,zx,y,z -оси соответственно.
Какова форма компонента единичного вектора вдоль оси x» role=»presentation»>xx?
Ответ: ‘i» role=»presentation»>ii’ в обычном соглашении о представлении компонента по оси x с использованием i» role=»presentation»>ii.
сводка
Классификация векторов
» Классификация по величине
→ нулевой или нулевой вектор: величина 0″ не 0″ роль=»презентация»>00<
»По сходству двух векторов
→ равные векторы: все соответствующие компоненты равны
→ Несмотря на векторы: те же направления
→ В отличие линейные векторы: на одной линии
→ компланарные векторы: на одной плоскости
→ некомпланарные векторы: не на одной плоскости
Контур
Схема материала для изучения векторной алгебры выглядит следующим образом.

 11.17
11.17


 co/j3zGC5Q6m8 #алгебра #backtoschool #homeschool pic.twitter.com/dzdb9M73Rl
co/j3zGC5Q6m8 #алгебра #backtoschool #homeschool pic.twitter.com/dzdb9M73Rl «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, и направление ветра (откуда дует), и модуль (то есть абсолютная величина) его скорости.
«Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, и направление ветра (откуда дует), и модуль (то есть абсолютная величина) его скорости. Конечным результатом является его движение из точки А в точку Б, т.е. движение по вектору.
Конечным результатом является его движение из точки А в точку Б, т.е. движение по вектору. Это означает, что вектор можно перемещать параллельно самому себе в любую точку плоскости.
Это означает, что вектор можно перемещать параллельно самому себе в любую точку плоскости. 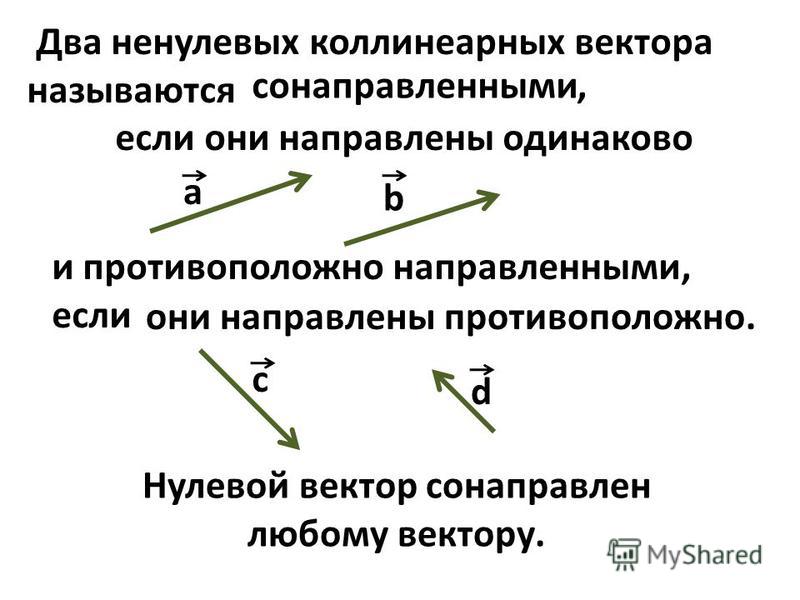 Это будет сумма векторов и .
Это будет сумма векторов и .
 Задача 14 часто решается векторным методом в несколько раз быстрее, чем классическим.
Задача 14 часто решается векторным методом в несколько раз быстрее, чем классическим. 2). При этом начало вектора совпадает с началом заданных векторов.
2). При этом начало вектора совпадает с началом заданных векторов.
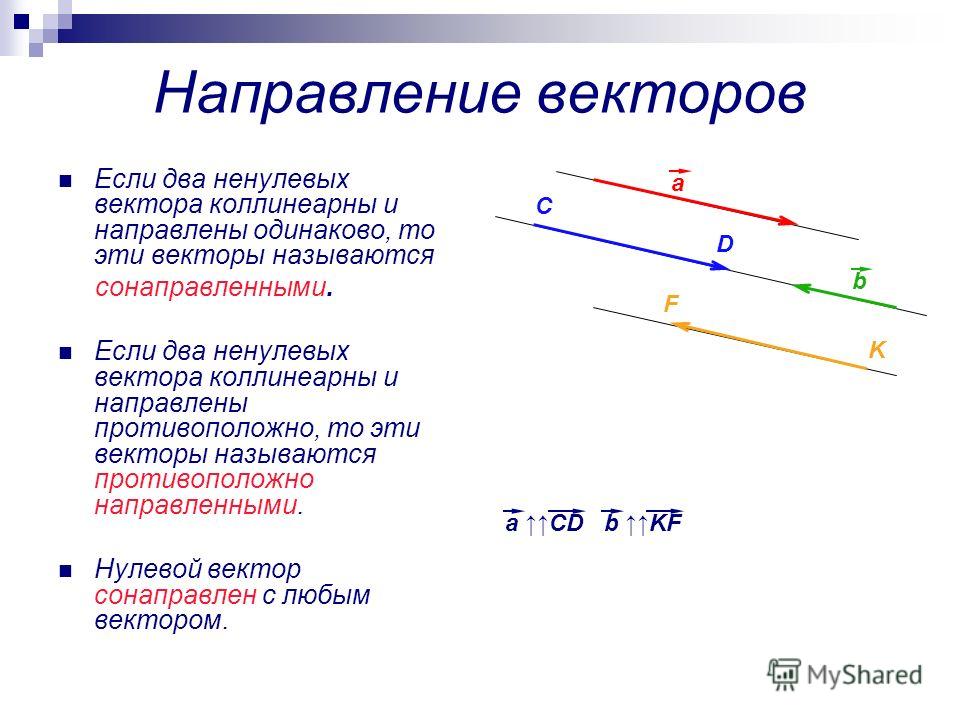 Это определение используется в основном в функциональном анализе, в частности для гильбертова пространства ,
Это определение используется в основном в функциональном анализе, в частности для гильбертова пространства , Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативностью ) и, в отличие от скалярного произведения векторов , является вектором. Широко используется во многих технических и физических приложениях. Например, углового момента и силы Лоренца математически записываются как векторное произведение. Взаимное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны или антипараллельны.
Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативностью ) и, в отличие от скалярного произведения векторов , является вектором. Широко используется во многих технических и физических приложениях. Например, углового момента и силы Лоренца математически записываются как векторное произведение. Взаимное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны или антипараллельны.

 1).
1).

 Точки \(K\) и \(L\) лежат на сторонах \(BC\) и \(CD\) соответственно, причем \(BK:KC = 3:1\) и \(L\) это середина \ (CD\) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(KL) = x\cdot\vec(a ) + y\cdot\vec(b)\), где \(x\) и \(y\) — некоторые числа. Найдите число, равное \(x + y\) .
Точки \(K\) и \(L\) лежат на сторонах \(BC\) и \(CD\) соответственно, причем \(BK:KC = 3:1\) и \(L\) это середина \ (CD\) . Пусть \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), тогда \(\overrightarrow(KL) = x\cdot\vec(a ) + y\cdot\vec(b)\), где \(x\) и \(y\) — некоторые числа. Найдите число, равное \(x + y\) .
 и \(ABCO\) — параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow (AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\]\(\Rightarrow\) \(x = 1\) , \(y = 1\) \(\Rightarrow\) \(х + у = 2\) .
и \(ABCO\) — параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow (AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\]\(\Rightarrow\) \(x = 1\) , \(y = 1\) \(\Rightarrow\) \(х + у = 2\) . Наш ресурс построен таким образом, чтобы студенты могли выделить для себя самые сложные разделы и восполнить пробелы в знаниях. Специалисты Школково подготовили и систематизировали весь необходимый материал для подготовки к сертификационному испытанию.
Наш ресурс построен таким образом, чтобы студенты могли выделить для себя самые сложные разделы и восполнить пробелы в знаниях. Специалисты Школково подготовили и систематизировали весь необходимый материал для подготовки к сертификационному испытанию.
 Почему необходимо выполнять операции над векторными величинами, такие как сложение или вычитание? Это необходимо для того, чтобы можно было определить результат действия векторной системы, состоящей из 2-х и более элементов.
Почему необходимо выполнять операции над векторными величинами, такие как сложение или вычитание? Это необходимо для того, чтобы можно было определить результат действия векторной системы, состоящей из 2-х и более элементов.

 Алгоритм построения будет выглядеть так:
Алгоритм построения будет выглядеть так: Формула для аналитического решения плоской задачи обсуждалась ранее: c = a — b координаты имеют вид ( с₁; c₂ } = { a₁ – b₁; а₂ – б₂ ). Для конкретного случая можно написать:
Формула для аналитического решения плоской задачи обсуждалась ранее: c = a — b координаты имеют вид ( с₁; c₂ } = { a₁ – b₁; а₂ – б₂ ). Для конкретного случая можно написать: В нашем случае разностный вектор начинается там же, где и вычитаемый. с.п.
В нашем случае разностный вектор начинается там же, где и вычитаемый. с.п. 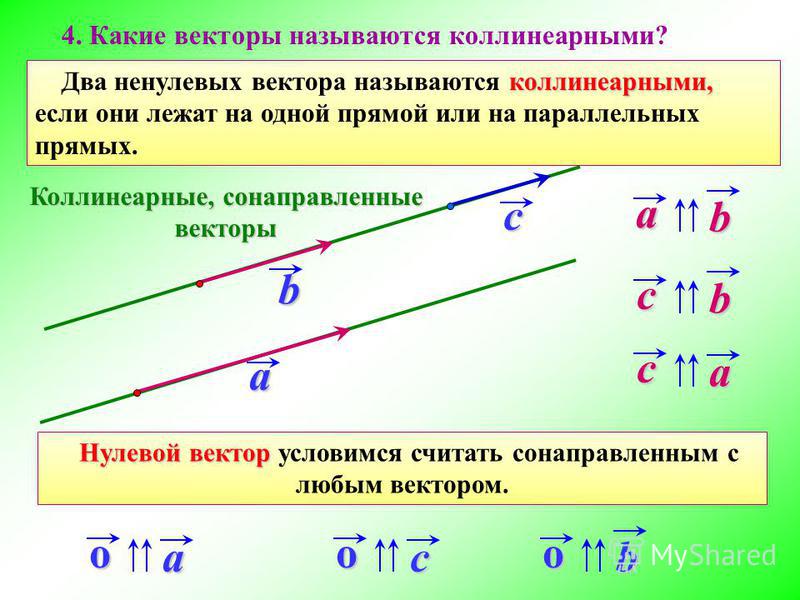 Построим разность двух заданных векторов с помощью разностной теоремы. Ответ показан на изображении ниже (красный цвет указывает на промежуточный результат, а зеленый — на окончательный).
Построим разность двух заданных векторов с помощью разностной теоремы. Ответ показан на изображении ниже (красный цвет указывает на промежуточный результат, а зеленый — на окончательный).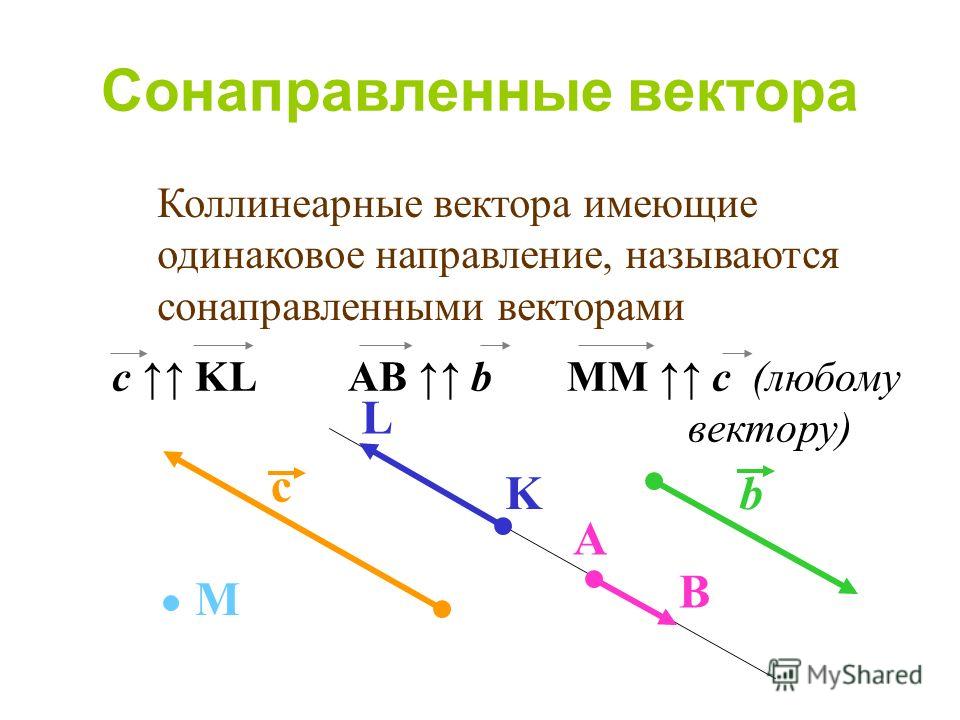 В этой статье мы разберем задачи, связанные с нахождением длины вектора, а также суммы (разности) векторов. Некоторые теоретические моменты:
В этой статье мы разберем задачи, связанные с нахождением длины вектора, а также суммы (разности) векторов. Некоторые теоретические моменты:

 Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO.
Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO. Найдите длину вектора AO –BO.
Найдите длину вектора AO –BO.


 Начальное положение вектора должно быть указано отдельно, а если оно не указано, то векторы могут располагаться где угодно.
Начальное положение вектора должно быть указано отдельно, а если оно не указано, то векторы могут располагаться где угодно.