Умножение и деление рациональных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.
Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Таким образом, значение выражения равно
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:
Решение для данного примера можно записать покороче:
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
Второе действие:
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.
Затем применяются правила умножения рациональных чисел.
Пример 1. Выполнить деление:
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение можно записать так:
Пример 2. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение можно записать так:
Пример 3. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь
Обратная для второй дроби это дробь
Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Выполнить деление
В данном случае нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:
Пример 5. Выполнить деление
Умнóжим первую дробь на число, обратное числу 4.
Обратное числу 4 это дробь . На неё и умножим первую дробь
Пример 6. Выполнить деление
Умнóжим первую дробь на число, обратное числу −3
Обратное числу −3 это дробь
Пример 7. Найти значение выражение −14,4 : 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 8. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0
Пример 9. Найти значение выражения −7,2 : (−0,6)
Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.
Пример 2. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )
А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.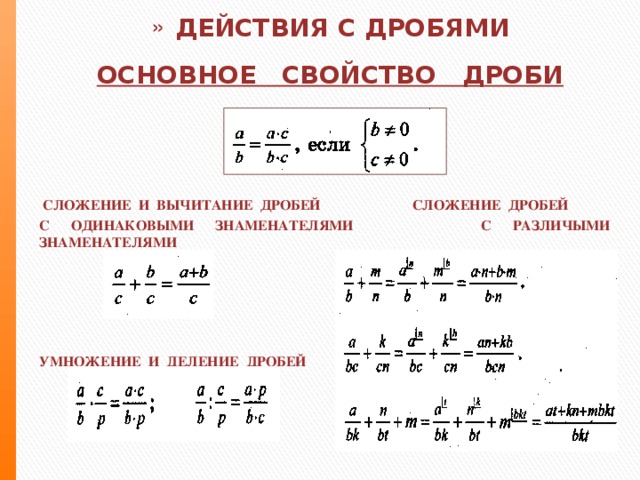
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Задания для самостоятельного решения
Задание 1. Выполните умножение:
Решение:
Показать решение
Задание 2. Выполните умножение:
Решение:
Показать решение
Задание 3. Выполните умножение:
Решение:
Показать решение
Задание 4. Выполните умножение:
Решение:
Показать решение
Задание 5. Выполните умножение:
Решение:
Показать решение
Задание 6. Выполните умножение:
Решение:
Показать решение
Задание 7. Выполните умножение:
Решение:
Показать решение
Задание 8. Выполните умножение:
Решение:
Показать решение
Задание 9. Выполните деление:
Решение:
Показать решение
Задание 10. Выполните деление:
Решение:
Показать решение
Задание 11. Выполните деление:
Решение:
Показать решение
Задание 12. Выполните деление:
Решение:
Показать решение
Задание 13. Выполните деление:
Решение:
Показать решение
Задание 14.
Решение:
Показать решение
Задание 15. Выполните деление:
Решение:
Показать решение
Задание 16. Выполните деление:
Решение:
Показать решение
Задание 17. Выполните деление:
Решение:
Показать решение
Задание 18. Вычислите выражение:
Решение:
Показать решение
Задание 19. Вычислите выражение:
Решение:
Показать решение
Задание 20. Вычислите выражение:
Решение:
Показать решение
Задание 21. Вычислите выражение:
Решение:
Показать решение
Задание 22. Вычислите выражение:
Решение:
Показать решение
Задание 23. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Показать решение
Задание 24. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Показать решение
Задание 25. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Показать решение
Задание 26. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 27. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 28. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 29. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 30. Найдите значение выражения:
Решение:
Показать решение
Задание 31. Найдите значение выражения:
Решение:
Показать решение
Задание 32. Найдите значение выражения:
Решение:
Показать решение
Задание 33. Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Степень с натуральным показателем.
 Действия со степенями
Действия со степенями
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что происходит со степенями при сложении чисел
Содержание
- Свойство № 1 Произведение степеней
- Свойство № 2 Частное степеней
- Свойство № 3 Возведение степени в степень
- Свойства 4 Степень произведения
- Свойства 5 Степень частного (дроби)
- Сложение и вычитание степеней
- Умножение степеней
- Деление степеней
- Примеры решения примеров с дробями, содержащими числа со степенями
- Что представляют собой степенные выражения?
- Основные виды преобразований степенных выражений
- Работа с основанием и показателем степени
- Использование свойств степеней
- Преобразование дробей, содержащих степени
- Преобразование выражений с корнями и степенями
- Преобразование степеней с переменными в показателе
- Преобразование выражений со степенями и логарифмами
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2 ) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2 ) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
m : a n =–>
| a m |
| a n |
= a m − n , где « a » — любое число, не равное нулю, а « m », « n » — любые натуральные числа такие, что « m > n ».
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2 : 4 4m + 3 = 4 5m + 6 + m + 2 : 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
| 512 · 4 |
| 32 |
=
| 512 · 4 |
| 32 |
=
| 2 9 · 2 2 |
| 2 5 |
=
| 2 9 + 2 |
| 2 5 |
=
| 2 11 |
| 2 5 |
= 2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2 ) на 4 1 . Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n ) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
- Пример.
(a 4 ) 6 = a 4 · 6 = a 24 - Пример. Представить 3 20 в виде степени с основанием 3 2 .
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
Свойства 4
Степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c ) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.

(−x 2 · y) 6 = ( (−1) 6 · x 2 · 6 · y 1 · 6 ) = x 12 · y 6
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n )= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b) n = a n : b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3) 12 = 5 12 : 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 – b n и h 5 -d 4 есть a 3 – b n + h 5 – d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
| Из | 2a 4 | 3h 2 b 6 | 5(a – h) 6 |
| Вычитаем | -6a 4 | 4h 2 b 6 | 2(a – h) 6 |
| Результат | 8a 4 | -h 2 b 6 | 3(a – h) 6 |
Или:
2a 4 – (-6a 4 ) = 8a 4
3h 2 b 6 – 4h 2 b 6 = -h 2 b 6
5(a – h) 6 – 2(a – h) 6 = 3(a – h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
| Первый множитель | x -3 | 3a 6 y 2 | a 2 b 3 y 2 |
| Второй множитель | a m | -2x | a 3 b 2 y |
| Результат | a m x -3 | -6a 6 xy 2 | a 2 b 3 y 2 a 3 b 2 y |
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат – это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 – это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
| Первый множитель | 4a n | b 2 y 3 | (b + h – y) n |
| Второй множитель | 2a n | b 4 y | (b + h – y) |
| Результат | 8a 2n | b 6 y 4 | (b + h – y) n+1 |
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h – y) n ⋅ (b + h – y) = (b + h – y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3 ) ⋅ (x – y).
Ответ: x 4 – y 4 .
Умножьте (x 3 + x – 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых – отрицательные.
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a – b, результат будет равен a 2 – b 2 : то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a – y).(a + y) = a 2 – y 2 .
(a 2 – y 2 )⋅(a 2 + y 2 ) = a 4 – y 4 .
(a 4 – y 4 )⋅(a 4 + y 4 ) = a 8 – y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
| Делимое | 9a 3 y 4 | a 2 b + 3a 2 | d⋅(a – h + y) 3 |
| Делитель | -3a 3 | a 2 | (a – h + y) 3 |
| Результат | -3y 4 | b + 3 | d |
Запись a 5 , делённого на a 3 , выглядит как $frac$. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 5>$. Ответ: $frac<2x><1>$ или 2x.
5>$. Ответ: $frac<2x><1>$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a – b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 – 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) – 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 – 3 · 3 · 3 1 2 , 2 3 , 5 · 2 – 2 2 – 1 , 5 , 1 a 1 4 · a 1 2 – 2 · a – 1 6 · b 1 2 , x π · x 1 – π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x – 54 – 7 · 3 x – 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · ( 4 2 − 12 ) = 32 .
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Представьте выражение со степенями 9 – b 3 · π – 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 – b 3 · π – 1 2 = 3 2 – b 3 · π – 1 2 = = 3 – b 3 · π – 1 3 + b 3 · π – 1
Ответ: 9 – b 3 · π – 1 2 = 3 – b 3 · π – 1 3 + b 3 · π – 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s – произвольные действительные числа:
Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s – произвольные действительные числа:
- a r · a s = a r + s ;
- a r : a s = a r − s ;
- ( a · b ) r = a r · b r ;
- ( a : b ) r = a r : b r ;
- ( a r ) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .
Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 – 5 – 2 3 1 + 2 · x 2 – 3 – 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 – 5 – 2 3 1 + 2 · x 2 – 3 – 3 · x 2 = 3 · 5 2 3 · 5 1 3 – 3 · 5 2 3 · 5 – 2 3 – 2 – x 2 = = 3 · 5 2 3 + 1 3 – 3 · 5 2 3 + – 2 3 – 2 – x 2 = 3 · 5 1 – 3 · 5 0 – 2 – x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 – 2 – x 2 = – 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 – 5 – 2 3 1 + 2 · x 2 – 3 – 3 · x 2 = – 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 – 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 – 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 – x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 – 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 – 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 – 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 – 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 – 5 3 , б) a 1 4 – b 1 4 a 1 2 – b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 – 5 3 .
Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 – 5 3 .
30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 – 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 – 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 – b 1 4 a 1 2 – b 1 2 = a 1 4 – b 1 4 a 1 4 2 – b 1 2 2 = = a 1 4 – b 1 4 a 1 4 + b 1 4 · a 1 4 – b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 – 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 – 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 – b 1 4 a 1 2 – b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Выполните действия x 1 2 + 1 x 1 2 – 1 – x 1 2 – 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 – 1 · x 1 2 + 1
x 1 2 + 1 x 1 2 – 1 – x 1 2 – 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 – 1 · x 1 2 + 1 – x 1 2 – 1 · x 1 2 – 1 x 1 2 + 1 · x 1 2 – 1 · 1 x 1 2 = = x 1 2 + 1 2 – x 1 2 – 1 2 x 1 2 – 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 – x 1 2 2 – 2 · x 1 2 + 1 x 1 2 – 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 – 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 – 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 – 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 – 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 – 1 · x 1 2 + 1 = 4 x 1 2 2 – 1 2 = 4 x – 1 .
Ответ: x 1 2 + 1 x 1 2 – 1 – x 1 2 – 1 x 1 2 + 1 · 1 x 1 2 = 4 x – 1
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x – 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x – 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x – 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x – 5 8 · 1 x 2 , 7 + 1 = x 3 4 – – 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x – 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) – 0 , 2 3 · x – 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 – 3 · 5 x · 7 x – 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x – 3 · 5 x · 7 x 7 2 · x – 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x – 3 · 5 x · 7 x 7 x · 7 x – 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x – 3 · 5 x 7 x – 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x – 3 · 5 7 x – 2 = 0 , которое равносильно 5 · 5 7 x 2 – 3 · 5 7 x – 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 – 5 · log 2 3 или log 3 27 9 + 5 ( 1 – log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Калькулятор степени умножения | Правила
Создано Анной Щепанек, доктором философии
Рецензировано Домиником Черниа, кандидатом наук и Джеком Боуотером
Последнее обновление: 11 марта 2022 г.
Содержание:- Что такое экспонента?
- Неположительные показатели степени
- Как использовать калькулятор Omni для умножения показателей степени?
- Как умножать показатели степени? Правила умножения степеней
- Умножение степеней с одинаковым основанием
- Умножение показателей степени с различными основаниями
Приходите и используйте Omni калькулятор умножения показателей степени всякий раз, когда вам нужна помощь в решении задач, связанных с возведением в степень. Этот калькулятор может показать вам шаг за шагом, как умножать показатели степени , используя наиболее важные правила, такие как произведение степени на правило и степень на правило произведения .
Этот калькулятор может показать вам шаг за шагом, как умножать показатели степени , используя наиболее важные правила, такие как произведение степени на правило и степень на правило произведения .
Чтобы узнать больше и увидеть несколько примеров, прокрутите вниз!
Что такое экспонента?
Возведение в степень — важная математическая операция. Показатели степени появляются во многих различных областях, от квадратных уравнений (и многочленов в целом) до вероятности.
Напомним, что показатель степени — это способ выражения многократного умножения. Например, 7 4 означает, что мы хотим 7 умножить на себя 4 раз:
7 4 = 7 * 7 * 7 * 7 = 2402
7 в приведенном выше примере) называется базой . Число, указывающее, сколько раз основание умножается само на себя ( 4 в приведенном выше примере), называется показателем степени .
Неположительные показатели степени
Выше мы сказали, что показатель степени говорит нам, сколько раз умножать основание само на себя. Однако есть особые случаи, требующие дальнейшего объяснения; а именно, что делать, если показатель степени равен нулю или какому-то отрицательному числу?
Нулевой показатель . Если a ≠ 0 , то
a 0 = 1
Прописью: Любое ненулевое основание , возведенное в нулевую степень, равно единице.
❌ Ноль в степени нуля 0 0 — неопределенный символ. Другими словами, нет смысла выполнять этот расчет.
Отрицательный показатель . Если а ≠ 0 , затем
a -n = 1 / a n
Прописью: Чтобы определить отрицательную степень, игнорируем на некоторое время знак минус и возводим основание в положительную степень. Тогда берите взаимность.
Тогда берите взаимность.
Можно также сказать, что отрицательные показатели представляют многократное деление на основание, то есть многократное умножение на обратную величину основания:
a -n = 1 / (a * ... * a) = (1/год) * ... * (1/год)
Как пользоваться калькулятором умножения в степени Omni?
Вот краткая инструкция по использованию нашего инструмента:
Введите основания x и y и показатели степени a и b .
Наш калькулятор степени умножения показывает шаг за шагом как определить произведение x a * y b
Калькулятор также показывает, как умножать отрицательные степени. В таком случае в конечном результате могут быть дроби, и вы можете захотеть найти их десятичные приближения . Чтобы включить эту опцию, перейдите в расширенный режим .
В расширенном режиме вы также можете настроить точность отображения приближений. По умолчанию наш калькулятор использует 5 значащих цифр.
Как умножить показатели степени? Правила умножения степеней
Что ж, лучший способ умножения степеней - это использовать наш калькулятор умножения степеней! 😉 Если вам когда-либо приходилось выполнять умножение показателей вручную, здесь мы перечисляем самые полезные правила:
Произведение степеней:
w a * w b = w a + b
Прописью: сложить показатели степени, если основания совпадают.
Мощность правила продукта:
w a * u a = (w * u) a
Прописью: умножьте основания, если степени одинаковы.
Двигаясь в другом направлении, т. е. справа налево, мы можем выразить правило следующим образом: если основание записать в виде произведения нескольких множителей, то мы можем распределить показатель степени на каждый из этих множителей.
е. справа налево, мы можем выразить правило следующим образом: если основание записать в виде произведения нескольких множителей, то мы можем распределить показатель степени на каждый из этих множителей.
Правило силы полномочий:
(w a ) b = w a * b
Прописью: при возведении одного показателя в другой показатель умножить два показателя степени.
В оставшейся части статьи мы покажем вам несколько примеров того, как умножать степени с помощью этих правил.
Умножение степеней с одинаковым основанием
Имеют ли степени, которые вы хотите перемножить, одинаковые основания? Повезло тебе! Это самый простой случай умножения показателей! Единственное, что вам нужно помнить, это складывать показатели вместе. В следующем примере мы покажем вам, как это сделать.
Пример 1. Решим 7 11 * 7 -9
Мы видим, что оба основания равны 7 , а показатели степени равны 11 и -9 . Мы используем произведение степеней и суммируем два показателя степени:
Мы используем произведение степеней и суммируем два показателя степени:
7 11 * 7 -9 = 7 11 + (-9) = 7 2
Получаем:
7 11 * 7 -9 = 7 * 7 = 49
Умножение показателей степени с разными основаниями
Если основания разные, то ваша задача немного сложнее, но вы справитесь! Давайте обсудим два примера, из которых вы можете научиться умножать показатели степени с разными основаниями.
Пример 2. Вычислим 5 4 * 2 4
Как видим, показатели степени одинаковы и равны 4 , а основания 5 и 2 . Это означает, что мы можем использовать степень правила произведения , то есть мы можем перемножить основания вместе:
5 4 * 2 4 = (5 * 2) 4 = 10 4
Напомним, что возведение 10 в любую степень очень просто: после ведущего 1 записываем столько нулей, сколько говорит показатель степени. В данном случае это четыре нуля:
В данном случае это четыре нуля:
. 5 4 * 2 4 = 10 4 = 10000
Что делать, если показатели степени разные и основания тоже разные? В отличие от двух особых случаев, которые мы обсуждали до сих пор, здесь нет быстрого пути.
Лучшее, что вы можете сделать, это упростить задачу, используя три приведенных выше правила вместе с простой факторизацией обоих оснований. Факторизация простых чисел означает, что мы представляем число как произведение простых чисел, возведенных в подходящие степени. Например, простая факторизация 24 -следующее:
24 = 2 * 2 * 2 * 3 = 2 3 * 3
Пример 3. Давайте обсудим, как разобраться с
24 -4 * 90 3 .
Основания равны 24 и 90 , а показатели степени равны -4 и 3 . Выполним простую факторизацию по основаниям:
24 = 2 * 2 * 2 * 3 = 2 3 * 3
90 = 2 * 3 * 3 * 5 = 2 * 3 2 * 5
Применяем силу правила продукта:
24 -4 = (2 3 * 3) -4 = (2 3 ) -4 * 3 -4
90 3 = (2 * 3 2 * 5) 3 = 2 3 * (3 2 ) 3 1 * 3 5 4
Применяем силу силы правило:
(2 3 ) -4 = 2 3 * (-4) = 2 -12
(3 2 ) 3 = 3 2 * 3 = 3 6
В итоге получаем:
24 -4 = 2 -12 * 3 -4
90 3 = 2 3 * 3 6 * 5 3
Следовательно:
24 -4 * 90 3 = 2 -12 * 3 -4 * 2 3 * 3 6 * 5 3
2
Применяем правило произведения степеней:
2 -12 * 2 3 = 2 -12 + 3 = 2 -9
3 -4 * 3 6 = 3 -4 + 6 = 3 2
Отсюда следует, что:
24 -4 * 90 3 = 2 -9 * 3 2 * 5 3
Это самая простая форма, которую мы можем получить. Если вы хотите избавиться от показателей степени, вычислите множители один за другим:
Если вы хотите избавиться от показателей степени, вычислите множители один за другим:
2 -9 = 1/2 9 = 1/512
3 2 = 9
5 3 = 125
В итоге получаем:
24 -4 * 90 3 = (1/512) * 9 * 125 = 1125/512 ≈ 2,1973
Anna Szczepanek, PhD
Этот калькулятор упрощает и вычисляет продукт экспонентов:
x A ⋅ Y B Expence Base
. из 14 похожих калькуляторов степеней и логарифмов 🇪 AntilogИзменение основной формулыКонденсированные логарифмы… еще 11
Как умножить X с разными показателями степени
Вы еще помните понятие переменных и показателей? Прежде чем мы перейдем к рассматриваемой теме, давайте рассмотрим.
x 3
x является переменной , или чем-то, что имеет неизвестное значение. Значение x может варьироваться (отсюда и название). В одном уравнении x может быть равно 4. В другом уравнении x может быть равно 7 или более сложному числу, например 75/2. Мы выражаем переменную с помощью символа. В большинстве уравнений чаще всего используются символы 9.0027 x , y и z .
Значение x может варьироваться (отсюда и название). В одном уравнении x может быть равно 4. В другом уравнении x может быть равно 7 или более сложному числу, например 75/2. Мы выражаем переменную с помощью символа. В большинстве уравнений чаще всего используются символы 9.0027 x , y и z .
С другой стороны, число 3 над " x" в " x 3" - это то, что люди называют показателем степени . Показатель степени говорит нам, сколько раз он использует число или переменную при умножении. Число или переменная, которую мы умножаем, называется по основанию .
Давайте рассмотрим простой пример, используя целое число вместо переменной в качестве основы. Вы знаете значение числа 43?
43 означает 4 умножить на 4 умножить на 4. Число 4 возводится в третью степень или возводится в куб.
43 = 4 * 4 * 4 = 64
Это не отличается для переменных. Для x 3 оно равно xxx . В алгебре размещение двух или более переменных рядом друг с другом означает их умножение. x умножить на x умножить на x .
В алгебре размещение двух или более переменных рядом друг с другом означает их умножение. x умножить на x умножить на x .
x 3 = xxx
Как только вы поймете эти основные понятия, мы сможем перейти к основной теме.
Умножение X с разными показателями степени
Правило продукта
Умножение X с разными показателями означает, что вы умножаете одни и те же переменные — в данном случае «X» — но разное количество раз.
(X4) (X7) = (XXXX)(XXXXXXX)
Как видите, мы расширяем переменные с показателями степени на разное количество итераций переменных. Количество записанных переменных равно значению каждого показателя степени.
Для дальнейшего упрощения удалим ненужные скобки.
(Х4) (Х7) = ХХХХХХХХХХ
Ну, это много Х. Сколько X справа от знака равенства? Бинго! Это 11. Существует 11 копий одной и той же переменной. Вы также можете упростить ситуацию, заменив результат на «X11». Давайте сложим их все вместе.
Давайте сложим их все вместе.
(X4) (X7) = (XXXX) (XXXXXXX)
= XXXXXXXXXXX
= X11
Следовательно, (X4)(X7) равно X11. Чтобы сделать это более интуитивным, мы также можем записать это как (X4)(X7) равно X(4 + 7).
Расчет, приведенный выше, знакомит нас с основным правилом экспоненты, которое называется « Product Rule" :
(Xa) (Xb) = X(a + b)
Имейте в виду, что приведенное выше правило применяется только в том случае, если основания двух показателей степени одинаковы. В приведенном выше примере показатели степени числа 4 и 7 имеют одно и то же основание: "X". у) =?
Чтобы решить эту задачу, сначала сгруппируем одинаковые переменные.
(x5 y6) (x2 y) = (x5 x2) (y6 y)
Как только они хорошо сгруппированы, мы можем применить правило произведения, сложив степени с одинаковым основанием.
(x5 x2) (y6 y) = (x(5 + 2)) (y(6 + 1))
Вы видели, что произошло? Для основания "y" мы добавляем показатель степени 6 и 1, хотя у второго "y", похоже, нет показателя степени.
Для любого числа или переменной, над которой не написан показатель степени, показатель степени равен 1. В этом случае "y" имеет показатель степени 1. То же самое относится к любому числу. Все числа имеют степень 1, если над ними не указан показатель степени.
Почему? Потому что все в степени 1 имеет «одну копию» самого себя. 51 = 5; 271 = 27; у1 = у.
Продолжим нашу работу.
(x(5 + 2)) (y(6 + 1)) = (x7) (y7)
Сложив их вместе, мы можем определить, что значение (x5 y6)(x2 y) равно (х7)(у7).
(x5 y6) (x2 y) = (x5 x2) (y6 y)
= (x(5 + 2)) (y(6 + 1))
= (x7) (y7)
Частное Правило
Если Правило Произведения позволяет нам сложить два показателя степени, то Правило Частного даст нам возможность вычесть два показателя степени. Рассмотрим это выражение.
Х6/Х3 = ?
Можете ли вы определить результат?
К этому моменту вы, возможно, поняли, что мы можем расширять базы, чтобы выявить их копии на основе значения каждого показателя степени.
X6 / X3 = XXXXXX / XXX
Отсюда мы можем стереть три X как из числителя, так и из знаменателя дроби.
Мы можем собрать все шаги вместе, чтобы увидеть полную картину.
X6 / X3 = XXXXXX / XXX
= XXX
= X3
Таким образом, X6/X3 равно X3. Или мы также можем записать это как X6/X3 равно X(6 - 3).
И снова наша работа подводит нас ко второму правилу экспонент: Частному правилу .
Xa / Xb = X(a – b)
Аналогично правилу произведения, правило частного может работать, только если все основания имеют одинаковое значение. В нашем случае основаниями являются одинаковые переменные «Х».
Степенное правило
В следующем разделе рассматривается основание с видимым показателем степени, возведенным в определенную степень. Взгляните на приведенное ниже уравнение.
(Х3)4 =?
Можете ли вы определить, сколько это X?
Если это слишком запутанно, давайте представим его в более осязаемой форме.
(X3)4 = (XXX)4
Сначала мы расширяем показатель степени в скобках. Таким образом, мы можем присвоить каждому X внешний показатель степени «4».
(Х3)4 = (ХХХ)4
= (Х4) (Х4) (Х4)
= X(4 + 4 + 4)
= X12
Таким образом, мы можем определить, что (X3)4 равно X12. Записав это иначе, мы увидим, что (X3)4 равно X(3 x 4)
. Благодаря приведенным выше вычислениям мы можем ознакомиться с третьим важным правилом экспонент: степенным правилом .
(Xa)b = X(ab)
Дополнительные примеры со степенным правилом
Давайте рассмотрим более сложный пример.
Вы можете упростить это?
(x5y9z2)3
Во-первых, помните, что все основания имеют разные переменные, поэтому мы не можем складывать показатели степени, используя правило произведения.
В этом случае, используя правило степени, мы можем вместо этого умножить внутренние показатели на внешние. С помощью этого метода мы можем легко и быстро увидеть результат.
(x5 y9 z2)3 = (x(5 x 3)) (y(9 x 3)) (z(2 x 3))
= x15 y27 z6
Правило нуля
Прежде чем мы углубимся в Правило нуля, рассмотрим выражение ниже.
Х4 / Х4 = ?
С первого взгляда видно, что и числитель, и знаменатель имеют одно и то же значение. Деление всего с одинаковым значением равно 1. Таким образом, результат уравнения равен 1.
X4 / X4 = 1
С учетом сказанного, вы помните правило частного? Правило гласит, что мы можем вычесть два показателя степени, если разделить две степени с одинаковыми основаниями.
X4 / X4 = X(4 -4)
= X0
Этот расчет приводит нас к правилу нуля 9.0024 .
X0 = 1
X ≠ 0
Условие X ≠ 0 имеет место, поскольку 0 разделить на 0 не определено. Кроме того, наш предыдущий расчет действителен только в том случае, если X не равен 0.
Отрицательные показатели степени
Даже показатели степени могут иметь отрицательную форму. Однако, как бы это ни звучало, это не очень сложная концепция. Это означает только то, что основание должно быть на противоположной стороне дробной линии. Взгляните на пример ниже.
Это означает только то, что основание должно быть на противоположной стороне дробной линии. Взгляните на пример ниже.
Х-3 = 1 / Х3
Как видите, мы переворачиваем основание из позиции числителя в знаменатель или наоборот, чтобы превратить отрицательную степень в положительную.
Обладая этими знаниями, сможете ли вы решить это уравнение?
2x-3 / x-5 = ?
Не торопитесь и помните, что нам нужно всего лишь изменить положение базы.
2x-3 / x-5 = 2x5 / x3
Мы не переворачиваем число «2», потому что оно имеет степень 1.
Final Words
шагов по сравнению с другими людьми. Это хорошо. Математика довольно гибкая, поэтому вам не нужно заставлять себя использовать одни и те же шаги для решения задач, если ваш ответ правильный.
Объяснение урока: Степени и степени
В этом объяснении мы научимся определять основание и показатель степени в формулах степени, записывать их в экспоненциальной, расширенной и словесной формах, а также оценивать простые степени.
Повторное сложение может быть записано как умножение. Итак, если мы получим 10 сообщений в один день, 10
на следующий день и 10 на следующий день мы получили всего 10+10+10=3×10 сообщений.
Многократное сложение числа 10 записывается как умножение 10 на количество
раз 10 появляется в повторном сложении. (Можно также сказать, что это на единицу больше, чем число
умноженное на 10 прибавляется к самому себе.)
Аналогичным образом можно записать повторяющееся умножение. Например, предположим, что
кто-то получает изображение в социальных сетях. Этот человек делится им в первую минуту до четырех
из его или ее друзей. В следующую минуту каждый из четырех друзей делится этим с другим
четыре человека. И, на третьей минуте, каждый из людей, получивших картинку в
предыдущая минута делится ею еще с четырьмя людьми. Количество людей, получивших эту фотографию в
третья минута 1⋅4⋅4⋅4.
Это многократное умножение данного множителя (здесь 4) может быть записано как степень этого
фактор; а именно, 1⋅4⋅4⋅4=4=64.
Число 4 называется степенью числа 4. Повторяющийся множитель 4 равен
называется основанием, а показатель степени 3 — это количество раз, когда множитель появляется в повторяющемся
умножение. (Можно также сказать, что это на единицу больше, чем 4 умножается на
сам.)
Подведем итог тому, что мы только что узнали о силах.
Определение: Степени и экспоненциальная форма
Степени - это числа, полученные в результате многократного умножения множителя. Их общая форма
это 𝑏, где 𝑏 называется
основание и 𝑚 показатель степени.
Основание 𝑏 — это множитель, многократно умноженный сам на себя, а
показатель 𝑚 — это количество раз, которое 𝑏 появляется в
многократное умножение.
Когда число записывается в виде степени, мы говорим, что оно записано в экспоненциальной форме .
Когда степень записывается как многократное умножение, мы говорим, что она написана в расширенном виде.
форма.
Возможно, вы уже узнали о квадрате и кубе числа. Квадрат - это то же самое, что
возведение во вторую степень; это умножение числа само на себя: 𝑎=𝑎×𝑎. Число, возведенное в третью степень или степень троицы, возводится в куб:
𝑎=𝑎×𝑎×𝑎.
Обратите внимание, что любое число может быть записано как первая степень самого себя, 3=3.
Умножение свойства тождества говорит нам, что умножение любого числа на 1 не
изменить этот номер. Отсюда следует, что все степени 1 равны просто 1: 1=1,
1=1, 1=1, 1=1 и так далее.
Кроме того, возведение любого ненулевого числа в нулевую степень дает 1.
Давайте рассмотрим несколько примеров, чтобы проверить и углубить наше понимание.
Пример 1. Запись повторяющегося умножения в экспоненциальной форме
Запись 7×7×7×7 в экспоненциальной форме.
Ответ
Выражение 7×7×7×7 является повторяющимся
умножение на множитель 7. Его можно записать в экспоненциальной форме, т. е. в
форма 𝑏, где 𝑏 — многократно
умножается сам на себя, здесь 7, а 𝑚 — количество раз, когда этот множитель
появляется при повторном умножении, здесь 4. Следовательно, 7×7×7×7=7.
е. в
форма 𝑏, где 𝑏 — многократно
умножается сам на себя, здесь 7, а 𝑚 — количество раз, когда этот множитель
появляется при повторном умножении, здесь 4. Следовательно, 7×7×7×7=7.
Пример 2: Написание степени в развернутой форме
Напишите 3 в развернутой форме.
Ответ
Степень записывается в виде 𝑏. Это сокращение от повторяющегося
умножение множителя 𝑏, где 𝑚 - это число
раз этот множитель появляется при повторном умножении. Здесь 𝑏=3
и 𝑚=4.
Следовательно, 3=3×3×3×3.
Пример 3: Запись степени по ее названию
Запишите семь в четвертой степени, используя цифры.
Ответ
Нас просят записать семь в четвертой степени. Напомним, что мощность записывается в
форма 𝑏. Это сокращение для многократного умножения множителя
𝑏, где 𝑚 — количество раз, когда этот коэффициент
появляется при повторном умножении. Есть разные способы вызова
𝑏: 𝑏 возведен в 𝑚-ю степень или
в степени 𝑚 или 𝑏 в степени 𝑚
сила. Здесь у нас есть семь в четвертой степени, поэтому мы находим, что 𝑏=7
и 𝑚=4. Следовательно, он записывается как 7.
Здесь у нас есть семь в четвертой степени, поэтому мы находим, что 𝑏=7
и 𝑚=4. Следовательно, он записывается как 7.
Пример 4. Запись степени в развернутой форме и вычисление ее
Выразите 3 как произведение одного и того же множителя, а затем найдите его
ценность.
Ответ
Число 3 записано в экспоненциальной форме, и мы хотим сначала написать
это в развернутом виде.
Показательная форма 𝑏 является сокращением для повторного умножения
множителя 𝑏, где 𝑚 — количество раз, когда это
множитель появляется при повторном умножении. Следовательно, 3 в расширенном
форма 3⋅3⋅3⋅3.
Затем нам нужно оценить этот продукт. Используя ассоциативность, мы можем написать 3⋅3⋅3⋅3=(3⋅3)⋅(3⋅3)=9⋅9=81.
Рассмотрим теперь пример умножения степеней разных оснований.
Пример 5: Расширение умножения двух степеней
Что из следующего эквивалентно 7⋅10?
Ответ
Выражение 7⋅10 включает умножение двух степеней,
7 и 10. Расширим каждую из них. Напомним, что
сила, записанная в форме 𝑏, является сокращением для повторяющегося
умножение множителя 𝑏, где 𝑚 - это число
раз этот множитель появляется при повторном умножении. Следовательно, имеем 7=7⋅7⋅7⋅7 и 10=10⋅10⋅10⋅10⋅10⋅10.
Расширим каждую из них. Напомним, что
сила, записанная в форме 𝑏, является сокращением для повторяющегося
умножение множителя 𝑏, где 𝑚 - это число
раз этот множитель появляется при повторном умножении. Следовательно, имеем 7=7⋅7⋅7⋅7 и 10=10⋅10⋅10⋅10⋅10⋅10.
Теперь мы просто перемножим их вместе, чтобы найти выражение, эквивалентное 7⋅10: 7⋅7⋅7⋅7⋅10⋅10⋅10⋅10⋅10⋅10.
Давайте посмотрим на другой пример, чтобы понять, что происходит, когда две степени одного основания
умножаются. В этом примере у нас есть степень переменной 𝑥 вместо
числа, и мы увидим, что это ничего не меняет в том, как мы обращаемся с силами.
Пример 6. Умножение степеней одного основания
Упростить 𝑥×𝑥.
Ответ
Мы хотим выразить 𝑥×𝑥 в виде одной степени. визуализировать
как можно упростить это выражение, давайте сначала перепишем его, расширив оба
силы. Мы находим, что наше выражение равно (𝑥⋅𝑥⋅𝑥⋅𝑥⋅𝑥)⋅(𝑥⋅𝑥).
Скобки здесь можно убрать, используя ассоциативное свойство умножения. Это повторное умножение множителя 𝑥 включает всего 5+2=7𝑥s. Следовательно, это можно записать как 𝑥.
В предыдущих двух примерах мы видели, что при умножении двух степеней одного и того же основания
мы получаем
Это известно как правило продукта.
Правило произведения
Произведение двух степеней, имеющих одно и то же основание, является степенью того же основания с
показатель степени равен сумме показателей степени: 𝑏⋅𝑏=𝑏.()
В следующих двух примерах мы увидим, как
умножение используется для перезаписи выражений, включающих многократное умножение различных
факторы.
Пример 7. Переписывание выражений с использованием экспонент
Какое из следующих выражений эквивалентно 7⋅5⋅7⋅3⋅5⋅5?
- 105
- 3 порядка 5om7
- 105
- 3Z5–7
Ответ
умножение с участием разных факторов. Поэтому его нельзя выразить в виде единого
сила. Однако мы замечаем, что факторы 7 и 5 повторяются. Мы собираемся использовать
коммутативное свойство умножения сначала переписать наше выражение так, чтобы все
идентичные факторы группируются вместе.
Поэтому его нельзя выразить в виде единого
сила. Однако мы замечаем, что факторы 7 и 5 повторяются. Мы собираемся использовать
коммутативное свойство умножения сначала переписать наше выражение так, чтобы все
идентичные факторы группируются вместе.
Например, мы можем переписать 7⋅5⋅7⋅3⋅5⋅5
как 7⋅7⋅3⋅5⋅5⋅5.
Теперь легко увидеть, что 7 используется дважды, 3 — один раз, а 5 — трижды. Напомним, что сила,
записанный в форме 𝑏, является сокращением для повторного умножения
множителя 𝑏, где 𝑚 — количество раз, когда это
множитель появляется при повторном умножении. Следовательно, это выражение эквивалентно
7⋅3⋅5.
Снова используя коммутативность, мы можем изменить порядок множителей и записать это как 3⋅5⋅7.
Пример 8. Поиск эквивалентных выражений для повторяющихся умножений
Какое из следующих выражений эквивалентно 2⋅5⋅2⋅2⋅5⋅2⋅5⋅5?
- 2=5
- 2 порядка 5
- 2 порядка 5
- 4 порядка
Ответ
Выражение 2 порядка 5 %2 ОТ ⋅5
это умножение с участием разных множителей. Поэтому его нельзя выразить как
единая мощность. Однако мы замечаем, что факторы 2 и 5 повторяются. С использованием
коммутативное свойство умножения, мы можем переписать наше выражение, сгруппировав двойки
вместе и пятерки вместе. Получаем 2⋅2⋅2⋅2⋅5⋅5⋅5⋅5.
Поэтому его нельзя выразить как
единая мощность. Однако мы замечаем, что факторы 2 и 5 повторяются. С использованием
коммутативное свойство умножения, мы можем переписать наше выражение, сгруппировав двойки
вместе и пятерки вместе. Получаем 2⋅2⋅2⋅2⋅5⋅5⋅5⋅5.
Напомним, что степень, записанная в форме 𝑏, является сокращением для
повторное умножение фактора 𝑏, где 𝑚
количество раз, когда этот множитель появляется при повторном умножении. Следовательно, наш
выражение эквивалентно 2⋅5.
Все еще используя коммутативное свойство умножения, мы можем также переписать наше первое
выражение в виде 2⋅5⋅2⋅5⋅2⋅5⋅2⋅5, что, используя на этот раз ассоциативное свойство, эквивалентно
(2⋅5)⋅(2⋅5)⋅(2⋅5)⋅(2⋅5).
Мы видим, что число внутри каждой пары скобок равно 2⋅5, т.е.
равно 10.
Следовательно, наше выражение также эквивалентно 10⋅10⋅10⋅10, что можно записать как четвертую степень числа 10:
10.
Когда мы оцениваем 10, мы находим, что это 10 000.
В итоге мы нашли, что 2⋅5⋅2⋅2⋅5⋅2⋅5⋅5=2⋅5=10=10000.
Следовательно, правильный ответ – вариант А: 2⋅5 .
В этом последнем примере обратите внимание, что как только вы поняли метод, вам не нужно группировать
все одинаковые факторы. Вы можете просто подсчитать, сколько раз появляется каждый фактор, и
затем запишите эквивалентную степень повторному умножению каждого множителя.
В предыдущих двух примерах мы обнаружили, что при возведении произведения двух множителей в
𝑚я степень, у нас есть
Это можно резюмировать таким образом.
Мощность продукта
Заданная мощность произведения факторов представляет собой произведение каждого фактора, возведенного до данного
мощность: (𝑎𝑏)=𝑎⋅𝑏.
Пример 9. Выражение многократного умножения дроби со степенью
Что такое 411×411×411×411×411×411×411?
Ответ
Показатель степени показывает, сколько раз рациональное число умножается само на себя.

 Сокращение дробей (интерактивное задание)
Сокращение дробей (интерактивное задание)




 Нахождение числа по его дроби (интерактивное задание)
Нахождение числа по его дроби (интерактивное задание) Нахождение числа по его дроби (интерактивное задание)
Нахождение числа по его дроби (интерактивное задание)







 ru
ru

 Тогда берите взаимность.
Тогда берите взаимность. 
 е. справа налево, мы можем выразить правило следующим образом: если основание записать в виде произведения нескольких множителей, то мы можем распределить показатель степени на каждый из этих множителей.
е. справа налево, мы можем выразить правило следующим образом: если основание записать в виде произведения нескольких множителей, то мы можем распределить показатель степени на каждый из этих множителей.  Мы используем произведение степеней и суммируем два показателя степени:
Мы используем произведение степеней и суммируем два показателя степени: В данном случае это четыре нуля:
В данном случае это четыре нуля: Если вы хотите избавиться от показателей степени, вычислите множители один за другим:
Если вы хотите избавиться от показателей степени, вычислите множители один за другим: Значение x может варьироваться (отсюда и название). В одном уравнении x может быть равно 4. В другом уравнении x может быть равно 7 или более сложному числу, например 75/2. Мы выражаем переменную с помощью символа. В большинстве уравнений чаще всего используются символы 9.0027 x , y и z .
Значение x может варьироваться (отсюда и название). В одном уравнении x может быть равно 4. В другом уравнении x может быть равно 7 или более сложному числу, например 75/2. Мы выражаем переменную с помощью символа. В большинстве уравнений чаще всего используются символы 9.0027 x , y и z . В алгебре размещение двух или более переменных рядом друг с другом означает их умножение. x умножить на x умножить на x .
В алгебре размещение двух или более переменных рядом друг с другом означает их умножение. x умножить на x умножить на x . Давайте сложим их все вместе.
Давайте сложим их все вместе.



 Это означает только то, что основание должно быть на противоположной стороне дробной линии. Взгляните на пример ниже.
Это означает только то, что основание должно быть на противоположной стороне дробной линии. Взгляните на пример ниже.


 е. в
форма 𝑏, где 𝑏 — многократно
умножается сам на себя, здесь 7, а 𝑚 — количество раз, когда этот множитель
появляется при повторном умножении, здесь 4. Следовательно, 7×7×7×7=7.
е. в
форма 𝑏, где 𝑏 — многократно
умножается сам на себя, здесь 7, а 𝑚 — количество раз, когда этот множитель
появляется при повторном умножении, здесь 4. Следовательно, 7×7×7×7=7.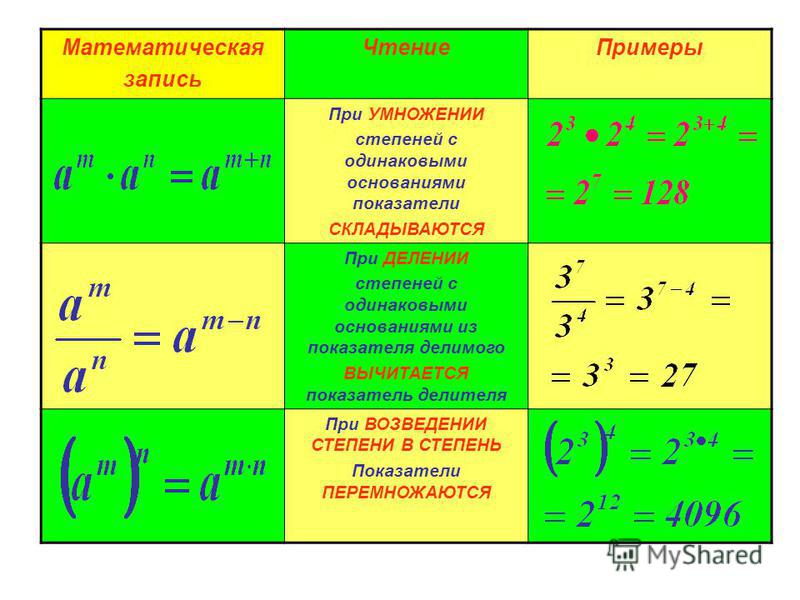 Здесь у нас есть семь в четвертой степени, поэтому мы находим, что 𝑏=7
и 𝑚=4. Следовательно, он записывается как 7.
Здесь у нас есть семь в четвертой степени, поэтому мы находим, что 𝑏=7
и 𝑚=4. Следовательно, он записывается как 7. Расширим каждую из них. Напомним, что
сила, записанная в форме 𝑏, является сокращением для повторяющегося
умножение множителя 𝑏, где 𝑚 - это число
раз этот множитель появляется при повторном умножении. Следовательно, имеем 7=7⋅7⋅7⋅7 и 10=10⋅10⋅10⋅10⋅10⋅10.
Расширим каждую из них. Напомним, что
сила, записанная в форме 𝑏, является сокращением для повторяющегося
умножение множителя 𝑏, где 𝑚 - это число
раз этот множитель появляется при повторном умножении. Следовательно, имеем 7=7⋅7⋅7⋅7 и 10=10⋅10⋅10⋅10⋅10⋅10.
 Поэтому его нельзя выразить в виде единого
сила. Однако мы замечаем, что факторы 7 и 5 повторяются. Мы собираемся использовать
коммутативное свойство умножения сначала переписать наше выражение так, чтобы все
идентичные факторы группируются вместе.
Поэтому его нельзя выразить в виде единого
сила. Однако мы замечаем, что факторы 7 и 5 повторяются. Мы собираемся использовать
коммутативное свойство умножения сначала переписать наше выражение так, чтобы все
идентичные факторы группируются вместе. Поэтому его нельзя выразить как
единая мощность. Однако мы замечаем, что факторы 2 и 5 повторяются. С использованием
коммутативное свойство умножения, мы можем переписать наше выражение, сгруппировав двойки
вместе и пятерки вместе. Получаем 2⋅2⋅2⋅2⋅5⋅5⋅5⋅5.
Поэтому его нельзя выразить как
единая мощность. Однако мы замечаем, что факторы 2 и 5 повторяются. С использованием
коммутативное свойство умножения, мы можем переписать наше выражение, сгруппировав двойки
вместе и пятерки вместе. Получаем 2⋅2⋅2⋅2⋅5⋅5⋅5⋅5.
