Комбинаторные задачи как решать: К сожалению, что-то пошло не так

Мерзляк 5 класс — § 24. Комбинаторные задачи

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Вопросы к параграфу

1. Какие задачи называют комбинаторными?

Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).

2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?

Дерево возможных вариантов.

Решаем устно

1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?

Найдём площадь поверхности куба:

S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.

Ответ: 54 дм².

2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:

1) 4 см, 6 см, 12 см

4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

2) 5 см, 6 см, 8 см

5 • 6 • 8 = 30 •  8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.

3) 3 см, 5 см, 10 см

3 • 5 • 10 = 15 •  10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

4) 10 см, 10 см, 24 см

10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

Ответ: числа 5 см, 6 см и 8 см.

3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?

1) 8 • 2 • 1 = 16 (м²) — объём бункера.

2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.

Ответ: 128 центнеров.

4. Что больше и на сколько:

1) квадрат суммы чисел 4 и 3 или сумма их квадратов

(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25

2) разность квадратов чисел 10 и 8 или квадрат их разности

10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4

3) разность кубов чисел 5 и 3 или куб их разности

5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8

Упражнения

645.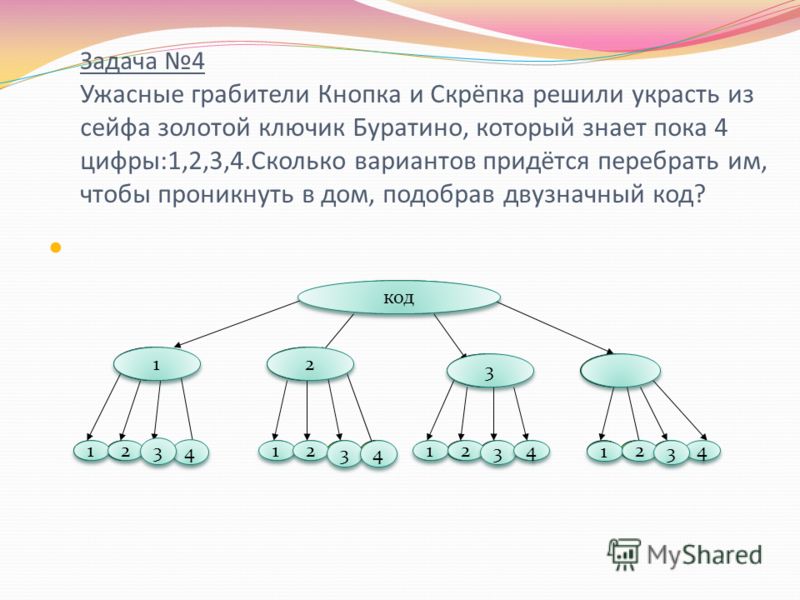 Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).

Таких двузначных чисел всего 9:

• 11, 12, 13
• 22, 21, 23
• 33, 31, 32

646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).

Таких двузначных чисел всего 6:

• 11, 12, 10
• 22, 21, 20

647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?

Решим задачу при помощи схемы «Дерево возможных вариантов».

Итак, у нас получилось шесть возможных вариантов:

	Винни-Пуха	Пятачок	Кролик
Вариант 1	Зелёный	Красный	Жёлтый
Вариант 2	Зелёный	Жёлтый	Красный
Вариант 3	Красный	Зелёный	Жёлтый
Вариант 4	Красный	Жёлтый	Зелёный
Вариант 5	Жёлтый	Зелёный	Красный
Вариант 6	Жёлтый	Красный	Зелёный

Ответ: 6 вариантов.

648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?

Таких двузначных чисел всего 4:

• 12, 10
• 21, 20

649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645—648 аналогично решению этой задачи?

Решим задачу при помощи схемы «Дерево возможных вариантов».

Итак, у нас получилось шесть возможных вариантов (последовательно места, занятые 5″А», 5″Б» и 5″В»):

Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):

	5″А»	5″Б»	5″В»
Вариант 1	1	2	—
Вариант 2	1	—	2
Вариант 3	2	1	—
Вариант 4	2	—	1
Вариант 5	—	1	2
Вариант 6	—	2	1

Задача аналогична задаче № 647.

Ответ: 6 вариантов.

650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):

1) 3, 4 и 6

• 346, 364
• 436, 463
• 634, 643

2) 4, 7 и 0

• 470, 407
• 740, 704

651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):

1) 1 и 2

• 111, 112, 121, 122
• 222, 221, 212, 211

Ответ: 8 чисел.

2) 0 и 1

• 111, 110, 101, 100

Ответ: 4 числа.

652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)

• 22, 24, 29, 20
• 42, 44, 49, 40
• 92, 94, 99, 90

653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?

• 67, 68, 69
• 78, 79
• 89

Ответ: 6 чисел.

654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?

• 98, 97, 96
• 87, 86
• 76

Ответ: 6 чисел.

655. Сколько существует двузначных чисел, сумма цифр которых равна 5?

Всего 5 чисел: 14, 23, 32, 41, 50.

Ответ: 5 чисел.

656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?

Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.

Ответ: 8 чисел.

657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?

Всего 6 чисел: 10, 12, 21, 23, 30, 32.

Ответ: 6 чисел.

658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3.

Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?

Составим таблицу:

• в первом столбце запишем возможные варианты первой цифры кода
• в верхней строке — возможные варианты второй цифры кода
• на пересечении строк и столбцов — возможные варианты кодов.

	0	1	2	3
0	00	01	02	03
1	10	11	12	13
2	20	21	22	23
3	30	31	32	33

Итак, возможное количество вариантов кода — 16.

Ответ: 16 вариантов.

659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?

P = (a + b) • 2

Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.

Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:

1. 1 см и 11 см
2. 2 см и 10 см
3. 3 см и 9 см
4. 4 см и 8 см
5. 5 см и 7 см
6. 6 см и 6 см (квадрат, который также соответствует определению прямоугольника).

Ответ: 6 прямоугольников.

660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?

V = abc

Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:

1. 30 • 1 • 1 = 30 
2. 15 • 2 • 1 = 30 
3. 10 • 3 • 1 = 30 
4. 6 • 5 • 1 = 30 
5. 5 • 3 • 2 = 30 

Ответ: 5 вариантов.

661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?

Для решения этой задачи можно ориентироваться на рисунок 184 § 24:

Но лучше сделать свой рисунок для этой конкретно задачи:

• AB, AC, AD
• BC, BD
• CD

Ответ: 6 отрезков.

662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?

Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:

• O — вершина горы
• A — первая точка у подножия горы
• B — вторая точка у подножия горы
• C — третья точка у подножия горы.

Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):

• AOA, AOB, AOC
• BOA, BOB, BOC
• COA, COB, COC

Итого — 9 вариантов маршрутов.

Ответ: 9 вариантов.

663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?

Составим таблицу:

• в первом столбце запишем возможные варианты шорт
• в верхней строке — возможные варианты футболок
• на пересечении строк и столбцов — возможные варианты формы

Форма		Футболки
		Красные	Зелёные	Синие
Шорты	Белые	Красная футболка белые шорты	Зелёная футболка белые шорты	Синяя футболка белые шорты
	Жёлтые	Красная футболка жёлтые шорты	Зелёная футболка жёлтые шорты	Синяя футболка жёлтые шорты

Итак, возможное количество вариантов формы — 6.

Ответ: 6 вариантов.

664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?

Составим таблицу:

• в первом столбце запишем возможные варианты туфель
• в верхней строке — возможные варианты платьев
• на пересечении строк и столбцов — возможные варианты наряда

Наряд		Платья
		1	2	3	4
Туфли	1	Платье № 1 Туфли № 1	Платье № 2 Туфли № 1	Платье № 3 Туфли № 1	Платье № 4 Туфли № 1
	2	Платье № 1 Туфли № 2	Платье № 2 Туфли № 2	Платье № 3 Туфли № 2	Платье № 4 Туфли № 2

Итак, возможное количество вариантов нарядов — 8.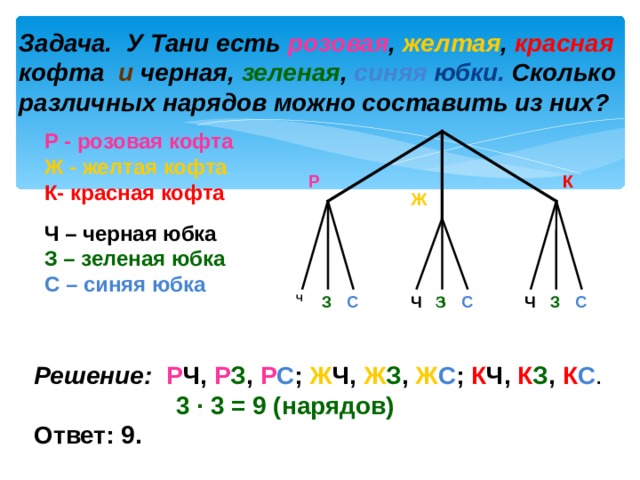

Ответ: 8 вариантов.

665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?

Составим таблицу:

• в первом столбце запишем возможные варианты инженеров
• в верхней строке — возможные варианты пилотов
• на пересечении строк и столбцов — возможные варианты экипажа

Экипаж		Пилоты
		1	2	3
Инженеры	1	Пилот 1 Инженер 1	Пилот 2 Инженер 1	Пилот 3 Инженер 1
	2	Пилот 1 Инженер 2	Пилот 2 Инженер 2	Пилот 3 Инженер 2

Итак, возможное количество вариантов нарядов — 6.

Ответ: 6 вариантов.

666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?

Существуют следующие варианты маршрутов:

1. Вверх — вверх — вправо — вправо
2. Вверх — вправо — вверх — вправо
3. Вверх — вправо — вправо — вверх
4. Вправо — вверх — вверх — вправо
5. Вправо — вверх — вправо — вверх
6. Вправо — вправо — вверх — вверх

Итак, возможное количество вариантов маршрутов — 6.

Ответ: 6 вариантов.

667. В записи 1 * 2 * 3 * 4 вместо каждой звёздочки можно поставить один из знаков «+» или «•». Чему равно наибольшее значение выражения, которое можно получить?

Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:

1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.

Упражнения для повторения

668. Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?

1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.

2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.

Ответ: 2 часа.

669. Решите уравнение:

670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?

Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.

(14х + х) : х = 15х : х = 15

Ответ: в 15 раз.

2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?

Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).

(12х + х) : х = 13х : х = 13

Ответ: в 13 раз.

671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?

1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.

2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.

3) 1 680 литров < 1 872 литра, значит 42 бидона не хватит для вывоза всего надоенного за день молока.

Ответ: Нет, не хватит.

672. Решите кроссворд.

По горизонтали:

2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)

По вертикали:
1. «Царица наук» (Математика)

Задача от мудрой совы

673. В классе 30 учащихся.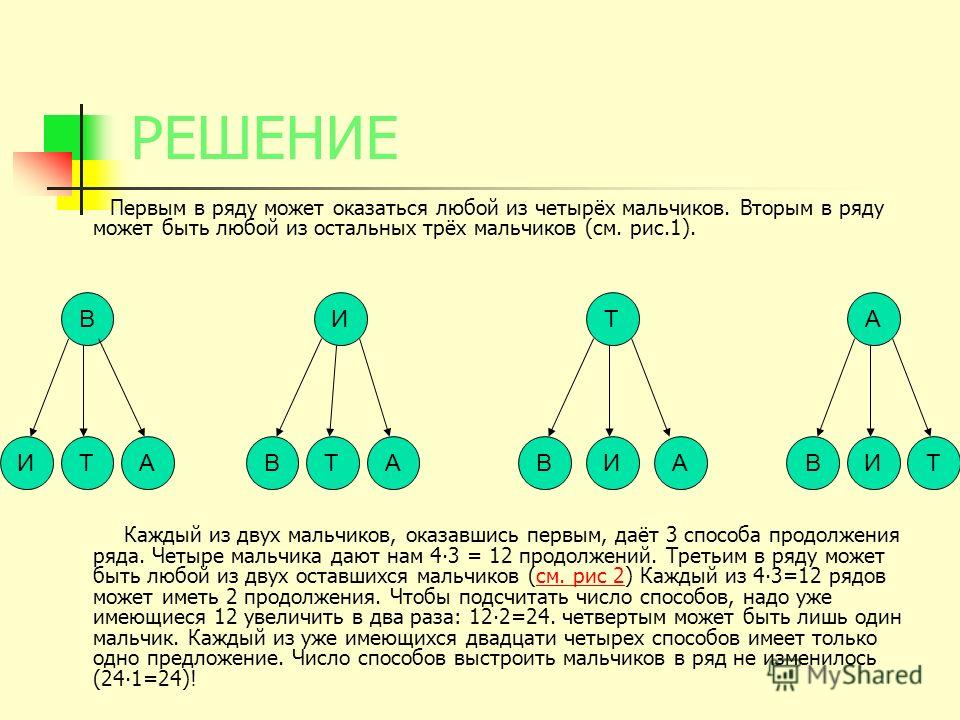 Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?

1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.

2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.

3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом. 

4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.

5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.

Ответ: Нет, нельзя. 

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Открытый урок по теме: решение комбинаторных задач

Урок №3 по комбинаторике в 9-м классе «Решение комбинаторных задач .»

Задачи урока:

Обучающие:

·         знакомство учащихся с комбинаторными задачами,                                                                     и научить учащихся решать комбинаторные задачи  ,

·         познакомить учащихся с правилом умножения при решении комбинаторных задач,

Развивающие:

·         развитие комбинаторного мышления учащихся,

·         формирование интеллектуальных умений: анализировать, выделять главное, сравнивать, обобщать и систематизировать, разрешать проблемы,

·         развитие умений владеть собой,

·         развитие инициативы, уверенности в своих силах, умения преодолевать трудности в учении.

Воспитывающие:

·         содействовать формированию основных мировоззренческих идей,

·         содействовать профориентации учащихся.

Тип урока. Урок изучения нового материала.

Структура урока.

1.      Организационный момент.

2.      Мотивация и сообщение темы урока.

3.      Формирование новых понятий и способов действий.

4.      Применение знаний, умений и навыков в различных ситуациях (стандартных и нестандартных)

5.      Подведение итогов, задание на дом.

Ход урока

1.. Организационный момент. (Вступительное слово учителя)

Здравствуйте, ребята, садитесь. Сегодня у нас открытый урок. Мы на уроке продолжим отрабатывать навыки решения комбинаторных задач. К уроку я подготовила вам различные  задачи по комбинаторике,  которые предлагаю решить разными способами: каждый из Вас может  высказать свою точку зрения на решение задач. Хотя в «споре рождается истина», но я Вас попрошу, быть очень внимательными друг к другу.

 

 

Мотивация и сообщение темы урока.

Вступление:

Переходим к уроку.

Презентация.

Тема нашего урока: «Решение комбинаторных задач

Проблемный вопрос:  Почему нам нужно научиться решать комбинаторные задачи? Как вы думаете?

Кроме того, что задачи из комбинаторики находятся в разделе «Реальная математика» и входят в материалы ГИА? Где еще нам пригодятся такие  знания ?

Может ли нам комбинаторика помочь в реальной жизни?

Ответ: Решение комбинаторных задач развивает творческие способности, помогает при решении олимпиадных задач.

В каких областях применяется комбинаторика?

 

Области применения  комбинаторики:
—учебные заведения ( составление расписаний)

-сфера общественного питания (составление меню)

-лингвистика (рассмотрение вариантов комбинаций букв)

-спортивные соревнования (расчёт количества игр между участниками)

-агротехника (размещение посевов на нескольких полях)

-география (раскраска карт)

—биология (расшифровка кода ДНК)

-химия (анализ возможных связей между химическими элементами)

-экономика (анализ вариантов купли-продажи акций) азартные игры (подсчёт частоты выигрышей)

—криптография (разработка методов шифрования)

—доставка почты (рассмотрение вариантов пересылки)

-военное дело (расположение подразделений)

 

  Учитель: Люди, которые умело владеют техникой решения комбинаторных задач, а следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций.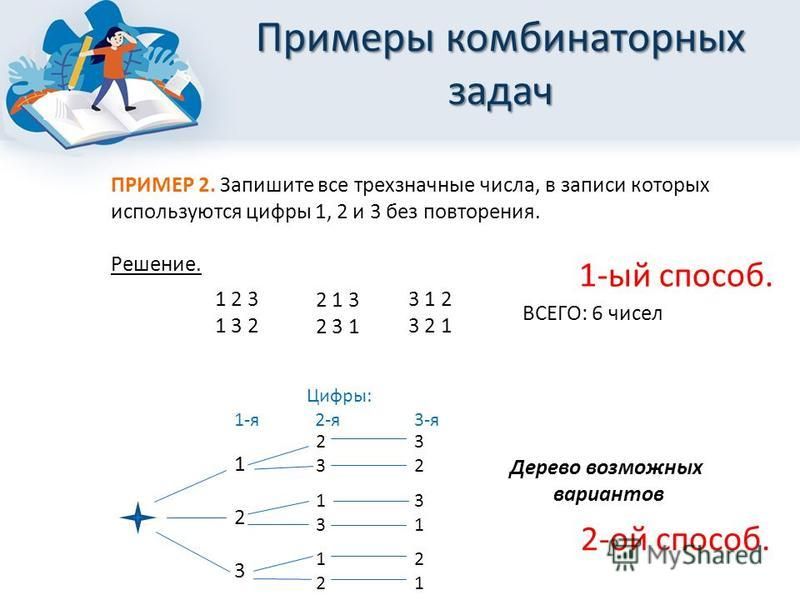

 

2..Проверка домашнего задания.

 Но, сначала, проверим домашнее задание. Я задавала вам решить дома №715 и №714 . кто пойдет к доске и кратко запишет д\з?

№714 и №715

3. Фронтальный опрос

 Пока они записывают домашнее задание на доске , ответим на вопросы

1.     Что такое комбинаторика?

2.     От какого слова произошло слово «комбинаторика»?

3.     Какие приемы решения комбинаторных задач вы знаете?

 

Задача 1. (желательно продемонстрировать.)

Итак, продолжим знакомство с новыми для вас понятиями начнем с двух простых задач.

            В одной пачке лежит 10 тетрадей в клеточку, в другой – 15 тетрадей в линию. Сколькими способами можно выбрать 1 тетрадь в клетку или 1 тетрадь в линию?

Решение. Из первой пачки тетрадь в клетку можно взять 10 способами, а из второй – 15 способами. Значит, всего существует 10+15=25 способов.

Поэтому, если объект  а  можно выбрать п способами, а объект в – т способами, то выбор «или а или в» можно осуществить (п+т) способами.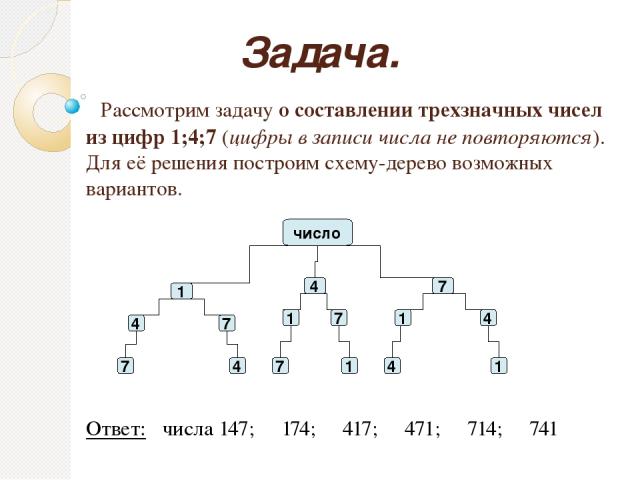

Это правило в комбинаторике получило название «правило суммы».

Задача 2 ( желательно продемонстрировать.)

Мне подарили  три книги. Сколькими способами можно расставить 3 различные книги на книжной полке?

 

 Решение:  123; 132; 213;231; 312;321.

Ответ: 6 способов

А сейчас проверим, правильно ли ребята решили задачи?

Итак,  первая задача №714                                            №715

 У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана.

Она решила двух из них пригласить в кино.

Укажите все возможные варианты выбора подруг.

 Сколько таких вариантов?

Обед

 

Борщ       Рассольник 

4.Формирование новых понятий и способов действий.

Обратимся к презентации

 

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

Рассмотрим еще одну задачу. На цветочной клумбе сидели шмель, жук, бабочка и муха. Два насекомых улетели. Какие пары насекомых могли улететь? Укажите все возможные варианты. Сколько таких вариантов?

Всего  3+2+1=6      Ответ:6 вариантов

 

Задача №2 Сколько двузначных чисел можно составить, используя цифры  3; 5; 7?

Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:

33;35;37; (начали с 3)

53;55;57; (начали с 4)

73;75;77; (начали с 7)

               Таким образом, из трёх данных цифр  можно составить всего 9 различных двузначных чисел.

                       Ответ: 9 чисел.

Задача №3 Решим аналогичную задачу о составлении трехзначных чисел из цифр 1;4;7, так чтобы цифры не повторялись. Для её решения построим схему — дерево возможных вариантов.                                                  

Ответ: числа 147;174;417;471;714;741

Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так.

    Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению

3х2х1=6

Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения

«Если объект А можно выбрать m  способами, а другой объект В можно выбрать k способами, то объект «А и В» можно выбрать m ∙ k  способами».

Задача: У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету.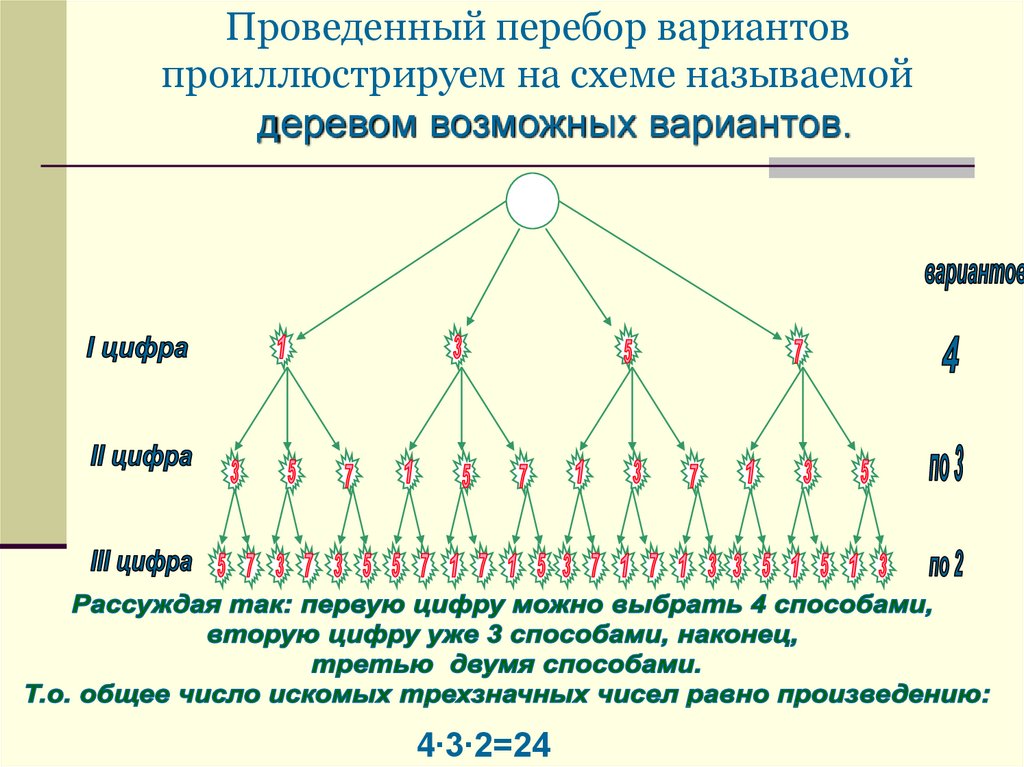 Сколько различных комбинаций одежды имеется у Светы?

Решение.  3·5 = 15

 

Самостоятельная работа

 

Задача 1

Составляя расписание на  понедельник в 9 классе, завуч может поставить 6 уроков: алгебра, физика, биология, труд, история, физкультура.  Сколько существует вариантов расписания?

Задача 2

Сколько рукопожатий делают наши юноши каждое утро,   учитывая,  что их 17 человек?

 

Задача 3 Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

Решение: ребята найдут ответ, начертив граф. (Презентация, задача 1)

Задача решается с помощью полного графа с четырьмя вершинами А,Б,В,Г, обозначенными по первым буквам имён каждого из мальчиков. В полном графе проводятся всевозможные рёбра. В данном случае отрезки-рёбра обозначают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 рёбер, значит, и партий сыграно 6 партий.

Ответ: 6 партий.

Задание для самостоятельной работы: придумайте задачи с похожим условием.

Математика повсюду — 
Глазом только поведешь
И примеров сразу уйму
Ты вокруг себя найдешь:

Задача№4.

Андрей, Борис, Виктор и Григорий подарили на память друг другу свои фотографии. Причём каждый мальчик подарил каждому из своих друзей по одной фотографии. Сколько всего фотографий было подарено?

Решение: ребята легко найдут ответ, начертив граф. (Презентация, задача 2)

Решение.

·         1 способ. С помощью стрелок на рёбрах полного графа показан процесс обмена фотографиями. Очевидно, что стрелок в 2 раза больше, чем рёбер, т.е. 12.

·         2 способ. Каждый из 4 мальчиков подарил друзьям 3 фотографии, следовательно, всего было подарено 3*4=12 фотографий.

Ответ: 12 фотографий.

Задача №5

У Лёвы 2 конверта: обычный и авиа, и 3 марки: прямоугольная , квадратная и треугольная. Сколькими способами он может выбрать конверт и марку ,чтобы отправить письмо?

Решение задачи. (Презентация, задача 3)

Сначала выбирается конверт, а затем выбирается марка.

Ответ: 6 вариантов.

Отличается ли данный граф от- предыдущих? Он имеет внешнее сходство с деревом, поэтому он так и называется — граф-дерево. Рёбра графа- дерева иногда называют ветвями, а сам граф -деревом вариантов. Вычерчивать дерево полезно, когда требуется записать все существующие комбинации элементов.

Решим следующую задачу с помощью графа-дерева.

Задача №6

Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько вариантов придётся перебрать им, чтобы проникнуть в дом, подобрав двузначный код?

Решение .

(Презентация, задача 4)

Ответ: 16 вариантов.

Задача №7.

Сколько двузначных чисел можно составить из чисел 1,2,3. 4 ,используя в записи числа каждую из них не более одного раза?

(Презентация, задача 5)

Решение задачи.

Ответ: 12 чисел.

Задача №8

Сколько трёхзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?

Решение. Первую цифру трёхзначного числа можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру, из оставшихся, можно выбрать тремя способами. Наконец третью цифру можно выбрать, из оставшихся, двумя способами.

(Презентация, задача 6)

Ответ.24 числа.

 

Задача №9.

Антон, Борис и Василий купили 3 билета на 1-е, 2-е и 3-е места первого ряда на футбольный матч. Сколькими способами они могут занять имеющиеся места?

Решение.

(Презентация, задача 8)

Ответ: 6 способов.

Задача №10

В пятницу у вас 4 уроков: алгебра, русский, физика, история. Сколькими способами можно составить расписание на пятницу?

Решение.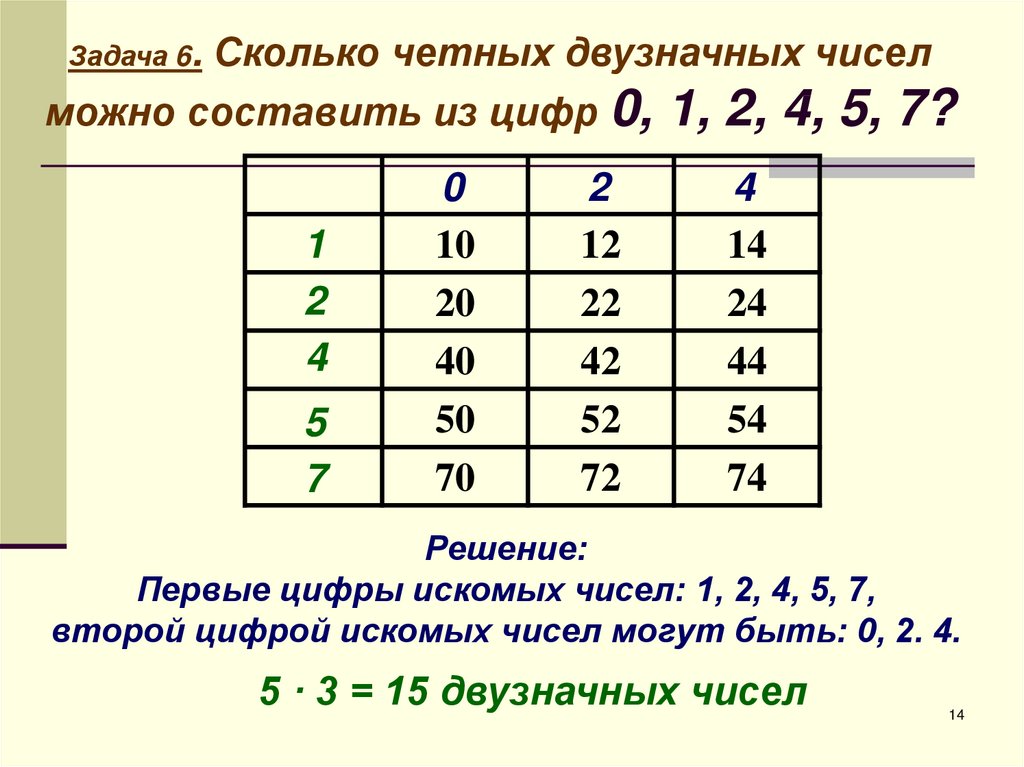

(Презентация, задача 9)

Ответ. 24 способа.

5. Подведение итогов урока.

Ребята, на все ли поставленные вопросы мы ответили? Ещё раз обратим на них внимание и дадим на них ответы.

Дома вы решите похожие задачи и найдёте ответы на вопросы, поставленные в начале урока.

Задание на дом.

Подготовьте материал по темам:

История её возникновения комбинаторики и этапы её развития. Учёные, внёсшие вклад в развитие комбинаторики. Проблемы комбинаторики. История возникновения теории графов. Терминология теории графов. Некоторые задачи теории графов.

Решите задачи:

1. Сколько различных трёхзначных чисел можно записать с помощью цифр:1)1 и 2;2)0 и 1?

2. Сколько различных трёхзначных чисел можно записать с помощью цифр 5,6,7,8,9,если:

1) цифры в числе могут повторяться;

2) цифры в числе должны быть различны?

Надеюсь, что наш урок поможет вам в изучении комбинаторики и теории вероятностей и сдачи экзамена по математики. Спасибо вам за урок.

Презентация.

История: Комбинаторика является древнейшей наукой. Некоторые комбинаторные задачи решали еще в Индии во 2 веке до нашей эры, в древнем Китае, в Римской империи. Термин комбинаторика происходит от латинского слова «комбина», что в переводе на русский язык — «сочетать», «соединять». Элементарные сведения комбинаторного характера были известны очень давно, но они носили разрозненный характер. Определенный вклад в их систематизацию был сделан в 17 веке Блезом Паскалем и Пьером Ферма. В том же 17 веке попытку рассмотреть комбинаторику как единую теоретическую дисциплину предпринял Готфрид Лейбниц. (Слайд 4) Он отводил комбинаторике роль универсального математического аппарата логических рассуждений, кроме того, именно Лейбниц ввел в математику термин «комбинаторика». Немало для развития математики в целом и комбинаторики в частности сделали такие ученые как Рене Декарт, Леонард Эйлер и Даниил Бернулли. В результате деятельности таких крупных математиков комбинаторика получила успешное развитие, в это время были получены почти все формулы современной комбинаторики.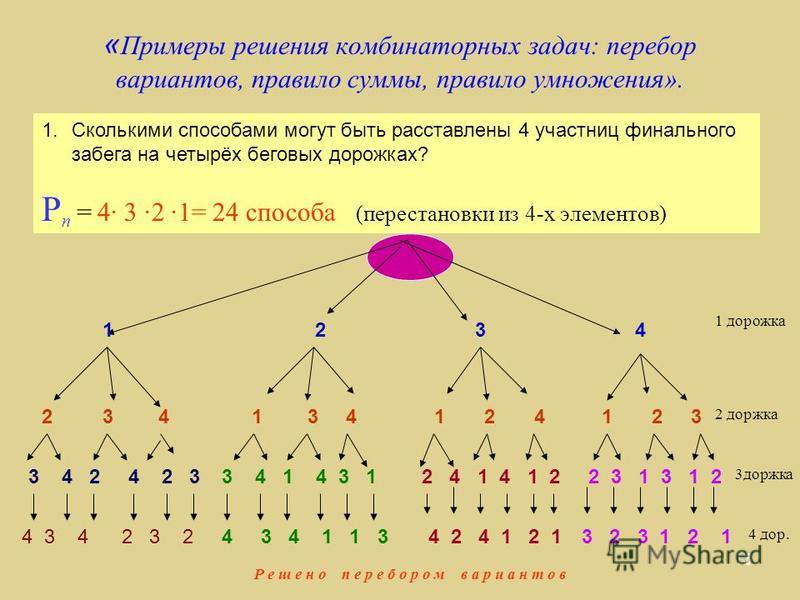

Решение комбинаторных задач: Головоломка на 15

Решение комбинаторных задач: Головоломка на 15

Скачать PDF

Скачать PDF

• Опубликовано: Сентябрь 2005 г.

• Зигмунт Пизло ¹ и
• Чжэн Ли ¹  

Память и познание том 33 , страницы 1069–1084 (2005 г.)Процитировать эту статью

• 4717 доступов

• 20 цитирований

• 1 Альтметрика

• Сведения о показателях

Abstract

Мы представляем серию экспериментов, в которых испытуемые решали хорошо известную комбинаторную задачу, называемую 15-пазл и в вариантах разного размера этого пазла. Испытуемые могут надежно решать эти головоломки, систематически выстраивая путь решения, не выполняя долгих поисков и не используя расстояния между состояниями задачи. Вычислительная сложность лежащих в основе психических механизмов очень низка. Мы сформулировали вычислительную модель лежащих в основе когнитивных процессов на основе наших результатов. В этой модели алгоритм пирамиды применялся к отдельным этапам каждой проблемы. Производительность модели оказалась очень похожей на производительность испытуемых. Частичную поддержку этому исследованию оказало Управление научных исследований ВВС.

Скачайте, чтобы прочитать полный текст статьи

Ссылки

• Bartlett, F.C. (1958). Мышление: экспериментальное и социальное исследование . Лондон: Аллен и Анвин.

  Google ученый

• Боуман, К., и Лю, Б. (1991). Сегментация текстурированных изображений с несколькими разрешениями. Транзакции IEEE по анализу шаблонов и машинному интеллекту , 13 , 99–113.

  Артикул Google ученый

• Коуэн, Н. (2001). Волшебное число 4 в кратковременной памяти: анализ умственной емкости памяти. Науки о поведении и мозге , 24 , 87–185.

  Артикул Google ученый

• Гэри, М. Р., и Джонсон, Д. С. (1979). Компьютеры и неразрешимость: Руководство по теории NP-полноты . Нью-Йорк: Фримен.

  Google ученый

• Грэм С.М., Джоши А. и Пизло З. (2000). Задача коммивояжера: иерархическая модель. Память и познание , 28 , 1191–1204.

  Google ученый

• Гутин Г. и Паннен А. П. (2002). Задача коммивояжера и ее разновидности . Бостон: Клувер.

  Google ученый

• Джолион, Дж. -М., и Розенфельд, А. (1994). Структура пирамиды для раннего зрения: компьютерное зрение с несколькими разрешениями . Дордрехт: Клювер.

  Google ученый

• Корф, Р. Э. (1985). Итеративное углубление в глубину: поиск оптимального допустимого дерева. Искусственный интеллект , 27 , 97–109.

  Артикул Google ученый

• Кропач В.Г., Леонардис А. и Бишоф Х. (1999). Иерархические, адаптивные и надежные методы понимания изображений. Обзоры по математике для промышленности , 9 , 1–47.

  Google ученый

• Лоулер, Э.Л., Ленстра, Дж.К., Ринноой Кан, А.Х.Г., и Шмойс, Д.Б. (1985). Задача коммивояжера: обзор комбинаторной оптимизации . Нью-Йорк: Уайли.

  Google ученый

• МакГрегор, Дж. Н., и Ормерод, Т. (1996). Действия человека в задаче о коммивояжере. Восприятие и психофизика , 58 , 527–539.

  Google ученый

• Майер, Н.Р.Ф. (1930). Рассуждения у людей: по направлению. Журнал сравнительной психологии , 10 , 115–143.

  Артикул Google ученый

• Меткалф, Дж., и Вибе, Д. (1987). Интуиция в решении проблем с пониманием и без понимания. Память и познание , 15 , 238–246.

  Google ученый

• Ньюэлл, А., и Эрнст, Г. (1965). Поиск общности. В WA Kalenich (Ed.), Обработка информации: Труды Конгресса IFIP (Том 1, стр. 17–24). Вашингтон, округ Колумбия: Спартанец.

  Google ученый

• Нильссон, Нью-Джерси (1971). Методы решения задач в области искусственного интеллекта . Нью-Йорк: Макгроу-Хилл.

  Google ученый

• Нильссон, Нью-Джерси (1980). Принципы искусственного интеллекта . Пало-Альто, Калифорния: Морган Кауфманн.

  Google ученый

• О’Хара, К.П., и Пейн, С.Дж. (1998). Влияние затрат на реализацию оператора на планомерность решения проблем и обучения. Когнитивная психология , 35 , 34–70.

  Артикул пабмед Google ученый

• Пизло З. и Ли З. (2003). Алгоритмы пирамиды как модели человеческого познания. В CA Bouman & RL Stevenson (Eds.), Computational Imaging (Материалы SPIE-IS&T Conference on Electronic Imaging , Vol. 5016, стр. 1–12). Беллингем, Вашингтон: SPIE.

  Google ученый

• Пизло, З., и Ли, З. (2004). Графические пирамиды как модели решения задач человеком. В CA Bouman & EL Miller (Eds.), Computational Imaging II (Материалы SPIE-IS&T Conference on Electronic Imaging, Computational Imaging , Vol. 5299, стр. 205–215). Беллингем, Вашингтон: SPIE.

  Google ученый

• Пизло З., Розенфельд А. и Эпельбойм Дж. (1995). Экспоненциальная модель пирамиды обработки размера во времени. Vision Research , 35 , 1089–1107.

  Артикул пабмед Google ученый

• Пизло, З., Салах-Голиска, М., и Розенфельд, А. (1997). Обнаружение кривой на зашумленном изображении. Vision Research , 37 , 1217–1241.

  Артикул пабмед Google ученый

• Ратнер, Д., и Вармут, М.К. (1986). Нахождение кратчайшего решения для n × n расширение головоломки с 15 неразрешимо. Материалы Пятой национальной конференции по искусственному интеллекту (том 1, стр. 168–172). Сан-Матео, Калифорния: Морган Кауфманн.

  Google ученый

• Ричардс, В. , и Кендеринк, Дж. Дж. (1995). Отображение траекторий: новый метод неметрического масштабирования. Восприятие , 24 , 1315–1331.

  Артикул пабмед Google ученый

• Розенфельд, А., и Терстон, М. (1971). Обнаружение краев и кривых для визуального анализа сцены. Транзакции IEEE на компьютерах , C — 20 , 562–569.

  Артикул Google ученый

• Рассел С.Дж. и Норвиг П. (1995). Искусственный интеллект. Современный подход . Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл.

  Google ученый

• Шофилд, PDA (1967). Полное решение восьмерки. В Э. Дейл и Д. Мичи (ред.), Машинный интеллект (том 2, стр. 125–133). Нью-Йорк: Эльзевир.

  Google ученый

• Шепард, Р. Н. (1962). Анализ близости: многомерное шкалирование с неизвестной функцией расстояния. Часть I. Психометрика , 27 , 125–140.

  Артикул Google ученый

• Толман, Э. К., Ричи, Б. Ф., и Калиш, Д. (1946). Исследования в области пространственного обучения: I. Ориентация и короткий путь. Журнал экспериментальной психологии , 36 , 13–24.

  Артикул пабмед Google ученый

• Викерс, Д., Ли, М.Д., Драй, М., и Хьюз, П. (2003). Роль выпуклой оболочки и количества потенциальных пересечений в решении визуально представленных задач коммивояжера. Память и познание , 31 , 1094–1104.

  Google ученый

• Weisstein, EW (2003). CRC Краткая энциклопедия математики . Нью-Йорк: Чепмен и Холл.

  Google ученый

Ссылки на скачивание

Информация об авторе

Авторы и организации

1. Факультет психологических наук, Университет Пердью, 703 Third Street, 47907-2081, West Lafayette, IN

   Zygmunt Pizlo & Zheng Li

Авторы

1. Zygmunt Pizlo

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

2. Zheng Li

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

Автор, ответственный за переписку

Зигмунт Пизло.

Дополнительная информация

Частичная поддержка этого исследования была предоставлена ​​Управлением научных исследований ВВС.

Права и разрешения

Перепечатка и разрешения

Об этой статье

AC Рекурсивное решение комбинаторных задач

В этом разделе мы представляем примеры комбинаторных задач, для которых решения могут быть вычислены рекурсивно. В главе 9 мы возвращаемся к этим проблемам и получаем еще более компактные решения. Наша первая проблема обсуждается во вводной главе.

Пример 3.3.

На плоскости нарисовано семейство из \(n\) прямых, причем (1) все пары пересекаются, а (2) никакие три прямые не пересекаются в одной и той же точке. Пусть \(r(n)\) обозначает число областей, на которые плоскость разбивается этими прямыми. Очевидно, \(r(1)=2\text{,}\) \(r(2)=4\text{,}\) \(r(3)=7\) и \(r(4)= 11\text{.}\) Чтобы определить \(r(n)\) для всех натуральных чисел, достаточно заметить, что \(r(1)=2\text{,}\) и когда \(n> 1\text{,}\) \(r(n)=n+r(n-1)\text{. }\) Эта формула следует из наблюдения, что если мы пометим строки как \(L_1\text{, }\) \(L_2, \dots, L_n\text{,}\) тогда \(n-1\) указывает на линию \(L_n\), где она пересекает другие линии в семейном делении \(L_n\) на \(n\) отрезков, два из которых бесконечны. Каждый из этих сегментов связан с областью, определяемой первыми \(n-1\) линиями, которая теперь была разделена на две, что дает нам \(n\) больше областей, чем было определено \(n-1\) линиями. . Эта ситуация показана на рис. 3.4, где линия, содержащая три точки, — это \(L_4\text{.}\). Другие линии делят ее на четыре сегмента, которые затем делят более крупные области, создавая области \(1\) и \ (5\текст{,}\) \(2\) и \(6\текст{,}\) \(7\) и \(8\текст{,}\) и \(4\) и \( 9\текст{.}\)

Рисунок 3.4. Линии и области на плоскости

Таким образом, используя рекурсивную формулу, мы имеем \(r(5)=5+11=16\text{,}\) \(r(6)=6+16=22\) и \ (r(7)=7+22=29\text{.}\) Даже вручную вычислить \(r(100)\text{.}\) не составит большого труда. Мы могли бы это сделать до обеда.

Пример 3.5.

Шахматная доска \(2\times n\) будет замощена прямоугольниками размером \(2\times1\) и \(1\times2\text{.}\) Найдите рекурсивную формулу для числа \(t(n )\) мозаик. Ясно, что \(t(1)=1\) и \(t(2)=2\text{.}\) Когда \(n>2\text{,}\) рассмотрим прямоугольник, который покрывает квадрат в верхний правый угол. Если он вертикальный, то ему предшествует замощение первых \(n-1\) столбцов. Если он горизонтален, то таким же является и прямоугольник, находящийся непосредственно под ним, а следующий за ним фрагмент представляет собой мозаику из первых \(n-2\) столбцов. Это показывает, что \(t(n)=t(n-1)+t(n-2)\text{.}\) В частности, \(t(3)=1+2=3\text{,} \) \(t(4)=2+3=5\) и \(t(5)= 3+5=8\text{.}\)

Опять же, при необходимости мы могли бы получить \(t(100)\) вручную, а система компьютерной алгебры могла бы получить \(t(1000)\text{.}\)

Пример 3.6.

Назовите троичную строку хорошей , если она никогда не содержит \(2\), за которой сразу следует \(0\текст{;}\), в противном случае назовите ее плохой . Пусть \(g(n)\) будет количеством хороших строк длины \(n\text{.}\) Очевидно, \(g(1)=3\text{,}\), так как все строки длины \( 1\) хороши. Кроме того, \(g(2)=8\), поскольку единственная неверная строка длины \(2\) – это \((2,0)\text{.}\). Теперь рассмотрим значение \(n\) больше чем \(2\текст{.}\)

Разделить набор хороших строк длины \(n\) на три части в соответствии с последним символом. Хорошим строкам, оканчивающимся на \(1\), может предшествовать любая хорошая строка длины \(n-1\text{,}\), поэтому таких строк \(g(n-1)\). То же самое относится и к хорошим строкам, оканчивающимся на \(2\text{.}\). Однако для хороших строк, заканчивающихся на \(0\text{,}\), мы должны быть более осторожными. Мы можем предшествовать \(0\) хорошей строкой длины \(n-1\) при условии, что строка не заканчивается на \(2\text{.}\). \) хорошие строки длины \(n-1\), из них ровно \(g(n-2)\) заканчиваются на \(2\text{.}\). Следовательно, существуют \(g(n- 1)-g(n-2)\) хороших строк длины \(n\), оканчивающихся на \(0\text{. }\). Следовательно, общее количество хороших строк длины \(n\) удовлетворяет рекурсивная формула \(g(n) = 3g(n-1) — g(n-2)\text{.}\) Таким образом, \(g(3) = 3\cdot8 -3= 21\) и \(g (4)= 3\cdot21-8= 55\текст{.}\)

Опять же, \(g(100)\) можно выполнить вручную, а даже скромный компьютер можно уговорить выдать нам \(g(5000)\text{.}\)

Подраздел 3.5.1 Нахождение наибольших общих делителей

В следующей элементарной теореме гораздо больше смысла, чем вы думаете, которая, кажется, просто констатирует факт, известный вам со второго класса.

Теорема 3.7. Теорема деления.

Пусть \(m\) и \(n\) — натуральные числа. Тогда существуют уникальные целые числа \(q\) и \(r\) такие, что

\begin{уравнение*} m = q\cdot n+r\quad\text{and} \quad 0 \le r \lt n. \end{уравнение*}

Мы называем \(q\) частное и \(r\) остаток .

Доказательство.

Мы урегулируем претензию на существование. Часть уникальности — это просто школьная алгебра. Если теорема не выполняется, то пусть \(t\) будет наименьшим положительным целым числом, для которого существуют целые числа \(m\) и \(n\) с \(m+n=t\text{,}\) но не существует целых чисел \(q\) и \(r\) с \(m=qn+r\) и \(0\le r\lt n\text{.}\)

Во-первых, отметим, что \(n\neq 1\text{,}\) ибо если \(n=1\text{,}\), то мы могли бы взять \(q=m\) и \(r=0 \text{.}\) Кроме того, у нас не может быть \(m=1\text{,}\) ибо если \(m=1\text{,}\), то мы можем взять \(q=0\) и \(r=1\text{.}\) Теперь утверждение верно для пары \(m-1\text{,}\) \(n\), поэтому существуют целые числа \(q\) и \(r\ ), так что

\begin{уравнение*} m-1 = q\cdot n+r\quad\text{and} \quad 0 \le r \lt n. \end{уравнение*}

Поскольку \(r\lt n\text{,}\) мы знаем, что \(r+1\le n\text{.}\) Если \(r+1\lt n\text{,}\), то

\begin{уравнение*} m = q\cdot n+(r+1)\quad\text{and} \quad 0 \le r+1 \lt n. \end{уравнение*}

С другой стороны, если \(r+1=n\text{,}\), то

\begin{уравнение*} m = q\cdot n+(r+1)=nq+n=(q+1)n=(q+1)n+0. \end{уравнение*}

Противоречие завершает доказательство.

Напомним, что целое число \(n\) является делителем целого числа \(m\), если существует целое число \(q\) такое, что \(m=qn\text{.}\) (Мы пишем \(n\mid m\) и читать «\(n\) делит \(m\)».) Целое число \(d\) является общим делителем целых чисел \(m\) и \(n\), если \(d\) является делителем обоих \(m\ ) и \(n\text{.}\) наибольший общий делитель чисел \(m\) и \(n\text{,}\), записанный \(\gcd(m,n)\text{,} \) является наибольшим из всех общих делителей \(m\) и \(n\text{.}\)

Вот особенно изящное применение предыдущей основной теоремы:

Теорема 3.8. Евклидов алгоритм.

Пусть \(m,n\) — положительные целые числа с \(m\gt n\), а \(q\) и \(r\) — уникальные целые числа, для которых

\begin{уравнение*} m = q\cdot n+r\quad\text{and} \quad 0 \le r \lt n. \end{уравнение*}

Если \(r>0\text{,}\), то \(\gcd(m,n)=\gcd(n,r)\text{.}\) Если \(r=0\text{,} \) тогда \(n\) делит \(m\text{,}\) и \(\gcd(m,n) = n\text{. }\)

Доказательство.

Рассмотрим выражение \(m=q\cdot n+r\text{,}\), которое эквивалентно \(m-q\cdot n = r\text{.}\) Если число \(d\) делителем \(m\) и \(n\text{,}\), то \(d\) также должен делить \(r\text{.}\) Аналогично, если \(d\) является делителем \(n\) и \(r\text{,}\), то \(d\) также должно делить \(m\text{.}\)

Вот фрагмент кода, который вычисляет наибольший общий делитель \(m\) и \(n\), когда \(m\) и \(n\) являются положительными целыми числами с \(m\ge n\text{. }\) Мы используем знакомое обозначение m%n для обозначения остатка \(r\) в выражении \(m=q\cdot n+r\text{,}\) с \(0\le r \ л\текст{.}\)

Не стесняйтесь изменять значения 12 и 5 выше в ячейке SageMath в HTML-версии текста, чтобы вычислить наибольший общий делитель некоторых других целых чисел. Просто помните, что код предполагает \(m\geq n\), когда вы это делаете!

Недостатком этого подхода является несколько расточительное использование памяти из-за рекурсивных вызовов функций. Нетрудно разработать код для вычисления наибольшего общего делителя \(m\) и \(n\), используя только цикл, т. е. без рекурсивных вызовов. С минимальной дополнительной работой такой код также может быть разработан для решения следующей задачи диофантова уравнения:

Теорема 3.9.

Пусть \(m\text{,}\) \(n\text{,}\) и \(c\) — натуральные числа. Тогда существуют целые числа \(a\) и \(b\text{,}\), не обязательно неотрицательные, решающие линейное диофантово уравнение \(am+bn=c\) тогда и только тогда, когда \(c\) равно кратное наибольшему общему делителю \(m\) и \(n\text{.}\)

Давайте посмотрим, как можно использовать алгоритм Евклида для записи \(\gcd(m,n)\) в форме \(am+bn\) с \(a,b\in\ints\) на следующем примере. .

Пример 3.10.

Найдите наибольший общий делитель \(d\) чисел \(3920\) и \(252\) и найдите целые числа \(a\) и \(b\) такие, что \(d=3920a+252b\text{. }\)

Решение.

Решая задачу, мы демонстрируем, как выполнить алгоритм Евклида, чтобы мы могли найти \(a\) и \(b\), работая в обратном порядке. Во-первых, отметим, что

\begin{уравнение*} 3920 = 15\cdot 252 + 140. \end{equation*}

Теперь алгоритм Евклида говорит нам, что \(\gcd(3920,252)=\gcd(252,140)\text{,}\) поэтому мы пишем

\begin{equation*} 252 = 1\cdot 140 + 112. \end{equation*}

Продолжая, мы имеем \(140= 1\cdot 112 + 28\) и \(112 = 4\cdot 28+0\text{,}\), поэтому \(d=28\text {.}\)

Чтобы найти \(a\) и \(b\text{,}\), мы теперь действуем в обратном порядке через уравнения, которые мы нашли ранее, «решая» их для остаточного члена, а затем подставляя. Начнем с

\begin{уравнение*} 28 = 140-1\cdot 112. \end{equation*}

Но мы знаем, что \(112=252-1\cdot 140\text{,}\) поэтому

\begin{equation*} 28=140-1(252-1\cdot 140) = 2\cdot 140 — 1\cdot 252. \end{equation*}

Наконец, \(140 = 3920-15\cdot 252\text{,}\), так что теперь у нас есть

\begin{equation*} 28= 2(3920-15\cточка 252) — 1\cточка 252 = 2\cточка 3920-31\cточка 252. \end{equation*}

Следовательно, \(a=2\) и \(b=-31\text{. }\)

Подраздел 3.5.2 Сортировка

Одной из самых распространенных и основных вычислительных задач является сортировка. Дана последовательность \(a_1,a_2,\dots,a_n\) из \(n\) различных целых чисел, переставить их в порядке возрастания. Мы опишем здесь простую рекурсивную стратегию для выполнения этой задачи. Эта стратегия известна как Сортировка слиянием и является одним из нескольких оптимальных алгоритмов сортировки. Вводные курсы информатики рассматривают эту тему более подробно. В нашем курсе нам просто нужна хорошая стратегия, и сортировка слиянием прекрасно подходит для наших целей.

Чтобы представить сортировку слиянием, необходимо сначала разработать стратегию решения частного случая задачи сортировки. Предположим, что у нас есть \(s+t\) различных целых чисел

\begin{уравнение*} \{u_0,u_1,\dots,u_{s-1},v_0,v_1,\dots,v_{t-1}\} \end{уравнение*}

в виде двух списков с \(u_0\lt u_1\lt \dots\lt u_{s-1}\) и \(v_0\lt v_1\lt \dots\lt v_{t-1}\text{. } \) Как нам объединить эти две последовательности в одну возрастающую последовательность длины \(s+t\text{.}\) Представьте себе две последовательности, расположенные на двух горизонтальных линиях, одна непосредственно под другой. Тогда пусть \(u\) будет наименьшим целым числом в первой последовательности, а \(v\) — наименьшим целым числом во второй. На данный момент это означает, что \(u=u_0\) и \(v=v_0\text{,}\) но целые числа будут удалены из двух последовательностей по мере выполнения процесса. В любом случае значение \(u\) и \(v\) будет сохранено. Кроме того, установите \(i=0\text{.}\) Затем возьмите \(a_i\) как минимум \(u\) и \(v\) и удалите \(a_i\) из последовательности, в которой он имеет место. Затем увеличьте \(i\) на \(1\) и повторите. Вот фрагмент кода для выполнения операции слияния, где \(u_p\) теперь записывается как u[p] и \(v_q\) теперь записывается как v[q] .

Теперь, когда у нас есть хорошая стратегия слияния, легко разработать рекурсивную стратегию сортировки. Дана последовательность \(a_1,a_2,\dots,a_n\) из \(n\) различных целых чисел, мы устанавливаем \(s=\lceil n/2\rceil\) и \(t=\lfloor n/2\ rfloor\text{.}\) Тогда пусть \(u_i=a_i\) для \(i=1,2,\dots,s\) и \(v_j=a_{s+j}\text{,}\) for \(j=1,2,\dots,t\text{.}\) Отсортируйте две подпоследовательности, а затем объедините их. Для конкретного примера, учитывая последовательность \((2,8,5,9,3,7,4,1,6)\text{,}\) разбиваем на \((2,8,5,9,3)\) и \((7,4,1,6)\text {.}\) Эти подпоследовательности сортируются (рекурсивным вызовом) в \((2,3,5,8,9)\) и \((1,4,6,7)\текст{,}\) а затем эти две отсортированные последовательности объединяются.

Для времени выполнения, если \(S(n)\) — это количество операций, которое требуется для сортировки последовательности из \(n\) различных целых чисел, то \(S(2n)\le2 S(n) + 2n\ text{,}\), так как для слияния двух отсортированных последовательностей длины \(n\text{.}\) явно требуется \(2n\) шагов. Это приводит к ограничению \(S(n) \lt C n\log n\) для некоторой положительной константы \(C\text{,}\) и на курсах информатики вы узнаете (здесь это упражнение), что это оптимально.