Комплексные числа онлайн калькулятор в тригонометрической форме: Комплексные числа онлайн

Бесплатные онлайн научные калькуляторы

Высокофункциональные научные онлайн-калькуляторы, которые могут выполнять базовые и сложные операции как с действительными, так и с комплексными числами. В калькуляторы встроено множество полезных математических функций, а также ряд полезных физических констант. Вводите комплексные числа в полярной форме, указывая их модуль и аргумент, или в декартовой форме (обратите внимание на их построение, для этого есть специальные клавиши). Вы можете выполнять операции с комплексными числами так же, как если бы это были действительные числа, поскольку их можно использовать везде, в сложениях, вычитаниях, умножениях, делениях, степенях, корнях, логарифмах, тригонометрических, гиперболических и обратных функциях. Найдите модуль и аргумент комплексного числа и измените знак действительного или комплексного числа. Для измерения углов и дуг можно выбирать между радианами, градусами и градианами. Вычислять и выполнять операции между тригонометрическими функциями синус, косинус, тангенс, котангенс, секанс, косеканс, а также гиперболическими функциями, гиперболическим синусом, гиперболическим косинусом, гиперболическим тангенсом, гиперболическим котангенсом, гиперболическим секансом, гиперболическим косекансом и их инверсиями.

Выбрав радианы в качестве единицы измерения, все вышеперечисленные функции также принимают комплексные числа в качестве аргументов. Найти вещественные или комплексные корни квадратного уравнения с вещественными коэффициентами. Добавить или удалить НДС из заданной цены. Рассчитать сумму НДС, включенную в цену брутто, а также сумму, которую нужно добавить к цене нетто. Вычислять проценты, добавлять наценки и вычитать скидки с помощью клавиш +, -, x, ÷. Выполнять основные операции, такие как сложение, вычитание, умножение, деление и факториал. Вы можете найти наибольший общий делитель, наименьшее общее кратное двух или более целых чисел и остаток при евклидовом делении двух целых чисел. Оценивать числовые выражения со степенями, корнями и круглыми скобками. Найти обратную величину действительного или комплексного числа, возвести в квадрат действительное или комплексное число, найти квадратный корень из действительного или комплексного числа, вычислить n-й корень из действительного или комплексного числа, найти мощность, в которой основание и экспонента могут быть комплексными числами, вычислить мощность с основанием e и экспонентой действительного или комплексного числа. Вычислите натуральный логарифм действительного или комплексного числа. Также вычислите логарифм действительного или комплексного числа на основе действительного или комплексного числа. Создать статистическую выборку и сохранить ее. Затем вы можете отсортировать ее, найти размер, минимальное и максимальное значения, сумму элементов, сумму квадратов, произведение, медиану, среднее арифметическое, стандартное отклонение, дисперсию, среднее абсолютное отклонение и моду. Встроенный генератор случайных чисел позволяет создавать выборки случайных чисел нужного диапазона и размера. Калькулятор предоставляет широкий набор встроенных физических констант, которые могут быть использованы в ваших расчетах. Для каждой константы указаны значение и единица измерения. Доступны универсальные константы, электромагнитные константы, атомные и ядерные константы, физико-химические константы, принятые значения и натуральные единицы.

Calculator

Κομπιουτεράκι

Calculator

Αριθμομηχανή

Κομπιουτεράκι

Calculator

Online Calculator

Online Scientific Calculator

Scientific Calculator

Комплексные числа онлайн.

Портал тоэ

Начнем с любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :

Для комплексного числа легко вывести свою формулу сокращенного умножения:

Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:

Просто до безобразия.

Пример 10

Дано комплексное число , найти.

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра:

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа ,,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Извлечение корней из комплексных чисел.

Квадратное уравнение с комплексными корнями

Рассмотрим пример:

Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:

Действительно ли найденные корни являются решением уравнения ? Выполним проверку:

Что и требовалось проверить.

Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .

Такие корни также называют сопряженными комплексными корнями .

Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.

Начнем с любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :

Для комплексного числа легко вывести свою формулу сокращенного умножения:

Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:

Просто до безобразия.

Пример 10

Дано комплексное число , найти.

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра:

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа ,,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями

Рассмотрим пример:

Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:

Действительно ли найденные корни являются решением уравнения ? Выполним проверку:

Что и требовалось проверить.

Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .

Такие корни также называют сопряженными комплексными корнями .

Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.

Пример 13

Решить квадратное уравнение

Вычислим дискриминант:

Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!

По известным школьным формулам получаем два корня: – сопряженные комплексные корни

Таким образом, уравнение имеет два сопряженных комплексных корня:,

Теперь вы сможете решить любое квадратное уравнение!

И вообще, любое уравнение с многочленом «энной» степени имеет ровнокорней, часть из которых может быть комплексными. {i1{,}25\pi}}\]

В калькуляторе возможно использование констант, математических функций, дополнительных операций и более сложных выражений, ознакомиться с этими возможностями вы можете на странице общих правил использования калькуляторов на этом сайте.

Сайт находится в разработке, некоторые страницы могут быть недоступны.

Новости

07.07.2016
Добавлен калькулятор для решения систем нелинейных алгебраических уравнений: .

30.06.2016
На сайте реализован адаптивный дизайн, страницы адекватно отображаются как на больших мониторах, так и на мобильных устройствах.

Спонсор

РГРОнлайн.ru – мгновенное решение работ по электротехнике онлайн.

Калькулятор тригонометрических функций — ezcalc.me

---

Этот онлайн-калькулятор тригонометрических функций вычисляет тригонометрические функции комплексного числа (переменной). При вводе мнимой части комплексного числа в соответствующее поле калькулятора следите за тем, чтобы символ « i », обозначающий мнимую единицу, стоял рядом с числовой частью без пробела.

---

---

Этот онлайн-калькулятор вычисляет следующие тригонометрические функции комплексной переменной \(z=x+yi\), где \(x\) и \(y\) — действительные числа. 9{ -iz }) } .$$

• csc() – функция косеканса

Функция косеканса определяется следующим образом:

$$ csc(z)=\frac { 1 }{ sin(z ) }.$$

• sec() – функция секанса

Функция секанса определяется следующим образом:

$$ sec(z)=\frac { 1 }{cos(z) }.$ $

• cot() – функция котангенса

Функция котангенса определяется следующим образом:

$$ cot(z)=\frac { 1 }{ tan(z) }.$$

Обратные тригонометрические функции — это обратные функции тригонометрических функций. В частности, они являются обратными функциями синуса, косинуса, тангенса, котангенса, косеканса и секанса. Эти функции могут быть выражены с помощью комплексных логарифмов. Это естественным образом расширяет их домены до сложной плоскости. Следующие тождества для главных значений функций выполняются везде, где они определены, даже на их ветвях. 2} – iz \right ),$$ 92}} – \frac{i}{z} \right).$$

Связанные калькуляторы

Ознакомьтесь с другими нашими математическими калькуляторами, такими как калькулятор комплексных чисел или калькулятор гиперболических функций.

---

Комплексные числа — Уроки Wyzant

Написано преподавателем Колином Д.

Как представить сложные числа графически: комплексная плоскость

• Комплексное число x + yi соответствует точке с координатами (x, y)
• Ось X — это реальная ось
• Ось Y является воображаемой осью
• Вещественные числа связаны с точками на оси x
  Например: x = x + 0i <- -=””> (x,0)
  
• Мнимые числа связаны с точками на оси Y
  Например: yi = 0 + yi <- -=””> (0,y)
  

Как найти точку (P) на комплексной плоскости

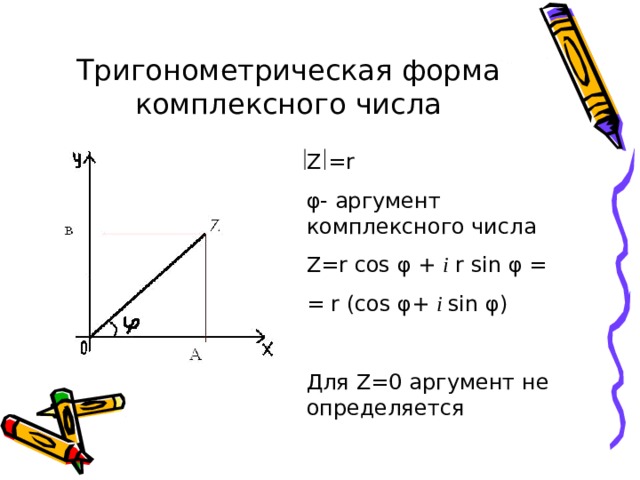
Тригонометрическая (полярная) форма

• Тригонометрическая форма «x + yi» равна r(cos θ + i sin θ)
  -Это может быть получено из более ранних эквивалентностей. Поскольку, когда у нас было
  x + yi, мы нашли x = r cos θ и
  y = r sin θ, мы можем заменить x и y на r cos θ
  и r sin θ соответственно:
  x + yi = (r cos θ) + (r sin θ)i
  — Если вынести «r» и умножить на «i», получится:
  r(cos θ + i sin θ)
• r = модуль или абсолютное значение
  r = (x ² + y ² ) ^1/2
  r = должен быть НЕотрицательным
• θ = Аргумент комплексного числа
  — Любой угол, котерминальный θ, также является аргументом для того же комплексного числа
  tan θ = y/x -> θ = arc tan (y/x)

Прямоугольная (стандартная) форма

• Прямоугольная форма «x + yi»

Как изменить прямоугольную форму на тригонометрическую

Как изменить тригонометрическую форму на прямоугольную

• Если B = 3√3 (cos 330° + i sin 330°)
  r = 3√3
  cos 330° = √(3/2)
  sin 330° = -1/2
• Тогда 3√3 (√(3/2) + -1/2 i) -> 9/2 – i(3√3)/2

Как выражать комплексные числа в

Правильная Тригонометрическая форма

• Всегда помните несколько важных правил правильной тригонометрической формы:
  — Модуль (r) всегда должен быть неотрицательным
  Это абсолютное значение диагонали от самой точки до начала координат.
  -Выражение в скобках должно иметь вид: cos θ + i sin θ.
  Убедитесь, что каждое слагаемое записано как положительное число.
• Пример: z = 2(cos 30° – i sin 30°)
  — Сначала представим z в прямоугольной форме:
  2(√(3/2) – 1/2 i) -> √3 – 1i
  -Таким образом , на графике это будет состоять из перемещения на √3 единицы вправо и на 1 единицу вниз, в результате чего появится точка в квадранте IV
  .
  г = √((√3) ² + 1 ² ) -> √4 -> √2

  Используя тангенс θ = y/x, получаем:

  тангенс θ = 1/√3 -> арктангенс 1/√3 = -30° -> следовательно, θ = -30°
  -Наконец, замена:

  z = 2[cos (-30°) + i sin (-30°)]

Умножение и деление в тригонометрической форме

• ПРИМЕЧАНИЕ. В то время как прямоугольная форма облегчает понимание сложения/вычитания комплексных чисел, тригонометрическая форма является лучшим методом
  представления сложных чисел для целей умножения/деления.
• Если вы собираетесь умножить два комплексных числа, z1 = r1 (cos θ1 + i sin θ1) и z2 = r2 (cos θ2 + i sin θ2), произведение
  можно вывести, выполнив несколько простых шагов:
  – Умножьте модули , чтобы найти модуль произведения: r1 умножить на r2
  – Добавьте аргументы , чтобы найти аргумент суммы : cos (θ1 + θ2)
  + i sin (θ1 + θ2)
  -Умножить модуль произведения на аргумент суммы: r1r2 [cos (θ1 + θ2) +
  i sin (θ1 + θ2)]
• Чтобы разделить два комплексных числа:
  – Разделите модули , чтобы получить частное модуля : r1/r2
  – Вычтите аргументы , чтобы получить аргумент разности : cos (θ1 – θ2)
  + i sin (θ1 – θ2)
  -Умножить модуль частного на аргумент разности: r1/r2 [cos (θ1 – θ2)
  + i sin ( θ1 – θ2)]
• Пример:
  z1 = √(3/2 + (1/2)i
  z2 = -2 – 2i
  Найти z1 * z2:
  (1) Выразить каждое в тригонометрической форме
  z1 = 2(cos 30° + i sin 30°)
  z2 = 2√2(cos 225° + i sin 225°)
  (2) Модули умножения:
  2 * 2√2 = 4√2
  (3) Добавить аргументы:
  cos(30° + 225°) + i (sin 30° + 225°)
  (4) Треугольная форма = 4√2 [cos(30° + 225°) + i (sin 30° + 225°)]
  4√2[cos (255°) + i (sin 255°)]
  найдите в прямоугольной форме, оцените cos 255° и sin 255° и упростите:
  4√2 [cos (255°) + i (sin 255°)]
  С помощью формулы суммы и разности:
  cos (a+b) = cos a cos b – sin a sin b
  sin (a+b) = sin a cos b + sin b cos a
  С калькулятором:
  cos 255° = -0,2588
  sin 255° = -0,9659
  -1,464 – 5. 464i

Теорема ДеМойвера

• Повторяя описанную выше процедуру умножения, можно вывести теорему Де Муавра, позволяющую вычислять степени
  и корни комплексных чисел.
• Чтобы проиллюстрировать это, если бы мы продолжали умножать z = r (cos θ + i sin θ) само по себе, мы получили бы: ³ = r ³ (cos 3θ + i sin 3θ)
  z ⁴ = r ⁴ (cos 4θ + i sin 4θ)
• Для отрицательных показателей он разворачивается по следующему шаблону:
  z ^-1 = r ^-1 [(cos(-θ)) + i sin (-θ)]
  z ^-2 = r ^-2 [(cos(-2θ)) + i грех (-2θ)]
• Формально сформулированная теорема Де Муавра, как правило, гласит:
• ПРИМЕР:
  (1 + √3i) ⁵
  -В тригонометрической форме:
  2(cos 60° + i sin 60°)
  -Применить теорему Де Муавра:
  2 ⁵ [cos 5(60°) + i sin 5(60°)]
  32 (cos 300° + i sin 300°)
  32 (1/2 + i(-√3)/2)
  16 — (16√3)i

Корни комплексных чисел

• Некоторые основы визуализации корней комплексных чисел:
  — n корней комплексного числа лежат на окружности, образованной внутри комплексной плоскости с центром в начале координат и радиусом = (r) ^(1/n)
  — n корней на указанном круге расположены через равные промежутки, начиная с K = 0 и продолжая до k = n-1, прогрессируя с аргументами (т.

  No related posts.