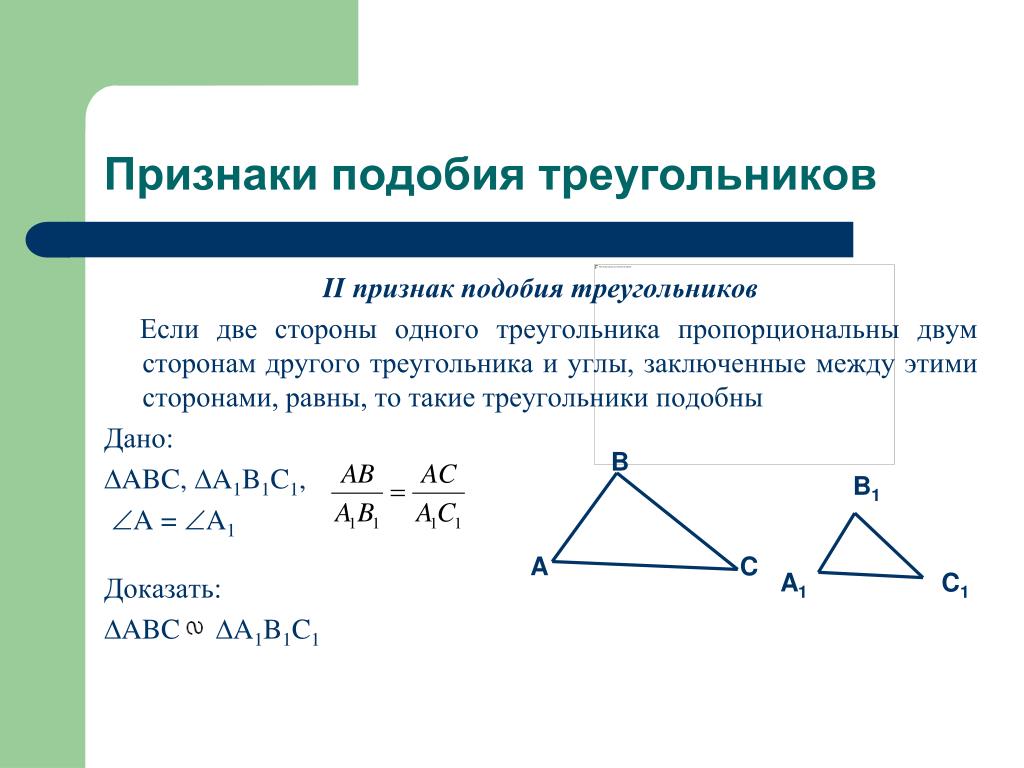
Шпаргалка: признаки подобия треугольников, 8 класс. 3 признака: по двум углам, по двум сторонам и углу, по трем сторонам
31 октября, 2022
1 мин
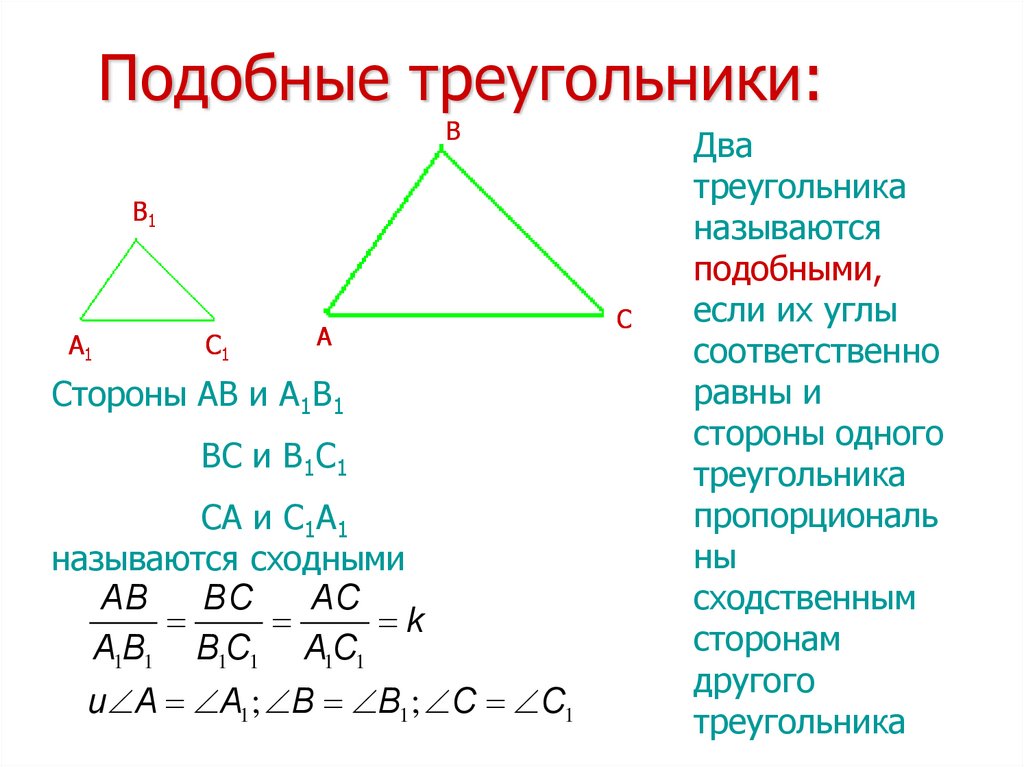
Треугольники называются подобными, если их стороны пропорциональны.
Запись подобия выглядит так:
∆ABC ~ ∆A1B1C1
I признак. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
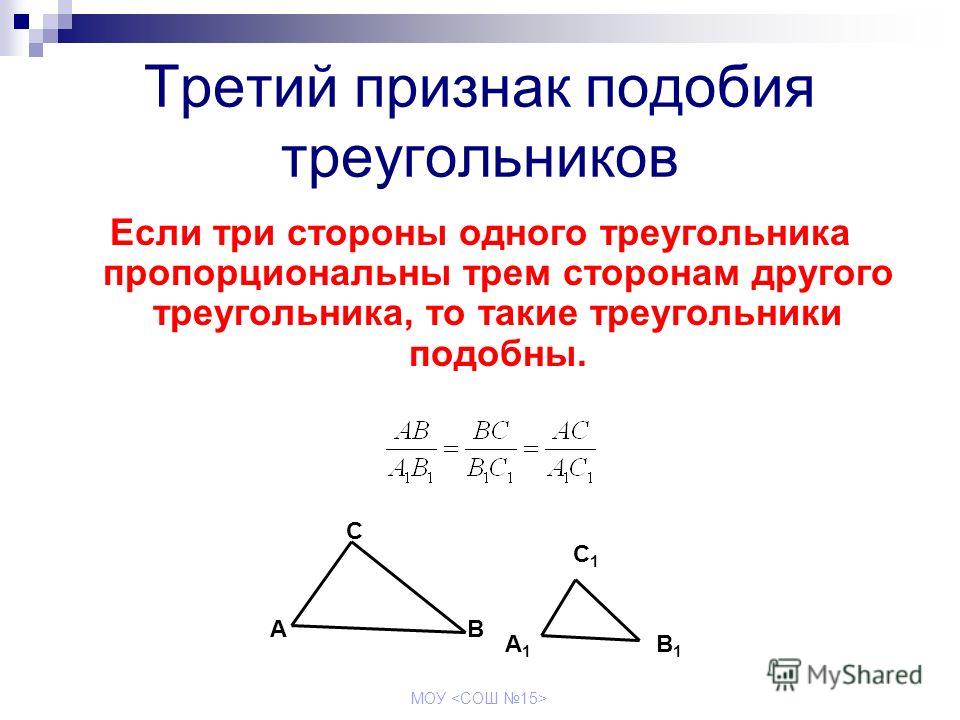
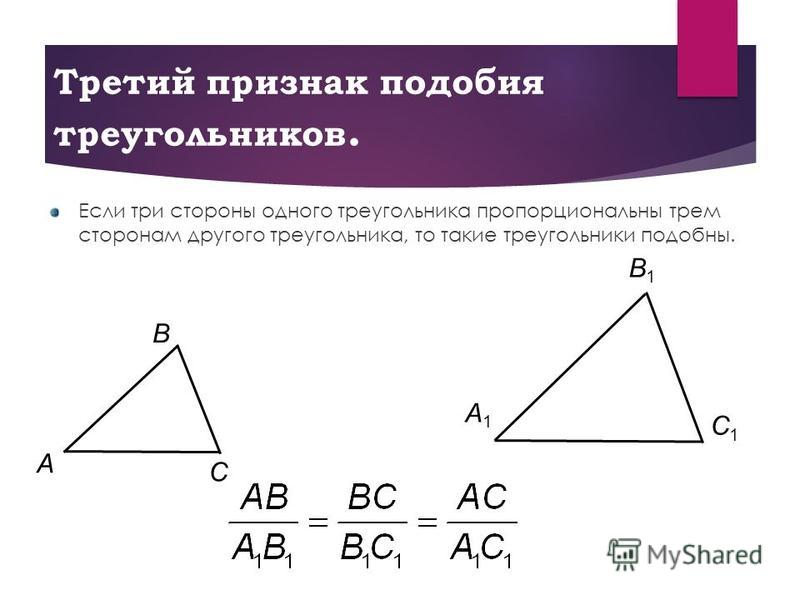
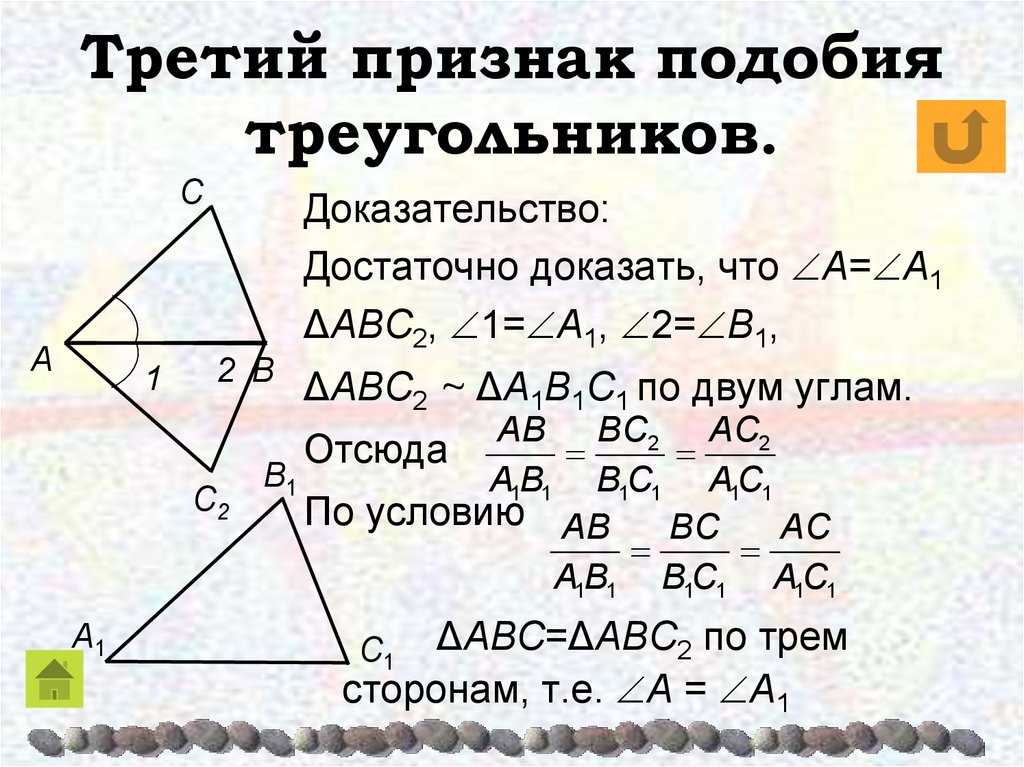
III признак. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно.
44 подписчиков
+ Подписаться
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Азотфиксаторы
Нитраты повсюду 😱 Особенно в помидорах, так по телеку сказали — мы все умрём! Или нет? 🍅 Так,…
Редакция Без Сменки
01 июля, 2022
1 мин
Хим 🧪
Химические свойства толуола
Толуол — брат и напарник бензола из семейства ароматических углеводородов 👌
Толуол —. ..
..
Редакция Без Сменки
06 июня, 2022
1 мин
Англ 🇬🇧
Как подготовиться к аудированию?
Так-так, признавайся, не любишь аудирование? Понимаю…🧐 Особенно когда на пробниках в школе…
06 июня, 2022
1 мин
Англ 🇬🇧
Чтение
— Когда откроешь задание 10, то увидишь там 7 отрывков и 8 заголовков, которые нужно соотнести друг…
Редакция Без Сменки
03 мая, 2022
1 мин
Хим 🧪
Химические термины
Хей, ловите новую подборку химических терминов, которые точно вам пригодятся при подготовке к ЕГЭ.
Редакция Без Сменки
29 июня, 2022
1 мин
Физ 🔬
КОЛИЧЕСТВО ТЕПЛОТЫ
👉 Внутренняя энергия тела может изменяться за счёт работы внешних сил. Для характеристики изменения…
Геометрия 7-9 класс. Признаки подобия треугольников — math200.ru
Skip to contentГеометрия 7-9 класс. Признаки подобия треугольниковadmin2022-12-23T09:29:10+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Признаки подобия треугольников
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
- Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны, то треугольники подобны.

- Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Признаки подобия прямоугольных треугольников
- Они имеют по равному острому углу.
- Катеты одного треугольника пропорциональны катетам другого треугольника.
- Гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.
Площади подобных треугольников: отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение сторон подобных треугольников равно отношению любых соответствующих линейных размеров.
| Задача 1. По данным на рисунке найдите SK, если \(ST\parallel KL.\) Ответ ОТВЕТ: 2,5. | |
| Задача 2. По данным на рисунке найдите ВЕ, если \(DE\parallel AC.\) Ответ ОТВЕТ: 13. | |
Задача 3. По данным на рисунке найдите СВ – AF. По данным на рисунке найдите СВ – AF.Ответ ОТВЕТ: 7. | |
| Задача 4. По данным на рисунке найдите СВ – МЕ. Ответ ОТВЕТ: 24. | |
| Задача 5. По данным на рисунке найдите площадь треугольника RKO. Ответ ОТВЕТ: 216. | |
| Задача 6. По данным на рисунке найдите TF, если STFE – трапеция. Ответ ОТВЕТ: 20. | |
| Задача 7. По данным на рисунке найдите периметр треугольника EFM, если MPKN параллелограмм. Ответ ОТВЕТ: 44. | |
| Задача 8. По данным на рисунке найдите CF, если ABCD параллелограмм и АВ = 14. Ответ ОТВЕТ: 10. | |
| Задача 9. По данным на рисунке найдите RE, если RT = 20. Ответ ОТВЕТ: 5. | |
| Задача 10. По данным на рисунке найдите AD, если ВС = 24. Ответ ОТВЕТ: 4. | |
| Задача 11. По данным на рисунке найдите ОС, если ABCD трапеция и АС = 14. Ответ ОТВЕТ: 10. | |
| Задача 12. По данным на рисунке найдите BO, если ABCD трапеция и BD = 21. Ответ ОТВЕТ: 6,3. | |
| Задача 13. По данным на рисунке найдите TL, если MNPT параллелограмм, NK = MT, NK : MN = 1 : 4 и ML = 20. Ответ ОТВЕТ: 16. | |
| Задача 14. По данным на рисунке найдите МN, если RKLN параллелограмм и KQ = 15. Ответ ОТВЕТ: 8. | |
| Задача 15. В остроугольном треугольнике АВС высоты АК и BH пересекаются в точке Ответ ОТВЕТ: 4. | |
| Задача 16. В остроугольном треугольнике АВС высоты СК и BH пересекаются в точке О. Найдите ОК, если СО = 5 и \(BO \cdot OH = 12.\) Ответ ОТВЕТ: 2,4. | |
Задача 17. В трапеции ABCD с основаниями AD и BC = 4 известно, что АС = 8 и \(\angle \,BAC = \angle \,ADC.\) Найдите длину основания AD. Ответ ОТВЕТ: 16. | |
| Задача 18. В трапеции ABCD с основаниями AD = 25 и BC = 4 известно, что \(\angle \,ABD = \angle \,BCD.\) Найдите длину диагонали ВD. Ответ ОТВЕТ: 10. | |
| Задача 19. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке О, \({P_{\Delta \,AOD}}:{P_{\Delta \,BOC}} = 5:2.\) Найдите АО, если АС = 14. Ответ ОТВЕТ: 10. | |
| Задача 20. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке О, \({S_{\Delta \,AOD}}:{S_{\Delta \,BOC}} = 9:1.\) Найдите АО, если АС = 16. Ответ ОТВЕТ: 12. | |
Задача 21. По данным на рисунке найдите сторону 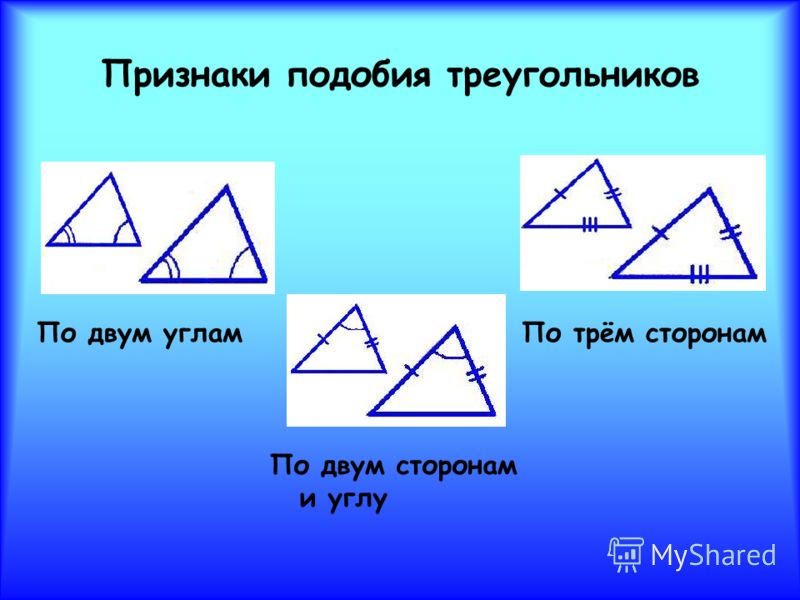 \) \)Ответ ОТВЕТ: \(12\sqrt 3 .\) | |
| Задача 22. По данным на рисунке найдите периметр треугольника NML. Ответ ОТВЕТ: 34. | |
| Задача 23. В остроугольном треугольнике АВС проведены высоты АК и СМ. Докажите подобие треугольников АВС и МВК. | |
| Задача 24. В остроугольном треугольнике АВС проведены высоты АК и СМ. Найдите КС, если МВ = 3, ВК = 4 и АМ = 9. Ответ ОТВЕТ: 5. | |
Задача 25. В трапеции АВСD с основаниями AD и ВС = 5 диагонали пересекаются в точке О. Через точку О проведена прямая параллельно основаниям, пересекающая боковые стороны трапеции в точках Е и F. Найдите длину основания AD, если EF = 8. Найдите длину основания AD, если EF = 8.Ответ ОТВЕТ: 20. | |
| Задача 26. В трапеции АВСD с основаниями AD = 20 и ВС = 5 диагонали пересекаются в точке О. Через точку О проведена прямая параллельно основаниям, пересекающая боковые стороны трапеции в точках Е и F. Найдите длину отрезка EF. Ответ ОТВЕТ: 8. | |
| Задача 27. В треугольнике АВС точки N, M и D принадлежат сторонам АВ, ВС и AС соответственно, причем \(MN\parallel AC\), а прямые MN и BD пересекаются в точке К. Известно, что площадь треугольника NBK равна 18, площадь трапеции ANKD равна 14 и КМ = 9. Найдите длину отрезка DC. Ответ ОТВЕТ: 12. | |
Задача 28.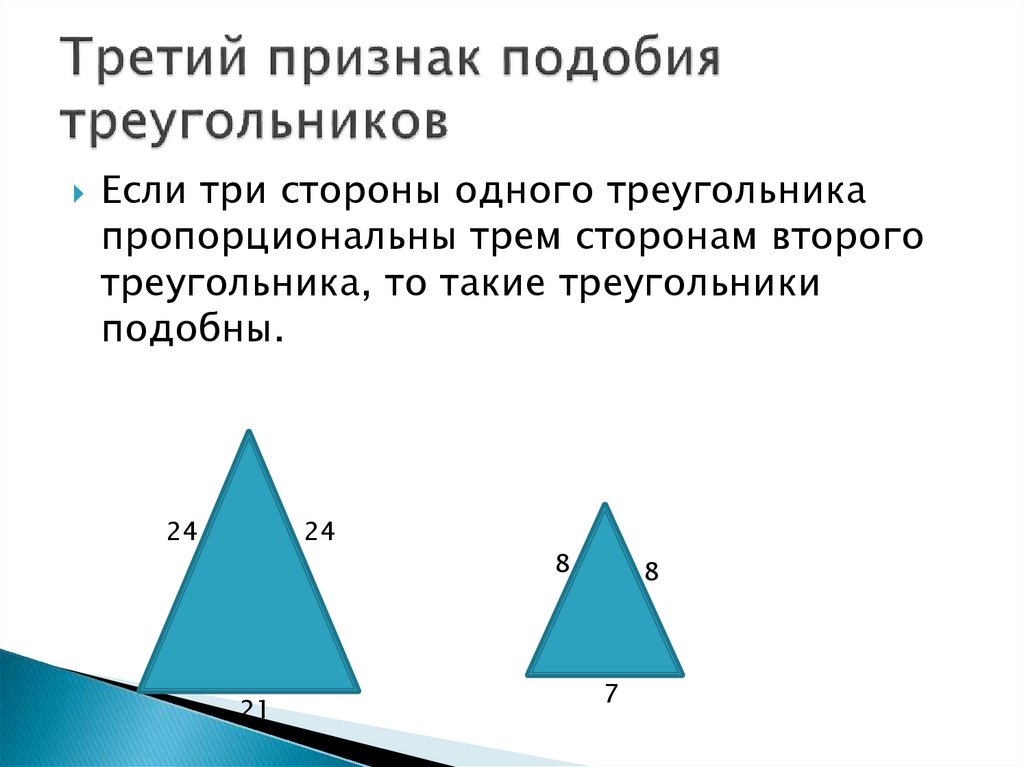 В прямоугольном треугольнике АВС проведена высота СК к гипотенузе АВ. При этом площади треугольников АКС и ВСК равны соответственно 4 и 16. Найдите длину гипотенузы АВ. В прямоугольном треугольнике АВС проведена высота СК к гипотенузе АВ. При этом площади треугольников АКС и ВСК равны соответственно 4 и 16. Найдите длину гипотенузы АВ.Ответ ОТВЕТ: 10. | |
| Задача 29. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Площади треугольников ВОС и AOD равны соответственно 2 и 50. Найдите площадь трапеции. Ответ ОТВЕТ: 72. | |
| Задача 30. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Площади треугольников ВОС и СOD равны соответственно 4 и 16. Найдите площадь трапеции. Ответ ОТВЕТ: 100. | |
Задача 31. В параллелограмме ABCD точка М принадлежит стороне ВС. \circ }.\) Найдите площадь параллелограмма. \circ }.\) Найдите площадь параллелограмма.Ответ ОТВЕТ: 144. | |
Реклама
Поддержать нас
Калькулятор площади треугольника с 3 сторонами
Создано Стивеном Вудингом
Отзыв Александры Зайонц, доктор медицины
Последнее обновление: 02 февраля 2023 г. Как пользоваться этим калькулятором площади трехстороннего треугольника
Калькулятор площади трехстороннего треугольника здесь, чтобы помочь, если вам нужно вычислить площадь треугольника, но известны только длины трех сторон . Хорошим примером является попытка вычислить площадь комнаты треугольной формы — с помощью этого калькулятора вы узнаете, как найти квадратные метры треугольной комнаты.
Читайте дальше, чтобы узнать о:
- Вычисление площади треугольника с 3 сторонами.
- Формула Герона.

- Как найти третью сторону треугольника без углов.
Расчет площади треугольника с 3 сторонами – формула Герона
Вычислить площадь треугольника по длинам трех сторон на удивление сложно. Если мы знаем высоту , то площадь находится простым умножением высоты на длину основания и делением на два. Мы построили калькулятор площади треугольника — 3 стороны и без высоты.
Область можно найти с помощью формулы Герона , впервые опубликованной Героном (или Героем) Александрийским примерно в 60 году нашей эры. Считается, что Архимед знал формулу на 200 лет раньше, но, насколько нам известно, в то время она так и не была опубликована.
Формулу Герона можно выразить разными способами. Самая длинная форма состоит в том, чтобы взять три стороны (aaa, bbb и ccc), суммировать их вместе, затем умножить еще на три суммы, но каждый раз вычитается одна из сторон. Затем из берется квадратный корень из , и мы делим на четыре, чтобы получить площадь ААА.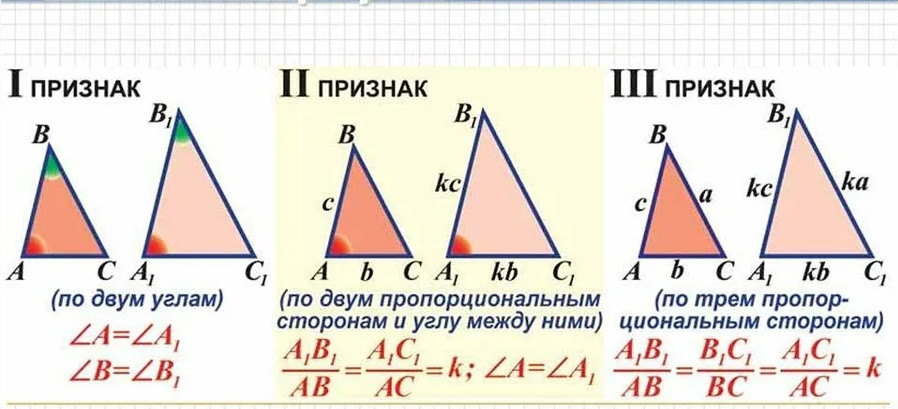 Вот это математически:
Вот это математически:
A=14[(a+b+c)(-a+b+c)(a-b+c)(a+b-c)]\footnotesize \начать{выравнивать*} A = \frac{1}{4}\sqrt{}[(a + b + c)(-a + b + c)\\[0,5em] (а-б+в)(а+б-в)] \end{выравнивание*}A=41 92}A=414a2b2−(a2+b2−c2)2
Все довольно сложно. Так почему бы просто не использовать наш калькулятор площади трехстороннего треугольника, чтобы упростить жизнь.
Как пользоваться калькулятором площади трехстороннего треугольника
Пользоваться калькулятором очень просто. Просто введите три длины сторон, и калькулятор мгновенно покажет результат площади.
Вы даже можете попробовать использовать калькулятор, чтобы найти недостающую длину стороны, если вы знаете площадь и длины двух других сторон:
- Введите значение для области треугольника.
- Введите другие две известные длины сторон треугольника.
- Затем будет рассчитана третья, недостающая длина стороны .

Вот как найти третью сторону треугольника без углов.
Другие калькуляторы площади треугольника
Вот некоторые другие калькуляторы площади треугольника, которые вы можете изучить здесь, на веб-сайте Omni Calculator:
- Площадь треугольника;
- Подобные треугольники;
- квадратных футов треугольника;
- Область разностороннего треугольника;
- Площадь тупоугольного треугольника;
- Площадь косоугольного треугольника;
- Площадь треугольника с координатами; и
- Площадь треугольника SAS.
Часто задаваемые вопросы
Могут ли любые 3 стороны составить треугольник?
Нет , это не тот случай, когда любые 3 стороны могут составить треугольник. Если одна сторона треугольника длиннее суммы двух других сторон, то вы не можете построить треугольник.
Как найти площадь треугольника?
Чтобы найти площадь треугольника в квадратных футах, выполните следующие действия:
Измерьте каждой стороны треугольника в футах и обозначьте их
a,bиc.
Введите их в формулу Герона , показанную ниже:
А = √[4a²b² - (a² + b² - c²)²]/4Результатом является площадь вашего треугольника в квадратных футах.
Какова площадь треугольника со сторонами 9, 6 и 5 дюймов?
14,1 квадратных дюйма . Этот результат получается из формулы Герона :
A = √[4a²b² - (a² + b² - c²)²]/4
Подставляя значения, мы получаем:
A = √[4× 9²×6² - (9² + 6² - 5²)²]/4
A = √[11664 - 8464]/4
A = 56,57/4 = 14,1 дюйма²
Steven Wooding
3 аналогичный калькуляторы треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… еще 15
Треугольники | bartleby
Что такое треугольники?
Треугольник — это фигура, состоящая из трех прямых линий, проведенных в одной плоскости. В математике треугольники являются неотъемлемой частью геометрии. Поскольку любую замкнутую фигуру, имеющую более двух сторон, можно назвать многоугольником, треугольники также являются многоугольниками.
В математике треугольники являются неотъемлемой частью геометрии. Поскольку любую замкнутую фигуру, имеющую более двух сторон, можно назвать многоугольником, треугольники также являются многоугольниками.
Общие свойства треугольников
В треугольнике три стороны и три угла. Сумма внутренних углов всегда будет 180 градусов. Это свойство суммы углов треугольника. Точно так же сумма внешних углов треугольника всегда равна 360 градусов. Треугольник обозначается символом ∆. ∆ ABC обозначает треугольник, тремя вершинами которого являются A, B и C, а сторонами являются AB, BC и CA.
Что такое разные треугольники?
Существует шесть типов различных треугольников. Однако эти шесть типов можно разделить на две группы.
Типы треугольников основаны на измерениях углов треугольников и длин их сторон. Различные свойства этих типов треугольников также основаны на этих различиях сторон и углов.
Какие бывают типы треугольников в зависимости от их сторон?
В зависимости от длины сторон треугольники можно разделить на следующие категории:
- Разносторонняя
- Равнобедренная
- Равносторонняя
Мы подробно обсудим эти типы ниже.
Разносторонний треугольник
Разносторонний – это треугольник, все три стороны которого имеют разную длину. Невозможно определить, какова будет длина сторон разностороннего треугольника. Все три стороны будут разными. Поскольку разносторонние треугольники имеют разную длину сторон, их внутренние углы также имеют разные измерения. Это означает, что ни один из углов разностороннего треугольника не равен. Этот тип треугольника действительно случайный по своей природе.
Равнобедренный треугольник
Равнобедренный треугольник – это особый тип треугольника. В этом типе длина сторон также различна. Однако, в отличие от разностороннего, у равнобедренного треугольника две стороны одинаковой длины. Только третья сторона будет иметь другую длину, чем две другие.
Любые две стороны этого треугольника могут иметь одинаковую длину. Это означает, что внутренние углы, образованные напротив этих равных сторон , также равны по измерению. В равнобедренном треугольнике всего два равных угла и две равные стороны.
Равносторонний треугольник
Равносторонний треугольник — пожалуй, самый совершенный тип треугольника. В отличие от равнобедренных треугольников или разносторонних треугольников, в равностороннем треугольнике все три стороны точно равны по длине. Это означает, что если вы знаете длину любой стороны, вы будете знать длину всех трех сторон.
Поскольку три стороны имеют одинаковую длину, образующиеся внутренние углы также равны по своей природе. Поскольку общая сумма углов всегда 180 градусов для треугольника, каждый угол в равностороннем треугольнике равен 180/3, или 60 градусов. Другое название равностороннего треугольника – равнобедренный треугольник. Расчет на этом типе треугольника считается самым простым.
Какие типы различаются по углам?
Далее у нас есть типы треугольников, основанные на измерении их углов. Существуют следующие типы:
- Остроугольный
- Тупоугольный
- Прямоугольный
Эти типы треугольников обсуждаются ниже.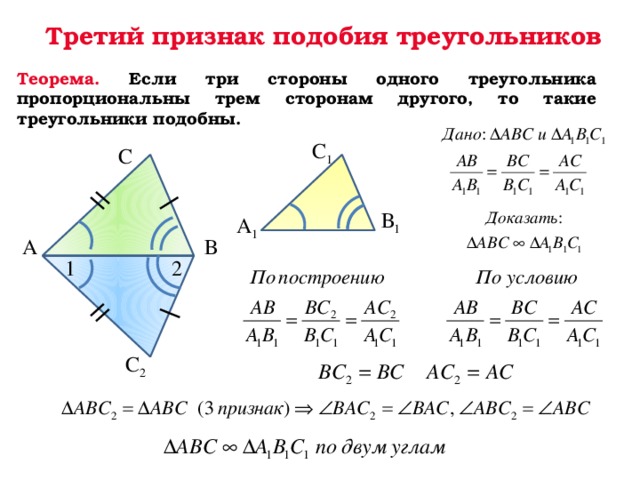
Остроугольный треугольник
В остроугольном треугольнике все три внутренних угла острые. Острый угол – это угол между 0 и 9 градусами.0 градусов. Если все углы треугольника острые, то такой треугольник называется остроугольным. Поскольку все углы равносторонних треугольников равны 60 градусам, это пример остроугольного треугольника.
Тупоугольный треугольник
Как следует из названия, тупоугольный треугольник — это треугольник, в котором любой из трех внутренних углов является тупым по своей природе. Тупой угол – это угол от 90 до 180 градусов. Поскольку общая сумма углов в треугольнике всегда равна 180 градусов, все три угла никогда не могут быть тупыми. В тупоугольном треугольнике один угол тупой, а два других по своей природе всегда острые.
Прямоугольный треугольник
В прямоугольном треугольнике один из углов прямой. Другими словами, один угол равен ровно 90 градусам. Это означает, что два других угла по своей природе острые, в соответствии со свойством суммы углов треугольников.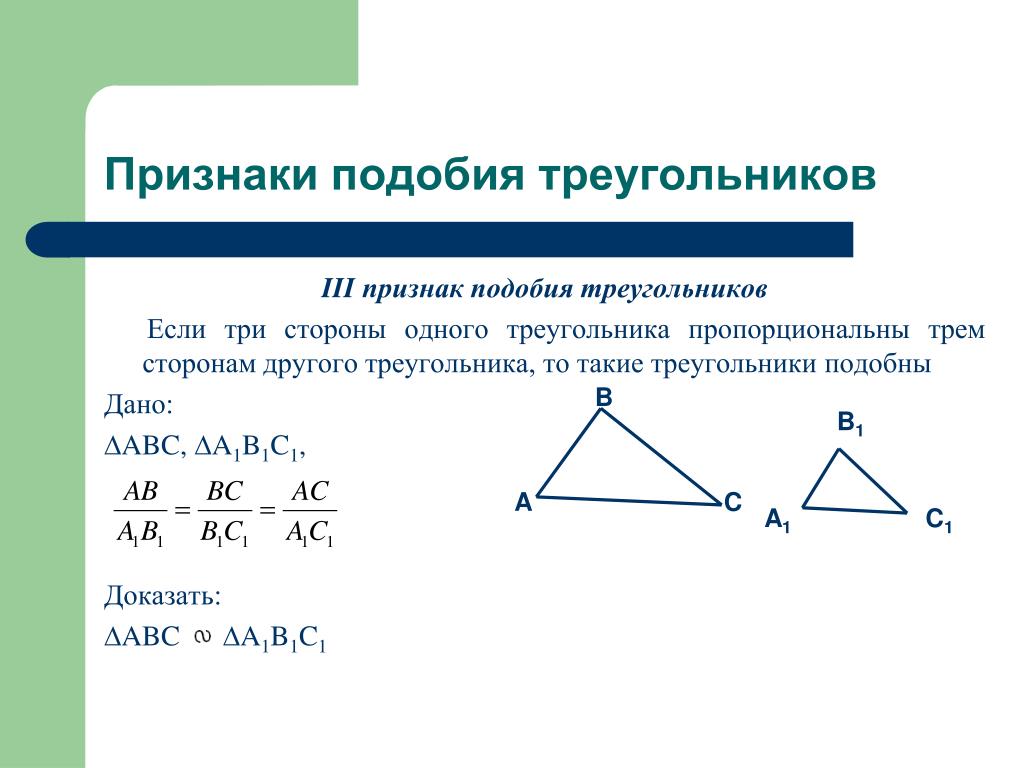
В этом типе две стороны, образующие прямой угол, всегда перпендикулярны друг другу. Третья сторона – противоположная сторона прямого угла – называется гипотенузой. Эта сторона также имеет наибольшую длину из трех сторон прямоугольного треугольника. Это также можно назвать прямоугольным равнобедренным, если две перпендикулярные стороны имеют одинаковую длину.
Что такое подобные треугольники?
Два треугольника называются подобными, если оба треугольника удовлетворяют некоторым критериям. Есть четыре способа определить подобие двух треугольников. Они следующие:
SSS или сходство стороны-стороны-стороны
Два треугольника будут подобны, если длины их соответствующих сторон имеют одинаковое отношение. В таком случае соответствующие углы двух треугольников также будут иметь одинаковую величину.
AAA или сходство угол-угол-угол
Два треугольника подобны, если их соответствующие углы имеют одинаковую величину. Это следствие подобия SSS (side-side-side). В таких случаях соответствующие стороны двух треугольников также будут иметь одинаковое отношение.
В таких случаях соответствующие стороны двух треугольников также будут иметь одинаковое отношение.
SAS или Side-Angle-Side Similarity
Два треугольника подобны, если они имеют угол одинакового значения, и стороны, образующие этот угол в двух треугольниках, также имеют одинаковое отношение.
AA или сходство углов
Если два треугольника имеют пару углов одинакового значения, то они подобны. В таких случаях значение любых двух углов первого треугольника будет таким же, как значение любых двух углов второго треугольника.
Практическая задача
Если ∆ ABC прямоугольный в точке B, а также является равнобедренным треугольником, найдите значение A и C. будет иметь одинаковую длину.
Так как B = 90 градусов, сумма углов A и C будет 180 – 90 градусов или 90 градусов.
Также здесь B = C, так как треугольник ABC равнобедренный.
Следовательно, мы имеем B + C = 90 градусов.
Или 2B = 2C = 90 градусов B = C = 90/2 = 45 градусов – это требуемый ответ.
Формулы
- В ∆ ABC m∠A+m∠B+m∠C=180°.
- Если ∆ ABC равнобедренный, так что AB=AC, то m∠B=m∠C.
Контекст и приложения
В реальной жизни треугольники являются важными фигурами, которые необходимы в сложных строительных процедурах. Кроме того, свойства треугольников пригодятся, когда необходимо определить измерение наклонных углов.
Эта тема важна для профессиональных экзаменов как для студентов, так и для выпускников, особенно для:
- B.S. по математике
- М.С. in Mathematics
Мы предоставим вам пошаговые решения для миллионов задач из учебников, круглосуточную помощь экспертов в данной области, если вы запутались, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по тригонометрии здесь!
*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.