Координаты середины отрезка формула в пространстве: Середина отрезка. Координаты середины отрезка

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. 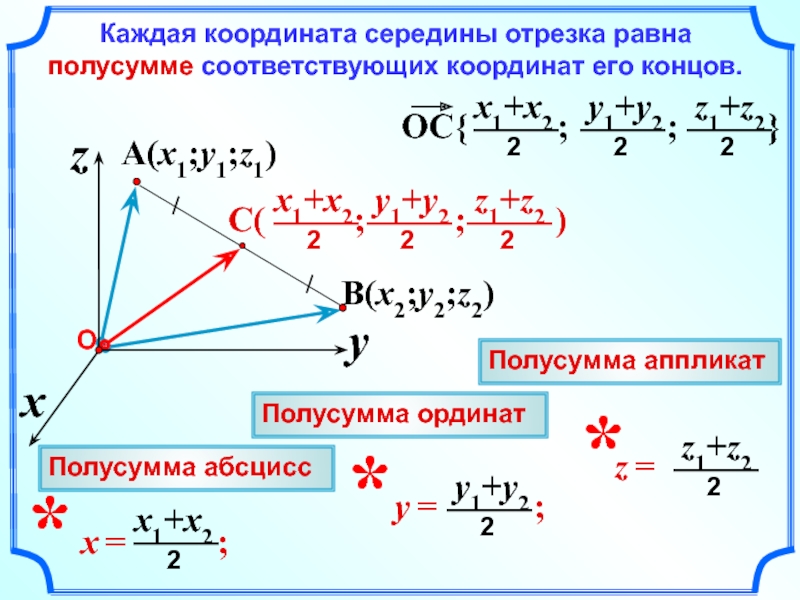3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Тема 4

1. Тема 1-11. Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Уравнение прямой на плоскости.

Раздел III. Аналитическая геометрия
Тема 1-11.
Расстояние между двумя точками. Середина
отрезка. Координаты середины отрезка.
Уравнение прямой на плоскости. Уравнение
прямой в пространстве. Уравнение
плоскости. Расстояние от точки до плоскости.
Расстояние между плоскостями. Расстояние
от точки до прямой на плоскости. Расстояние
от точки до прямой в пространстве. Угол
между плоскостями. Угол между прямой и
плоскостью

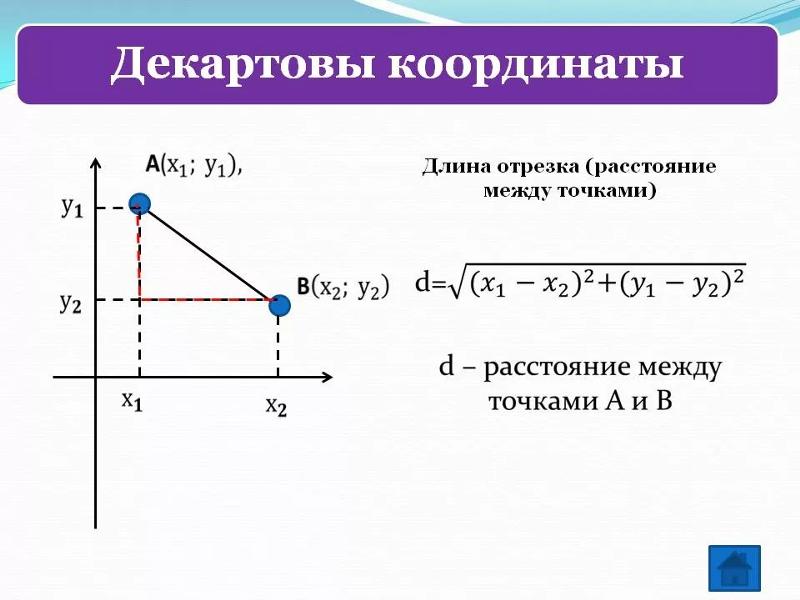
2. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.

Расстояние между двумя точками — это
длина отрезка, что соединяет эти точки.
• Формула вычисления расстояния между двумя
точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb — xa)2 + (yb — ya)2
• Формула вычисления расстояния между двумя
точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2

3. Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.

Середина отрезка — это точка, которая
лежит на отрезке и находится на равном
расстоянии от конечных точек.
• Формула вычисления координат середины
отрезка с концами A(xa, ya) и B(xb, yb) на
плоскости:
x a + xb
ya + yb
xc =
yc =
2
2
• Формула вычисления координат середины
отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в
пространстве:
xa + xb
ya + yb
za + zb
xc =
yc =
zc =
2
2
2

4.

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.Прямая (прямая линия) — это
бесконечная линия, по которой
проходит кратчайший путь между
любыми двумя её точками.
• Любую прямую на плоскости можно
задать уравнением прямой первой степени
вида
A x + B y + C = 0,
где A и B не могут быть одновременно равны
нулю.

5. Уравнение прямой с угловым коэффициентом

• Общее уравнение прямой при B≠0 можно
привести к виду
y = k x + b,
где k — угловой коэффициент равный тангенсу
угла, образованного данной прямой и
положительным направлением оси ОХ.

6. Уравнение прямой в отрезках на осях

• Если прямая пересекает оси OX и OY в
точках с координатами (a, 0) и (0, b), то она
может быть найдена используя
формулу уравнения прямой в отрезках
x
a
+
y
b
=1

7. Уравнение прямой, проходящей через две различные точки на плоскости

• Если прямая проходит через две точки
A(x1, y1) и B(x2, y2), такие
что x1 ≠ x2 и y1 ≠ y2 то уравнение
прямой можно найти, используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 — y1

8.

Параметрическое уравнение прямой на плоскости• Параметрические уравнения прямой могут
быть записаны следующим образом
x = l t +x0
y = m t + y0
где (x0, y0) — координаты точки лежащей на
прямой,
{l,m} — координаты направляющего вектора
прямой.

9. Каноническое уравнение прямой на плоскости

• Если известны координаты точки A(x0, y0)
лежащей на прямой и направляющего
вектора n ={l;m}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y — y0
m

10. Уравнение прямой, проходящей через две различные точки в пространстве

• Если прямая проходит через две точки
A(x1,y1,z1) и B(x2,y2,z2), такие что
x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2 то уравнение
прямой можно найти используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 -y1
=
z -z1
z2 — z1

11. Параметрическое уравнение прямой в пространстве

• Параметрические уравнения прямой могут
быть записаны следующим образом
x = l t +x0
y = m t + y0
z = n t + z0
где (x0, y0, z0) — координаты точки лежащей на
прямой,
{l; m; n} — координаты направляющего вектора
прямой.

12. Каноническое уравнение прямой в пространстве

• Если известны координаты точки A(x0, y0, z0)
лежащей на прямой и направляющего
вектора n={l;m;n}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y -y0
m
=
z -z0
n

13. Прямая как линия пересечения двух плоскостей

• Если прямая является пересечением двух
плоскостей, то ее уравнение можно задать
следующей системой уравнений
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0
при условии, что не имеет место равенство
A1
A2
=
B1
B2
=
C1
C2
.

14. Плоскость — есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.

Плоскость — есть поверхность, полностью
содержащая, каждую прямую,
соединяющую любые её точки.
• Любую плоскость можно
задать уравнением плоскости первой
степени вида
Ax+By+Cz+D=0
где A, B и C не могут быть одновременно
равны нулю.

15. Уравнение плоскости в отрезках

• Если плоскость пересекает оси OX, OY и OZ в
точках с координатами (a, 0, 0), (0, b, 0) и (0,
0, с), то она может быть найдена, используя
формулу уравнения плоскости в отрезках
x
a
+
y
b
+
z
c
=1

16. Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

• Чтобы составить уравнение плоскости, зная
координаты точки плоскости M(x0, y0, z0) и
вектора нормали плоскости n = {A; B; C} можно
использовать следующую формулу.
A(x — x0) + B(y — y0) + C(z — z0) = 0

17. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

• Если заданы координаты трех точек
A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3),
лежащих на плоскости, то уравнение
плоскости можно найти по следующей
формуле
x — x1 y — y1 z — z1
x2 — x1 y2 — y1 z2 — z1
x3 — x1 y3 — y1 z3 — z1
=0

18. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Расстояние от точки до плоскости —
равно длине перпендикуляра,
опущенного из точки на плоскость.
• Если задано уравнение плоскости Ax + By +
Cz + D = 0, то расстояние от точки M(Mx, My,
Mz) до плоскости можно найти, используя
следующую формулу:
|A·Mx + B·My + C·Mz + D|
d=
√A2 + B2 + C2

19. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.

Расстояние между плоскостями — равно
длине перпендикуляра, опущенного с
одной плоскости на другую.
• Если заданы уравнения параллельных
плоскостей Ax + By + Cz + D1 = 0 и
Ax + By + Cz + D2 = 0, то расстояние между
плоскостями можно найти, используя
следующую формулу
|D2 — D1|
d=
√A2 + B2 + C2

20. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Расстояние от точки до прямой — равно
длине перпендикуляра, опущенного из
точки на прямую.
• Если задано уравнение прямой Ax + By + C = 0,
то расстояние от точки M(Mx, My) до прямой
можно найти, используя следующую формулу
|A·Mx + B·My + C|
d=
√A2 + B2

21.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.Расстояние от точки до прямой —
равно длине перпендикуляра,
опущенного из точки на прямую.
• Если s = {m; n; p} — направляющий вектор
прямой l, M1(x1, y1, z1) — точка лежащей на
прямой, тогда расстояние от точки
M0(x0, y0, z0) до прямой l можно найти,
используя формулу
d=
|M0M1×s|
|s|
• Двугранный угол между плоскостями равен углу
образованному нормальными векторами этих
плоскостей.
• Двугранный угол между плоскостями равен углу
образованному прямыми l1 и l2, лежащими в
соответствующих плоскостях и перпендикулярными
линии пересечения плоскостей.
• Если заданы уравнения плоскостей A1x + B1y + C1z +
D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между
плоскостями можно найти, используя следующую
формулу
|A1·A2 + B1·B2 + C1·C2|
cos α =
√A12 + B12 + C12√A22 + B22 + C22

23. Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Угол между прямой и плоскостью — это угол
между прямой и ее проекцией на эту
плоскость.
• Если в пространстве заданы направляющий
вектор прямой L s = {l; m; n} и уравнение
плоскости Ax + By + Cz + D = 0, то угол
между этой прямой и плоскостью можно
найти используя формулу
|A·l+B· m+C· n|
sin φ =
√A2 + B2 + C2 · √l2 + m2 + n2

Пояснение к уроку: Точки, средние точки и расстояния в пространстве

В этом объяснении мы научимся найдите координаты точки в 3D, расстояние между двумя точками в 3D, а также координаты средней и конечной точек в 3D, используя формулу.

Мы уже должны знать, как найти все это в двух измерениях. Любая точка в двух измерениях будет иметь 𝑥- и 𝑦-координату и может быть записана в виде (𝑥,𝑦). Каждое из действительных чисел в упорядоченной паре представляет собой смещение этой точки от начала координат, другими словами, положительное или отрицательное расстояние от точки (0,0).

Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то мы можем вычислить их середину по формуле 𝑥+𝑥2,𝑦+𝑦2.

Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то мы можем вычислить расстояние между ними, используя формулу расстояния, полученную из теоремы Пифагора, (𝑥−𝑥)+(𝑦−𝑦).

В этом объяснении мы исследуем, как мы можем расширить эти формулы, чтобы включить третью координату при работе с точками в трех измерениях.

Определение: Координаты точки в трехмерном пространстве

Любая точка в трех измерениях будет иметь 𝑥-, 𝑦-, и 𝑧-координат и может быть записан в виде (𝑥,𝑦,𝑧). Каждое из действительных чисел в упорядоченной тройке дает расстояние от начала координат, измеренное вдоль соответствующей оси.

В нашем первом примере мы рассмотрим, в какой плоскости лежит точка, одна из координат которой равна нулю.

Пример 1. Определение плоскости, в которой находится заданная координата

В какой из следующих координатных плоскостей находится точка (−7,−8,0) ложь?

1. 𝑥𝑦
2. 𝑥𝑧
3. 𝑦𝑧

Ответ

Мы знаем, что точка в 3D будет иметь 𝑥-, 𝑦- и 𝑧-координаты. В этом вопросе 𝑥=−7, 𝑦=−8 и 𝑧=0.

Поскольку 𝑧-координата равна нулю, точка находится на нулевом расстоянии от начала координат в 𝑧-направлении. Это означает, что он будет лежать на 𝑥𝑦-плоскости. В самом деле, любая точка с координаты (𝑥,𝑦,0) будут лежать на этой плоскости.

Таким образом, мы можем заключить, что точка (−7,−8,0) лежит на 𝑥𝑦-плоскости.

Определение: Три координатные плоскости

Любая точка с координатами (𝑥,𝑦,0) будет лежать на 𝑥𝑦-плоскости.

Аналогично, любая точка с координатами (𝑥,0,𝑧) будет лежать на 𝑥𝑧-плоскость, и любая точка с координатами (0,𝑦,𝑧) будет лежать на 𝑦𝑧-плоскости.

В нашем следующем вопросе мы рассмотрим, как мы можем определить координаты точки в трех измерениях.

Пример 2. Нахождение координат заданной точки в 3D

Определить координаты точки 𝐴.

Ответ

Любая точка в трех измерениях будет иметь 𝑥-, 𝑦- и 𝑧-координаты и может быть записана в виде (𝑥,𝑦,𝑧).

Двигаясь от начала координат, мы проходим 3 единицы в положительном 𝑥-направлении, −3 единицы в 𝑦-направлении и, наконец, 3 единицы в 𝑧-направлении.

Это означает, что 𝑥=3, 𝑦=−3 и 𝑧=3.

Координаты точки 𝐴 равны (3,−3,3).

Напомним, что формула средней точки в двух измерениях просто говорит нам найти среднее значение двух точек. Находим среднее значение 𝑥-координат и среднее значение 𝑦-координат. Теперь мы расширим эту идею на три измерения, найдя также среднее значение 𝑧-координат.

Чтобы найти среднее любых двух чисел, мы складываем их, а затем делим их сумму на два.

Определение: середина двух точек в трехмерном пространстве

Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) соответственно, то можно вычислить их среднюю точку, используя следующую формулу: 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.

В нашем следующем примере мы будем использовать эту формулу для определения середины двух точек в пространстве.

Пример 3: Нахождение координат средней точки в 3D

Баллы 𝐴 и 𝐵 имеют координаты (8,−8,−12) и (−8,5,−8) соответственно. Определить координаты середины 𝐴𝐵.

Ответ

Чтобы найти середину двух точек в трех измерениях, мы будем использовать формулу для вычисления середины координат (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧): 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2. 

Пусть точка 𝐴 имеет координаты (𝑥,𝑦,𝑧), а точка 𝐵 имеет координаты (𝑥 ,𝑦,𝑧 ).

Середина между точками 𝐴 и 𝐵 равна =8+(−8)2,−8+52,−12+(−8)2=02,−32,−202=0,−32 ,−10.

Координаты середины 𝐴𝐵 составляют 0,−32,−10.

В нашем следующем примере мы будем использовать формулу средней точки для определения конечной точки по средней точке двух точек в пространстве и другой конечной точке.

Пример 4: Нахождение координат конечной точки отрезка линии по координатам середины и координатам начальной точки

Учитывая, что точка (0,17,−10) является средней точкой 𝐴𝐵 и это 𝐴(−19,7,14), каковы координаты 𝐵?

Ответ

Чтобы найти середину двух точек в трех измерениях, мы будем использовать формулу для вычисления середины координат (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) : 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.

Мы знаем, что точка 𝐴 имеет координаты (−19,7,14) и пусть точка 𝐵 имеет координаты (𝑥,𝑦,𝑧). Середина между этими двумя точками имеет координаты (0,17,−10).

Подставив эти значения в формулу, получим (0,17,−10)=−19+𝑥2,7+𝑦2,14+𝑧2.

Затем мы можем приравнять отдельные компоненты, что даст нам решение трех уравнений.

Во-первых, 𝑥-координата дает нам 0=−19+𝑥2.

Умножая обе части уравнения на 2, получаем 0=−19+𝑥.

Итак, 19=𝑥.

Во-вторых, 𝑦-координата дает нам 17=7+𝑦2.

Умножив обе части уравнения на 2, мы получим 34=7+𝑦.

Итак, 27=𝑦.

Наконец, 𝑧-координата дает нам −10=14+𝑧2.

Умножая обе части уравнения на 2, мы получаем −20=14+𝑧.

Итак, −34=𝑧.

Координаты точки 𝐵 равны (19,27,−34).

В двух измерениях мы можем вычислить расстояние между двумя точками, используя адаптацию теоремы Пифагора. Это утверждает, что 𝑎+𝑏=𝑐, где 𝑐 — длина самой длинной стороны, известной как гипотенуза, прямоугольного треугольника.

Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то можно вычислить расстояние между ними по следующей формуле: (𝑥−𝑥)+(𝑦−𝑦). 

Теперь мы рассмотрим, как мы можем вычислить расстояние между двумя точками в три измерения.

Рассмотрим трехмерную прямоугольную призму 𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻, нарисованную ниже, и предположим, что мы хотим пройти от самого нижнего левого переднего угла, 𝐴, до самого верхнего правого заднего угла, 𝐺.

Сначала рассмотрим треугольник 𝐴𝐵𝐹 в основании призмы. Теорема Пифагора говорит нам, что 𝐴𝐹=𝐴𝐵+𝐵𝐹.

Итак, 𝐴𝐹=√𝑥+𝑦.

Теперь делаем еще один треугольник 𝐴𝐹𝐺, с основанием вдоль 𝐴𝐹 и высотой 𝐹𝐺.

Мы можем снова использовать теорему Пифагора так, чтобы 𝐴𝐺=𝐴𝐹+𝐹𝐺. Подставляя длины 𝐴𝐹 и 𝐹𝐺, мы видим, что 𝐴𝐺=√𝑥+𝑦+𝑧.

Следовательно, 𝐴𝐺=√𝑥+𝑦+𝑧.

Определение: расстояние между двумя точками в трехмерном пространстве

Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧), соответственно, то мы можем рассчитать расстояние между ними по следующей формуле: (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧). теоремы Пифагора в трех измерениях; мы находим сумму квадратов разницы между каждой координатой и затем квадратный корень этого ответа.

В наших последних двух вопросах мы вычислим кратчайшее расстояние между точкой и одной из осей, а также расстояние между двумя точками в пространстве.

Пример 5. Нахождение расстояния между двумя точками по их координатам в трех измерениях

Нахождение расстояния между двумя точками 𝐴(−7,12,3) и 𝐵(−4,−1,−8).

Ответ

Чтобы вычислить расстояние между двумя точками в трех измерениях, мы будем использовать следующую формулу, где две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) соответственно: (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧).

Пусть точка 𝐴 имеет координаты (𝑥,𝑦,𝑧), а точка 𝐵 имеет координаты (𝑥,𝑦,𝑧).

Расстояние между ними равно =√(−4−(−7))+(−1−12)+(−8−3)=√(3)+(−13)+(−11)=√9+169+121=√299 .

Расстояние между двумя точками 𝐴(−7,12,3) и 𝐵(−4,−1,−8) составляет √299 единиц длины.

Пример 6: Нахождение расстояния между точкой и осью в 3D

Каково расстояние между точкой (19,5,5) и осью 𝑥?

Ответ

Мы знаем, что любая точка будет лежать на оси 𝑥, если и ее 𝑦-координата, и ее 𝑧-координата равны нулю. Это означает, что мы можем определить точку на оси 𝑥 как (𝑥,0,0).

Признаем, что искомое расстояние — это перпендикулярное расстояние от точки до оси 𝑥, что означает проекцию точки на 𝑥-ось будет в точке (19,0,0).

Расстояние между двумя точками можно рассчитать по формуле следующим образом √(19−19)+(5−0)+(5−0)=√0+(5)+(5)=√50=5√2.

Расстояние между точка (19,5,5) и ось 𝑥 составляют 5√2 единиц длины.

Мы закончим это объяснение повторением некоторых ключевых моментов.

Ключевые точки

• Любая точка в трех измерениях имеет координаты, записанные в виде (𝑥,𝑦,𝑧).
• Если 𝑧-координата равна нулю, то мы знаем, что точка лежит в 𝑥𝑦-плоскости; если 𝑦-координата равна нулю, то мы знаем, что точка лежит в 𝑥𝑧-плоскость; а если 𝑥-координата равна нулю, то мы знаем, что точка лежит в 𝑦𝑧-плоскости.
• Если и 𝑦-координата, и 𝑧-координата равны нулю, то точка лежит на 𝑥-оси; если и 𝑥-координата, и 𝑧-координата равна нулю, то точка лежит на 𝑦-оси; и если и 𝑥-координата, и 𝑦-координата равны равна нулю, то точка лежит на оси 𝑧.
• Середина двух точек с координатами (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) лежит в точке 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
• Мы также можем использовать формулу средней точки для вычисления конечной точки отрезка, учитывая среднюю точку и другую конечную точку.
• Расстояние между двумя точками с координатами (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) это равно (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧).

Центр отрезка.

Произношение: /ˈmɪdˌpɔɪnt/ Объяснение

Середина — это точка равноудаленный между двумя точками. Середина находится на отрезке, соединяющем две точки и делит отрезок ровно пополам. Точное математическое определение средней точки:

Средняя точка A M между точками А и В точка на прямой AB такая, что АМ = МБ .

Как построить среднюю точку

Шаг	Иллюстрация	Описание
1		Начните с точек A и Б .
2		Нарисуйте отрезок АВ.
3		Нарисуйте круг с центром в точке А и радиус AB .
4		Нарисуйте круг с центром в точке B и радиус AB
5		Отметить одно пересечение двух кругов как точку C и другой перекресток двух круги как точка D .
6		Нарисуйте отрезок CD.
7		Отметить точку пересечения сегмента линии АВ и отрезок CD как М . Точка M — средняя точка.
Таблица 1: Построение средней точки.

Как вычислить среднюю точку в одномерном метрическом пространстве

Нажмите на синие точки и перетащите их, чтобы изменить фигуру. Что произойдет, если B окажется слева от A?

Манипулятивное 8 — Расчет средней точки в одном измерении Создано с помощью GeoGebra.

Формула средней точки в одномерном пространстве между А и В есть . Нажать на синие точки в манипуляции 1 и перетащите их, чтобы изменить фигуру.

Как вычислить среднюю точку в метрическом двумерном пространстве

Нажмите на синие точки и перетащите их, чтобы изменить фигуру.

Манипулятивное 9 — Расчет средней точки в двух измерениях Создано с помощью GeoGebra.

Середина делит отрезок ровно пополам. Этот факт можно использовать найти формулу для середины отрезка в двумерном пространстве. Евклидово пространство, такое как декартова система координат. X-координата средняя точка будет на полпути между x-координатами двух точек, и y-координата средней точки будет на полпути между y-координатами две точки. Формула середины отрезка с концами и является .

Как вычислить среднюю точку в метрическом n-мерном пространстве

Алгоритм вычисления конечной точки в двумерном пространство может быть обобщено для n-мерного пространства. Учитывая две точки и середина .

Доказательство: Если

M является средней точкой АБ, затем утра = MB

Это доказательство является доказательством абзаца или неофициальным доказательством.

Определение середины отрезка таково, что 902:01 AM = МБ . Другими словами, длины двух отрезков равны. По определению конгруэнтности АМ конгруэнтно МБ тогда и только тогда, когда AM и MB имеют одинаковую меру. Так как по определению середины АМ и МБ имеют одинаковую меру, утра = МБ.

Ссылки

1. МакАдамс, Дэвид Э.. Словарь всех математических слов, середина . 2-й классный выпуск 20150108-4799968. стр. 117. Life is a Story Problem LLC. 8 января 2015. Купить книгу

Дополнительная информация

• Евклид Александрийский. Элементы . Университет Кларка. 06.09.2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Цитируйте эту статью как:

МакАдамс, Дэвид Э. Середина . 25.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/m/midpoint.html.

Авторы изображений

• Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

История изменений

25.