Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA. Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Прикладная статистика: Исследование зависимостей
Прикладная статистика: Исследование зависимостей
ОглавлениеПРЕДИСЛОВИЕВведение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ В.2. Какова конечная прикладная цель статистического исследования зависимостей? В.3. Математический инструментарий В.4. Некоторые типовые задачи практики В.5. Основные типы зависимостей между количественными переменными В.6. Основные этапы статистического исследования зависимостей ВЫВОДЫ Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ) 1. 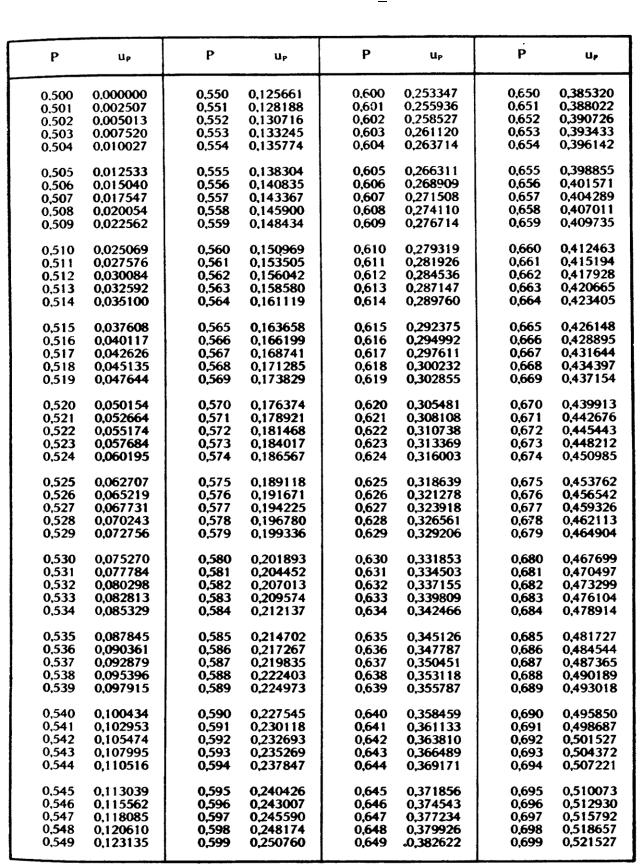 1.1. Понятие индекса корреляции. 1.1. Понятие индекса корреляции.1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах. 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи. 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции. 1.1.5. Измерение степени тесноты связи при нелинейной зависимости. 1.2. Анализ частных («очищенных») связей 1.2.2. Частные коэффициенты корреляции и их выборочные значения. 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы). 1.3. Анализ множественных связей 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай). 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей. 1.3.4. Примеры. ВЫВОДЫ Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ 2.  1. Ранговая корреляция 1. Ранговая корреляция2.1.2. Понятие ранговой корреляции. 2.1.3. Основные задачи статистического анализа связей между ранжировками. 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5]. 2.2. Анализ и измерение парных ранговых статистических связей 2.2.1. Ранговый коэффициент корреляции Спирмэна. 2.2.2. Ранговый коэффициент корреляции Кендалла. 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла. 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи. 2.3. Анализ множественных ранговых связей 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации. 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей. 2.3.4. Примеры. ВЫВОДЫ Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ 3.1. Таблицы сопряженности 3.  1.2. Логарифмически-линейная. параметризация таблиц сопряженности. 1.2. Логарифмически-линейная. параметризация таблиц сопряженности.3.1.3. Проверка гипотез. 3.1.4. Меры связи между строками и столбцами таблицы. 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование) 3.2.1. Методическое место дуального шкалирования. 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений. 3.2.3. Двойственность в определении V и W. 3.2.4. Максимизация коэффициента корреляции. 3.2.5. Изучение оптимального решения. 3.2.6. Таблицы «объект—многомерный отклик». ВЫВОДЫ Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА 4.1.1. Цепи Маркова. 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ. 4.2. Распределение с древообразной структурой зависимостей 4.2.1. Предварительные сведения из теории графов. 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ). 4.3. Оценка графа структуры зависимостей компонент нормального вектора 4. 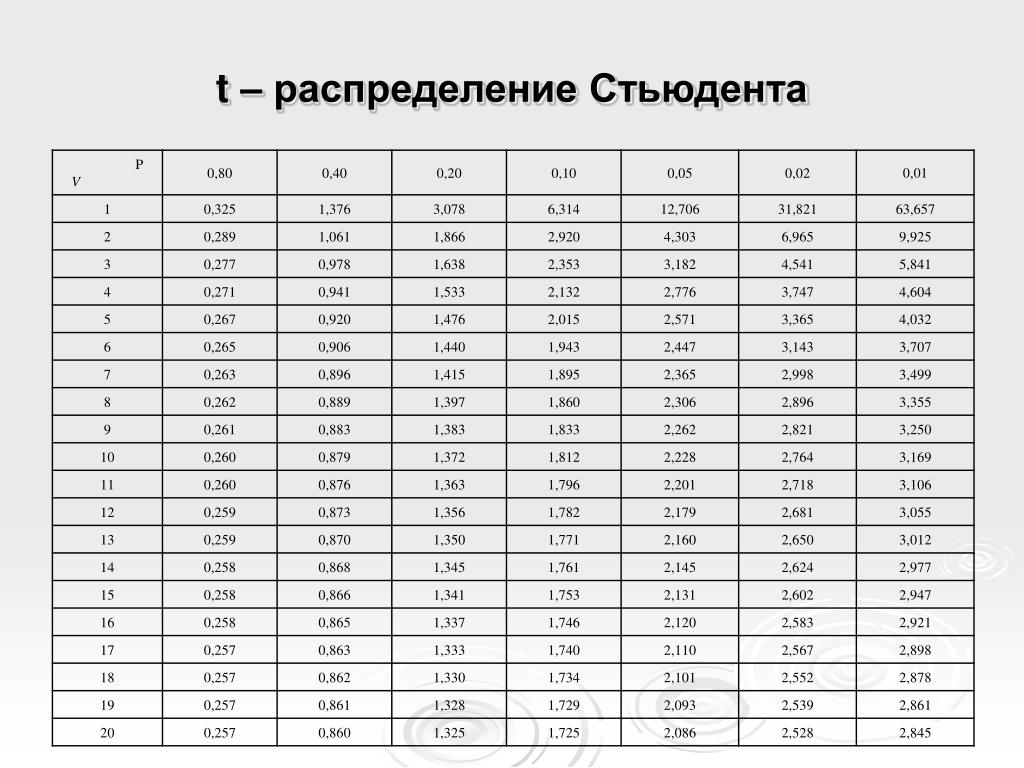 3.2. Построение графа структуры зависимостей по корреляционной матрице. 3.2. Построение графа структуры зависимостей по корреляционной матрице.4.3.3. Асимптотика Колмогорова — Деева. 4.4. R(k)-распределения 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ. 4.4.2. Нормальное R(k)-распределение. 4.4.3. Восстановление графа структуры зависимостей. 4.5. Структура связей нормального вектора (общий случай) 4.5.1. Марковская тройка. Структура многомерного вектора. 4.5.2. Информационная интерпретация структуры связей. 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений. ВЫВОДЫ Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ) 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи 5.3. Взаимоотношения различных регрессий ВЫВОДЫ Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 6.  1. Использование априорной информации о содержательной сущности анализируемой зависимости 1. Использование априорной информации о содержательной сущности анализируемой зависимости6.2. Предварительный анализ геометрической структуры исходных данных 6.2.1. Содержание геометрического анализа парных корреляционных полей. 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии. 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость. 6.3. Математико-статистические методы в задаче параметризации модели регрессии 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания. 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается. 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии. ВЫВОДЫ Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ 7.1. Метод наименьших квадратов 7.1.2. Свойства мнк-оценок. 7.1.3. Ортогональная матрица плана.  7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева. 7.1.5. Обобщенный мнк. 7.2. Функции потерь, отличные от квадратичной 7.2.1. Функция потерь. 7.2.3. Функции потерь, имеющие горизонтальную асимптоту. 7.2.4. Эв-регрессия («лямбда»-регрессия). 7.2.5. Минимизация систематической ошибки. 7.3. Байесовское оценивание 7.3.1. Введение априорной плотности распределения параметров. 7.3.2. Апостериорное распределение параметров. 7.3.3. Повторная выборка из той же совокупности. 7.4. Многомерная регрессия 7.4.1. Случай известной ковариационной матрицы ошибок. 7.4.3. Эв-оценки. 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений. 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ) 7.5.1. Основные типы задач конфлюэнтного анализа. 7.5.2. Модифицированный мнк для схемы активного эксперимента. 7.5.3. Пассивные наблюдения.  7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84). 7.5.5. Неявное задание отклика. 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода) 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры). 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры). 7.6.4. Случай неизвестных. ВЫВОДЫ Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки 8.2. Регрессия на главные компоненты 8.3. Смещенное оценивание коэффициентов регрессии 8.4. Редуцированные оценки для стандартной модели линейной регрессии 8.4.2. Редуцированная оценка Мейера — Уилке. 8.5. Оценки, связанные с ортогональным разложением 8.5.1. Оптимальное взвешивание вклада главных компонент. 8. 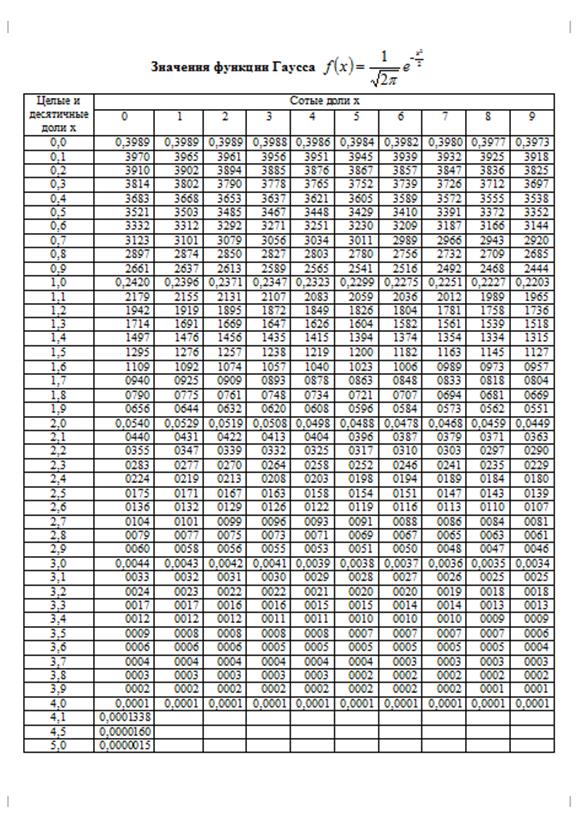 5.2. Оценка оптимальных вкладов главных компонент. 5.2. Оценка оптимальных вкладов главных компонент.8.6. Вопросы точности вычислительной реализации процедур линейного оценивания 8.6.1. Два метода получения мнк-оценок. 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений. 8.6.3. Центрирование и нормирование матрицы данных. 8.6.4. Вычисление элементов ковариационной матрицы. 8.7. Отбор существенных переменных в задачах линейной регрессии 8.7.1. Влияние отбора переменных на оценку уравнения регрессии. 8.7.2. Критерии качества уравнения регрессии. 8.7.3. Схемы генерации наборов переменных. 8.7.4. Пошаговые процедуры генерации наборов. 8.7.5. Оператор симметричного выметания. 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных. ВЫВОДЫ Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок) 9.1.2.  Алгоритмы квазиградиентного типа. Алгоритмы квазиградиентного типа.9.2. Градиентный спуск 9.3. Метод Ньютона 9.4 Метод Ньютона-Гаусса и его модификации 9.4.2. Обсуждение скорости сходимости процедуры. 9.4.3. Рекомендации по правилу остановки итерационной процедуры. 9.5. Методы, не использующие вычисления производных 9.6. Способы нахождения начального приближения 9.7. Вопросы существования и единственности мнк-оценки ВЫВОДЫ Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ 10.1. Непараметрическое оценивание регрессии 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей 10.3.1. Определение одномерных сплайнов. 10.3.2. Выбор порядка сплайна, числа и положения узлов. 10.3.3. Оценка параметров и проверка гипотез. 10.3.4. Билинейные сплайны. ВЫВОДЫ Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ 11.  1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости 1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости11.1.2. Решение основных задач по оценке точности регрессионной модели. 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии. 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели. 11.3. Исследование точности регрессионной модели в реалистической ситуации ВЫВОДЫ Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ 12.1. Дискретные динамические модели 12.2. Авторегрессия первого порядка 12.3. Авторегрессия произвольного порядка ВЫВОДЫ Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных 13. 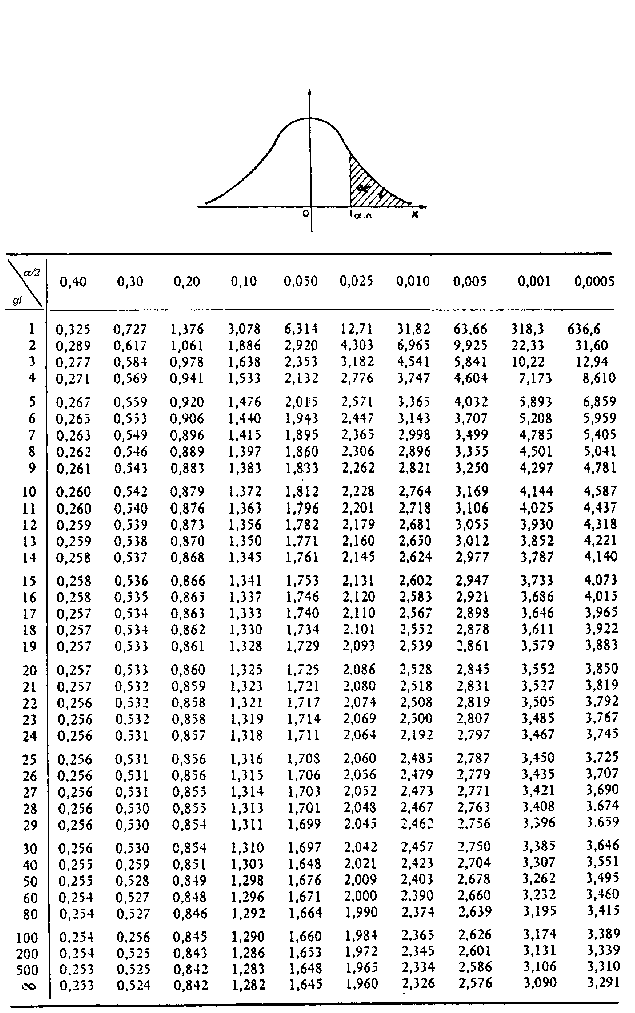 2. Однофакторный дисперсионный анализ 2. Однофакторный дисперсионный анализ13.3. Полный двухфакторный дисперсионный анализ 13.4. Модели дисперсионного анализа со случайными факторами 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений 13.6. Влияние нарушений основных предположений ВЫВОДЫ Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ 14.1. Системы одновременных уравнений 14.2. Спецификация модели и проблема идентифицируемости 14.3. Рекурсивные системы 14.4. Двух- и трехшаговый методы наименьших квадратов 14.5. Метод неподвижной точки 14.6. Сравнение методов ВЫВОДЫ Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ Таблица П.1. Значения функции плотности стандартного нормального закона распределения Таблица П.2. Значения функции стандартного нормального распределения ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ СПИСОК ЛИТЕРАТУРЫ |
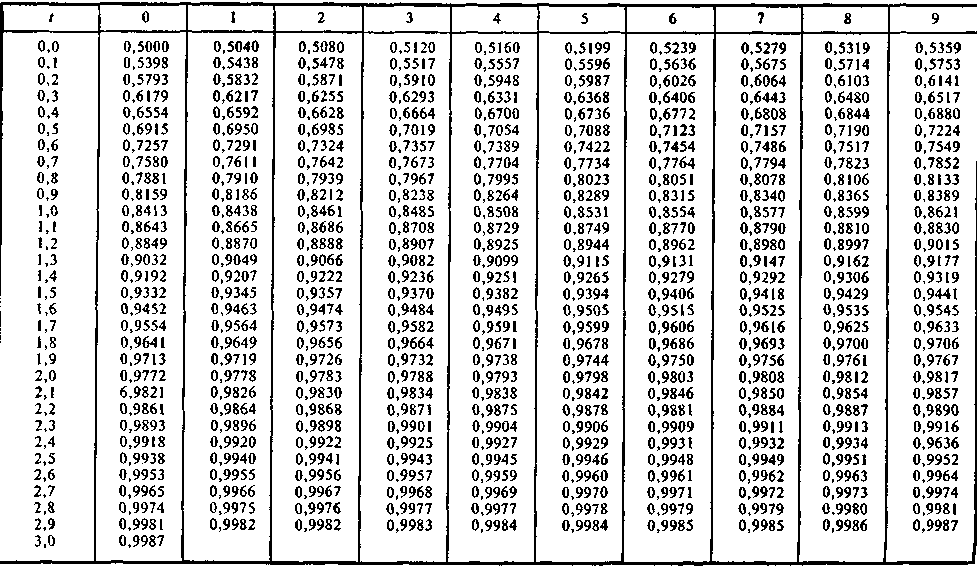
Стандартная таблица нормального распределения
изображения / normal-dist.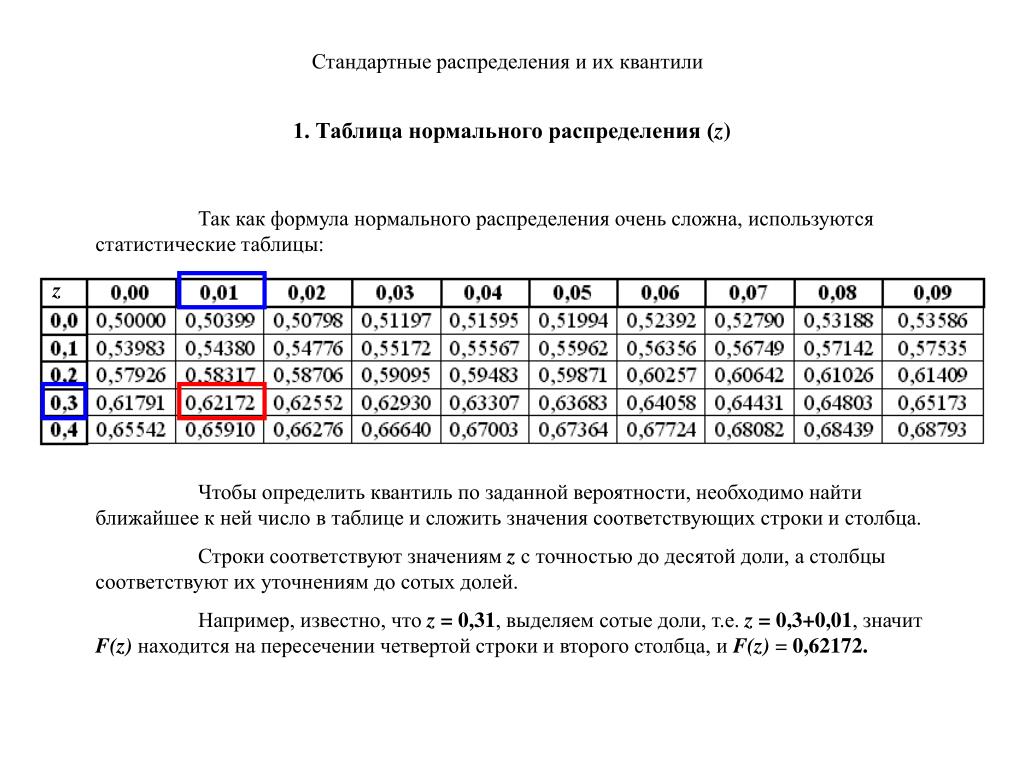 js
js
Это колоколообразная кривая стандартного нормального распределения.
Это нормальное распределение со средним значением 0 и стандартным отклонением 1.
Показывает процент населения:
- между 0 и Z (опция «0 до Z»)
- меньше Z (опция «До Z»)
- больше, чем Z (опция «Z и далее»)
Отображает только значения до 0,01%
Вы также можете использовать приведенную ниже таблицу. В таблице показана область от 0 до Z.
Вместо одной ДЛИННОЙ таблицы мы поместили « 0.1 » вниз, а затем « 0.01 «. (Пример использования ниже)
| З | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,0 | 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 |
| 0,1 | 0,0398 | 0,0438 | 0,0478 | 0,0517 | 0,0557 | 0,0596 | 0,0636 | 0,0675 | 0,0714 | 0,0753 |
| 0,2 | 0,0793 | 0,0832 | 0,0871 | 0,0910 | 0,0948 | 0,0987 | 0,1026 | 0,1064 | 0,1103 | 0,1141 |
| 0,3 | 0,1179 | 0,1217 | 0,1255 | 0,1293 | 0,1331 | 0,1368 | 0,1406 | 0,1443 | 0,1480 | 0,1517 |
| 0,4 | 0,1554 | 0,1591 | 0,1628 | 0,1664 | 0,1700 | 0,1736 | 0,1772 | 0,1808 | 0,1844 | 0,1879 |
| 0,5 | 0,1915 | 0,1950 | 0,1985 | 0,2019 | 0,2054 | 0,2088 | 0,2123 | 0,2157 | 0,2190 | 0,2224 |
| 0,6 | 0,2257 | 0,2291 | 0,2324 | 0,2357 | 0,2389 | 0,2422 | 0,2454 | 0,2486 | 0,2517 | 0,2549 |
| 0,7 | 0,2580 | 0,2611 | 0,2642 | 0,2673 | 0,2704 | 0,2734 | 0,2764 | 0,2794 | 0,2823 | 0,2852 |
| 0,8 | 0,2881 | 0,2910 | 0,2939 | 0,2967 | 0,2995 | 0,3023 | 0,3051 | 0,3078 | 0,3106 | 0,3133 |
| 0,9 | 0,3159 | 0,3186 | 0,3212 | 0,3238 | 0,3264 | 0,3289 | 0,3315 | 0,3340 | 0,3365 | 0,3389 |
| 1,0 | 0,3413 | 0,3438 | 0,3461 | 0,3485 | 0,3508 | 0,3531 | 0,3554 | 0,3577 | 0,3599 | 0,3621 |
1.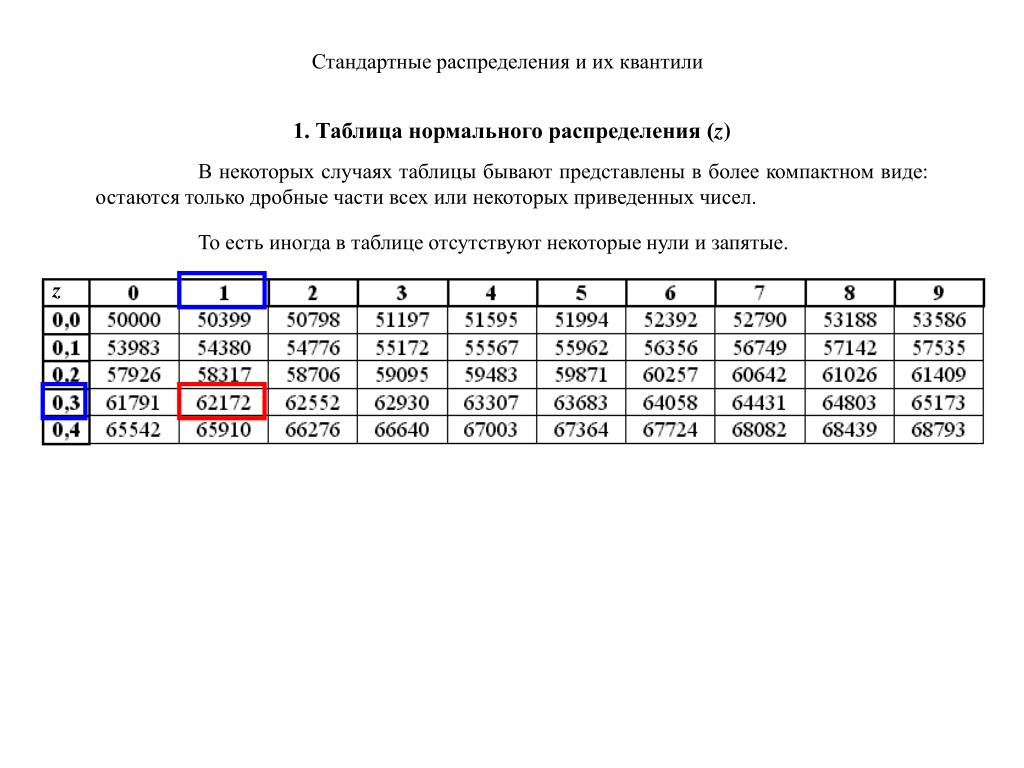 1 1 | 0,3643 | 0,3665 | 0,3686 | 0,3708 | 0,3729 | 0,3749 | 0,3770 | 0,3790 | 0,3810 | 0,3830 |
| 1,2 | 0,3849 | 0,3869 | 0,3888 | 0,3907 | 0,3925 | 0,3944 | 0,3962 | 0,3980 | 0,3997 | 0,4015 |
| 1,3 | 0,4032 | 0,4049 | 0,4066 | 0,4082 | 0,4099 | 0,4115 | 0,4131 | 0,4147 | 0,4162 | 0,4177 |
| 1,4 | 0,4192 | 0,4207 | 0,4222 | 0,4236 | 0,4251 | 0,4265 | 0,4279 | 0,4292 | 0,4306 | 0,4319 |
| 1,5 | 0,4332 | 0,4345 | 0,4357 | 0,4370 | 0,4382 | 0,4394 | 0,4406 | 0,4418 | 0,4429 | 0,4441 |
| 1,6 | 0,4452 | 0,4463 | 0,4474 | 0,4484 | 0,4495 | 0,4505 | 0,4515 | 0,4525 | 0,4535 | 0,4545 |
| 1,7 | 0,4554 | 0,4564 | 0,4573 | 0,4582 | 0,4591 | 0,4599 | 0,4608 | 0,4616 | 0,4625 | 0,4633 |
| 1,8 | 0,4641 | 0,4649 | 0,4656 | 0,4664 | 0,4671 | 0,4678 | 0,4686 | 0,4693 | 0,4699 | 0,4706 |
| 1,9 | 0,4713 | 0,4719 | 0,4726 | 0,4732 | 0,4738 | 0,4744 | 0,4750 | 0,4756 | 0,4761 | 0,4767 |
| 2,0 | 0,4772 | 0,4778 | 0,4783 | 0,4788 | 0,4793 | 0,4798 | 0,4803 | 0,4808 | 0,4812 | 0,4817 |
2. 1 1 | 0,4821 | 0,4826 | 0,4830 | 0,4834 | 0,4838 | 0,4842 | 0,4846 | 0,4850 | 0,4854 | 0,4857 |
| 2.2 | 0,4861 | 0,4864 | 0,4868 | 0,4871 | 0,4875 | 0,4878 | 0,4881 | 0,4884 | 0,4887 | 0,4890 |
| 2,3 | 0,4893 | 0,4896 | 0,4898 | 0,4901 | 0,4904 | 0,4906 | 0,4909 | 0,4911 | 0,4913 | 0,4916 |
| 2,4 | 0,4918 | 0,4920 | 0,4922 | 0,4925 | 0,4927 | 0,4929 | 0,4931 | 0,4932 | 0,4934 | 0,4936 |
| 2,5 | 0,4938 | 0,4940 | 0,4941 | 0,4943 | 0,4945 | 0,4946 | 0,4948 | 0,4949 | 0,4951 | 0,4952 |
| 2,6 | 0,4953 | 0,4955 | 0,4956 | 0,4957 | 0,4959 | 0,4960 | 0,4961 | 0,4962 | 0,4963 | 0,4964 |
| 2,7 | 0,4965 | 0,4966 | 0,4967 | 0,4968 | 0,4969 | 0,4970 | 0,4971 | 0,4972 | 0,4973 | 0,4974 |
| 2,8 | 0,4974 | 0,4975 | 0,4976 | 0,4977 | 0,4977 | 0,4978 | 0,4979 | 0,4979 | 0,4980 | 0,4981 |
| 2,9 | 0,4981 | 0,4982 | 0,4982 | 0,4983 | 0,4984 | 0,4984 | 0,4985 | 0,4985 | 0,4986 | 0,4986 |
| 3,0 | 0,4987 | 0,4987 | 0,4987 | 0,4988 | 0,4988 | 0,4989 | 0,4989 | 0,4989 | 0,4990 | 0,4990 |
Пример: Процент населения от 0 до 0,45
Начните со строки 0,4 и читайте дальше до 0,45: есть значение 0,1736
А 0,1736 — это 17,36%
Итак, 17,36% населения находятся в диапазоне от 0 до 0,45 стандартных отклонений от среднего.
Поскольку кривая симметрична, одну и ту же таблицу можно использовать для значений, идущих в любом направлении, поэтому отрицательный 0,45 также имеет площадь 0,1736
Пример: Процент населения Z Между −1 и 2
От от −1 до 0 то же, что и от 0 до +1 :
В строке для 1,0, первый столбец 1,00, есть значение 0,3413
От 0 до +2 :
В строке для 2,0, первый столбец 2,00, есть значение 0,4772
Добавьте два, чтобы получить сумму от -1 до 2:
0,3413 + 0,4772 = 0,8185
И 0,8185 9002 3 равно 81,85%
Таким образом, 81,85% населения находятся между -1 и +2 стандартных отклонения от среднего.
1486, 1487, 1488, 1489, 1490, 1491, 3846, 3847, 3848, 3849
Квантиль — это ключ к пониманию распределения вероятностей
Если вы когда-нибудь чувствовали себя запутанными при использовании распределения вероятностей, эта статья для вас.
Agnieszka Kujawska, PhD
·
Читать
Опубликовано в
·
13 мин чтения
·
Июн 26, 2021
Photo by Joshua Earle on UnsplashВы много раз встречались с распределением вероятностей. Вы знаете, что есть несколько разных типов. Но в глубине души вы чувствуете смущение, когда вам нужно использовать его на практике. В чем, черт возьми, разница между распределением вероятностей и кумулятивным распределением вероятностей? Должен ли я проверять уровень достоверности или альфу по оси X или Y? Если да, то эта статья для вас. В конце концов, вы будете чувствовать себя комфортно, используя распределения вероятностей для дискретных или непрерывных случайных величин. Давайте погрузимся в это!
В этой статье мы рассмотрим следующие темы:
- Функция плотности вероятности (PDF)
- Функция массы вероятности (PMF)
- Кумулятивное распределение вероятностей (CDF)
3. 1 Кумулятивное распределение вероятностей для ДИСКРЕТНЫХ случайных величин (CMF) 9000 5 3.2 Кумулятивное распределение вероятностей для НЕПРЕРЫВНЫХ случайных величин (CDF)
1 Кумулятивное распределение вероятностей для ДИСКРЕТНЫХ случайных величин (CMF) 9000 5 3.2 Кумулятивное распределение вероятностей для НЕПРЕРЫВНЫХ случайных величин (CDF) - Сводка распределений вероятностей
- Функция квантилей
- Спасибо за чтение и ссылки
Распределение плотности вероятности нормального распределения — это то, о чем люди чаще всего думают, когда слышат слово «распределение». Он имеет специфическую форму колокола:
PDF стандартного нормального распределения (нулевое среднее и стандартное отклонение 1). Источник: изображение автораФункция плотности вероятности (PDF) сопоставляет значение с его плотностью вероятности [1]. Это понятие похоже на физику, где плотность вещества — это его масса на единицу объема. Например, 1 литр воды весит примерно 1 кг, поэтому плотность воды составляет примерно 1 кг/л или 1000 кг/м³. Аналогично, плотность вероятности измеряет вероятность на единицу х .
PDF относится к непрерывной случайной величине , что означает, что переменная может принимать любое значение в пределах определенного диапазона действительных чисел. Random показывает неопределенность того, какие значения может принимать переменная. Это дает бесконечное количество возможностей, например 0,1, но также и 0,101, 0,1001 и т. д. Таким образом, вероятность того, что непрерывная случайная величина будет равна заданному значению, равна нулю.
Random показывает неопределенность того, какие значения может принимать переменная. Это дает бесконечное количество возможностей, например 0,1, но также и 0,101, 0,1001 и т. д. Таким образом, вероятность того, что непрерывная случайная величина будет равна заданному значению, равна нулю.
Вероятность на графике PDF представлена площадью под кривой плотности. Площадь под точкой равна нулю. Вот почему PDF используется для проверки вероятности того, что случайная величина попадает в заданный диапазон значений, а не для принятия какого-либо конкретного значения. Например, какова вероятность того, что мы потеряем деньги, инвестируя в фонд так, что доходность будет отрицательной? Здесь мы рассматриваем все доходы меньше нуля.
Интуитивно PDF представляет собой линию, описывающую гистограмму. Например, мы хотим разделить 992 участника эксперимента на возрастные группы (0–10, 11–20 и т. д.). Мы подсчитываем, сколько участников попадает в каждую группу, и представляем это в виде столбцов на гистограмме:
Гистограмма из 992 участников, разделенных на возрастные группы. Данные, полученные из нормального распределения. Изображение автора.
Данные, полученные из нормального распределения. Изображение автора.Насколько высока вероятность того, что человек, которого мы случайно выберем, будет членом данной возрастной группы? Во-первых, мы должны преобразовать распределение частот в распределение вероятностей. Это означает вычисление плотности вероятности на основе количества участников в каждой группе. Так как бары имеют прямоугольную форму и площадь под функцией плотности вероятности всегда равна 1, мы можем использовать упрощенное уравнение:
Для частот, представленных на предыдущем графике, мы имеем:
Теперь мы можем построить наши данные, используя плотности вместо подсчетов по оси Y. Красная кривая соединяет расчетные точки и обозначает функцию плотности вероятности:
PDF-график автора. Красная линия — функция плотности вероятности. Но обратите внимание, что я сгенерировал данные для этого графика из нормального распределения. Вот почему PDF и гистограмма так хорошо подходят. PDF имеет «закрытую» форму, что требует предварительного определения распределения и параметров (среднее значение и стандартное отклонение в случае нормального распределения).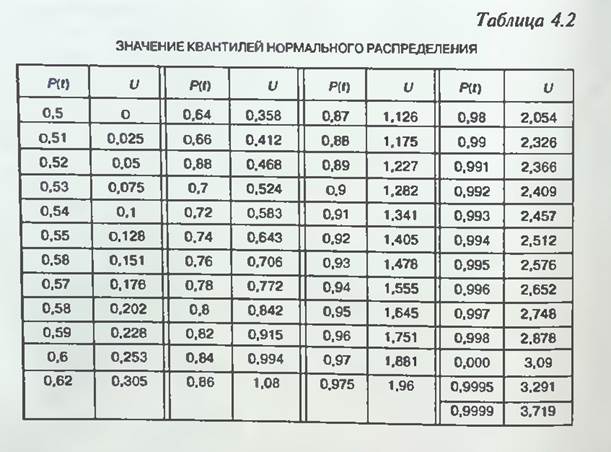 Гистограмма использует необработанные данные, поэтому она показывает реальное распределение. Это позволяет обнаруживать аномалии, особенно при большом количестве баров.
Гистограмма использует необработанные данные, поэтому она показывает реальное распределение. Это позволяет обнаруживать аномалии, особенно при большом количестве баров.
Интересуют другие параметры, используемые для описания распределения (математическое ожидание, дисперсия, асимметрия и эксцесс)? Перейти сюда:
Статистические моменты в интервью по науке о данных
Основная математика для специалистов по данным, объясненная с нуля
в направлении datascience.com
Ключевые моменты, которые следует помнить из приведенного выше анализа:
- Вероятность — это площадь под вероятностью кривая плотности (PDF).
- Вероятность того, что непрерывная случайная величина примет заданное значение, равна нулю. Итак, для заданного значения x мы можем проверить только плотность вероятности, что не очень полезно.
- Поэтому мы ориентируемся на интервалы значений. Это позволяет нам делать вероятностные утверждения о диапазоне значений.
 Например, есть вероятность 50%, что участнику будет не менее 40 лет.
Например, есть вероятность 50%, что участнику будет не менее 40 лет.
Функция массы вероятности (PMF) относится к дискретным случайным величинам. В отличие от непрерывных случайных величин, дискретные случайные величины могут принимать только счетное число дискретных значений, таких как 0, 1, 2,…. Простыми примерами являются бросание игральной кости, подбрасывание монеты или обнаружение мошеннических транзакций (мошенничество либо есть, либо его нет).
Подобно непрерывным случайным величинам, мы можем создать гистограмму дискретных данных. Но нет необходимости агрегировать значения в интервалы. Рассмотрим сумму бросков пары игральных костей. Количество результатов конечно, так как значения на обоих кубиках от 1 до 6. На графике ниже показан пример гистограммы для 1000 бросков правильной пары игральных костей:
Гистограмма сумм при 1000-кратном броске правильной пары игральных костей . Изображение автора. Оба кубика являются правильными, что означает, что вероятность выпадения каждого числа от 1 до 6 одинакова, равная 1/6. Таким образом, самая популярная сумма равна 7. Как и в случае с непрерывными случайными величинами, мы можем выразить каждый результат как вероятность.
Таким образом, самая популярная сумма равна 7. Как и в случае с непрерывными случайными величинами, мы можем выразить каждый результат как вероятность.
Если мы бросим пару кубиков, возможны 36 исходов (по 6 вариантов на каждом кубике). Если сумма равна 2, возможна только одна комбинация: (1,1). Таким образом, вероятность получить сумму, равную 2, равна 1/36 = 0,0278. Аналогично для суммы 12, возможно только для (6,6). Точно так же мы можем рассчитать вероятности других возможных исходов. Результаты, представленные на графике, создают функцию массы вероятности (PMF):
PMF суммы справедливой пары игральных костей. Изображение автора.Подводя итог, мы рассмотрели следующие типы графиков:
- Гистограмма — это график, показывающий, сколько раз каждый диапазон значений появляется в наборе данных. Он не требует каких-либо предположений о распределении, но мы должны заранее указать количество баров. Гистограмма строится из конечного числа выборок.
 Сумма значений гистограммы для всех баров равна общему количеству выборок.
Сумма значений гистограммы для всех баров равна общему количеству выборок. - Функция плотности вероятности (PDF) описывает плотность вероятности непрерывных случайных величин . Вероятность на PDF представляет собой площадь под кривой плотности. Поскольку вероятность данного значения равна нулю для непрерывных случайных величин, PDF используется для проверки вероятности того, что переменная попадает в заданный интервал. Вся площадь под PDF равна единице.
- Функция массы вероятности (PMF) описывает вероятность дискретных случайных величин . Это означает, что переменная может принимать только счетное число дискретных значений, таких как 0, 1, 2 и т. д. Сумма вероятностей всех дискретных значений в PMF равна единице.
Хотя все они очень полезны и широко используются в отрасли, есть еще одно важное распределение вероятностей — кумулятивная функция распределения (CDF).
Кумулятивная функция распределения (CDF) случайной величины X описывает вероятность (шансы) того, что X примет значение, равное или меньшее x. Математически это можно выразить так:
Математически это можно выразить так:
Взяв предыдущий пример с подбрасыванием правильной пары игральных костей, мы можем спросить: какова вероятность того, что сумма двух игральных костей меньше или равна 3? Нам нужно добавить вероятность суммы, равной 2 (0,0278), и вероятность суммы 3 (0,0556), поэтому совокупная вероятность для x = 3 составляет 0,0278 + 0,0556 = 0,0834. Затем мы повторяем процесс добавления для каждого дискретного значения, чтобы получить кумулятивную функцию распределения дискретного распределения вероятностей:
Кумулятивную функцию вероятности дискретного распределения вероятностей. Изображение автора.Как видно на графике, кумулятивная функция вероятности для максимально возможного исхода равна 1. Поскольку сумма двух игральных костей может принимать только целые значения, график можно выразить с помощью столбцов:
Накопительная функция вероятности дискретное распределение вероятностей. Изображение автора. 3.2. Кумулятивная функция распределения НЕПРЕРЫВНОГО распределения вероятностей (CDF)
Изображение автора. 3.2. Кумулятивная функция распределения НЕПРЕРЫВНОГО распределения вероятностей (CDF) Идея CDF для непрерывных переменных такая же, как и для дискретных переменных. Ось Y показывает вероятность того, что X примет значения, равные или меньшие, чем x. Отличие в том, что вероятность меняется даже при небольших перемещениях по оси x.
В примере с групповым возрастом участников кумулятивная функция распределения выглядит следующим образом:
Графики ниже сравнивают PDF и CDF нормального распределения с нулевым средним и стандартным отклонением, равным единице:
PDF и CDF нормального распределения N(0,1). Изображение автора.Мы можем сделать вывод, что:
- CDF является неубывающей функцией. Он показывает вероятность того, что переменная равна или меньше x, поэтому она может увеличиваться только с увеличением значения x.

- Мы можем проверить вероятность по обоим графикам, но использование CDF более просто. CDF показывает вероятность по оси y, а PDF имеет плотность вероятности по оси y. В случае PDF вероятность представляет собой площадь под кривой PDF.
- Поскольку нормальное распределение симметрично, CDF при x=0 (что означает среднее значение) составляет 0,5.
- Функция CDF с левой стороны асимптотична к 0 и 1 с правой стороны графика. Точные значения x зависят от типа распределения и параметров (среднее значение и стандартное отклонение для нормального распределения).
До сих пор мы рассмотрели три способа описания распределения вероятностей: функция плотности вероятности (PDF), функция массы вероятности (PMF) и кумулятивная функция распределения (CDF). Основные различия между PDF и PMF представлены в таблице ниже:
Основные различия между PDF и PMF. Изображение автора. Кумулятивная функция распределения показывает вероятность того, что X примет максимальное значение x.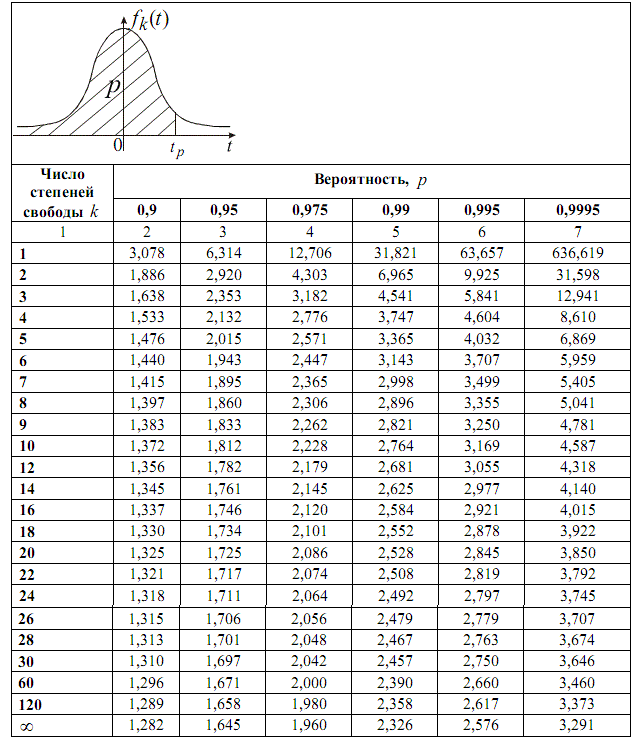 Он суммирует шансы для всех меньших значений и шансов, равных x. Поскольку ось Y представляет собой вероятность, использование CDF часто более просто, чем для PDF.
Он суммирует шансы для всех меньших значений и шансов, равных x. Поскольку ось Y представляет собой вероятность, использование CDF часто более просто, чем для PDF.
На следующей схеме показаны типичные графики каждого распределения, по часовой стрелке и начиная с верхнего левого угла: PDF, PMF, CMF, CDF. Он обобщает высокоуровневую характеристику и описывает отношения между заданными типами функций распределения.
Сравнение различных типов дистрибутивов. Изображение автора вдохновлено [1,2].Как видно выше, существует некоторая связь между различными способами отображения распределения вероятностей.
- Для непрерывных случайных величин мы можем легко построить PDF и CDF. Область под PDF — это вероятность, поэтому нам нужно интегрировать, чтобы преобразовать PDF в CDF, или дифференцировать, чтобы перейти от CDF к PDF.
- Для дискретных случайных величин PMF показывает вероятность, а CDF (CMF) — кумулятивную вероятность. Чтобы получить CMF из PMF, мы должны сложить вероятности до заданного x.
 Чтобы пойти наоборот (от CMF к PMF), мы должны вычислить разницу между шагами.
Чтобы пойти наоборот (от CMF к PMF), мы должны вычислить разницу между шагами. - Если мы разделим все значения на набор бинов (см. примеры с гистограммами выше), мы можем перейти от PDF к виду PMF. Он использует диапазон значений/интервалов и может рассматриваться как аппроксимация PDF. Чтобы перейти от дискретного кумулятивного распределения к непрерывной функции, необходима некоторая форма сглаживания. Это можно сделать, предположив, что данные поступают из определенного непрерывного распределения, такого как нормальное или экспоненциальное, и оценив параметры этого распределения. Изменение дискретной и непрерывной случайной величины в обоих направлениях следует рассматривать как аппроксимацию.
Позвольте представить суперзвезду распределений — функцию квантилей. Это позволяет использовать распределения для многих практических целей, таких как поиск доверительных интервалов и проверка гипотез.
Математическое определение состоит в том, что квантильная функция является обратной функцией распределения при α. Он определяет значение случайной величины так, что вероятность того, что переменная меньше или равна этому значению, равна заданной вероятности:
Он определяет значение случайной величины так, что вероятность того, что переменная меньше или равна этому значению, равна заданной вероятности:
Где F⁻¹(α) обозначает α-квантиль X.
Сейчас это может показаться немного загадочным, но при ближайшем рассмотрении сомнения развеются. Предположим, что мы хотим проверить 5% общей площади в нижнем хвосте распределения. Мы называем это нижним 5% квантилем X и записываем как F⁻¹(0,05). Квантиль — это распределение вероятностей, разделенное на области с равной вероятностью. Если рассматривать проценты, то сначала делим раздачу на 100 штук. Когда мы смотрим в PDF, 5-й квантиль — это точка, которая отсекает площадь 5% в нижней части распределения:
Нижний 5% квантиль для нормального распределения N(0,1). Изображение автора. Площадь под PDF слева от красной линии составляет ровно 5% от общей площади под кривой. Это подразумевает вероятность 5%. Первым шагом к рисованию красной линии было вычисление, где заканчивается 0,05 общей площади (здесь x=-1,645).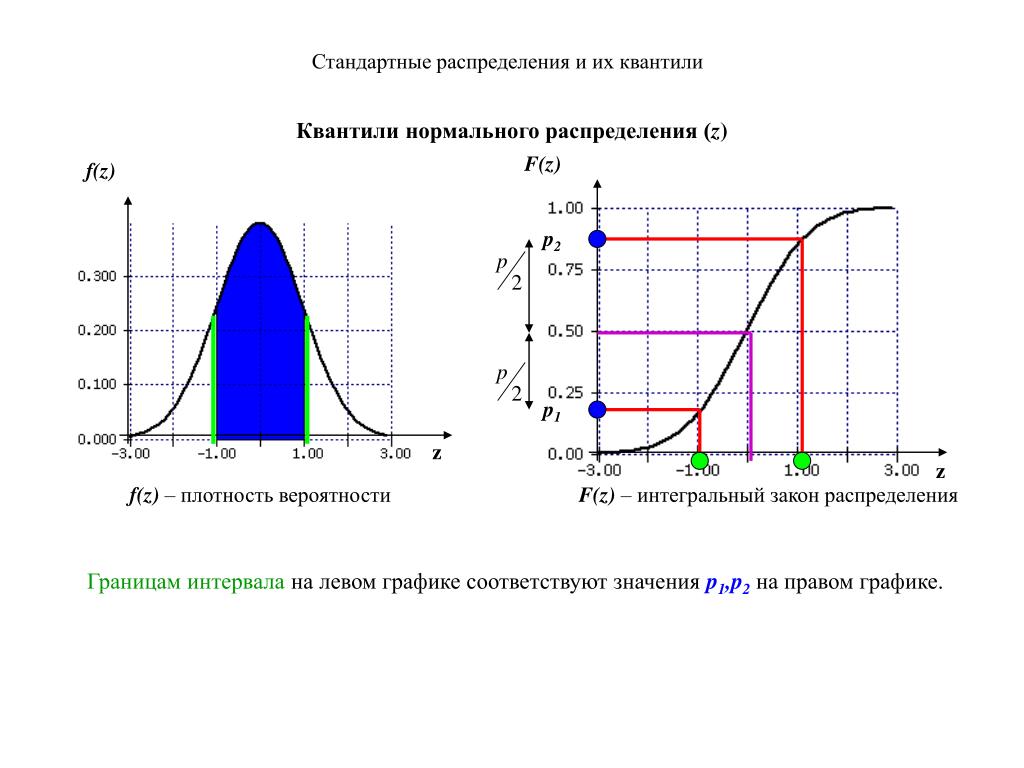 Это можно сделать с помощью программного обеспечения (например, функция qnorm() в R или scipy.stats.norm.ppf() в Python) или вручную с использованием z-таблиц (пример здесь).
Это можно сделать с помощью программного обеспечения (например, функция qnorm() в R или scipy.stats.norm.ppf() в Python) или вручную с использованием z-таблиц (пример здесь).
Поскольку CDF имеет вероятность (α) по оси y, проще найти это значение здесь:
Нижний 5% квантиль для нормального распределения N(0,1). Изображение автора.Это показывает, насколько полезны графики CDF. Мы можем использовать CDF в обоих направлениях:
- Если у нас есть значение z (или значение x, значение на оси x), мы можем проверить вероятность того, что X примет значение, равное или меньшее, чем x. Например, какова вероятность того, что средняя продолжительность пребывания клиента в интернет-магазине составляет полчаса или меньше?
- Если у нас есть вероятность, мы можем проверить значение, которое отсекает область данной альфы. Например, с 90% уверенности, можно сказать, что клиент проводит в интернет-магазинах не менее X часов.
В приведенном выше примере мы рассмотрели только односторонний 5% квантиль (нижний хвост). Мы можем сделать то же самое для 5% вероятности с двух сторон. Это означает, что мы ищем 5% общей площади под PDF, но разделены на 2,5% нижнего квантиля (слева) и 2,5% верхнего квантиля (на правой стороне графика).
Мы можем сделать то же самое для 5% вероятности с двух сторон. Это означает, что мы ищем 5% общей площади под PDF, но разделены на 2,5% нижнего квантиля (слева) и 2,5% верхнего квантиля (на правой стороне графика).
Таким образом, квантили являются прямой связью между этими графиками.
Основываясь на графиках, мы можем сказать, что у нас есть 95% уверенность в том, что истинный параметр (среднее значение) находится между -1,96 и 1,96. Или что существует 5% вероятность того, что оно находится за пределами диапазона от -1,96 до 1,96.
Приведенная выше интерпретация подчеркивает, что:
- уровень достоверности говорит нам, насколько вероятно рассматриваемое событие или каковы шансы того, что данный параметр находится в заданном диапазоне значений.
- альфа или уровень значимости — это вероятность. Мы можем проверить это по оси Y на графике CDF. Альфа — это один минус уровень достоверности.
Несколько замечаний:
- Обратная функция Φ⁻¹(α) является α-квантилем
- Когда α мало, квантиль также называется критическим значением 0010 Некоторые квантили имеют специальные имена .
 Если мы разделим вероятность на 100 частей, мы получим процентили. Мы можем сказать 5-й процентиль вместо 5% квантиля. 4-квантили называются квартилями и делятся на 4 части с разбивкой по значениям 25%, 50% (медиана) и 75%.
Если мы разделим вероятность на 100 частей, мы получим процентили. Мы можем сказать 5-й процентиль вместо 5% квантиля. 4-квантили называются квартилями и делятся на 4 части с разбивкой по значениям 25%, 50% (медиана) и 75%. - Для стандартного нормального распределения (нормальное распределение с нулевым средним значением и стандартным отклонением, равным единице N(0,1)), которое симметрично относительно нуля, мы имеем:
Это доказано на графиках выше, поскольку мы получаем — 1,96 на нижнем оперении и 1,96 на верхнем оперении.
Используя квантили, PDF, CDF, мы можем ответить на разные вопросы в зависимости от информации, которой мы владеем, например:
- Учитывая выборочное среднее, каков диапазон значений, содержащих среднее значение генеральной совокупности, в котором мы достаточно уверены? «Разумно» может принимать различные процентные значения и зависит от цели нашего исследования.
- С какой степенью уверенности можно сказать, что доходность не будет отрицательной?
Я рад, что вы дочитали до конца этой статьи. Мы рассмотрели различные типы распределений вероятностей: функция плотности вероятности (PDF), функция массы вероятности (PMF) и кумулятивная функция плотности (CDF). Затем мы обсудили функцию количества. Он связывает различные способы описания дистрибутивов (PDF и CDF) и позволяет нам использовать эти дистрибутивы очень практичным образом. Надеюсь, это было увлекательное путешествие для вас.
Мы рассмотрели различные типы распределений вероятностей: функция плотности вероятности (PDF), функция массы вероятности (PMF) и кумулятивная функция плотности (CDF). Затем мы обсудили функцию количества. Он связывает различные способы описания дистрибутивов (PDF и CDF) и позволяет нам использовать эти дистрибутивы очень практичным образом. Надеюсь, это было увлекательное путешествие для вас.
Помните, что самый эффективный способ выучить (математические) навыки — это практика . Так что не ждите, пока вы почувствуете себя «готовым», просто возьмите ручку и бумагу (или ваше любимое программное обеспечение) и попробуйте несколько примеров самостоятельно. Держу за тебя пальцы скрещенными.
Я буду рад услышать ваши мысли и вопросы в разделе комментариев ниже, связавшись со мной напрямую через мой профиль LinkedIn или по телефону [email protected]. До скорой встречи!
Вам также может понравиться:
Statistical Moments in Data Science интервью
Основная математика для специалистов по данным: объяснение с нуля
в направлении datascience.

 Математическая статистика. Комбинаторика. / / Таблица. Функция распределения вероятностей стандартного нормального закона. Таблица квантилей стандартного нормального закона распределения.
Математическая статистика. Комбинаторика. / / Таблица. Функция распределения вероятностей стандартного нормального закона. Таблица квантилей стандартного нормального закона распределения. 00
00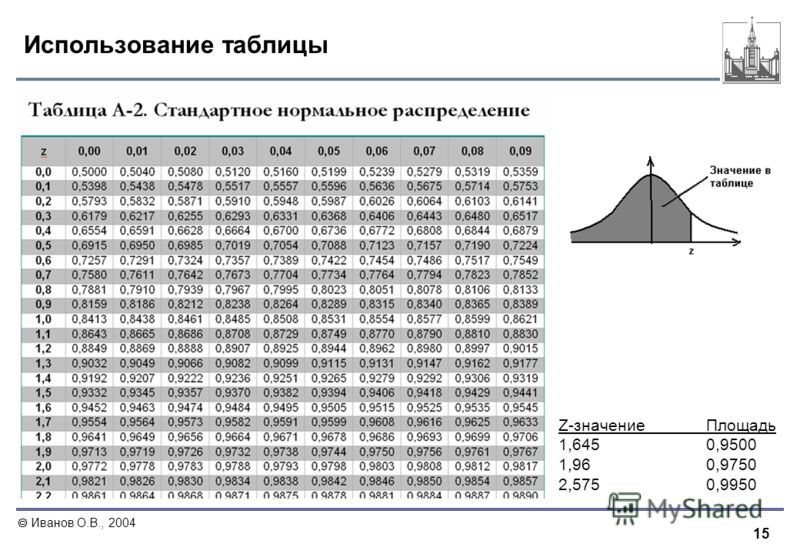
 6844
6844 8
8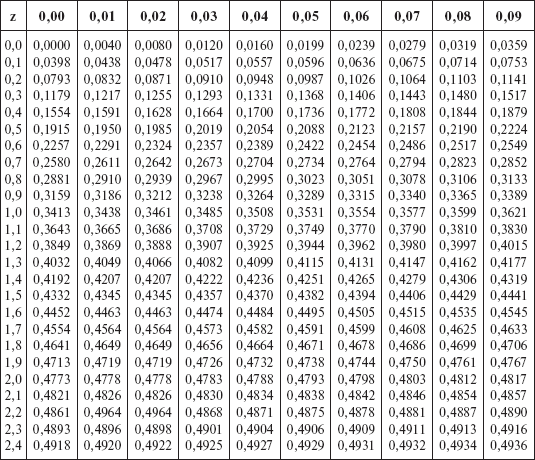 8686
8686 9265
9265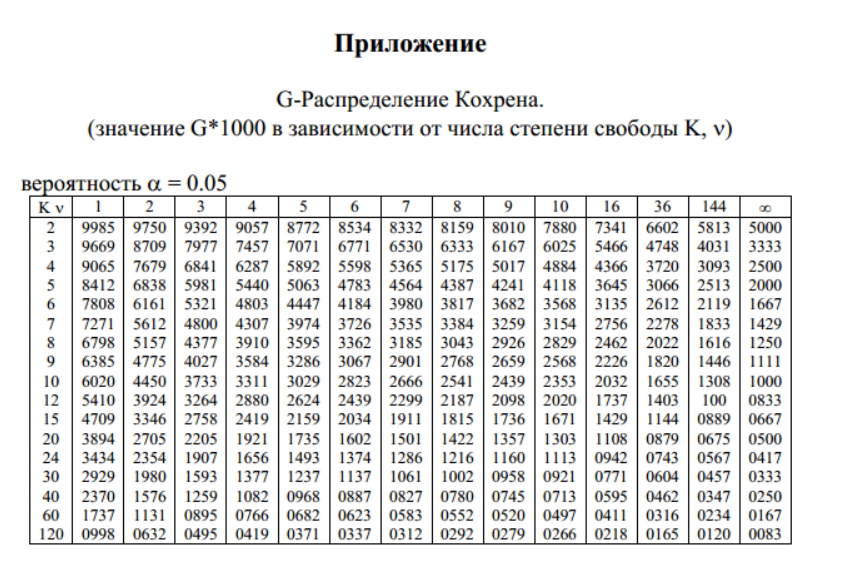 9625
9625 1
1 9922
9922 9970
9970 9990
9990 4
4 50
50 70
70 90
90 ru
ru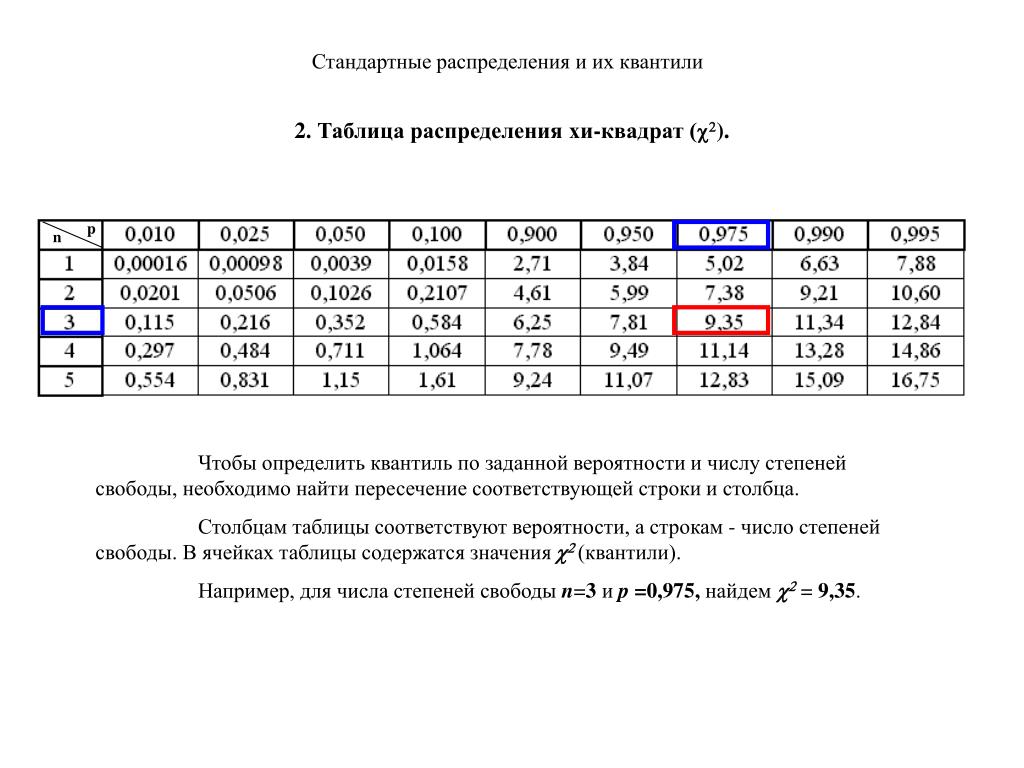 — 487 с.
— 487 с.
 1 Кумулятивное распределение вероятностей для ДИСКРЕТНЫХ случайных величин (CMF) 9000 5 3.2 Кумулятивное распределение вероятностей для НЕПРЕРЫВНЫХ случайных величин (CDF)
1 Кумулятивное распределение вероятностей для ДИСКРЕТНЫХ случайных величин (CMF) 9000 5 3.2 Кумулятивное распределение вероятностей для НЕПРЕРЫВНЫХ случайных величин (CDF) Например, есть вероятность 50%, что участнику будет не менее 40 лет.
Например, есть вероятность 50%, что участнику будет не менее 40 лет.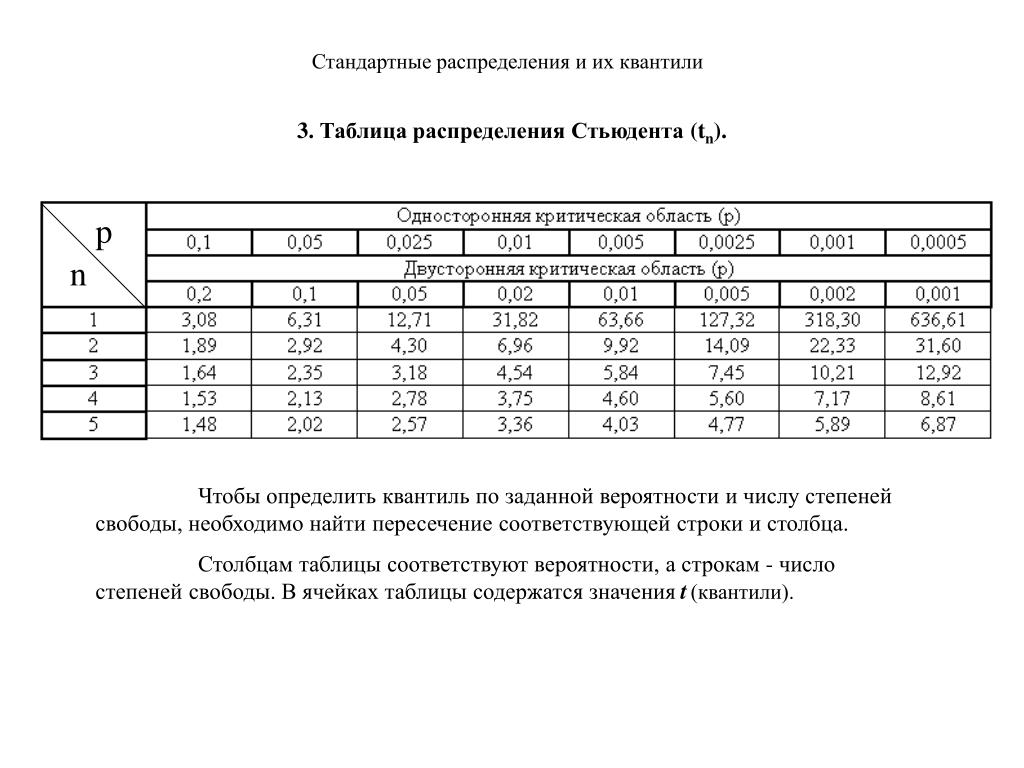 Сумма значений гистограммы для всех баров равна общему количеству выборок.
Сумма значений гистограммы для всех баров равна общему количеству выборок.
 Чтобы пойти наоборот (от CMF к PMF), мы должны вычислить разницу между шагами.
Чтобы пойти наоборот (от CMF к PMF), мы должны вычислить разницу между шагами. Если мы разделим вероятность на 100 частей, мы получим процентили. Мы можем сказать 5-й процентиль вместо 5% квантиля. 4-квантили называются квартилями и делятся на 4 части с разбивкой по значениям 25%, 50% (медиана) и 75%.
Если мы разделим вероятность на 100 частей, мы получим процентили. Мы можем сказать 5-й процентиль вместо 5% квантиля. 4-квантили называются квартилями и делятся на 4 части с разбивкой по значениям 25%, 50% (медиана) и 75%.