Корень 13 степени из произвольного числа из ста знаков за 4 секунды • иллюстрации
Корень 13 степени из произвольного числа из ста знаков за 4 секунды • иллюстрацииИстории и иллюстрации Талант
27-летний Алексис Лемэр установил новый рекорд в скорости вычислений во вторник в британском Музее науки. Число, из которого он должен был извлечь корень, выбрал компьютер. Лемер без ошибки выдал ответ всего через 70,2 секунды. Его предыдущий рекорд составлял 72,4 сек.
Как рассказывает куратор математического отдела музея Джейн Уэсс, «он сел, и установилась полная тишина. Вдруг стало ясно, что он каким-то чудом решил задачу».
«Я думаю, что это было самое сложное математическое вычисление, которое когда-либо выполнялась в уме, — указывает он. — Похоже, у Алексиса феноменальная память, и, кроме того, он всю жизнь занимается этим. Очень интересно было наблюдать за ним. Немногие обладают такими способностями, наверное, всего несколько человек».
Лемэр, который учится в университете города Реймс на севере Франции, вначале демонстрировал способность извлекать корень 13 степени из произвольного числа из ста знаков. Однако после того, как в 2004 году он дал ответ менее, чем за 4 секунды, он больше не пытался улучшить свой результат.
Как все спортсмены, Алексис Лемер ежедневно тренирует память на более сложных примерах с 200-значными числами.
Сообщество Вконтакте
Понравилось?
оцените
Свежие иллюстрации:
- Праздничное ограбление канадского магазина Food Basics
- Морковь, яйцо и молотый кофе
- Сколько будет бесконечность плюс бесконечность?
- Сто лет с момента основания Тель-Авива
Q.Информация:
добавить
иллюстрацию
- авторов:
- 178
- историй:
- 1097
46455 просмотров за эту неделю
Q.Ресурсы:
Q.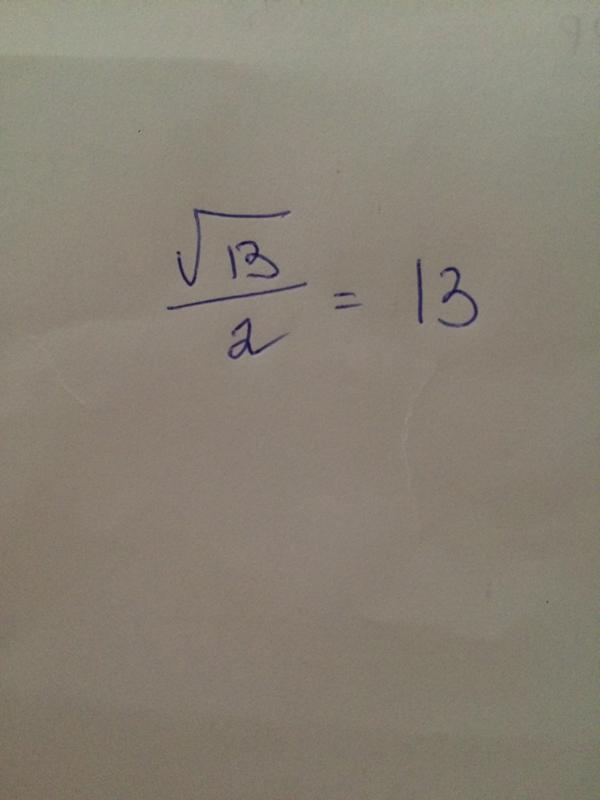 Орфография:
Орфография:
Если Вы заметили любого рода ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter. Мы рассматриваем каждый Ваш сигнал с благодарностью за Вашу помощь!
Разделы сайта:
- » Видео
- » Загадки
- » Игры
- » Идеи
- » Илл-ции
- » Комиксы
- » Лагерь
- » Новости
- » Опросы
- » Ответы
- » Открытки
- » Песни
- » Послания
- » Поделки
- » Поэзия
- » Психология
- » Рассказы
- » info»>Свадьбы
- » Статистика
- » Страсти Хр.
- » Сценки
- » Тесты
- » Фильмы
- » Фразы
- » Шутки
Авторские права на размещенные материалы [если не оговорено иначе] принадлежат авторам; в случае заимствования материалов для дальнейшей публикации их в электронных или печатных изданиях обязательно наличие явной активной ссылки на сайт Uucyc.ru.
Все права сохранены.
© 2000-2023, Uucyc.ruGT: [0.0022]
Квадратный корень из 13 (√13)
В этой статье мы собираемся вычислить квадратный корень из 13, узнать, что такое квадратный корень, и ответить на некоторые часто задаваемые вопросы. Мы также рассмотрим различные методы вычисления квадратного корня из 13 (как с компьютером/калькулятором, так и без него).
Квадратный корень из 13 Определение
В математической форме мы можем представить квадратный корень из 13, используя знак радикала, например: √13. Это обычно называют квадратным корнем из 13 в радикальной форме.
Так что же такое квадратный корень? В этом случае квадратный корень из 13 — это количество (которое мы будем называть q), которое при умножении само на себя будет равно 13.
√13 = q × q = q 2
Является ли число 13 идеальным квадратом?
В математике мы называем число 13 полным квадратом, если квадратный корень из 13 представляет собой целое число.
В этом случае, как мы увидим в вычислениях ниже, мы видим, что 13 не является полным квадратом.
Чтобы узнать больше о идеальных квадратах, вы можете прочитать о них и просмотреть список из 1000 из них в нашем разделе Что такое идеальный квадрат? статья.
Является ли квадратный корень из 13 рациональным или иррациональным?
Обычный вопрос состоит в том, является ли квадратный корень из 13 рациональным или иррациональным. Рациональные числа можно записать в виде дроби, а иррациональные — нет.
Рациональные числа можно записать в виде дроби, а иррациональные — нет.
Быстрый способ проверить это — посмотреть, является ли число 13 правильным квадратом. Если да, то это рациональное число. Если это не идеальный квадрат, то это иррациональное число.
Мы уже знаем, является ли 13 полным квадратом, поэтому мы также можем видеть, что √13 — иррациональное число.
Можно ли упростить квадратный корень из 13?
13 можно упростить, только если вы можете уменьшить 13 внутри радикального символа. Это процесс, который называется упрощением сурда. В этом примере квадратный корень из 13 не может быть упрощен.
√13 уже находится в простейшей радикальной форме.
Как вычислить квадратный корень из 13 с помощью калькулятора
Если у вас есть калькулятор, то самый простой способ вычислить квадратный корень из 13 — воспользоваться этим калькулятором. На большинстве калькуляторов это можно сделать, набрав 13 и нажав клавишу √x. Вы должны получить следующий результат:
√13 ≈ 3,6056
Как вычислить квадратный корень из 13 с помощью компьютера
На компьютере вы также можете вычислить квадратный корень из 13 с помощью Excel, Numbers или Google Sheets и функции SQRT, например:
SQRT(13) ≈ 3,605551275464
Чему равен квадратный корень из 13 с округлением?
Иногда вам может понадобиться округлить квадратный корень из 13 до определенного числа знаков после запятой. Вот решения для этого, если это необходимо.
Вот решения для этого, если это необходимо.
10-й: √13 ≈ 3,6
100-й: √13 ≈ 3,61
1000-й: √13 ≈ 3,606
Что такое квадратный корень из 13 в виде дроби?
Ранее в этой статье мы говорили о том, что только рациональное число может быть представлено в виде дроби, а иррациональное число — нет.
Как мы сказали выше, поскольку квадратный корень из 13 является иррациональным числом, мы не можем превратить его в точную дробь. Однако мы можем превратить его в приблизительную дробь, используя квадратный корень из 13, округленный до сотых.
√13
≈ 3,6/1
≈ 361/100
≈ 3 61/100
Что такое квадратный корень из 13, записанный с показателем степени?
Все вычисления квадратного корня могут быть преобразованы в число (называемое основанием) с дробным показателем степени. Давайте посмотрим, как это сделать с квадратным корнем из 13:
√b = b ½
√13 = 13 ½
используйте метод длинного деления для вычисления квадратного корня из 13.
 Это очень полезно для тестов на длинное деление, и именно так математики вычисляли квадратный корень из числа до изобретения калькуляторов и компьютеров.
Это очень полезно для тестов на длинное деление, и именно так математики вычисляли квадратный корень из числа до изобретения калькуляторов и компьютеров.Шаг 1
Разместите 13 в парах из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный знак:
Шаг 2
Начиная с первого набора: самый большой совершенный квадрат меньше или 13 равно 9, а квадратный корень из 9 равен 3. Поэтому поставьте 3 сверху и 9 снизу вот так:
| 3 | |
13 | 00 |
9 |
Шаг 3
Вычислите 13 минус 9 и запишите разницу ниже. Затем переместитесь вниз к следующему набору чисел.
| 3 | |
13 | 00 |
4 | 00 |
Шаг 4
Удвойте число, выделенное зеленым сверху: 3 × 2 = 6. Затем используйте 6 и нижнее число, чтобы решить эту задачу:
Затем используйте 6 и нижнее число, чтобы решить эту задачу:
6? × ? ≤ 400
Знаки вопроса «пробел» и такие же «пробел». Путем проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 6.
Теперь введите 6 сверху:
| 3 | 6 |
13 | 00 |
9 | |
4 | 00 |
Вот и все! Ответ показан вверху зеленым цветом. Квадратный корень из 13 с точностью до одной цифры после запятой равен 3,6. Обратите внимание, что последние два шага фактически повторяют два предыдущих. Чтобы добавить десятичные знаки к вашему ответу, вы можете просто добавить больше наборов 00 и повторить последние два шага.
Квадратный корень из 13 | Thinkster Math
Методы
Что такое квадратный корень из 13?
Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5 x 5 = 25. Выражаясь в радикальной форме: √25 = 5. Следовательно, находя квадратный корень из 13, мы находим, что квадратный корень из 13 3,606 . Всегда помните: ваш ответ может быть как целым, так и десятичным числом.
Например, квадратный корень из 25 равен 5, потому что 5 x 5 = 25. Выражаясь в радикальной форме: √25 = 5. Следовательно, находя квадратный корень из 13, мы находим, что квадратный корень из 13 3,606 . Всегда помните: ваш ответ может быть как целым, так и десятичным числом.
Является ли квадратный корень из 13 иррациональным?
Числа можно разделить на подмножества, называемые рациональными и иррациональными числами. Примером иррациональных чисел являются десятичные дроби, которые не имеют конца или не заканчиваются. Распространенная путаница заключается в том, что, поскольку у десятичной дроби нет конца, это большое число, стремящееся к бесконечности, хотя это неверно.
Взгляните на экспоненциальную константу e, e имеет значение 2,7182818… и является неограниченным, но не огромным значением, потому что в конце дня e никогда не будет больше 3. С другой стороны, рациональные числа — это десятичные дроби, которые можно записать в виде дробей, делящих два целых числа (если знаменатель не равен 0). Таким образом, для этой задачи, поскольку квадратный корень из 13, или 3,606, является неконечной десятичной дробью, квадратный корень из 13 иррационален.
Таким образом, для этой задачи, поскольку квадратный корень из 13, или 3,606, является неконечной десятичной дробью, квадратный корень из 13 иррационален.
Методы нахождения квадратного корня из 13
Начнем с того, что есть два способа вычисления квадратного корня из числа: разложение на простые множители и длинное деление. Обычно простая факторизация используется для идеальных квадратов, а длинное деление используется, когда значение квадратного корня является десятичным.
Поскольку мы знаем, что 13 — десятичное число, мы знаем, что подходящим методом будет деление в длинную сторону. Этот метод работает очень похоже на обычное длинное деление, за исключением того, что в этом методе есть еще несколько правил, которые помогают нам получить ответ. Взгляните на этот пример, в котором подробно рассказывается о том, что представляет собой этот метод, как его использовать, а также приводится несколько решенных примеров. Таким образом, результат после использования метода деления в большую сторону равен 3,606.
Нахождение квадратного корня из других чисел
Нахождение квадратного корня любого числа можно выполнить с помощью того же метода, который показан выше. Посмотрите, как найти квадратный корень из этих других конкретных примеров, нажав на любую из ссылок ниже:
Квадратный корень из 1493
Квадратный корень из 2950
Квадратный корень из 3869
Квадратный корень из 1817
Квадратный корень из 1774
Загрузите БЕСПЛАТНЫЕ математические ресурсы
Воспользуйтесь нашими бесплатными загружаемыми ресурсами и учебными материалами для обучения дома.
8 математических хитростей и хитростей, которые превратят вашего «хорошего» студента-математика в чемпиона по математике!
Одна вещь, которой мы учим наших студентов в Thinkster, состоит в том, что есть несколько способов решить математическую задачу. Это помогает нашим ученикам научиться мыслить гибко и нелинейно.
Получить PDFКак сделать так, чтобы ваш ребенок добился больших успехов и стал миллионером
Как родитель, вы надеетесь, что ваш ребенок станет очень успешным и, вероятно, станет следующим Гейтсом, Цукербергом или Мег Уитман.
