Корень 27 в степени 3: Найдите значение выражения: √27/√3 — ответ на Uchi.ru

2

Корень n-ой степени и его свойства

Цели урока:

Образовательная: создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач.

Развивающая: создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.

Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.

Ход урока

1. Организационный момент.

Добрый день! Добрый час!

Как я рада видеть вас.

Прозвенел уже звонок

Начинается урок.

Улыбнулись. Подравнялись.

Друг на друга поглядели

И тихонько дружно сели.

 

2. Мотивация урока.

Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

— Что есть больше всего на свете? – Пространство.

— Что быстрее всего? – Ум.

— Что мудрее всего? – Время.

— Что приятнее всего? – Достичь желаемого.

Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

 

3. Актуализация знаний.

1. Назовите взаимообратные алгебраические операции над числами. (Сложение и вычитание, умножение и деление)

2. Всегда ли можно выполнить такую алгебраическую операцию, как деление? (Нет, делить на нуль нельзя)

3. Какую еще операцию вы можете выполнять с числами? (Возведение в степень)

4. Какая операция будет ей обратной? (Извлечение корня)

5. Корень какой степени вы можете извлекать? (Корень второй степени)

6. Какие свойства квадратного корня вы знаете? (Извлечение квадратного корня из произведения, из частного, из корня, возведение в степень)

7. Найдите значения выражений:

, , , ,

Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин (при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.

 

4. Изучение нового материала.

Очевидно, что в соответствии с основными свой­ствами степеней с натуральными показателями, из любого положительного числа существует два проти­воположных значения корня четной степени, напри­мер, числа 4 и -4 являются корнями квадратными из 16, так как (-4)2 = 42 = 16, а числа 3 и -3 являют­ся корнями четвертой степени из 81, так как (-3)4 = З4 = 81.

Кроме того, не существует корня четной степени из отрицательного числа, поскольку четная степень любого действительного числа неотрицательна. Что же касается корня нечетной степени, то для любого действительного числа существует только один ко­рень нечетной степени из этого числа. Например, 3 есть корень третьей степени из 27, так как З3 = 27, а -2 есть корень пятой степени из -32, так как (-2)5 = 32.

В связи с существованием двух корней четной сте­пени из положительного числа, введем понятие ариф­метического корня, чтобы устранить эту двузначность корня.

Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.

Обозначение: – корень n-й степени.

Число n называется степенью арифметического корня. Если n = 2, то степень корня не указывается и пишется. Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.

= b, b2 = а, а ≥ 0, b ≥ 0

= b, bп = а, п – четное а ≥ 0, b ≥ 0

п – нечетное а, b – любые

Свойства

1. , а ≥ 0, b ≥ 0

2. , а ≥ 0, b >0

3. , а ≥ 0

4. , m, n, k – натуральные числа

 

5. Закрепление нового материала.

Устная работа

а) Какие выражения имеют смысл?

; ; ; ;

; ; ; ;

; ; ; ;

; ; ; .

б) При каких значениях переменной а имеет смысл выражение?

 

в) Вычислите:

Решить № 3, 4, 7, 9, 11.

 

6. Физкультминутка.

Во всех делах умеренность нужна,

Пусть будет главным правилом она.

Гимнастикой займись, коль мыслил долго,

Болезни чтоб прогнать и сохранить здоровье.

Гимнастика не изнуряет тела,

Но очищает организм всецело!

Закройте глаза, расслабьте тело,

Представьте – вы птицы, вы вдруг полетели!

Теперь в океане дельфином плывете,

Теперь в саду яблоки спелые рвете.

Налево, направо, вокруг посмотрели,

Открыли глаза, и снова за дело!

 

7.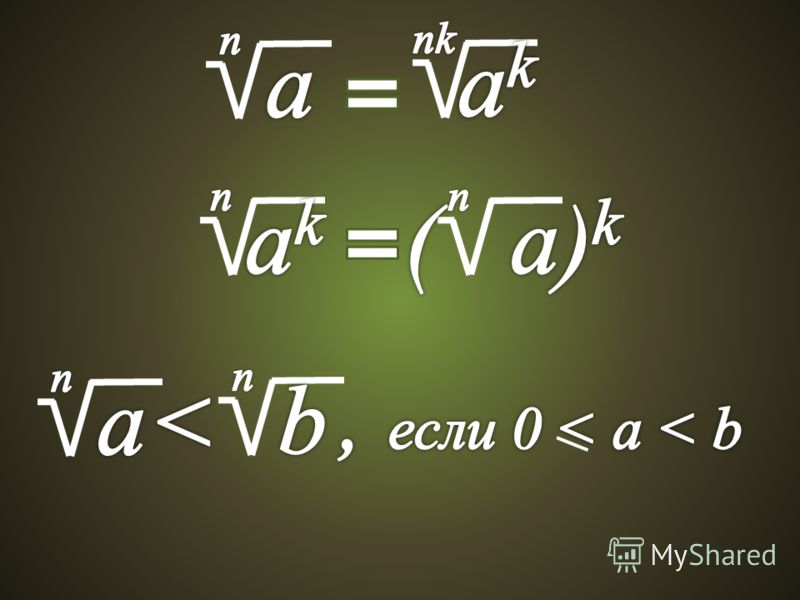 Самостоятельная работа.

Работа в парах с. 178 №1, №2.

 

8. Д/з. Выучить п.10 (с.160-161), решить № 5, 6, 8, 12, 16(1, 2).

 

9. Итоги урока. Рефлексия деятельности.

Достиг ли урок своей цели?

Чему вы научились?

Видео с вопросами: Упрощение алгебраических выражений с использованием законов экспонент, включающих рациональные и отрицательные экспоненты

Стенограмма видео

Определите простейшую форму числа 16, возведенного в степень три над двумя 𝑥 умножить на 27 в степени 𝑥 минус один над тремя все разделить на 144, возведенное в степень три над двумя 𝑥, умноженное на квадратный корень из 81.

Нам дано показательное выражение в виде дроби, где и числитель, и знаменатель состоят из произведений самих экспоненциальных выражений. Чтобы упростить это, мы будем использовать законы показателей степени вместе с простой факторизацией оснований, напомнив, что основание 𝑎 — это натуральное число, не равное единице, возведенной в степень 𝑏. Мы рассмотрим наше выражение почленно. Итак, давайте сначала посмотрим на квадратный корень из 81 в знаменателе. Мы знаем, что девять в квадрате равно 81, так что на самом деле девять равно квадратному корню из 81. Итак, мы можем заменить квадратный корень из 81 в нашем знаменателе на девять.

Теперь давайте разобьем наши основания 16, 27, 144 и девять на их простые множители. Мы знаем, что 16 — это четыре в квадрате, то есть два, умноженные сами на себя четыре раза, так что 16 — это два, возведенные в степень четыре. 27 — это девять умножить на три, то есть три, умноженное само на себя трижды. И это три в кубе, три в степени три. 144 — это 12 в квадрате, то есть четыре раза по три в квадрате. И это два в степени четыре, умноженное на три в квадрате, а затем девять, то есть три в квадрате, трижды три. Освободив немного места, мы можем поместить их в наше выражение.

Итак, наше выражение теперь равно двум в степени четыре все в степени три над двумя 𝑥 умножить на три в степени три все в степени 𝑥 минус один на три разделить на три в квадрате умножить на два в степени в степени четырех все в степени три над двумя 𝑥 умножить на три в квадрате.

Теперь давайте рассмотрим первый член нашего знаменателя. Чтобы разбить это, мы можем использовать силу правила произведения для показателей. Это говорит нам о том, что 𝑎, умноженное на 𝑏, возведенное в степень 𝑚, равно 𝑎, возведенное в степень 𝑚, умноженное на 𝑏, возведенное в степень 𝑚. Это дает нам три в квадрате, возведенные в степень три над двумя 𝑥, умноженные на два в четвертой степени, возведенные в степень три над двумя 𝑥.

Итак, теперь, если мы разделим их в нашем знаменателе, мы увидим, что у нас есть общий множитель в нашем числителе и знаменателе двух, возведенных в степень четыре, и всех, возведенных в степень три над двумя 𝑥. И мы можем затем разделить верх и низ на этот коэффициент. Теперь у нас осталось три в степени трех, все возведенные в степень 𝑥 минус один на три, деленное на три в квадрате, в степень три на два 𝑥, умноженное на три в квадрате.

Итак, все наши базы теперь имеют степень 3. И мы можем использовать степенной закон для показателей степени, чтобы упростить каждый термин. Тогда показатель степени в нашем числителе становится равным трем, умноженным на 𝑥 минус один на три, то есть три 𝑥 минус один. И показатель степени в левой части нашего знаменателя становится два, умноженные на три над двумя 𝑥, то есть три 𝑥. Тогда наш числитель равен трем, возведенным в степень три 𝑥 минус один, а наш знаменатель три возведен в степень три 𝑥, умноженный на три в квадрате.

Таким образом, у нас есть три, возведенные в степень три 𝑥 минус единица, деленная на три, возведенная в степень три 𝑥, умноженная на три в квадрате. Теперь в числителе мы можем использовать закон произведения для показателей степени. То есть 𝑎 в степени 𝑚 плюс 𝑛 ​​равно 𝑎 в степени 𝑚, умноженной на 𝑎 в степени 𝑛. В нашем случае основание 𝑎 равно трем, первый показатель 𝑚 равен трем 𝑥, а второй показатель 𝑛 отрицателен.

Итак, наш числитель превращается в три в степени три 𝑥, умноженные на три в степени минус один. Теперь мы снова видим, что у нас есть общий делитель в нашем числителе и знаменателе трех, возведенных в степень три 𝑥. Итак, разделив и числитель, и знаменатель на три в степени три 𝑥, у нас останется три в степени минус один на три в квадрате.

Итак, наконец, используя закон для отрицательных показателей, то есть 𝑎, возведенное в отрицательную степень, 𝑚 равно единице над 𝑎, возведенной в степень 𝑚, где в нашем случае 𝑚 равно единице. Итак, у нас есть один на три в квадрате, умноженный на три, возведенный в степень один. Итак, в нашем знаменателе мы снова можем использовать правило произведения. И это дает нам один на три, возведенный в степень два плюс один. Это один к трем в кубе, то есть один к 27.

Следовательно, простейшая форма данного выражения — один к 27. 9(2/3)

RD SHARMA АНГЛИЙСКИЙ-ЭКСПОНЕНТЫ РЕАЛЬНОГО ЧИСЛА-Все вопросы

20 видео

РЕКЛАМА

Ab Padhai karo bina ads ke

Khareedo DN Pro and dekho sari videos bina kisi ad ki rukaavat!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.