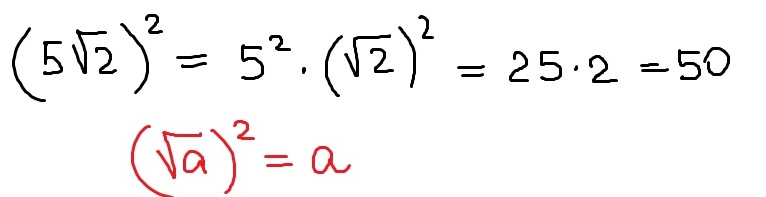Квадратный корень из произведения и дроби. 8-й класс
Тип урока: повторение и систематизация знаний
Цели:
- Образовательные:
- изучить способы преобразования выражений, содержащих разность квадратов под знаком корня;
- ознакомиться со свойствами квадратного корня из произведения и дроби.
- Развивающие:
- развивать умения учащихся решать задачи с использованием свойств квадратного корня из произведения и дроби;
- совершенствовать практические умения для преобразования выражений, содержащих квадратные корни; переноса знаний в новую ситуацию;
- развивать умения учащихся анализировать,
сравнивать, обобщать.
- Воспитательные:
- воспитывать такие качества личности, как способность к самоанализу, доброжелательность;
- способствовать эстетическому воспитанию школьников.
ХОД УРОКА:
I. Организационный момент
II. Мотивация
Сегодняшний урок я хотела бы начать со слов Фридриха Адольфа Вильгельма Дистервега — немецкого педагога, прогрессивного либерального политика, который выступал за секуляризацию школ.
«Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь».
Сегодня нам предстоит проверить, как мы понимаем и искусно применяем наши знания, полученные по теме: «Квадратный корень из произведения и дроби»
Мотивация: Ребята, знания, полученные по этой
теме, помогут вам в дальнейшем изучении
математики, а именно при изучении темы «
Преобразования выражений, содержащих квадратные
корни».
Сегодня мы обобщим, и проанализировать наши знания и умения по плану:
- Вспомним формулы, с помощью которых можно найти квадратный корень из произведения и дроби.
- Устно решим несколько заданий на применение этих формул.
- Работа с учебником.
- Напишем самостоятельную работу.
- Вы самостоятельно проведете самоанализ: «Как вы знаете и применяете материал по данной теме.
III. Актуализация знаний
I.
1. Чему равен квадратный корень из
произведения?
– Корень из произведения неотрицательных
множителей равен произведению корней из этих
множителей:
а > 0, b > 0, = ·
2. Чему равно произведение квадратных корней?
– Произведение квадратных корней равно
квадратному корню из произведения:
· =
3.
Чему равен квадратный корень из дроби?
– Корень из дроби, числитель которой
неотрицателен, а знаменатель положителен, равен
корню из числителя, деленному на корень из
знаменателя:
а > 0, b > 0, =
4. Чему равно частное квадратных корней?
– Частное квадратных корней равно квадратному корню из дроби:
=
II. Верно ли равенство:
1. = –
10 (нет)
2. 2· =
2.4 (нет)
4. = – 4 (нет)
5. = 660 (да)
III. Вместо треугольника написать число, чтобы получилось верное равенство:
1. =
2. = 3 ? = 30
3. =
4. = = 40
5. = = 2
IV. Примените формулу разности квадратов а2– b2 = (а – b)(а + b) для вычисления следующих числовых выражений:
а) 52 – 32 = (5 – 3)(5 + 3) = 2 • 8 = 16
б) 2,52 – 1,52 = (2,5 – 1,5)(2,5 + 1,5) = 1 • 4 = 4
в) 2 – 2 = = • 1=
V.
Как бы вы стали вычислять значение
следующего выражения?
– ?
Учащиеся предлагают два способа:
I способ: = = =7
II способ: = = = 7
Какое решение более рациональное?
IV. Самостоятельная работа
| 1 вариант: | 2 вариант: | |
|
1б 1б 2б 1б 3б 3б |
1) 2) 3) 4) • 5) 6) |
Критерии:
«5» – 9-11 баллов;
«4» – 6-8 баллов;
«3» – 3-5 баллов.
Резервное задание для обеспечения занятости и развития наиболее подготовленных учащихся.
Задание на смекалку: Используя 6 раз число и знаки действия, получить число 6.
Решение:
(= 6
(3+=6
9 – 3 = 6
6 = 6
V. Итог урока
VI. Домашнее задание: № 364(в, г, е), №469(в), №470(б)
VII. Рефлексия
Согласно словам Дистервега: «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь», проведите самоанализ, ответив на вопросы на бланке. Как я знаю и применяю материал по теме: «Квадратный корень из произведения и дроби»:
а) на отлично;
б) хорошо;
в) удовлетворительно;
г) совсем не знаю и не могу применять.
Рационализация знаменателя с более высокими корнями — Концепция
Когда знаменатель имеет более высокий корень, умножение на подкоренное не удаляет корень.
рационализация знаменателя высший корень
Рационализация знаменателя — это, по сути, способ сказать: «Извлеките квадратный корень из глубины». Хорошо. Мы можем спросить, почему он внизу. Не совсем уверен, почему, но по какой-то причине мы не можем, и когда мы это делаем, нам нужно умножить на что-то, чтобы избавиться от квадратного корня.
Итак, мы собираемся сделать пример, будем надеяться, что вы помните, как это сделать. И это будет 4 больше квадратного корня из 8, хорошо? Мы могли бы умножить его на квадратный корень из 8 на квадратный корень из 8, тогда квадратный корень из 8 отменяется, оставляя нас с 8. Но я хочу, чтобы вы привыкли делать это искать, есть ли способ что мы можем сначала упростить знаменатель.
Таким образом, чтобы рационализировать знаменатель, умножьте корень 2 на корень 2. Наш числитель станет 4, корень 2, наша 2 все еще там, и тогда у нас есть корень 2, умноженный на корень 2, что равно 2. Вы можете упростить это до 4 на 2. умножить на 2, они все отменяются, оставляя нас с квадратным корнем из 2, хорошо. Так что, надеюсь, это не слишком ново для вас.
Сейчас я хочу поговорить в основном о знаменателе, когда вы имеете дело с корнем, отличным от 2. Итак, этот пример, о котором мы говорим, — это кубический корень. И одна распространенная ошибка заключается в том, что люди хотят умножить на кубический корень из 2, а не на кубический корень из 2. Хорошо? Когда мы умножаем радикалы, мы [IB] основываем корни одинаковыми. Мы совмещаем это. Таким образом, мы на самом деле получаем здесь кубический корень из 2 в квадрате или из 4. Это нам совсем не помогает, потому что кубический корень из 4 мы не знаем. Так что вам действительно нужно подумать о том, сколько этого термина вам нужно, чтобы получить его из кубического корня? Хорошо? Чтобы получить что-то из кубического корня, вам нужно их 3, хорошо? Кубический корень из 2 в кубе равен 2, кубический корень из 8 равен 2. Итак, чтобы получить что-то из кубического корня, вам нужно 3 предмета], а чтобы получить что-то из четвертого корня, вам нужно 4. Итак, размышляя об этом , мне нужен кубический корень из 2 в квадрате.
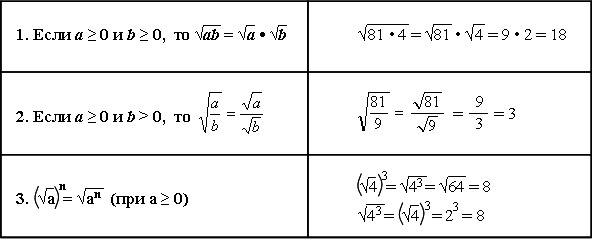У меня есть один 2, мне нужно еще два, чтобы сделать три. Хорошо? Умножая верх и низ на то же самое, кубический корень из 2 в квадрате. Теперь у нас есть 3 умножения кубического корня из 2 в квадрате на кубический корень из 2 в третьей степени. Кубический корень из 2 в третьем равен всего 2. Таким образом, мы получаем только 3, кубический корень из 4 на 2. Это 3 выглядит не очень хорошо, давайте перепишем это. Итак, всякий раз, когда мы имеем дело с корнем, отличным от квадратного, вам нужно серьезно подумать о своем индексе. Подумайте о корне и убедитесь, что у вас есть такой номер элемента, чтобы вытащить его, хорошо? Вы не можете просто использовать тот же подход, что и здесь, умноженный на корень чего угодно. Тебе действительно нужно подумать об этом, сказать «хорошо». У меня есть пятый корень, поэтому мне понадобится 5 предметов для того, что есть под рукой.
упростить калькулятор квадратного корня — Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
Square Root Calculator
www.
calculatorsoup.com › Algebra
Используйте этот калькулятор, чтобы найти главный квадратный корень и корни действительных чисел. Входными данными для подкоренного числа x могут быть положительные или отрицательные действительные числа. Ответ …
Упростите радикальное, рациональное выражение с помощью пошаговой математической задачи …
quickmath.com › алгебра › упрощает › базовый
упростите рациональные или радикальные выражения с помощью нашего бесплатного пошагового математического калькулятора.
Калькулятор квадратного корня и решатель — Math Warehouse
www.mathwarehouse.com › арифметика › квадратный корень…
Калькулятор квадратного корня и решатель. Бесплатный калькулятор сводит квадратные корни к простейшей радикальной форме. Рабочий лист Упрощение радикалов.
Solve — Упрощение калькулятора квадратных корней — Алгебратор
softmath.com › факторинг-выражения › упрощение-квадра.
..
Упрощенный калькулятор квадратных корней. Посетители Google нашли наш веб-сайт вчера, введя следующие термины алгебры: симметрия бесплатных распечаток; Как разместить …
Калькулятор уравнений радикалов — Symbolab
www.symbolab.com › … › Алгебра › Уравнения
Калькулятор уравнений свободных радикалов — шаг за шагом решайте уравнения радикалов. … упростить, решить, расширить, факторизовать, рационализировать. See All, чередующийся тест …
Ähnliche Fragen
Как решить √128?
Как решить √200?
Как решить √10?
Калькулятор квадратного корня — Mathway
www.mathway.com › Калькулятор › Калькулятор квадратного корня
Бесплатный калькулятор квадратного корня — пошаговые решения, помогающие вычислить квадратный корень из подкоренного выражения.
Калькулятор квадратного корня онлайн — Simplify_surd — Solumaths
www.solumaths.com › калькулятор › вычислить › просто.
..
Упростить сурд, онлайн-исчисление. Резюме : онлайн-калькулятор surds, который позволяет производить расчеты в точной форме с квадратными корнями: сумма, …
Калькулятор упрощения квадратных корней — Решение квадратных уравнений
www.solve-variable.com › правила экспоненты › упрощение…
Опубликовано: Суббота, 30 декабря, 08:59. Привет всем, я только начал свой класс по упрощенному калькулятору квадратных корней. Мальчик! Эта вещь действительно ужасна!
Упрощенный калькулятор извлечения квадратного корня
online-calculator.org ›simplify-square-root-calculator
Упрощенный калькулятор извлечения квадратного корня для нахождения простейшей формы квадратного корня любого числа. Калькулятор упрощения радикалов покажет вам шаг за шагом …
Калькулятор извлечения квадратного корня — Math.com
www.math.com › студенты › калькуляторы › источник › s…
Калькулятор извлечения квадратного корня найдет квадратный корень из введенного вами числа.