Решение дробных неравенств: Дробные неравенства и их решение

Содержание

дробно рациональные неравенства примеры с решением

Вы искали дробно рациональные неравенства примеры с решением? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и дробное неравенство, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробно рациональные неравенства примеры с решением».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как дробно рациональные неравенства примеры с решением,дробное неравенство,дробное неравенство как решать,дробные квадратные неравенства,дробные квадратные неравенства как решать,дробные неравенства,дробные неравенства как решать,дробные неравенства как решаются,дробные неравенства примеры,дробные неравенства примеры решения,дробные неравенства решение,дробные рациональные неравенства примеры с решением,как решать дробные квадратные неравенства,как решать дробные неравенства,как решать квадратные дробные неравенства,как решать квадратные неравенства дробные,как решать методом интервалов дробные неравенства,как решать неравенства дробные квадратные,как решать неравенства с дробью,как решать неравенства с дробями,как решать неравенство дробное,как решать неравенство с дробью,как решать систему неравенств с дробями,как решать системы рациональных неравенств,как решаются дробные неравенства,как решаются неравенства дробные,как решить дробное неравенство,как решить неравенство с дробью,квадратные дробные неравенства,квадратные неравенства дробные,квадратные неравенства рациональные неравенства,метод интервалов дробные неравенства,неравенства дробные,неравенства дробные примеры,неравенства дробные решение,неравенства квадратные дробные,неравенства с дробью,неравенства с дробью как решать,неравенства с дробями,неравенство дробное,неравенство с дробью,неравенство с дробью как решать,неравенство с дробями,решение дробно рациональных неравенств,решение дробно рациональных неравенств методом интервалов,решение дробного неравенства,решение дробные неравенства,решение дробных квадратных неравенств,решение дробных неравенств,решение дробных неравенств квадратных,решение дробных неравенств методом интервалов,решение дробных рациональных неравенств,решение квадратных дробных неравенств,решение квадратных неравенств дробных,решение неравенств дробных,решение неравенств с дробью,решение неравенств с дробями,решение неравенства дробного,решение неравенства дробные,решение рациональных дробных неравенств,решите дробное неравенство,решите неравенство дробное,решите неравенство дробное неравенство,решить дробное неравенство,решить неравенство дробное,решить неравенство с дробью,системы рациональных неравенств как решать,собери выражение для частей неравенства,собери выражения для частей неравенства.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и дробно рациональные неравенства примеры с решением. Просто введите задачу в окошко и нажмите «решить» здесь (например, дробное неравенство как решать).

Где можно решить любую задачу по математике, а так же дробно рациональные неравенства примеры с решением Онлайн?

Решить задачу дробно рациональные неравенства примеры с решением вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Система рациональных неравенств примеры.

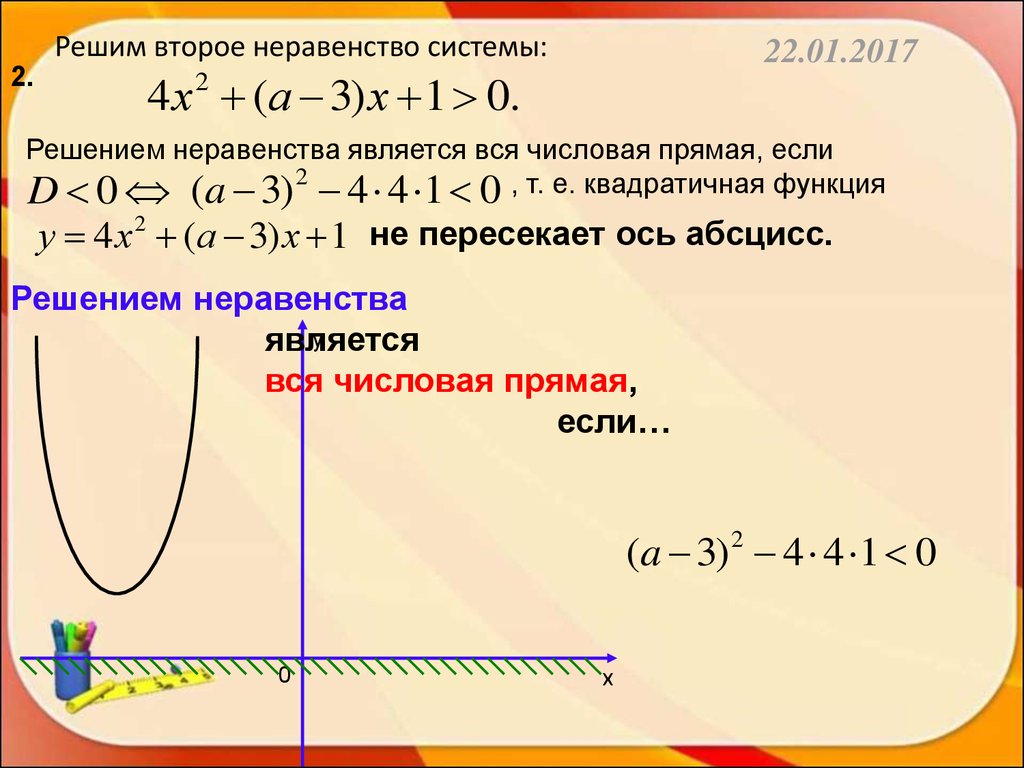Рациональные неравенства и их системы

Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.

Yandex.RTB R-A-339285-1

Понятие рациональных равенств

Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:

Определение 1

Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.

Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много. Следовательно, возможны рациональные неравенства с 1 , 2 , 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.

Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:

x > 4 x 3 + 2 · y ≤ 5 · (y − 1) · (x 2 + 1) 2 · x x — 1 ≥ 1 + 1 1 + 3 x + 3 · x 2

А вот неравенство вида 5 + x + 1

Все рациональные неравенства делятся на целые и дробные.

Определение 2

Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).

Определение 3

Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.

Например, неравенства вида 1 + x — 1 1 3 2 2 + 2 3 + 2 11 — 2 · 1 3 · x — 1 > 4 — x 4 и 1 — 2 3 5 — y > 1 x 2 — y 2 являются дробно рациональными, а 0 , 5 · x ≤ 3 · (2 − 5 · y) и 1: x + 3 > 0 – целыми.

Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.

Допустим, что нам требуется найти решения целого рационального неравенства r (x) , которое включает в себя только одну переменную x . При этом r (x) и s (x) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.

Начнем с перенесения выражения из правой части в левую. Получим следующее:

вида r (x) − s (x) , ≥)

Мы знаем, что r (x) − s (x) будет целым значением, а любое целое выражение допустимо преобразовать в многочлен. Преобразуем r (x) − s (x) в h (x) . Это выражение будет тождественно равным многочленом. Учитывая, что у r (x) − s (x) и h (x) область допустимых значений x одинакова, мы можем перейти к неравенствам h (x) , ≥) , которое будет равносильно исходному.

Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.

Пример 1

Условие: решите целое рациональное неравенство x · (x + 3) + 2 · x ≤ (x + 1) 2 + 1 .

Решение

Начнем с переноса выражения из правой части в левую с противоположным знаком.

x · (x + 3) + 2 · x − (x + 1) 2 − 1 ≤ 0

Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3 · x − 2 ≤ 0 , равносильному тому, что было дано в условии. Решить его несложно:

3 · x ≤ 2 x ≤ 2 3

Ответ: x ≤ 2 3 .

Пример 2

Условие: найдите решение неравенства (x 2 + 1) 2 − 3 · x 2 > (x 2 − x) · (x 2 + x) .

Решение

Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.

(x 2 + 1) 2 − 3 · x 2 − (x 2 − x) · (x 2 + x) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0

В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x , следовательно, решением исходного неравенства может быть любое действительное число.

Ответ: любое действительно число.

Пример 3

Условие: решите неравенство x + 6 + 2 · x 3 − 2 · x · (x 2 + x − 5) > 0 .

Решение

Из правой части мы ничего переносить не будем, поскольку там 0 . Начнем сразу с преобразования левой части в многочлен:

x + 6 + 2 · x 3 − 2 · x 3 − 2 · x 2 + 10 · x > 0 − 2 · x 2 + 11 · x + 6 > 0 .

Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.

Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :

D = 11 2 — 4 · (- 2) · 6 = 169 x 1 = — 11 + 169 2 · — 2 , x 2 = — 11 — 169 2 · — 2 x 1 = — 0 , 5 , x 2 = 6

Теперь на схеме отметим все необходимые нули.

Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.

Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак > . Нужный интервал равен (− 0 , 5 , 6) , следовательно, эта область значений и будет нужным нам решением.

Ответ: (− 0 , 5 , 6) .

Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h (x) , что чаще всего делается с помощью разложения многочлена на множители.

Пример 4

Условие: вычислите (x 2 + 2) · (x + 4) .

Решение

Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.

(x 2 + 2) · (x + 4) − 14 + 9 · x

В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.

Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x 3 + 4 · x 2 + 11 · x − 6 = 0 . Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ± 1 , ± 2 , ± 3 , ± 6 . Подставим их по очереди в исходное уравнение и выясним, что числа 1 , 2 и 3 будут его корнями.

Значит, многочлен x 3 + 4 · x 2 + 11 · x − 6 может быть описан в виде произведения (x − 1) · (x − 2) · (x − 3) , и неравенство x 3 + 4 · x 2 + 11 · x − 6 может быть представлено как (x − 1) · (x − 2) · (x − 3) . С неравенством такого вида нам потом будет легче определить знаки на промежутках.

Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1 , 2 , 3 . Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак

Нам осталось только записать готовый ответ: (− ∞ , 1) ∪ (2 , 3) .

Ответ: (− ∞ , 1) ∪ (2 , 3) .

В некоторых случаях выполнять переход от неравенства r (x) − s (x) , ≥) к h (x) , ≥) , где h (x) – многочлен в степени выше 2 , нецелесообразно. Это распространяется на те случаи, когда представить r (x) − s (x) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h (x) на отдельные множители. Разберем такую задачу.

Пример 5

Условие: найдите решение неравенства (x 2 − 2 · x − 1) · (x 2 − 19) ≥ 2 · x · (x 2 − 2 · x − 1) .

Решение

Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим x 4 − 4 · x 3 − 16 · x 2 + 40 · x + 19 ≥ 0 .

Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1 , − 1 , 19 или − 19 не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.

Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:

(x 2 − 2 · x − 1) · (x 2 − 19) − 2 · x · (x 2 − 2 · x − 1) ≥ 0 (x 2 − 2 · x − 1) · (x 2 − 2 · x − 19) ≥ 0 .

Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения x 2 − 2 · x − 1 = 0 и x 2 − 2 · x − 19 = 0 . Их корни – 1 ± 2 , 1 ± 2 5 . Переходим к равенству x — 1 + 2 · x — 1 — 2 · x — 1 + 2 5 · x — 1 — 2 5 ≥ 0 , которое можно решить методом интервалов:

Согласно рисунку, ответом будет — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Ответ: — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Добавим, что иногда нет возможности найти все корни многочлена h (x) , следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h (x) , ≥) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.

Допустим, надо решить дробно рационально неравенств вида r (x) , ≥) , где r (x) и s (x) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:

Определяем область допустимых значений переменной x .
Переносим выражение из правой части неравенства налево, а получившееся выражение r (x) − s (x) представляем в виде дроби. При этом где p (x) и q (x) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
Далее решаем полученное неравенство методом интервалов.
Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x , которую мы определили в начале.

Это и есть алгоритм решения дробно рационального неравенства. Большая часть его понятна, небольшие пояснения требуются только для п. 2 . Мы перенесли выражение из правой части налево и получили r (x) − s (x) , ≥) , а как потом привести его к виду p (x) q (x) , ≥) ?

Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n -ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.

На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4 . Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.

Далее нам надо решить, будет ли полученное неравенство p (x) q (x) , ≥) равносильным по отношению к r (x) − s (x) , ≥) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.

Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p (x) q (x) совпадет с областью значений выражения r (x) − s (x) . Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.

Но область значений для p (x) q (x) может оказаться шире, чем у r (x) − s (x) , например, за счет сокращения дробей. Примером может быть переход от x · x — 1 3 x — 1 2 · x + 3 к x · x — 1 x + 3 . Либо это может происходить при приведении подобных слагаемых, например, здесь:

x + 5 x — 2 2 · x — x + 5 x — 2 2 · x + 1 x + 3 к 1 x + 3

Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.

Пример 6

Условие: найдите решения рационального равенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x x — 3 2 · x + 1 .

Решение

Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x + 1 · x — 3 ≠ 0 x — 3 2 ≠ 0 x — 3 2 · (x + 1) ≠ 0 , решением которой будет множество (− ∞ , − 1) ∪ (− 1 , 3) ∪ (3 , + ∞) .

x x + 1 · x — 3 + 4 (x — 3) 2 + 3 · x (x — 3) 2 · (x + 1) ≥ 0

После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю (x − 3) 2 · (x + 1) :

x x + 1 · x — 3 + 4 (x — 3) 2 + 3 · x (x — 3) 2 · (x + 1) = = x · x — 3 + 4 · x + 1 + 3 · x x — 3 2 · x + 1 = x 2 + 4 · x + 4 (x — 3) 2 · (x + 1)

Сворачиваем выражение в числителе, применяя формулу квадрата суммы:

x 2 + 4 · x + 4 x — 3 2 · x + 1 = x + 2 2 x — 3 2 · x + 1

Областью допустимых значений получившегося выражения является (− ∞ , − 1) ∪ (− 1 , 3) ∪ (3 , + ∞) . Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x + 2 2 x — 3 2 · x + 1 ≥ 0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.

Используем метод интервалов:

Видим решение { − 2 } ∪ (− 1 , 3) ∪ (3 , + ∞) , которое и будет решением исходного рационального неравенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x (x — 3) 2 · (x + 1) .

Ответ: { − 2 } ∪ (− 1 , 3) ∪ (3 , + ∞) .

Пример 7

Условие: вычислите решение x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 .

Решение

Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме − 2 , − 1 , 0 и 1 .

Переносим выражения из правой части в левую:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 > 0

x + 3 x — 1 — 3 x x + 2 = x + 3 — x — 3 x x + 2 = 0 x x + 2 = 0 x + 2 = 0

Учитывая получившийся результат, запишем:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 0 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 (x + 1) · x — 1 = = — x — 1 (x + 1) · x — 1 = — x + 1 (x + 1) · x — 1 = — 1 x — 1

Для выражения — 1 x — 1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены − 2 , − 1 и 0 . Значит, нам нужно выполнить последний шаг алгоритма.

Поскольку мы пришли к неравенству — 1 x — 1 > 0 , можем записать равносильное ему 1 x — 1 (− ∞ , 1) .

Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из (− ∞ , 1) числа − 2 , − 1 и 0 . Таким образом, решением рационального неравенства x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 будут значения (− ∞ , − 2) ∪ (− 2 , − 1) ∪ (− 1 , 0) ∪ (0 , 1) .

Ответ: (− ∞ , − 2) ∪ (− 2 , − 1) ∪ (− 1 , 0) ∪ (0 , 1) .

В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.

Пример 8

Условие: найдите решение неравенства 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 .

Решение

Область допустимых значений неравенства, заданного в условии, определяет система x 2 ≠ 0 x 2 — x + 1 ≠ 0 x — 1 ≠ 0 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≠ 0 .

Решений у этой системы нет, поскольку

x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 = = (x + 1) · x 2 — x + 1 x 2 — x + 1 — (x — 1) · x + 1 x — 1 = = x + 1 — (x + 1) = 0

Значит, исходное равенство 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.

Ответ: решений нет.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. 2-5x}{x+1}\) .

При решении дробных рациональных неравенств используется метод интервалов. Поэтому если алгоритм, приведенный ниже, вызовет у вас затруднения, посмотрите статью по .

Как решать дробные рациональные неравенства:

Алгоритм решения дробно-рациональных неравенств.

Примеры:

Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:

Определяем знак в самом крайнем правом интервале — берем число с этого интервала и подставляем его в неравенство вместо икса. После этого определяем знаки в скобках и результат перемножения этих знаков;

Примеры:

Выделите нужные промежутки. Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести его в ответ (см. пример ниже).

Примеры:

Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).

Примеры:
Ответ: \((-∞;-1)∪(-1;1,2]∪}

Исчисление

— Почему мы учитываем нули выражения при решении рациональных неравенств?

спросил 2 года 4 месяца назад

Изменено 2 года, 4 месяца назад

Просмотрено 328 раз

$\begingroup$

Почему при нахождении решения множества рациональных неравенств (вида $ {x-3\over x+2} \geq 0 $ и т. д.) мы учитываем «нули» выражения.

Итак, меня учили решать это следующим образом:

Во-первых, $x-3 = 0 \подразумевает x = 3 \quad и \quad x+2\not= 0 \подразумевает x\not=-2 \,\text{(b/c, undefined)} $ являются «достопримечательностями» «.

Нарисуйте числовую линию от $-∞$ до $+∞$, пометив точки интереса ($-2$ и $3$). Затем мы проверяем каждую область, связанную этими числами, чтобы увидеть, являются ли они положительными или отрицательными, и помечаем их соответствующим образом.

Меня смущает то, почему мы проверяем эти нули? Что говорит нам о том, что знаки не перевернутся внезапно при каком-то другом случайном значении? Может ли кто-нибудь подробно объяснить эту работу, предложить лучший метод или указать мне на другие ресурсы, которые «доказывают» то, о чем я говорю.

исчисление
алгебра-предварительное исчисление
неравенство

$\endgroup$

$\begingroup$

Например, рассмотрим $$\frac{x-a}{x-b} \ge 0, \ a\gt b$$ Чтобы дробь была неотрицательной, нам нужно, чтобы числитель и знаменатель имели одинаковую четность, или чтобы числитель был равен нулю.

Если оба положительны, то $$x-a\ge 0 \подразумевает x\ge a$$ и $$x-b \gt 0 \подразумевает x\gt b \hspace{1 см} \потому что x-b\ne 0$$ пересечение двух требований, мы получаем $$x\ge a \hspace{2 cm} (\mathbf 1)$$

Если оба отрицательны, то $$x-a \lt 0 \подразумевает x\lt a \\ x-b \lt 0 \подразумевает x\lt b $$ Это означает $$x\lt b \hspace{2 cm} (\ mathbf 2)$$ Теперь возможен любой из двух случаев, поэтому возьмем объединение $(\mathbf 1)$ и $(\mathbf 2)$: $$x\in(-\infty, b) \ cup [a, \infty) $$ Чтобы ответить на ваш вопрос более прямо, рассмотрим нули каждого множителя, потому что именно там множитель меняет знак.

$\endgroup$

$\begingroup$

Как заявил в своем комментарии Питер Форман (принимая во внимание мой собственный комментарий), неравенства $$\frac{x-3}{x+2}\ge0$$ и $$(x-3)(x+2)\ge 0$$ эквивалентны. Это наглядно видно на графике ниже:

На графике видно, что $$\operatorname{sgn}\left(\frac{x-3}{x+2}\right)=\operatorname{sgn}\left( (x-3)(x+2)\право), \ \ x \neq -2$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Необходимые условия существования глобальных решений нелинейных дробно-дифференциальных неравенств и систем

На этой странице

АннотацияВведениеПредварительные сведенияЗаключениеДоступность данныхКонфликты интересовВклад авторовБлагодарностиСсылкиАвторское правоСтатьи по теме

В этой статье исследуются дробные дифференциальные неравенства и системы дробных дифференциальных неравенств, включающие дробные производные в смысле Капуто. А именно, получены необходимые условия существования глобальных решений. Наш подход основан на методе пробных функций и некоторых интегральных неравенствах.

1. Введение и основные результаты

В нескольких исследованиях была продемонстрирована полезность дробных производных при математическом моделировании различных явлений физики и техники (см., например, [1–7] и ссылки в них). В связи с этим изучению дифференциальных уравнений дробного порядка уделяется большое внимание многих исследователей. Существование решений — одна из важнейших тем дифференциальных уравнений дробного порядка. Изучение достаточных условий существования решений исследовалось многими авторами с использованием различных подходов функционального анализа (см., например, [8–18] и ссылки в них). Изучение необходимых условий существования глобальных решений в контексте дифференциальных уравнений дробного порядка было начато Киране и его сотрудниками (см., например, [19].–24] и ссылки в нем).

В [19] Фурати и Киране исследовали систему дробных дифференциальных уравнений: где , и . Здесь , , обозначает дробную производную Капуто порядка . А именно, было показано, что если то (1) не допускает глобального решения.

По мотивам Фурати и Киране [19] в этой статье мы сначала рассмотрим дробно-дифференциальное неравенство где , , , , , , и . Предполагается, что это функция и удовлетворяет

(A1) для всех

(A2)

(A3) для всех

Нашей целью является изучение влияния на поведение решений при больших временах. Под глобальным решением задачи (3) понимается функция (абсолютно непрерывная), удовлетворяющая почти всюду дробно-дифференциальному неравенству в (3) и начальному условию . Наша цель — получить достаточные условия, при которых (3) не допускает глобального решения. А именно, получен следующий результат.

Теорема 1. Предположим, что Тогда (3) не допускает глобального решения.

Ниже мы приводим несколько примеров, когда (4) выполняется.

Пример 2. Рассмотрим задачу (3) с , , , и . Затем,

Отсюда по теореме 1 получаем, что при всех (3) не имеет глобального решения.

Пример 3. Рассмотрим задачу (3) с , , , и . затем

Отсюда по теореме 1 получаем, что при всех (3) не имеет глобального решения.

Пример 4. Рассмотрим задачу (3) с и куда

В этом случае после элементарных вычислений получаем где – константа, не зависящая от . Отсюда по теореме 1 получаем, что при всех уравнение (3) не допускает глобального решения.

Пример 5. Рассмотрим задачу (3) с и куда

Во второй части этой статьи мы расширяем предыдущее исследование на систему дробных дифференциальных неравенств: где для , , , , , , , и . При этом предполагается, что является функцией и удовлетворяет (A1)–(A3). Обратите внимание, что в частном случае , и , (13) сводится к (1).

Под глобальным решением (13) мы понимаем пару функций, удовлетворяющих дробным дифференциальным неравенствам в (13) почти всюду и начальному условию .

Мы получили следующий результат.

Теорема 6. (i) Пусть и . Если , то (13) не допускает глобального решения (ii) Пусть и . Если , то (13) не допускает глобального решения

Ниже мы приведем несколько примеров, для которых выполняются (14) или (15).

Пример 7. Рассмотрим (1), т.е. Систему (13) с , , , и , для всех . затем

Отсюда по теореме 6 получаем, что при всех (1) не имеет глобального решения. Это улучшает [19] (теорема 1), где отсутствие глобального решения было получено только при .

Пример 8. Рассмотрим систему (13) с

В этом случае после элементарных вычислений получаем

Отсюда по теореме 6 получаем, что при всех и уравнение (13) не допускает глобального решения.

Остальная часть этого документа организована следующим образом. В разделе 2 мы кратко напоминаем некоторые понятия, связанные с дробным исчислением, и приводим некоторые леммы, которые будут использоваться в доказательствах наших основных результатов. В разделе 3 мы доказываем теоремы 1 и 6.

2. Предварительные сведения

Сначала напомним некоторые основные понятия и свойства, связанные с дробным исчислением (см., например, [25, 26]).

Пусть и . Левосторонний дробный интеграл Римана-Лиувилля порядка функции определяется выражением почти везде , где – гамма-функция. Правосторонний дробный интеграл Римана-Лиувилля порядка функции определяется выражением почти везде.

Дробная производная Капуто порядка функции определяется выражением почти везде.

Лемма 9 (см. [25, лемма 2.7]). Пусть , , и (, , в случае ). Если , то Для ( достаточно велико), пусть

Следующие результаты можно найти в [19].

Лемма 10. Пусть . затем для всех.

3. Доказательства основных результатов

Доказательства наших основных результатов основаны на методе основных функций, разработанном Митидиери и Похозаевым [27].

Доказательство теоремы 1. Используем аргумент от противного. А именно, предположим, что это глобальное решение (3). Умножая дробно-дифференциальное неравенство в (3) на функцию, определяемую (24) при , и интегрируя по , , получаем По начальному условию имеем

Обратите внимание, что по определению у нас есть и . Следовательно, считается, что

Далее, используя лемму 9, получаем

Интегрируя по частям и используя начальное условие , получаем

С другой стороны, по лемме 10 имеем и . Следовательно,

Объединяя (29) с (31), получаем, что

Отсюда из (28) и (29) следует, что

Рассмотрим теперь члены левой части (26). Заменой переменной, используя свойства (A1)–(A3) и свойство убывания , получаем

Далее, по (24) и с учетом этого (имеем также ), получаем

Объединяя (34) с (35), получаем, что

Отсюда из (26), (33) и (36) следует, что куда

Далее, используя неравенство Юнга, получаем где обозначает положительную константу (независимую от ), значение которой может меняться от строки к строке. Тогда из (37), (39) и (40) следует, что куда

Оценим члены , . Для всех по (24) и (38) имеем

Интегрируя по , получаем

Далее, по (38) и лемме 10 для всех имеем

Интегрируя по , получаем

Следовательно, из (41), (44) и (46) следует, что который дает

Отсюда делаем вывод, что что противоречит (4). Доказательство завершено.

Доказательство теоремы 6. Предположим, что это глобальное решение (13). Умножая первое дробно-дифференциальное неравенство в (13) на функцию, определяемую (24) при , и интегрируя по , получаем

Следуя тем же шагам, что и в доказательстве теоремы 1, получаем

Отсюда из (50), (51) и (52) следует, что куда

Рассуждая аналогично второму неравенству в (13), получаем куда

Далее, по неравенству Гёльдера имеем

Аналогично имеем

Для , пусть

Из (53), (57) и (58) следует, что

Аналогично, в силу (55), (59) и (60) получаем

Теперь рассмотрим случай и . В этом случае, используя (62) и (63), получаем

С другой стороны, используя неравенство Юнга, получаем

Следовательно, объединяя (64) с (65), получаем, что который дает

Далее, используя оценки (44) и (46), получаем (после элементарных вычислений)

Объединяя (67) с (68), получаем что противоречит (14).

Во втором случае при и , проделав те же действия, что и в предыдущем случае, получим что противоречит (15). Доказательство завершено.

4. Заключение

В работе исследуются задачи (3) и (13). А именно, с помощью метода основных функций и некоторых интегральных неравенств получены достаточные условия отсутствия глобальных решений (или, что то же самое, необходимые условия существования глобальных решений) рассматриваемых задач. Для задачи (3) мы доказали, что (см. теорему 1) при предположениях (A1), (A2) и (A3), если то (3) не допускает глобального решения. Для системы дробных дифференциальных неравенств (13) всегда при предположениях (A1), (A2) и (A3) мы доказали, что (см. теорему 6), если и

или и

, то (13) не допускает глобального решения.

Доступность данных

Данные не использовались для поддержки этого исследования.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Вклады авторов

Все авторы внесли равный вклад, прочитали и поддержали последнюю оригинальную копию.

Благодарности

Авторы выражают признательность деканату научных исследований Исламского университета имени Имама Мохаммада ибн Сауда за финансирование этой работы через Исследовательскую группу №. РГ-21-09-01.

Ссылки

М. Капуто и М. Фабрицио, «О понятии дробной производной и применении к явлениям гистерезиса», Meccanica , vol. 13, стр. 1–10, 2017 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Лай, С. Мао, Дж. Цю и др., «Прогресс исследования и применение модели дробной производной в геотехнической инженерии», Математические проблемы в инженерии , том. 2016, номер статьи 9183296, 2016.
Посмотреть по адресу:
Google Scholar
Ф. Майнарди, «Исторический взгляд на дробное исчисление в линейной вязкоупругости», Applicable Analysis , vol. 15, нет. 4, стр. 712–717, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Д. Ортигейра, Исчисление дробей для ученых и инженеров , Springer, Нидерланды, 2011 г.
Посмотреть по адресу:
Сайт издателя
Р. Рагхаван, «Дробные производные: применение к нестационарному потоку», Journal of Petroleum Science and Engineering , vol. 80, нет. 1, стр. 7–13, 2011 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Вейцнер и Г. М. Заславский, «Некоторые приложения дробных уравнений», , Связь в нелинейной науке и численном моделировании , том. 8, нет. 3–4, стр. 273–281, 2003.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Чжан, Д. А. Бенсон и Д. М. Ривз, «Нелокальности времени и пространства, лежащие в основе моделей с дробными производными: различие и обзор литературы по полевым приложениям», Advances in Water Resources , vol. 32, нет. 4, стр. 561–581, 2009.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Аббас, М. Бенчохра, Дж. Э. Лагрег, А. Алсаеди и Ю. Чжоу, «Существование и устойчивость по Уламу для дробных дифференциальных уравнений типа Гильфера-Адамара», Успехи в дифференциальных уравнениях , vol. 2017, нет. 1, с. 180, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. И. Аббас и М. А. Рагуза, «О гибридных дробных дифференциальных уравнениях с дробно-пропорциональными производными функции по отношению к некоторой функции», Symmetry , vol. 13, нет. 2, с. 264, 2021.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. И. Аббас и М. Алессандра Рагуза, «Разрешимость уравнений Ланжевена с двумя дробными производными Адамара с помощью функций Миттаг-Леффлера», Применимый анализ , стр. 1–15, 2021 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Айди, М. Джлели и Б. Самет, «О положительных решениях для модели дробного термостата с выпукло-вогнутым исходным членом через дробную производную \psi-Caputo», Mediterranean Journal of Mathematics , том. 17, нет. 1, стр. 1–15, 2020 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
З. Бай, «О положительных решениях нелокальной дробной краевой задачи», Нелинейный анализ , том. 72, нет. 2, стр. 916–924, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Бенчохра и Б. А. Слимани, «Существование и уникальность решений дробно-импульсных дифференциальных уравнений», Electronic Journal of Differential Equations , vol. 2009, стр. 1–11, 2009.
Посмотреть по адресу:
Google Scholar
К. С. Гудрич, «Существование положительного решения класса дробных дифференциальных уравнений», Письма по прикладной математике , том. 23, нет. 9, стр. 1050–1055, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Гу и Дж. Дж. Трухильо, «Существование мягкого решения уравнения эволюции с дробной производной Гильфера», Applied Mathematics and Computation , vol. 257, стр. 344–354, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Джлели и Б. Самет, «Существование положительных решений дробного дифференциального уравнения произвольного порядка с помощью метода смешанного монотонного оператора», Нелинейный анализ , том. 20, нет. 3, стр. 367–376, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
В. Лакшмикантам и А. С. Ватсала, «Общая уникальность и монотонный итерационный метод для дробных дифференциальных уравнений», Applied Mathematics Letters , vol. 21, нет. 8, стр. 828–834, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Ян и К. Ван, «Существование мягких решений для класса дробных эволюционных уравнений Гильфера с нелокальными условиями», Дробное исчисление и прикладной анализ , vol. 20, нет. 3, стр. 679–705, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
К. М. Фурати и М. Киране, «Необходимые условия существования глобальных решений систем дробных дифференциальных уравнений», Fractional Calculus & Applied Analysis , vol. 11, pp. 281–298, 2008.
Посмотреть по адресу:
Google Scholar
М. Киране, Б. Ахмад, А. Алсаеди и М. Аль-Ями, «Несуществование глобальных решений для система уравнений дробной диффузии» Acta Applicandae Mathematicae , vol. 133, нет. 1, стр. 235–248, 2014.
Посмотреть по адресу:
Сайт издателя | Google Scholar. 286, нет. 17–18, стр. 1797–1804, 2013.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Киране и С. А. Малик, «Профиль раздутых решений нелинейной системы дробных дифференциальных уравнений», Нелинейный анализ , том. 73, нет. 12, стр. 3723–3736, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Киране и Н.-Э. Татар, «Отсутствие решений гиперболического уравнения с дробным затуханием по времени», Journal for Analysis and its Applications , vol. 25, нет. 2, стр. 131–142, 2006 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
N.-E. Татар, «Результаты несуществования для дробной задачи, возникающей при термодиффузии во фрактальных средах», Хаос, солитоны и фракталы , том. 36, нет. 5, стр. 1205–1214, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. А. Килбас, Х. М. Сривастава и Дж. Дж. Трухильо, Теория и приложения дробных дифференциальных уравнений, North-Holland Mathematics Studies , vol. 204, Elsevier, Amsterdam, 2006.
С. Г. Самко, А. А. Килбас, О. И. Маричев, Дробные интегралы и производные: теория и приложения , Gordon and Breach, Yverdon, Switzerland, 1993.
No related posts.