| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | cos(pi/2) | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
1 3 радиан. Перевод градусов в радианы и обратно, формулы, примеры
Давай посмотрим на рисунке. Вектор \(AB \)
«повернулся» относительно точки \(A \)
на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \(\alpha \) .
\circ \)
. Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Yandex.RTB R-A-339285-1
Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.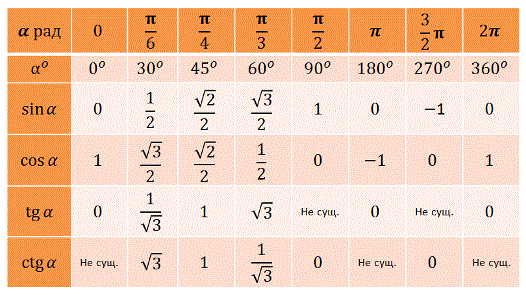
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
π радиан = 180 °
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.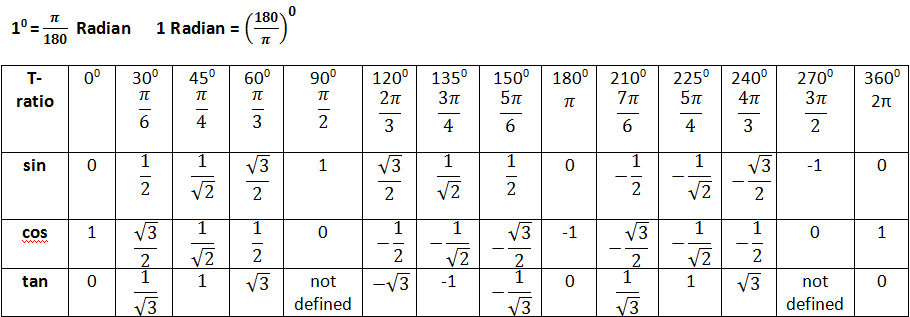
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Рассмотрим пример.
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решениидифференциальныхи функциональных уравнений.
К
тригонометрическим функциям относятся
следующие 6 функций: синус , косинус , тангенс , котангенс , секанс и косеканс .
Для каждой из указанных функций
существует обратная
тригонометрическая функция.
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r = 1. На окружности обозначена точка M (x,y ). Угол между радиус-вектором OM и положительным направлением оси Ox равен α .
Синусом угла α y точки M (x,y ) к радиусу r : sin α = y /r . Поскольку r = 1, то синус равен ординате точки M (x,y ).
Косинусом угла α x точки M (x,y ) к радиусу r : cos α = x /r = x
Тангенсом угла α называется отношение ординаты y точки M (x,y ) к ee абсциссе x : tan α = y /x , x ≠ 0
Котангенсом угла α называется отношение абсциссы x точки M (x,y ) к ее ординате y : cot α = x /y , y ≠ 0
Секанс угла α − это отношение радиуса r к абсциссе x точки M (x,y ): sec α = r /x = 1/x , x ≠ 0
Косеканс угла α − это отношение радиуса r к ординате y точки M (x,y ): cosec α = r /y = 1/y , y ≠ 0
В
единичном круге проекции x , y точки M (x,y )
и радиус r образуют прямоугольный треугольник,
в котором x,
y являются
катетами, а r − гипотенузой.
Поэтому, приведенные
выше определения тригонометрических
функций в приложении к прямоугольному
треугольнику формулируются таким
образом: Синусом угла α называется отношение противолежащего
катета к гипотенузе. Косинусом угла α называется отношение прилежащего
катета к гипотенузе. Тангенсом угла α называется противолежащего катета
к прилежащему. Котангенсом угла α называется прилежащего катета к
противолежащему.
График функции синус y = sin x , область определения: x ∈ ℜ , область значений: −1 ≤ sin x ≤ 1
График функции косинус y = cos x , область определения: x ∈ ℜ , область значений: −1 ≤ cos x ≤ 1
График функции тангенс y = ttg x , область определения: x ∈ ℜ , x ≠ (2k + 1)π /2, область значений: −∞ x
График функции котангенс y = ctg x , область определения: x ∈ ℜ , x ≠ kπ , область значений: −∞ x
Градусная мера угла.
Радианная мера угла. Перевод градусов в радианы и обратно.Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы освоили отсчёт углов на тригонометрическом круге. Узнали, как отсчитывать положительные и отрицательные углы. Осознали, как нарисовать угол больше 360 градусов. Пришла пора разобраться с измерением углов. Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да…
Стандартные задания по тригонометрии с числом «Пи» решаются неплохо. Зрительная память выручает. А вот любое отклонение от шаблона — валит наповал! Чтобы не свалиться — понимать надо. Что мы с успехом сейчас и сделаем. В смысле — всё поймём!
Итак, в чём считаются углы? В школьном курсе тригонометрии используются две меры: градусная мера угла и радианная мера угла . Разберём эти меры. Без этого в тригонометрии — никуда.
Градусная мера угла.
К градусам мы как-то привыкли. Геометрию худо-бедно проходили… Да и в жизни частенько встречаемся с фразой «повернул на 180 градусов», например. Градус, короче, штука простая…
Да? Ответьте мне тогда, что такое градус? Что, не получается с ходу? То-то…
Градусы придумали в Древнем Вавилоне. Давненько это было… Веков 40 назад… И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно… Но они, египтяне не виноваты. После них ещё веков 35 мучились.
Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя… В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926… раз.
Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой. Запоминаем:
Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:
Где L — длина окружности, а d — её диаметр.
В геометрии пригодится.
Для общего образования добавлю, что число «Пи» сидит не только в геометрии… В самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно! Само по себе.
Вне наших желаний. Вот так.
Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? Нет? Ну ладно. Выскажу версию. У древних вавилонян не спросишь… Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие — 360? И в каком варианте этих делителей нацело — больше? Людям такое деление очень удобно. Но…
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена. И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245… И что мне делать? Нет уж…» Пришлось послушаться. Природу не обманешь…
Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь — радиан!
Радианная мера угла.
Что такое радиан? В основе определения радиана — всё равно окружность.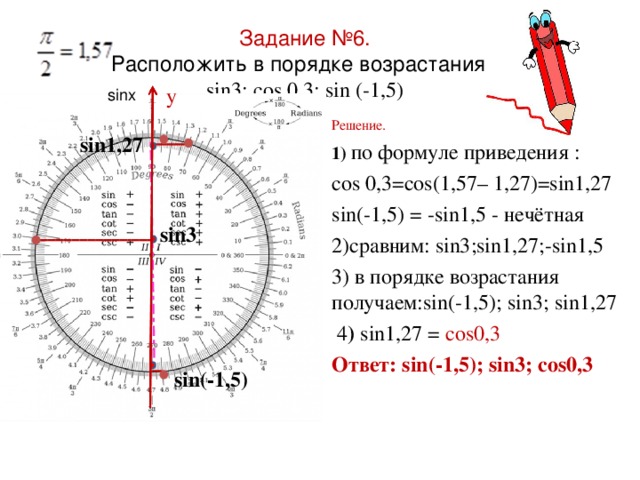
Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L ) равна длине радиуса (R ). Смотрим картинки.
Маленький такой угол, почти и нет его… Наводим курсор на картинку (или коснёмся картинки на планшете) и видим примерно один радиан . L = R
Чувствуете разницу?
Один радиан много больше одного градуса. А во сколько раз?
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.
Кто угадает, чему равен этот хвостик!?
Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
А вот в Интернете число
писать неудобно.
.. Поэтому я в тексте пишу его по имени — «Пи». Не запутаетесь, поди?…
Вот теперь совершенно осмысленно можно записать приближённое равенство:
Или точное равенство:
Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:
Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
Но главное умение этой темы — перевод градусов в радианы и обратно.
Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан ? Вот и пишем:
Или, более экзотическое выражение:
Легко, верно?
Обратный перевод чуть сложнее.
Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:
Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:
Или, аналогично:
Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы — это очень просто. Да и перевод без проблем… И «Пи» — вполне терпимая штука… Так откуда путаница!?
Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов — пишется. Всегда. Например, sin35°. Это синус 35 градусов . А значок радианов (рад ) — не пишется! Он подразумевается.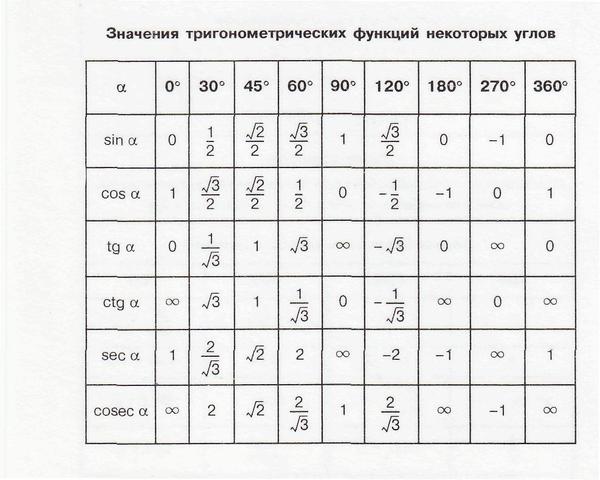
То ли лень математиков обуяла, то ли ещё что… Но решили не писать. Если внутри синуса — котангенса нет никаких значков, то угол — в радианах ! Например, cos3 — это косинус трёх радианов .
Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!
Ещё раз: «Пи» — это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
«Пи» — это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?
Или, что меньше?
Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать…
Если вы тоже в ступор впали, вспоминаем заклинание: «Пи» — это число! 3,14.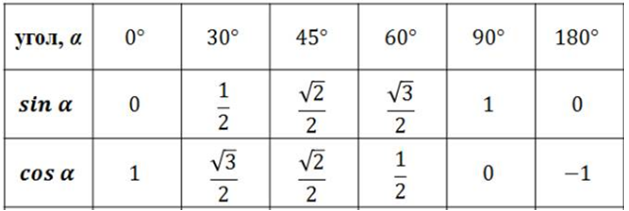
В самом первом синусе четко указано, что угол — в градусах ! Стало быть, заменять «Пи» на 180° — нельзя! «Пи» градусов — это примерно 3,14°. Следовательно, можно записать:
Во втором синусе обозначений никаких нет. Значит, там — радианы ! Вот здесь замена «Пи» на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:
Осталось сравнить эти два синуса. Что. забыли, как? С помощью тригонометрического круга, конечно! Рисуем круг, рисуем примерные углы в 60° и 1,05°. Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Совершенно аналогично поступим и с косинусами. На круге нарисуем углы примерно 4 градуса и 4 радиана (не забыли, чему примерно равен 1 радиан?). Круг всё и скажет! Конечно, cos4 меньше cos4°.
Потренируемся в обращении с мерами угла.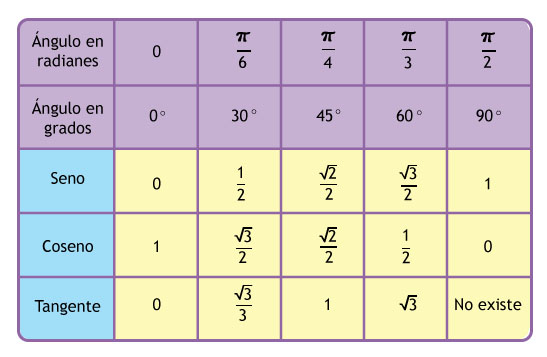
Переведите эти углы из градусной меры в радианную:
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
У вас должны получиться такие значения в радианах (в другом порядке!)
Я, между прочим, специально выделил ответы в две строчки. Ну-ка, сообразим, что за углы в первой строчке? Хоть в градусах, хоть в радианах?
Да! Это оси системы координат! Если смотреть по тригонометрическому кругу, то подвижная сторона угла при этих значениях точно попадает на оси . Эти значения нужно знать железно. И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
Во второй строчке — тоже углы специальные… Это 30°, 45° и 60°. И что в них такого специального? Особо — ничего. Единственное отличие этих углов от всех остальных — именно про эти углы вы должны знать всё .
И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° — уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего… Но об этом подробнее — в следующем уроке.
А пока продолжим тренировку. Переведите эти углы из радианной меры в градусную:
У вас должны получиться такие результаты (в беспорядке):
210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.
Получилось? Тогда можно считать, что перевод градусов в радианы и обратно — уже не ваша проблема.) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…
Второй мощный шаг — это умение определять положение любого угла на тригонометрическом круге. И в градусах, и в радианах. Про это самое умение я буду вам во всей тригонометрии занудно намекать, да…) Если вы всё знаете (или думаете, что всё знаете) про тригонометрический круг, и отсчёт углов на тригонометрическом круге, можете провериться.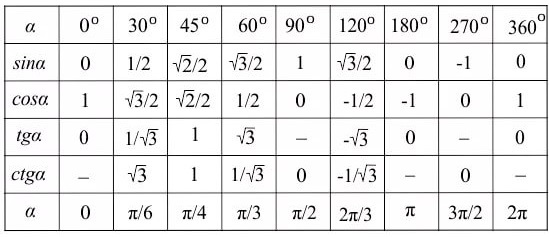
Решите эти несложные задания:
1. В какую четверть попадают углы:
45°, 175°, 355°, 91°, 355° ?
Легко? Продолжаем:
2. В какую четверть попадают углы:
402°, 535°, 3000°, -45°, -325°, -3000°?
Тоже без проблем? Ну, смотрите…)
3. Сможете разместить по четвертям углы:
Смогли? Ну вы даёте..)
4. На какие оси попадёт уголок:
и уголок:
Тоже легко? Хм…)
5. В какую четверть попадают углы:
И это получилось!? Ну, тогда я прям не знаю…)
6. Определить, в какую четверть попадают углы:
1, 2, 3 и 20 радианов.
Ответ дам только на последний вопрос (он слегка хитрый) последнего задания. Угол в 20 радианов попадёт в первую четверть.
Остальные ответы не дам не из жадности.) Просто, если вы не решили чего-то, сомневаетесь в результате, или на задание №4 потратили больше 10 секунд, вы слабо ориентируетесь в круге.
Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Там рассказано, как просто и правильно решать такие задания. Ну и эти задания решены, разумеется. И четвёртое задание решено за 10 секунд. Да так решено, что любой сможет!
Если же вы абсолютно уверены в своих ответах и вас не интересуют простые и безотказные способы работы с радианами — можете не посещать 555. Не настаиваю.)
Хорошее понимание — достаточно веская причина, чтобы двигаться дальше!)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер паропроницаемости и скорости переноса пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
1 радиан [рад] = 57,2957795130823 градус [°]
Исходная величина
Преобразованная величина
градус радиан град гон минута секунда зодиакальный сектор тысячная оборот окружность оборот квадрант прямой угол секстант
Общие сведения
Плоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча.
Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Виды углов
Прямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются развернутыми , углы в 360° называются полными , а углы больше развернутых но меньше полных называются невыпуклыми . Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными смежными , а если же до 360° — то сопряженными
Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными . Если они дополняют друг друга до 180°, они называются смежными , а если же до 360° — то сопряженными . В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными .
Они равны.
Измерение углов
Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы.
Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла.
Транспортир
Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.
Использование углов в архитектуре и искусстве
Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике.
Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля.
В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.
В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба.
Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.
Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок.
Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».
Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.
5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Что больше sin 1 или cos 1
Обновлено: 05.10.2022
Вот такое задание по теме «Формулы приведения». Не знаю, как решать. Подайте идею, пожалуйста. И как тут применить формулы приведения, понятия не имею.
Ну, например, воспользовавшись формулами приведения, представьте второй косинус как синус какого-то аргумента (какого?). А потом воспользуйтесь монотонностью синуса на отрезке [m][0,\pi/2][/m], сравнив аргументы двух синусов. (А для этого Вам понадобится оценить сумму синуса и косинуса одинаковых аргументов.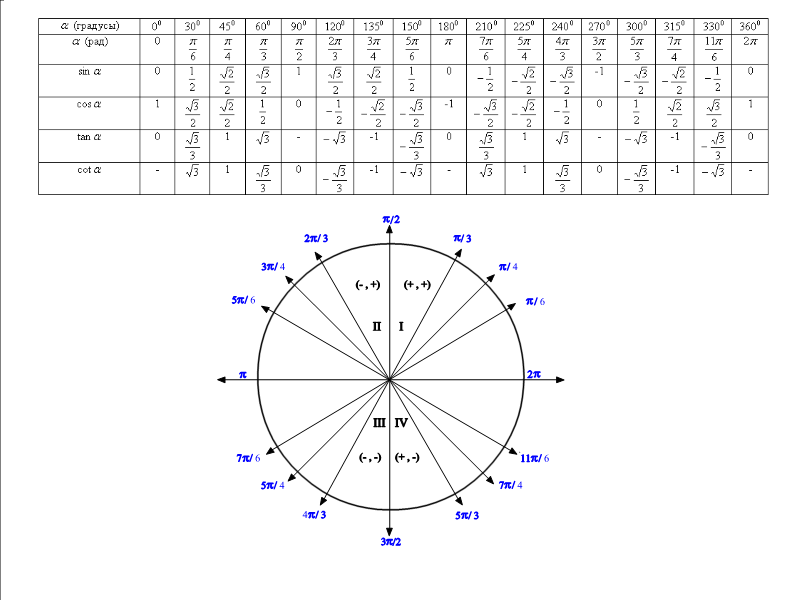
)
cos(cos1)=sin(тт/2-cos1) => Сравнить sin1 и тт/2-cos1.
Так? А как дальше?
Или так: cos1=sin(тт/2-1) ? Тогда вообще непонятно, как сравнивать.
Именно так, сравнить sin1 и тт/2-cos1. А для этого нужно сравнить sin1+cos1 и тт/2. В каких пределах изменяется сумма синуса и косинуса одинаковых аргументов? Если Вы этого не знаете, снова воспользуйтесь формулой приведения, выразите cos1 через синус, а затем воспользуйтесь формулой для суммы синусов.
Сравните числа: sin(-1) и cos 1
ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО! НОМЕРА 2.1;2.3;2.4;. СПАСИБО!
на рисунке изображен график функции y=q(x) областью определения функции служит промежуток [-5;6] с помощью графика функции найдите a) q(-2) q(0) q(2) … q(6) б) значения х при которых q(x)= -2 q(x)= 4 q(x)= 0 в) наибольшее меньшее значение функции г) область значения функции
Изобразите множество точек, заданных системой неравенств:
Упражнения 120 Тело брошено вертикально Вверх начальной ростью Uо (м/с) с высоты h, (м).
Высота һ(м), на ко- торой окажется тело через t (c), выражае … тся формулой gt2 +vot +ho (g=10 м/с2). На рисунке 34 показан гра- фик зависимости от t для случая, когда һо = 20, vo = 15. Найдите по графику: а) сколько времени тело поднималось вверх; б) сколько времени оно опускалось вниз; в) какой наибольшей высо- ты достигло тело; г) через сколько секунд те- ло упало на землю.
1.Выберите неверные утверждения:а)Параллелограмм — это четырёхугольник, в котором все стороны имеют различные длины.б)Непараллельные стороны параллело … грамма не равны.в)Диагонали параллелограмма равны.г)Углы, прилежащие к одной из сторон параллелограмма, в сумме составляют 180°.д)Сумма любых двух углов параллелограмма равна 180°.е)Диагонали параллелограмма делят его на два треугольника, периметры которых равны.2.Диагональ AC параллелограмма ABCD образует с его сторонами углы BCA и ACD, равные 35° и 19° соответственно. Найдите больший угол параллелограмма. Ответ дайте в градусах.3.Один из углов параллелограмма равен 158°.
Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.4.Найдите тупой угол параллелограмма ABCD, если биссектриса угла В образует со стороной AD угол, равный 49°. Ответ дайте в градусах.5.Периметр параллелограмма равен 58 см. Одна из его сторон на 6 см больше другой. Найдите большую сторону параллелограмма. Ответ дайте в сантиметрах.6.Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 53, BD = 21, BС = 29. Найдите АO. Если в ответе получается десятичная дробь, запишите её с помощью точки (например, 1.2).25 баллов
Длина одной стороны прямоугольника-7 см. Какой может быть длина второй стороны если известно, что периметр прямоугольника больше, чем 56 см, но меньше … , чем 62 см
Задайте свой вопрос по математике
профессионаламДругие вопросы на эту тему:
Тригонометрия,10 класс
Решить тригонометрическое уравнение
Подскажите, пожалуйста, идею! Решу сама.
Триг уравнение
Каким методом лучше решать это уравнение, покажите как, надо проверить свое решение
[m]^>x+^>x=\frac^>x>[/m]
Тригонометрия
1) 3 sin ^2 x+10+3 cos^2 x
2) cos^2 15 градусов+cos^2 75 градусов
3) cos^2 15 градусов — sin^2 75 градусов
4) 3 сos^2 x +1 — cos^2 x — 3 sin^2 x, если cos 2x = — 0,2
5) (sin x-cos x)^2, если sin 2x =0,4
Тригонометрия.
2(2*SQRT(|x|)+1) = 122) Решить уравнение:
pi*sin x = | x-pi/4 | — | x-3pi/4|
Во 2-м случае получаем одно из уравнений при х от pi/4 до 3pi/4:
pi*sin(x) = 2x-pi/2
А дальше — ступор
Сравнить числа a и в : а = sin1 в =cos 1
В корзине 4 шара: два красных, лдин синий и один зеленый. Девочки взяли из корзины по одному шару. У Саши и Полины не зелёные шары, у Ани и Саши не си … ние. В корзине остался один шар и он не красный. У полины и Саши шары разного цвета. Какой шар остался в корзине? Какие шары у девочек?
дайте развёрнутый ответ. Площадь футбольного поля 587,47 ×10¹⁸мм². Запишите чему равна площадь в дм², см²
Знайти значення параметра а, при якому рівняння має безліч коренів
Первый дворник может убрать территорию на 2 часа быстрее второго. Сколько потребуется времени на уборку территории первому дворнику, если вдвоем два д … ворника убирают весь двор за 1 7/8 часа?
Читайте также:
- Как отменить способность в apex legends
- Horizon zero dawn как узнать версию игры
- Luna яхта кому принадлежит
- Factorio как создать персонажа в песочнице
- Можно ли играть в геншин импакт без скачивания
Краткий обзор графического калькулятора TI-92
Краткий обзор графического калькулятора TI-92 Введение по алгебре по ТИ-92 Х 1997 г.
, Натан О. Найлз
Ассоциированный профессор (на пенсии)
Военно-морская академия США
15. Инверсные триггерные функции
Значения обратных тригонометрических функций могут быть получены с помощью калькулятор или из таблиц. ТИ-92 Графический калькулятор имеет ключи SIN — 1 , COS -1 и TAN -1 . Это вторая функция клавиш SIN, COS и TAN, требующая клавиша, которую нужно нажать первый. При использовании калькулятора мода должна быть в радианах, когда реальная желательно число или угол в радианах. Когда требуется угол в градусах мода должна быть градусов.
Пример . Найдите число для каждого из следующих, используя ТИ-92 Графический калькулятор.
(а) Sin -1 (0,2337). (б) Грех -1 (- 0,567). (в) Cos -1 (- 0,9211). (г) Тан -1 (1,743).
Решение: Поскольку ответ должен быть числом, режим должен быть
радианы.
Включите TI-92, очистите главный экран и строку ввода: 8
Проверить режим: (если
четвертая строка: Угол .. РАДИАН нажмите
)
(если четвертая строка: Угол ГРАДУС нажмите
1 )
(а) [SIN -1 ] 0,2337 Отображает: .235881
(б) [SIN -1 ] 0,567 Дисплеи: — .602859
(c) [COS -1 ] 0,9211 Отображений: 2,74169
(г) [TAN -1 ] 1,743 Отображает: 1.04992
Проблема . Найдите число для каждого из следующих, используя Графический калькулятор TI-92.
(а) Грех -1 (0,7833). (б) Грех -1 (- 0,9425). (в) Cos -1 (0,4713). (г) Cos -1 (- 0,4713).
(e) Тан -1 (1,557). (е) Тан -1 (- 1,557). (g) Sin -1 (1,557). (Почему сообщение об ошибке?)
Пример . Найдите угол в градусах для каждого из следующих
с помощью графического калькулятора TI-92.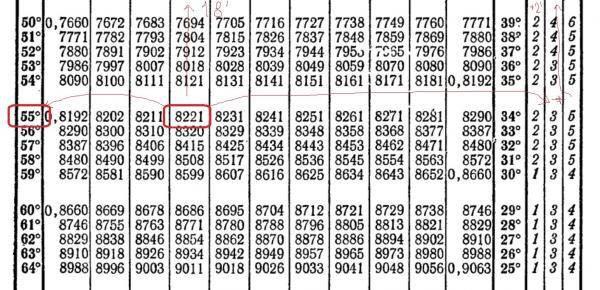
(а) Sin -1 (0,2337). (б) Грех -1 (- 0,567). (в) Cos -1 (- 0,9211). (г) Тан -1 (1,743).
Решение: Так как нам нужен угол в градусах, мы должны использовать ГРАДУС режим.
2 (а) [СИН -1 ] 0,2337 Дисплеи: 13,515 (что составляет 13,515°)(б) [SIN -1 ] 0,567 Отображает: — 34,5413 (то есть — 34,5413°)
(c) [COS -1 ] 0,9211 Отображает: 157,087 (что составляет 157,087°)
(д) [TAN -1 ] 1,743 Отображает: 60,1561 (60,1561°)
Проблема . Найдите угол в градусах для каждого из следующих с помощью графического калькулятора TI-92.
(а) Sin -1 (0,7833). (б) Грех -1 (- 0,9425). (в) Cos -1 (0,4713). (г) Cos -1 (- 0,4713).
(e) Тан -1 (1,557). (е) Тан -1 (-
1,557). (ж) Грех -1 (1.557).
(Почему
сообщение об ошибке?)
TI-92 можно использовать для решения некоторых тригонометрических уравнений.
Пример . Используйте калькулятор TI-92, чтобы решить 2 cos u = — 1, для 0 £ и < 2р.
Решение : Включите, очистите главный экран и строку ввода: 8
Режим проверки радианов. В нижней строке должен отображаться RAD.
Получить меню алгебры и решить: 1Введите уравнение: 2 ты 1 u
На дисплее отображается:
Этот ответ требует некоторых объяснений и манипуляций, чтобы согласиться с ответом. когда пример был сделан ранее. Символ @n1 указывает на произвольное целое число, представляющее любое целое число . В предыдущем обсуждении мы использовали u ± 2p n , n = 0, 1, 2, ¼ В произвольный целочисленный символ, число после n может быть любым числом от 1 до 255, то есть @n1¼ @n255. Каждый раз это используется число увеличивается. (Если очистить память, [ПАМЯТЬ] 1 , число снова начинается с 1.
Возможно, вам придется отрегулировать контрастность дисплея.
по
а также .) Поскольку @n1 — произвольное целое число, выберем его равным 0. Тогда u = и u = . 2р/3 в промежутке, но — 2р/3 нет. Итак, пусть @n1 = 1, тогда и = 8п/3 и и = 4п /3. 8п/3 не в антракте, а 4п /3 есть.
Следовательно, ответ u = 2p/3, 4p /3
, что согласуется с ответом, найденным ранее. Вы должны проверить другие значения для @n1, чтобы показать, что они находятся за пределами требуемого интервала.
Проблема . Используйте калькулятор TI-92, чтобы решить 2 sin u = — 1, для 0 £ и < 2р.
Факторинг иногда бывает полезен.
Пример . Решите 2 sinq cosq = sinq для 0° £ д < 360°.
Решение: Транспонировать sinq и factor. sinq (2 cosq — 1) = 0.
Приравняв каждый множитель к нулю и упростив, получим
sinq = 0 и 2 cosq — 1 = 0
Таким образом, sinq = 0 и cosq = 1/2
что приводит к q = 0° , 180° и q = 60°, 300°
Решение может быть записано как q = 0° , 60° , 180° , 300°
Вы должны проверить каждое из этих значений в исходном уравнении.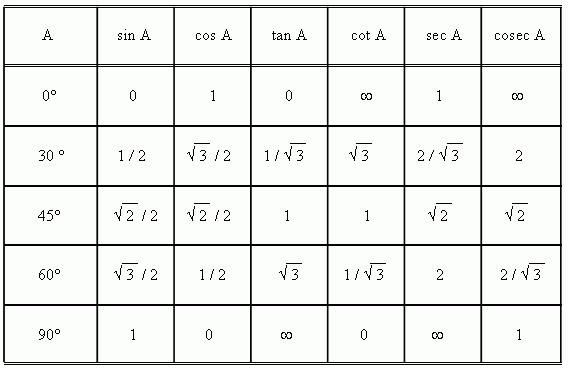
Проблема . Решите 2 sinq cosq = cosq для 0° £ д < 360°.
Пример . Используйте TI-92, чтобы решить 2 sinq cosq = sinq для 0° £ д < 360°.
Изменить РЕЖИМ на ГРАДУС: 2 2 [к] [к] [к] [к] На дисплее отображается: q = 60× (6× @n3 + 1) или q = 60× (6× @n3 — 1) или q = 180 × @n4 (закрашенный прямоугольный треугольник ú означает нажать B для большей части дисплея. Строка должна быть выделена. Если это не так, нажмите С или Д пока не будет.) Теперь мы выбираем целые значения для @n3 и @n4, пока не получим все значения в интервале 0° £ д < 360° . При @n3 = 0, q = 60 и - 60. При @n3 = 1 q = 420 и 300. При @n3 = 2, q = 780 и 660.При @n4 = 0, q = 0. При @n4 = 1, q = 180. При @n4 = 2 q = 360.
Таким образом, в интервале 0° £ д < 360° , у нас есть2 = 0° , 60° , 180° , 300°.
Проблема . Используйте TI-92, чтобы решить 2 sinq cosq = cosq для 0° £ д < 360°.
Пример .
Решить 2 sin4 u — 9
sin2 u + 4 = 0 для 0 £ u < 2р.
Решение: Факторинг получаем (2 sin2 u — 1)(sin2 и — 4) = 0
Приравняв каждый множитель к нулю и упростив, получим,
sin2 u = и sin2 и = 4
При извлечении квадратных корней имеем
sin u = и sin u = ± 2
Для первого выражения находим
u =
Второе выражение, sin u = ± 2, не имеет решения , так как абсолютное значение sin u не может превышать 1.
Проблема . Решите 2 cos4 u — 19 cos2 u + 9 = 0 для 0 £ u < 2р.
Пример . Используйте TI-92, чтобы решить 2 sin4 u — 9 sin2 u + 4 = 0 для 0 £ u < 2р.
Решение: Убедитесь, что MODE установлен на RAD.
1 2с В у д г Z 4 9 с В у д г Z 2 4 А 0 б у д ¸
На дисплее отображается: u = 71,4712 или u = 7,06858 или u = 5,49779 ú
(нажмите C и B
много раз, чтобы увидеть больше значений) или u = 3,02699 или u = 2,35619 или u = 0,785398
или и = — .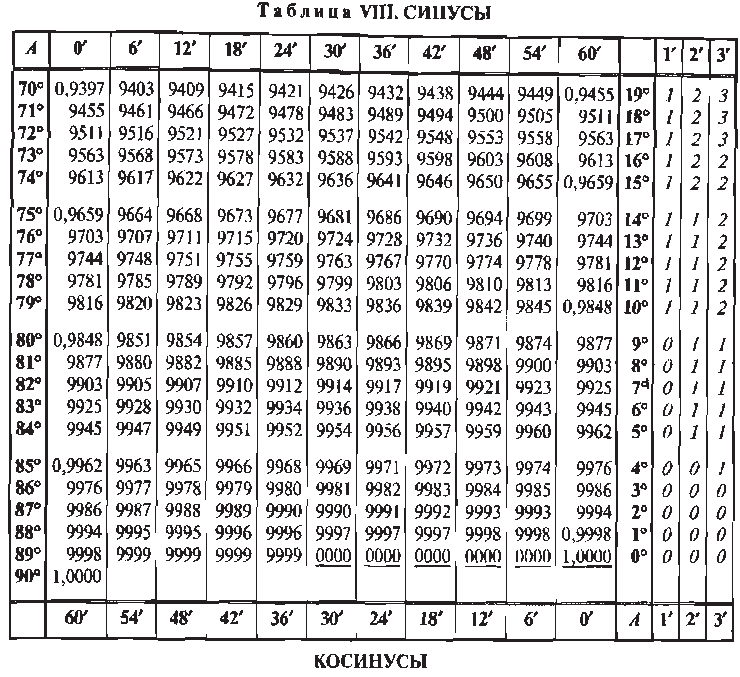
785398 или и = —
2,35619 или и = — 3,02699
или и = — 5,49779 или и = —
7,06858 или и = — 71,4712
Для требуемого интервала имеем
u = 0,785398, 2,35619, 3,02699, 5,49779
Иногда мы можем указать требуемый интервал в качестве ограничения домена используя оператор with, | , это набирается как 2 н (или 2 К). Мы можем добавить это обозначение к строку ввода, нажав D и B несколько раз, пока курсор не окажется в правом конце строки ввода. затем Нажмите:
2 л и 2 Ã 0 и ты 2 2 2 Т ¸ Дисплей: u = 5,49779 или u = 3,92699 или u = 2,35619 или u = 0,785398Проблема . Используйте TI-92, чтобы решить 2 cos4 u — 19 cos2 u + 9 = 0 для 0 £ u < 2р.
Пример . Решить — 2 sin и + 3 cos u = 1 для 0 £ u < 2р.
Решение: Переставить 3 cos на и возвести в квадрат обе стороны, у нас есть
4 sin2 u = 1 — 6 cos u + 9 cos2 и
, что упрощается до 13 cos2 u — 6 cos и — 3 = 0
Решив cos u по квадратичной формуле, получим
или cos u = 0,764 и cos u = — 0,302
Для cos u = 0,764 и u в нужном интервале у является номером QI или QIV.
Чтобы найти номер ссылки, u r , мы используем калькулятор.
u r = cos-1 0,764 = 0,701
В I квартале u = u r и u = 0,701.
В QIV, и = 2р — u r и u = 6,28 — 0,701 = 5,58
Для cos u = — 0,302 и u в требуемом интервале, u — это номер QII или QIII.
Соответствующий номер ссылки
u r = cos- 1½ — 0,302½ = cos-1 0,302 = 1,26
Во II квартале u = p — u r и u = 3,14 — 1,26 = 1,88
В III квартале и = р + и г и и = 3,14 + 1,26 = 4,4
Поскольку мы возвели обе части уравнения в квадрат, мы могли ввести посторонние корни. Мы должны проверить их в исходном уравнении, — 2 грех и + 3 потому что и = 1.
Для и = 5,58. находим — 2 sin 5.58
+ 3 cos 5,58 = — 2(-
0,647) + 3(0,763) = 3,583, что не равно 1.
Аналогично для u = 1,88. (Вы должны проверить это и два других корнеплоды.)
Таким образом, искомые корни равны u = 0,701, 4,4.
Проблема . Решите 2 потому что и — 3 sin u = 1 для 0 £ и < 2р.
Пример . Используйте TI-92, чтобы решить — 2 sin u + 3 cos u = 1 с ограничением домена 0 £ и < 2р .
Решение: 1 · 2 В у д 3 х у д Á 1b уд 2 0 2 Â Á ты и и 2 Â 2 2 т ¸
На дисплее отображается u = 4,40542 или u = 0,701759
Проблема . Используйте TI-92, чтобы решить 2 cos u — 3 sin u = 1 с ограничением домена 0 £ и < 2р .
Иногда проще решить для кратного угла, такого как 2q
, 3q , q/2 и т. д.,
сначала, а не для q . Когда это будет сделано,
необходимо соблюдать осторожность, чтобы найти углы в желаемом интервале. То есть,
если q должно лежать между 0 °
и 360°, 2q
должен лежать между 0° и 720°
.
Пример . Решите sinq cosq = для 0° £ q < 360° .
Решение: Заменить sinq cosq по греху 2q . Тогда sin 2q =
И sin 2q =
Так как q находится в интервале 0° £ q < 360° , 2q находится в интервале 0° £ q < 720° .
Таким образом, 2q = 240° , 300° , 600° , 660°
и решения равны q = 120° , 150° , 300° , 330°
Проблема . Решите sinq cosq = для 0° £ q < 360° .
Пример . Решите 2 x = тангенс x для x .
Решение: С помощью калькулятора ТИ-92 имеем
1 2x Á Г х д б х г ¸На дисплее отображается: x = 92,6716 или x = 7,78988 или x = 4,60422ú (выделите эту строку на C и получить больше значений на B ) или х = 0 или х = — 4,60422 или х = — 7,78988 или х = — 92,6716
Но, что-то не так! Из наших знаний о графах следует быть корнем между 0 и 4,60422.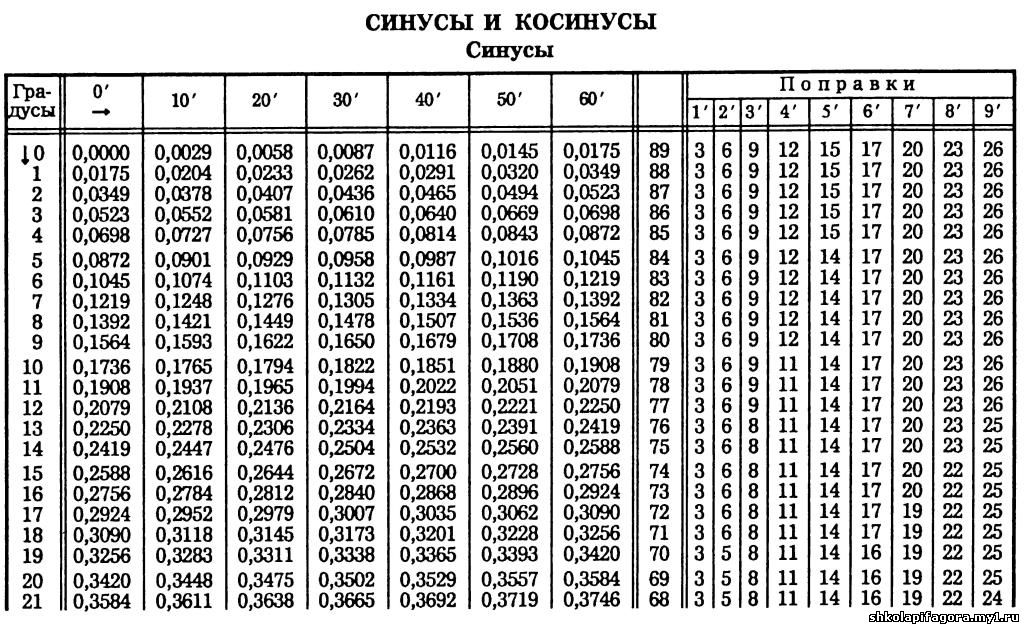
Потому что, если мы допустим, что y 1 = 2 x и y 2 = тангенс x и зарисовав их графики видим, что они пересекаются около х = 1.
Давайте посмотрим, что произойдет, если мы установим ограничение на x из 0 < x < p/2.
1 2x Á Г х д б х г 2 н 0 2 В х и х 2 Т е 2 ¸На дисплее отображается: x = 1,16556
Это больше похоже на него. Этот пример показывает, что разумное использование калькулятора вы должны иметь хорошее представление о том, каких результатов следует ожидать. Проблема . Используйте TI-92, чтобы решить 3 x = тангенс x для x .
Отсутствует ли корень, когда ограничения не используются?
| К оглавлению | К Разделу 14. Тригонометрические функции |
Обратные тригонометрические функции — Разделы по тригонометрии
Темы | Дом
19
Диапазон y = arcsin x
sin −1 x .
Обратный синус
Диапазон y = арктангенс x
Диапазон y = arccos x
Обратные отношения
Диапазон y = угловых секунд x
УГЛЫ в исчислении будут измеряться в радианах. Таким образом, если нам дан, например, угол в радианах, мы можем оценить его функцию.
| грех | № 6 | = | ½. |
(Тема 8.)
Обратно, если нам дано, что значение функции синуса равно ½, то задача состоит в том, чтобы назвать угол x в радианах.
грех х = ½.
«Синус какого угла равен ½?»
Однако мы пишем: Оценить
угловой синус ½ .
« угол , синус которого равен ½.»
Функция
y = арксинус x
называется обратной функцией
. у = грех х .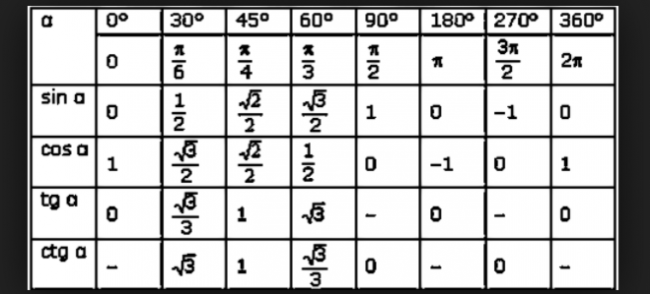
угловых углов в x – это угол , синус которого – число x .
Строго говоря, arcsin x — это дуги , синус которой равен x . Потому что в единичном круге длина этой дуги измеряется в радианах. Тема 15.
Теперь есть много углов, у которых синус равен ½. Это будет любой угол, соответствующий острый угол которого равен . Следовательно, мы должны ограничить диапазон y = arcsin x — значения этого угла — так, чтобы он действительно был функцией; чтобы оно было однозначным.
Как мы это сделаем? Мы ограничим их теми углами, которые имеют наименьшее абсолютное значение.
Они называются главными значениями y = arcsin x .
Следовательно,
угловых синусов ½ = .
Первый квадрант угла — это угол с наименьшим абсолютным значением, синус которого равен ½.
Пример 1. Вычислите arcsin (−½).
Раствор.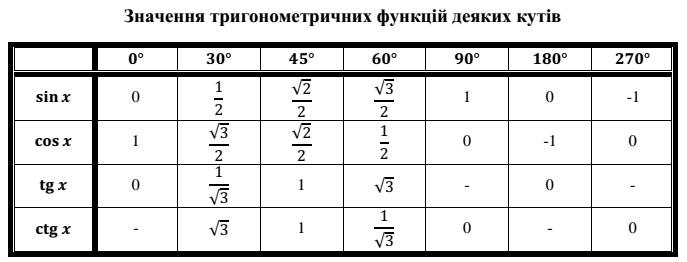
Углы, синусы которых отрицательны, попадают в 3-й и 4-й квадранты. Угол наименьшего абсолютного значения находится в 4-м квадранте между 0 и -.
Угол, синус которого равен − x , является просто отрицательным значением угла, синус которого равен x .
арксинус (-½) = -арксинус (½) = -.
Таким образом, диапазоном функции y = arcsin x будут углы, попадающие в 1-й и 4-й квадранты между — и .
Углы, синусы которых положительны, будут углами 1-го квадранта. Углы, синусы которых отрицательны, попадают в четвертую четверть.
Ограничение диапазона arcsin x эквивалентно ограничению домена sin x теми же значениями. Это будет иметь место со всеми ограниченными диапазонами, которые следуют.
sin −1 x . Обратный синус
Другое обозначение для arcsin x – это sin −1 x .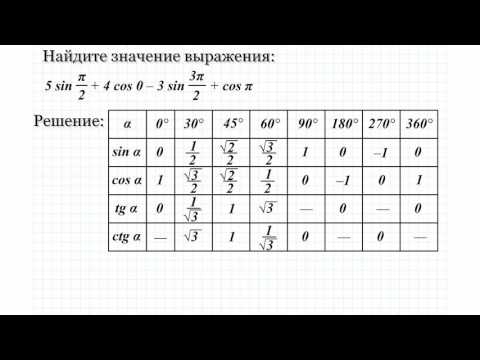
Прочтите: «Обратный синус x «. −1 здесь , а не показатель степени. (См. Тему 19 Предварительного исчисления.)
Задача 1. Оцените следующее в радианах.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова прикрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
а) arcsin 0 = 0. (Тема 15.)
б) arcsin 1 = π/2. (Тема 15.)
c) sin −1 (−1) = −π/2. (Тема 15.)
| π/3. (Тема4.) |
| -π/3. |
| -π/6. |
Каждой тригонометрической функции соответствует обратная ей функция.
arcsin x ,
арккос х ,
арктан x ,
arccsc x ,
угловых секунд x ,
арккот x .
В каждом из них нам дано значение x тригонометрической функции. Мы должны назвать радиан углом , который имеет это значение.
В каждом случае мы должны ограничить его диапазон, чтобы функция была однозначной.
Диапазон y = арктангенс x
Как y = arcsin x , y = arctan x имеет наименьшие абсолютные значения в 1-м и 4-м квадрантах.
Обратите внимание, что y — угол , тангенс которого равен x — должен быть больше — и меньше . Ибо при этих квадрантных углах касательная не существует.
Углы, касательные которых положительны, будут углами 1-го квадранта. Углы, тангенсы которых отрицательны, попадут в четвертую четверть.
То же самое, что и с arcsin (− x ).
Угол, тангенс которого равен − x , является просто отрицательным значением угла, тангенс которого равен x .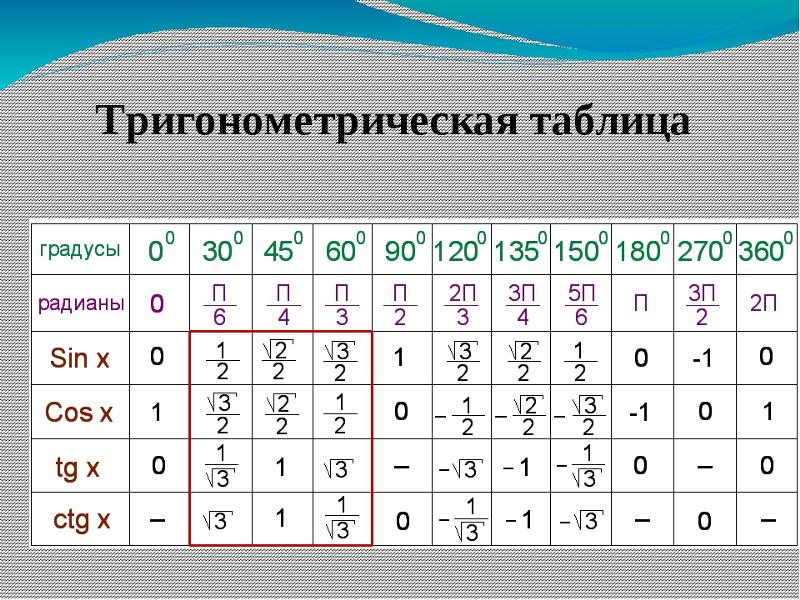
| = | -θ. | |
| = | θ. | |
| Следовательно, | ||
| арктан(− x ) | = | −арктан x . |
Проблема 2. Оцените следующее.
| а) арктан 1 = | № 4 | b) арктан (−1) = | − | № 4 |
| c) tan −1 | = | № 3 | d) tan −1 (−) | = | − | № 3 |
| д) арктан 0 = | 0 | е) | = | − | № 6 |
Ассортимент у = arccos x
Пример 2.
Вычислите arccos ½.
| Решение . | arccos ½ = | № 3 | . |
| Угол в радианах, косинус которого равен ½, равен | № 3 | (60°). |
Проблема 3. Почему это не так?
arccos (−½) = −.
— угол 4-го квадранта. А в четвертом квадранте косинус положительный.
Урок 15.
Угол, косинус которого отрицательный, попадет во 2-й квадрант, где он будет иметь наименьшее абсолютное значение. (Тема 15.)
Косинус угла 2 четверти θ — это минус косинуса соответствующего острого угла, который является его дополнением.
Другими словами:
Угол, косинус которого равен − x
, является дополнением угла, косинус которого равен x .
arccos (− x ) = π − arccos x .
Пример 3. Вычислите arccos (−½).
Раствор . Мы видели:
arccos ½ = .
Следовательно, arccos (−½) — это дополнение к углу — θ , который мы должны прибавить, чтобы получить π.
+ θ = π.
Теперь составляет одну — треть числа π. Следовательно, его дополнение θ будет равно двум -третям числа π: .
arccos (−½) = .
Тогда диапазон y = arccos x будет от 0 до π.
Угол, косинус которого положителен, будет углом 1-го квадранта; угол, косинус которого отрицателен, будет лежать во 2-й четверти. Он будет дополнением угла 1-го квадранта.
Проблема 4. Оцените следующее.
| а) arccos 1 = | 0 | б) arccos (−1) = | № |
| c) cos −1 | 2 | = | № 4 | d) cos −1 (− | 2 | ) = | π − | № 4 | = | 3π 4 |
| д) | = | № 6 | е) | = | π − | № 6 | = | 5π 6 |
| g) arccos 0 = | № 2 |
Обратные отношения
Если поставить
f ( х ) = грех х
и
г ( x ) = arcsin x ,
, то по определению обратных функций:
f ( г ( x )) = x и г ( f ( x )) = x .
sin (arcsin x ) = x , а arcsin (sin x ) = x .
Отсюда следует:
arcsin x = θ тогда и только тогда, когда x = sin θ.
Мы взяли обратную функцию — синус — обеих частей уравнения слева. Мы извлекли аргумент х .
Тема 19 предварительного исчисления.
Например,
| угловой синус ½ = | № 6 | если и только если ½ = sin | № 6 | . |
Обычно это так.
Задача 5.
а) арктан t = β тогда и только тогда, когда t = тангенс β.
b) угл.сек u = α тогда и только тогда, когда u = сек α.
c) arccos 1 = 0 тогда и только тогда, когда 1 = cos 0.
| d) arccot 1 = | № 4 | тогда и только тогда | 1 | = кроватка | № 4 | . |
Этот принцип позволяет решать многие тригонометрические уравнения.
Пример 4. Решите для x :
| арксинус ( x — 1) = | . |
Раствор . Взяв обратную функцию — синус — обеих сторон, мы можем освободить аргумент x − 1. Пишем сразу:
| х − 1 | = грех | = | 2 |
Следовательно,
| х | = 1 + | 2 | . |
Задача 6. Решите для х :
тангенс ( х + 2) = 1.
| х + 2 | = | арктангенса 1 = | № 4 | . |
| х | = | № 4 | − 2. |
Задача 7. Решите для x :
, потому что х 2 = −1.
x 2 = arccos (−1) = π.
х = ±.
Задача 8. Решите для x :
| sin −1 ( x 2 − 1) | = | 0. | |
| x 2 − 1 | = | угловой синус 0 | = 0 |
| x 2 | = | 1 | |
| x | = | ±1. | |
Диапазон y = угловых секунд x
В исчислении sin −1 x , tan −1 x и cos −1 x являются наиболее важными обратными тригонометрическими функциями.
Тем не менее, вот диапазоны, которые делают остальные однозначными.
Если x положительное, то значение обратной функции всегда равно первому квадранту угла или 0. Если x отрицательное, значение обратной функции попадет в квадрант, в котором прямая функция отрицательна. Таким образом, если 90 939 x 90 940 – отрицательное значение, то 90 939 x 90 940 угловых секунд попадет во 2-й квадрант, потому что именно там значение sec x отрицательно.
Единственная обратная функция ниже, в которой x может быть 0, это arccot x . аркот 0 = π/2.
Опять же, мы ограничиваем значения y теми углами, которые имеют наименьшее абсолютное значение.
Теорема. Если
y = угловая секунда x ,
затем товар
sec y tan y никогда не бывает отрицательным.
Действительно, если y = угловые секунды x , то угол y попадает либо в первый, либо во второй квадрант.