Сведение матрицы к треугольному виду онлайн: Приведение матрицы к треугольному виду онлайн

3. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду с помощью элементарных преобразований. Метод Гаусса.

3.1. Элементарные преобразования. Будем называть элементарным преобразованием типа I перестановку двух строк матрицы.

Элементарным преобразованием типа II будем называть следующую операцию: все строки матрицы, кроме одной, остаются прежними, но к этой одной строке прибавляется другая (любая), умноженная на некоторое число.

Утверждение 1. Преобразование, обратное к элементарному, является элементарным, т.е. если матрица В получена из матрицы А с помощью элементарного преобразования, то и матрица А может быть получена из матрицы В с помощью элементарного преобразования. Доказательство очевидно.

Утверждение 2. Пусть — расширенная матрица системы линейных уравнений. Элементарные преобразования этой матрицы не меняют множества решений системы.

Доказательство. Пусть — матрица, получившаяся из с помощью элементарного преобразования и пусть — решение исходной системы. Этот же набор чисел будет являться и решением системы с матрицей — в каждом из двух возможных случаев это очевидно. Значит, решений меньше не стало. А так как обратный переход от к осуществляется тоже с помощью элементарного преобразования, то каждое решение системы с матрицей будет решением системы с матрицей . Утверждение доказано.

3.2. Приведение матрицы к ступенчатому виду. С помощью элементарных преобразований можно перейти от исходной матрицы к матрице более простого вида. Алгоритм следующий: Пусть дана матрица

Рассмотрим первый столбец. Пусть в нем есть хотя бы один ненулевой элемент (если такого нет, перейдем ко второму столбцу). Поставим строку, где находится этот элемент, на первое место (элементарное преобразование первого типа).

Теперь прибавим ко 2-й строке 1-ю, умноженную на подходящий коэффициент , подобрав его так, чтобы элемент стал равен 0: . Так же поступим с остальными строками: к -й строке прибавим 1-ю, умноженную на коэффициент Получим матрицу вида

Теперь на время забудем о первой строке. Повторим описанную процедуру для матрицы из элементов , . Если во втором столбце, начиная со второй строки, нет ненулевых элементов, перейдем к третьему столбцу. Если же есть ненулевой элемент, поставим его на вторую строку, поменяв строки местами. Затем к остальным строкам, начиная с третьей, прибавим вторую, умноженную на подходящий коэффициент так, чтобы элемент из второго столбца стал равен 0. Матрица примет вид:

.

Таким способом за конечное число шагов из любой матрицы мы получим матрицу следующего вида:

.

Такую матрицу называют ступенчатой (трапецевидной, квазитреугольной). В углу каждой ступеньки стоит ненулевой элемент.

4.1. Определение обратной матрицы. Мы по-прежнему будем рассматривать квадратные матрицы.

Определение. Пусть дана матрица А. Назовем матрицу правой обратной для А, если (– единичная матрица соответствующего порядка).

Аналогично, назовем левой обратной для А, если выполняется равенство .

Утверждение 1. .

Доказательство. Действительно,

Значит, можно говорить просто об

обратной матрице. Будем ее обозначать А^-1. Итак,

.

Заметим, что не каждая матрица имеет обратную. Так как , то , и если (такие матрицы называются вырожденными), то матрица А не может иметь обратной матрицы.

Утверждение 2. Если обратная матрица существует, то она единственна. Иначе, если АВ = ВА = Е и АС = СА = Е, то В = С.

Доказательство:

4.2. Существование обратной матрицы. Мы уже заметили, что если определитель матрицы равен нулю, то она не имеет обратной. Оказывается, что если определитель матрицы не равен нулю, то она имеет обратную матрицу. Мы сейчас ее построим.

Составим сначала матрицу из алгебраических дополнений:

.

Затем транспонируем эту матрицу:

.

Получившаяся матрица называется присоединенной. Умножим на :

,

так как

. Тогда .

4.3. Матричные уравнения. Умея находить обратные матрицы, можно решать матричные уравнения. Например, чтобы решить уравнение АХ = В, где А и В — квадратные матрицы одинакового размера, причем А – невырожденная, достаточно умножить обе части равенства слева на А^-1:

Аналогично, решением матричного уравнения

ХА = В будет являться матрица Х = ВА^-1.

4.4. Решение систем линейных уравнений с помощью обратной матрицы. Пусть дана система линейных уравнений с квадратной матрицей, т.е. количество уравнений равно количеству неизвестных. В матричном виде эту систему можно записать . Если матрица А невырождена, т.е. ее определитель не равен нулю, то существует обратная матрица А^-1, и тогда

Мы получили решение такой системы линейных уравнений с помощью обратной матрицы и заодно показали единственность решения такой системы.

3.3. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения переменных). Пусть дана система линейных уравнений

(*)

Составим расширенную матрицу системы (*):

С помощью элементарных преобразований из мы можем получить другую матрицу, соответствующую другой системе уравнений, но, напомним, множество решений получившейся системы будет совпадать с множеством решений исходной системы (утверждение 2). Значит, если привести матрицу к ступенчатому виду, множество решений не изменится:

Тогда соответствующая система линейных уравнений выглядит так:

(**)

Очевидно, что если в матрице оказалась строка причем то система уравнений несовместна.

Пусть таких строк нет.

Тогда неизвестные назовем главными (они соответствуют нашим «ступенькам»). Количество главных неизвестных равно . Остальные неизвестные назовем свободными. Очевидно, их .

Для удобства записи будем считать, что главными оказались переменные , а свободными — (в конце концов, всегда можно переобозначить неизвестные величины). Расширенная матрица системы имеет вид:

,

причем .

До сих пор мы двигались сверху вниз – это был так называемый прямой ход метода Гаусса. Теперь начнем движение снизу вверх – обратный ход. Прибавим к -й строке -ю, умноженную на подходящий коэффициент , чтобы элемент стал равен нулю. Этот коэффициент нетрудно найти: . То же самое сделаем с остальными строками. (Заметьте: эти преобразования изменяют только элементы, стоящие в столбцах с номерами от до ). Теперь в -м столбце только элемент не равен нулю.

Поднимемся на строку выше. Так как , то можно добиться того, чтобы все элементы в -м столбце, кроме самого элемента , были равны нулю. Постепенно мы дойдем до первой строки и получим матрицу вида

.

Вспомним, что за каждой строкой матрицы стоит линейное уравнение:

Из этих уравнений сразу получаем выражения для главных неизвестных:

(***)

Придадим свободным неизвестным произвольные значения. Тогда значения главных неизвестных будут определяться однозначно. Система (***) описывает все решения исходной системы (*).

Сформулируем некоторые, теперь уже очевидные, утверждения.

1. Система (*) совместна в получившейся ступенчатой системе (**) нет уравнений вида , где .

2. Совместная система является определенной в ступенчатой системе (**) .

3. Однородная система нетривиально совместна (т.е. имеет ненулевое решение) <.

Метод Гаусса решения систем линейных уравнений весьма удобен для небольших систем с небольшим количеством неизвестных.. Но в практических задачах, когда коэффициенты при неизвестных даны с определенной точностью и с определенной точностью ищутся решения, при использовании этого метода возникают некоторые проблемы, но это уже вопросы, которые излагаются в курсе «Численные методы».

Пока мы только описали множество решений системы линейных уравнений. О структуре этого множества мы поговорим позднее, когда будет введено понятие линейного пространства и линейной зависимости.

4.5. Правило Крамера в простейшем случае. Пусть дана система из двух линейных уравнений с двумя неизвестными:

Умножим первое уравнение на , а второе — на :

Вычитая из первого уравнения второе, получим выражение для неизвестной :

откуда, если ,

.

Аналогично получается выражение для :

.

Заметим, что в знаменателе обоих выражений стоит определитель матрицы коэффициентов, а в числителе – определитель, получившийся из матрицы коэффициентов заменой соответствующего столбца на столбец правых частей.

Оказывается, этот симпатичный результат можно обобщить на случай произвольного числа уравнений . Напомним, речь идет только о системах линейных уравнений с квадратными матрицами коэффициентов.

4.6. Правило Крамера в общем случае. Пусть АХ = В — система линейных уравнений с квадратной матрицей коэффициентов, причем определитель матрицы не равен нулю. Тогда решением такой системы являются значения неизвестных

где , а — определитель матрицы, получившейся из матрицы заменой -го столбца на столбец правых частей.

Покажем, что набор чисел действительно является решением системы.

Так как матрица А невырождена, то существует обратная матрица А^-1. Умножим обе части равенства АХ = В слева на А^-1, получим

.

Заметим, что -я компонента получившегося вектор-столбца — это разложение определителя по -му столбцу. Значит,

.

Несмотря на привлекательность формулировки, практическое значение правила Крамера невелико: чтобы найти решение системы с неизвестными, приходится вычислять определитель -го порядка. Это оправдано при или .

Треугольный вид матрицы. Свойства верхней треугольной матрицы

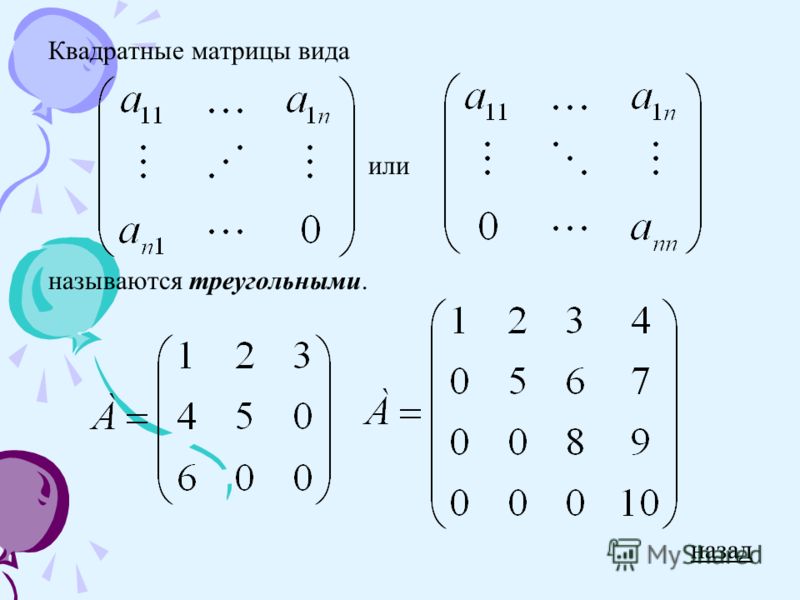
Верхняя треугольная матрица

Треугольная матрица — квадратная матрица , в которой все элементы ниже или выше главной диагонали равны нулю.

Пример верхнетреугольной матрицы

Верхнетреугольная матрица — квадратная матрица , в которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.

Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.

Треугольные матрицы используются в первую очередь при решении линейных систем уравнений , когда матрица системы сводится к треугольному виду используя следующую теорему:

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.

Свойства

• Определитель треугольной матрицы равен произведению элементов на её главной диагонали.
• Определитель унитреугольной матрицы равен единице.
• Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу , которая обозначается UT (n , k ) или UT n (k ).
• Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT (n , k ) или LT n (k ).
• Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT n (k ) по умножению, которая обозначается SUT (n , k ) или SUT n (k ). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT (n , k ) или SLT n (k ).
• Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
• Группа UT n разрешима , а её унитреугольная подгруппа SUT n нильпотентна .

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Верхняя треугольная матрица» в других словарях:

Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица … Википедия

Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия

Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия

Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Проставив сноски, внести более точные указания на источники. Добавить иллюстрации … Википедия

Представление симметричной положительно определённой матрицы в виде, где нижняя треугольная матрица со строго положительными элементами на диагонали. Иногда разложение записывается в эквивалентной форме: , где верхняя треугольная матрица.… … Википедия

SFLASH асимметричный алгоритм цифровой подписи рекомендованный проектом NESSIE European в 2003 году. SFLASH основан на Matsumoto Imai(MI) схеме, так же называемой C*. Алгоритм принадлежит к семейству многомерных схем с открытым ключом, то… … Википедия

Процесс ортогонализации, алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V. Наиболее известным является… … Математическая энциклопедия

Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора

Ослабления м е т о д, метод итерационного решения системы линейных алгебраич. уравнений Ах=b, элементарный шаг к рого состоит в изменении только одной компоненты вектора неизвестных, причем номера изменяемых компонент выбираются в нек ром циклич … Математическая энциклопедия

В которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.

Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.

Треугольные матрицы используются в первую очередь при решении линейных систем уравнений , когда матрица системы сводится к треугольному виду используя следующую теорему:

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.

Свойства

• Определитель треугольной матрицы равен произведению элементов на её главной диагонали.
• Определитель унитреугольной матрицы равен единице.
• Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу , которая обозначается UT (n , k ) или UT n (k ).
• Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT (n , k ) или LT n (k ).
• Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT n (k ) по умножению, которая обозначается SUT (n , k ) или SUT n (k ). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT (n , k ) или SLT n (k ).
• Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
• Группа UT n разрешима , а её унитреугольная подгруппа SUT n нильпотентна .

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Треугольная матрица» в других словарях:

треугольная матрица — — треугольная матрица Квадратная матрица, у которой равны нулю все элементы, расположенные под или над главной диагональю (ср. Диагональная матрица). В первом случае имеем… …

Треугольная матрица — квадратная матрица, у которой равны нулю все элементы, расположенные под или над главной диагональю (ср. Диагональная матрица). В первом случае имеем верхнюю Т.м. во втором нижнюю …

Квадратная матрица, у к рой все элементы, расположенные ниже (или выше) главной диагонали, равны нулю. В первом случае матрица наз. верхней треугольной матрицей, во втором нижней треугольной матрицей. Определитель Т. м. равен произведению всех ее … Математическая энциклопедия

Треугольная матрица МОБ — матрица коэффициентов межотраслевого баланса (МОБ), соответствующая такой производственной системе, в которой любой продукт может затрачиваться в своем собственном производстве и в производстве любого следующего… … Экономико-математический словарь

треугольная матрица МОБ — Матрица коэффициентов межотраслевого баланса (МОБ), соответствующая такой производственной системе, в которой любой продукт может затрачиваться в своем собственном производстве и в производстве любого следующего за ним продукта, но никакой… … Справочник технического переводчика

Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия

Блочно-треугольная матрица — – матрица, которую можно разбить на подматрицы таким образом, чтобы по одну сторону ее «главной диагонали«, составленной из подматриц, стояли нули. Примерами блочно треугольных матриц могут служить… … Экономико-математический словарь

блочно-треугольная матрица — Матрица, которую можно разбить на подматрицы таким образом, чтобы по одну сторону ее «главной диагонали«, составленной из подматриц, стояли нули. Примерами блочно треугольных матриц могут служить треугольная матрица и блочно диагональная матрица … Справочник технического переводчика

Матрица — система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь

матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика

Матрица — это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Однако для начала давайте разберемся, какие виды матриц выделяют математики.

Нулевой тип

Все компоненты этого вида матрицы — нули. Между тем, число ее строк и столбцов абсолютно различно.

Квадратный тип

Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы «квадрат». Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.

Вектор-стобец

Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.

Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.

Диагональный тип

Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в правом верхнем углу, а заканчивается числом в третьем столбце третьей строки. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.

Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.

Канонический тип

Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.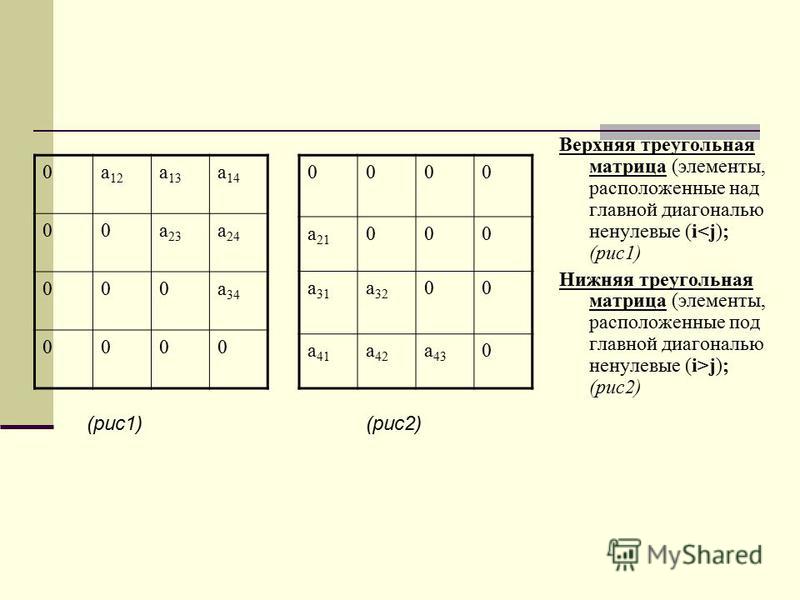

Треугольный тип

Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.

В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.

В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.

Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю.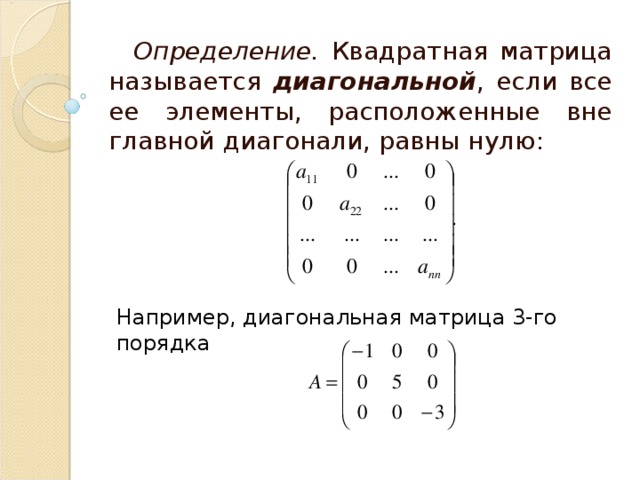 Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Приведение к треугольному виду

Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно «сохранить» главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.

Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.

Задание 1

Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.

Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.

Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы — с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки.

Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.

Осталось только последнее значение — элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую.

Выполним проверку:

detA = 2 x (-1) x 11 = -22.

Значит, ответ к заданию: -22.

Задание 2

Нужно найти детерминант матрицы методом приведения его к треугольному виду.

Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.

Начнем приведение ее с элемента, находящегося в нижнем углу слева, — с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Запишем итог первого этапа преобразования.

Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.

Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 — элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы.

Снова начнем с нижней части — с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) — элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.

В данном столбце нам нужно обратить в нуль только одно число — 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль.

После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.

Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.

Приведение к ступенчатому виду

При элементарных операциях над матрицами ступенчатый вид является менее «востребованным», чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.

Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.

Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.

Задание 1. Найти ранг данной матричной таблицы.

Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) — (1 x 1 x 4) — (2 x 3 x 0) — (6 x 5 x 2) = 12.

Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.

Начнем его с элемента левого столбца третьей строки — числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 — элемент второго столбца третьей строки — обратились в нуль.

Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.

Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) — 3. Ответ к заданию: 3.

Задание 2. Определить количество линейно независимых строк данной матрицы.

Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.

Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла — числа (-1).

Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию — 3.

Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.

На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!

Cтраница 2

Треугольной матрицей называется матрица, у которой все элементы по одну сторону от главной или побочной диагонали равны нулю. Чему равен определитель треугольной матрицы.  

Треугольной матрицей называется матрица, у которой все элементы, стоящие по одну сторону от главной или побочной диагонали, равны нулю. Чему равен определитель треугольной матрицы.  

Операции по выполнению прямого хода метода Гаусса в соответствии с теоремами линейной алгебры не изменяют величины определителя. Очевидно, что определитель треугольной матрицы равен произведению ее диагональных элементов.  

Это интуитивное представление находит в некоторых случаях точное количественное выражение. Например, мы знаем (см. (6) из § 1), что определитель треугольной матрицы (верхней или нижней) равен произведению элементов, стоящих на главной диагонали.  

Треугольные матрицы имеют много замечательных свойств, в силу которых они широко используются в построении самых различных методов решения задач алгебры. Так, например, для квадратных матриц сумма и произведение одноименных треугольных матриц есть треугольная матрица того же наименования, определитель треугольной матрицы равен произведению диагональных элементов, собственные значения треугольной матрицы совпадают с ее диагональными элементами, треугольная матрица легко обращается и обратная к ней также будет треугольной.  

Ранее уже отмечалось, что непосредственное нахождение определителя требует большого объема вычислений. Вместе с тем легко вычисляется определитель треугольной матрицы: он равен произведению ее диагональных элементов.  

Чем больше нулей среди элементов матрицы А и чем лучше они расположены, тем легче вычислять определитель det А. Это интуитивное представление находит в некоторых случаях точное количественное вьфажение. Например, мы знаем (см. (6) из § 1), что определитель треугольной матрицы (верхней или нижней) равен произведению элементов, стоящих на главной диагонали.  

Например, умножение определителя на скаляр эквивалентно умножению элементов любой строки или любого столбца матрицы на этот скаляр. Из уравнения (40) и из того, что разложение применимо к алгебраическому дополнению так же, как к определителю, следует, что определитель треугольной матрицы равен произведению ее диагональных элементов.  

Эта возможность вытекает из трех основных свойств определителей. Прибавление кратного одной строки к другой не меняет определителя. Перестановка двух строк изменяет знак определителя. Определитель треугольной матрицы равен попросту произведению ее диагональных элементов. DECOMP использует последнюю компоненту вектора ведущих элементов, чтобы поместить туда значение 1, если было произведено четное число перестановок, и значение — 1, если нечетное. Чтобы получить определитель, это значение нужно умножить на произведение диагональных элементов выходной матрицы.  

Последовательном исключении неизвестных из уравнений — КиберПедия

2. Сведении матрицы коэффициентов к треугольному виду

3. Вычислении определителя, составленного из коэффициентов уравнения

4.(3)

Решение системы линейных уравнений методом Жордана состоит в:

Последовательном исключении неизвестных из уравнений

2. Сведении матрицы коэффициентов к диагональному виду

3. Вычислении определителя, составленного из коэффициентов уравнения

5.(4)

Сведение матрицы коэффициентов к диагональному виду

— суть метода решения систем линейных уравнений методом

_________________

6(5)

Сведение матрицы коэффициентов к треугольному виду

— суть метода решения систем линейных уравнений методом

__________.

7. (5)

При решении систем линейных уравнений методами Гаусса-Зейделя и простых итераций быстрее сходится к решению метод

___________

 

8.(5)

Решение систем линейных уравнений прямым методом Гаусса сводится к приведению матрицы коэффициентов к _____________

9. (5).

 

Решение систем линейных уравнений прямым методом Жордана сводится к приведению матрицы коэффициентов к _________________

10.(5).

Из прямых методов решения систем линейных уравнений обратный ход имеет метод ________.

11.(4)

Привести в соответствие:

слева

1. Решение систем линейных уравнений прямым методом Гаусса сводится к тому, что матрица коэффициентов имеет вид

2. Решение систем линейных уравнений прямым методом Жордана сводится к тому, что матрица коэффициентов имеет вид

справа

а) треугольный

б) диагональный

12.(4)

При решении систем линейных уравнений методом простых итераций, необходимо проверить условие:_(записать)

13.(3)

При решении систем линейных уравнений процесс итераций сходится к единственному решению, независимо от выбора начального приближения, если выполняется условие:____________.

14. (4)

Достаточное условие сходимости решения системы линейных уравнений можно проверить по формуле:_____________

15. (4)

Решение системы линейных уравнений методом Гаусса-Зейделя состоит из этапов (Указать последовательность):

1. Приведение системы к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк

2. Проверка достаточного условия сходимости

3. Вычисление неизвестных , при котором предыдущие вычисленные значения неизвестных используются в последующих

4. Сравнение результатов с заданной точностью.

 

16(3).

Функциональная зависимость между У и Х ,полученная в результате экспериментальных данных называется:

Эмпирической

Аппроксимирующей функцией

3. Теоретической кривой

17 (3).

Для получения коэффициентов уравнения сглаживающей кривой обычно используется метод:

Наименьших квадратов

Гаусса

3. неопределенных коэффициентов

18.(3).

При нахождении коэффициентов уравнения сглаживающей кривой, имеющей вид нелинейного уравнения, необходимо привести его к линейному виду путем:

Замены переменных

2. Алгебраического преобразования

3. Разложения в ряд Тейлора

19.(3).

Показателем адекватности выбора аналитической зависимости, отражающей эмпирические данные, коэффициенты которой получены с использованием метода наименьших квадратов, является:

1. Стандартизированная ошибка аппроксимации:

2. Погрешность, вычисленная на основе ошибки измерения исходных данных

3. Индекс детерминации

 

 

20.(5)

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных можно записать, используя обозначения неизвестной х и коэффициентов а, в так:

Степенная — y=

Экспонента- y=

Показательная- y=

Правую часть записывает студент

21.(5)

 

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных через коэффициенты а,в можно записать так:

Гиперболическая – у=

Степенная – у=

Обратная — у=

Правую часть уравнения записывает студент

22. (5).

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных через коэффициенты а, в можно записать так:

Дробно-линейная – у=

Логарифмическая — у=

Правую часть уравнения записывает студент

23.(4)

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных

Привести в соответствие:

1.Степенная — а) y=ba^x —

2. Экспонента- б) y=be^ax

3. Показательная- — и) y=bx^a

24.(4)

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных

Привести в соответствие

1. Гиперболическая – а) у=в+а/х

2. Степенная – б) у=вх^а

3. Обратная — в) у=1/(ах+в)

25.(4)

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных

Привести в соответствие

1. Степенная — а) y= be^ax

2. Экспонента- б) y= bx^a

 

3. Показательная- в) y=ba^x

26.(4)

Наиболее часто используемые нелинейные зависимости для описания эмпирических данных

Привести в соответствие:

1. Гиперболическая – а) у=в+а/х

3. Обратная — в) у=1/(ах+в)

4. Дробно-линейная – г) у= х/(вх+а)

27.(5)

Привести в соответствие:

Слева.

1.Подбор приближенной похожей функции – это

2. Если функция проходит через узлы интерполяции, то эо

3.Найти значение функции в точке, принадлежащей области задания функции, но не совпадающей ни с одним узлом интерполяции, это

Справа:

1. Постановка задачи интерполяции

2. Аппроксимация

3. Интерполяци

28.(4)

Для нахождения неизвестных параметров по методу наименьших квадратов функцию надо привести к _______________виду.

29.(5)

Для нахождения неизвестных параметров «а» и «в» по методу наименьших квадратов функцию надо привести к линейному виду, сделав ________________ преобразования и _____________________

30. (5)

Сколько дробей будет в интерполяционном многочлене Лагранжа, если он проходит через 5 точек.

31.(5)

По сколько скобок в числителе и знаменателе будет в записи интерполяционного многочлена Лагранжа, если он записан для 5 точек

 

32.(5)

Можно ли получить уравнение прямой, проходящей через 2 точки, пользуясь формулой интерполяционного многочлена Лагранжа.

33.(5).

Сколько точек (минимально) необходимо взять для решения задачи квадратичной интерполяции

34 .(4)

 

Показателем адекватности выбора аналитической зависимости, отражающей эмпирические данные, коэффициенты которой получены с использованием метода наименьших квадратов является

Стандартизированная _____________ аппроксимации:

35(3).

Теорема о существовании определенного интеграла формулируется так:

1. Если функция F(x) определена и непрерывна на (а,в), то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка (а,в) на элементарные отрезки, ни от выбора точки

2. Если функция F(x) кусочно непрерывна на (а, в), то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка (а, в) на элементарные отрезки, ни от выбора точки

3. Если функция F(x) определена и непрерывна на (а, в), то предел интегральной суммы существует и зависит от способа разбиения отрезка (а, в) на элементарные отрезки, и не зависит от выбора точки

36.(3).

Приближенно вычислить интеграл можно представив подинтегральную функцию в виде: 1,2,3:

 

37.(3)

Приближенно вычислить интеграл можно воспользовавшись формулой прямоугольников (1,2,3)

38. (3)

Вычислить интеграл можно воспользовавшись формулой трапеции.

 

39.(3)

Приближенно вычислить интеграл можно воспользовавшись формулой Симпсона:

 

 

40.(3)

Какие из этих формул не являются формулами для вычисления интеграла трапеций

41.(4)

Привести в соответствие:

Приближенно вычислить интеграл можно представив подынтегральную функцию в виде:

Слева:

1.Площадей прямоугольников

2. Площадей трапеций

3. Площадей парабол

Справа: а,б,в

42.(3)

Результат приближенного вычисления интеграла по формуле трапеций можно оценить, вычислив остаточный член по формуле: (1,2,3)

 

 

43. (3)

 

Результат приближенного вычисления интеграла по формуле Симпсона можно оценить, вычислив остаточный член по формулеL1,2,3)

 

 

 

44.(3)

Привести в соответствие:

Результаты приближенных вычислений интеграла можно оценить для всех формул:

Слева:

1. Трапеций

2. Симпсона

3. Ньютона

Справа (а,б,в)

 

 

45(3)

Планирование эксперимента – это: (выбрать один ответ )

1. процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

2. стремление к минимизации числа опытов.

46(3)

 

Модель «черного ящика » предполагает:

1. Наличие входных и выходных параметров

2. Задание ограничений на входные параметры

3. Задание ограничений на выходные параметры

47(3)

Для проведения эксперимента необходима:

1. Возможность влияния на воздействие фактора

2. Способность алгоритма привести к расчету критериев значимости факторов

3. Возможность изменять условия во время проведения каждого опыта

48(3)

Уравнение, связывающее входные и выходной параметр, называется:

1. Функцией отклика

2. Интерполяционным многочленом

3. Квадратным трехчленом

49(3)

Каждый фактор может принимать при проведении опытов несколько значений, которые называются:

1. Средними

2. Уровнями

3. Значениями для построения линий одинакового выхода

50(3)

Параметром оптимизации может быть:

1. Любая функция, связывающая «вход» и «выход»

2. Функция, описывающая изменение поведения фактора во время проведения опыта

3. Функция, дающая наибольшее отклонение от ее среднего значения

 

 

51(4)

 

В матрице планирования эксперимента используются значения факторов:

1. Нормированные

2. Натуральные

3. Средние

52(3)

Оценка коэффициентов уравнения регрессии на значимость проводится по критерию

1. Фишера

2. Стьюдента

3. Чебышева

53(3)

Проверка уравнения на адекватность проводится по критерию:

1. Фишера

2 .Стьюдента

3 Чебышева

4. Гаусса

54.(3)

Алгоритм нахождения корня нелинейного уравнения итерационными методами состоит из: (выбрать)

1.Отыскания приближенного значения корня или содержащего его отрезка и уточнения до заданной степени точности.

2.Нахождения приближенного значения корня при начальных условиях, заданных системой неравенств

3.Получение области допустимых значений на основе решения системы уравнений

4.Вычисления производной и нахождения критической точки и уточнения до заданной точности

5.Нахождения суммы приращений

55.(4)

Отыскание приближенного значения корня или содержащего его отрезка и уточнение до заданной степени точности в этом суть алгоритма нахождения корня _____________ уравнения ___________________________ методами .

56.(4)

Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется он с помощью метода (выбрать):

1. Бисекции

2.Ньютона

3.Простых итераций

4.Хорд

5.Лина

57. (4)

Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется метод хорд

58.(3).

При решении нелинейного уравнения численными методами уравнение касательной используется в методе (выбрать):

1.Бисекции

2.Ньютона

3.Хорд

4.Простых итераций

5.Лина

59.(4)

Если при решении нелинейного уравнения численными методами используется уравнение прямой, имеющей одну общую точку с кривой, то реализуется

метод касательных (Ньютона)

60.(4).

 

При решении нелинейного уравнения численными методами принцип деления отрезка пополам используется в методе (выбрать):

1.Бисекции

2.Ньютона

3.Хорд

4.Простых итераций

5.Лина

61. (4)

Если при решении нелинейного уравнения численными методами, используется принцип деления отрезка пополам реализуется метод бисекции

62. (4)

Привести в соответствие:

Слева:

1.Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется он с помощью метода:

2.При решении нелинейного уравнения численными методами уравнение касательной используется в методе:

3.При решении нелинейного уравнения численными методами принцип деления отрезка пополам используется в методе:

Справа:

1.Хорд

2.Ньютона

3.Бисекций

 

. 63.(3)

Если при отделении корня строим график функции и выбираем отрезок, включающий точку пересечения кривой с осью ОХ, то такой подход называется :________________ способом отделения корня.

64.(3)

Для отделения корня аналитически сначала необходимо функцию ___________________, а затем выбрать интервал, в котором функция меняет _____.

65.(5).

Первым этапом при решении нелинейного уравнения численными методами является

Отделение _______

66. (4)

Первым этапом при решении нелинейного уравнения численными методами является

__________ корня

 

67.(5)

 

При решении нелинейного уравнения численными методами используется принцип деления отрезка , в котором находится корень, пополам в методе

__________.

68.(5).

При решении нелинейного уравнения численными методами используется принцип, по которому проводится касательная к кривой в методе ________

69.(3)

Линейная интерполяция состоит в том, что:

Матричные операции с элементарными строками (видео)

TranscriptPractice

Привет, и добро пожаловать в это видео о манипуляциях с матрицей ! В этом видео мы рассмотрим:

• Элементарные операции со строками
• Эшелонированную форму строк матрицы
• Сокращенную эшелонированную форму строк матрицы
• и нахождение обратной матрицы

Матрицы любых размер можно манипулировать с помощью трех элементарных операций со строками :

1. Любые две строки можно поменять местами.
2. Любую строку можно умножить на ненулевой скаляр.
3. Несколько строк могут быть добавлены к другой строке.

Процесс использования операций со строками в матрице называется сокращением строк .

Конечная цель редукции строк — получить верхнюю треугольную матрицу — матрицу со всеми нулевыми элементами ниже главной диагонали. Когда это достигается, говорят, что матрица находится в -й эшелонированной форме строки 9.0022 . В частности, чтобы быть в форме эшелона строк:

1. Строки со всеми нулевыми элементами должны быть внизу матрицы
2. Первый ненулевой элемент строки должен быть справа от первого ненулевого элемента в матрице. ряд выше.

Давайте посмотрим на сокращение строк в действии! Имейте в виду, что последовательность операций над строками не уникальна. Кроме того, эшелонированная форма матрицы строк не уникальна. Разные люди могут использовать разные серии операций, чтобы в итоге получить разные эшелонированные формы одной и той же матрицы. Вот матрица X :

Моя первая операция будет состоять в том, чтобы использовать 2, чтобы превратить 4 под ней в 0. Я хочу вычесть 2 строки 1 из строки 2 и заменить строку 2. В сокращении это выглядит как R2 минус 2R1 равняется R2. Теперь я хочу снова использовать 2, чтобы превратить 3 в левом нижнем углу в 0. Чтобы упростить задачу, я использую два шага: 2R3 равно R3, а затем R3 минус 3R1 равно R3. Теперь остался только один шаг, чтобы привести эту матрицу в форму эшелона строк. Мне нужно использовать 1, чтобы превратить отрицательную 9 в третьей строке в 0. Итак, R3 плюс 9R2 равен R3.

Это одна из версий X в форме эшелона строк. Другой вариант мог бы выглядеть так

, если бы мы решили, например, разделить строку 3 на строку 2.

Как видите, мы закончили с верхней треугольной матрицей. Первая ненулевая запись в каждой строке находится справа от ненулевой записи в строке выше. Другими словами, 1 находится справа от 2, а минус 78 — справа от 1.

Мы могли бы пойти дальше и получить X в виде сокращенного эшелона строк . Приведенную эшелонную форму строки можно получить, используя различные последовательности операций над строками, но эта форма уникальна. Матрица имеет только одну уменьшенную ступенчатую форму строки. Для того, чтобы быть в форме редуцированного эшелона строк, матрица должна удовлетворять следующим условиям:

• Быть в форме эшелона строк.
• Начальная запись в каждой ненулевой строке должна быть 1.
• Везде, где есть ведущая 1, записи в остальной части столбца должны быть нулями.

Давайте продолжим с X, где мы остановились:

Во-первых, мне нужно превратить 2 в 1; половина R1 равна R1. Первая колонка выглядит хорошо. Теперь к столбцу 2. Мне нужно использовать 1, чтобы превратить три половины над ним в 0; R1 минус три половинки R2 равно R1. Теперь столбцы 1 и 2 выглядят хорошо. Время превратить это отрицательное 78 в 1; отрицательный 1 на 78 R3 равен R3. Ряд 3 выглядит хорошо. Все, что осталось, это использовать строку 3, чтобы заменить 16 и минус 9 на нули; минус 16R3 плюс R1 равен R1, а R2 плюс 9R3 равен R2. {3}\). С квадратными матрицами это будет происходить часто, но не обязательно. Эти матрицы также имеют уменьшенную эшелонированную форму строк: 9{-1}А=I\).

Например, здесь у нас есть матрица B и матрица, обратная матрице B.

Давайте попробуем B умножить B на обратную. Для этого мы делаем 4, умноженное на 4, равно 16, плюс 3 раза, отрицательное число 5, равно отрицательному числу 15. Для нашего следующего элемента мы сделаем 4 раза, отрицательное значение 3, равно отрицательному значению 12, плюс 3 раза, умноженное на 4, равно 12. Здесь мы собираемся сделать 5 умножить на 4 будет 20, плюс 4 умножить на минус 5 будет на минус 20. Тогда мы сделаем 5 умножить на минус 3 будет минус 15, плюс 4 раза на 4 будет 16. Если мы упростим это, мы получим 16 плюс минус 15 будет 1, минус 12 плюс 12 равно 0, 20 плюс минус 20 равно 0, а минус 15 плюс 16 равно 1.

Это наша единичная матрица для матрицы 2 на 2. Если вы продолжите и умножите B обратно на B, вы получите то же самое.

и

Для того чтобы матрица имела обратную или была обратимой , должны быть выполнены два условия:

1. Матрица должна быть квадратной матрицей
2. Определитель матрицы не должен быть равен 0.

Давайте поработаем с матрицей 3 на 3 Y:

Является ли Y квадратной матрицей? Проверять!

Разве определитель Y не равен 0? Посмотрим…

Определитель Y равен 2 умножить на 4, умножить на минус 1, получить отрицательное число 4, минус 1, умножить на 0, будет 0, значит, отрицательное 4, умножить на 3, умножить на отрицательное, умножить на 4, умножить на отрицательное, 1 будет 4, минус 1, умножить на 3, будет 3, поэтому 4 минус 3 равно 1, плюс минус 2, умножить на минус 4 умножить на 0 равно 0, минус 4 умножить на 3 будет 12 — получится минус 12. Таким образом, определитель у равен минус 8 минус 3 плюс 24, что равно 13.

\(det(Y) =2(-4)-3(1)±2(-12)=-8-3+24=13\)

Да, определитель Y не равен 0 Итак, теперь давайте выясним, что является инверсией Y.

Вот два шага для нахождения обратной матрицы:

1. Дополнить матрицу единичной матрицей соответствующего размера

Y дополнить I выглядит следующим образом: [Y|I]

2. Строка уменьшить расширенную матрицу . Когда он находится в форме сокращенного эшелонированного ряда, структура будет I увеличить Y инверсной [I|Y-1], и можно будет идентифицировать инверсию.

Вот как выглядит этот процесс. Во-первых, давайте превратим 2 в 1; половина R1 равна R1. Далее, давайте получим нули ниже 1 в столбце 1; R2 плюс 4R1 равно R2, а R3 минус 3R1 равно R3. Теперь нам нужно превратить 10 в столбце 2 в 1; одна десятая R2 равна R2. Остальные записи в столбце 2 должны быть равны 0; таким образом, R1 минус три половины R2 равняется R1, а R3 плюс девять половинок R2 равняется R3. Теперь 13 больше 20 в столбце 3 нужно изменить на 1; 20 больше 13R3 равно R3. Наконец, две оставшиеся записи в столбце 3 должны быть равны 0; R1 плюс 11 к 20 R3 равно R1, а R2 плюс три десятых R3 равно R2. 9{-1}\)].

Спасибо за просмотр и удачной учебы!

Вопрос №1:

 
Дана матрица X.
\(X=\begin{bmatrix}
1 & 2 & 1\\
5 & 3 &0 \\
9 & 8 & 4
\end{bmatrix}
\)

Какой шаг изменит 5 в строке два в ноль?

\(R_1-5R_2=R_2\)

\(R_2-5R_1=R_2\)

\(R_3-5R_2=R_2\)

\(R_2-5R_3=R_2\)

Показать ответ

0 Показать ответ

Ответ:

Мы можем использовать значения в матрицах вместо Rs таким же образом, как мы подставляем переменные, чтобы увидеть, какая из них приведет к изменению \(5\) на \(0\). Мы видим, что при подстановке значений в уравнение \(R_2-5R_1=R_2\) мы получаем следующее \(5-5(1)=0\), следовательно, \(R_2-5R_1=R_2\) изменится \(5\) в \(0\).

Скрыть ответ

Вопрос № 2:

 
Какая матрица имеет форму эшелона строк?

\(\begin{bmatrix}
2 & 6 & -9\\
0 & 5 & 7\\
0 & 0 & 18
\end{bmatrix}
\)

\(\begin{bmatrix}
1 & 0 & 0\\
7& 9 & 0\\
4 & -3 & -1
\end{bmatrix}
\)

\(\begin{bmatrix}
0 & 0 & 0\\
0 & -1 & 20\\
-4 &5 & 6
\end{bmatrix}
\)

\(\begin{bmatrix}
6 & 4 & 2\\
9 & -8 & 0\\
0 & 0 & 0
\end{ bматрица}
\)

Показать ответ

Ответ:

Для того, чтобы матрица была в виде эшелона строк, она должна иметь все нулевые элементы ниже главной диагональной линии. Значения \(2\), \(5\) и \(18\) составляют диагональную линию матрицы в выборе A, а элементы ниже этой строки являются нулями.

Скрыть ответ

Вопрос №3:

 
Какая матрица представлена ​​в виде редуцированного эшелона строк?

\(\begin{bmatrix}
0 & 1 & 1 \\
0 & 1 & 0\\
1 & 1 & 0
\end{bmatrix}
\)

\(\begin{bmatrix}
1 & 1 & 1\\
0 & 0 & 0\\
0 & 1 & 0
\end{bmatrix}
\)

\(\begin{bmatrix}
1 & 0 & 0\\
0 & 1 &0 \\
0 & 0 & 1
\end{bmatrix}
\)

\(\begin{bmatrix}
1 & 0 & 0\\
0 & 0 & 1\\
1 & 0 & 1
\end{bmatrix}
\)

Показать Ответ

Ответ:

Определение матрицы в сокращенной ступенчатой ​​форме состоит в том, что она должна быть в форме ступенчатой ​​строки, первая запись для каждой строки, которая не равна нулю, должна быть единицей, а там, где есть ведущая единица, остальные записи должны быть нулями. Следовательно, единственная матрица, удовлетворяющая этим условиям, это \(\begin{bmatrix}
1 & 0 & 0\\
0 & 1 &0 \\
0 & 0 & 1
\end{bmatrix}
\).

Скрыть ответ 9{-1}\times A=I)\) говорит.

Скрыть ответ

Вопрос № 5:

 
Какое утверждение верно относительно обратимой матрицы?

Матрица обратима, если она квадратная и ее определитель равен нулю.

Матрица обратима, если она квадратная и ее определитель не равен нулю.

Матрица обратима, если она не является квадратной матрицей и ее определитель равен нулю.

Матрица обратима, если она не является квадратной матрицей и ее определитель не равен нулю.

Показать Ответ

Ответ:

Матрица обратима, если она квадратная и ее определитель не равен нулю.

Чтобы матрица была обратимой, она должна удовлетворять двум условиям: матрица должна быть квадратной, а определитель не может быть нулем.

Скрыть ответ

 

Вернуться к видео Algebra II

493170

Калькулятор RREF — MathCracker.com

Инструкции: Используйте этот пошаговый калькулятор калькулятора формы эшелона с уменьшенной строкой (RREF), чтобы поместить заданную матрицу, которую вы предоставляете, в уменьшенный рядно-кулисная форма.

При необходимости измените размер матрицы, указав количество строк и количество столбцов. Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицу (вводя числа и перемещая матрица с помощью «TAB»)

Сокращенная форма эшелона строк — один из самых полезных процессов в линейной алгебре, и он может служить нескольким целям.

RREF обычно достигается с помощью метода исключения Гаусса. С точки зрения приложений, уменьшенная форма эшелона строк может использоваться для решения систем линейных уравнений, для вычисления обратной матрицы или для нахождения полезные матричные разложения

Что такое rref матрицы?

Идея эшелонированной формы строк состоит в том, чтобы систематически строить эквивалентную матрицу с помощью обратимых элементарные матрицы таким образом получают эшелонированную форму строк, которая является обобщенной формой треугольной формы.

Используя метод сокращения строк, мы можем получить матрицу в форме эшелона строк, используя ненулевые опорные точки.

Преимущества RREF

• Этот калькулятор RREF преобразует матрицу в форму, удобную для многих целей
• Например, если конечной формой RREF данной матрицы является тождество, матрица обратима
• Дополнение исходной матрицы, нахождение формы RREF позволяет построить обратную по элементарным матрицам
• Обеспечивает систематический способ решения систем линейных уравнений.

Как рассчитать сокращенную форму эшелона строк?

Существуют различные подходы, которые можно использовать. Но основная идея состоит в том, чтобы использовать ненулевые опорные точки для устранения всех значений в таблице. столбца, которые находятся ниже ненулевой опорной точки, которая лежит в основе процедуры, называемой гауссовым исключением.

Одним из важнейших элементов этого сокращения является знание того, находится ли матрица в rref, поэтому мы останавливаем процесс, когда это происходит.

Необходимо выполнить следующие шаги:

Шаг 1 : Проверьте, не находится ли матрица уже в форме сокращенного эшелона строк. Если это так, то остановитесь, мы закончили.

Шаг 2 : Посмотрите на первый столбец. Если значение в первой строке не равно нулю, используйте его как точку опоры. Если нет, проверьте столбец на наличие ненулевой элемент и при необходимости переставить строки так, чтобы стержень находился в первой строке столбца. Если первый столбец равен нулю, переходите к следующему столбцу справа, пока не найдете ненулевой столбец.

Шаг 3 : Используйте опорную точку, чтобы исключить все ненулевые значения ниже опорной.

Шаг 4 : нормализуйте значение разворота до 1.

Шаг 5 : Используйте опорную точку, чтобы исключить все ненулевые значения над опорной точкой.

Шаг 6 : После этого, если матрица все еще не в виде эшелона строк, переместите один столбец вправо и на одну строку ниже, чтобы найти следующую точку поворота.

Шаг 7 : Повторите процесс, как описано выше. Ищите опору. Если ни один элемент не отличен от нуля в новой опорной точке позиция или ниже, посмотрите справа на столбец с ненулевым элементом в опорной позиции или ниже и переставьте ряды при необходимости. Затем удалите значения ниже опорной точки.

Шаг 7 : Продолжайте процесс поворота до тех пор, пока матрица не примет уменьшенную форму строки-эшелона.

Как рассчитать уменьшенный эшелон ряда на калькуляторе?

Не все калькуляторы могут проводить исключение Гаусса-Жордана, но некоторые из них это делают. Как правило, все, что вам нужно сделать, это ввести соответствующую матрицу, для которой вы хотите привести форму RREF.

Обратите внимание, что для того, чтобы иметь уменьшенную эшелонированную форму строки, вам также необходимо иметь нули НАД опорной точкой. Если вам это не нужно вы можете использовать этот калькулятор формы эшелона строки, который не уменьшает значения выше точки поворота

Этот калькулятор позволит вам определить матрицу (с любым выражением, например дроби и корни, а не только числа), а затем будут показаны все шаги процесса, как прийти к окончательной форме эшелона сокращенной строки.

Большинство калькуляторов будут использовать элементарные операции со строками для выполнения вычислений, но наш калькулятор покажет вам точно и подробно, какие используются элементарные матрицы на каждом шагу.

Как найти решение RREF

Это немного зависит от контекста, но один из способов — начать с системы линейных уравнений, представить ее в матричной форме, и в этом случае Решение RREF при увеличении правыми значениями.

Другой вариант — начать с матрицы и дополнить ее единичной матрицей, и в этом случае решение RREF приведет к обратному результату исходная матрица.

Пример формы сокращенного эшелона строк

Вопрос: Предположим, что у вас есть следующая матрица:

\[A = \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0. 6em]\displaystyle 2&\displaystyle 7&\displaystyle 2\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 1 \end{bmatrix} \]

Найдите его уменьшенную форму эшелона, показав все шаги и соответствующие элементарные матрицы.

Решение: Предоставленная матрица является матрицей \(3 \times 3\).

Нам нужно найти сокращенную ступенчатую форму строки этой матрицы.

Шаг 1 : Операции, используемые для сокращения столбца \(1\):
\((1) — R_{ 1} + R_{ 2} \rightarrow R_{ 2}, \quad (2) — R_{ 1 } + R_{ 3} \rightarrow R_{ 3}\)

\( \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 7&\displaystyle 2\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 1 \end{bmatrix} \rightarrow \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 0&\displaystyle 4&\displaystyle 1\\[0. 6em]\displaystyle 0&\displaystyle 0&\displaystyle 0 \end{bmatrix} \)

Шаг 2 : Операция, используемая для сокращения столбца \(1\):
\((1) \frac{1}{2} R_{1}\)

\( \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 0&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 0&\displaystyle 0&\displaystyle 0 \end{bmatrix} \rightarrow \begin{bmatrix} \displaystyle 1&\displaystyle \frac{3}{2}&\displaystyle \frac{1}{2}\\[0.6em]\displaystyle 0&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 0&\displaystyle 0&\стиль отображения 0 \end{bmatrix} \)

Для столбца \(2\) все элементы ниже опорной точки уже равны нулю, поэтому исключать их не нужно.

Шаг 3 : Операции, используемые для уменьшения столбца \(2\) над точкой опоры:
\((1) \frac{1}{4} R_{2}, \quad (2) -\frac{3 {2} R_{ 2} + R_{ 1} \rightarrow R_{ 1}\)

\( \begin{bmatrix} \displaystyle 1&\displaystyle \frac{3}{2}&\displaystyle \frac{1}{2}\\[0. 6em]\displaystyle 0&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 0&\displaystyle 0&\стиль отображения 0 \end{bmatrix} \rightarrow \begin{bmatrix} \displaystyle 1&\displaystyle 0&\displaystyle \frac{1}{8}\\[0.6em]\displaystyle 0&\displaystyle 1&\displaystyle \frac{1}{4}\\[0.6em]\displaystyle 0&\displaystyle 0& \displaystyle 0 \end{bmatrix} \)

Шаг 4 : Для столбца \(3\) мы не находим опорную точку, потому что столбец равен нулю, поэтому мы переходим к следующему столбцу.

Отсюда заключаем, что матрица в форме RREF:

\[ \begin{bmatrix} \displaystyle 1&\displaystyle 0&\displaystyle \frac{1}{8}\\[0.6em]\displaystyle 0&\displaystyle 1&\displaystyle \frac{1}{4}\\[0.6em]\displaystyle 0&\displaystyle 0& \displaystyle 0 \end{bmatrix} \]

Онлайн калькулятор: Определитель матрицы

Разложение первой строки

Для вычисления определителя матрицы путем разложения первой строки необходимо каждый элемент данной строки умножить на соответствующий минор;

Миноры, соответствующие определенному элементу, находятся путем исключения i-й строки, j-го столбца из матрицы A, после чего находится определитель полученной матрицы;
i, j — номера строки и столбца, в которых находится данный элемент;

После вычисления произведений каждого элемента первой строки в соответствующем миноре необходимо их сложить и вычесть;
Знак сложения и вычитания меняется по порядку, начиная со знака сложения;
Near the first product there is a plus sign, near the second a minus sign, etc.

det(A) =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=

= a ₁₁ * A ₁₁ — а ₁₂ * А ₁₂ + а ₁₃ * А ₁₃ — а ₁₄ * А ₁₄ ;

Итак, мы находим миноры каждого элемента первой строки.

Найти младший элемент с индексом 11
Для этого необходимо исключить 1 строку и 1 столбец из матрицы А, после чего получим следующую матрицу:

000	8	5	2	000
	5	8	7
	5	5	2

Next, we calculate the определитель этой матрицы.
It is equal to -57, this is the minor of element 11.

A ₁₁ =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=

000	8	5	2	000
	5	8	7
	5	5	2

= -57;

Найти второстепенный элемент с индексом 12
Для этого необходимо исключить из матрицы А 1-ю строку и 2-й столбец, после чего получим следующую матрицу: 2 8 7 4 5 2

Далее вычисляем определитель этой матрицы.
Равно -57, это минор элемента 12.

A ₁₂ =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=

000	7	5	2	000
	2	8	7
	4	5	2

= -57;

Найти младший элемент с индексом 13
Для этого необходимо исключить из матрицы А 1 строку и 3 столбец, после чего получим следующую матрицу: 2 000 2 5 7 4 5 2

Далее вычисляем определитель этой матрицы.
It is equal to -3, this is the minor of element 13.

A ₁₃ =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=

000	7	8	2	000
	2	5	7
	4	5	2

= — 3;

Найти младший элемент с индексом 14
Для этого необходимо исключить из матрицы А 1 строку и 4 столбец, после чего получим следующую матрицу:

000	7	8	5	000
	2	5	8
	4	5	5

Next, we calculate the determinant of this matrix.
It is equal to 21, this is the minor of element 14.

A ₁₄ =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=;

Теперь нам нужно вычислить произведение первого элемента на соответствующий ему минор.
71 * (-57) = -4047;

Далее из этого произведения необходимо вычесть произведение второго элемента на соответствующий минор.
-4047 — (8 * (-57)) = -4047 — (-456) = -3591;

Теперь к результату нужно прибавить произведение третьего элемента на соответствующий минор.
-3591 (8 * (-3)) = -3591 (-24) = -3615;

И, наконец, из полученного результата необходимо вычесть произведение четвертого элемента на соответствующий минор
-3615 — (2*21) = -3615 — 42 = -3657;

Результатом этого вычитания является определитель матрицы A

det(A) = (71 * (-57)) — (8 * (-57)) + (8 * (-3)) — ( 2 * 21) = -3657;

Ответ: DET (A) = -3657

Sarrus

Дайте следующую матрицу A:

000	7	8	5	000
	2	5	8
	4	5	5		5	5

000	2	5		2	5		2	5		2	5		.	8	2
	3	5		7

Справа от матрицы А добавляем первые два столбца;

000	2	5	6	000	2	5
	5	8	2		5	8
	3	5	7		3	5

=

Произведения элементов на главной диагонали и на параллельных ей диагоналях берем со знаком плюс;

= (A ₁₁ A ₂₂ A ₃₃ ) + (A ₁₂ A ₂₃ A ₃₁ ) + (A ₁₃ A ₂₁ ) + ( ₁₃ A ₂₁ ) + ( ₁₃ A ₂₁ ). Произведения элементов побочной диагонали и параллельных ей диагоналей берем со знаком минус;

= (A ₁₃ A ₂₂ A ₃₁ ) — (A ₁₁ A ₂₃ A ₃₂ ) — ( ₁₂ A _{21 2113 3.} 3. 3) — ₁₂ A _{21. 210513) — A 12 A 21.1) — 12 A 32 ). = (2 * 8 * 7) + (5 * 2 * 3) + (6 * 5 * 5) — (6 * 8 * 3) + (2 * 2 * 5) + (5 * 5 * 7) = — 47;}

Ответ: det(A) = -47

Приведение к треугольной форме

Приведем матрицу к треугольной форме, тогда произведение элементов главной диагонали даст нам определитель;

det(A) =

000	71	8	8	2	000
	7	8	5	2
	2	5	8	7
	4	5	5	2

=

из 2 ряда вычитаем 8 10 ряд, 0 умножаем на 10;

из 3 ряда вычитаем 1 ряд, умноженный на 0,02817;

из 4 ряда вычитаем 1 ряд, умноженный на 0,05634;

=

000	71	8	8	2	000
	0	7. 21128	4.21128	1.80282
	0	4.77464	7.77464	6.94366
	0	4.54928	4.54928	1.88732

=

from 3 row we subtruct 2 row, multiplied by 0.66211;

из 4 ряда вычитаем 2 ряд, умноженный на 0,63086;

=

000	71	8	8	2	000
	0	7. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт