Калькулятор обратимой матрицы
Инструкции: Используйте этот калькулятор, чтобы найти обратную матрицу, которую вы предоставили, показывая шаг за шагом. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.
Затем щелкните первую ячейку и введите значение и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы определить ВСЕ значения матрицы.
Подробнее об этом Калькулятор обратимой матрицы с шагами
Понятие обратной матрицы будет появляться во многих контекстах алгебры. Во-первых, для матриц идея состоит в том, чтобы иметь возможность работать с ними так же, как с числами.
Одним из важнейших свойств этой инверсии является то, что при умножении на исходное число получается 1, это \(3 \cdot \displaystyle \frac{1}{3} = 1\).
Как определить и обратимую матрицу
- Найдите, что его определитель отличается от нуля
- Получите его рядно-кулисная форма и получить диагональную матрицу без нулей
- Найдите, что RREF матрицы это личность
Как определить обратную матрицу?
Для матриц роль «1» играет единичная матрица \(I\), и, учитывая матрицу \(A\), мы будем говорить, что \(A^{-1}\) является обратной матрицей \(A\). {-1} A\).
{-1} A\).
Другими словами, матрица, обратная данной матрице \(A\), является матрицей, обладающей тем свойством, что умножение этой матрицы на исходную , приводит к единичной матрице I.
Как вычислить обратную матрицу?
Существует множество различных способов вычисления обратной матрицы \(A\). Одним из наиболее часто используемых методов является
сопряженная формула
, который основан на вычислителе целой кучи определителей подматриц, полученных удалением одной строки и одного столбца \(A\). {-1} = \displaystyle \frac{1}{\det(A)} adj(A)\]
{-1} = \displaystyle \frac{1}{\det(A)} adj(A)\]
На первый взгляд это выглядит просто! Но это не так много, когда размер матрицы большой. Действительно, приведенная выше формула говорит вам, что для того, чтобы найти обратную, вам нужно вычислить определитель матрицы, а также вам нужно вычислить сопряженную матрицу.
В отличие от того, что может показаться на первый взгляд, это может быть очень трудоемким, поскольку размер матрицы большой (например, \(n > 4\)). Итак, хорошо, что у нас компактная формула, но это не обязательно означает, что она не будет трудоемкой.
Как можно инвертировать матрицу 2×2?
Во-первых, вы должны убедиться, что \(\det(A) \ne 0\). T = \displaystyle \frac{1}{ad — bc} \begin{bmatrix}
d & -b \\ -c & a
\end{bmatrix}\]
T = \displaystyle \frac{1}{ad — bc} \begin{bmatrix}
d & -b \\ -c & a
\end{bmatrix}\]
Достаточно легко, да? Вы хотите попробовать для 3×3?
Как найти обратную матрицу 3×3?
Первое требование, как и для всех матриц, состоит в том, чтобы вычислить определитель и убедиться, что \(\det(A) \ne 0\). Затем нам нужно вспомнить общую сопряженную формулу
\[ A^{-1} = \displaystyle \frac{1}{\det(A)} adj(A) = \displaystyle \frac{1}{\det(A)} C^T\]
где \(C\) — матрица кофакторов. {3+3} \begin{vmatrix} a & b\\\\ d & e \end{vmatrix} \end{bmatrix}\]
\[ = \begin{bmatrix} ei-fh & — (di — gf) & dh — ge \\ — (bi — hc) &
ai — gc & — (ah — gb) \\ bf — ec & — (af-dc) & ae — db \end{bmatrix}\]
\[ = \begin{bmatrix} ei-fh & gf — di & dh — ge \\ hc — bi &
ai — gc & gb — ah \\ bf — ec & dc — af & ae — db \end{bmatrix}\]
{3+3} \begin{vmatrix} a & b\\\\ d & e \end{vmatrix} \end{bmatrix}\]
\[ = \begin{bmatrix} ei-fh & — (di — gf) & dh — ge \\ — (bi — hc) &
ai — gc & — (ah — gb) \\ bf — ec & — (af-dc) & ae — db \end{bmatrix}\]
\[ = \begin{bmatrix} ei-fh & gf — di & dh — ge \\ hc — bi &
ai — gc & gb — ah \\ bf — ec & dc — af & ae — db \end{bmatrix}\]
Итак, теперь нам нужно транспонировать матрицу \(C\):
\[ C^T = \begin{bmatrix} ei-fh & gf — di & dh — ge \\ hc — bi & ai — gc & gb — ah \\ bf — ec & dc — af & ae — db \end{bmatrix}^T = \begin{bmatrix} ei — fh & hc — bi & bf — ec \\ gf — di & ai — gc & dc — af \\ dh — ge & gb — ah & ae — db \end{bmatrix}\]
Итак, наконец, у нас есть формула для обратного:
\[ A^{-1} = \displaystyle \frac{1}{\det(A)} C^T = \displaystyle \frac{1}{a(e i — hf) — b(d i — g f) + c(d h — g e))} \begin{bmatrix} ei — fh & hc — bi & bf — ec \\ gf — di & ai — gc & dc — af \\ dh — ge & gb — ah & ae — db \end{bmatrix} \]
Готовы это запомнить? Конечно нет. Не то, чтобы вы должны, на самом деле. Это всего лишь тизер того, насколько сложно становится, когда вы пытаетесь получить общую формулу для простой матрицы 3×3. Это становится очень грязным и довольно бесполезным для \(n > 3\).
Не то, чтобы вы должны, на самом деле. Это всего лишь тизер того, насколько сложно становится, когда вы пытаетесь получить общую формулу для простой матрицы 3×3. Это становится очень грязным и довольно бесполезным для \(n > 3\).
Таким образом, гораздо практичнее применить набор шагов для нахождения обратного:
Какие шаги нужно выполнить, чтобы вычислить обратную матрицу?
Шаг 1: Вычислите определитель заданной матрицы A. Обратите внимание, что это может потребовать вычислений для больших матриц, поэтому используйте для вычисления определителя строку/столбец с наибольшим количеством нулей.
Шаг 2:
Вычислите матрицу кофакторов, связанную с матрицей A. {i+j}\). Опять же, при вычислении вспомогательных определителей убедитесь, что вы выбрали строку/столбец с наибольшим количеством нулей.
{i+j}\). Опять же, при вычислении вспомогательных определителей убедитесь, что вы выбрали строку/столбец с наибольшим количеством нулей.
Шаг 3: Получив определитель исходной матрицы и матрицу кофакторов, разделите каждый компонент матрицы кофакторов на определитель, и в результате получится обратная матрица.
Как использовать этот обратный калькулятор
- Укажите размер матрицы
- Введите числа, определяющие матрицу
-
Выберите метод, который вы предпочитаете использовать для вычисления обратного: «Сопряженная формула» или «Эшелонная форма с уменьшенной строкой».

- Нажмите «Рассчитать инверсию».
Пример: вычисление обратной заданной матрицы
Вопрос: Рассмотрим следующую матрицу:
\[A = \begin{bmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix} \]
Найдите его обратную по формуле сопряжения.
Отвечать: Нам нужно вычислить обратную матрицу \(3 \times 3\), которая была предоставлена.
Шаг 1: вычислить определитель матрицы
По формуле субдетерминанта получаем:
\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) — 2 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) + 1 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -3 \right) — 2 \cdot \left( -2 \right) + 1 \cdot \left( 1 \right) = 2\]
Так как \(\det(A) = 2 \ne 0\), мы заключаем, что матрица обратима, и мы можем продолжить вычисление обратной данной матрицы \(A\). { 3 3} = \begin{vmatrix}
\displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 2&\displaystyle 1
\end{vmatrix}
= 1 \cdot \left( 1 \right) — 2 \cdot \left(2 \right) = -3\]
{ 3 3} = \begin{vmatrix}
\displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 2&\displaystyle 1
\end{vmatrix}
= 1 \cdot \left( 1 \right) — 2 \cdot \left(2 \right) = -3\]
Подводя итог, матрица несовершеннолетних выглядит следующим образом:
\[M = \begin{bmatrix} \displaystyle -3&\displaystyle -2&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -1\\[0.6em]\displaystyle 7&\displaystyle 2&\displaystyle -3 \end{bmatrix} \]
Теперь мы можем вычислить элементы матрицы кофакторов \(C\), используя формулу
\[ C_{ij} = (-1)^{i+j}M_{ij}\]
Приведенную выше формулу можно использовать напрямую, поскольку миноры уже известны. {-1} = \frac{1}{\det(A)} adj(A) = \frac{1}{2} \begin{bmatrix}
\displaystyle -3&\displaystyle -1&\displaystyle -7\\[0.6em]\displaystyle 2&\displaystyle 0&\displaystyle -2\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle \frac{1}{2}\times\left(-3\right)&\displaystyle \frac{1}{2}\times\left(-1\right)&\displaystyle \frac{1}{2}\times\left(-7\right)\\[0.6em]\displaystyle \frac{1}{2}\times2&\displaystyle \frac{1}{2}\times0&\displaystyle \frac{1}{2}\times\left(-2\right)\\[0.6em]\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{2}\times3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle -\frac{3}{2}&\displaystyle -\frac{1}{2}&\displaystyle -\frac{7}{2}\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -1\\[0.6em]\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}&\displaystyle \frac{3}{2}
\end{bmatrix}
\]
{-1} = \frac{1}{\det(A)} adj(A) = \frac{1}{2} \begin{bmatrix}
\displaystyle -3&\displaystyle -1&\displaystyle -7\\[0.6em]\displaystyle 2&\displaystyle 0&\displaystyle -2\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle \frac{1}{2}\times\left(-3\right)&\displaystyle \frac{1}{2}\times\left(-1\right)&\displaystyle \frac{1}{2}\times\left(-7\right)\\[0.6em]\displaystyle \frac{1}{2}\times2&\displaystyle \frac{1}{2}\times0&\displaystyle \frac{1}{2}\times\left(-2\right)\\[0.6em]\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{2}\times3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle -\frac{3}{2}&\displaystyle -\frac{1}{2}&\displaystyle -\frac{7}{2}\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -1\\[0.6em]\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}&\displaystyle \frac{3}{2}
\end{bmatrix}
\]
что завершает вычисление обратной матрицы \(A\).
Матричные вычисления в SciLab
МАТРИЧНЫЕ ВЫЧИСЛЕНИЯ И ЧИСЛЕННЫЙ АНАЛИЗ В SCILAB
1. Функции и операции по обработке матриц
В системе SciLab основной единицей данных является матрица, поэтому система имеет обширный набор стандартных функций и операций по обработке матриц, который позволяет:
— формировать новые матрицы стандартного вида;
— выполнять матричные арифметические операции;
— вычислять матричные характеристики и математические функции.
Для формирования новых матриц стандартного вида применяются следующие системные функции:
rand(M,N) – формирует прямоугольную матрицу
размерностью M×N,
элементами которой являются случайные
числа в интервале (0.0; 1.0), функция rand
без параметров формирует одно случайное
число в том же интервале.
ones(M,N) формирует единичную матрицу размерностью M×N.
zeros(M,N) формирует матрицу размерностью M×N, состоящую из нулей.
diag(V) создает диагональную матрицу, в которой элементы вектора V являются элементами главной диагонали.
Матричные арифметические операции представлены следующими:
A+B , A—B матричное сложение и вычитание. Оба операнда этой операции должны иметь одинаковую размерность, если они являются матрицами. Один из операндов может выть скалярной величиной.
A*B матричное умножение. Операция выполняется по правилам матричного умножения, число столбцов матрицы A должно быть равно числу строк матрицы B.
A \ B левое деление матриц. поэлементное возведение матрицы в
степень.
поэлементное возведение матрицы в
степень.
Оба операнда этих операций должны иметь одинаковую размерность, или один из них должен являться скалярной величиной.
Операция «апостроф» ′ вычисляет комплексно сопряженную транспонированную матрицу.
Операция «точка апостроф» .′ вычисляет транспонированную матрицу.
Ниже приведены примеры выполнения матричных арифметических операций.
Формирование новой матрицы | Матричные операции | Поэлементные матричные операции |
>> rand(2,3) ans = 0.9218 0.1763 0.9355 0. ans = 158 201 335 426 >> x=[2 3 4; 5 6 7]; >> t=[3; 6; 9]; >> z=x*t z = 60 114 | >> x=[2 3 4; 5 6 7]; >> y=[9 8 7 ; 6 5 4]; >> z=x .*y z = 18 24 28 30 30 28 >>f=y./x f = 4.5000 2.6667 1.7500 1.2000 0.8333 0.5714 >> w=y.’ w = 9 6 8 5 7 4 |
Система содержит стандартные функции, позволяющие вычислять различные характеристики матриц:
det(A) вычисляет определитель матрицы;
trace(A) вычисление следа матрицы;
rank(A) вычисление ранга матрицы;
inv(A) вычисление обратной матрицы.
Ниже приведены примеры вычисления этих характеристик для матриц А и В.
Определитель матрицы | Обратная матрица |
>> x=[2 3 4; 5 6 7; 1 2 2]; >> d=det(x) d = 3 | >> x=[2 3 4; 5 6 7; 1 2 2]; >> inv(x) ans = -0.6667 0.6667 -1.0000 -1.0000 0 2.0000 1.3333 -0.3333 -1.0000 |
Над массивами можно выполнять различные операции, заданные системными функциями.
max(А) вычисление максимального элемента массива;
min(А) вычисление минимального элемента массива;
sum(A) вычисление суммы элементов массива;
prod(A) вычисление произведения элементов массива;
mean(A) вычисление среднего значения элементов
массива.
Порядок применения этих функций и результаты их выполнения рассмотрены на примерах.
Минимум и максимум | Сумма и произведение | Среднее значение |
>> x=[2 3 4; 55 6 7; 1 12 2]; >> m=max(x) m = 55 12 7 m = 55 >> z=min(x) z = 1 3 2 | >> x=[2 3 4; 5 6 7; 1 2 2]; >> s=sum(x) s = 8 11 13 >> s1=sum(sum(x)) s1 = 32 >> z=prod(x) z = 10 36 56 | > x=[2 3 4; 5 6 7; 2 3 7]; >> z=mean(x) z = 3 4 6 >> z1=mean(mean(x)) z1 = 4. |
Матрицы в Excel
Автор Амина С. На чтение 9 мин Опубликовано
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Содержание
- Формулы массива
- Что можно делать с матрицами
- Транспонирование
- Сложение
- Умножение
- Обратная матрица
- Поиск определителя матрицы
- Несколько примеров
- Умножение и деление
- Метод 1
- Метод 2
- Сложение и вычитание
- Метод 1
- Метод 2
- Пример транспонирования матрицы
- Поиск обратной матрицы
- Выводы
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
- Выделить набор ячеек, где будут выводиться значения.
- Непосредственно введение формулы.
- Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
- Выделить набор ячеек, отведенных под транспонированную матрицу.
- Нажать клавишу F2.
- Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
Предположим, у нас есть такая таблица, которую следует умножить на 12.
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:h21). Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке h5. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку h5, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
=B3+h4
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().
Выделяем диапазон для ячеек матрицы АТ.
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Оцените качество статьи. Нам важно ваше мнение:
Нам важно ваше мнение:
Матрицы – умножение, деление, сложение и вычитание
Перейти к содержимомуУмножение
Умножение
Деление
Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.
Умножить матрицу на одно число очень просто –
Вычисления выполняются по следующей формуле –
Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 st и столбца 1 st .
Скалярный продукт — это умножение совпадающих членов и их суммирование —
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —
(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для 2 -й -й ряд и 1-й столбец –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
И тогда для 2 -й строки и 2-го столбца –
(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда мы окончательно получим результат.
Надеюсь, теперь вы разобрались с методом и решениями?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.
X / Y = X * (1/Y) = X * B -1
Где B обратная означает обратную матрицу B. Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание
Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры. Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Давайте решим несколько примеров и разберемся в них глубже –
Пример – 1
[1 2] + [2 -3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.
[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]
Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.
Пример – 2
[4 5] – [2 1]
Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Сложение матрицы очень простое и выполняется с каждой записью.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте следующие матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.
Итак, окончательный ответ —
До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.
Оцените приведенную ниже задачу или, если это невозможно, укажите причину.
Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –
Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.
Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.
Это касается как сложения, так и вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –
, Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1
And
2y – 3 = -5
Y = -5 + 3 / 2
Y = -2 / 2
Д = -1
Перейти к началу
Умножение двух матриц в одну строку с использованием Numpy в Python
Умножение матриц — это операция, которая принимает две матрицы в качестве входных данных и создает одну матрицу путем умножения строк первой матрицы на столбец второй матрицы. При умножении матриц убедитесь, что количество столбцов первой матрицы должно быть равно количеству строк второй матрицы .
Пример: Умножение двух матриц друг на друга размера 3×3.
Ввод:matrix1 = ([1, 2, 3],
[3, 4, 5],
[7, 6, 4])
матрица2 = ([5, 2, 6],
[5, 6, 7],
[7, 6, 4])
Выход: [[36 32 32]
[70 60 66]
[93 74 100]] Рекомендуется: попробуйте свой подход на {IDE} сначала, прежде чем перейти к решению.
Методы умножения двух матриц в python
1. Использование явных циклов for: Это простой метод умножения матриц, но один из дорогостоящих методов для больших наборов входных данных. Здесь мы используем вложенные для циклов. для повторения каждой строки и каждого столбца.
Если матрица1 представляет собой матрицу n x m , а матрица2 представляет собой матрицу м x l .
Implementation:
Python3
|
Выход
[114, 160, 60], [74, 97, 73], [114], 904, 904, 904, 904, 904, 904, 9018], [114, 160, 60]. В этой программе мы использовали вложенные циклы for для вычисления результата, который будет перебирать каждую строку и столбец матрицы, в конце концов он будет накапливать сумму произведения в результате.2. Использование Numpy : Умножение с использованием Numpy, также известное как векторизация, основная цель которого уменьшить или удалить явное использование циклов for в программе, благодаря чему вычисления становятся быстрее.
Numpy — это сборка пакета на python для обработки массивов и манипулирования ими. Для больших операций с матрицами мы используем пакет numpy python, который в 1000 раз быстрее, чем итеративный метод.
For detail about Numpy please visit the LinkImplementation:
Python3
|
|
Вывод:
[[ 63 320 83] [ 77 484 102 ] [ 84 248 117]]
Используя numpy
Python3
|
Output:
[[ 63 320 83] [ 77 484 102 ] [ 84 248 117]]
В приведенном выше примере мы использовали скалярное произведение, а в математике скалярное произведение — это алгебраическая операция, которая берет два вектора одинакового размера и возвращает одно число.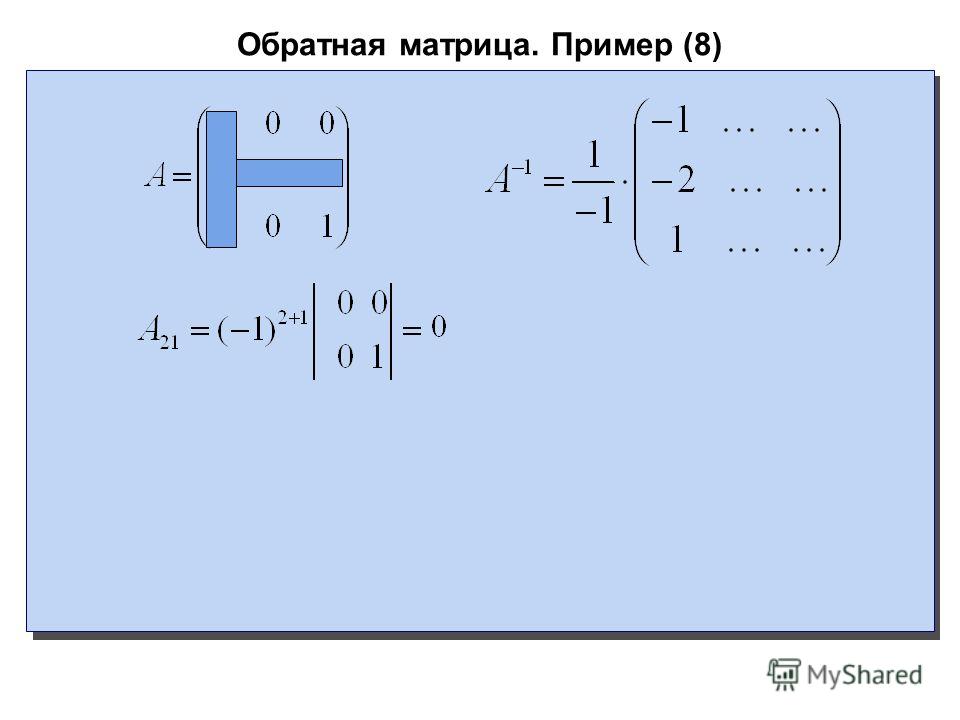 Результат рассчитывается путем умножения соответствующих записей и сложения этих продуктов.
Результат рассчитывается путем умножения соответствующих записей и сложения этих продуктов.
Эта статья предоставлена Dheeraj Sharma . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
scipy.sparse.csr_matrix — Руководство по SciPy v1.9.1
- class scipy.sparse.csr_matrix( arg1 , shape=None , dtype=None , copy=False )[источник]
Сжатая матрица разреженных строк
- Это можно реализовать несколькими способами:
- csr_matrix(D)
с плотной матрицей или ndarray ранга 2 D
- csr_matrix(S)
с другой разреженной матрицей S (эквивалентно S.tocsr())
- csr_matrix((M, N), [dtype])
для построения пустой матрицы формы (M, N) dtype является необязательным, по умолчанию dtype=’d’.

- csr_matrix((data, (row_ind, col_ind)), [shape=(M, N)])
где
data,row_indиcol_indудовлетворяют отношениеa[row_ind[k], col_ind[k]] = data[k].- csr_matrix((данные, индексы, indptr), [shape=(M, N)])
— это стандартное представление CSR, в котором индексы столбцов для строка i хранится в индексах
[indptr[i]:indptr[i+1]]и их соответствующие значения хранятся вdata[indptr[i]:indptr[i+1]]. Если параметр формы не указан, размеры матрицы выводятся из индексных массивов.
Примечания
Разреженные матрицы можно использовать в арифметических операциях: они поддерживают сложение, вычитание, умножение, деление и степень матрицы.
- Преимущества формата CSR
эффективные арифметические операции CSR + CSR, CSR * CSR и т. д.
эффективная нарезка рядов
быстрые матричные векторные произведения
- Недостатки формата CSR
Примеры
>>> импортировать numpy как np >>> из scipy.
 sparse импортировать csr_matrix
>>> csr_matrix((3, 4), dtype=np.int8).toarray()
массив([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)
sparse импортировать csr_matrix
>>> csr_matrix((3, 4), dtype=np.int8).toarray()
массив([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)
>>> строка = np.массив ([0, 0, 1, 2, 2, 2]) >>> col = np.array([0, 2, 2, 0, 1, 2]) >>> данные = np.массив ([1, 2, 3, 4, 5, 6]) >>> csr_matrix((данные, (строка, столбец)), shape=(3, 3)).toarray() массив([[1, 0, 2], [0, 0, 3], [4, 5, 6]])>>> indptr = np.array([0, 2, 3, 6]) >>> индексы = np.array ([0, 2, 2, 0, 1, 2]) >>> данные = np.массив ([1, 2, 3, 4, 5, 6]) >>> csr_matrix((данные, индексы, indptr), shape=(3, 3)).toarray() массив([[1, 0, 2], [0, 0, 3], [4, 5, 6]])Повторяющиеся записи суммируются:
>>> строка = np.массив ([0, 1, 2, 0]) >>> столбец = np.массив ([0, 1, 1, 0]) >>> данные = np.массив ([1, 2, 4, 8]) >>> csr_matrix((данные, (строка, столбец)), shape=(3, 3)).toarray() массив([[9, 0, 0], [0, 2, 0], [0, 4, 0]])В качестве примера постепенного построения матрицы CSR: следующий фрагмент строит матрицу терминов-документов из текстов:
>>> docs = [["привет", "мир", "привет"], ["до свидания", "жестокий", "мир"]] >>> индптр = [0] >>> индексы = [] >>> данные = [] >>> словарный запас = {} >>> для d в документах: . .. для срока в d:
... индекс = словарь.setdefault (термин, длина (словарь))
... index.append(индекс)
... data.append(1)
... indptr.append (длина (индексы))
...
>>> csr_matrix((данные, индексы, indptr), dtype=int).toarray()
массив([[2, 1, 0, 0],
[0, 1, 1, 1]])
.. для срока в d:
... индекс = словарь.setdefault (термин, длина (словарь))
... index.append(индекс)
... data.append(1)
... indptr.append (длина (индексы))
...
>>> csr_matrix((данные, индексы, indptr), dtype=int).toarray()
массив([[2, 1, 0, 0],
[0, 1, 1, 1]])
- Атрибуты
- dtype dtype
Тип данных матрицы
-
shape2-tuple Получить форму матрицы.
- ndim int
Количество измерений (всегда 2)
-
nnz Количество сохраненных значений, включая явные нули.
- данные
CSR формат данных массив матрицы
- индексы
индекс формата CSR массив матрицы
- indptr
Массив указателей индекса формата CSR матрицы
-
has_sorted_indices Определить, имеет ли матрица отсортированные индексы
Методы
__len__()arcsin()Поэлементный арксинус.

угловой синус()Поэлементный угл.
арктан()Поэлементный арктангенс.
арктанг()Поэлементный арктанг.
аргмакс([ось, выход])Возвращает индексы максимальных элементов вдоль оси.
аргмин([ось, выход])Возвращает индексы минимальных элементов вдоль оси.
в формате(формат[ копия])Вернуть эту матрицу в переданном формате.
тип asfp()Преобразование матрицы в формат с плавающей запятой (при необходимости)
astype(dtype[ литье, копия])Приведение элементов матрицы к указанному типу.

потолок()Поэлементный потолок.
check_format([full_check])проверить правильность формата матрицы
соединение([копия])Поэлементное комплексное сопряжение.
сопряженный([копия])Поэлементное комплексное сопряжение.
копия()Возвращает копию этой матрицы.
count_nonzero()Количество ненулевых записей, эквивалентное
град2рад(+)Поэлементно град2рад.
диагональ([k])Возвращает k-ю диагональ матрицы.
точка(другое)Обычное скалярное произведение
исключить_нули()Удаление нулевых записей из матрицы
экспм1(+)Поэлементный expm1.

этаж()Поэлементный пол.
getH()Вернуть эрмитову транспонированную эту матрицу.
get_shape()Получить форму матрицы.
геткол(и)Возвращает копию столбца i матрицы в виде матрицы CSR (m x 1) (вектор-столбец).
формат()Формат представления матрицы в виде строки.
getmaxprint()Максимальное количество отображаемых элементов при печати.
getnnz([ось])Количество сохраненных значений, включая явные нули.
получить(i)Возвращает копию строки i матрицы в виде CSR-матрицы (1 x n) (вектор-строка).

log1p()Поэлементный log1p.
макс.([ось, выход])Возвращает максимум матрицы или максимум по оси.
максимум(другое)Поэлементный максимум между этой и другой матрицей.
среднее значение([ось, тип d, выход])Вычислить среднее арифметическое вдоль указанной оси.
мин([ось, выход])Возвращает минимум матрицы или максимум по оси.
минимум(другое)Поэлементный минимум между этой и другой матрицей.
многократный(другой)Поточечное умножение на другую матрицу, вектор или скаляр.
ненулевой()ненулевые индексы
мощность(n[ dtype])Эта функция выполняет поэлементное питание.

чернослив()Удалить пустое пространство после всех ненулевых элементов.
рад2град()Поэлементно rad2deg.
изменить форму(самостоятельно, сформировать [ заказать, скопировать])Придает новую форму разреженной матрице без изменения ее данных.
изменение размера(*форма)Изменение размера матрицы на месте до размеров, заданных формой
ринт()Поэлементный ринт.
set_shape(форма)См.
изменение формы.setdiag(значения [ k])Установить диагональные или недиагональные элементы массива.
знак()Поэлементный знак.

грех()Поэлементный грех.
синх()Поэлементный синх.
sort_indices()Отсортировать индексы этой матрицы по месту
отсортированные_индексы()Вернуть копию этой матрицы с отсортированными индексами
кв()Поэлементная кв.
сумма([ось, тип d, выход])Суммируйте элементы матрицы по заданной оси.
сумма_дубликатов()Удаление повторяющихся элементов матрицы путем их сложения
желто-коричневый()Поэлементный тан.
танх()Поэлементный танх.

массив([заказ, выход])Вернуть плотное представление этой матрицы в формате ndarray.
tobsr([размер блока, копия])Преобразуйте эту матрицу в формат Block Sparse Row.
tocoo([копия])Преобразуйте эту матрицу в формат COOrdinate.
tocsc([копия])Преобразуйте эту матрицу в формат сжатого разреженного столбца.
tocsr([копия])Преобразуйте эту матрицу в формат Compressed Sparse Row.
плотный([заказ, исходящий])Возвращает плотное матричное представление этой матрицы.
тодиа([копия])Преобразуйте эту матрицу в разреженный формат DIAgonal.



 3
3 3333
3333
 dot(mat1,mat2)
dot(mat1,mat2) 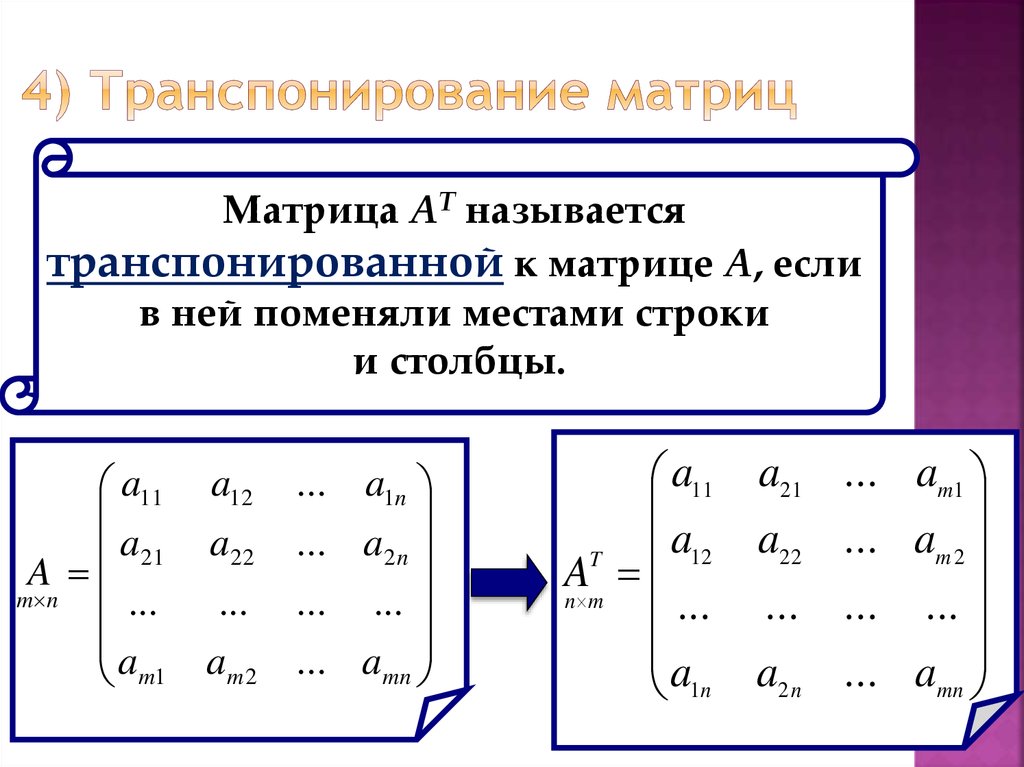
 sparse импортировать csr_matrix
>>> csr_matrix((3, 4), dtype=np.int8).toarray()
массив([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)
sparse импортировать csr_matrix
>>> csr_matrix((3, 4), dtype=np.int8).toarray()
массив([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)
 .. для срока в d:
... индекс = словарь.setdefault (термин, длина (словарь))
... index.append(индекс)
... data.append(1)
... indptr.append (длина (индексы))
...
>>> csr_matrix((данные, индексы, indptr), dtype=int).toarray()
массив([[2, 1, 0, 0],
[0, 1, 1, 1]])
.. для срока в d:
... индекс = словарь.setdefault (термин, длина (словарь))
... index.append(индекс)
... data.append(1)
... indptr.append (длина (индексы))
...
>>> csr_matrix((данные, индексы, indptr), dtype=int).toarray()
массив([[2, 1, 0, 0],
[0, 1, 1, 1]])







