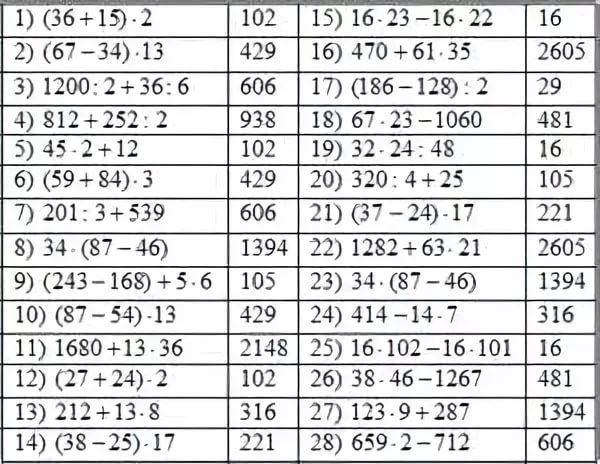
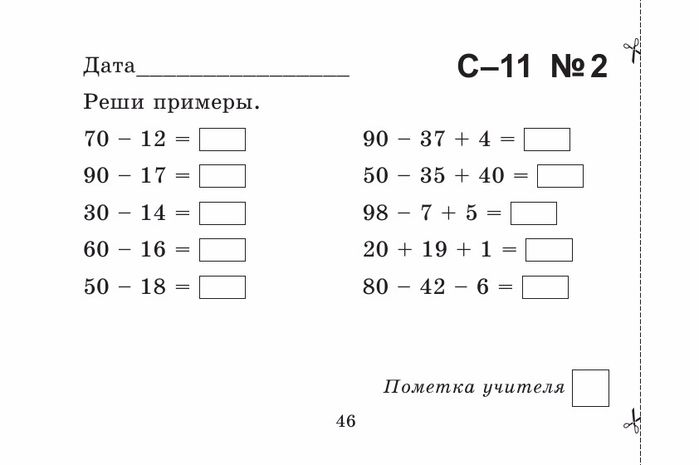
Математика приклади: приклади на додавання і віднімання в межах 10 — Раскраски и прописи для девочек и мальчиков l Загадки l… — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

alexxlab / / Разное

Содержание

Математика для 1 класу – скачати завдання безкоштовно – Розвиток дитини

Математика для дітей 6-7 років (1 клас)

Величезна кількість завдань школярі опрацьовують самостійно. Батьки першокласників часто губляться, шукаючи де дістати необхідні посібники. На сайті Childdevelop зібрані розвиваючі картки, приклади, логічні задачі, лабіринти. Матеріали розділу «Математика для 1 класу» обов’язково зацікавить юних школярів та їхніх батьків.

Чому потрібні додаткові завдання з математики для 1 класу

Похід в школу — великий стрес. Мінімізувати його допоможе підготовка і додаткове навчання. Серед запропонованих посібників є збірники з такого роду вправами.

Прописи

За програмою математики для 1 класу прописам приділяється мало часу, тому починати тренування варто обов’язково. Першокласникам можна запропонувати домалювати геометричну фігуру, намалювати малюнок по клітинках. Після освоєння простих вправ варто переходити до прописів цифр. У каталозі представлено кілька варіантів прописів і завдань для тренування пальців. Серед них можна знайти матеріали навіть для самого неслухняного школяра.

Картки

Популярністю в навчанні користуються картки. З ними простіше освоїти рахунок і математичні операції додавання-віднімання.

Тренування на визначення розміру одного предмета по відношенню до іншого також краще проводити з картками. Постійно працюючи з цією вправою, дитина легко розпізнає предмети за ознакою «високий», «низький», «великий», «маленький».

Загальний розвиток

Математика для першокласників призначена не тільки для освоєння дітьми математичних операцій. Це тренування логіки, просторової уяви. Навчальні матеріали, спрямовані на загальний розвиток дітей:

  • пошук однакових фігур;
  • виключення зайвого;
  • малюнки по клітинам;
  • вибір вірної відповіді серед кількох хибних;
  • визначення часу.

Цікаві завдання мають практичну основу. Їх мета — навчання основам арифметики, розвиток мислення, вміння застосовувати отримані навички.

Допомога з математикою в 1 класі

У школі діти отримують відразу великий обсяг інформації. Нерідко малюк не встигає розібратися і освоїти одну тему, як слідом вже йде інша. Щоб допомогти дитині, на сайті складена добірка посібників по декількох напрямках. З її допомогою простіше систематизувати знання, пояснити незрозумілий предмет.

Цікава математика

Дітей зацікавлять незвичайні приклади з математики для 1 класу. Цікаві розвиваючі ігри тренують логіку, просторове мислення. Відмінний приклад цікавих математичних вправ:

  • арифметичні розмальовки;
  • пошук відсутніх фігур;
  • математичні кросворди;
  • пошук правильних прикладів.

Рішення прикладів подається в ігровій формі. Навчаючись у такий спосіб, першокласник не буде перевтомлюватися.

Приклади рішень математичних задач

Розділ зібрав типові завдання для 1 класу з математики. Вони подаються в доступній формі. Для початківців, зовсім юних математиків роз’яснюються завдання, проілюстровані рішення. Незвичайні вправи допоможуть закріпити навички. Для цього можна використовувати арифметичну піраміду або лабіринт.

Практичні завдання йдуть з ілюстраціями. Якщо супроводити завдання з математики для 1 класу картинками, воно краще сприймається дітьми 6-7 років, ніж сухий текст.

Логічні завдання

Батькам не варто зациклюватися на вирішенні завдань. Вирішуючи тільки приклади для 1 класу з математики, можна відбити у дітей бажання вчитися. Завдання по шкільній програмі варто розбавити логічними задачами і загадками, лабіринтами, головоломками. Навчатися з цікавими і веселими вправами — простіше і швидше.

Математика для першокласників — наука не нудна. Знайомити дитину з предметом можна за допомогою ігрових завдань і конкурсів. Зробивши цікаву добірку логічних лабіринтів, можна надовго захопити чада.

Матеріали з математики для 1 класу вчителям

Перед учителем стоїть важливе завдання. Школярам потрібно дати необхідний обсяг знань, проконтролювати правильність розуміння теми. Вправи, зібрані на порталі, позбавляють від необхідності нескінченно складати приклади для першокласників з математики. За допомогою навчальних матеріалів можна організувати вікторину, провести математичні конкурси.

На сайті можна підібрати завдання для першокласників з математики для самостійного розбору на літо. Є кілька рівнів складності. Є й найпростіші приклади, і завдання для олімпіади. Посібники можна роздрукувати або зробити презентацію для наочного пояснення.

Доступність матеріалів з математики для 1 класу

Прекрасно знаючи про всі складнощі математики для першокласників, був створений проект з підбіркою навчальних матеріалів.

Завдання поділяються за складністю. Серед них знайдуться матеріали на будь-який смак. Посібники доступні онлайн. Завантажити їх можна безкоштовно.

Математика для 1 класу — предмет, що вимагає повного розуміння і освоєння матеріалу. У розділі зібрані якісні і сучасні посібники, що в цьому допоможуть.

Учебно-методические пособия | Кафедра прикладной математики

На этой странице представлена информация о некоторых из наших учебных пособий.

На кафедре разработана литература, охватывающая как общий курс математики, так и специальные главы и отдельные разделы, а также научные монографии и книги сотрудников кафедры.

ОБЩИЙ КУРС ВЫСШЕЙ МАТЕМАТИКИ.

 ▲ Вища математика в прикладах і задачах: у двох томах (під ред. проф. Л.В. Курпи).

 

Вища математика в прикладах і задачах: у 2 т. Т.1: Аналітична геометрія та лінійна алгебра. Диференціальне та інтегральне числення функцій однієї змінної: навч. посібник / Л.В.Курпа, Ж.Б.Кашуба, Г.Б.Лінник [та ін.]; за ред. Л.В.Курпи. – Харків: НТУ «ХПІ», 2009. – 532с.

 

 

 

 

 

 

  • Скачать книгу можно в цифровом репозитарии НТУ «ХПИ».

 

Вища математика в прикладах і задачах: у 2 т. Т.2: Диференціальне числення функцій багатьох змінних. Диференціальні рівняння та ряди: навч. посібник / Л.В.Курпа, Н.О.Кириллова, Г.Б.Лінник [та ін.]; за ред. Л.В.Курпи. – Харків: НТУ «ХПІ», 2009. – 432с

 

 

 

 

 

 

  • Скачать книгу можно в цифровом репозитарии НТУ «ХПИ».

 

▲ Высшая математика. Решение задач и варианты типовых расчетов  (под ред. проф. Л.В. Курпы) = 

Higher Mathematics. Problem solving and variants of typical calculations 

Авторы первого тома: Курпа Л.В., Кашуба Ж.Б., Линник А.Б., Ярошенко А.Р., Манучарян Г.В., Одинцова Е.В., Чистилина А.В., Шматко Т.В. , Буйвол О.В.

Авторы второго тома: Курпа Л.В., Кашуба Ж.Б., Столбовая Т.В., Линник А.Б., Ярошенко А.Р., Манучарян Г.В., Одинцова Е.В., Чистилина А.В., Шматко Т.В., Буйвол О.В.

Авторы третьего тома: Курпа Л.В., Васильченко В.Ф., Кириллова Н.А., Столбовая Т.В., Линник А.Б., Ярошенко А.Р., Манучарян Г.В., Одинцова Е.В., Чистилина А.В., Буйвол О.В., Курилов Е.А.

Авторы четвертого тома: Курпа Л.В., Щербинина Т.Е., Линник А.Б., Манучарян Г.В., Одинцова Е.В., Чистилина А.В., Буйвол О.В., Курилов Е.А.

В основу учебного пособия «Высшая математика» в четырех томах положены материалы опубликованных ранее учебных пособий «Вища математика» и «Higher mathematics» под редакцией проф. Курпа Л.В. в двух томах (в 2002 и 2004 гг.). Настоящее издание существенным образом переработано, расширено, дополнено и представлено параллельно на двух языках: русском и английском. По каждой теме приведены лишь основные систематизированные теоретические сведения.

Особое внимание уделяется разбору решения задач, чтобы помочь студенту более глубоко понять теоретический материал, научить применять математический аппарат к решению конкретных задач. По каждой теме представлены индивидуальные задания (по 30 вариантов), а также тестовые вопросы и задания, с помощью которых студент может проверить свою готовность к самостоятельному выполнению индивидуального задания. Как тестовые задачи, так и задачи индивидуальных заданий снабжены ответами, что поможет студенту проверить правильность их решения. Отличительной особенностью данного учебного пособия являются примеры решения задач в Maple, представленные вместе с текстами программ. Учитывая современные требования к квалификации инженера, а так же высокий уровень развития информационных технологий, авторы сочли необходимым включить в учебное пособие первичную информацию для ознакомления с одной из современных математических систем Maple. Авторы считают, что параллельное решение многих задач курса высшей математики с использованием пакета Maple и без него позволяет проверить решение, полученное студентом самостоятельно, а также закладывает базу у студентов для свободного обращения с различного рода математическими пакетами.
Использование подобных пакетов в будущем сможет освободить инженера от рутинных математических вычислений и преобразований, что, безусловно, будет способствовать интенсификации их работы и развитию творческих подходов для выполнения тех или иных заданий. Книга будет весьма полезной не только студентам из стран СНГ, но и зарубежным студентам, обучающимся на Украине, в России или Белоруссии. Авторы глубоко признательны многим преподавателям, которые представили ответы для индивидуальных домашних заданий, в том числе Архиповой Е.С., Болотиной Л.В., Корниль Т.Л., Лемешевой Л.П., Ясницкой Н.Н.

 

▲ Higher Mathematics Problem solving and variants of typical calculations. (Edited by Prof. Kurpa L.V.)

     

Авторы первого тома: Архипова Е.С., Болотина Л.В., Кашуба Ж.Б., Корниль Т.Л., Курпа Л.В., Курпа Л.И., Лемешева Л.П., Линник А.Б., Протопопова В.П., Ярошенко А.Р., Ясницкая Н.Н.

Авторы второго тома: Архипова Е. С., Болотина Л.В., Васильченко В.Ф., Вовк В.Н., Волкова Н.Н., Кашуба Ж.Б., Кириллова Н.А., Корниль Т.Л., Курпа Л.В., Курпа Л.И., Линник А.Б., Столбовая Т.В., Щербинина Т.Е., Ярошенко А.Р., Ясницкая Н.Н.

Учебный учебник включает теоретический материал по основным разделам высшей математики: линейная алгебра, аналитическая геометрия и исчисление, основы дифференциального исчисления функций многих переменных, множественные, криволинейные и поверхностные интегралы, теория поля и множества, примеры решения типовых задач и вариантов Типичных расчетов.

 

▲ Пособие по элементарной математике для абитуриентов и студентов ХГПУ / Л. В. Курпа, Л. В. Болотина, Е. С. Архипова, Л. И. Курпа.  Харьков, ХГПУ, 2000. 244 с. ISBN 966-593-142-3

Авторы: Л. В. Курпа, Л. В. Болотина, Е. С. Архипова, Л. И. Курпа

Прекрасная книга для абитуриентов, решивших поступать в ХПИ, и студентов-первокурсников. В сжатом виде, но достаточно полно изложена теория, выделены основные формулы, определения и правила. Есть много примеров и задач с решениями и для самостоятельной работы. Есть более 20 реальных вариантов заданий на вступительных экзаменах с прошлых лет. Имея эту книгу, Вы сможете повторить весь школьный курс математики, начиная с азов (действия с дробями, деление в столбик и т.п.) и до самого конца.

В пособии есть следующие главы: арифметика, алгебра, прогрессии, уравнения и системы, показательные и логарифмические уравнения, неравенства, тригонометрия, планиметрия, стереометрия, математический анализ, образцы вариантов заданий, предлагавшихся на вступительных экзаменах в ХПИ, образцы вопросов к собеседованию для абитуриетов ХПИ, примеры решения вариантов заданий, предлагавшихся на письменных вступительных экзаменах в хгпу, примеры заданий по элементарной математике, которые должен уметь решить каждый потенциальный студент, варианты индивидуальных домашних заданий по элементарной математике для студентов 1-го курса ХПИ.

▲ Высшая математика. Решение задач и варианты типовых расчётов. Части 1, 2. (под ред. проф. Л.В. Курпы)

Главная цель данной книги — помочь студентам в их самостоятельной работе при решении практических задач по курсу высшей математики. В начале каждой главы приводятся сведения из теории. Подробно разобраны примеры. Имеется по 30 вариантов индивидуальных домашних заданий по каждой теме. По этой книге преподаватели кафедры выдают ИДЗ студентам механических, информационных и инженерно-физических специальностей. Много примеров и вариантов разного уровня сложности. Из них можно выбрать варианты ИДЗ практически для любых специальностей. Для студентов экономических специальностей разработан сокращённый вариант книги. Издан украиноязычный вариант этого учебника.

Авторы первой части: Л. В. Курпа, Е. С. Архипова, Н. Н. Ясницкая, Т. Л. Корниль, Л. В. Болотина, Ж. Б. Кашуба, А. Р. Ярошенко, Л. И. Курпа, А. Б. Линник.

Л. В. Курпа, Е. С. Архипова, Н. Н. Ясницкая, Т. Л. Корниль, Л. В. Болотина, Ж. Б. Кашуба, А. Р. Ярошенко, Л. И. Курпа, А. Б. Линник. Высшая математика. Решение задач и варианты типовых расчётов. Ч.1. Харьков, ХГПУ, 1999. 288 с. ISBN 966-593-085-0, ISBN 966-593-088-5

 В 1-ю часть пособия включены такие главы: матрицы, определители, решение систем,  векторная алгебра, поверхности и линии 1-го и 2-го порядка,  пределы и непрерывность функции одной переменной,  основы дифференциального исчисления для функции одной переменной,  неопределённый интеграл, методы интегрирования, определённый интеграл, приложения,  несобственные интегралы, вопросы их сходимости.

 

Авторы второй части: Л. В. Курпа, Е. С. Архипова, Н. Н. Ясницкая, А. Р. Ярошенко, О. И. Бабакова, Л. П. Лемешева, Н. Н. Волкова, Ж. Б. Кашуба, В. Н. Вовк, Т. Л. Корниль, В. Ф. Васильченко, Т. В. Столбовая, Л. В. Болотина, Н. А. Кириллова, Л. И. Курпа, А. Б. Линник.

Л. В. Курпа, Е. С. Архипова, Н. Н. Ясницкая, А. Р. Ярошенко, О. И. Бабакова, Л. П. Лемешева, Н. Н. Волкова, Ж. Б. Кашуба, В. Н. Вовк, Т. Л. Корниль, В. Ф. Васильченко, Т. В. Столбовая, Л. В. Болотина, Н. А. Кириллова, Л. И. Курпа, А. Б. Линник. Высшая математика. Решение задач и варианты типовых расчётов. Ч.2. Харьков, ХГПУ, 1999. 280 с. ISBN 966-593-085-0, ISBN 966-593-103-2

Во 2-ю часть пособия входят такие главы: функции многих переменных, дифференциальные уравнения, числовые и функциональные ряды, кратные интегралы, криволинейные и поверхностные интегралы, элементы теории поля.

 

 

▲ Вища математика. Розв’язання задач та варіанти типових розрахунків. Частини 1 та 2 (під ред. проф. Л.В. Курпи). 

Авторы первой части: Архіпова О.С., Болотіна Л.В, Кашуба Ж.Б., Кірілова Н.О., Корніль Т.Л., Курпа Л.В., Курпа Л.І., Лемешева Л.П., Лінник Г.Б., Протопопова В.П., Ярошенко О.Р., Ясницька Н.М. 

Вища математика. Розв’язання задач та варіанти типових розрахунків. Т.1.: Навч. Посібник  / За ред. Л.В.Курпа. — Харків: НТУ “ХПІ”, 2002 – 316с.–Укр.мовою.

Учебное пособие содержит теоретический справочный материал по основным разделам высшей математики: линейной алгебры, аналитической геометрии и математического анализа для функции одной переменной, образцы решения типовых задач и варианты типовых расчетов. В первом томе пособия рассмотрено более 250 примеров. Типовые задачи для индивидуального исполнения состоят из 30 вариантов.

Пособие предназначается для студентов инженерно-физических, машиностроительных и экономических специальностей, а также может быть полезным преподавателям, аспирантам, научным работникам и всем, кто имеет дело с применением высшей математики для решения научно-технических

Авторы второй части: Архіпова О.С., Болотіна Л.В., Васильченко В.Ф., Вовк В.М., Волкова Н.М.,Кашуба Ж.Б., Кірілова Н.О., Корніль Т.Л., Курпа Л.В., Курпа Л.І., Лінник Г.Б., Столбова Т.В., Щербініна Т.Є., Ярошенко О.Р., Ясницька Н.М.

Вища математика. Розв’язання задач  та варіанти типових розрахунків. Т.ІІ.: Навч. Посібник  / За ред. Л.В.Курпа. — Харків: НТУ “ХПІ”, 2002 – 312с.–Укр.мовою.

Второй том учебного пособия содержит теоретический справочный материал по дифференциального и интегрального исчисления функций многих переменных, образцы решения типовых задач и варианты типовых расчетов. В этом томе назад более 190 примеров и задач. Типовые расчеты содержат от 5 до 20 заданий, каждое из которых состоит из 30 вариантов для индивидуального исполнения.

Пособие предназначается для студентов инженерно-физических, машиностроительных и экономических специальностей, а также может быть полезным преподавателям, аспирантам, научным работникам и всем, кто имеет дело с применением высшей математики для решения научно-технических проблем.

 

▲ Математика для экономистов. Решение задач и варианты индивидуальных заданий (под ред. проф. Л.В. Курпы).

Авторы: Л. В. Курпа, Е. С. Архипова, Т. Л. Корниль, Л. В. Болотина, О. И. Бабакова, Ж. Б. Кашуба, Л. П. Лемешева, А. Р. Ярошенко

Л. В. Курпа, Е. С. Архипова, Т. Л. Корниль, Л. В. Болотина, О. И. Бабакова, Ж. Б. Кашуба, Л. П. Лемешева, А. Р. Ярошенко. Математика для экономистов. Решение задач и варианты индивидуальных заданий. Харьков, ХГПУ, 2000. 333 с. ISBN 966-593-141-5

Вместо двух частей, которые используются для студентов при изучении стандартного курса высшей математики, в данном пособии в одном томе собраны все разделы упрощённого курса высшей математики, которые изучаются студентами-экономистами. Все главы дополнены задачами экономического содержания. Отобраны наиболее простые и типичные примеры. Особое внимание уделено темам, которые в дальнейшем применяются в теории вероятностей и математической статистике, математическом программировании, макро- и микроэкономике.

Структура каждой главы книги: теория, решение примеров, 30 вариантов ИДЗ по каждой теме. Если Вы преподаёте на экономических специальностях, эта книга Вам, несомненно, пригодится: Вы можете выдавать готовые варианты ИДЗ по каждой теме. Особенно интересны будут студентам задачи с экономическим содержанием.

Главы: матрицы, определители, решение систем линейных уравнений, векторная алгебра, поверхности и линии 1-го и 2-го порядка, пределы и непрерывность функции одной переменной, основы дифференциального исчисления для функции одной переменной, неопределённый интеграл, методы интегрирования, определённый интеграл (приложения), несобственные интегралы, вопросы их сходимости, функции многих переменных, дифференциальные уравнения, числовые и функциональные ряды, кратные интегралы.

 

▲ Математический анализ для инженеров.Часть 1.

Автор: Сенчук Ю.Ф.

Книга написана на базе курса лекций по математическому анализу, который автор читал студентам НТУ «ХПИ» с усиленной математической подготовкой. В первой части изложены теория пределов, дифференциальное и интегральное исчисление функций, кратные интегралы. Материал изложен последовательно, четко, на достаточном уровне строгости и в доступной форме. Книга содержит большое количество иллюстраций, примеров и задач.

 

 

 

 

  • Скачать книгу можно в цифровом репозитарии НТУ «ХПИ».

▲ Математический анализ для инженеров.Часть 2.

Автор: Сенчук Ю.Ф.

Изложены разделы: криволинейные и поверхностные интерралы, теория поля, числовые и функциональные ряды, интеграл Фурье, дифференциальные уравнения и системы дифференциальных уравнений, а также дополнительные разделы: интегралы, зависящие от параметра и приближенные методы решения обыкновенных дифференциальных уравнений и их систем. Все изложенные теоретические факты доказаны и проиллюстрированы большим количеством примеров и задач.

 

 

 

  •  Скачать книгу можно в цифровом репозитарии НТУ «ХПИ».

 

ОТДЕЛЬНЫЕ ГЛАВЫ И РАЗДЕЛЫ ВЫСШЕЙ МАТЕМАТИКИ

 ▲ Дифференциальное и интегральное исчисление функций одной переменной. / L.V. Kurpa, T.V.Shmatko. Differential and Integral Calculus for One Variable Functions// Диференціальне та інтегральне числення функцій однієї змінної. Навчальний посібник . – Х.: ТНУ „ХПІ”,  2017. – 324с. (англ. мовою)

Авторы: Курпа Л.В.,  Шматко Т.В.

В учебном пособии рассматривается теоретический материал по таким разделам высшей математики: теории пределов, непрерывность функций, дифференциальное и интегральное исчисление для функций одной переменной. Пособие содержит в себе доказательства всех необходимых теорем, предположениях рабочей программой по математическому анализу относительно рассмотренных тем, и иллюстрацию их на конкретных примерах.

Предназначено для студентов технических университетов, изучающих высшую математику на английском языке.

 

 

 

 

▲ Краткое руководство высшей математики. Т.1: Аналитическая геометрия и элементы линейной алгебры / Г.М.Тимченко, О.В.Одинцова, О.С.Мазур, Н.О.Кириллова. Стислий курс вищої математики. Т.1: Аналітична геометрія та елементи лінійної алгебри: навч. посібн. – К.: Кондор-Видавництво, 2016.- 176 с.

Авторы: Г.М.Тимченко, О.В.Одинцова, О.С.Мазур, Н.О.Кириллова.

Учебное пособие содержит теоретический материал по линейной алгебре, аналитической геометрии и векторной алгебры, а также образцы решения типовых задач, тестовые вопросы и задачи, индивидуальные варианты типовых расчетов.

Предназначено для студентов технических специальностей.

 

 

 

 

 

▲ Введение в функциональный анализ / Курпа Л. В., Лінник Г.Б., Щєрбініна Т.Є. Введение в функциональный анализ. – Харків: НТУ ХПІ, 2015. -72с

Авторы: Курпа Л.В., Линник Г.Б., Щербинина Т.Е.

 

Учебное пособие содержит теоретический материал по базовым разделам; функционального анализа. Приведены основные определения, формулы, примеры относительно рассмотренных тем. Пособие содержит доказательства все необходимые теорем, предположениях рабочей программой по функциональному анализу.

Предназначено для студентов инженерно-физического факультета дневной формы обучения

 

 

 

 

 ▲Теория графов. Лекции и варианты индивидуальных домашних заданий: Электронное пособие. / Иглин С.П. Теория графов. Лекции и варианты индивидуальных домашних заданий. — Харьков: НТУ ХПИ, 2015

Автор: Иглин С.П.

Разработан Graph Theory Toolbox — инструментарий для решения задач на графах. Он размещен на сайте Mathworks для свободного скачивания и использования. Некоторые его функции описаны в книге «Математические расчёты на базе MATLAB» (третья часть). В электронной версии книги примеры использования этих функций. Но время идет, пакет постоянно пополняется, и теперь в него включены 27 функций.

  • Электронное пособие можно читать на сайте автора …

 

▲ Линейная алгебра. Сборник задач и методика решения. / Л.П. Дзюбак, С.П. Іглін, Г.Б. Лінник, І.О. Морачковська. Лінійна алгебра. Збірка завдань та методика розв’язання: навч.-метод. посібник // – Х.: НТУ „ХПІ”, 2013. – 240с. ISBN 978-617-05-0074-8

Авторы: Л.П. Дзюбак, С.П. Иглин, Г.Б. Линник, И.О. Морачковская

 

 

Рассматривается методика решения типовых задач по линейной алгебре. Приведенные варианты типовых расчетов. Предназначено для студентов и аспирантов технических вузов.

 

 

 

 

 

▲ Теория функций комплексного переменного/ В. В. Веретельник, Г.М. Тимченко. Теорія функцій комплексної змінної: навч. посібник. – Х.: НТУ „ХПІ”, 2012. – 208с.

Авторы: В.В. Веретельник, Г.Н. Тимченко

Обучающее пособие содержит теоретический материал по тeopии функций комплексной переменной, приведены основные теоремы и формулы, необходимые для решения задач, а также образцы решения типовых задач. Представлены индивидуальные варианты типовых расчетов. Предназначено для студентов технических университетов.

 

 

 

 

 

▲ Уравнения математической физики. / Курпа Л.В. Рівняння математичної фізики: навч. посіб. / Л.В. Курпа, Г.Б. Лінник. – Харків : Вид-во «Підручник НТУ “ХПІ”», 2011. – 312 с.

Авторы: Курпа Л.В., Линник Г.Б.

В этом пособии изучаются основные разделы математической физики в объеме, рекомендованном для инженерно-технических специальностей высших учебных заведений. При подготовке пособия авторы учитывали большой опыт, который был накоплен в течение 40 лет на кафедре прикладной математики НТУ «ХПИ» при преподавании этого курса для студентов специальности «Динамика и прочность машин. Издание охватывает как теоретический материал, так и практический, что необходимо для лучшего усвоения курса математической физики.

Подано теорию линейных уравнений с частными производными в основном второго порядка. Подробно приведены вывода некоторых уравнений и основные типы уравнений классической математической физики.

Среди методов решения основное внимание уделено методам Фурье, Даламбера и метода функций Грина. Рассматриваются не только точные, но и приближенные методы решения задач математической физики. В частности, освещены один из эффективных современных приближенных методов, основанный на применении вариационных методов и теории R-функций. Этот метод известен в литературе как вариационно-структурный метод или метод R-функций (международная аббревиатура RFM).

  • Скачать книгу можно в цифровом репозитарии НТУ «ХПИ».

 

▲ Уравнения математической физики. / Учебное пособие к аудиторной и самостоятельной работы студентов инженерных специальностей. -Х .: Бизнес Информ, НТУ «ХПИ», 2002. — 288с. — Рус. языке.

Авторы: Бойко Б.Т., Курпа Л.В., Сенчук Ю.Ф.

Учебно-методическое пособие содержит материал теоретического характера по курсу математической физики, хорошо проиллюстрировано большим количеством задач прикладного характера. Особое внимание уделяется применению метода Фурье, физическом толкованию полученных решений, а также вариационным методам математической физики. Первый раздел носит вспомогательный характер. Практическое освоение второго и третьего разделов целесообразно проводить с помощью лабораторного практикума, представленного в учебном пособии Л.В. Курпей, Ж.Б. Кашуба «Уравнения математической физики. Лабораторный практикум «.

Учебное пособие разработано по материалам конспекта лекций, прочитанных Н.И Ахиезером в харьковском политехническом институте, и предназначен для студентов инженерно-физического, физико-технического и др. факультетов, также может быть полезно студентам политехнических университетов, аспирантам и преподавателям.

 

▲ Уравнения математической физики. Лабораторный практикум. / Л. В. Курпа, Ж. Б. Кашуба. Уравнения математической физики. Лабораторный практикум. Харьков, ХГПУ, 2000. 217 с. ISBN 966-593-123-7

Авторы: Л. В. Курпа, Ж. Б. Кашуба

Учебное пособие составлено в виде набора лабораторных работ как по основным разделам традиционного курса математической физики (лабораторные работы No 1-9), так и по вопросам, связанным с применением приближённых (вариационных) методов с использованием теории R-функций для построения координатных последовательностей (лабораторные работы No 10-17). Каждой лабораторной работе предпослан теоретический материал, разобраны типичные задачи и приведены варианты индивидуальных домашних заданий.

Список лабораторных работ:

  1. Решение простейших дифференциальных уравнений с частными производными первого и второго порядка
  2. Дифференциальные уравнения с частными производными второго порядка с двумя независимыми переменными, их классификация и приведение к канонической форме
  3. Метод характеристик для уравнения колебаний струны (метод Даламбера)
  4. Краевая задача Штурма-Лиувилля
  5. Метод Фурье (разделения переменных) для уравнений гиперболического типа на отрезке
  6. Метод Фурье (разделения переменных) для уравнений параболического типа на отрезке
  7. Метод Фурье (разделения переменных) для уравнений эллиптического типа
  8. Метод Фурье (разделения переменных) для уравнений гиперболического и параболического типов в многомерной области
  9. Решение задач математической физики с сосредоточенными параметрами
  10. Построение уравнений границы области
  11. Построение уравнений отрезков
  12. Обобщённая интерполяционная формула Лагранжа
  13. Приближённое интегрирование функций и их производных в областях сложной формы
  14. Обработка результатов наблюдений методом наименьших квадратов
  15. Решение задачи Дирихле для уравнения Пуассона в области сложной формы
  16. Решение смешанной краевой задачи для уравнения Пуассона в области сложной формы
  17. Изгиб и собственные колебания пластин сложной формы в плане

Первая часть лабораторных работ предназначена для аналитического решения. Есть по 30 вариантов каждой работы, подробно разобранные примеры, теория. Для проведения лабораторных работ из второй части требуются компьютеры.

 

▲ Дифференциальное исчисление функций одной переменной. / Kurpa L.V., Shmatko Т.V. Differential calculus for one variable functions: Навчальний посібник для студентів технічних університетів. – Харків: НТУ “ХПІ”, 2008. – 160 с. Англ. мовою.

Авторы: Курпа Л.В., Шматко Т.В.

Курпа Л.В., Шматко Т.В. Диференціальне числення функцій однієї змінної / Kurpa L.V., Shmatko Т.V. Differential calculus for one variable functions: Навчальний посібник для студентів технічних університетів. – Харків: НТУ “ХПІ”, 2008. – 160 с. Англ. мовою.

 

 

 

 

 

 

 

 

▲ Differential and integral calculus for functions with several variables = Диференціальне та інтегральне числення функцій багатьох змінних : навч. посіб. / Л. В. Курпа, Т. В. Шматко. — X. : НТУ “ХПІ”, 2012 — 252 с. — Англ. мовою. ISBN 978-617-05-0030-4

Автори: Курпа Л.В., Шматко Т.В.

Differential and integral calculus for functions with several variables

Рассматривается теоретический материал по следующим разделам: дифференциальное исчисления функций многих переменных, кратные и криволинейные интегралы В пособие также включены задачи, рекомендуется для решения в аудитории вместе с преподавателем, а также домашние задания. Для каждой темы предлагаются варианты контрольных заданий. Предназначено для студентов и преподавателей технических специальностей.

 

 

 

 

▲ Элементы линейной алгебры и аналитической геометрии: учеб. пособие./ Руднєва Г.В. Elements of linear algebra and analytic geometry = Елементи лінійної алгебри та аналітичної геометрії: навч. посібник . – Харків: НТУ «ХПІ», 2008. – 168с. (Англ. мовою).

Автор: Руднева Г.В.

 

Учебное пособие содержит на английском языке теоретический материал по линейной алгебре и аналитической геометрии, доведенные основные теоремы и утверждения и формулы, необходимые для решения практических задач. Применение предоставленного материала продемонстрировано большим количеством примеров и иллюстраций.
Предназначено для студентов технических университетов, изучающих курс высшей математики на английском языке, иностранных студентов и преподавателей высшей математики

 

 

 

 

▲ Приложения векторной алгебры к решению задач геометрии. / Бурлаенко В.Н., Димитрова С.Д. Приложения векторной алгебры к решению задач геометрии. Практикум по высшие математики. Харьков, НТУ «ХПИ», 2005. 50 с.

Авторы: Бурлаенко В.Н., Димитрова С.Д.

В учебном пособии показано использование методов векторной алгебры на примерах решения геометрических задач. Пособие составлено в виде практикума, демонстрирующего технику векторных преобразований. Каждая задача сформулированна и решена в не зависящем от системы координат виде. Некоторые примеры имеют также и координатное представление.

Пособие предназначено для самостоятельной работы студентов инженерных специальностей.

 

 

 

 

▲ Элементы дифференциальной геометрии. (под ред. проф. Михлина Ю.В.) 

Элементы дифференциальной геометрии.(под ред. проф. Михлина Ю.В.) Харьков, НТУ «ХПИ», 2005. 51 с.

В предлагаемом пособии представлена дифференциальная геометрия пространственных кривых и поверхностей. Первый раздел посвящен вектор-функции скалярного аргумента и правилам ее дифференцирования, рассмотрены касательная к кривой, а также кривизна кривой и вычисление кривизны. Во втором разделе вводится естественный базис в каждой точке кривой, а также анализируется изменяемость базиса в виде формул Френе. Третий раздел посвящен дифференциальной геометрии поверхностей. Рассмотрены уравнения касательной плоскости и нормали к поверхности, вводятся первая и вторая дифференциальные формы поверхности, нормальная кривизна в каждой точке поверхности, определяются главные кривизны и главные направления. Введение в теорию огибающих семейств кривых и поверхностей изложено в четвертом разделе.

 

 

▲ Методология интегрального исчисления.

Авторы: Босин М.Е., Дзюбак Л.П.

В основу изложения основных положений интегрального исчисления положены прикладные идеи, что оправдано для физических и инженерных специальностей. С этой целью изначально вводится не интеграл Лебега, а интеграл Римана, причем вводится один определенный интеграл — интеграл по мере, вне зависимости от мерности и кривизны пространства. Подробно классифицированы приложения определенных интегралов в физике, рассмотрены примеры (в том числе и классические) соответствующих задач.

 

 

 

 

 

▲ Теория вероятностей и математическая статистика. (Н.А. Кириллова и др.)

Авторы: Л. С. Тимченко, Н. А. Кириллова, С. Е. Гардер, С. П. Иглин, Ю. И. Зайцев, В. П. Протопопова.

Л. С. Тимченко, Н. А. Кириллова, С. Е. Гардер, С. П. Иглин, Ю. И. Зайцев, В. П. Протопопова. Теория вероятностей и математическая статистика. Учебно-методическое пособие для самостоятельной работы студентов экономических специальностей. Харьков, ХГПУ, 1999. 154 с. ISBN 966-593-112-1

Пособие включает большой объём разнообразных задач, охватывающих банковское и страховое дело, рыночные отношения и маркетинг. Предназначено для студентов /pэкономических специальностей. В пособие включены необходимые теоретические сведения, примеры решения задач, задачи для решения в аудитории, 30 вариантов ИДЗ по каждой теме.

Разделы книги:

  1. Основные понятия теории вероятностей (элементы комбинаторики, случайные события, операции над событиями)
  2. Основные теоремы теории вероятностей (зависимые и независимые события, теоремы сложения и умножения вероятностей, формула полной вероятности, формулы Байеса)
  3. Повторение испытаний (формула Бернулли, наивероятнейшее число появлений события, асимптотические формулы, локальная и интегральная теоремы Лапласа, формула Пуассона)
  4. Случайные величины (понятие случайной величины, дискретные случайные величины и законы их распределения, функция распределения, плотность распределения, числовые характеристики случайных величин
  5. Наиболее распространённые законы распределения случайных величин и их числовые характеристики (биномиальное, геометрическое, гипергеометрическое, пуассоновское, равномерное, показательное, нормальное)
  6. Системы случайных величин (законb распределения системы случайных величин, числовые характеристики, законы равномерного и нормального распределения системы случайных величин)
  7. Функции одного и двух случайных аргументов (функции одного случайного аргумента: законы распределения, числовые характеристики, закон распределения функции двух случайных аргументов и числовые характеристики, теоремы о числовых характеристиках)
  8. Элементы математической статистики (построение статистической совокупности, точечные оценки параметров распределения, интервальные оценки, проверка статистических гипотез, построение теоретической кривой по методу наименьших квадратов)

 

▲ An introduction to probability theory and mathematical statistics. = Введення в теорію ймовірностей та математичну статистику : навч. посіб. / В. М. Бурлаєнко, Г. В. Руднева, С. Д. Дімітрова-Бурлаєнко. — X. : НТУ “ХПІ”, 2013. — 264 с. — Англ. мовою. ISBN 978-617-05-0066-3

Авторы: Бурлаенко B.H., Руднева Г.В., Димитрова С.Д.

Учебное пособие содержит на английском языке теоретический материал по теории вероятностей и математической статистики, доведенные основные теоремы и утверждение и формулы, необходимые для решения практических задач, даны набор типовых задач для индивидуальной работы. Применение материла продемонстрировано большим количеством примеров и иллюстраций.

Предназначено для студентов технических специальностей, изучающих курс «Теория вероятностей и математическая статистика» на английском языке, иностранных студентов и преподавателей высшей математики.

 

 

 

▲ Обыкновенные дифференциальные уравнения и системы дифференциальных уравнений (ред. Волкова Н.Н.)

Авторы: Антипко И. И., Бабакова О.И., Вовк В.М., Волкова Н.Н., Кашуба Ж.Б., Щербинина Т.Е.

Антипко І.І., Бабакова О.І., Вовк В.М., Волкова Н.М., Кашуба Ж.Б., Щербініна Т.Є. Звичайні диференційні рівняння та системи диференційних рівнянь: Навч. методич. посібник до самостійної роботи студентів інженерно-фізичних, хімічних та машинобудівних спеціальностей / За редакцією Волкової Н.М. – Харків, ХДПУ, 2000 – 108с. –Рос. мовою.

Учебно-методическое пособие содержит материал теоретического характера, который необходим для решении задач, подробно разобраны примеры, большое количество задач для самостоятельного решения, набор типовых задач для индивидуальной работы и охватывает все разделы курса «Обычные дифференциальные уравнения и системы дифференциальных уравнений» .

Предназначен для студентов инженерно-физических, химических и машиностроительных специальностей, может быть полезным преподавателям при подготовке методического материала к практическим занятиям.

 

▲ Differential Equations and Series = Диференціальні рівняння та ряди / Л. В. Курпа, О. С. Мазур, Т. В. Шматко : навч. посіб. — Харків : НТУ “ХПІ”, 2013. — 288 с. — Англ. мовою. ISBN 978-617-05-0064-9

Авторы: Л.В. Курпа, О.С. Мазур, Т.В. Шматко

Differential Equations and Series

Навчальний посібник присвячено викладенню теоретичного матеріалу з наступних розділів: диференціальні рівняння; ряди. Посібник містить доведення всіх необхідних теорем, передбачених робочою програмою з математичного аналізу стосовно розглянутих тем, а також задачі, що рекомендовано для розв’язання в аудиторії ра¬зом з викладачем, і домашні завдання. Для кожної теми пропонуються варіанти контрольних завдань. Призначено для викладачів і студентів технічних університетів, які використовують англійську мову для викладання курсу вищої математики.

 

 

 

▲ Линейная алгебра. Теория линейных пространств. / Учеб. пособие для студентов специальности «Прикладная математика». — Харьков: НТУ «ХПИ», 2001. — 200 с. — Рус. языке.

Автор: Сенчук Ю.Ф.

Лінійна алгебра. Теорія лінійних просторів

Изложен курс линейной алгебры по объему, предусмотренным программой для специальности «Прикладная математика» технических вузов. Изучаются теория определителей и матриц с применением к решению и исследования СЛАУ, теория линейных пространств и подпространств, линейные операторы в аффинных и в евклидовых пространствах, Билинейные и квадратичные формы, а также теория выпуклых множеств в пространстве Rn.

В конце каждого раздела приводятся контрольные вопросы по теории, задачи и упражнения.

Пособие может быть использовано студентами и аспирантами всех специальностей, изучающих линейную алгебру.

 

 

▲ Линейная алгебра. Сборник заданий и методика решения. / Н. Н. Склепус, Ю. Ф. Сенчук, И. В. Ушакова, Ж. Б. Кашуба, Е. В. Одинцова. Линейная алгебра. Сборник заданий и методика решения. Харьков, ХГПУ, 2000. 178 с. ISBN 966-593-111-3

Авторы: Н. Н. Склепус, Ю. Ф. Сенчук, И. В. Ушакова, Ж. Б. Кашуба, Е. В. Одинцова

Это учебно-методическое пособие предназначено для студентов специальности «Прикладная математика» и других специальностей с углублённым изучением курса высшей математики. Главы пособия: матрицы и определители, системы линейных алгебраических уравнений, линейные пространства и подпространства, линейные операторы в конечномерных линейных пространствах, эвклидово пространство и ортонормированный базис. ортогональное проектирование, линейные операторы в евклидовом пространстве, квадратичные формы, выпуклые множества.

Структура каждой главы: теоретические сведения, решение примеров, варианты ИДЗ. Это учебное пособие из серии «продвинутых»: оно предназначено не для всех студентов. Но если Вы ведёте достаточно серьёзный курс линейной алгебры, то это книга для Вас.

 

▲ Функции комплексного переменного. (под ред. Ясницкой Н.Н.)

Авторы: Болотина Л.В., Веретельник В. В., Волкова Н.Н., Щербинина Т.Е., Ясницкая Н.Н.

Учебно-методическое пособие содержит материал теоретического характера, необходимый для решения задач, подробно разобранные примеры и набор типовых заданий для индивидуальной работы студентов. Особое внимание уделено наиболее сложным разделам курса «Функции комплексного переменного»: разложению функций в ряд Лорана, классификации особых точек, а также применению теории вычетов для вычисления несобственных интегралов, часто встречающихся при решении задач прикладного характера.

 

 

 

 

▲ Математическое программирование. / / Т. Л. Корниль, Н. О. Кириллова, Л. С. Тимченко. Математическое программирование: Учеб. Пособие  — Харьков: НТУ «ХПИ», 2002. — 135 с.- Рус. язык.

Авторы: Т.Л. Корниль, Н.А. Кириллова, Л.С. Тимченко.

В пособии изложены основные разделы курса математического программирования для студентов экономических специальностей. Есть краткие теоретические сведения, примеры решения задач, 30 вариантов ИДЗ по каждой теме.

Разделы пособия:

  1. Линейное программирование (общая и основная задачи линейного программирования, основные свойства, геометрический смысл, симплекс-метод решения)
  2. Двойственные задачи линейного программирования. Связь между решениями прямой и двойственной задач
  3. Транспортная задача по критерию стоимости перевозок (постановка задачи, построение начального базисного плана перевозок, метод потенциалов)
  4. Элементы матричной игры

 

▲ Вариационное исчисление с применением MATLAB. / С. П. Иглин. Вариационное исчисление с применением MATLAB. ХПИ, Харьков, 2001, 112с.

Автор: С.П. Иглин.

В пособии изложены основные разделы курса вариационного исчисления для студентов инженерно-физических специальностей. Есть краткие теоретические сведения, примеры решения задач, 30 вариантов ИДЗ по каждой теме. Разделы пособия: элементарная задача вариационного исчисления, экстремаль функционала, зависящего от нескольких функций, экстремаль функционала, зависящего от производных высших порядков, экстремаль функционала, зависящего от функции нескольких переменных, естественные граничные условия, условия трансверсальности, отражение экстремалей, преломление экстремалей, односторонние вариации, изопериметрическая задача, метод начальных параметров, метод конечных разностей, метод Ритца.

 

  • Скачать книгу можно в на сайте автора.

 

НАУЧНЫЕ МОНОГРАФИИ И КНИГИ

▲Применение теории R-функций к решению нелинейных задач динамики многослойных пластин. / Курпа Л. В. Применение теории R-функций к решению нелинейных задач динамики многослойных пластин: / Л. В. Курпа, О. С. Мазур, Т. В. Шматко. – Харьков: ООО «В деле», 2016. – 492 с. – На рус. яз.

Авторы: Л. В. Курпа, О. С. Мазур, Т. В. Шматко

Монография посвящена разработке методов решения нелинейных задач динамики многослойных и однослойных пластин сложной геометрической формы, а именно, задач о геометрически нелинейных колебаниях, динамической и статической устойчивости пластин. Предложенные методы базируются на использовании теории R- функций, вариационных и проекционных методах, а также методе Рунге-Кутта. Предложена оригинальная схема линеаризации исходной нелинейной системы дифференциальных уравнений движения. Особое внимание в монографии уделено численному решению задач. Для научных работников, аспирантов и студентов, работающих в области механики деформируемого твердого тела, динамики и прочности машин.

▲ Метод R-функций для решения линейних задач изгиба и колебаний пластин и пологих оболочек. / Курпа Л.В. Метод R-функций для решения линейных задач изгиба и колебаний пластин и пологих оболочек. – Харків: НТУ “ХПІ”, 2009. – 408 с.

Автор: Курпа Л.В.

 

 

 

 

 

 

 

 

 

 

▲ Normal Modes and Localization in Nonlinear Systems. / Vakakis, A. F., Manevitch, L. I., Mikhlin, Y. v., Pilipchuk, V. N., and Zevin A. A.  Wiley, New York, 1996.

Авторы: А.Ф. Вакакис, Л.И. Маневич, Ю.В. Михлин, В.Н. Пилипчук

Этот знаковый том открывает совершенно новый ракурс исследования колебаний в дискретных или непрерывных нелинейных осцилляторах. В нем описывается использование нелинейных нормальных режимов для анализа колебаний нелинейных систем и систем проектирования с ограничениями движения.

Основные черты Normal Modes and Localization in Nonlinear Systems

  • Новые и разработанные математические методы могут быть использованы для более точного дизайна конструкций виброизоляции гибких конструкциях
  • Охватывает свободные и вынужденные колебания в системах со слабой или сильной нелинейностью, включая результаты, которые нельзя получить существующими линейными или квазилинейными методами
  • Новый метод анализа сильно нелинейных систем, который допускает анализ возмущений систем с существенными нелинейностями
  • Теоретическая связь между нелинейными нормальными модами и стоячими уединенными волнами
  • Первые экспериментальные проверки локализации нелинейного режима и нелинейного ограничения движения в гибких инженерных структурах

Смотреть книгу можно на сайте …

 

▲ Нелинейная динамика упругих систем. Том 1:  Модели, методы, явления / К. В. Аврамов, Ю. В. Михлин . – М. : Регулярная и хаотическая динамика ; Ижевск : Ин-т компьют. исслед., 2010 . – 704 с. 

Авторы: К.В. Аврамов, Ю.В. Михлин.

Рассматриваются дискретные и континуальные модели нелинейной динамики механических систем. Представлены подходы и методы решения задач нелинейной динамики, встречающихся в инженерной практике. Большое внимание уделяется нелинейным явлениям, которые не описываются в квазилинейной теории. Рассматриваются аналитические и численные методы исследования периодических, квазипериодических и хаотических колебаний, их устойчивости и бифуркаций. С единых позиций изложены как классические, так и современные асимптотические методы нелинейной динамики. Подробно излагаются идеи и методы теории нелинейных нормальных форм колебаний.

Для специалистов, занимающихся проблемами теории колебаний, механики и прикладной математики, инженеров-исследователей, аспирантов и студентов старших курсов технических и механико-математических специальностей.

  • Читать книгу можно на сайте ….

 

▲ Нелинейная динамика упругих систем. Том 2: Приложения. / Аврамов К.В., Михлин Ю. В. — М. : R&C Dynamics ; Ижевск : Ин-т компьютер. исслед., 2015. — 699 с.

Авторы: К.В. Аврамов, Ю.В. Михлин.

Во втором томе представленные ранее теоретические результаты применяются для исследования нелинейных колебаний разнообразных упругих систем, имеющих приложения в технике. Выбор задач определяется в первую очередь научными интересами авторов книги. Наряду с использованием представленных в первом томе методов для построе­ния и исследования устойчивости режимов движения нелинейных упру­гих систем большое внимание уделяется также качественному анализу тех нелинейных явлений, которые наблюдаются в технических системах.

 

 

  • Читать книгу можно на сайте ….

 

▲  Оптимизация формы элементов конструкций. / С.П Іглін. Оптимізація форми елементів конструкцій.– Харків: НТУ “ХПІ”, 2009. –240 с.

Автор: Іглін С.П.

Рассматриваются задачи оптимизации различных элементов машиностроительных конструкций: стержней, пластин, оболочек, трехмерных тел. Изменяется их геометрия в заданных границах. Используются квазиньютоновский метод оптимизации с линейными и нелинейными ограничениями. 3адача анализа решается с помощью МКЭ. Градиенты целевых функций на нелинейных ограничениях находятся аналитически, без численного дифференцирования. В книгу включены функции MATLAB для вычисления матриц MKE и производных от них. Приведенные примеры.

Предназначено для студентов, аспирантов, преподавателей, научных работников, занимающихся проблемами оптимизации.

 

 

  •  Скачать книгу можно в на сайте автора.

▲ Математические расчеты на базе MATLAB

Автор: Иглин С.П.

Рассматриваются три раздела математики: вариационное исчисление, математическая статистика и теория графов. Основная направленность книги — применение MATLAB и его расширений: Symbolic Math Toolbox, PDE Toolbox, Optimization Toolbox, Statistics Toolbox и разработанного автором Graph Theory Toolbox. Для всех рассмотренных задач приведены программы их решения.

 

 

 

 

 

  •  Скачать книгу можно в на сайте автора.

Математические функции — Visual Basic

  • Статья
  • Чтение занимает 4 мин

Методы System.Math класса предоставляют тригонометрические, логарифмические и другие распространенные математические функции.

В следующей System.Math таблице перечислены методы класса. Их можно использовать в программе Visual Basic:

Метод .NETОписание
AbsВозвращает абсолютное значение числа.
AcosВозвращает угол, косинус которого равен указанному числу.
AsinВозвращает угол, синус которого равен указанному числу.
AtanВозвращает угол, тангенс которого равен указанному числу.
Atan2Возвращает угол, тангенс которого равен отношению двух указанных чисел.
BigMulВозвращает полный продукт двух 32-разрядных чисел.
CeilingВозвращает наименьшее целочисленное значение, большее или равное указанному или Doubleравному значениюDecimal.
CosВозвращает косинус указанного угла.
CoshВозвращает гиперболический косинус указанного угла.
DivRemВозвращает 32-разрядные или 64-разрядные целые числа со знаком, а также возвращает оставшуюся часть в выходном параметре.
ExpВозвращает e (основание естественных логарифмов), поднятых до указанной мощности.
FloorВозвращает наибольшее целое число, которое меньше или равно указанному Decimal или Double числу.
IEEERemainderВозвращает оставшуюся часть, полученную из деления указанного числа на другое указанное число.
LogВозвращает естественный (базовый e) логарифм указанного числа или логарифм указанного числа в указанной базе.
Log10Возвращает логарифм с основанием 10 указанного числа.
MaxВозвращает большее из двух чисел.
MinВозвращает меньшее из двух чисел.
PowВозвращает указанное число, возведенное в указанную степень.
RoundDecimal Возвращает или Double округляет значение, округленное до ближайшего целого значения или до указанного числа дробных цифр.
SignВозвращает значение, Integer указывающее знак числа.
SinВозвращает синус указанного угла.
SinhВозвращает гиперболический синус указанного угла.
SqrtВозвращает квадратный корень из указанного числа.
TanВозвращает тангенс указанного угла.
TanhВозвращает гиперболический тангенс указанного угла.
TruncateВычисляет неотъемлемую часть указанного Decimal или Double числа.

В следующей таблице перечислены методы System.Math класса, которые не существуют в платформа .NET Framework, но добавляются в .NET Standard или .NET Core:

Метод .NETОписаниеДоступно в
AcoshВозвращает угол, гиперболический косинус которого равен указанному числу.Начиная с .NET Core 2.1 и .NET Standard 2.1
AsinhВозвращает угол, гиперболический синус которого равен указанному числу.Начиная с .NET Core 2.1 и .NET Standard 2.1
AtanhВозвращает угол, гиперболический тангенс которого равен указанному числу.Начиная с .NET Core 2.1 и .NET Standard 2.1
BitDecrementВозвращает ближайшее самое маленькое значение, которое меньше, чем x.Начиная с .NET Core 3.0
BitIncrementВозвращает ближайшее самое большое значение, превышающее x.Начиная с .NET Core 3.0
CbrtВозвращает кубический корень из указанного числа.Начиная с .NET Core 2.1 и .NET Standard 2.1
ClampВозвращает value, ограниченное диапазоном от min до max включительно.Начиная с .NET Core 2.0 и .NET Standard 2.1
CopySignВозвращает значение с величиной x и знаком y.Начиная с .NET Core 3.0
FusedMultiplyAddВозвращает значение (x * y) + z, округленное в рамках одной тернарной операции.Начиная с .NET Core 3.0
ILogBВозвращает целочисленный логарифм с основанием 2 указанного числа. n, вычисленное эффективно.Начиная с .NET Core 3.0

Чтобы использовать эти функции без квалификации, импортируйте System.Math пространство имен в проект, добавив следующий код в начало исходного файла:

Imports System.Math

Пример — Abs

В этом примере метод класса используется AbsMath для вычисления абсолютного значения числа.

Dim x As Double = Math.Abs(50.3)
Dim y As Double = Math.Abs(-50.3)
Console.WriteLine(x)
Console.WriteLine(y)
' This example produces the following output:
' 50.3
' 50.3

Пример — Atan

В этом примере метод класса используется AtanMath для вычисления значения pi.

Public Function GetPi() As Double
    ' Calculate the value of pi.
    Return 4.0 * Math.Atan(1.0)
End Function

Примечание

Класс System.Math содержит Math.PI поле константы. Его можно использовать, а не вычислять.

Пример: Cos

В этом примере метод класса используется CosMath для возврата косиуса угла.

Public Function Sec(angle As Double) As Double
    ' Calculate the secant of angle, in radians.
    Return 1.0 / Math.Cos(angle)
End Function

Пример— Exp

В этом примере используется Exp метод Math класса для возврата e, возвращаемого в силу.

Public Function Sinh(angle As Double) As Double
    ' Calculate hyperbolic sine of an angle, in radians.
    Return (Math.Exp(angle) - Math.Exp(-angle)) / 2.0
End Function

Пример. Журнал

В этом примере метод класса используется LogMath для возврата естественного логарифма числа.

Public Function Asinh(value As Double) As Double
    ' Calculate inverse hyperbolic sine, in radians.
    Return Math.Log(value + Math.Sqrt(value * value + 1.0))
End Function

Пример — округление

В этом примере метод Math класса используется Round для округления числа до ближайшего целого числа.

Dim myVar2 As Double = Math.Round(2.8)
Console.WriteLine(myVar2)
' The code produces the following output:
' 3

В этом примере метод класса используется SignMath для определения знака числа.

Dim mySign1 As Integer = Math.Sign(12)
Dim mySign2 As Integer = Math.Sign(-2.4)
Dim mySign3 As Integer = Math.Sign(0)
Console.WriteLine(mySign1)
Console.WriteLine(mySign2)
Console.WriteLine(mySign3)
' The code produces the following output:
' 1
' -1
' 0

Пример. Sin

В этом примере метод класса используется SinMath для возврата синуса угла.

Public Function Csc(angle As Double) As Double
    ' Calculate cosecant of an angle, in radians.
    Return 1.0 / Math.Sin(angle)
End Function

Пример— Sqrt

В этом примере используется Sqrt метод Math класса для вычисления квадратного корня числа.

Dim mySqrt1 As Double = Math.Sqrt(4)
Dim mySqrt2 As Double = Math.Sqrt(23)
Dim mySqrt3 As Double = Math.Sqrt(0)
Dim mySqrt4 As Double = Math.Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN

Пример — Tan

В этом примере метод класса используется TanMath для возврата тангенсов угла.

Public Function Ctan(angle As Double) As Double
    ' Calculate cotangent of an angle, in radians.
    Return 1.0 / Math.Tan(angle)
End Function

См. также раздел

  • Rnd
  • Randomize
  • NaN
  • Производные математические функции
  • Арифметические операторы

Как подать заявку | Департамент математики

Последнее обновление: 23 июня 2022 г. для поступления осенью 2023 года.

Важно внимательно прочитать все указания, прежде чем приступить к подаче заявления в аспирантуру. Поскольку все курсы для выпускников начального уровня рассчитаны на год и начинаются осенью, заявки на поступление обычно принимаются только на осенний квартал. Веб-сайт приложений открывается примерно в начале сентября для приема следующей осенью. В дополнение к требованиям, приведенным ниже, см. также страницы о требованиях к поступающим и иностранных абитуриентах.

Крайний срок:   Все материалы заявки должны быть получены в электронном виде до  пятницы, 9 декабря 2022 г.  , чтобы их можно было принять на следующий осенний квартал.

 

Портал онлайн-заявок UW открыт с сентября 2022 года для приема осенью 2023 года. При заполнении онлайн-заявки всем заявителям будет предложено предоставить следующее:

Неофициальные стенограммы: Посещены учебные заведения бакалавриата и магистратуры, включая неофициальные стенограммы из соответствующих учебных заведений. Допущенные кандидаты должны будут предоставить официальные стенограммы.

Курсы продвинутой математики: Загрузите документ в формате PDF, содержащий подробный список всех курсов математики, выходящих за рамки элементарного исчисления, дифференциальных уравнений и линейной алгебры, которые вы изучали или будете изучать до того, как начнете выпускную работу в Вашингтонском университете. . Для каждого пройденного курса укажите следующую информацию:
— Номер и название курса
— Полученная оценка (если вы в процессе, укажите это вместо оценки)
— Школа
— Преподаватель
— Даты
— Название и автор использованного(ых) учебника(ов)
— Пройденный материал (примерно столько информации, сколько можно было бы найти в каталоге колледжа. )

Анкета о математических знаниях: В этой анкете спрашивается, были ли и на каких курсах вы познакомитесь со следующими математическими темами:

  1. Конечные абелевы группы
  2. Классы смежности и факторгруппы
  3. Уникальные домены факторизации
  4. Теория Галуа
  5. Равномерная сходимость
  6. Метрические ячейки
  7. Компактные наборы, связанные наборы
  8. Теоретическое развитие дифференцирования и интегрирования по Риману
  9. Теоремы об обратной и неявной функциях
  10. Интеграция Лебега

Резюме или биографическая справка : Загрузите 1-2-страничный PDF-документ на веб-сайт приложения. Должны быть включены следующие компоненты: история трудоустройства (включая стажировки, неполный рабочий день, научные стажировки и опыт преподавания), специальные математические программы, в которых вы участвовали (например, исследовательский опыт для студентов или будапештские семестры по математике), награды и награды, публикации, специальные навыки и нынешнее положение или деятельность.

Личное заявление: На веб-сайте приложения вам будет предложено загрузить личное заявление в виде документа PDF. Рекомендуемая длина составляет примерно 1000 слов. Вот некоторые из тем, которые вы могли бы затронуть (не предполагается, что вы охватите все эти темы):

  • Опишите недавний математический опыт, который повлиял на ваше решение подать заявление в аспирантуру по математике.
  • Какой академический или научный опыт был для вас самым сложным и как вы с ним справились?
  • Опишите любой опыт в вашей личной истории, который повлиял на ваше интеллектуальное развитие, интересы, карьерные планы и цели, например, семья, образование, культурное происхождение, экономическое положение, предыдущий опыт работы.
  • Вы инициировали или участвовали в мероприятиях, направленных на расширение участия недопредставленных групп населения в математических науках?
  • Есть ли что-нибудь еще, что вы хотели бы, чтобы мы знали о вас, что мы должны рассмотреть как часть вашего заявления?

Наконец, ваше личное заявление должно отвечать на вопрос: Почему вы хотите получить ученую степень по математике, в частности, в Вашингтонском университете?

Баллы GRE:   Предметный тест GRE по математике настоятельно рекомендуется, но не является обязательным.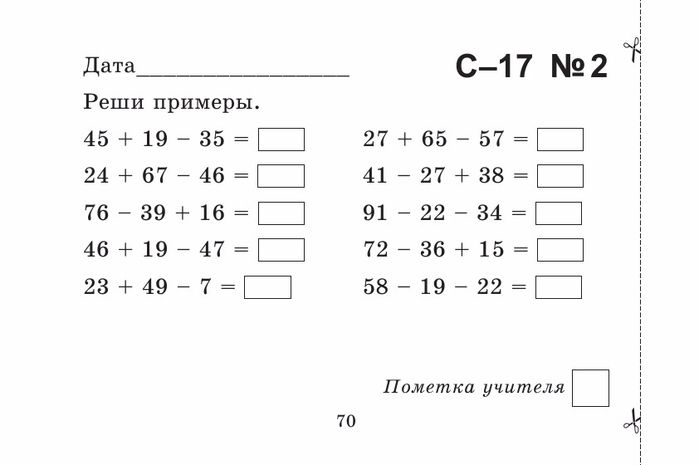 Помимо предоставления нам полезной информации, мы считаем, что подготовка к предметному тесту GRE полезна для ознакомления с материалом бакалавриата, который вам потребуется знать в качестве ассистента по нашей программе. На веб-сайте GRE Math Subject Test доступны бесплатные материалы для подготовки к экзамену.

Чтобы подать свои баллы GRE, вам нужно будет организовать отправку ETS официальных результатов в электронном виде непосредственно в UW с использованием кода учебного заведения 4854. (Код факультета не требуется.) Чтобы уложиться в срок подачи заявок, вам необходимо сдать анализы до 1 декабря . После подачи заявки официальные результаты должны появиться в течение 48 часов.

Рекомендательные письма: Вам будет предложено ввести имена и контактную информацию (организация, электронная почта, телефон) как минимум для трех рекомендательных писем, а затем активировать запросы на рекомендательные письма. Пожалуйста, попросите своих рекомендателей заблаговременно, чтобы они могли отправить свои письма до 9 часов.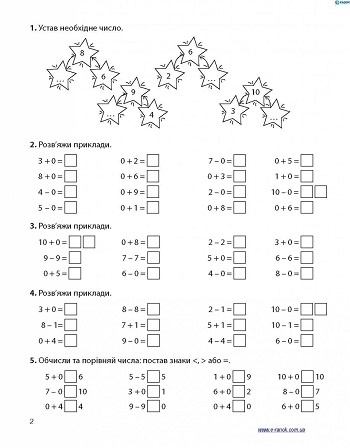 0007 9 декабря .

Плата за подачу заявления:   Приемная комиссия Высшей школы Вашингтонского университета взимает невозмещаемый сбор за рассмотрение заявления в размере 85 долларов США. Плата оплачивается онлайн с помощью Mastercard или Visa для того, чтобы ваша заявка была заполнена. См. страницу приложения Высшей школы для получения более подробной информации.

Освобождение от платы за поступление:   В некоторых случаях Вашингтонский университет предлагает освобождение от платы за поступление в аспирантуру. Ниже приведен список программ освобождения от платы, о которых нам известно в настоящее время. Все запросы на отмену должны быть поданы не менее чем за 7 дней до крайнего срока подачи заявок 9 декабря. их онлайн-приложение. Международные заявители не имеют права на освобождение от платы на основе потребностей. Более подробная информация доступна на странице инструкций Высшей школы по освобождению от платы.

  • Программы, признанные UW: Высшая школа Вашингтонского университета предлагает освобождение от платы для стипендиатов McNair Scholars и PPIA Fellows, которые представили документацию. Подробнее см. на странице инструкций по освобождению от платы.
  • Математический факультет UW, признанные программы: Математический факультет предлагает освобождение от платы для ученых-докторантов Math Alliance и участников MSRI-UP. Чтобы запросить отказ, связанный с программой математического факультета, отправьте электронное письмо на адрес [email protected] с документацией о вашем участии в конкретной программе.
  • Обязательство по разнообразию: Мы понимаем, что могут быть обстоятельства, при которых учащиеся не принадлежат ни к одной из вышеперечисленных категорий, но все же нуждаются в поддержке и поощрении. В таких случаях мы можем предложить ограниченное количество льгот для исключительных кандидатов. Пожалуйста, отправьте копию своего резюме и стенограммы на [email protected]. В электронном письме объясните, почему вы просите об отказе, сообщите нам свое гражданство и опишите любые аспекты вашей личности или опыта, которые недостаточно представлены в математике.

    • НЕ ЗАПРАШИВАЙТЕ ОТКАЗ, ПОКА НЕ БУДЕТЕ ГОТОВЫ ПОДАТЬ ЗАЯВЛЕНИЕ. Если отказ будет предоставлен и применен, вы больше не сможете вносить изменения в свое заявление.

    Иностранные заявители, не являющиеся носителями английского языка, также должны предоставить подтверждение владения английским языком для получения финансовой поддержки. Подробную информацию о требованиях к владению английским языком для поступления в аспирантуру и назначений на получение технической помощи см. в разделе «Иностранные заявители».

    Баллы TOEFL: Если вы должны предоставить баллы TOEFL в качестве иностранного абитуриента, попросите ETS отправить ваши официальные баллы в Вашингтонский университет в электронном виде, используя код учебного заведения 4854. (Код факультета не требуется). Чтобы получить баллы до крайнего срока подачи заявок 9 декабря, необходимо пройти тесты не позднее 1 декабря.

    Приглашенные студенты: Математический факультет принимает заявки на получение статуса приглашенного аспиранта, но процедура подачи заявок несколько отличается; см. соответствующую страницу для получения дополнительной информации.

    Если у вас есть дополнительные вопросы о подаче заявки на участие в нашей программе, свяжитесь с нами по адресу [email protected]. Спасибо за интерес к нашим программам.

    Подайте заявку сейчас, перейдя на приемный портал: Портал онлайн-приложений, создайте учетную запись для себя и следуйте инструкциям в приложении. Мы не принимаем бумажные заявления или рекомендательные письма.

     

    Как подать заявку | Кафедра математики

    Примечание:
    • Крайний срок подачи заявок на осень 2023 года – 1 декабря 2022 года.
    •  (общие и расширенные) тесты GRE больше не принимаются. Пожалуйста, не отправляйте эти баллы.

    Чтобы подать заявку, вам необходимо заполнить онлайн-форму заявки.

    Помимо ответов на все вопросы формы, вы также должны использовать форму для подачи следующих документов. Приемная комиссия не будет официально рассматривать ваше заявление до тех пор, пока не будут получены все материалы, перечисленные ниже.

    • Оригиналы стенограмм и официальные переводы из всех учебных заведений, в которых учились студенты и выпускники
    • Балл GRE по предмету «Математика» — не требуется и не должен быть представлен.
    • Общий балл GRE не требуется и не должен предоставляться.
    • Не менее трех рекомендательных писем
    • Баллы TOEFL или IELTS, если необходимо (см. ниже)
    • Невозмещаемый регистрационный сбор в размере 90 долларов США

    Крайний срок подачи заполненных и поданных заявок 1 декабря  для поступления на программу PhD, которая начнется в следующем осеннем квартале. Обратите внимание, что мы не разрешаем студентам начинать занятия в середине учебного года.

    Приемная комиссия обычно заканчивает принимать решения к 31 марта. Как только решение по вашему заявлению будет принято, вы будете уведомлены либо по электронной почте, либо по почте первого класса, либо авиапочтой (для иностранных абитуриентов).

    Ниже приведены некоторые более конкретные комментарии по каждому из необходимых документов.

    Стенограммы

    Кандидаты, которые посещали международные учебные заведения, чьи стенограммы не на английском языке, должны загрузить эти стенограммы или заверенные свидетельства об обучении с заверенными переводами на английский язык. Как оригинал стенограммы, так и заверенные переводы должны быть загружены в ваше онлайн-приложение.

    Если вы приняты и принимаете наше предложение, мы потребуем, чтобы вы прислали в наш офис официальную выписку из регистратуры всех школ, которые вы посещали. Ожидается, что кандидаты на программы магистратуры Чикагского университета будут зачислены или получили степень бакалавра или эквивалентную степень в аккредитованном колледже или университете. Перед началом осенних занятий потребуются официальные стенограммы, подтверждающие получение вами степени бакалавра и дату присвоения. Мы оставляем за собой право отозвать предложение о приеме, если есть какие-либо необъяснимые расхождения.

    Заявление о цели

    Это возможность для вас объяснить причины вашего желания продолжить обучение в аспирантуре по математике. Вы можете обсудить любые относящиеся к делу факты о вашем образовании или опыте работы с математикой, которые не отражены в других материалах, которые вы отправляете, вид математики, который вы находите интересным или хотите изучать в аспирантуре, и что вы планируете делать после получения диплома. Кандидат наук.

    Рекомендательные письма

    Рекомендательные письма принимаются через нашу онлайн-систему подачи заявок. Они должны быть написаны людьми, которые хорошо знают вашу работу и могут оценить ваш потенциал для достижения успеха в аспирантуре. Предпочтение отдается рекомендателям, которые могут предложить подробную и откровенную оценку вашей квалификации и мотивации для обучения в аспирантуре.

    GRE/Mathematics Subject Test не требуется и не должен быть отправлен.

    TOEFL или IELTS

    Кандидаты, которые не соответствуют приведенным здесь критериям отказа, должны предоставить подтверждение владения английским языком. Только тесты TOEFL iBT или IELTS Academic принимаются в качестве подтверждения квалификации. Для факультета математики требуется минимальный общий балл TOEFL 90 и минимальный общий балл IELTS 7.0.

    Для TOEFL код нашего учебного заведения — 1832, а код факультета — 72.

    Посетите веб-сайт UChicagoGRAD, чтобы узнать больше о подтверждении владения английским языком.

    Плата за подачу заявления

    Плата за подачу заявления составляет 90 долларов США. Чикагский университет не возвращает и не откладывает оплату за подачу заявления. Если вы считаете, что имеете право на освобождение от платы за подачу заявления, найдите ссылку для отказа от подачи заявления в Интернете и следуйте инструкциям. Если вы подаете заявку на освобождение от платы за подачу заявки, не подавайте заявку онлайн. Если вам будет отказано в отказе, вам необходимо будет оплатить пошлину онлайн. Отказы не могут быть предоставлены иностранным заявителям. Заявки не будут рассматриваться без соответствующей платы.

    Финансовая помощь

    Всем студентам, которым предлагается зачисление, также будет предложена полная финансовая помощь, которая включает полную стипендию на обучение и стипендию на проживание. В течение первого года нет преподавательских обязанностей. Финансовая помощь гарантируется принятым студентам на срок до пяти лет при условии удовлетворительной успеваемости и удовлетворительной работы в качестве учителя. Помимо формы финансовых данных, прилагаемой к онлайн-заявке, не требуется никакой специальной формы финансовой помощи или заявки GAPFAS.

    Вопросы? Электронная почта по адресу: math.uchicago.edu.

    Кроме того, кафедра предлагает отдельную степень магистра наук в области финансовой математики. Пожалуйста, свяжитесь с Мередит Мьюир, [email protected] для получения дополнительной информации, 773-702-1902.

    Как подать заявку – математика

    Прежде чем подать заявку, ознакомьтесь с полным описанием нашей программы для выпускников и на веб-сайте Высшей школы Украины. Важно проверить наши области исследований, чтобы увидеть, соответствуют ли они вашим интересам. Нет необходимости связываться с кем-либо из преподавателей, но будет полезно, если у вас есть одобрение некоторых преподавателей. Математический факультет принимает заявления от граждан США, постоянных жителей и иностранных абитуриентов.

    Крайние сроки

    Прием в магистратуру и докторантуру. программы обычно проводятся в осеннем семестре, но мы допускаем студентов к началу занятий весной. Мы не принимаем студентов летом.  Чтобы максимизировать ваши шансы на поступление, вам следует организовать доставку всех материалов заявки в аспирантуру в указанные ниже сроки.

    • Начало осеннего семестра: 15 января
    • Начало весеннего семестра: 19 октября.0037

    Поздние заявки принимаются и будут рассмотрены в зависимости от наличия вакансий.

    Финансовая поддержка

    Все кандидаты автоматически рассматриваются для получения финансовой поддержки. Нет никакого дополнительного процесса подачи заявки. Посетите веб-страницу финансовой поддержки, чтобы получить дополнительную информацию.

    Подача

    Заявки на факультет подаются онлайн через страницу приложений Высшей школы. Заявка должна включать компоненты, перечисленные ниже, поданные в электронном виде. Не отправляйте бумажные копии документов на факультет математики или в аспирантуру. Приведенная ниже информация дает общий обзор политик, но полное описание можно найти на странице критериев приема в каталоге UA.

    Компоненты заявок

    Плата за подачу заявления

    Чтобы подать заявку на UA, аспирантура взимает с соискателей фиксированную сумму. При определенных обстоятельствах вы можете претендовать на освобождение от платы. Посетите страницу подачи заявок в аспирантуру для получения дополнительной информации о программах освобождения от платы за обучение в университете. Мы понимаем, что плата за подачу заявления может быть бременем для многих студентов. Неделя с 17 октября 2022 г. является неделей бесплатной подачи заявок. Воспользуйтесь этой возможностью.

    Резюме или биографические данные

    Кандидаты должны приложить резюме или биографические данные с указанием своего образовательного опыта, любой научной деятельности и опыта работы в данной области.

    Стенограммы и требования к среднему баллу

    Кандидаты должны иметь степень бакалавра, полученную в аккредитованном на региональном уровне колледже или университете в области математики или тесно связанной области. Для поступления на программу PhD степень магистра не требуется. Высшая школа требует, чтобы соискатели имели средний балл бакалавриата 3,0 в целом, 3,0 за последние 60 семестровых часов программы на получение степени или 3,0 за завершенную программу магистратуры (см Каталог выпускников UA).

    В процессе подачи заявки загрузите копии стенограмм (при необходимости с переводом на английский язык) на портал подачи заявок. Неофициальные стенограммы подходят для подачи заявки. После поступления иностранные заявители должны предоставить одну заверенную копию на родном языке вместе с заверенными переводами на английский язык всех стенограмм, дипломов и свидетельств об образовании. Копии транскрипта и диплома, представляемые после поступления, должны быть заверены выдавшим учреждением. Нотариальные копии НЕ принимаются. (со страницы приема в аспирантуру)

    Заявление о целях

    Кандидаты должны предоставить письменное заявление с описанием своих академических и карьерных целей, а также своих особых интересов в области математики. Заявление не должно занимать более двух страниц.

    Рекомендательные письма

    Требуются три рекомендательных письма. Они должны быть написаны людьми, которые знают академическую успеваемость заявителя и его потенциал для обучения в аспирантуре. Наиболее важные из них будут от профессоров математики или смежных областей, которые обучали соискателя или руководили исследованиями. Заявитель предоставляет адреса электронной почты для авторов писем в онлайн-системе подачи заявок. Эти письма должны быть отправлены онлайн авторами писем.

    Результаты общего экзамена GRE

    Результаты общего экзамена GRE не являются обязательными. Мы призываем абитуриентов предоставлять баллы GRE, особенно если они считают, что это сделает их заявки сильнее и повысит их шансы на поступление. Тем не менее, заявки с баллами GRE и без них будут рассмотрены в полном объеме.

    Результаты предметного экзамена GRE не требуются.

    Уровень владения английским языком

    По данным Высшей школы, лица, не являющиеся носителями языка, должны представить результаты TOEFL, IELTS, Duolingo или PTE, если они не соответствуют хотя бы одному из следующих критериев:

    1. на момент первоначальной регистрации они будут иметь степень, полученную в учреждении США или учреждении в одной из англоязычных стран или регионов, перечисленных ниже;
    2. на момент первоначальной регистрации, они должны быть зачислены на курсовые работы в течение как минимум двух лет в учреждении США или учреждении в одной из англоязычных стран или регионов, перечисленных ниже;
    3. они являются гражданами или законными резидентами одной из англоязычных стран или регионов, перечисленных ниже.

    Англоязычные страны или регионы:

    Американское Самоа, Ангилья, Антигуа, Австралия, Багамы, Барбадос, Бермудские острова, Белиз, Ботсвана, Британские Виргинские острова, Канада (кроме Квебека), Каймановы острова, Острова Рождества, Кука , Доминика, Фолклендские острова, Федеративные Штаты Микронезии, Фиджи, Гибралтар, Гамбия, Гайана, Гана, Гренада, Гуам, Гонконг, Ирландия, Ямайка, Кения, Кирибати, Лесото, Либерия, Малави, Мальта, Маршалловы острова, Маврикий, Монтсеррат, Намибия, Науру, Новая Зеландия, Нигерия, Ниуэ, остров Норфолк, Северные Марианские острова, Палау, Папуа-Новая Гвинея, острова Питкэрн, остров Святой Елены, Сент-Китс и Невис, Сент-Люсия, Сент-Винсент и Гренадины, Самоа, Сандвичевы острова , Сьерра-Леоне, Сингапур, Соломоновы острова, Южная Африка (англоязычные, то есть не африкаанс), острова Южная Георгия, Свазиленд, Танзания, Тонга, Тринидад и Тобаго, острова Теркс и Кайкос, Тувалу, Уганда, Соединенные Штаты, Соединенное Королевство, Виргинские острова США ндс (св.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *