График параметрически заданной функции онлайн: IIS 7.0 Detailed Error — 404.11

6. Построение графика функции, заданной параметрически

Пусть имеем две функции и , где — общей для и области определения. Вычисляя при и считаем, что полученное значение есть функция от полученного . Тем самым получаем функцию . Такое приведение, параметрически заданной, функции к явной не всегда возможно и может быть потеряна часть информации. Параметрически заданную функцию удобно тракторвать как уравнение движения точки на плоскости. В момент времени мы знаем координаты точки . Множество всех точек , где , называетя графиком функции или траекторией движения точки. При построении графика получаем направление движения точки.

Основной метод построения графика функции, заданной параметрически, состоит в том, чтобы разбить весь график на монотонные и непрерывные куски (ветви). Монотонную и непрерывную ветвь можно строить по точкам, используя при этом исследование функции на концах промежутка, если на концах хотя бы одна из функций или разрывна.

6.1. Порядок построения графика параметрически заданной функции

• Найти — область определения по общую для и и отметить её на числовой оси , там же отметить точки разрыва функций.

• Найти производные и и их область определения и отметить её на той же числовой оси , также отметить точки разрыва производных.

• Решить уравнения , и нули производных отметить на той же оси.

Тем самым ось будет разбита на промежутки, на каждом из которых , и вместе с ними будут монотонны и непрерывны.

Результат исследования на монотонность функций и оформляют в виде таблицы (см. ниже в решении примера). По таблице строится черновик графика, который позже уточняется нахождением асимптот, участков выпуклости определённого знака и точек перегиба.

6. 2. Асимптоты параметрического графика

• Если при некотором или и , то — горизонтальная асимптота. Пределы слева и справа вычисляются отдельно, т.

к. это могут быть две разные асимптоты. Эти пределы уже бывают вычислены при заполнении таблицы.

• Если , или , то -вертикальная асимптота.

• Если или и или , то возможно, у этой ветви есть наклонная асимптота , где

Если существует, то ищем :

Если — существует, то у соответствующей ветви будет наклонная асимптота .

6. 3. Точки перегиба

Для нахождения участков выпуклости и точек перегиба нужна производная , которая находится по формуле

Исследуем знак , определяем направдение выпуклости, находим точки перегиба, если есть, и корректируем черновик графика.

6.4. Пример построения графика параметрически заданной функции

Пример 18. 21 Построить эскиз графика , .

Решение. Совокупная область определения: .

Найдем , :

Получаем, что не существует при , при , не существует при и в нуль не обращается.

На ось наносим точки , , (см. рис. 40):

Рис. 40. Ось .

Мы получили четыре интервала. На каждом интервале функции , , а вместе с ними и будут непрерывны и монотонны. Осталось найти промежутки изменения функций и . Другими словами, откуда и куда движется точка по плоскости. Результат такого иследования оформляем в виде таблицы. Основных трок в таблице четыре, а столбцов только, сколько отмечено интервалов на оси .

Таблица 14.

Знак
	Убывает	Убывает	Возрастает	Возрастает
	от до	от до	от до	от до
Знак
	Возрастает	Возрастает	Возрастает	Убывает
	от до	от до	от до	от до

Для заполнения первой клетки изменения функции вычисляем

Для первой клетки функции вычисляем

Аналогично заполняются остальные клетки.

В точках непрерывности вычисляем просто значение функции.

Для построения графика читаем таблицу по столбцам. Получаем, что переменная точка движется от точки неограниченно влнво ( — убывает) и одновременно поднимается от до .

В данном случае при имеем горизонтальную асимптоту . Получим монотонную ветвь по которой точка движется влево (см. рис. 41). Правый конец ветви на рис. 41 соответствует , левый — .

Рис. 41. Ветвь графика функции , при .

Остальные три ветви строим аналогично как движение точки в нужном направлении.

Для уточнения графика на ветви найдем хотя бы одну точку. Выберем получим округлённо . На ветви возьмем получим .

Исследуем направление выпуклости. Находим

Наносим на ось точки разрыва функций , и нули . Находим и проставляем знаки . (см. рис.

42).

Рис. 42. Ось и знаки .

При получаем точку перегиба .

При кривая будет выпукла вверх, при — выпукла вниз, при — выпукла вверх, при — выпукла вниз, при — выпукла вниз.

При имеем , , поэтому у ветви может быть наклонная асимптота. Проверим это:

Это значит, что асимптоты не существует. У ветви при проверка показывает отсутствие аимптоты. При — горизонтальная асимптота . Заметим также, что при любых , поэтому график функции находится выше оси .

График функции , изображен на рис. 43.

Рис. 43. График функции , .

Сообщество Экспонента

• вопрос
• 22.09.2022

Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

8 Ответов

• вопрос
• 20.09.2022

Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

1 Ответ

• MATLAB

20.09.2022

• Публикация
• 15.09.2022

Системы управления, Другое

Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

• Публикация
• 10.09.2022

Системы управления, Электропривод и силовая электроника, Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.

• Публикация
• 24.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &. ..

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

• вопрос
• 23.08.2022

Математика и статистика, Радиолокация, Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

• ЦОС
• цифровая обработка сигналов

23.08.2022

• Публикация
• 23.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &…

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

• Публикация
• 16.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                      

Здесь собрана литература по методам множественного доступа с пространственным разделением.

• вопрос
• 22.07.2022

Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1. txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

2 Ответа

• чтение

22.07.2022

• вопрос
• 17.07.2022

Математика и статистика, Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

• MATLAB
• Signal Processing

17.07.2022

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.

Определение 1

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.

Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):

S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt

Определение 2

Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.

Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Пример 1

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:

Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z

При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах).  Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2

Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.

Ответ: S(G)=6π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:

φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z

Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.

Разберем еще одну задачу.

Пример 2

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.

Теперь разберем подробно, как построить такую кривую.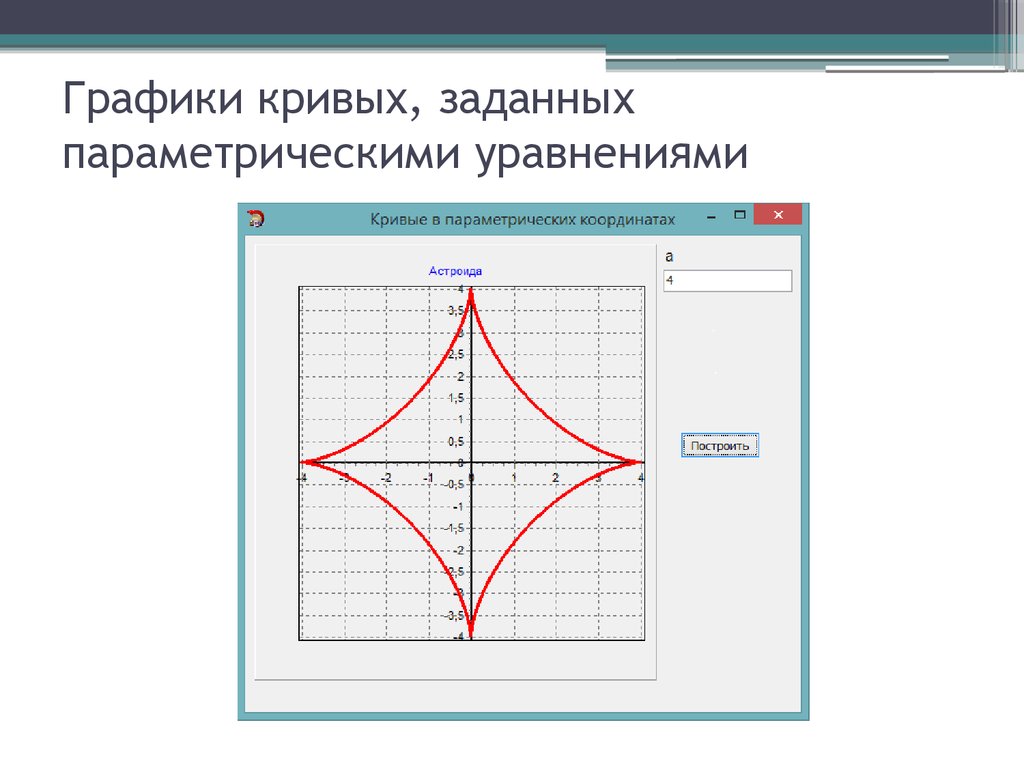 Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.

Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).

Составим таблицу итоговых значений:

t0	0	π8	π4	3π8	π2	5π8	3π4	7π8	π
x0=φ(t0)	3	2.36	1.06	0.16	0	-0.16	-1.06	-2.36	-3
y0=ψ(t0)	0	0.11	0.70	1. 57	2	1.57	0.70	0.11	0

 

t0	9π8	5π4	11π8	3π2	13π8	7π4	15π8	2π
x0=φ(t0)	-2.36	-1.06	-0.16	0	0.16	1.06	2.36	3
y0=ψ(t0)	-0.11	-0.70	-1.57	-2	-1.57	-0.70	-0.11	0

После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:

φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z

Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.

∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96

Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.

Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Как использовать калькулятор параметрических уравнений 3D

Калькулятор параметрических уравнений 3D, также называемый графопостроителем, представляет собой онлайн-инструмент, который позволяет отображать параметрические уравнения в режиме онлайн и создавать анимированные трехмерные графики параметрических функций. Вот как использовать его для визуализации параметрических кривых и поверхностей, которые вы хотите видеть. Первым шагом к использованию этого инструмента является определение того, хотите ли вы генерировать параметрические уравнения или параметрические поверхности; каждый генерирует свой собственный вид графа.

Введение

Допустим, у вас есть переменные x, y и z и функция от x и y, например f(x,y) = 2xy. Что делать, если вы хотите построить f(x,y) для разных значений y? Для этого лучше всего преобразовать ваши уравнения в параметрическую форму. В параметрической форме (также называемой t-переменными или t-координатами) и x, и y заменяются на t. (В стандартных координатах только одна переменная заменяется на t. Другая является независимой переменной.) Третье измерение (z) можно полностью исключить из уравнения, иначе уравнение необходимо будет переписать как ƒ (t, т). В этом примере:

Калькулятор параметрических уравнений 3d Учебное пособие по построению кривых – Узнайте, как использовать калькулятор параметрических уравнений 3d для построения кривых в деталях. Он имеет множество вариантов рисования, таких как линейная кривая, ступенчатая кривая, сплайновая кривая и т.д. еще одна переменная. Две наиболее распространенные формы параметрических уравнений: ƒ (t) = (x (t), y (t)) и x = f (t). Обе формы приводят к бесконечным семействам кривых. Например, возьмем ƒ(t) = (x, y) и пусть t находится в диапазоне от 0 до 10. Получившаяся кривая представляет собой эллипс, ширина которого увеличивается с увеличением t. Кривая также вращается против часовой стрелки вокруг начала координат с каждым значением t. (См. изображение ниже.) ## ## Графики + Формулы параметрического уравнения ## Возьмем функцию ƒ(t) = (x, y), где t находится в диапазоне от 0 до 10. Результирующая кривая представляет собой эллипс, ширина которого увеличивается с увеличением t . Кривая также вращается против часовой стрелки вокруг начала координат с каждым значением t. Из этих графиков видно, что при t=0 координаты x=0 и y=0. Когда t=10, координаты x=-5 и y=-5. Обратите внимание, что когда t=-2, обе координаты являются отрицательными числами.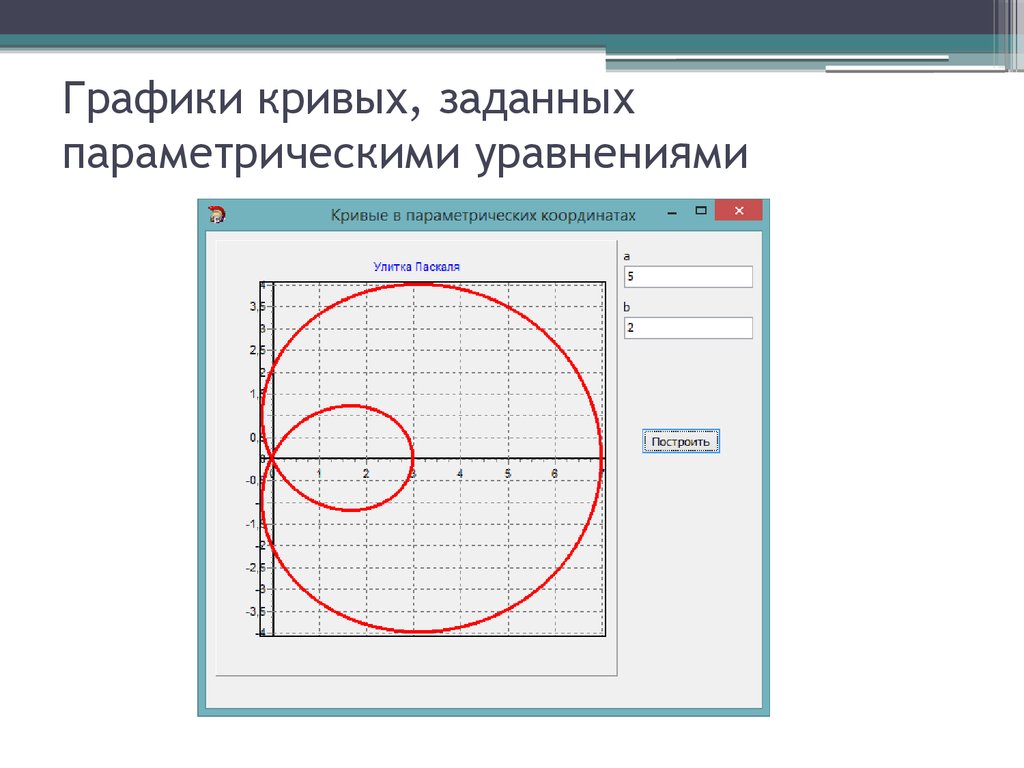 Аналогично, когда t=4, обе координаты являются положительными числами. График всегда будет вращаться в одном и том же направлении независимо от того, является ли координата положительной или отрицательной. Как вы можете видеть из этого калькулятор параметрических уравнений 3d позволяет нам создавать формы с бесконечным количеством решений, предоставляя только одну начальную точку? Изменяя только один параметр, такой как t в нашем уравнении выше, мы можем иметь разные размеры и направления. В дополнение к нашему параметрическому графику на экране под ним есть четыре графика, показывающие, как выглядят определенные параметрические уравнения в зависимости от значения t. Мы показали вам несколько примеров, но если вы хотите увидеть и другие, не стесняйтесь исследовать их, нажав «Показать больше».

Параметрические уравнения можно построить с помощью графика

График с известными параметрами по x и y (x1, y1) в зависимости от x и y (x2, y2). Это построено с использованием уравнений параболы, найденных с помощью графического калькулятора или калькулятора Sphere Equation Calculator . Для обоих параметрических уравнений можно использовать одно уравнение: XY=c и YX=c, где c = константа. В этом примере XY=6+Constance и YX=Constance являются двумя уравнениями. Затем они наносятся на график по абсциссе и ординате соответственно; ось X будет давать значения с шагом h, которые представляют единицы в горизонтальном направлении на графике, а ось Y будет давать значения с шагом k, которые представляют единицы в вертикальном направлении на графике. Кривая, сгенерированная из этих точек, затем определяется точкой (точками) пересечения с координатами (h0, k0), как показано ниже. Когда есть только одно параметризованное уравнение (например, XY=6+Constance), кривая следует прямой линии между точками, которые соответствуют каждой из констант вдоль нее.

При наличии двух параметризованных уравнений, таких как XY=(2-k)+5*k и YX=(-5*k)-10*k, которые пересекаются в точке P с координатами (-8,-4) , мы находим его значение, подставляя -8 вместо h и -4 вместо k в одно из наших уравнений и решая его для t:

t=-8/(5*(-4))=-32<0, поэтому это уравнение не генерирует никаких значений между 0≤t≤30, потому что, когда h>0 и k>0, наклон m=slope(k, h)=20 > наклон либо 6+(2-k), либо 5*(k- 10), которые равны m=14.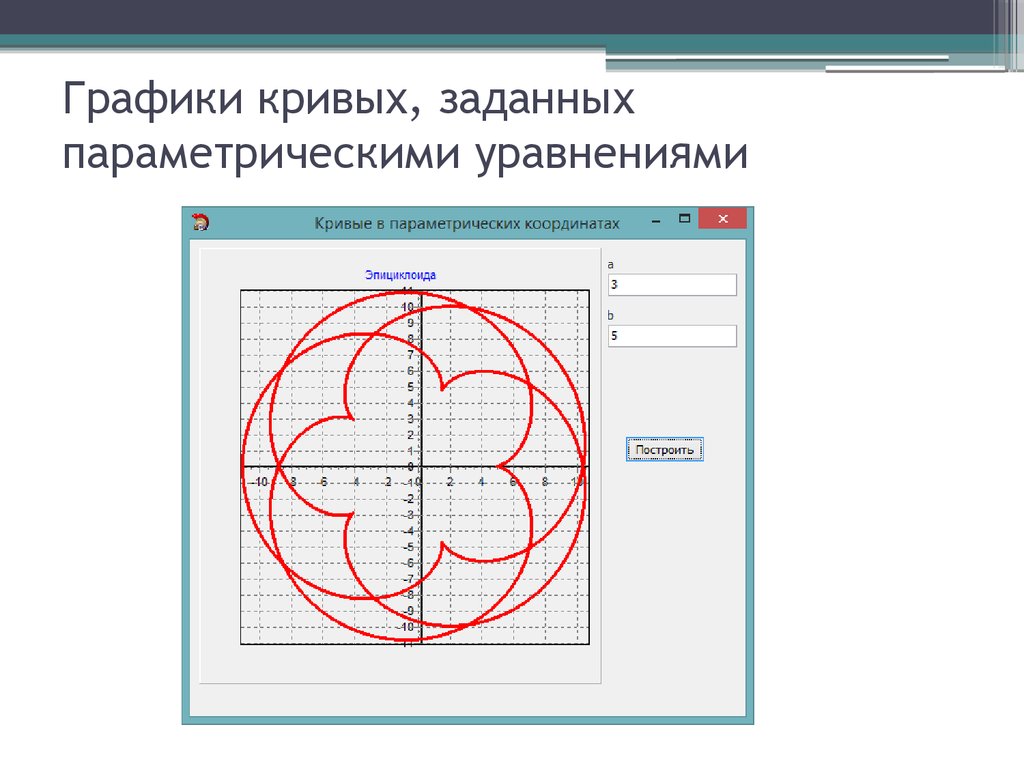 На графике, изображающем параметрические кривые с их уравнениями, нанесенными по оси абсцисс и ординат соответственно, видна параболическая форма.

Существует много интересных приложений для построения трехмерных графиков, предлагаемых онлайн-математическими калькуляторами:

Построение параметрических кривых также может выполняться в трех измерениях, а не только в двух измерениях! Для этого вы наносите на график все параметрические точки (x1, y1, z1) в зависимости от x2 и y2. Для этого нам понадобятся два уравнения: XYZ=c и YZX=c, где c = константа. Нам нужно рассчитать все значения координаты z, прежде чем переходить к нанесению их на график. Первый шаг — решить для z, используя любое уравнение, которое вы хотите сначала — обратите внимание, что если вы сначала решите для Z, ваш диапазон оси Z будет . Затем подставьте эти результаты в другое уравнение и снова решите — теперь у нас есть решение для всех четырех переменных!

Вычисление координат точек на кривых

Параметрические уравнения необходимы во многих областях науки, таких как электротехника, проектирование и других областях, где ученые и инженеры используют разные формулы для решения задач. Эти формулы строят трехмерные кривые, которые можно использовать для различных целей. Чтобы вычислить координаты точек на этих кривых, вы должны умножить любую точку на вашей кривой на параметр t. Параметр t равен времени в секундах. Вам также может понадобиться применить некоторые тригонометрические функции. Эти функции включают, среди прочего, косинус, синус и тангенс. Когда дело доходит до калькулятор параметрических уравнений 3d , плоскость xy разделена на четыре квадранта. Ось x идет от отрицательных чисел вверх к положительным числам, а ось y колеблется от отрицательных чисел вниз к положительным числам. Каждый квадрант имеет свой собственный набор значений at с двумя измерениями, соответствующими значениям высоты и ширины. Чтобы упростить расчеты при использовании параметрических уравнений, важно не только понимать, как они работают, но и знать, как они построены математически, чтобы вам было легче манипулировать ими позже.

Параметрические уравнения: Графики | Алгебра и тригонометрия

Цели обучения

В этом разделе вы:

• Изобразите плоские кривые, описываемые параметрическими уравнениями, с помощью точек.
• Граф параметрических уравнений.

Это конец девятого иннинга, с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Тесто раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом приблизительно [латекс]\,45°\,[/латекс] к горизонтали. Какое расстояние пролетит мяч? Сможет ли он очистить забор для победного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрические уравнения. В этом разделе мы обсудим параметрические уравнения и некоторые распространенные приложения, такие как задачи о движении снарядов.

Рисунок 1. Параметрические уравнения могут моделировать траекторию снаряда. (кредит: Пол Крехер, Flickr)

Построение графиков параметрических уравнений с помощью точек

Стандартным методом вместо графического калькулятора или компьютерной графической программы является построение точек для представления графика уравнения. {2}+1,\,\,y \влево(т\вправо)=2+т.[/латекс]

Показать решение

Анализ

По мере того, как значения [латекс]\,t\,[/латекс] увеличиваются в положительном направлении от 0 до 5, точки на графике очерчивают верхнюю половину параболы. Когда значения [latex]\,t\,[/latex] становятся отрицательными, они очерчивают нижнюю половину параболы. Ограничений по домену нет. Стрелки указывают направление в соответствии с возрастающими значениями [latex]\,t.\,[/latex] График не представляет функцию, так как он не пройдет тест вертикальной линии. График состоит из двух частей: положительные значения для [latex]t,[/latex] и отрицательные значения для [latex]t[/latex]

Попробуйте

Нарисуйте график параметрических уравнений[латекс]\,x=\sqrt{t},\,\,y=2t+3,\,\,\,0\le t\le 3. [/latex]

Показать решение

Построение графика тригонометрических параметрических уравнений

Построить таблицу значений заданных параметрических уравнений и начертить график:

[латекс]\begin{array}{l}\\ \begin{array}{l}x =2\mathrm{cos}\,t\hfill \\ y=4\mathrm{sin}\,t\hfill \end{массив}\end{массив}[/latex]

Показать решение

Анализ

Мы видели, что параметрические уравнения можно изобразить в виде графика, нанеся точки. Однако графический калькулятор сэкономит некоторое время и выявит нюансы на графике, которые могут быть слишком утомительными, чтобы обнаруживать их, используя только ручные вычисления.

Не забудьте изменить режим калькулятора на параметрический (PAR). Для подтверждения в окне [latex]\,Y=\,[/latex] должно отображаться

[latex]\begin{array}{c}{X}_{1T}=\\ {Y}_{1T} =\end{массив}[/latex]

вместо [latex]\,{Y}_{1}=.[/latex]

Попробуйте

Постройте график параметрических уравнений:[латекс]\,х=5\mathrm{cos}\,t,\,\,y=3\mathrm{sin}\,t.[/латекс]

Показать решение

Совместное графическое отображение параметрических уравнений и прямоугольной формы

Графическое отображение параметрических уравнений [латекс]\,x=5\mathrm{cos}\,t\,[/latex]и[латекс]\,y=2\mathrm{sin }\,t.\,[/latex]Сначала постройте график, используя точки данных, сгенерированные из параметрической формы. Затем начертите прямоугольную форму уравнения. Сравните два графика.

Показать решение

Анализ

На (рисунке) данные параметрических уравнений и прямоугольного уравнения нанесены вместе. Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического пунктирным красным цветом. Ясно, что обе формы дают один и тот же граф.

Рис. 5.

Графики параметрических уравнений и уравнений прямоугольной формы в системе координат sqrt{t},\,\,t\ge 0,\,[/latex] и прямоугольный эквивалент [latex]y=\sqrt{x-1}\,[/latex] в той же системе координат.

Показать решение

Анализ

С доменом [latex]\,t\,[/latex]restricted, мы наносим на график только положительные значения[latex]\,t.\,[/latex]. график прямоугольного уравнения заштрихован красным. И снова мы видим, что эти две формы пересекаются.

Попробуйте

Нарисуйте график параметрических уравнений[латекс]\,x=2\mathrm{cos}\,\theta \,\,\,\text{and}\,\,y=4\mathrm {sin}\,\theta ,\,[/latex] вместе с прямоугольным уравнением на той же сетке.

Показать решение

Применение параметрических уравнений

Многие преимущества параметрических уравнений становятся очевидными при их применении для решения реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не раскрывают положение объекта в определенное время. Параметрические уравнения, однако, иллюстрируют, как значения x и y изменяются в зависимости от t , как местоположение движущегося объекта в определенное время.

Обычно параметрические уравнения применяются при решении задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в направлении вверх, образуя угол [латекс]\тета [/латекс] с горизонтом, с начальной скоростью [латекс]{v}_{0},\, [/latex]и на высоте [latex]h[/latex] над горизонталью.

Путь объекта, движущегося с наклоном [латекс]\тета[/латекс] к горизонту, с начальной скоростью [латекс]{v}_{0},\,[/латекс] и на высоте [ латекс]h[/латекс] над горизонталью равен 9{2}. \,[/latex]Уравнение для [латекс]\,x\,[/латекс] дает расстояние по горизонтали, а уравнение для [латекс]\,у\,[/латекс] дает расстояние по вертикали.

Как сделать

Дана задача о движении снаряда. Для ее решения используйте параметрические уравнения.

1. Горизонтальное расстояние определяется как [латекс]\,x=\left({v}_{0}\mathrm{cos}\,\theta \right)t.\,[/latex]Замените начальное скорость объекта for[latex]\,{v}_{0}.[/latex]
2. Выражение[латекс]\,\mathrm{cos}\,\theta \,[/латекс] указывает угол, под которым перемещается объект. Подставьте этот угол в градусах вместо [латекс]\,\mathrm{cos}\,\theta .[/латекс] 9{2}.\,[/latex]Снова подставьте начальную скорость вместо [латекс]\,{v}_{0},\,[/латекс] и высоту, на которую объект был брошен вместо [латекс]\ ,ч.[/латекс]
3. Продолжайте вычислять каждый член для решения для [латекс]\,t.[/латекс]

Поиск параметрических уравнений для описания движения бейсбольного мяча

Решите задачу, представленную в начале этого раздела. Удастся ли отбивающему сделать победный хоумран? Предположим, что по мячу ударили с начальной скоростью 140 футов в секунду под углом [латекс]\,45°\,[/латекс] к горизонту, и он коснулся мяча на высоте 3 фута над землей.

1. Найдите параметрические уравнения для моделирования траектории бейсбольного мяча.
2. Где мяч через 2 секунды?
3. Как долго мяч находится в воздухе?
4. Это хоумран?

Показать раствор

Доступ к следующему онлайн-ресурсу для получения дополнительных инструкций и практики с графиками параметрических уравнений.

• Графические параметрические уравнения на TI-84

Ключевые понятия

• Когда есть третья переменная, третий параметр, от которого зависят [латекс]\,х\,[/латекс]и[латекс]\,у\,[/латекс], параметрические уравнения могут быть использовал.
• Чтобы построить параметрические уравнения с помощью точек, составьте таблицу с тремя столбцами, помеченными [латекс]\,t,x\left(t\right),\,[/latex] и [латекс]\,y\left(t\ right). \,[/latex]Выберите значения для[latex]\,t\,[/latex] в порядке возрастания. Постройте два последних столбца для [латекс]\,х\,[/латекс]и[латекс]\,у.\,[/латекс] См. (Рисунок) и (Рисунок).
• При построении параметрической кривой с помощью точек обратите внимание на соответствующие значения t и покажите на графике стрелки, указывающие ориентацию кривой. См. (Рисунок) и (Рисунок). 9{2}+\left({v}_{0}\mathrm{sin}\,\theta \right)t+h.\,[/latex]Начальная скорость обозначается как[latex]\,{v}_ {0}.\,\theta [/latex] представляет собой начальный угол объекта при броске, а [latex]\,h\,[/latex] представляет высоту, на которую движется объект.

Упражнения по разделам

Вербальные

Какие два метода используются для построения графиков параметрических уравнений?

Показать решение

В чем отличие параметрических уравнений точечного построения от декартовых уравнений? 9{2}-1\hfill \end{массив}[/latex]

The first row is labeled t, the second is labeled x, and the third is labeled y. The first columns contains the numbers -3, -2, -1, 0, 1, 2, 3. The other two columns are left blank for completion.»> 9{2}\hfill \end{массив}[/latex]

[латекс]т[/латекс]	[латекс]x[/латекс]	[латекс]у[/латекс]
[латекс]-3[/латекс]
[латекс]-2[/латекс]
[латекс]-1[/латекс]
[латекс]0[/латекс]
[латекс]1[/латекс]

[латекс]т[/латекс]	[латекс]-3[/латекс]	[латекс]-2[/латекс]	[латекс]-1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

Показать решение

[латекс] \{\ begin {массив} {l} x (t) = 2 + t \ hfill \\ y (t) = 3-2t \ hfill \ end {массив} [/ латекс]

The first row is labeled t, the second is labeled x, and the third is labeled y. The first row contains the numbers -2, -1, 0, 1, 2, 3. The other two columns are left blank for completion.»>

[латекс]т[/латекс]	[латекс]-2[/латекс]	[латекс]-1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]	[латекс]3[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

[латекс] \{\ begin {массив} {l} x (t) = -2-2t \ hfill \\ y (t) = 3 + t \ hfill \ end {массив} [/ латекс]

«> 9{3}\hfill \\ y(t)=t+2\hfill \end{массив}[/latex]

[латекс]т[/латекс]	[латекс]-3[/латекс]	[латекс]-2[/латекс]	[латекс]-1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]

9{2}\hfill \\ y(t)=t+3\hfill \end{массив}[/latex]

[латекс]т[/латекс]	[латекс]-2[/латекс]	[латекс]-1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

The first row is labeled t, the second is labeled x, and the third is labeled y. The first row contains the numbers — -2, -1, 0, 1, 2. The other two columns are left blank for completion.»>

[латекс]т[/латекс]	[латекс]-2[/латекс]	[латекс]-1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

Показать решение

Для следующих упражнений нарисуйте кривую и включите ориентацию.

[латекс] \{\ begin {массив} {l} x (t) = t \\ y (t) = \ sqrt {t} \ end {массив} [/ латекс]

[латекс] \ {\ begin{array}{l}x(t)=-\,\sqrt{t}\\ y(t)=t\end{array}[/latex]

Показать решение

[латекс] \{\ begin {массив} {l} x (t) = 5- | t | \\ y (t) = t + 2 \ end {массив} [/ латекс]

[латекс] \ {\begin{массив}{l}x(t)=-t+2\\ y(t)=5-|t|\end{массив}[/latex]

Показать решение

9{2}},\,0

[латекс]x\left(t\right)=-t,y\left(t\right)=\sqrt{t},\ ,t\ge 0[/latex]

Показать решение

[латекс]x=-2\mathrm{cos}\,t,\,y=6\,\mathrm{sin}\,t,\,0\le t\le \pi [/latex]

[латекс] x = — \ mathrm {sec} \, t, \, y = \ mathrm {tan} \, t, \, — \ frac {\, \ pi} {2}

Показать решение

В следующих упражнениях используйте параметрические уравнения для целых чисел a и b :

[латекс]\begin{array}{l}x\left(t\right)=a\mathrm{cos}\ влево (\ влево (a + b \ вправо) t \ вправо) \\ y \ влево (t \ вправо) = a \ mathrm {cos} \ влево (\ влево (a-b \ вправо) t \ вправо) \ конец {массив }[/латекс]

Граф в области [латекс]\,\слева[-\пи ,0\справа],\,[/латекс]где[латекс]\,а=2\,[/латекс]и[латекс]\, b=1,\,[/latex] и укажите ориентацию.

Граф в области [латекс]\,\слева[-\pi ,0\справа],\,[/латекс]где[латекс]\,а=3\,[/латекс]и[латекс]\, b=2[/latex] и укажите ориентацию.

Показать решение

Граф в домене [латекс]\,\слева[-\pi ,0\справа],\,[/латекс],где[латекс]\,а=4\,[/латекс]и[латекс]\, b=3[/latex] и укажите ориентацию.

Граф в области [латекс]\,\слева[-\пи ,0\справа],\,[/латекс]где[латекс]\,а=5\,[/латекс]и[латекс]\, b=4[/latex] и укажите ориентацию.

Показать решение

Если [латекс]\,а\,[/латекс] на 1 больше, чем [латекс]\,b,\,[/латекс], опишите эффект значения [латекс]\,а\,[/латекс] и [латекс]\,b\,[/латекс] имеют на графике параметрические уравнения.

Опишите график, если[латекс]\,а=100\,[/латекс]и[латекс]\,b=99.[/латекс]

Показать решение

Что произойдет, если [латекс]\,b\,[/латекс]на 1 больше, чем [латекс]\,а?\,[/латекс]Опишите график.

Если параметрические уравнения [латекс]\,х\влево(т\вправо)={т}^{2}\,[/латекс] и [латекс]\,у\влево(т\вправо)=6- 3t\,[/latex]есть график горизонтальной параболы, открывающейся вправо, что изменит направление кривой? 9{2}\,[/latex]и[латекс]\,x\left(t\right)\,[/latex]линейно

Запишите параметрические уравнения окружности с центром[латекс]\,\left( 0,0\right),[/latex]радиус 5 и ориентация против часовой стрелки.

Показать решение

Напишите параметрические уравнения эллипса с центром[латекс]\,\влево(0,0\вправо),[/латекс]большой осью длины 10, малой осью длины 6 и ориентацией против часовой стрелки.

В следующих упражнениях используйте графическую утилиту для построения графика в окне[латекс]\,\слева[-3,3\справа]\,[/латекс]по[латекс]\,\слева[-3,3 \right]\,[/latex]в домене[latex]\,\left[0,2\pi \right)\,[/latex]для следующих значений [latex]\,a\,[/latex ]and[latex]\,b[/latex] и укажите ориентацию.

[латекс] \{\ begin {array} {l} x (t) = \ mathrm {sin} (at) \\ y (t) = \ mathrm {sin} (bt) \ end {array} [/ латекс]

[латекс]a=1,b=2[/латекс]

Показать решение

[латекс]a=2,b=1[/латекс]

[латекс]a=3,b=3[/латекс]

Показать решение

[латекс]a=5,b=5[/латекс]

[латекс]a=2,b=5[/латекс]

Показать решение

[латекс]a=5,b=2[/латекс]

Технология

В следующих упражнениях посмотрите на графики, созданные с помощью параметрических уравнений вида [латекс]\,\{\begin{массив }{l}x(t)=a\text{cos}(bt)\hfill \\ y(t)=c\text{sin}(dt)\hfill \end{массив}. \,[/latex] Используйте параметрический режим графического калькулятора, чтобы найти значения [латекс]a,b,c,[/латекс] и [латекс]d[/латекс] для построения каждого графика.

Показать решение

Показать решение

В следующих упражнениях используйте графическую утилиту для построения графиков заданных параметрических уравнений.

1. [латекс] \{\ begin {array} {l} x (t) = \ mathrm {cos} t-1 \\ y (t) = \ mathrm {sin} t + t \ end {array} [ /латекс]
2. [латекс] \{\ begin {array} {l} x (t) = \ mathrm {cos} t + t \\ y (t) = \ mathrm {sin} t-1 \ end {array} [/latex ]
3. [латекс] \{\ begin {array} {l} x (t) = t- \ mathrm {sin} t \\ y (t) = \ mathrm {cos} t-1 \ end {array} [/latex ]

Постройте график всех трех наборов параметрических уравнений в области [латекс]\,\влево[0,\,2\пи \вправо].[/латекс]

Показать решение

Построить график всех трех наборов параметрических уравнений в области [латекс]\,\left[0,4\pi \right]. [/latex]

Построить график всех трех наборов параметрических уравнений в области [латекс]\, \left[-4\pi ,6\pi \right].[/latex]

Показать решение

График каждого набора параметрических уравнений «ползет» по одной из осей. Что определяет, по какой оси ползет график?

Объясните влияние на график параметрического уравнения, когда мы поменяли местами [латекс]\,\mathrm{sin}\,t\,[/латекс]и [латекс]\,\mathrm{cos}\,t[/ латекс]. 9{2}+10t+5.\text{}[/latex]Напишите параметрические уравнения для положения мяча, а затем освободите время для записи высоты как функции горизонтального положения.

Для следующих упражнений используйте этот сценарий: Дротик брошен вверх с начальной скоростью 65 футов/с под углом возвышения 52°. Учитывайте положение дротика в любой момент[latex]\,t.\,[/latex]Сопротивлением воздуха пренебрегайте.

Найдите параметрические уравнения, моделирующие проблемную ситуацию.

Показать решение

Найдите все возможные значения [latex]\,x\,[/latex], представляющие ситуацию.

Когда дротик упадет на землю?

Показать решение

Найдите максимальную высоту дротика.

Когда дротик достигнет максимальной высоты?

Показать решение

В следующих упражнениях посмотрите на графики каждого из четырех параметрических уравнений. Хотя они выглядят необычно и красиво, они настолько распространены, что имеют имена, указанные в каждом упражнении. Используйте графическую утилиту, чтобы построить график каждого в указанном домене.

Эпициклоида: [латекс]\,\{\begin{array}{l}x(t)=14\mathrm{cos}\,t-\mathrm{cos}(14t)\hfill \\ y(t )=14\mathrm{sin}\,t+\mathrm{sin}(14t)\hfill \end{array}\,[/latex]в домене[latex]\,[0,2\pi ][/latex ].

Гипоциклоида: [латекс] \{\ begin {array} {l} x (t) = 6 \ mathrm {sin} \, t + 2 \ mathrm {sin} (6t) \ hfill \\ y (t) =6\mathrm{cos}\,t-2\mathrm{cos}(6t)\hfill \end{array}\,[/latex]в домене[latex]\,[0,2\pi ][/ латекс].

Показать решение

Гипотрохоид: [латекс] \{\ begin {array} {l} x (t) = 2 \ mathrm {sin} \, t + 5 \ mathrm {cos} (6t) \ hfill \\ y (t) =5\mathrm{cos}\,t-2\mathrm{sin}(6t)\hfill \end{массив}\,[/latex]в домене[latex]\,\left[0,2\pi \ справа][/латекс].

A rose: [латекс] \, \ {\ begin {array} {l} x (t) = 5 \ mathrm {sin} (2t) \ mathrm {sin} t \ hfill \\ y (t) = 5 \mathrm{sin}(2t)\mathrm{cos}t\hfill \end{array}\,[/latex]в домене[latex]\,\left[0,2\pi \right][/latex] .

Показать решение

Калькулятор параметрических уравнений — Mathauditor

Как использовать калькулятор параметрических уравнений?

Существует большое количество уравнений и формул, доступных в математика, которая используется для различных видов математических проблемы. Однако эти теоремы и уравнения также полезны. для реальных приложений. Среди них самые простые в использовании и это уравнение необходимо для изучения концепции. Как будто вы узнаете сложности для расчета уравнений вручную, вы также можете использовать такие онлайн-инструменты, такие как калькулятор параметрических уравнений. Независимо от того, доступно несколько онлайн-калькуляторов; такой инструмент по-прежнему используется для определенной цели и соответствующих методов и уравнения.

Для использования калькулятора параметрических уравнений необходимо знать о точном значении всех терминов. Это слово используется для определения и описать методы в математике, которые вводят и обсудить дополнительные и независимые переменные, известные как параметр для заставить их работать. Это уравнение определяет набор или группу величин (которые рассматриваются как функции) независимых переменные, называемые параметрами. В основном используется для изучения координаты точек, определяющих геометрический объект. Чтобы получить четкое представление об этом термине и его уравнении, пройдите ниже пример. Давайте возьмем пример этих уравнений окружности, который определяется, как указано ниже, с использованием двух уравнений.

X = r cos (t)
Y = r sin (t).

В приведенных выше уравнениях t является параметром, который является переменной но не реальная часть круга. Тем не менее, параметр T будет генерировать значение пары значений X и Y, которое зависит от круга радиус р. Вы можете использовать любую геометрическую форму, чтобы определить эти уравнения. Кроме того, вы можете использовать его в параметрическом калькулятор уравнений.

Шаги по использованию калькулятора параметрических уравнений

Приведенные шаги необходимо выполнить при использовании калькулятор параметрических уравнений.

1. Шаг 1: Найдите набор уравнений для заданной функции любого геометрическая форма.
2. Шаг 2: Затем присвойте любую переменную, равную t, которая является параметр.
3. Шаг 3: Узнайте значение второй переменной относительно переменная т.
4. Шаг 4: Затем вы получите набор или пару этих уравнений.
5. Шаг 5: Введите оба уравнения в параметрические уравнения калькулятор.
6. Шаг 6: Нажмите кнопку отправки, и вы получите решение.

Вы можете получить график вывода в отдельном окне решатель параметрических уравнений.

Зачем использовать параметрический калькулятор формы?

При изменении формы стандартного уравнения на это форма, инструмент также используется в качестве параметрического калькулятора формы, который определяет окружной путь относительно переменной t. Изначально, вы можете найти этот процесс преобразования немного сложным, но после использования калькулятора параметрических уравнений; это конвертирует в простую процедуру за меньшее время.

После преобразования функции в этот процесс вы можете вернуть это также путем устранения этого калькулятора. в исключения, вы исключите параметр, который используется в калькулятор параметрических уравнений.

Также известен как процесс трансформации. Как вы преобразовывая эти уравнения в нормальное, нужно исключить или удалить параметр t, который добавляется, чтобы узнать пару или набор, который используется для расчета различных форм в калькулятор параметрических уравнений.

Чтобы выполнить исключение, сначала нужно решить x=f (t) уравнения и удалить его из него, используя процесс вывода и затем поместите значение t в Y. Затем вы получите значение X и Y. На выходе будет нормальная функция, состоящая только из x и y, в котором y основан на x, который можно найти на отдельное окно решателя параметрического уравнения.

No related posts.