Косинус 7 пи 6: Найдите значение выражение cos 7п/6

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68
Найти точное значение		tan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значение tan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значение
sin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление.

Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.

Обозначаем числа \(2π\), \(π\), \(\frac{π}{2}\), \(-\frac{π}{2}\), \(\frac{3π}{2}\)

Как вы знаете из прошлой статьи, радиус числовой окружности равен \(1\). Значит, длина окружности равняется \(2π\) (вычислили по формуле \(l=2πR\)). С учетом этого отметим \(2π\) на числовой окружности. Чтобы отметить это число нужно пройти от \(0\) по числовой окружности расстояние равно \(2π\) в положительном направлении, а так как длина окружности \(2π\), то получается, что мы сделаем полный оборот. То есть, числу \(2π\) и \(0\) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.


Теперь обозначим на числовой окружности число \(π\). \(π\) – это половина от \(2π\). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от \(0\) в положительном направлении половину окружности.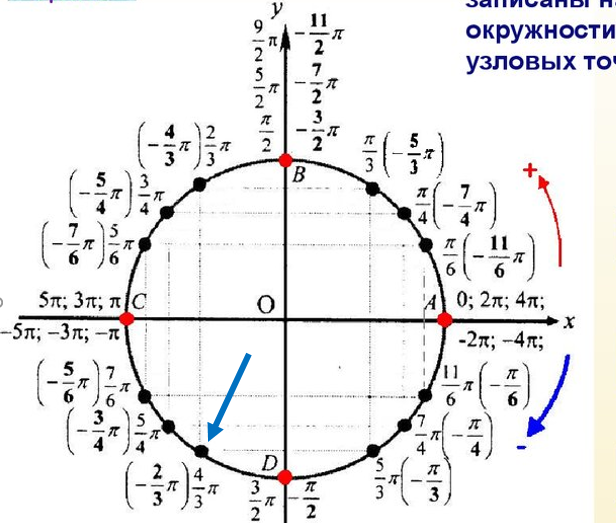


Отметим точку \(\frac{π}{2}\). \(\frac{π}{2}\) – это половина от \(π\), следовательно чтобы отметить это число, нужно от \(0\) пройти в положительном направлении расстояние равное половине \(π\), то есть четверть окружности.


Обозначим на окружности точки \(-\)\(\frac{π}{2}\). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.


Нанесем \(-π\). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.


Теперь рассмотрим пример посложнее. Отметим на окружности число \(\frac{3π}{2}\). Для этого дробь \(\frac{3}{2}\) переведем в смешанный вид \(\frac{3}{2}\)\(=1\)\(\frac{1}{2}\), т.е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

                                    

 

Задание 1. Отметьте на числовой окружности точки \(-2π\),\(-\)\(\frac{3π}{2}\).


Обозначаем числа \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\)

Выше мы нашли значения в точках пересечения числовой окружности с осями \(x\) и \(y\). Теперь определим положение промежуточных точек. Для начала нанесем точки \(\frac{π}{4}\), \(\frac{π}{3}\) и \(\frac{π}{6}\).
\(\frac{π}{4}\) – это половина от \(\frac{π}{2}\) (то есть, \(\frac{π}{4}\) \(=\)\(\frac{π}{2}\)\(:2)\) , поэтому расстояние \(\frac{π}{4}\) – это половина четверти окружности.

                                   

\(\frac{π}{4}\) – это треть от \(π\) (иначе говоря,\(\frac{π}{3}\)\(=π:3\)), поэтому расстояние \(\frac{π}{3}\) – это треть от полукруга.

           

\(\frac{π}{6}\) – это половина \(\frac{π}{3}\) (ведь \(\frac{π}{6}\)\(=\)\(\frac{π}{3}\)\(:2\)) поэтому расстояние \(\frac{π}{6}\) – это половина от расстояния \(\frac{π}{3}\).


Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением \(0\), \(\frac{π}{2}\),\(π\), \(\frac{3π}{2}\), \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

     

     

 

Обозначаем числа \(\frac{7π}{6}\), \(-\frac{4π}{3}\), \(\frac{7π}{4}\)

Обозначим на окружности точку \(\frac{7π}{6}\), для этого выполним следующие преобразования: \(\frac{7π}{6}\)\(=\)\(\frac{6π + π}{6}\)\(=\)\(\frac{6π}{6}\)\(+\)\(\frac{π}{6}\)\(=π+\)\(\frac{π}{6}\). Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).

                                  

Отметим на окружности точку \(-\)\(\frac{4π}{3}\). Преобразовываем: \(-\)\(\frac{4π}{3}\)\(=-\)\(\frac{3π}{3}\)\(-\)\(\frac{π}{3}\)\(=-π-\)\(\frac{π}{3}\). Значит надо от \(0\) пройти в отрицательную сторону расстояние \(π\) и еще \(\frac{π}{3}\).

                               

Нанесем точку \(\frac{7π}{4}\), для этого преобразуем \(\frac{7π}{4}\)\(=\)\(\frac{8π-π}{4}\)\(=\)\(\frac{8π}{4}\)\(-\)\(\frac{π}{4}\)\(=2π-\)\(\frac{π}{4}\). Значит, чтобы поставить точку со значением \(\frac{7π}{4}\), надо от точки со значением \(2π\) пройти в отрицательную сторону расстояние \(\frac{π}{4}\).

                     

Задание 2. Отметьте на числовой окружности точки \(-\)\(\frac{π}{6}\),\(-\)\(\frac{π}{4}\),\(-\)\(\frac{π}{3}\),\(\frac{5π}{4}\),\(-\)\(\frac{7π}{6}\),\(\frac{11π}{6}\), \(\frac{2π}{3}\),\(-\)\(\frac{3π}{4}\).

Обозначаем числа \(10π\), \(-3π\), \(\frac{7π}{2}\) ,\(\frac{16π}{3}\), \(-\frac{21π}{2}\), \(-\frac{29π}{6}\)

Запишем \(10π\) в виде \(5 \cdot 2π\).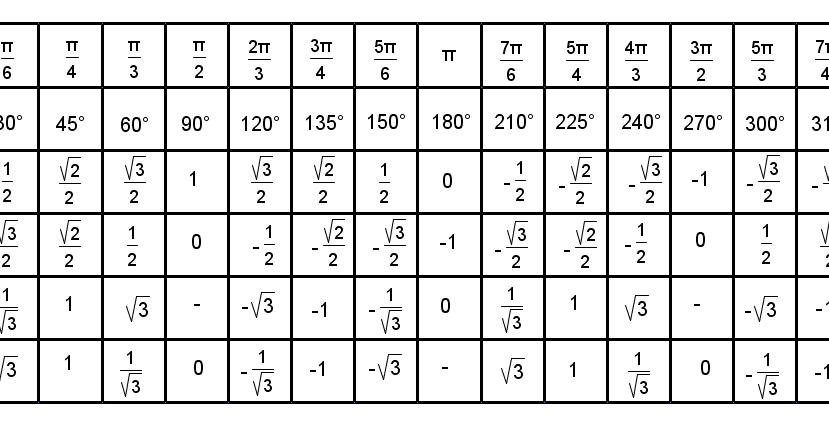 Вспоминаем, что \(2π\) – это расстояние равное длине окружности, поэтому чтобы отметить точку \(10π\), нужно от нуля пройти расстояние равное \(5\) окружностям. Нетрудно догадаться, что мы окажемся снова в точке \(0\), просто сделаем пять оборотов.


Из этого примера можно сделать вывод:

Числам с разницей в \(2πn\), где \(n∈Z\) (то есть \(n\) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше \(2π\) (или меньше \(-2π\)), надо выделить из него целое четное количество \(π\) (\(2π\), \(8π\), \(-10π\)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Еще один вывод:

Точке, которой соответствует \(0\), также соответствуют все четные количества \(π\) (\(±2π\),\(±4π\),\(±6π\)…).

Теперь нанесем на окружность \(-3π\). \(-3π=-π-2π\), значит \(-3π\) и \(–π\) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в \(-2π\)).


Кстати, там же будут находиться все нечетные \(π\).

Точке, которой соответствует \(π\), также соответствуют все нечетные количества \(π\) (\(±π\),\(±3π\),\(±5π\)…).

Сейчас обозначим число \(\frac{7π}{2}\). Как обычно, преобразовываем: \(\frac{7π}{2}\)\(=\)\(\frac{6π}{2}\)\(+\)\(\frac{π}{2}\)\(=3π+\)\(\frac{π}{2}\)\(=2π+π+\)\(\frac{π}{2}\). Два пи – отбрасываем, и получается что, для обозначения числа \(\frac{7π}{2}\) нужно от нуля в положительную сторону пройти расстояние равное \(π+\)\(\frac{π}{2}\) (т.е. половину окружности и еще четверть).


Отметим \(\frac{16π}{3}\). Вновь преобразования: \(\frac{16π}{3}\)\(=\)\(\frac{15π + π}{3}\)\(=\)\(\frac{15π}{3}\)\(+\)\(\frac{π}{3}\)\(=5π+\)\(\frac{π}{3}\)\(=4π+π+\)\(\frac{π}{3}\). Ясно, что от нуля надо пройти расстояние равное \(π+\)\(\frac{π}{3}\) – и мы найдем место точки \(\frac{16π}{3}\).


Нанесем на окружность число \(-\)\(\frac{21π}{2}\).
\(-\)\(\frac{21π}{2}\)\(= -\)\(\frac{20π}{2}\)\(-\)\(\frac{π}{2}\)\(=-10π-\)\(\frac{π}{2}\). Значит, место \(-\)\(\frac{21π}{2}\) совпадает с местом числа \(-\)\(\frac{π}{2}\).


Обозначим \(-\)\(\frac{29π}{6}\).
\(-\)\(\frac{29π}{6}\)\(=-\)\(\frac{30π}{6}\)\(+\)\(\frac{π}{6}\)\(=-5π+\)\(\frac{π}{6}\)\(=-4π-π+\)\(\frac{π}{6}\). Для обозначение \(-\)\(\frac{29π}{6}\), на числовой окружности надо от точки со значением \(–π\) пройти в положительную сторону \(\frac{π}{6}\).


Задание 3. Отметьте на числовой окружности точки \(-8π\),\(-7π\), \(\frac{11π}{4}\),\(-\)\(\frac{7π}{3}\),\(\frac{17π}{6}\),\(-\)\(\frac{20π}{3}\),\(-\)\(\frac{11π}{2}\).

Скачать статью

найти значение выражения cos 7П/6 — sin 4П/3 — Учеба и наука

Ответы

cos 7П/6 — sin 4П/3=cos (П+П/6) — sin (П+П/3)=-cos П/6 +sin П/3=-sqrt(3)/2+sqrt(3)/2=0

13. 05.14

Ответ понравился автору вопроса

Андрей Андреевич
Читать ответы

Eleonora Gabrielyan
Читать ответы

Галина Владимировна
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

Собственная скорость полета голубя 55 км/ч, а скорость ветра 5. 5км/ч. Голубь летел 0,2 ч против ветра и 0,4 часа по ветру. Какой путь пролетел голубь за все это время?

Задача

Решено

3 землекопа за 2 часа…

Решено

Решение задачи по математике 4 класс по программе «Школа-2100»

Пользуйтесь нашим приложением

Cos 7pi/6 — Найдите значение Cos 7pi/6

LearnPracticeDownload

Значение cos 7pi/6 равно -0,8660254. . . . Cos 7pi/6 радиан в градусах записывается как cos ((7π/6) × 180°/π), т. е. cos (210°). В этой статье мы обсудим методы определения значения cos 7pi/6 на примерах.

  • Cos 7pi/6: -√(3)/2
  • Cos 7pi/6 в десятичном формате: -0,8660254. . .
  • Cos (-7pi/6): -0,8660254. . . или −√3/2
  • Cos 7pi/6 в градусах: cos (210°)

Каково значение Cos 7pi/6?

Значение cos 7pi/6 в десятичном виде равно -0,866025403.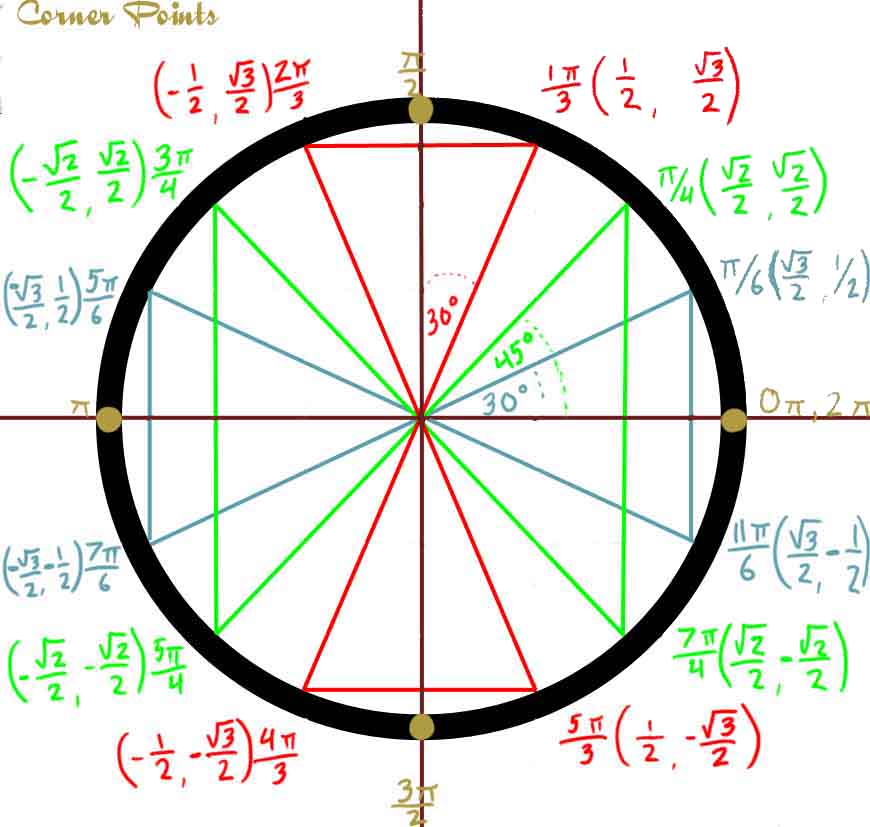 . .. Cos 7pi/6 также можно выразить с помощью эквивалента заданного угла (7pi/6) в градусах (210°).

Мы знаем, используя преобразование радиан в градусы, θ в градусах = θ в радианах × (180°/pi)
⇒ 7pi/6 радиан = 7pi/6 × (180°/pi) = 210° или 210 градусов
∴ cos 7pi/6 = cos 7π/6 = cos(210°) = -√(3)/2 или -0,8660254. . .

Объяснение:

Для cos 7pi/6 угол 7pi/6 лежит между pi и 3pi/2 (третий квадрант). Поскольку функция косинуса в третьем квадранте отрицательна, значение cos 7pi/6 = -√(3)/2 или -0,8660254. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 7pi/6 как cos 7pi/6 = cos(7pi/6 + n × 2pi), n ∈ Z.
⇒ cos 7pi/6 = cos 19pi/6 = cos 31pi/6 и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-7pi/6) = cos(7pi/6).

Методы определения значения Cos 7pi/6

Функция косинуса отрицательна в 3-м квадранте. Значение cos 7pi/6 определяется как -0,86602. . .. Мы можем найти значение cos 7pi/6 по:

  • Используя Unit Circle
  • Использование тригонометрических функций

Cos 7pi/6 с помощью единичной окружности

Чтобы найти значение cos 7π/6 с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 7pi/6 с положительной осью x.
  • Космос 7pi/6 равен x-координате (-0,866) точки пересечения (-0,866, -0,5) единичной окружности и r.

Следовательно, значение cos 7pi/6 = x = -0,866 (приблизительно)

Cos 7pi/6 в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить cos 7pi/6 как:

  • ± √ (1-sin²(7pi/6))
  • ± 1/√(1 + tan²(7pi/6))
  • ± раскладушка(7pi/6)/√(1 + раскладушка²(7pi/6))
  • ±√(косек²(7pi/6) — 1)/косек(7pi/6)
  • 1/сек (7pi/6)

Примечание: Поскольку 7pi/6 лежит в 3-м квадранте, окончательное значение cos 7pi/6 будет отрицательным.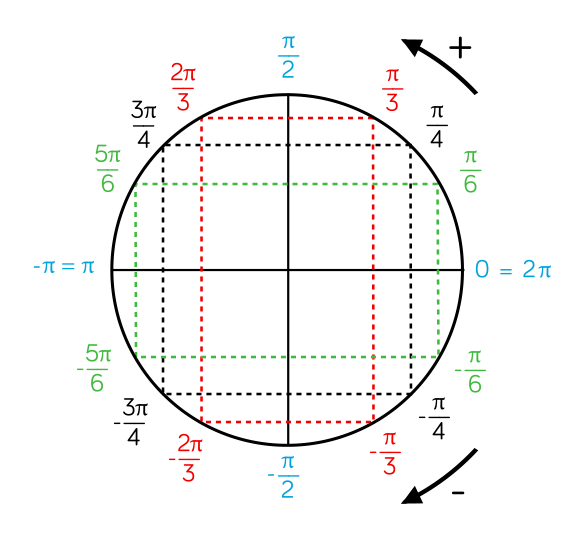

Мы можем использовать тригонометрические тождества для представления cos 7pi/6 как

  • -cos(pi — 7pi/6) = -cos(-pi/6)
  • -cos(pi + 7pi/6) = -cos 13pi/6
  • sin(pi/2 + 7pi/6) = sin 5pi/3
  • sin(pi/2 — 7pi/6) = sin(-2pi/3)

☛ Также проверьте:

  • потому что 2pi
  • тан пи/12
  • желтовато-коричневый 4pi/3
  • грех 2pi
  • грех 11pi/12
  • грех 11pi/6

Примеры использования Cos 7pi/6

  1. Пример 1: Найдите значение (cos² 7pi/12 — sin² 7pi/12). [Подсказка: используйте cos 7pi/6 = -0,866]

    Решение:

    Используя формулу cos 2a,
    (cos² 7pi/12 — sin² 7pi/12) = cos(2 × 7pi/12) = cos 7pi/6
    ∵ cos 7pi/6 = -0,866
    ⇒ (cos² 7pi/12 — sin² 7pi/12) = -0,866

  2. Пример 2: Упростить: 9 (cos(7pi/6)/sin(5pi/3))

    Решение:

    Мы знаем cos 7pi/6 = sin 5pi/3
    ⇒ 9 cos(7pi/6)/sin(5pi/3) = 9 (cos(7pi/6)/cos(7pi/6))
    = 9(1) = 9

  3. Пример 3. Найдите значение 2 cos(7pi/6)/3 sin(-2pi/3).

    Решение:

    Используя тригонометрические тождества, мы знаем, что cos(7pi/6) = sin(pi/2 — 7pi/6) = sin(-2pi/3).
    ⇒ cos(7pi/6) = sin(-2pi/3)
    ⇒ Значение 2 cos(7pi/6)/3 sin(-2pi/3) = 2/3

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы посмотреть на мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Cos 7pi/6

Что такое Cos 7pi/6?

Cos 7pi/6 — значение тригонометрической функции косинуса для угла, равного 7π/6 радиан. Значение cos 7pi/6 составляет -√(3)/2 или -0,866 (приблизительно)

Каково значение Cos 7pi/6 с точки зрения Sec 7pi/6?

Поскольку функция секанса является обратной функцией косинуса, мы можем записать cos 7pi/6 как 1/sec(7pi/6).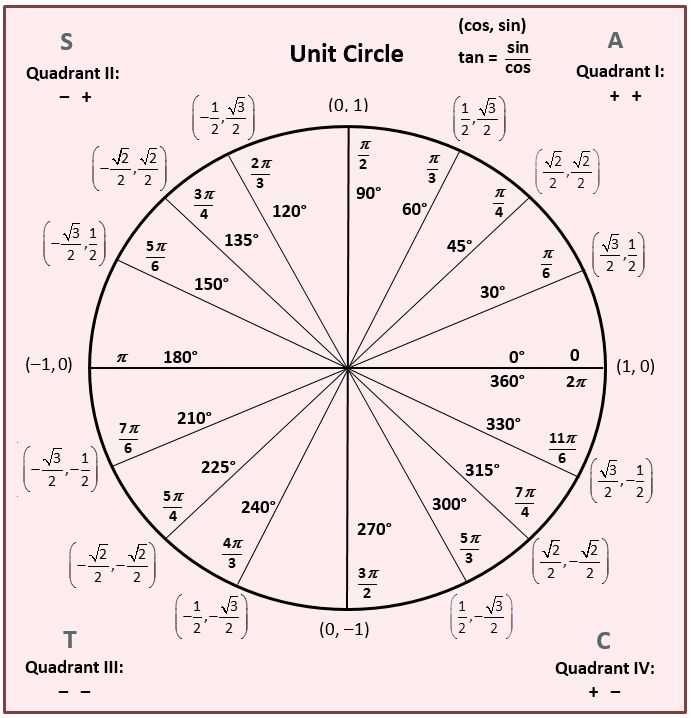 Значение sec 7pi/6 равно -1,154700.

Каково значение Cos 7pi/6 относительно Cot 7pi/6?

Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 7pi/6 можно записать как -cot(7pi/6)/√(1 + cot²(7pi/6)). Здесь значение cot 7pi/6 равно 1,73205.

Как найти значение Cos 7pi/6?

Значение cos 7pi/6 можно рассчитать, построив угол 7π/6 радиан с осью x, а затем найдя координаты соответствующей точки (-0,866, -0,5) на единичной окружности. Значение cos 7pi/6 равно координате x (-0,866). ∴ cos 7pi/6 = -0,866.

Как найти Cos 7pi/6 с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение cos 7pi/6 может быть выражено через другие тригонометрические функции следующим образом:

  • ± √(1-sin²(7pi/6))
  • ± 1/√(1 + tan²(7pi/6))
  • ± раскладушка(7pi/6)/√(1 + раскладушка²(7pi/6))
  • ±√(косек²(7pi/6) — 1)/косек(7pi/6)
  • 1/сек (7pi/6)

☛ Также проверьте: тригонометрическую таблицу

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядная программа

Mathway | Популярные проблемы

92
1 Найдите точное значение грех(30)
2 Найдите точное значение грех(45)
3 Найдите точное значение грех(30 градусов)
4 Найдите точное значение грех(60 градусов)
5 Найдите точное значение загар (30 градусов)
6 Найти точное значение угловой синус (-1)
7 Найдите точное значение грех(пи/6)
8 Найдите точное значение cos(pi/4)
9 Найдите точное значение грех(45 градусов)
10 Найдите точное значение грех(пи/3)
11 Найдите точное значение арктический(-1)
12 Найдите точное значение cos(45 градусов)
13 Найдите точное значение cos(30 градусов)
14 Найдите точное значение желтовато-коричневый(60)
15 Найдите точное значение csc(45 градусов)
16 Найдите точное значение загар (60 градусов)
17 Найдите точное значение сек (30 градусов)
18 Найдите точное значение cos(60 градусов)
19 Найдите точное значение соз(150)
20 Найдите точное значение грех(60)
21 Найдите точное значение cos(pi/2)
22 Найдите точное значение загар (45 градусов)
23 Найдите точное значение arctan(- квадратный корень из 3)
24 Найдите точное значение csc(60 градусов)
25 Найдите точное значение сек (45 градусов)
26 Найдите точное значение csc(30 градусов)
27 Найдите точное значение грех(0)
28 Найти точное значение грех(120)
29 Найдите точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найдите точное значение
35 Преобразовать из радианов в градусы пи/6
36 Найдите точное значение детская кроватка(30 градусов)
37 Найдите точное значение арккос(-1)
38 Найдите точное значение арктический(0)
39 Найдите точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найдите точное значение sin((5pi)/3)
43 Найдите точное значение sin((3pi)/4)
44 Найдите точное значение желтовато-коричневый (pi/2)
45 Найдите точное значение грех(300)
46 Найдите точное значение соз(30)
47 Найдите точное значение соз(60)
48 Найдите точное значение соз(0)
49 Найдите точное значение соз(135)
50 Найдите точное значение cos((5pi)/3)
51 Найдите точное значение соз(210)
52 Найдите точное значение сек (60 градусов)
53 Найдите точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найдите точное значение грех(135 градусов)
61 Найдите точное значение грех(150)
62 Найдите точное значение грех(240 градусов)
63 Найдите точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найдите точное значение грех(225)
66 Найдите точное значение грех(240)
67 Найдите точное значение cos(150 градусов)
68 Найдите точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найдите точное значение сек(0)
71 Найдите точное значение cos((5pi)/6)
72 Найдите точное значение КСК(30)
73 Найдите точное значение arcsin(( квадратный корень из 2)/2)
74 Найдите точное значение желтовато-коричневый ((5pi)/3)
75 Найдите точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найдите точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 шт. )/4
79 Найдите точное значение sin((7pi)/4)
80 Найдите точное значение угловой синус(-1/2)
81 Найдите точное значение грех((4pi)/3)
82 Найдите точное значение КСК(45)
83 Упростить арктан( квадратный корень из 3)
84 Найдите точное значение грех(135)
85 Найти точное значение грех(105)
86 Найдите точное значение грех(150 градусов)
87 Найдите точное значение грех((2pi)/3)
88 Найдите точное значение желтовато-коричневый ((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найдите точное значение грех(пи/2)
91 Найдите точное значение сек(45)
92 Найдите точное значение cos((5pi)/4)
93 Найдите точное значение cos((7pi)/6)
94 Найдите точное значение угловой синус(0)
95 Найдите точное значение грех(120 градусов)
96 Найдите точное значение желтовато-коричневый ((7pi)/6)
97 Найдите точное значение соз(270)
98 Найдите точное значение sin((7pi)/6)
99 Найдите точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Как найти значение cos((7pi)/6)?

Тригонометрия

Наука
  • Анатомия и физиология
  • астрономия
  • Астрофизика
  • Биология
  • Химия
  • науки о Земле
  • Наука об окружающей среде
  • Органическая химия
  • Физика
Математика
  • Алгебра
  • Исчисление
  • Геометрия
  • Преалгебра
  • Предварительный расчет
  • Статистика
  • Тригонометрия
Гуманитарные науки
  • Английская грамматика
  • История США
  • Всемирная история
    .

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *