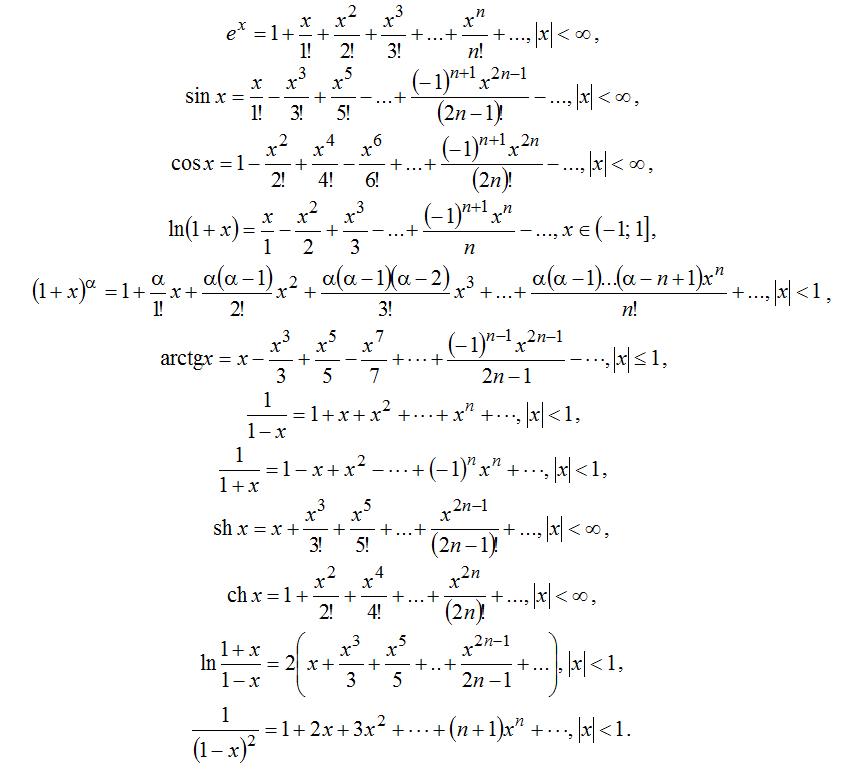Формулы Маклорена и Тейлора
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Многочлен Тейлора и остаточный член
2. Формула Тейлора
3. Формула Маклорена
Многочлен Тейлора и остаточный член
Пусть задана функция f(x), которая некоторое число раз дифференцируется в точке x0. Найдем многочлен n-й степени вида
Для которого выполняются равенства
Для того, чтобы вычислить коэффициенты многочлена, найдем его производные и рассчитаем их значения в точке х0.
Таким образом, коэффициенты имеют вид:
А многочлен называемый многочленом Тейлора:
Разность между функцией и многочленом носит название остаточного члена.
Формула Тейлора
Формула Тейлора в общем виде:
Формула Маклорена
Формула Маклорена это упрощенное представление формулы Тейлора при х0=0
Пример 1
Разложить в ряд Тейлора функцию в точке x0 = 1.
{4} \]
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 14.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
4.
23. Формулы Маклорена и ТейлораВ предыдущем параграфе был получен простейший вариант формулы Тейлора – формула (5.9). Эта формула приближенная, и она тем точнее, чем меньше . Но хотелось бы знать больше. Хотелось бы иметь оценку погрешности этой формулы. А еще лучше – иметь возможность заменить эту формулу на более точную, такую, чтобы ее погрешностью заведомо можно было бы пренебречь. С этой целью проведем в формуле (5.9) переобозначения:
· старое обозначение X – новое обозначение X0;
· старое обозначение – новое обозначение X;
· старое обозначение – новое обозначение .
Тогда формула (5.9) пример вид:
(6.1)
То есть получаем приближенную формулу вида
, (6.2)
Где ; . Использование этой приближенной формулы равносильно замене кривой на прямую с уравнением , которая является касательной, проведенной к графику функции в точке
Действительно, прямая проходит через точку .
Кроме того, она имеет угловой коэффициент . А это и есть, согласно геометрического смысла производной (см. 1.11), угловой коэффициент касательной, проведенной к графику функции в точке M0. Для приближенная формула (6.2) становится точной. А для она, очевидно, тем точнее, чем ближе X к X0.
Для X, очень близких к X0, замена кривой на касательную к ней, или как еще говорят, Аппроксимация кривой её касательной, очевидно, вполне оправдана. Но с удалением X от X0 расхождение между кривой и касательной к ней может стать существенным, а формула (6.2) может стать слишком грубой.
Возникает естественная мысль: поискать замену кривой не на прямую, а на другую кривую, только более простую (на параболу, гиперболу, и т. д.). В соответствии с этой мыслью приближенные значения функции для X, близких к X0, будем искать по обобщению формулы (6.2):
(6.3)
В простейшем случае формула (6.3) совпадает формулой (6.
2). А при мы вправе ожидать, что формула (6.3) окажется более точной, чем формула (6.2), и что ее точность будет возрастать с увеличением числа N. Действительно, аппроксимация кривой параболой (при ), кубической параболой (при ) и т. д. более естественна, чем аппроксимация кривой какой угодной прямой. И чем сложнее аппроксимирующая кривая, тем качественнее может быть осуществлена эта аппроксимация. В том числе и для X, достаточно удаленных от X0.
Потребуем, чтобы формула (6.3), как и ее частный случай (6.2), была точной при . Тогда получим:
(6.4)
Найдем остальные коэффициенты формулы (6.3). Предположим, что функцию можно сколько угодно раз дифференцировать в некоторой окрестности точки , и продифференцируем обе части приближенного равенства (6.3) до N-го порядка включительно:
;
; (6.5)
————————————————————————-
Здесь использовано обозначение:
(эн – факториал) (6.
6)
В частности,
; ; ; … (по определению) (6.7)
Приближенные равенства (6.5), как и исходное равенство (6.3), должны быть тем точнее, чем ближе X к X0. Потребовав, чтобы при все они стали точными, получим:
; ; ; …
Отсюда
; ; ; … (6.8)
Подставляя выражения (6.8) в (6.3), получим для X, близких к X0:
(6.9)
Полученная ранее формула (6.1) является простейшим частным случаем этой формулы при .
Формула (6.9) – приближенная. Следует ожидать, что ее точность должна повышаться как при приближении X к X0, так и при увеличении числа ее слагаемых N. Но чтобы убедиться в этом окончательно, следует получить оценку погрешности этой формулы для всех N, начиная с .
Обозначим символом эту погрешность ( – разность между левой и правой частями формулы (6.9)). Тогда получим Точно Для любых х и N:
(6.10)
Формула (6.10) называется Формулой Тейлора.
Последнее слагаемое называется Остаточным членом формулы Тейлора. Поэтому еще говорят, что (6.10) – это Формула Тейлора с остаточным членом.
При практическом использовании формулы Тейлора ее остаточный член отбрасывают, переходя тем самым к приближенной формуле (6.9), которую называют Формулой Тейлора без остаточного члена
(6.11)
Если – допустимая погрешность вычисления функции , то для данных X и X0 подбирают такое значение N, чтобы .
При формула Тейлора (6.10) принимает вид
(6.12)
И называется Формулой Маклорена. Ее остаточный член оценивается по формуле (6.13), вытекающей из (6.11) при :
(6.13)
Формулой Маклорена, после оценки и отбрасывания ее остаточного члена, пользуются для приближенного вычисления значений при X, близких к нулю.
Пример 1. Вычислить с точностью до 0,001.
Решение. Рассмотрим функцию (X – в радианах). Тогда . То есть при . Так как и близок к нулю, то для приближенного вычисления воспользуется формулой Маклорена (6.12). Но для этого сначала нужно найти такое значение N, чтобы остаточный член этой формулы по абсолютной величине был заведомо меньше 0,001. Тогда, отбросив его в формуле Маклорена (6.12) и подсчитав сумму оставшихся слагаемых, получим нужное значение с точностью до 0,001.
Сначала оценим первый множитель в формуле (6.13):
. (6.14)
Имеем:
;; ; …
Таким образом, производные функции любого порядка равны либо , либо . А значит, при любых X они по абсолютной величине не превосходят единицы. Следовательно, при любых и любых N имеем:
(6.15)
С учетом (6.15) оценка (6.13) остаточного члена формулы Маклорена при принимает вид:
(N = 1, 2,…) (6.16)
Оценим значение правой части этого неравенства при различных N:
; ;
; ;
; .
Для правая часть неравенства (6.16), а следовательно, и его левая часть, будут еще меньше, чем при . Таким образом, если мы возьмем , то – это нас устроит. Тогда записывая формулу Маклорена (6.12) для при и отбрасывая в ней остаточный член, получим:
Итак, – с точностью до 0,001. Сверяя это значение с табличным (по таблице Брадиса ), видим, что у нас нет расхождения даже в десятитысячных.
Кстати, если бы в формуле Маклорена (6.12) мы взяли (, и т. д.), то получили бы значение еще точнее. В принципе – как угодно точно.
Совершенно аналогично с помощью формулы Маклорена (если X близок к 0), или с помощью формулы Тейлора (если X далек от 0, но близок к некоторому удобному для расчетов значению X0), можно вычислять приближенные значения И других многократно дифференцируемых функций. Именно на использовании этих формул и основано составление таблиц значений различных функций.
Упражнения
1. Вычислить с точностью до 0,01 (учесть, что ).
Ответ: .
2. Вычислить с точностью до 0,01 (учесть, что ).
Ответ: .
3. Вычислить с точностью до 0,00001 (учесть, что ).
Ответ: .
| < Предыдущая | Следующая > |
|---|
Формула Тейлора и ее применение с примерами решения
Содержание:
Формула Тейлора
Теорема: Если функция
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора называется остаточным членом, вид которого установил Лагранж: величина
В этой формуле неизвестной является только величина причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид:
При a = 0 формула Тейлора переходит в формулу Маклoрена:
Пример:
Представить по формуле Маклорена функцию ограничившись n=2.
Решение:
Вычислим три первых производных заданной функции:
При х = 0 получим Остаточный член имеет вид Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид: Отметим, что полученное выражение справедливо при Решим найденное равенство относительно величины Отсюда получаем Следовательно, Так как выражение под радикалом 4-ой степени должно быть неотрицательным и Таким образом, из двух корней теореме Тейлора удовлетворяет только корень который действительно лежит между нулем и х.
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
(см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем Если положить то получим формулу
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора.
Для оценки погрешности вычислений необходимо помнить, что величина в остаточном члене в форме Лагранжа лежит в пределах от а до х.
Пример:
Представить функцию по формуле Маклорена.
Решение:
Так как Следовательно, где Отсюда следует,
Пример:
Вычислить с точностью
Решение:
Так как основание Следовательно, при х = 1/2 остаточный член равен При n = 3: остаточный член Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что
Пример:
Вычислить число е с точностью
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа
При n = 6 имеем
при n = 7 получаем
Итак,
Если вычислять значение числа е с точностью то потребуется взять 13 первых слагаемых, при этом Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций.
Например, для вычисления натуральных логарифмов используется формула:причем
Пример:
Вычислить с точностью
Решение:
В данном примере х = -0,1. Так как следовательно, остаточный член При n = 1 получаем Следовательно, достаточно взять первый член в формуле Маклорена-Тейлора
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке . Тогда (см. формулу (9.5)) ее приращение
Пусть тогда (14.1) перепишется в виде
Рассмотрим многочлен
Многочлен обладает следующими свойствами:
Пусть функция y=f(x) n раз дифференцируема в точке . Найдем многочлен
обладающий аналогичными свойствами:
Из (14.2), (14.3) следует, что
Поэтому коэффициенты многочлена (14.2) задаются формулой
Далее
Таким образом свойства (14.3) выполняются (при этом коэффициенты
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке , тогда
где – бесконечно малая функция более высокого порядка
малости, чем
Формула (14.5) называется формулой Тейлора, многочлен
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности в виде – остаточным членом в форме Пеано.
Если функция то (14.5) перепишется в виде
формула Маклорена.
Если функция раз дифференцируема в некоторой окрестности
точки , то остаточный член можно представить в виде
остаточный член в форме Лагранжа и формула
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа:
Поэтому
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x:
(см. упражнение 10.1)
Таким образом, и по формуле (14.6)
Аналогично
Формулы (14.7)–(14.11) называются основными разложениями.
- Заказать решение задач по высшей математике
Пример 14.3
Разложить по формуле Маклорена до члена используя основные разложения. Оценить погрешность при
Решение
Пусть Тогда (см. формулу (14.10))
Остаточный член запишем в форме Лагранжа:
поэтому
Таким образом, и погрешность при меньше чем
Пример 14.4
Найти
Решение
Воспользуемся разложением (14.7):
Тогда
Серия Маклорена | Brilliant Math & Science Wiki
Содержание
- Вывод
- Интервал и радиус сходимости
- Часто используемая серия Maclaurin
- Серия Тейлора 9{(k)}(0) = 0f(k)(0)=0 в противном случае.
- Численный анализ
- Серия
- Серия Тейлор
k}{k} ∑k=1∞kxk. 9k}{k}∑k=1∞k(−1)k. Это знакопеременный гармонический ряд, который сходится по критерию знакопеременного ряда.Следовательно, интервал сходимости равен [−1, 1)[-1, \, 1)[−1,1), а радиус сходимости равен 111. □_\square□
Полезно отметить, что для простых функций, таких как приведенная выше, 111 и ∞\infty∞ являются общими радиусами сходимости.
Большинство рядов Маклорена, выразимых в терминах элементарных функций, можно определить через состав и комбинацию следующих функций: 9{2k + 1}.\ _\squaref(t)=∫0tk=0∑∞(−u2)kdu=k=0∑∞∫0t(−1)ku2kdt=k=0∑∞ 2k+1(−1)kt2k+1. □
1 2 3 4 5 6 Ничего из вышеперечисленного
Найдите значение константы nnn, удовлетворяющее
9n+\cdots.
n=0∑∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+2!f′′(a )(x−a)2+⋯+k!f(k)(a)(x−a)n+⋯.Цитировать как: Серия Маклорена. Brilliant.org . Извлекаются из https://brilliant.org/wiki/maclaurin-series/
Новое открытие одной из самых замечательных математических формул | Каспер Мюллер
Доказательство красивой и невероятно полезной формулы суммирования Эйлера–Маклорена — с нуля
Якоб Бернулли — Изображение с Wikimedia Commons .Хотя это скорее шутка, чем правда, каждый раз, когда это случалось со мной, вскоре после этого я обнаруживал числа Бернулли.
Сначала они прятались в расчетах, но потом как будто выскочили повсюду. Это случалось со мной несколько раз, и я подозреваю, что это случалось со многими людьми до меня.
Вам не нужно ничего знать о числах Бернулли, чтобы следовать этой статье.
На самом деле, вам вообще не нужно много знать, потому что мы начнем с самого начала, с суммы по функции.
Отсюда мы будем наблюдать, как красота разворачивается на другой стороне уравнения, пока мы не получим красивую формулу, известную как формула Эйлера-Маклорена.
Мы даже докажем его версию с явным остаточным членом.
По пути мы приобретем некоторые предпосылки, в том числе кое-что из этих загадочных чисел Бернулли. На данный момент единственное, что вы должны знать о них, это то, что они являются рациональными числами, их бесконечно много, и они появляются повсюду в поле 9.0173 теория чисел . Это делает их, без тени сомнения, одними из самых важных рациональных чисел, которые у нас есть.
Начнем с довольно общего случая суммы. В частности, предположим, что вы хотите вычислить следующее:
, где m и n — целые числа, такие что m ≤ n и f — дифференцируемая функция. Через минуту вы поймете, почему мы хотим, чтобы f было дифференцируемым.
Например, если f (x) = x³ и мы выбираем m=1 , наша вышеуказанная сумма становится 1³ + 2³ + ⋅⋅⋅ + n³ .
Подобно подстановкам в интегралах, мы можем манипулировать суммами, соответствующим образом изменяя индекс и слагаемые. Мы также воспользуемся тем, что сумма разности есть разность сумм. Рассмотрим следующие расчеты.
Обратите внимание на изменение индекса суммирования в третьей строке и на то, что наши попытки получить тот же индекс в двух суммах после изменения индекса добавили значения f(n)n — f(m)(m-1) . В конце мы используем фундаментальную теорему исчисления , чтобы записать разность в виде интеграла.
Прежде чем двигаться дальше, нам нужно познакомиться с некоторыми разрывными функциями.
В частности, нам нужно ознакомиться с двумя важными функциями, а именно с функцией пола и функцией дробной части .
Полная функция x, которую мы будем обозначать [x] , возвращает наибольшее целое число, меньшее или равное x , поэтому он «округляется» до ближайшего целого числа, например.
[2,3] = 2 .
Функция дробной части x , обозначенная как {x} , определяется как {x} = x — [x] или эквивалентно [x] = x — {x} и, таким образом, {2.3} = 0,3 . Дробная часть является периодической функцией периода 1 , что означает {x + 1} = {x} для всех x .
Продолжая вычислять приведенную выше сумму, мы замечаем, что если x ∈ [k, k+1) , то [x] = k , и поэтому мы можем немного переписать сумму выше. Рассмотрим следующее:
Это круто. Мы превратили сумму в интеграл. Подынтегральная функция может выглядеть немного неприятно из-за разрыва функции пола, но мы еще далеки от завершения.
Эта формула на самом деле является частным случаем более общего результата, известного как формула суммирования Абеля .
Прежде чем двигаться дальше, вспомним правило интегрирования по частям:
, где F(x) является производной f(x) .
Мы будем широко использовать это в этой статье, и на самом деле это также работает, даже если f не является непрерывным, чем мы и воспользуемся. Чтобы объяснить, почему это так, требуется теория интеграла Римана – Стилтьеса, которую я не буду здесь развивать.
Записав [x] = x — {x} , мы можем разделить интеграл.
, где мы использовали интегрирование по частям.
Обратите внимание, что эта формула на самом деле говорит о том, что сумма, подобная той, что в левой части, может быть аппроксимирована интегралом с ошибкой, связанной с дробной частью.
Следующий шаг требует некоторой математической интуиции. Мы интегрируем по целому интервалу чисел, и одним из множителей подынтегральной функции является функция дробной части.
Хотя этот интеграл «погрешности» не обязательно слишком велик, было бы определенно лучше, если бы мы сдвинули функцию дробной части вниз на 1/2, сделав интеграл от нее по целому интервалу чисел равным 0.
В других Словом, составим интеграл ошибки с коэффициентом {x} — 1/2.
Мы можем сделать это с помощью небольшого, но часто используемого и упускаемого из виду трюка: складывать и вычитать одно и то же число.
и у нас осталось нечто поразительное!
Прежде чем двигаться дальше, нам нужно знать, как интегрировать функцию дробной части. В частности, мы можем найти площадь под кривой от 0 до x как «первообразную» и использовать ее для интегрирования по частям интеграла выше.
Однако для этого нам нужен следующий результат:
Мы можем доказать это разными способами, и я позволю читателю сделать это небольшим упражнением.
Теперь понятно, что мы вычли 1/2, верно? При интегрировании {x} — 1/2 линейный член исчезает, и мы позаботились о том, чтобы результирующий фактор был периодическим и хорошо ограниченным.
Если мы проинтегрируем по частям вышеизложенное, используя наши интегралы с дробными частями, мы получим:
Мы еще не закончили, но пришло время отложить ручку и бумагу, пойти приготовить чашку теплого кофе и, возможно, сделать небольшое резюме того, что мы только что сделали в твоей голове.
Мы продолжим разработку вышеуказанной формулы, несмотря на то, что она уже достаточно хороша.
Но сначала нам нужно познакомиться с еще некоторыми теоретико-числовыми драгоценностями.
От разложения Тейлора функции тангенса до целых значений дзета-функции Римана числа Бернулли встречаются во всех видах выражений в теории чисел и анализе.
Первоначально они изучались из-за их появления в замкнутых формулах для сумм степеней. Первым, кто понял, что такая последовательность чисел существует, был швейцарский математик Якоб Бернулли (1654–1705).
Все числа Бернулли являются рациональными числами, и последовательность начинается с
Здесь уместно несколько комментариев. Прежде всего, обратите внимание на B1 = ±1/2. Это потому, что используются два соглашения. Одна последовательность, где B1 = 1/2, и одна последовательность, где B1 = -1/2.
Все нечетные индексированные числа Бернулли, за единственным исключением B1, равны 0, и кажется, что четные индексированные числа ведут себя довольно хорошо и становятся все меньше и меньше с 1 в числителе, но последовательности могут быть хитрыми.
По индексу 12 получаем -691/2730 и по индексу 20 получаем -174611/330 — к сожалению, они немного сложнее.
Так как же они определяются?
Существует множество определений и формул для получения чисел Бернулли. Одной из таких формул является
, где верхний индекс указывает, что B1 = -1/2 .
Существует множество формул с участием чисел Бернулли, и веселье никогда не заканчивается, однако нам нужно вернуться в нужное русло, потому что у нас есть «своя» формула, которую нужно доказать!
Мы получили интеграл с полиномом дробной части и второй производной от f , удалив линейный член после интегрирования множителя дробной части.
Оказывается, это полезно делать каждый раз, когда мы используем интегрирование по частям, получая множители дробных частей, умноженные на производные возрастающего порядка.
Например, мы видим, что интеграл от ({x} — {x}²)/2 с помощью формулы площади для функции дробной части равен n -я степень, 1/12(x — {x}) + 1/4{x}² — 1/6{x}³.
Если мы хотим удалить линейный множитель x/12, мы должны вычесть его из интеграла, что эквивалентно вычитанию константы 1/12 под знаком интеграла.
У нас есть следующее:
и после некоторого интегрирования по частям в последнем интеграле и большой очистки, мы приходим к:
Теперь, если вы продолжите в том же духе, получится закономерность, и наметанный глаз , там можно обнаружить спрятанные числа Бернулли. Последний интеграл в формуле будем называть «остаточным членом».
Записав некоторые рекуррентные соотношения от интегрирования по частям на множителях дробной части и внимательно изучив их, вы действительно можете доказать, как вписываются числа Бернулли, и, продолжая удалять линейные члены из подынтегральных выражений, мы, наконец, придем к это жемчужина короны формулы.
Об этом факте можно так много сказать, что я не знаю, с чего начать.
Во-первых, мы могли бы заметить, что если бы мы суммировали от k=0 вместо k=1, разность в скобках включала бы интеграл, таким образом, более естественной формой этой теоремы, возможно, была бы сумма от 0 вместо интеграл, однако, я хотел бы оставить его там, чтобы напомнить мне, что материал справа от интеграла на самом деле является способом выражения разницы между интегралом и суммой.
Также обратите внимание, что остаточный член, выраженный в терминах так называемых периодизированных полиномов Бернулли, естественным образом выпал из наших расчетов как побочный продукт нашего мышления.
Если вы посмотрите эту формулу, например. Википедия, вы не получите такого явного остаточного члена, а скорее некоторые повторения и начальные условия. Конечно, мы также должны убедиться, что функция f дифференцируема в r+1 раз.
Последний шаг, который мы предпримем, — дело вкуса. Видите ли, эта формула имеет множество версий. Мне лично нравится использовать его на сумме от м вместо м+1 в левой части уравнения. Это довольно легко получить, так как мы можем просто добавить f(m) с обеих сторон.
Красивая теорема состоит в следующем.
Формула суммирования Эйлера-Маклорена с явным остаточным членом:
Мы собираемся повеселиться с этой формулой, раскрывая ее истинную силу и показывая, что она не только красива, но и невероятно полезна.
У этой формулы очень много применений. Как для реальных вычислений, так и для асимптотического анализа. Поскольку я не ввел большое обозначение O и все другие приемы асимптотики, мы будем использовать его в основном для реальных вычислений в этом посте.
Треугольные числа
Говорят, что его учитель попросил Гаусса сложить все натуральные числа от 1 до 100. В то время как большинство учеников строчили как сумасшедшие, а учитель откинулся назад, ожидая долгого перерыва, юный Гаусс за считанные секунды нашел правильный ответ 5050.
Мы не знаем, верна ли эта история, но, вероятно, что-то в этом роде произошло. Давайте посчитаем эту сумму по приведенной выше формуле Эйлера-Маклорена.
В частности, пусть f(x) = x и m = 1 .
Подстановка n=100 , конечно же, дает нам желаемый результат. Что ж, это было почти слишком просто. Обратите внимание, что мы могли бы суммировать с 0 вместо 1, что упростило бы наши вычисления.
Мы немного воспользуемся этим наблюдением.
Дзета-функция Римана
В последние пару лет велись довольно горячие математические дебаты о расходящемся ряду 1 + 2 + 3 + … , и люди с трудом понимают, как формальная величина -1/12 можно отдать такому зверю. Как насчет того, чтобы попытаться оценить дзета-функцию Римана при -1? В определении ряда дзета-функции Римана это соответствовало бы приведенному выше расходящемуся ряду, если бы мы использовали определение ряда для ζ.
Применим формулу Эйлера-Маклорена к дзета-функции Римана. Мы начнем с предположения, что у нас есть комплексное число s с Re(s) > 1.
В этом случае ряд сходится, и мы имеем
, и удивительно то, что теперь мы можем оценить дзета функция всякий раз, когда остаточный член сходится.
Непонятно, почему это нормально, поскольку мы заставили все это работать, предположив, что действительная часть s больше, чем 1 . В противном случае у нас не было бы значимой серии для начала.
Причина связана с концепцией комплексного анализа, называемой аналитическим продолжением , но я пока оставлю это, чтобы сделать эту статью немного неформальной.
В частности, теперь мы можем подставить s=-1 и вуаля, остаточный член равен нулю, и мы получаем ζ(-1) = -1/12, как и ожидалось. Но обратите внимание, что мы не (незаконно) манипулировали какими-либо рядами, чтобы попасть туда, мы просто использовали формулу.
Произошла еще одна поразительная вещь. Если s=-2, остаточный член также обращается в нуль, показывая, что ζ(-2) = 0. Это «первый» из тривиальных нулей дзета-функции Римана. Также имеем ζ(0) = 1/2.
Все это по формуле Эйлера-Маклорена с r=2 . О, и это также объясняет, откуда берется якобы странное число -1/12. Оно отрицательно из-за отрицательного аргумента -1 и равно -B2/2!.
Формула Бернулли
Выведем формулу суммы степеней. Мы видели формулу для суммы первых n натуральных числа в степени 1 , а именно 1 + 2 + 3 + 4 + ⋅⋅⋅ + n = n(n+1)/2 .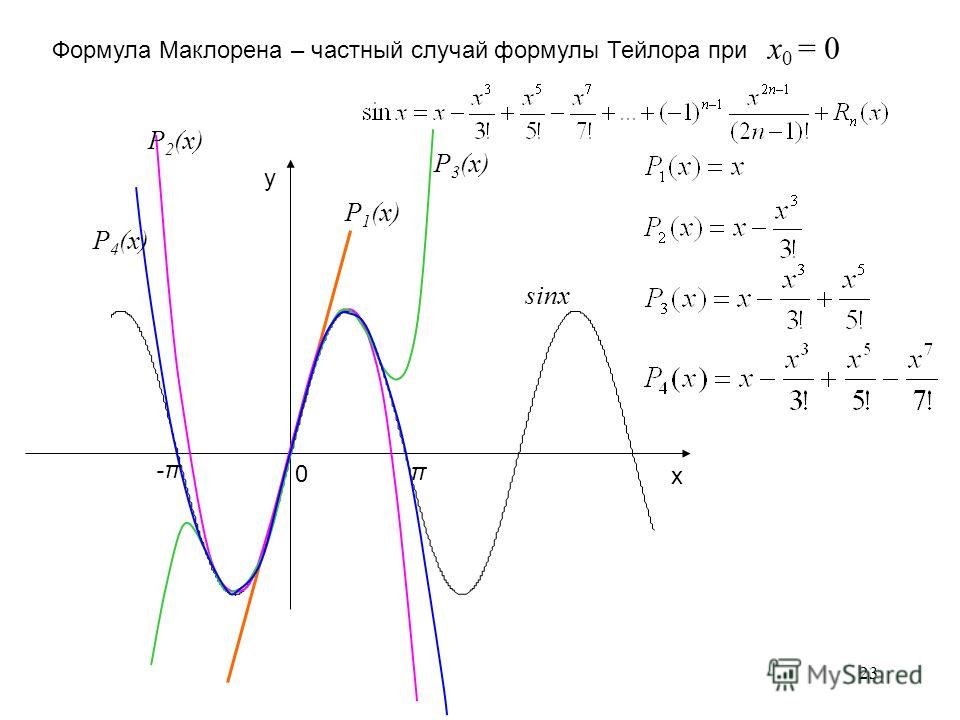
Но как насчет вторых степеней, третьих степеней и так далее?
Сам Якоб Бернулли нашел общую формулу для этих сумм, но, как ни странно, она не названа в его честь. Она называется Формула Фаульхабера . Применим формулу к этому случаю.
Обратите внимание, как мы упростили вычисление, просуммировав 0 вместо 1 . Мы, конечно, получили бы тот же результат, если бы просуммировали из 1 , но это упростило расчеты. Также обратите внимание, что мы разделили на p+1 вне суммы, чтобы записать слагаемые с биномиальными коэффициентами.
Мы можем записать это немного более компактно, используя также первые два числа Бернулли:
Формула Бернулли/Фаульхабера:
Эта удивительная формула просто выпала из суммирования Эйлера-Маклорена как самая естественная вещь! Без каких-либо усилий с нашей стороны.
Мы начали с простой суммы дифференцируемых арифметических функций. Сумма!
Затем мы применили к сумме некоторые полезные приемы и преобразования, в результате чего получили явную форму формулы суммирования Абеля.
Затем мы использовали некоторые свойства функции дробной части, в том числе формулу интеграла от степеней дробной части. Это оказалось полезным, когда мы попытались исключить линейный член этой формулы в нашем остаточном члене.
Это привело к постоянному использованию интегрирования по частям к взвешенной сумме разностей n Производные -го порядка от функции, по которой мы просуммировали в первую очередь.
Эти веса оказались Бк/к! и привели к красивой формуле суммирования Эйлера-Маклорена.
После открытия мы применили эту формулу к известным суммам с известными значениями и закрытыми формами.
В этой статье я стремился к интуитивности, красоте и пониманию. Не строгость… Я уверен, что вы можете заполнить необходимые детали относительно того, какое пространство арифметических функций и проблемы сходимости.
Кроме того, на данный момент, возможно, неясно, откуда именно взялись числа Бернулли. Я призываю вас узнать себя.
Это определенно было весело! Я надеюсь, что я помог некоторым из вас понять происхождение этой формулы.
Обычно вы доказываете формулу Эйлера-Маклорена по индукции, но, делая это таким образом, не только ясно, откуда она берется, но и мы получаем очень явный остаточный член.
Эта формула по-разному записывается в литературе. Это не значит, что существует много разных формул, это просто означает, что вы можете написать это разными способами.
Например, причина «отсутствия» r -й производной в нашем варианте формулы — дело вкуса. Мы избавились от постоянного члена, еще раз проинтегрировав по частям, и получили периодический множитель, но это просто наш выбор.
Если вам нравится читать подобные статьи на Medium, вы можете получить членство для полного доступа: просто нажмите здесь .
Mathwords: Серия Маклорена
Mathwords: Серия Маклорена
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
