Элементарные функции комплексного переменного
Показательная функция комплексного переменного определяется равенством
Из определения видно, что это периодическая функция с основным периодом:. Основное свойство (также как у показательной функции действительного переменного).
Логарифмическая функция. Эта функция определяется как обратная показательной: число w называется логарифмом числа z, если. Обозначение:. Следующее равенство можно принять за определение логарифмической функции комплексного переменного:
.
В отличие от функции действительного переменного Ln z является многозначной функцией; значение при k = 0 называется главным значением или главной ветвью логарифмической функции в комплексной области и обозначается ln z:
Из определения вытекают основные функциональные свойства логарифмической функции:
,
Общие показательные и общие степенные
функции.
Так называют функции комплексного переменного определяемые равенствами соответственно
Общая показательная и общая степенная функции комплексного переменного в являются многозначными. Тригонометрические функции определяются (посредством формулы Эйлера) через показательную:
Эти формулы также называются формулами Эйлера. По аналогии с функциями действительного переменного определяются функции tg z и ctg z:
Для тригонометрических функций комплексного переменного справедливы все формулы, справедливые для соответствующих функций действительного переменного. Для примера, исходя из формул (9.4) (9.5), докажите равенства
, ,
, .
Гиперболические функции определяются (как и тригонометрические) через показательную функцию.
Гиперболический синус
Гиперболический косинус
Гиперболический тангенс
Гиперболический котангенс
Из определений гиперболических и тригонометрических функций вытекают формулы
, ,
,
.
Замечание. Любое соотношение, справедливое между тригонометрическими функциями переходит в соответствующее соотношение между гиперболическими функциями в результате формальной замены функций и. Например, совершив указанную замену в соотношениях
,
получим следующие соотношения между гиперболическими функциями
, .
Обратные тригонометрические функции определяются как функции обратные тригонометрическим. Эти функции являются многозначными и выражаются через логарифмы комплексного переменного по формулам
,
,
Обратные гиперболические функции обозначаются соответственно Arsh z (ареасинус), Arch z (ареакосинус), Arth z (ареатангенс), Arcth z (ареакотангенс). Это опять многозначные функции, которые выражаются через логарифмы комплексного переменного по формулам
,
(2. 9)
9)
, . (2.10)
2.2 Примеры с решениями В задачах 1-7 значения соответствующих функций представить в алгебраической форме.
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 |
math.
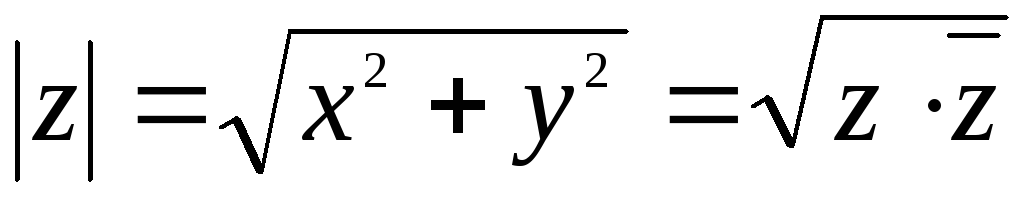 h — frwiki.wiki
h — frwiki.wikimath.h — это группа функций из стандартной библиотеки C, которая позволяет использовать набор основных математических функций с использованием чисел с плавающей запятой . Различные стандарты C реализуют их по-разному, но всегда остаются обратно совместимыми. Большинство этих функций также доступны в стандартной библиотеке C ++, хотя и в отдельном заголовке (заголовки C включены, но только для совместимости).
Резюме
- 1 Обзор функций
- 1.1 Среда с плавающей точкой
- 1.2 Комплексные числа
- 1.3 Генерация случайных чисел
- 2 библиотеки в минуту
- 3 Примечания и ссылки
- 4 Внешние ссылки
Обзор функций
Большинство функций содержится в заголовке math.h (или в заголовке cmath в C ++). Функции, которые работают с целыми числами, такие как abs, labs, div или ldiv, указаны в stdlib.h ( cstdlib в C ++).
Все функции, которые включают углы, используют радиан как единицу измерения.
Не все функции присутствуют в версии C89 стандарта C. Для тех, которые есть, функции принимают только тип double для операций с числами с плавающей запятой. В стандарте C99 это ограничение было снято путем введения новой серии функций, работающих с параметрами типа float или long double . Эти функции могут быть обозначены суффиксом f или l соответственно .
| Функция | Описание | |
|---|---|---|
abslabsllabs | вычисляет абсолютное значение целого числа | |
fabs | вычислить абсолютное значение числа типа float | |
divldivlldiv | вычислить частное и остаток от евклидова деления | |
fmod | остаток от деления чисел с плавающей запятой | |
| подписанный остаток от операции деления | |
remquo | остается подписанным, а также последние три бита операции деления | |
fma | Умножить, затем сложить (Умножить-накопить) | |
fmax | максимум два значения с плавающей запятой | |
fmin | минимум два значения с плавающей запятой | |
fdim | положительная разница двух значений с плавающей запятой | |
nannanfnanl | Возвращает не-число (NaN) | |
| Экспоненциальные функции | exp | возвращает e в запрошенной степени |
exp2 | возвращает 2 в запрошенной степени | |
expm1 | возвращает e high до запрошенной мощности минус 1 | |
log | вычислить натуральный логарифм (по основанию е) | |
log2 | вычислить двоичный логарифм (по основанию 2) | |
log10 | вычислить десятичный логарифм (по основанию 10) | |
log1p | вычислить натуральный логарифм (с основанием е) 1 плюс заданное число | |
ilogb | извлекает экспоненту числа | |
logb | извлекает экспоненту числа | |
| Силовые функции | sqrt | вычислить квадратный корень |
cbrt | вычислить кубический корень | |
hypot | вычислить квадратный корень из суммы квадратов двух заданных чисел | |
pow | возвести число в указанную степень | |
| Тригонометрические функции | sin | вычислить синус |
cos | вычислить косинус | |
tan | вычислить касательную | |
asin | вычислить арксинус | |
acos | вычислить арккосинус | |
atan | вычислить арктангенс | |
atan2 | вычислить арктангенс, используя знак для определения квадранта | |
| Гиперболические функции | sinh | вычислить гиперболический синус |
cosh | вычислить гиперболический косинус | |
tanh | вычислить гиперболический тангенс | |
asinh | вычислить дугу гиперболического синуса | |
acosh | вычислить гиперболический арккосинус | |
atanh | вычислить гиперболический арктангенс | |
| Функция ошибки и гамма-функция | erf | вычислить функцию ошибок |
erfc | вычислить дополнительную функцию ошибок | |
lgamma | вычислить натуральный логарифм модуля гамма-функции | |
tgamma | вычислить гамма-функцию | |
| Операции округления | ceil | возвращает ближайшее большее целое число |
floor | возвращает ближайшее меньшее целое число | |
trunc | возвращает ближайшее целое число, абсолютное значение которого меньше | |
roundlroundllround | возвращает ближайшее целое число, следуя правилам округления | |
nearbyint | возвращает ближайшее целое число, используя текущий метод округления | |
rintlrintllrint | возвращает ближайшее целое число, используя текущий метод округления, за исключением случаев, когда результат отличается | |
| Функции для управления числами с плавающей запятой | frexp | разложите параметр на число и степень двойки |
ldexp | умножить число на число в степени 2 | |
modf | разлагает число на целое и дробную часть. | |
scalbnscalbln | умножить число на FLT_RADIX в заданной степени | |
nextafternexttoward | возвращает следующее значение, которое может быть представлено как плавающая точка | |
copysign | копирует знак числа с плавающей запятой | |
| Классификация | fpclassify | классифицирует значение с плавающей запятой |
isfinite | проверяет, имеет ли данное число конечное значение | |
isinf | проверяет, имеет ли данное число бесконечное значение | |
isnan | проверьте, является ли данное число NaN | |
isnormal | проверьте, является ли данный номер нормальным | |
signbit | проверяет, является ли данное число отрицательным |
Среда с плавающей запятой
C99 добавляет несколько функций и типов для более точного управления средой с плавающей запятой. Эти функции могут использоваться для управления рядом параметров, которые влияют на вычисления с числами с плавающей запятой, например, режим округления, когда числа должны быть сброшены, и т. Д. Эти функции определены в fenv.h заголовке ( cfenv в C ++ ).
Эти функции могут использоваться для управления рядом параметров, которые влияют на вычисления с числами с плавающей запятой, например, режим округления, когда числа должны быть сброшены, и т. Д. Эти функции определены в fenv.h заголовке ( cfenv в C ++ ).
| Функция | Описание |
|---|---|
feclearexcept | удалить исключения (C99) |
fegetenv | сохраняет текущую среду (C99) |
fegetexceptflag | сохранить флаги состояния (C99) |
fegetround | получить текущее направление округления (C99) |
feholdexcept | сохранить текущую среду и очистить исключения (C99) |
feraiseexcept | вызвать исключение (C99) |
fesetenv | настраивает среду (C99) |
fesetexceptflag | устанавливает флаг состояния (C99) |
fesetround | выберите направление округления (C99) |
fetestexcept | проверить, не возникли ли какие-либо исключения (C99) |
feupdateenv | восстановить среду, сохраняя поднятые исключения (C99) |
Комплексные числа
C99 добавляет новое ключевое слово _Complex (и сложный макрос для удобства), который используется для обработки комплексных чисел. Они представлены в виде двух чисел с плавающей запятой.
Они представлены в виде двух чисел с плавающей запятой.
C ++ не обеспечивает обратной совместимости для комплексных чисел, но предоставляет класс std :: complex .
Все операции с комплексными числами определены в заголовке complex.h . Что касается функций с целыми числами, суффиксы f и l представляют собой варианты функции, использующие комплексный тип float и длинный двойной комплексный типы соответственно .
| Функция | Описание | |
|---|---|---|
| Основные операции | cabs | рассчитать абсолютное значение (C99) |
carg | вычислить аргумент (C99) | |
cimag | возвращает мнимую часть комплексного числа (C99) | |
creal | возвращает действительную часть комплексного числа (C99) | |
conj | возвращает сопряжение комплексного числа (C99) | |
cproj | вычислить проекцию комплексного числа на сферу Римана (C99) | |
| Экспоненциальные операции | cexp | вычислить экспоненту комплексного числа (C99) |
clog | вычислить логарифм комплексного числа (C99) | |
csqrt | вычислить квадратный корень комплексного числа (C99) | |
cpow | вычислить мощность комплексного числа (С99) | |
| Тригонометрические операции | csin | вычислить синус комплексного числа (C99) |
ccos | вычислить косинус комплексного числа (C99) | |
ctan | вычислить тангенс комплексного числа (C99) | |
casin | вычислить арксинус комплексного числа (C99) | |
cacos | вычислить арккосинус комплексного числа (C99) | |
catan | вычислить арктангенс комплексного числа (C99) | |
| Гиперболические операции | csinh | вычислить гиперболический синус комплексного числа (C99) |
ccosh | вычислить гиперболический косинус комплексного числа (C99) | |
ctanh | вычислить гиперболический тангенс комплексного числа (C99) | |
casinh | вычислить гиперболический арксинус комплексного числа (C99) | |
cacosh | вычислить гиперболический арккосинус комплексного числа (C99) | |
catanh | вычислить гиперболический арктангенс комплексного числа (C99) |
Генерация случайных чисел
Заголовок stdlib. h ( cstdlib в C ++) определяет несколько функций, которые можно использовать для генерации статических случайных чисел.
h ( cstdlib в C ++) определяет несколько функций, которые можно использовать для генерации статических случайных чисел.
| Функция | Описание |
|---|---|
rand | генерирует псевдослучайное число |
srand | инициализирует генератор псевдослучайных чисел |
libm
В Linux и FreeBSD математические функции (объявленные в math.h ) сгруппированы отдельно в математической библиотеке libm . Так что, если какие — либо из этих функций используется, -lm директива должна быть добавлена к линкеру.
Примечания и ссылки
- ↑ (in) Спецификация ISO / IEC 9899: 1999 ( читать онлайн ), стр. 212, § 7.12.
- ↑ (in) Стивен Прата, приоритет C над: включает индекс, Sams Publishing,, 959 с. ( ISBN 0-672-32696-5 ), Приложение B, Раздел V: Стандартная библиотека ANSI C с дополнениями C99.
- ↑ (in) Спецификация ISO / IEC 9899: 1999 ( читать онлайн ), стр. 212, § 7.12.
- ↑ Стивен Прата, C primer plus: Includes Index, Sams Publishing,, 959 с. ( ISBN 0-672-32696-5 ), Приложение B, Раздел VIII: Расширения числовых вычислений C99.
- ↑ (in) Стивен Прата, приоритет C над: включает индекс, Sams Publishing,, 959 с.
 ( ISBN 0-672-32696-5 ), Приложение B, Раздел VIII: Расширения числовых вычислений C99.
( ISBN 0-672-32696-5 ), Приложение B, Раздел VIII: Расширения числовых вычислений C99. - ↑ « Библиотека GNU C — ISO Random » (по состоянию на 18 июля 2018 г. ) .
- (fr) Эта статья частично или полностью взята из статьи в Википедии на английском языке, озаглавленной « Математические функции C » ( см. список авторов ) .
Внешние ссылки
- math.h : математические объявления — Справочник по базовым определениям , Единая спецификация UNIX®, выпуск 7 от The Open Group
- Справочник C по математическим функциям
<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Нахождение гиперболического косинуса комплексного числа в Голанге
Улучшить статью
Сохранить статью
- Последнее обновление: 01 апр, 2020
Улучшить статью
Сохранить статью
Язык Go обеспечивает встроенную поддержку основных констант и математических функций для комплексных чисел с помощью пакета cmplx. Вы можете найти гиперболический косинус указанного комплексного числа с помощью Функция Cosh() , предоставляемая пакетом math/cmplx. Итак, вам нужно добавить пакет math/cmplx в вашу программу с помощью ключевого слова import для доступа к функции Cosh().
Вы можете найти гиперболический косинус указанного комплексного числа с помощью Функция Cosh() , предоставляемая пакетом math/cmplx. Итак, вам нужно добавить пакет math/cmplx в вашу программу с помощью ключевого слова import для доступа к функции Cosh().
Syntax:
func Cosh(y complex128) complex128
Let us discuss this concept with the help of the given examples:
Example 1 :
|
Выход:
Результат 1: (0,43771362521767465-1,1269289521981367i) Результат 2: (-0,5473996002472885-3,5882642538552894i) Результат 3: (-0,64214812471552+1,068607421382778i)
Example 2 :
|
Вывод:
2
Комплекс номер 1: (0+2i)
Гиперболический косинус 1: (-0,4161468365471424+0i)
Комплекс номер 2: (4+6i)
Гиперболический косинус 2: (26,220553750072888-7,625225809442885и)
Сумма: (25,804406913525746-7,625225809442885i)
Функция Excel IMCOSH
Главная » Встроенные функции Excel » Инженерные функции Excel » Функция Excel-Imcosh
Связанные функции:
Функция IMCOS
IMSINH90 Функция Hyper Colic
3 90
Гиперболический косинус комплексного числа вычисляется по следующему уравнению:
ch(x + yi) = ch(x) cos(y) - sh(x) sin(y)i
Дополнительную информацию о комплексных числах см. в Википедии.
Описание функции
Функция Excel Imcosh возвращает гиперболический косинус заданного комплексного числа.
Примечание. Функция Imcosh была представлена только в Excel 2013, поэтому недоступна в более ранних версиях Excel.
Синтаксис функции:
IMCOSH(число)
, где аргумент числа — это комплексное число, для которого вы хотите вычислить гиперболический косинус.
Комплексные числа в Excel
Обратите внимание, что комплексные числа просто хранятся в виде текста в Excel. Когда текстовая строка в формате «a+bi» или «a+bj» передается одной из встроенных функций Excel для работы с комплексными числами, она интерпретируется как комплексное число.
Функции комплексных чисел также могут принимать простые числовые значения, поскольку они эквивалентны комплексным числам, у которых мнимый коэффициент равен 0.
Примеры функций Имкоша
Функция Имкоша. В каждом примере используется другой метод для предоставления комплексного числа функции.
Formulas:
| Results:
|
Обратите внимание, что в таблице выше:
Дополнительные сведения и примеры функции Excel Imcosh представлены на веб-сайте Microsoft Office. Распространенные ошибки
| #ЧИСЛО! | - | Происходит, если предоставленный аргумент числа не распознается как комплексное число.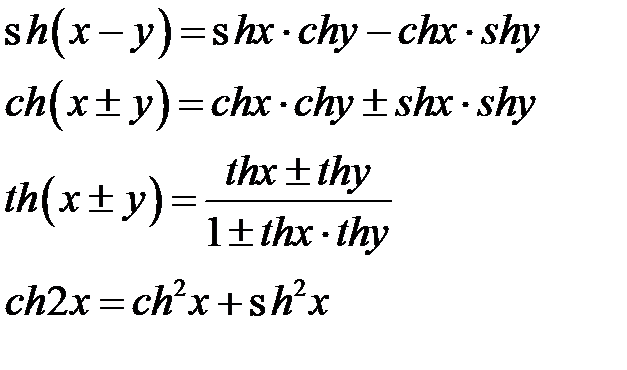 |

 ( ISBN 0-672-32696-5 ), Приложение B, Раздел VIII: Расширения числовых вычислений C99.
( ISBN 0-672-32696-5 ), Приложение B, Раздел VIII: Расширения числовых вычислений C99. COSH (1 + 5I)
COSH (1 + 5I)  0003
0003 Println(
Println(  5 )
5 )