Нужна помощь по геометрии. В окружности с центром …
Геометрия8 класс
А
Алексей
Нужна помощь по геометрии. В окружности с центром в точке О проведены два взаимно перпендикулярных диаметра AB и CD. Из точки М, лежащей на окружности, опущены два перпендикуляра ME и MN на диаметры. Найдите диаметр окружности, если EN = 5 см.
Елена АлександровнаПредметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ
MNOE — прямоугольник, т.к. \(ME\perp CD\), \(MN\perp AB\)
EN и MO — диагонали прямоугольника, значит EN = MO = 5 см
MO — радиус окружности, значит диаметр окружности будет равен 2MO = 10 см
Записаться на занятие к этому репетитору
Задайте свой вопрос!
Наши репетиторы максимально быстро дадут на него развёрнутый ответ. Это бесплатно!
Задать вопросНовые вопросы
Русский язык10 класс
А
Анастасия
ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ ТЕСТ
Ответ данНаталья ВасильевнаПредметы: Математика, Подготовка к школе, Окружающий мир, Начальные классы, Литературное чтение, Русский язык, Онлайн няня
Алгебра8 класс
М
Матвей
Решите уравнение 𝑥^2 = 5,5𝑥 + 3 сначала графически, азатем с помощью формулы корней.
Предметы: Математика, Подготовка к школе, Окружающий мир, Начальные классы, Литературное чтение, Русский язык, Онлайн няня
Всеобщая история7 класс
М
Макар
Помогите пожалуйста. сравнение уровня социально экономического развития германских государств с развитием англии или франции и укажи на основе различия.
Ответ данНаталья ВасильевнаПредметы: Математика, Подготовка к школе, Окружающий мир, Начальные классы, Литературное чтение, Русский язык, Онлайн няня
Геометрия8 класс
М
Матвей
Из вершины 𝐵 треугольника 𝐴𝐵𝐶 проведеныбиссектриса 𝐵𝐸 и высота 𝐵𝐻, равная 12, причем высота делитсторону 𝐴𝐶 на отрезки 𝐴𝐻 и 𝐻𝐶, равные 9 и 16 соответственно.Найдите стороны треугольника и отрезки, на которые биссектриса делит сторону 𝐴𝐶.
Ответ данНаталья СергеевнаПредметы: Математика, Геометрия, Алгебра, Окружающий мир, Начальные классы, Литературное чтение, Подготовка к ОГЭ, Русский язык
Геометрия8 класс
М
Матвей
Периметр треугольника 𝐴𝐵𝐶 равен 60 см. На сторонах𝐴𝐵, 𝐵𝐶, 𝐴𝐶 лежат точки 𝐷, 𝐸, 𝐹 соответственно так, что 𝐷𝐵𝐸𝐹 −ромб. Найдите стороны 𝐴𝐵 и 𝐵𝐶 треугольника, если 𝐴𝐹 = 10,𝐹𝐶 = 15.
На сторонах𝐴𝐵, 𝐵𝐶, 𝐴𝐶 лежат точки 𝐷, 𝐸, 𝐹 соответственно так, что 𝐷𝐵𝐸𝐹 −ромб. Найдите стороны 𝐴𝐵 и 𝐵𝐶 треугольника, если 𝐴𝐹 = 10,𝐹𝐶 = 15.
Тепаева Мария
История России6 класс
И
Ирина
Не могу найти значимые события в 982 году ? по истории 6 класс
Ответ данИнна ИгоревнаПредметы: Математика, Подготовка к школе, История России, Окружающий мир, Подготовка к ЕГЭ, Обществознание, Всеобщая история, ИЗО, МХК, Литературное чтение, Русский язык
Русский язык8 класс
М
Матвей
Найдите предложения с несогласованным определением, запишите только номера предложений: 1. Солнце гуляло по мокрым от вчерашнего дождя жнивьям. 2. Я не мог забыть девушку с синими глазами. 3. Дальше по оврагу еще лежал снег в желтых, в синих пятнах. 4. После душной ночи потянул на рассвете свежий ве…
Ответ данНаталья ВасильевнаПредметы: Математика, Подготовка к школе, Окружающий мир, Начальные классы, Литературное чтение, Русский язык, Онлайн няня
Алгебра8 класс
М
Матвей
Решите графически уравнения:1.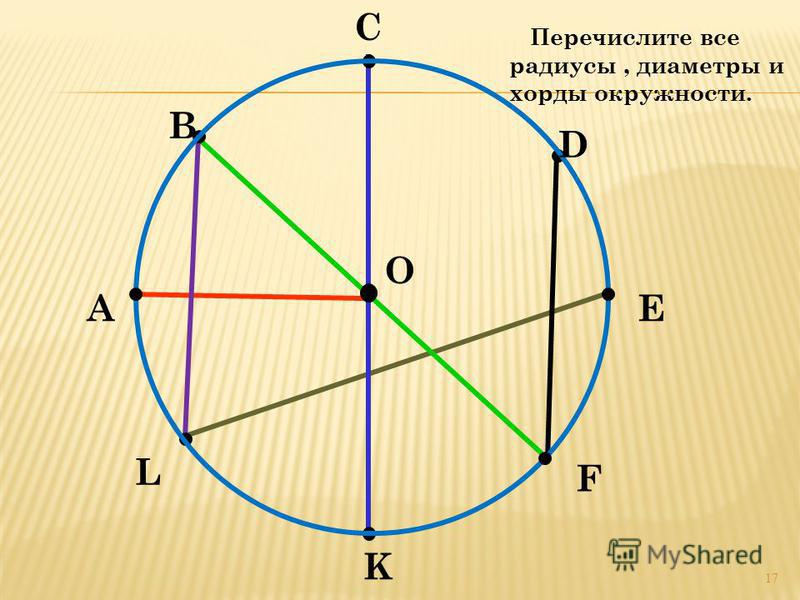 √𝑥 = 6 − 𝑥;2. 2√𝑥 = 2𝑥 − 4.
√𝑥 = 6 − 𝑥;2. 2√𝑥 = 2𝑥 − 4.
Предметы: Математика, Геометрия, Алгебра, Окружающий мир, Начальные классы, Литературное чтение, Подготовка к ОГЭ, Русский язык
Русский язык8 класс
М
Матвей
Выполните морфемный разбор слов: существование, горевший.
Ответ данНаталья ВасильевнаПредметы: Математика, Подготовка к школе, Окружающий мир, Начальные классы, Литературное чтение, Русский язык, Онлайн няня
Физика8 класс
М
Матвей
Рассчитайте, сколько энергии требуется затратить, чтобырасплавить медь массой 5 кг:а) при температуре плавления;б) при температуре 30°C
Ответ данОльга ВалерьевнаПредметы: Логопедия, Дефектология
Решение задач по теме «Уравнение окружности» 9 класс онлайн-подготовка на Ростелеком Лицей
Уравнение окружности
Уравнение окружности с центром в точке и радиусом имеет вид:
и – это координаты точки , лежащей на этой окружности.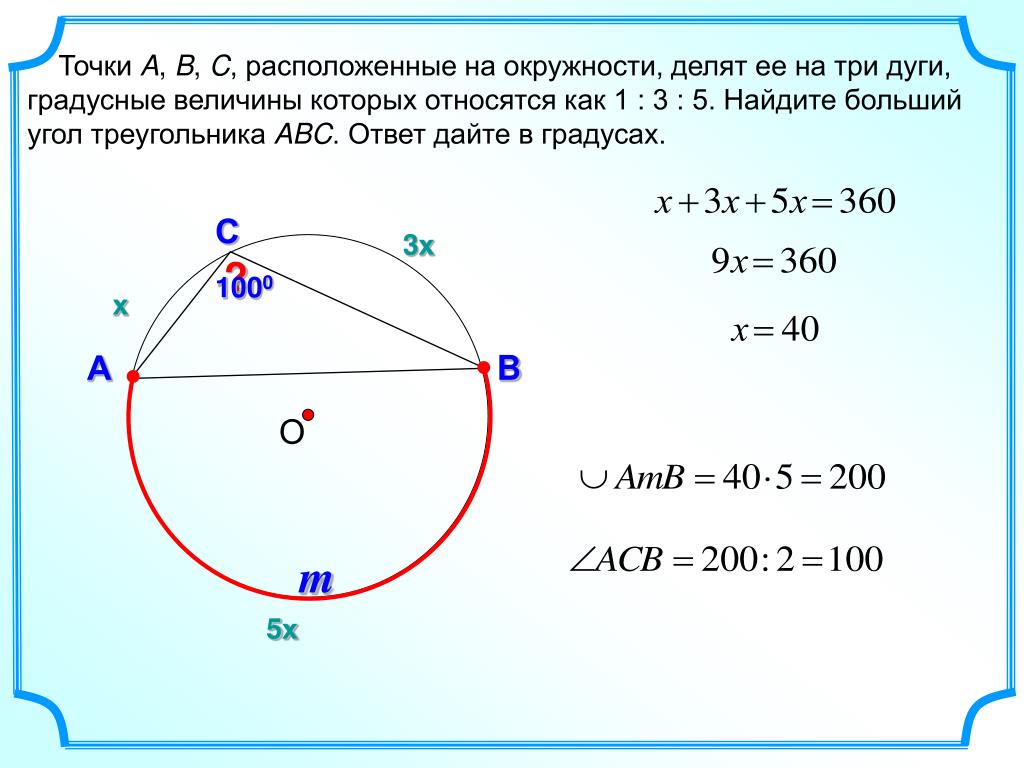
Задача 1
Выясните, какие из данных уравнений являются уравнениями окружности, найдите центр окружности и ее радиус:
1.
2.
Решение
1.
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
2.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Воспользуемся формулой квадрата суммы и разности. В обеих скобках есть квадрат первого выражения и удвоенное произведение, не хватает квадрата второго выражения, прибавим и отнимем его:
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
Центр окружности – это точка с координатами ; радиус окружности – .
Задачи с использованием метода выделения полного квадрата
Выясните, является ли данное уравнение уравнением окружности, найдите центр окружности и ее радиус:
1.
2.
Решение
1.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Так как и (квадрат выражения больше или равен нулю), то выражение в левой части уравнения больше нуля. Следовательно, это уравнение не имеет решения и не является уравнением окружности.
Доказать отсутствие решений у исходного уравнения можно также с помощью дискриминанта. Для этого рассмотрим это уравнение как квадратное относительно с параметром .
Мы получили квадратный трехчлен с такими коэффициентами:
— коэффициент при – ;
— коэффициент при – ;
— свободный член зависит от параметра – .
Найдем корни данного уравнения по известной формуле:
Выделим полный квадрат в подкоренном выражении:
Видно, что подкоренное выражение меньше нуля. А так как подкоренное выражение равно четверти дискриминанта, то и дискриминант будет отрицательным числом.
Следовательно, исходное уравнение не имеет решений.
2.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
Задача 2
Напишите уравнение окружности, проходящей через три заданные точки.
Дано: ; ; .
Найти: уравнение окружности, проходящей через данные точки.
Решение
Уравнение окружности задается тремя параметрами , , , поэтому необходимо найти эти параметры.
Так как данные точки лежат на окружности, то их координаты удовлетворяют уравнению искомой окружности. Подставим координаты точек в уравнение окружности в общем виде:
:
:
:
Мы получили систему из трех уравнений относительно трех неизвестных:
Решим эту систему. Вычтем из третьего уравнения первое:
Разложим выражение как разность квадратов:
Подставляем найденное значение во все три уравнения системы:
Видно, что первое и третье уравнение одинаковые, поэтому оставляем только одно из них:
Вычтем из первого уравнение второе:
Подставим найденное значение a в уравнение системы:
Радиус больше нуля, следовательно:
Мы нашли необходимые три параметра, поэтому можно выписать искомое уравнение окружности:
Ответ:
Типовые задачи на нахождение координат точек на окружности
Задача А
Дано: – центр окружности; – точка на окружности (см. Рис. 1).
Рис. 1).
Найти: уравнение окружности.
Рис. 1. Иллюстрация к задаче
Решение
Уравнение окружности в общем виде:
Так как координаты центра окружности , то ; . Необходимо найти – радиус данной окружности.
Нам известны две точки, поэтому радиус определим по формуле:
Выпишем уравнение окружности:
Ответ: .
Уравнение окружности позволяет найти точки на окружности по одной из координат этих точек.
Задача Б
Дано: – уравнение окружности; ордината искомых точек равна 3 (см. Рис. 2).
Найти: точки окружности с ординатой, равной 3.
Рис. 2. Иллюстрация к задаче
Решение
Уравнение данной окружности , следовательно, координаты ее центра , а радиус равен 5.
На рисунке видно, что необходимо найти координаты точек и (абсциссы данных точек).
Точки и лежат на окружности, поэтому их координаты удовлетворяют уравнению этой окружности. Для этих точек известно, что их ординаты равны 3. Получаем систему уравнений:
или
Таким образом, координаты точки , а координаты точки .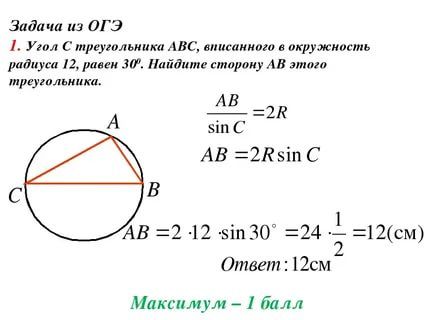
Ответ: , .
Задача 3
Напишите уравнение окружности, проходящей через две заданные точки , , если известно, что центр окружности лежит на оси ординат.
Дано:, , (см. Рис. 3).
Найти: уравнение окружности.
Рис. 3. Иллюстрация к задаче
Решение
Уравнение данной окружности будет иметь следующий вид:
Нам необходимо найти и .
1-й способ:
Так как окружность проходит через точки и , то их координаты удовлетворяют уравнению окружности. Подставляем эти координаты в уравнение и получаем систему уравнений:
Правые части данных уравнений равны, поэтому равны и левые части:
Подставим данное значение в одно из уравнений системы:
Радиус – это положительное число, поэтому радиус равен:
Мы нашли все три параметра, задающих уравнение окружности, выпишем это уравнение:
2-й способ
Центр окружности лежит на серединном перпендикуляре к отрезку .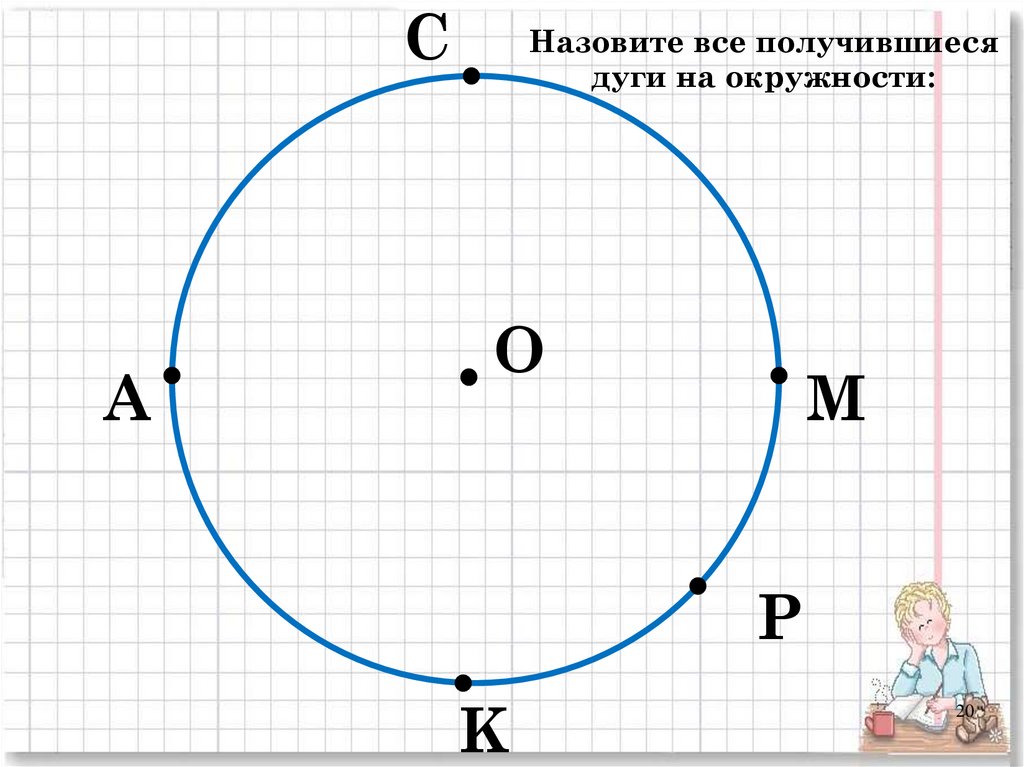 Теорема Пифагора для треугольника задает искомое уравнение (см. Рис. 4).
Теорема Пифагора для треугольника задает искомое уравнение (см. Рис. 4).
Рис. 4. Иллюстрация к задаче
В треугольнике : катет , гипотенуза , катет . Согласно теореме Пифагора:
Таким образом, ордината центра окружности будет равна:
Выпишем уравнение окружности:
Ответ: .
Задачи на геометрическое место точек
Геометрический смысл уравнения окружности и неравенств, вытекающих из этого уравнения (см. Рис. 5)
1.
2. Неравенству удовлетворяют все точки, лежащие внутри окружности с центром в точке с координатами и радиусом . Такое неравенство задает круг.
3. Неравенство задает внешность круга (без окружности).
Рис. 5. Геометрический смысл уравнения окружности и неравенств, вытекающих из этого уравнения
Задача А
Изобразите на координатной плоскости фигуру, заданную неравенством, и вычислите ее площадь.
Решение
1.
Выделяем полный квадрат:
Данное неравенство задает круг, ограниченный окружностью с центром в точке с координатами и радиусом (см. Рис. 6).
Рис. 6).
Рис. 6. Иллюстрация к задаче
2. Площадь круга вычисляется по формуле:
Подставляем известное значение радиуса:
Ответ: .
Задача Б
Изобразите на координатной плоскости фигуру, заданную неравенством, и вычислите ее площадь.
Решение
Рис. 7. Симметрия относительно
Таким образом, нам необходимо решить задачу при , а далее использовать симметрию относительно .
Пусть , тогда . Следовательно, имеем неравенство без модуля:
Следовательно, имеем неравенство без модуля:
Выделяем полный квадрат:
Данное неравенство задает круг, ограниченный окружностью с центром в точке с координатами и радиусом (см. Рис. 8).
Рис. 8. Иллюстрация к задаче
Используем симметрию относительно и получаем искомое геометрическое место точек, то есть множество всех точек, которые удовлетворяют неравенству (см. Рис. 9).Рис. 9. Иллюстрация к задаче
2. У нас получились два одинаковых круга, поэтому для нахождения площади этой фигуры необходимо площадь круга умножить на 2:
Подставляем значение радиуса:
Ответ: .
Задача В
Изобразите на координатной плоскости фигуру, заданную неравенством, и вычислите ее площадь.
Решение
Из данного неравенства видно симметрию по и по , то есть допускается замена на , на . Таким образом, если – это одно из решений неравенства, то и , , – тоже одно из решений (см. Рис. 10).
Нам необходимо решить задачу при , , а далее использовать симметрию относительно и .
Рис. 10. Симметрия относительно и
Пусть, , тогда , . Следовательно, имеем неравенство без модуля:
Выделяем полный квадрат:
Данное неравенство задает круг, ограниченный окружностью с центром в точке с координатами и радиусом (см.
Рис. 11. Иллюстрация к задаче
Используем симметрию относительно и и получаем искомое геометрическое место точек, то есть множество всех точек, которые удовлетворяют неравенству (см. Рис. 12).
Рис. 12. Иллюстрация к задаче
2. У нас получилось 4 одинаковых круга, поэтому для нахождения площади этой фигуры необходимо площадь круга умножить на 4:
Подставляем значение радиуса:
Ответ: .
Список литературы
1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Pm298.ru» (Источник)
2. Интернет портал «Profmeter.com.ua» (Источник)
3. Видеохостинг «YouTube» (Источник)
Домашнее задание
1. Задачи 961, 970 – Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия, 7-9.
2. Доказать, что уравнение является уравнением окружности. Найти ее центр и радиус.
Wassily Kandinsky — Круги по кругу, 1923
1923
Геометрическая абстракция
Нефть на Canvas
38,9 × 37,6 «(98,6.63
9.phi.phiphiphiphi.phia
9.phiphi.phia
9000. phi.ple.
phi.ple.
«Круги в круге» — компактная и замкнутая композиция. Кандинский начал вдумчивое изучение круга как художественной единицы, начиная с этой картины. В своем письме к Галке Шейер он писал: «Это первая моя картина, вывести тему кругов на передний план». Внешний черный круг, словно второй кадр для картины, побуждает сосредоточиться на взаимодействии внутренних кругов, а две пересекающиеся диагональные полосы усиливают эффект, добавляя композиции перспективу.0003
Подробнее от 1923
Композиция VIII
в Черном квадрате
Orange
Черный и фиолетовый
на белом II
Поперечная линия
Деликатный натяжение #85
Открыть зеленый
диаг.
Состав III
Состав I
Состав II
Фиолетовый
Белая точка
Без названия
Две черные точки
Три свободных круга
Composition (red,yellow,black)
All artworks by year
1896 1897 1898 1899 1900 1901 1902 1903 1904 1905 1906 1907 1908 1909 1910 1911 1912 1913 1914 1915 1916 1917 1918 1919 1920 1921 1922 1923 1924 1925 1926 1927 1928 1929 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940 1941 1942 1943 1944
20 Комментарии
21 марта 2022
Шарон: Это будет веселая живопись и урок для использования в день PI!
21 ноября 2019 г.
13 октября 2019 г.
Китти Ву: Почему и как этот художник использовал масло на холсте для создания «Кругов в круге»?
02 октября 2019 г.
Кристофер Нельсон: У меня есть коврик размером 8 x 10 футов, который выглядит как упрощенная версия этой картины Кандинского. Мне нужно больше информации о репродукциях RUG.
18 мая 2018 г.
Сумасшедший: Кандинский — хороший художник
18 мая 2018 г.
Сумасшедший: Любимая картина
28 августа 2017
кто-то: это произведение представляет начало большого взрыва Земли с шарами, представляющими планеты в будущем true a artpeice
21 марта 2017
Чарис Риден из Эссекса: Это великолепная композиция
18 ноября 2015 г.
Хейли Стейндорф из Нью-Виндзора: Эта картина — моя любимая.
23 января 2015 г.
Пенни Мартин из Великобритании: взято из Художественного музея Филадельфии об этом произведении
«Круги в круге» демонстрирует отличительный стиль Кандинского с начала 1920-х годов, когда он начал преподавать в Баухаузе в Веймаре, Германия, и впоследствии отошел от спонтанного стиля живописи к геометрической композиции. В этой работе толстый черный круг окружает двадцать шесть перекрывающихся кругов разного размера и цвета, многие из которых пересекаются прямыми черными линиями Две полосы синего и желтого цветов, идущие от верхних углов, пересекаются к центру фигуры, изменяя цвета кругов в местах их наложения. Хотя «Круги в круге» заметно отличаются от картин Кандинского начала двадцатого века, они отражают его неизменную веру в то, что определенные цвета и формы обозначают эмоции, которые можно систематизировать и объединить в единое целое, отражающее гармонию космоса.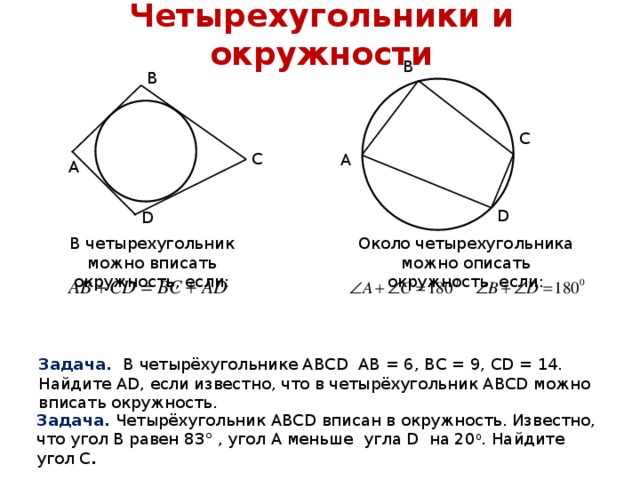 Кандинский, круг, самая элементарная из форм, имел символическое, космическое значение.Он писал, что «круг есть синтез великого ст оппозиции. Он сочетает в себе концентрическое и эксцентрическое в единой форме и в равновесии».31, он описал «Круги в круге» как «первую мою картину, в которой тема кругов выдвинута на передний план». 136.
Кандинский, круг, самая элементарная из форм, имел символическое, космическое значение.Он писал, что «круг есть синтез великого ст оппозиции. Он сочетает в себе концентрическое и эксцентрическое в единой форме и в равновесии».31, он описал «Круги в круге» как «первую мою картину, в которой тема кругов выдвинута на передний план». 136.
Примечания:
1) Кандинский в переводе Уилла Громана, Василий Кандинский: жизнь и работа, пер. Норберт Гутерман (Нью-Йорк: Гарри Н. Абрамс, 1958), с. 188.
2) Кандинский — Галке Шейер, Дессау, 9 мая 1931 г., в переводе Эми Бейкер Сэндбэк, «Голубые высоты», Artforum 28, вып. 7 (19 марта90), с. 127″.
22 апреля 2014 г.
Хейли из Нью-Виндзора: Круги по кругу снялись в фильме «Маленькие Эйнштейны: Погоня за дикими гусями».
Сикх из фонда: чем он рисовал это Мне нужна эта информация сейчас
06 марта 2013
Джонатан из Вашингтона: Какая замечательная картина!Я использую ее в своем отчете о художнике
06 марта 2013 г.
Эмили из Нью-Йорка: Где этапы рисования картины?!
Пожалуйста, добавьте больше! 🙂
22 мая 2012 г.
Джим из Лондона: Если вам это нравится, вы можете увидеть это вживую до 12 августа в рамках выставки Баухаус в Барбакане, Лондон. https://www.barbican.org.uk/artgallery/event-detail.asp?ID=12409
24 февраля 2012 г.
Ниха из Монагана: Картина великолепна, мне нравится
Мне нравятся все из них.
24 октября 2011 г.
wwwwwwwwww от wwwwwwwww: Информации об этом почти нет!!!!!!!!!!!!!!!! очень много информации нужно пожалуйста!!!!!!!!!!!!
27 марта 2011 г.
Диана из Уэст-Де-Мойн, штат Айова: Я преподаю в художественном центре маленьких детей рисованию и живописи, и я всегда пытаюсь найти разные способы преподавания живописи, отпочковавшись от «Мастеров», но достаточно интересно, чтобы запечатлеть их. Это великолепная картина, которую я планирую использовать — у вас есть другие идеи, полезные для детского творчества.
Это великолепная картина, которую я планирую использовать — у вас есть другие идеи, полезные для детского творчества.
20 сентября 2010
ashley from lusaka: пожалуйста, дайте мне больше информации о картине кандиски сделал именной круг в кругу
Ваш комментарий
Имя Электронная почта (необязательно):
Сообщение
Код
На данном рисунке дана окружность с центром O, в которой диаметр AB делит пополам хорду CD в точке…
Перейти к
- Круговое упражнение 12А
- Круговое упражнение 12B
- Круговое упражнение 12C
- Системы счисления
- Полиномы
- Факторизация многочленов
- Линейные уравнения с двумя переменными
- Координатная геометрия
- Введение в геометрию Евклида
- Линии и углы
- Треугольники
- Конгруэнтность треугольников и неравенства в треугольнике
- Четырехугольники
- Площади параллелограммов и треугольников
- Круги
- Геометрические построения
- Площади треугольников и четырехугольников
- Объем и площадь поверхности твердых тел
- Средняя медиана и режим разгруппированных данных
- Вероятность
Главная > Решения RS Aggarwal Класс 9 Математика > Глава 12 — Круги > Круговое упражнение 12А > Вопрос 7
Вопрос 7 Окружности Упражнение 12A
На данном рисунке дана окружность с центром O, в которой диаметр AB делит пополам хорду CD в точке E так, что CE = ED = 8см и EB = 4см. Найдите радиус окружности. 92 + 8r = 80
Найдите радиус окружности. 92 + 8r = 80
Получаем
8r = 80
Делением
r = 10 см
Следовательно, радиус окружности равен 10 см.
Связанные вопросы
В окружности радиусом 10 см проведена хорда длиной 16 см. Найдите расстояние от хорды до…
Найдите длину хорды, которая проходит на расстоянии 3 см от центра окружности радиусом 5 см.
На расстоянии 8 см от центра окружности проведена хорда длиной 30 см. Узнать радиус…
В окружности радиусом 5 см AB и CD проходят две параллельные хорды длиной 8 см и 6 см соответственно. Ка…
Две параллельные хорды длиной 30 см и 16 см проведены по разные стороны от центра окружности.
