Косинус икс равен косинус игрек: Решите уравнение cos(x)=y (косинус от (х) равно у)

alexxlab / / Разное
2

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21
Найти точное значение		cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )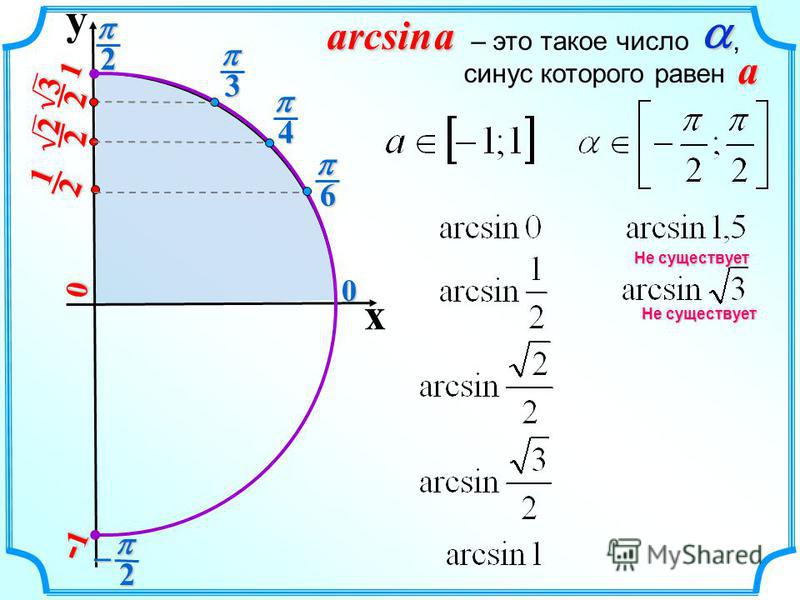
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74
Найти точное значение		tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81
Найти точное значение		sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

функций — Построение графика $\cos(x) >\cos(y) $

спросил

Изменено 4 года, 5 месяцев назад

Просмотрено 432 раза

$\begingroup$

Я новичок на веб-сайте, поэтому во многих местах могу ошибаться, но, пожалуйста, потерпите меня.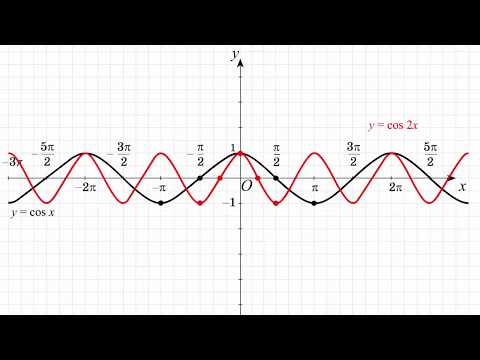 Я наткнулся на это: $$\cos (x) — \cos(y) > 0$$ и попытался построить его с помощью простой тригонометрии. Но я не смог этого сделать после неоднократных попыток. Моя работа: $$\cos(x) > \cos(y)$$ $$\поэтому 2\sin\left(\frac{x+y}{2}\right) \times\sin\left(\frac{x-y}{2}\right) > 0 $$ Из чего следует, что $$\sin \left(\frac{x+y}{2} \right)$$ и $$\sin \left(\frac{x-y}{2} \right)$$ должны иметь одинаковые знаки. . После этого я не мог сделать никаких дальнейших выводов. Любая помощь?

  • функции
  • тригонометрия
  • графические функции

$\endgroup$

2

$\begingroup$

Пусть $A$ — множество всех точек $(x,y)$ таких, что $\cos(x) > \cos(y)$. $A$ имеет несколько симметрий:

  • $(x,y) \in A \имеет (x \pm 2\pi, y) \in A$.
  • $(x,y) \in A \подразумевает (x, y \pm 2\pi) \in A$.
    • 9\звезда = А$.

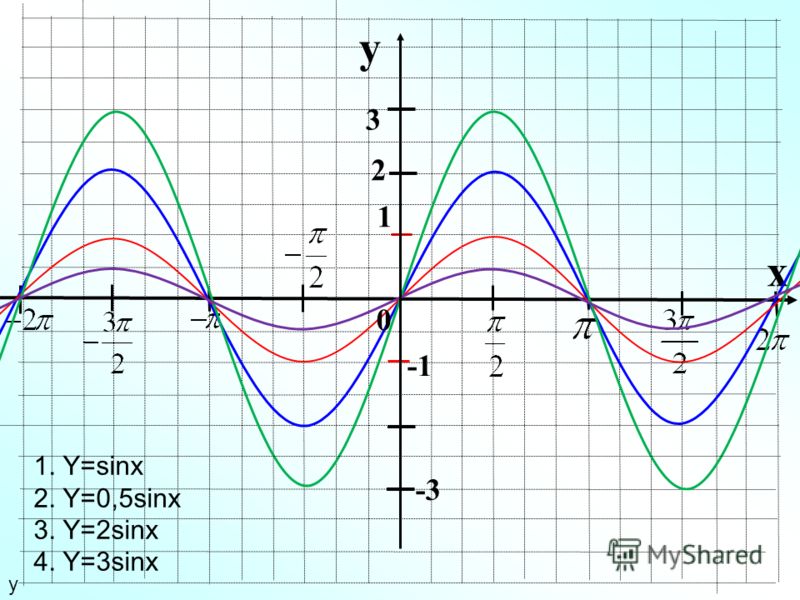
    $\endgroup$

    $\begingroup$

    Голубым цветом отмечена область $\cos(x)>\cos(y)$

    $\endgroup$

    $\begingroup$

    $$ \cos(x) > \cos(y) \quad\Leftrightarrow\quad x > y + 2k\pi \quad\vee\quad x > -y + 2k\pi, \qquad k \in \mathbb {Z} $$

    Примечание: $ x > -y + 2k\pi $, минус в $ y $ происходит из-за того, что $ \cos$ — четная функция, т. е. $\cos(a) = \cos( -а) $.

    PD: Мне не разрешено оставлять комментарии.

    $\endgroup$

    1

    $\begingroup$

    Обозначим для $\cos y \neq 1$

    $$z=\arccos y\neq0$$

    тогда

    $$\cos (x) — \cos(y) > 0 \iff \cos (х) > \cos(y) $$ $$\iff 0+2k\pi\le x< z+2k\pi, \quad 2\pi-z+2k\pi

    область в плоскости $x-y$, рассмотрим сначала условие $$\cos x=\cos y\iff y=x+2k\pi \,\lor \, y=-x+2k\pi $$

    , который представляет собой набор линий, параллельных биссектрисам.

    Тогда из начального наблюдения легко найти область, ограниченную линиями, для которых выполняется неравенство.

    $\endgroup$

    2

    Зарегистрируйтесь или войдите

    Зарегистрироваться через Google

    Зарегистрироваться через Facebook

    Зарегистрируйтесь, используя электронную почту и пароль

    Опубликовать как гость

    Электронная почта

    Требуется, но никогда не отображается

    Опубликовать как гость

    Электронная почта

    Требуется, но не отображается

    Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

    .

    исчисление — $ x\cos y + y \cos x = \pi$ , как мне найти $y»(0)$ самым простым способом?

    спросил

    Изменено 2 года назад

    Просмотрено 364 раза

    $\begingroup$

    Я рассматривал дифференциацию грубой силы, но это очень сложно. Я также пытался разложить косинусы и ‘$y$’ в ряд Тейлора, но я не думаю, что это сильно помогает

    • исчисление

    $\endgroup$

    $\begingroup$

    Дифференцируя обе части по $x$, получаем \begin{equation*}\cos y — x\sin y\frac{\mathop{}\!\mathrm{d}y}{\mathop{}\ ! \ mathrm {d} x} + \ frac {\ mathop {} \! \ mathrm {d} y} {\ mathop {} \! \ mathrm {d} x} \ cos xy \ sin x = 0 \ end { уравнение*} т. е. \begin{equation*}(\cos y-y\sin x)+(\cos x-x\sin y)\frac{\mathop{}\!\mathrm{d}y}{\mathop{}\! \mathrm{d}x}=0 \qquad (*)\end{equation*} Когда $x=0$, мы имеем $0+y(1)=\pi$, поэтому $y=\pi$. Таким образом, $(-1-0)+\left(1-0\right)\frac{\mathop{}\!\mathrm{d}y}{\mathop{}\!\mathrm{d}x}=0 $, поэтому $\frac{\mathop{}\!\mathrm{d}y}{\mathop{}\!\mathrm{d}x}=1$, когда $x=0$. 9{} = \pi\end{уравнение*}

    $\endgroup$

    3

    $\begingroup$

    Используйте теорему о неявной функции для $$f=x \cos(y)+y \cos(x)-\pi=0$$ $$f’_x=\cos(y)-y \sin(x)\qquad \qquad f’_y=-x \sin(y)+\cos(x)$$ $$y’=\frac{dy}{dx}=-\frac{f’_x}{f’_y}=-\frac{\cos(y)-y \sin(x)}{-x\sin (y)+\cos(x) }$$ и теперь продифференцируем по $x$; в правой части у вас будет $y’$.

    9\простое\sin у+у=\пи$.

    $\endgroup$

    $\begingroup$

    $x\cos y + y\cos x = \pi$

    Что такое $y(0)$?

    $0\cos (y(0)) + y(0)\cos 0 = \pi\ y(0) = \pi\

    Что такое $y’$?

    $\cos y -y\sin x + (-x\sin y + \cos x)y’ = 0\\ y’= \frac {y\sin x — \cos y}{\cos x — x\sin y} = \frac {u}{v}\\ $

    И $y'(0)$?

    $u(0) = \pi \sin 0 — \cos \pi = 1\\ v(0) = \cos 0 — 0\sin \pi = 1\\ у'(0) = 1$ 92}\\ u’ = y\cos x + (\sin x + \sin y) y’\\ и'(0) = \пи\\ v’ = -sin x — sin y + (-x\cos y) y’\\ v'(0) = 0\\ у»(0) = \pi$

    $\endgroup$

    $\begingroup$

    Поскольку $F(x,y(x)) = x\cos y + y\cos x$ дифференцируема, мы можем использовать формулу неявного дифференцирования:

    \begin{align*} y’ =\frac{dy }{dx} & = — \ frac {\ frac {\ partial F} {\ partial x}} {\ frac {\ partial F} {\ partial y}} \\ & = -\frac{\cos y -y\sin x}{\cos x — x\sin y}.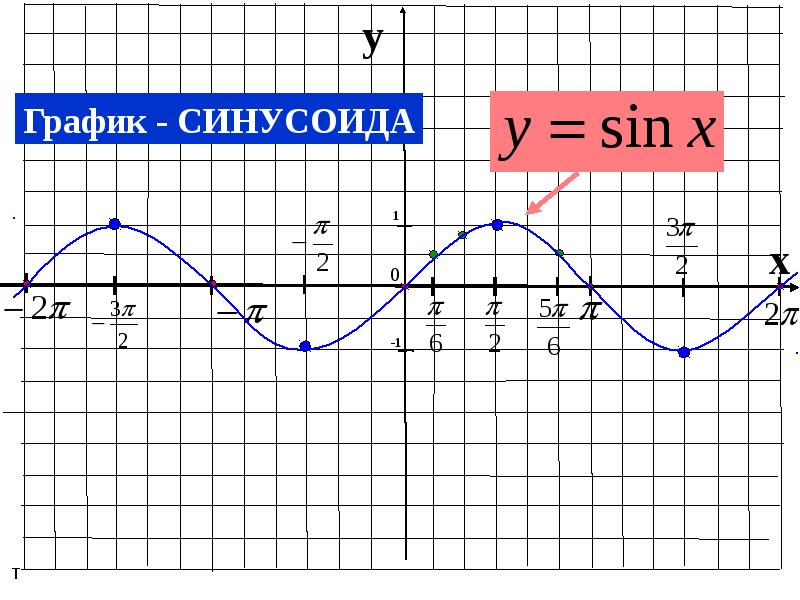 \end{выравнивание*}

    Теперь у нас есть $$y’\cos x — y’x\sin y -y\sin x + \cos y = 0.$$

    Продифференцировать по $x$ с обеих сторон и упростить .

    $\endgroup$

    1

    $\begingroup$

    Что ж, прошло больше шести месяцев, и недавно я нашел лучший способ сделать это.

    $$ x \cos y + y \cos x = \pi$$

    Теперь перепишем как:

    $$ Q(x,y) = x \cos y + y \cos x — \pi$$ р D.w.r.t.x и используйте теорему 9 о неявной функции0005

    $$ \frac{dQ}{dx} = \left[ \cos y — y \sin x \right] +y’ \left [ -x \sin y + \cos x \right] $$

    Сейчас обратите внимание, что $\frac{dQ}{dx} = G(x,y,y’)$ , снова используйте теорему о неявной функции:

    $$ \frac{dG}{dx} =( \left[ — y \cos x \right] + y’ \left[-\sin y — \sin x \right] )+ (\left[ — \sin y — \sin x \right] + y’ \left[ -x \cos y \right])y’ +\left[ (-x \sin y + \cos x) \right] y» $$

    Следовательно, наши три неявных уравнения, связывающие функцию и ее производные, таковы: $$ \left[ x \cos y + y \cos x — \pi \right]=0 \tag{0}$$ $$ \left[ \cos y — y \sin x \right] +y’ \left [ -x \sin y + \cos x \right] =0\tag{1} $$ $$( \left[ — y \cos x \right] + y’ \left[-\sin y — \sin x \right] )+ (\left[ — \sin y — \sin x \right] + y ‘ \left[ -x \cos y \right])y’ +\left[ (-x \sin y + \cos x) \right] y» =0 \tag{2}$$

    Заглушка $ x = 0$,

    $$ y- \pi = 0 \tag{0}$$

    $$ \left[ \cos(y) \right] + y’ =0$$

    $$ ( -y -y’ \sin y) + (- \sin y )y’ + \left[ 1 \right] y»=0$$

    Упрощение,

    $$ y= \pi$$ $$ у’=1$$ $$y»=\pi$$

    См.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *