Косинус в тангенс: Синус и косинус. Тангенс и котангенс — урок. Алгебра, 10 класс.

Урок геометрии «Синус, косинус и тангенс острого угла прямоугольного треугольника». 8-й класс

Цели урока:

• ввести понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника;
• показать, как используются синус, косинус и тангенс при решении задач;
• развитие умений наблюдать, сравнивать, анализировать и делать вывод.

Ход урока

Актуализация знаний (определение основной проблемы урока)

Проводится в форме фронтального опроса.

Учитель. На доске вы видите краткую запись 6 задач < Рисунок 1>. Вспомните , какие из этих задач вы уже умеете решать? Решите эти задачи. Сформулируйте соответствующие теоремы.

Рисунок 1

Учащиеся:

Задача 1. Ответ: 5. В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.

Задача 2. Ответ: 41°. Сумма внутренних углов треугольника равна 180°.

Задача 3. Ответ: 10 . Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Задачи 4-6 мы не можем решить.

Учитель. А почему вы не сумеете решить задачи 4-6? Какой вопрос возникает?

Учащиеся. Мы не знаем, что такое tgB, sinA, cosB.

Учитель. sinА, cosB, tgB читается: “синус угла А”, “косинус угла В” и “тангенс угла В”. Мы сегодня узнаем, что означает каждое из этих выражений, и научимся решать задачи типа 4-6.

Введение нового материала

Проводится в форме эвристической беседы.

Учитель. Начертите прямоугольные треугольники с катетами 3 и 4, 6 и 8. Обозначьте их АВС и А₁В₁С₁ так, чтобы В и В₁ были_{углами, противолежащими катетам 4 и 8, а прямыми углами были С, С1. Равны ли углы В и В1? Почему?}

Учащиеся

. Равны, потому что треугольники подобны. AC : BC = A₁C₁ : B₁C₁ (3 : 4 = 6 : 8) и углы между ними прямые.<Рисунок 2>

Учитель. Равенства каких ещё отношений следуют из подобия треугольников АВС и А₁В₁С₁?

Учащиеся. ВС : АВ = В₁С₁ : А₁В₁, АС : АВ = А₁С₁ : А₁В₁.

Учитель. АС : АВ = А₁С₁ : А₁В₁= sinB = sinB_1.

ВС : АВ = В₁С₁ : А₁В₁ = cosB = cosB_{1 .} AC : BC = A₁C₁ : B₁C₁ = tgB = tgB₁. Катет АС является противолежащим углу В, а катет ВС — прилежащим к этому углу. Сформулируйте определения синуса, косинуса и тангенса.

Учащиеся. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Учитель. Запишите сами синус, косинус и тангенс угла А (слайд 1). Получились формулы (1), (2), (3) :

(1)

 . (3)

.Итак , мы узнали что такое синус, косинус и тангенс острого угла прямоугольного треугольника. Вообще, понятия синуса косинуса и тангенса имеют длительную историю. Изучая зависимость между сторонами и углами треугольника, древние учёные нашли способы вычислений различных элементов треугольника. Эти знания, главным образом, использовались для решения задач практической астрономии, для определения недоступных расстояний.

Закрепление

Учитель. Решим задачу №591 (а,б) [1].

Задание выводится на экран (слайд 2). Задание “а” решается на доске с полным объяснением; “б” – самостоятельно с последующей проверкой друг друга.

Найдите синус, косинус и тангенс углов А и В треугольника АВС с прямым углом С, если: а) ВС = 8, АВ = 17; б) ВС = 21, АС = 20.

Решение. а) = . = , по теореме Пифагора найдём АС = 15,

= ; б) , по теореме Пифагора найдём АВ = 29, . . .

Учитель. А теперь вернёмся к задачам 4–6 <Рисунок 1>. Давайте обсудим, что известно в задачах 4–6 и что требуется найти?

Задача 4.

Что известно? Что надо найти?

Учащиеся. Известны ВС = 7 и tg В = 3,5. Надо найти АС.

Учитель. Что такое tg В?

Учащиеся. .

Учитель. Работаем с формулой. Формула состоит из трёх компонентов. Назовите их. Какие компоненты известны? Какой компонент неизвестен? Можете найти? Найдите.

Учащиеся. АС = ВС * tg B = 7 * 3,5 = 24,5

Учитель. По этому образцу решите задачи 5 и 6 <Рисунок 1>. 1 ученик работает на закрытой доске

Учитель.

1. Расскажите, удалось ли вам найти требуемые неизвестные?

2. Каков был порядок ваших действий?

3. Может быть есть другие решения?

Учащиеся.1. Да. Легко. По образцу. Задача 5. Ответ: 10. Задача 6. Ответ: 2,5

2. Сначала синус и косинус соответствующих углов заменяем по определению соответствующими отношениями, затем в полученных пропорциях проставляем известные данные, после этого находим искомые неизвестные.

Учитель. Какой общий вывод можно сделать после решения задач 4–6? Какие новые задачи мы научились решать в прямоугольном треугольнике? Подумайте и сформулируйте ваш вывод.

Учащиеся. Если в прямоугольном треугольнике известны одна сторона и отношение этой стороны к одной из других сторон, либо одна сторона и отношение одной из других сторон к известной стороне (либо синус, либо косинус, либо тангенс), то можно найти эту вторую сторону.

Решение задач.

А теперь попробуйте решить эти задачи 7–9 <Рисунок 3>.

Рисунок 3

Учащиеся. Мы не знаем, как их решать.

Учитель

. Вернёмся к задаче 1 <Рисунок 1>. Изменим условие задачи. Пусть NK = 5, NM = 10. Найти угол М.

Учащиеся. Угол М равен 30°, так как катет противолежащий углу М равен половине гипотенузы.

Учитель. То есть получается, что если синус угла равен 0,5, то угол равен 30°. А теперь решим задачи №592 (а,в,д) [1]

№592. Постройте угол a, если: а) в) д) .

Решение.

а) На сторонах прямого угла отложим отрезки длиной 1 и 2, соединим концы отрезков. В полученном треугольнике угол, лежащий против катета 1, и есть искомый угол a;

(слайд 3)

в) 0,2 = . На одной стороне прямого угла от его вершины отложим отрезок длины 1. Построим окружность радиуса 5 с центром в конце отложенного отрезка. Точку пересечения окружности со второй стороной прямого угла соединим с концом отложенного на первой стороне угла отрезка. В полученном треугольнике угол, прилежащий катету длины 1, и есть угол

a; (слайд 4)

д) На одной стороне прямого угла от его вершины отложим отрезок длины 1. Построим окружность радиуса 2 с центром в конце отложенного отрезка. Точку пересечения окружности со второй стороной прямого угла соединим с концом отложенного на первой стороне угла отрезка. В полученном треугольнике угол, противолежащий катету длины 1, и есть искомый угол a.(слайд 5)

Вы построили углы, а значит, вы нашли углы. Их можно измерить и оформить в виде таблицы.

Аналогично можно решить задачи 7-9 <Рисунок 3>

Подведение итогов

Учитель. Ответьте на вопросы:

1. Что называется синусом, косинусом и тангенсом прямого угла в прямоугольном треугольнике?

2. В прямоугольном треугольнике 6 элементов. Какие новые задачи вы сегодня научились решать? Каков при этом порядок ваших действий? Проверьте свои умения правильно выполнять эти действия (Раздаются индивидуальные карточки).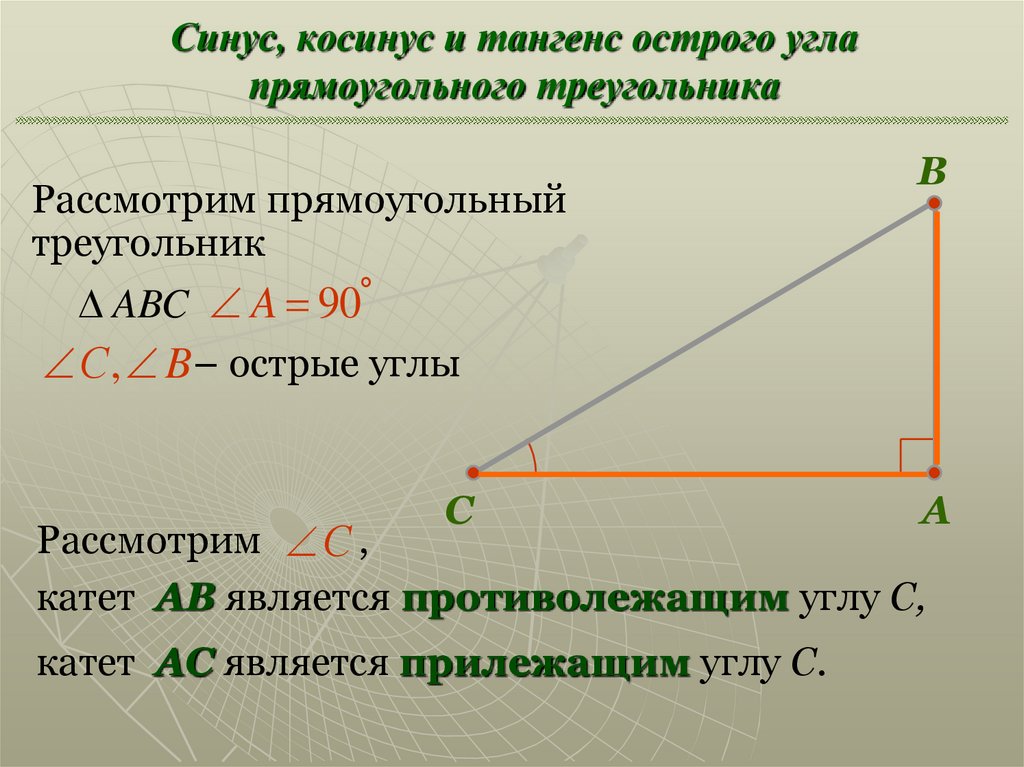

Примерное содержание карточек: 1. В треугольнике АВС угол С прямой, ВС = 2, Найдите АВ. 2. В треугольнике АВС угол С прямой, АС = 8, . Найдите АВ. 3. В треугольнике АВС угол С равен 90°, АС = 6, . Найдите ВС.

Учащиеся сверяют свою работу с готовыми решениями на соответствующих карточках.

Задания на дом: [1] вопрос 15 на стр.159; №591(в,г),592(б,г,е) (слайд 6)

Использованная литература

1. Геометрия. 7–9 классы: учеб. для общеобразовательных организаций / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014.

‎App Store: Синус Косинус Тангенс про

Описание

Здесь объясняется поведение основных функций синуса, косинуса и тангенса. Вы можете изменять амплитуду и частоту функции. Кроме того, вы можете ввести значение x или периодический шаг для нужного вам решения. Приложение показывает все важные вычисления, предоставляет информационное изображение и отображает график.

Поддерживаются десятичные и дробные числа, отрицательные значения и π. Решение показывается шаг за шагом. Все вычисления сохраняются в истории. Окончательным решением можно поделиться.

[ Содержание ]
— все важные величины для синуса, косинуса и тангенса
— область определения, область значений, длина периода, максимум, минимум, нули и полюса функций
— доказательство симметрии и периодического поведения функций
— результаты также вычисляются как π-значение
— графики для синуса, косинуса и тангенса
— функция истории для сохранения вводимых данных
— подробное решение
— поддерживаются отрицательные значения, десятичные числа, дроби и π

[ Использование ]
— имеются поля для ввода значений с помощью специальной клавиатуры
— нажмите кнопку с галочкой в правом нижнем углу, чтобы начать вычисления
— если значения отсутствуют, приложение будет использовать значения по умолчанию
— если значения неверны, соответствующее поле будет выделено красным цветом
— записи в истории можно удалять или сортировать
— если выбрать запись в истории, она будет автоматически загружена для расчета
— вся история может быть удалена нажатием одной кнопки
— решениями можно обмениваться

000Z» aria-label=»3 июня 2022 г.»>3 июн. 2022 г.

Версия 1.1

— Bugfix: red highlight now is placed correctly and shows the wrong input
— Minor fixes

Разработчик Flooki указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Связанные с пользова­телем данные

Может вестись сбор следующих данных, которые связаны с личностью пользователя:

• Геопозиция
• Идентифика­торы
• Данные об использова­нии
• Диагностика

Не связанные с пользова­телем данные

Может вестись сбор следующих данных, которые не связаны с личностью пользователя:

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер

Glindemann, Sennoun, Langer GbR

Размер

30,8 МБ

Категория

Образование

Возраст

4+

Copyright

© 2022 Glindemann, Sennoun, Langer GbR

Цена

179,00 ₽

• Сайт разработчика
• Поддержка приложения
• Политика конфиденциальности

Поддерживается

Другие приложения этого разработчика

Вам может понравиться

Понимание синуса, косинуса и тангенса

Все ресурсы по математике для старших классов

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

Справка по математике для старших классов » Тригонометрия » Тригонометрические операции » Понимание синуса, косинуса и тангенса

Если полярные координаты точки , то каковы ее прямоугольные координаты?

Возможные ответы:

Правильный ответ:

Объяснение:

Полярные координаты точки задаются как , где r представляет собой расстояние от точки до начала координат, а  представляет собой угол поворота. (Отрицательный угол поворота означает вращение по часовой стрелке, а положительный угол означает вращение против часовой стрелки.)

Следующие формулы используются для преобразования полярных координат в прямоугольные (x, y) координаты.

В этой задаче полярные координаты точки равны  , значит,  и . Мы можем применить формулы преобразования, чтобы найти значения x и y.

Прямоугольные координаты.

Ответ .

Сообщить об ошибке

Что такое ?

Возможные ответы:

Правильный ответ:

Объяснение:

 

Сообщить об ошибке

В прямоугольном треугольнике выше какое из следующих выражений дает длину y?

Возможные ответы:

Правильный ответ:

Объяснение:

 определяется как отношение прилежащей стороны к гипотенузе, или в данном случае . Решение для y дает правильное выражение.

Сообщить об ошибке

Что такое косинус ?

Возможные ответы:

Правильный ответ:

Объяснение:

Образец для стороны  треугольника  .

 С тех пор, мы можем подставить заданные нами значения.

Обратите внимание, что 

Сообщить об ошибке

Если , что если  между и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Напомним, .

Поэтому ищем  или .

Теперь у этого опорного угла  , но он находится в третьем квадранте. Это означает, что значение будет отрицательным. Значение  равно . Однако, учитывая квадрант нашего угла, это будет .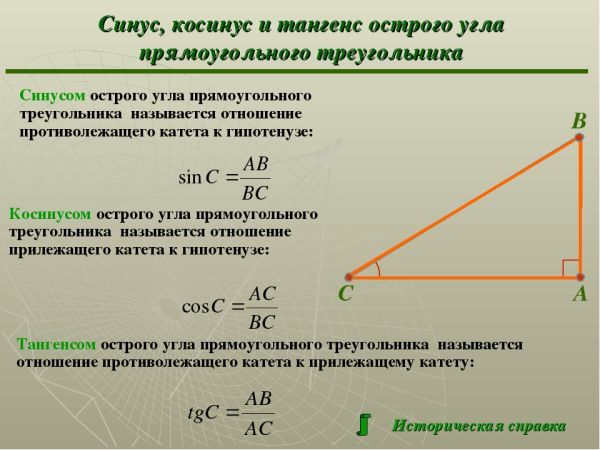

Сообщить об ошибке

Уведомление об авторских правах

Все математические ресурсы средней школы

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Учитесь по концепции

math — Вопросы о функциях синуса, косинуса и тангенса в Python

Задавать вопрос

спросил 1 год, 5 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 146 раз

Я начинаю изучать математический модуль в Python и пытаюсь разобраться в тригонометрических функциях синуса, косинуса и тангенса в Python.

Я потратил некоторое время, чтобы больше узнать о тригонометрии и понять, как работают основные формулы для прямоугольных треугольников:

Функция синуса:
sin(θ) равно противоположности/гипотенузе

Функция косинуса:
cos(θ) равно смежной/гипотенузе

Касательная функция:
tan(θ) равно Противоположный / Смежный

Но мне не ясно, как это применяется в Python, когда он принимает только одно значение. Я читал, что значение должно быть в радианах.

Итак, если x = 1 радиан и math.sin(x)

Результат равен 0,8414709848078965

Таким образом, синус 1 радиана равен 0,8414709848078965

Итак, мой вопрос: что функция синуса на самом деле сделала с радианом 1?

Я надеюсь, что ответ также поможет мне понять, что происходит, если я сделал косинус и тангенс к радиану 1. 2

python использует ряд Тейлора sin, чтобы найти значение sin 1. https://people.math.sc.edu/girardi/m142/handouts/10sTaylorPolySeries.pdf

Кроме того, когда вы сказали, как это верно, когда он принимает одно значение. Я думаю, у вас неправильное представление. Функции sin, cosine, tangent принимают один аргумент, т. е. тета, и выводят одно значение. Теперь это значение равно основанию/гипотенузе ( или любой другой функции триггера, которую вы использовали ) треугольника, угол которого вы вводите в функцию триггера. ТАК, что вы не должны ожидать, что триггерные функции будут выдавать два значения.