Первый замечательный предел — примеры решений
Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется первый замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.
Примеры решений
Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓, ⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Найти предел функции с помощью первого замечательного предела:
.
Решение
При , , . Это неопределенность вида 0/0.
Для ее раскрытия, преобразуем функцию за знаком предела и разделим числитель и знаменатель дроби на x:
.
Заметим, что функцию в числителе можно представить как сложную:
,
где . Функция не определена при , поскольку знаменатель дроби обращается в нуль. Поэтому, для вычисления предела , применим теорему о пределе сложной функции.
Поскольку функция непрерывна для всех x, и в том числе в точке , то
.
Первое условие теоремы выполнено.
Второе условие теоремы заключается в том, что должна существовать такая проколотая окрестность точки , на которой
при .
Если бы это условие не выполнялось, то в любой проколотой окрестности точки были значения , на которых функция не определена. Поэтому предел не существовал бы. В нашем случае, функция строго монотонна. Поэтому она может иметь значение только в одной точке. И это точка , которая не содержится ни в одной проколотой окрестности этой точки. То есть для любой проколотой окрестности точки , . Второе условие выполнено.
И, наконец, третьим условием теоремы является существование предела . В нашем случае он равен первому замечательному пределу:
.
Таким образом,
.
Аналогичным образом, находим предел функции в знаменателе:
;
при ;
.
И наконец, применяем арифметические свойства предела функции:
.
Ответ
.
Пример 2
Найдите предел:
.
Решение
При , , . Это неопределенность вида 0/0.
Преобразуем функцию за знаком предела:
.
Сделаем подстановку . Поскольку и при , то применим теорему о пределе сложной функции и первый замечательный предел:
.
Аналогичным образом имеем:
.
Поскольку функция косинус непрерывна на всей числовой оси, то
.
Применяем арифметические свойства пределов:
.
Ответ
.
Пример 3
Найти предел:
.
Решение
Подставим в числитель и знаменатель дроби:
;
.
Это неопределенность вида 0/0.
Попробуем решить этот пример с помощью первого замечательного предела. Поскольку в нем значение переменной стремится к нулю, то сделаем подстановку, чтобы новая переменная стремилась не к , а к нулю. Для этого от x перейдем к новой переменной t, сделав подстановку , . Тогда при , .
Предварительно преобразуем функцию за знаком предела, умножив числитель и знаменатель дроби на :
.
Подставим и воспользуемся приведенными выше тригонометрическими формулами.
;
;
.
Функция непрерывна при . Находим ее предел:
.
Преобразуем вторую дробь и применим первый замечательный предел:
.
В числителе дроби мы сделали подстановку .
Применяем свойство предела произведений функций:
.
Ответ
.Пример 4
Найти предел:
.
Решение
При , , . У нас неопределенность вида 0/0.
Преобразуем функцию под знаком предела. Применим формулу:
.
Подставим :
.
Преобразуем знаменатель:
.
Тогда
.
Поскольку и при , то сделаем подстановку , и применим теорему о пределе сложной функции и первый замечательный предел:
.
Применяем арифметические свойства предела функции:
.
Ответ
.
Пример 5
Найдите предел функции:
.
Решение
Нетрудно убедиться, что в этом примере мы имеем неопределенность вида 0/0. Для ее раскрытия, применим результат предыдущей задачи, согласно которому
.
Введем обозначение:
(П5.1) . Тогда
(П5.2) .
Из (П5.1) имеем:
.
Подставим в исходную функцию:
,
где ,
,
;
;
;
.
Используем (П5.2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
,
здесь m – отличное от нуля число, ;
;
;
.
Ответ
.
Пример 6
Найти предел:
.
Решение
При , числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 0/0. Для ее раскрытия, преобразуем числитель дроби:
.
Применим формулу:
.
Подставим :
;
,
где .
Применим формулу:
.
Подставим :
;
,
где .
Числитель дроби:
.
Функция за знаком предела примет вид:
.
Найдем предел последнего множителя, учитывая его непрерывность при :
.
Применим тригонометрическую формулу:
.
Подставим ,
. Тогда
.
Разделим числитель и знаменатель на , применим первый замечательный предел и одно из его следствий:
.
Окончательно имеем:
.
Также можно было применить формулу
, подставив .
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Первый замечательный предел, формула и следствия
Формула первого замечательного предела
Доказательство первого замечательного предела
Рассмотрим односторонние пределы
Докажем, что каждый из этих пределов равен единице. Тогда и предел также будет равняться единице.
Пусть и отложим этот угол на тригонометрической окружности (рис. 1).
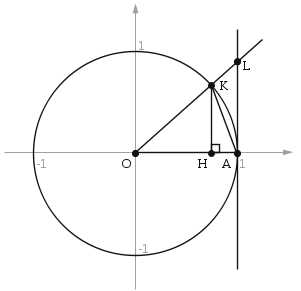
Рис. 1
Этот луч будет пересекать единичную окружность в точке , а вертикальную касательную, проведенную в точке , – в точке . Через точку обозначим проекцию точки на горизонтальную ось косинусов.
Рассмотрим треугольники и круговой сектор . Очевидно следующее двойное неравенство:
Абсцисса точки равна , а ее ордината – (равна высоте ). А тогда
Здесь как радиус тригонометрической окружности.
Площадь центрального сектора круга радиуса с центральным углом равна
Площадь
Итак, неравенство (1)перепишется в виде:
Так как для все части этого неравенства положительны, поэтому его можно записать следующим образом:
После умножения на получаем:
или
Переходя во всех частях последнего неравенства к пределу при , будем иметь:
По теореме о двухстороннем ограничении (теорема «про двух милиционеров») делаем вывод, что и
Вычислим теперь :
То есть .
А, таким образом, и .
Теорема доказана.
Следствия из первого замечательного предела
Примеры решения задач
ru.solverbook.com
теория и примеры — Студопедия.Нет
Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:
Приведённое выше равенство основано на эквивалентности бесконечно малых . Следовательно, верно равенство и следующего отношения:
.
Это разновидность первого замечательного предела.
Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.
При решении не обойтись без преобразований выражений. Для этого обязательно потребуется открыть в новых окнах пособия
Пример 1.Найти предел .
Решение. Подстановка вместо x нуля приводит к неопределённости:
.
В знаменателе — синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:
.
В знаменателе — синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе, а, когда тройки сократятся, получится первый замечательный предел в чистом виде. Умножаем икс на три и тут же делим и далее решаем:
.
Пример 2.Найти предел .
Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:
.
Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:
.
Пример 3.Найти предел .
Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:
.
Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
Пример 4.Найти предел .
Решение. Вновь получаем неопределённость «нуль делить на нуль»:
.
Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:
Пример 5.Найти предел .
Решение. И вновь неопределённость «нуль делить на нуль»:
.
Помним из тригонометрии, что тангенс — это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:
.
Пример 6.Найти предел .
Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.
.
Так как , то и
Пример 7.Найти предел .
Решение. И вновь неопределённость «ноль делить на ноль» и синус под знаком предела. Значит надо приводить к первому замечательному пределу. Умножим числитель и знаменатель на выражение сопряжённое числителю и получим
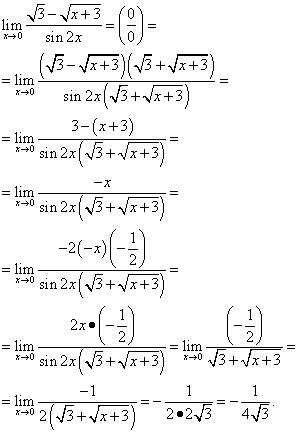
Пример 8.Найти предел .
Решение. Бороться с неопределённостью «ноль делить на ноль» будем приведением к первому замечательному пределу. Вспоминаем формулу тригонометрической единицы и подставляем её. Потом вспоминаем, что косинус в квадрате нуля и просто косинус нуля равны единице, а они у нас с противоположными знаками, значит взаимно уничтожаются. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё вышеописанное выглядит так:
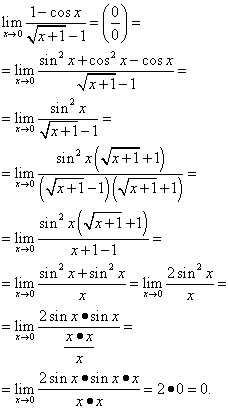
studopedia.net
Первый замечательный предел — 10 Августа 2015 — Примеры решений задач
Следствия первого замечательного предела:
Следствие 1:
Доказательство:
Следствие 2:
Доказательство: сделаем замену , тогда
Следствие 3:
Доказательство: сделаем замену , тогда
Пример 1. Найти предел
Решение.
Пример 2. Найти предел
Решение. Замена
Пример 3. Найти предел
Решение.
www.reshim.su
Второй замечательный предел — МегаЛекции
Первый замечательный предел
Рассмотрим следующий предел:
Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
Данный математический факт носит название Первого замечательного предела.
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
, , ,
Здесь , , , , и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
Пример 2
Найти предел
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
Собственно, ответ готов:
Пример 3
Найти предел
Подставляем ноль в выражение под знаком передела:
Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле ( В данном случае:
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел
Пробуем подставить ноль в числитель и знаменатель:
Получена неопределенность (косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
Постоянные множители вынесем за значок предела:
Организуем первый замечательный предел:
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
Избавимся от трехэтажности:
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
Второй замечательный предел
В теории математического анализа доказано, что:
Данный факт носит название второго замечательного предела.
Справка: – это иррациональное число.
В качестве параметра может выступать не только переменная , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти предел
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение , Нетрудно заметить, что при основание степени , а показатель – , то есть имеется, неопределенность вида :
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :
Когда задание оформляется от руки, карандашом помечаем:
Практически всё готово, страшная степень превратилась в симпатичную букву :
При этом сам значок предела перемещаем в показатель:
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7
Найти предел
Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.
Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :
Теперь можно почленно разделить числитель на знаменатель:
Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел .
Легко заметить, что в данном примере . Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :
Наконец-то долгожданное устроено, с чистой совестью превращаем его в букву :
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
