Интегральная круговая формула числа Пи, пи, разное, угол, текст png
Интегральная круговая формула числа Пи, пи, разное, угол, текст pngтеги
- разное,
- угол,
- текст,
- логотип,
- геометрическая форма,
- черный,
- число,
- пи,
- параллель,
- символ,
- танака,
- приближение,
- музыка,
- область,
- математика,
- марка,
- линия,
- исчисление,
- круг,
- окружность,
- диаграмма,
- уравнение,
- формула,
- функция,
- черныйА белый,
- цельный,
- трапециевидный,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 2100x826px
- Размер файла
- 42.94KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
22KB
63MB
84KB
org/ImageObject»> Пи день символ математики, пи, разное, текст, логотип png
600x588px
15.69KB
org/ImageObject»> Круг окружности символа Пи Пи, пи, разное, угол, текст png
2000x1935px
38.72KB
38KB
79KB
21KB
16KB
53KBИстория Пи Число Пи День Математика, пи, разное, угол png
История Пи Число Пи День Математика, пи, разное, угол pngтеги
- разное,
- угол,
- текст,
- чирок,
- логотип,
- пирог,
- число,
- пи,
- пи День,
- круговая диаграмма,
- соотношение,
- символ,
- математика,
- математика Шутка,
- аква,
- площадь,
- лазурь,
- круг,
- окружность,
- диаметр,
- зеленый,
- история Пи,
- линия,
- очередь,
- png,
- прозрачный png,
- без фона,
- бесплатная загрузка
- Размер изображения
- 1024x908px
- Размер файла
- 28.71KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Некоммерческое использование, DMCA Contact Us
org/ImageGallery» align=»middle»>
96KB
org/ImageObject»> Число математики в день Пи, математика пи, разное, текст png
1600x1593px
791.84KB
38KB
org/ImageObject»> День Математики Символ Пи История Пи, 100%, Разное, текст png
1058x1024px
28.99KB
25KB
org/ImageObject»> Круговая диаграмма Диаграмма Компьютерные иконки, круговая диаграмма, угол, текст png
512x512px
8.26KB
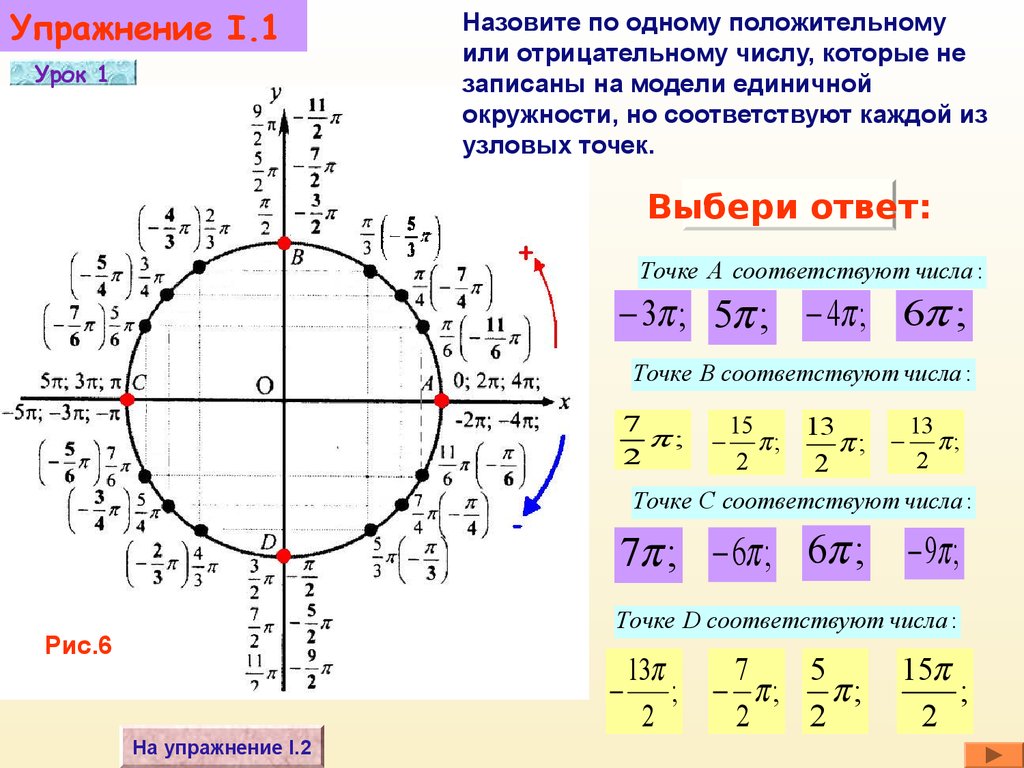58KB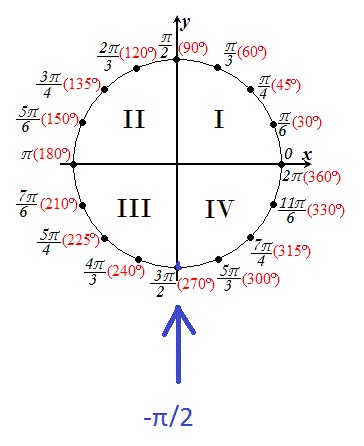
32KB
org/ImageObject»> Пи День Математический Символ, пи, Разное, текст png
1280x1238px
55.42KBПочему PI встречается в каждой круглой форме и по всей Вселенной
Происхождение числа Пи (π) восходит к древним цивилизациям около 4000 лет назад. Это математическая загадка, которая на протяжении веков привлекала внимание каждого любителя математики. В евклидовой геометрии число Пи определяется как отношение длины окружности к его диаметру, но оно имеет и другие эквивалентные определения. Пи называют математической константой, приблизительное значение которой равно 3,14159.. Всегда интересно попытаться вычислить значение числа Пи, так как это может продолжаться вечно! Что касается вычислений, число Пи было рассчитано более чем с 22 триллионами цифр. Для его вычисления потребовался всего один компьютер, неустанно работавший в течение 105 дней с 24 жесткими дисками.
История использования числа Пи с древних времен
Число Пи веками использовалось в нескольких разделах математики, статистики, геометрии и других областях.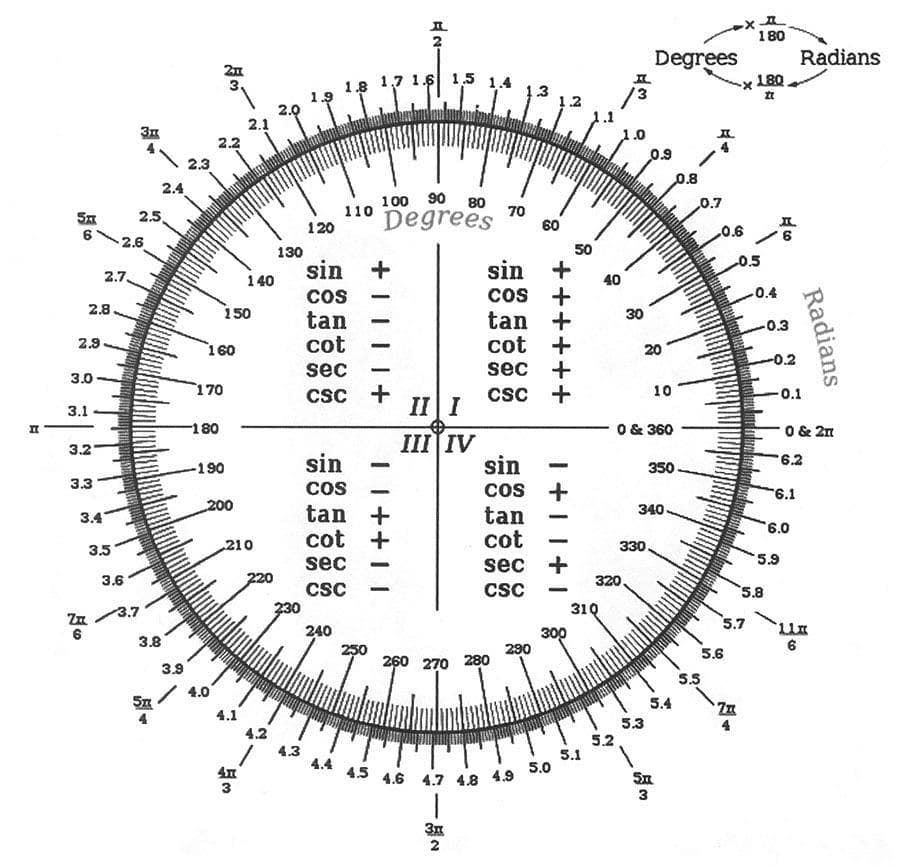
А вот имя «Пи» — это относительно недавняя деятельность. В 1706 году Уильям Джонс, британский математик, был первым, кто назвал это число Пи, соединив его с греческой буквой π.
Давайте посмотрим, как появилось число Пи, каким мы его знаем сегодня:
- В древнем Вавилоне площадь круга вычислялась путем умножения на три квадрата его радиуса, что давало значение числа Пи, которое равнялся трем. Число Пи, найденное на найденной вавилонской табличке, равнялось 3,125.
- Некоторые примеры египетской математики можно найти в папирусе Райнда около 1650 г. до н.э. Древние египтяне использовали формулу для определения площади круга, которая давала приблизительное значение Пи как 3,1605.
- Уильям Джонс ввел символ числа Пи в 1706 году, который впоследствии был популяризирован Леонардом Эйлером, принявшим его в 1737 году.
- Джордж Бюффон, французский математик, ввел способ вычисления числа Пи с использованием вероятности.
Теперь давайте попробуем провести простой эксперимент, чтобы получить число Пи.
Нарисуйте на любом листе бумаги круг (любого размера) с помощью циркуля. Поместите одну нить поверх круга и еще раз пройдитесь по ней, затем выпрямите нить. Его длина даст вам длину окружности. Диаметр круга в два раза больше радиуса (длина от любой точки круга до его центра). Наконец, разделите длину окружности на диаметр. Удивительно, но значение будет 3,14 ⏤ независимо от размера вашего круга! Если вы все правильно измерили и рассчитали, вы получили число Пи, равное 3,14.
Современные применения числа Пи в различных сферах жизни
Некоторые могут назвать число Пи самым известным числом в мире. Число Пи настолько популярно среди людей, что ему посвящен отдельный день ⏤ День числа Пи (π), который ежегодно отмечается 14 марта года года с большой помпой во всем мире. Хотя число Пи оказывает сильное влияние на математику и геометрию, оно также имеет и другие важные применения:
- Звук и свет. Звуковые и световые волны играют решающую роль в функционировании мира, например,
- Пи можно найти в синусоидах, которые в основном используются для обработки звуковых и световых сигналов.
- Пи также имеет другие применения, например, звуковые волны, используемые для проведения УЗИ ребенка в утробе матери.
- Пи помогает в изучении частоты, длины волны и амплитуды океанских волн.
Pi также помогает изучить, как прыгают пружины, вибрируют струны и качаются маятники.
- Генетика. Самой основной структурой человеческого тела является ДНК. Угадай, что? Пи можно найти в ДНК человека. Для того, чтобы длинная ДНК (около 1,8 метра в длину) поместилась на небольшом участке клетки тела (около 10 микрон в диаметре), она образует нуклеосомы, которые выглядят как бусины, и эта нить в 1,5 раза короче нашей ДНК. . Пи также находится в спирали двойной спирали ДНК. Структура двойной спирали скрепляется пи-связями, которые представляют собой стековые взаимодействия, помогающие удерживать структуру на месте.
- Природное окружение. К любому круглому объекту с диаметром и окружностью в нашем окружении можно применить Пи ⏤ из круглого зрачка наших глаз, луны, солнца и даже радуги. Пи находит свое применение во многих природных явлениях, таких как
Пи находит свое применение во многих природных явлениях, таких как- Его можно найти в пульсации сердца.
- Pi также используется для измерения пульсаций, исходящих из центральной точки.
- Используется для измерения извилистости рек.
- Пи также можно найти в Солнечной системе.
- Астрономия и астрофизика. С древних времен число Пи использовалось для изучения Вселенной и нашей Солнечной системы. Давайте посмотрим, как:
- Для поиска новых планет и их атмосфер
- Используется при расчете количества секунд в году.
- Многие космические центры также используют число Пи для расчета траектории космического корабля и изучения астероидов и метеоров.
- Пи в паттернах. Знаете ли вы, что паттерны таких животных, как зебра или леопард, зависят от числа Пи? Удивительно, как число Пи играет такую важную роль в животном мире. Алан Тьюринг, английский математик, предположил, что Пи — это константа, управляющая различными закономерностями, проявляемыми живыми существами, пока они еще находятся в эмбриональном состоянии. Он назвал этот процесс «морфогенезом».
Он назвал этот процесс «морфогенезом».Пи — одно из самых знаменитых чисел в мире, которое можно найти в нескольких разделах математики, физики, биологических наук и астрономии. Хотя может быть трудно собрать воедино все многочисленные варианты использования числа Пи, мы, конечно же, не можем этого отрицать. Он начал свой путь в древней математике и астрономии, но сегодня его можно найти почти во всех областях нашего физического мира и даже во Вселенной!
Что вы думаете о Pi и его приложениях? Дайте нам знать в разделе комментариев и ознакомьтесь с другими блогами BYJU’S FutureSchool.
Математика, Мир математики
Об авторе
Больше, чем просто программирование и математика! Наша запатентованная учебная программа, основанная на деятельности, с обучением в режиме реального времени облегчает: Решение проблем. Креативное мышление. Песок. Уверенность. Связь
Практические рабочие листы по классам:
Рабочие листы по математике для первого класса, Рабочие листы по математике для второго класса, Рабочие листы по математике для третьего класса, Рабочие листы по математике для четвертого класса, Рабочие листы по математике для пятого класса, Рабочие листы по математике для шестого класса, Рабочие листы по математике для седьмого класса, Рабочие листы по математике для восьмого класса
Вам также может понравиться
Как создать мобильную математическую игру? Нет сомнений в том, что мобильные устройства повсюду, и с появлением мощных смартфонов и планшетов не видно конца
Подробнее.
..
Пи прячется повсюду | WIRED
Photograph: Justin Paget/Getty Images
Rhett Allain
Science
Для Дня Пи давайте отследим удивительные места, где эта математическая константа поворачивается квантовый мир к повседневному.
Когда кто-то поздравляет вас с Днем Пи, вы, вероятно, сразу же думаете о кругах, и не только о пирогах. (День Пи — 14 марта или 3.14, если вы используете формат даты в США.) Это потому, что если вы измерите расстояние вокруг внешней стороны круга (окружность), а затем расстояние по ней (диаметр), число Пи — это длина окружности, деленная на по диаметру.
Иллюстрация: Getty Images
Поэтому каждый раз, когда вы имеете дело с кругами, кажется вполне логичным, что число Пи может появиться.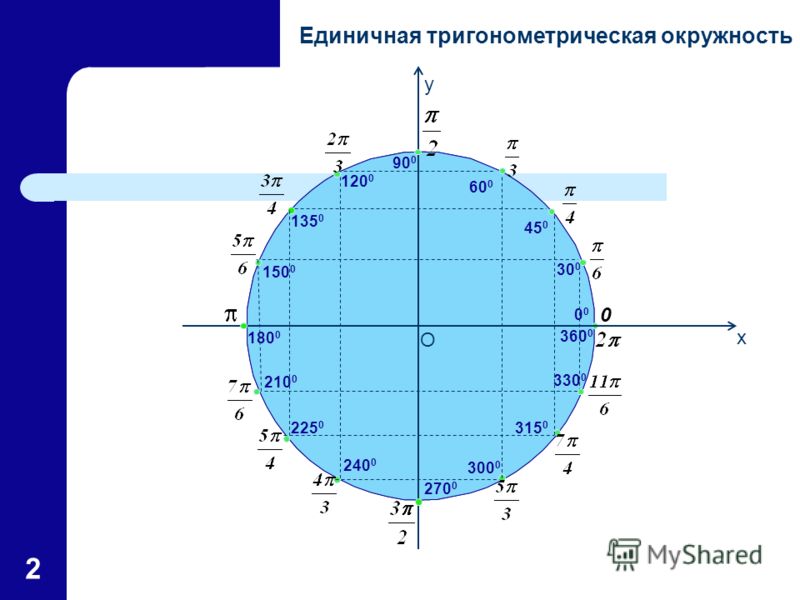
Но многие ситуации, когда появляется число пи, поначалу кажутся вообще не связанными с кругами. В квантовой механике это решение уравнения Шредингера, как мы моделируем электроны и протоны в атоме. Это константа магнитной проницаемости, которая используется для расчета магнитных полей. Он проявляется в движении массы, раскачивающейся на струне, иначе известной как маятник. Это электрическая постоянная, которая используется для расчета электрического поля из-за зарядов. И дело даже в принципе неопределенности, согласно которому нельзя точно знать и импульс, и положение частицы.
Почему он продолжает появляться? На самом деле есть две основные причины: симметрия и осцилляции.
Пи и симметрия
Давайте поговорим о симметрии на примере солнечного света. В частности, давайте рассмотрим интенсивность солнца. Самый простой способ подумать о силе солнца — это подумать о скорости его производства энергии или о том, сколько оно производит за определенный промежуток времени.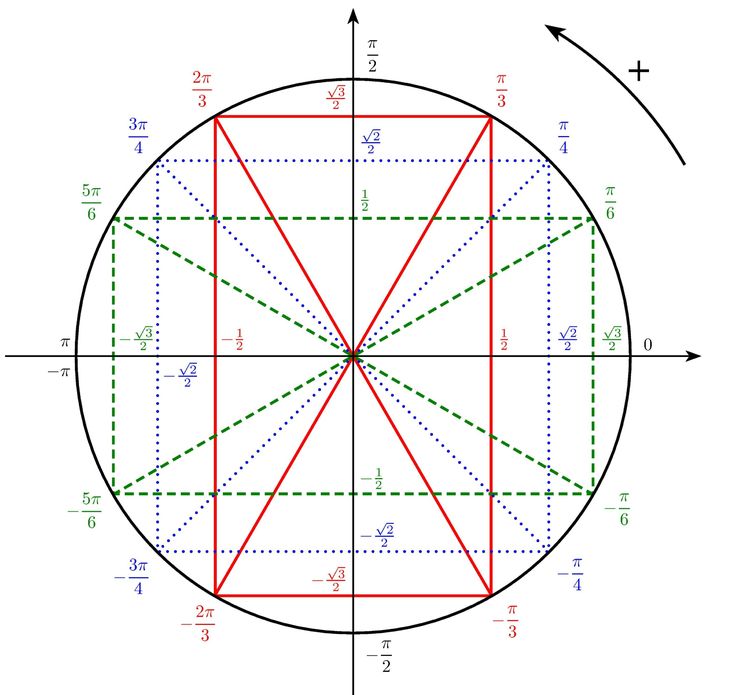
Это огромная. Каждую секунду Солнце излучает почти 4 x 10 26 ватт (это 4 x 10 26 джоулей) энергии.
Поскольку он излучает эту мощность во всех направлениях, мы можем описать мощность на единицу площади как солнечную интенсивность. Когда свет уходит от Солнца, он покрывает расширяющуюся сферу. По мере увеличения радиуса этой сферы увеличивается и площадь поверхности, по которой должна распределяться мощность. Это означает, что интенсивность солнечного излучения уменьшается по мере удаления от Солнца. К тому времени, когда свет, наконец, достигает Земли, его интенсивность составляет всего около 1000 ватт на квадратный метр. Возможно, эта двухмерная диаграмма поможет проиллюстрировать концепцию:
Иллюстрация: Ретт Аллен
Самые популярные
Угадайте, что? Площадь поверхности расширяющейся сферы зависит от значения числа пи, поскольку сфера — это всего лишь трехмерный круг. (Площадь сферы равна 4πR 2 .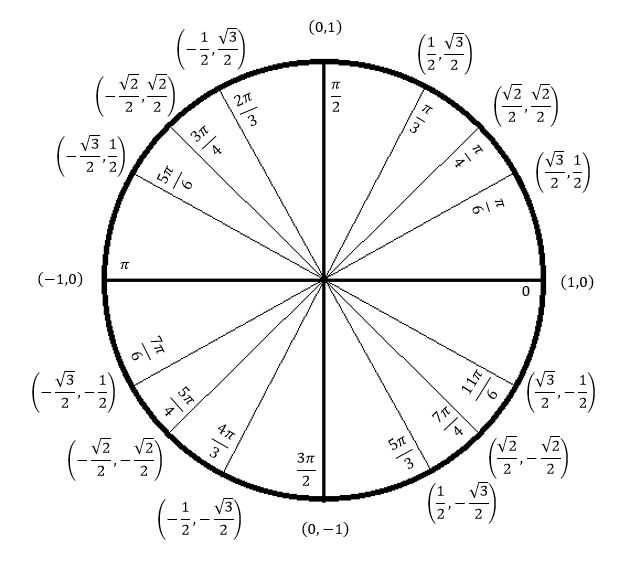
) Это дает следующее выражение для солнечной интенсивности:
Иллюстрация: Ретт Аллен
Свет — или любой другой объект — распространяясь равномерно во всех направлениях, создает сферическое распределение. Любое сферическое распределение симметрично, поскольку любая точка на сфере будет равноудалена от центра сферы.
Хорошо, попробуем другой пример. Представьте, что у меня есть электрический заряд, движущийся с некоторой скоростью (v). (Возьмем протон, но это применимо к любому заряду, включая заряды в атомах или даже заряды, движущиеся в электрическом токе.)
Движущийся электрический заряд создает магнитное поле, и мы можем вычислить это магнитное поле с помощью следующего уравнения :
Иллюстрация: Ретт Аллен
Самые популярные
Это сложное и очень красивое уравнение — и вот ваше число Пи. Это прямо в знаменателе. Это связано с тем, что магнитное поле, создаваемое движущейся заряженной частицей, имеет круговую симметрию.
Чтобы найти напряженность магнитного поля, представьте, что вы проводите линию от движущегося заряда к тому месту, где вы хотите найти значение поля. Сила этого поля зависит от расстояния до заряда, и это образует круг.
Вы можете увидеть симметрию в этом вычислении Python, показывающем заряд с вектором скорости (красная стрелка) и магнитное поле в разных местах (желтые стрелки).
Иллюстрация: Ретт Аллен
(Вот код.)
Хорошо, теперь посмотрим на другую переменную в уравнении магнитного поля, μ 0 . Это магнитная постоянная (также называемая проницаемостью вакуума), и она имеет значение, равное 4π x 10 -7 ньютонов на квадратный ампер. Как и все фундаментальные константы, она создает взаимосвязь между вещами, которые мы действительно можем измерить, например между силами и электрическими токами.
Но почему там тоже пи? Поначалу кажется, что эти два экземпляра пи должны компенсировать друг друга. Единица в уравнении магнитного поля стоит в числителе, а в знаменателе уже была единица.
Это справедливое замечание. На самом деле можно определить наши константы так, что число пи не будет фигурировать в выражении для магнитного поля. Однако есть и другое место, где эта магнитная постоянная проявляется — скорость света.
Если вы помните, свет — это электромагнитная волна. Это означает, что это действительно две волны в одной. Существует изменяющееся электрическое поле, которое создает изменяющееся магнитное поле, а изменяющееся магнитное поле создает изменяющееся электрическое поле. Таким образом, значение скорости этой электромагнитной волны (мы называем ее скоростью света, с) зависит как от магнитной постоянной , так и от электрической постоянной (ε 0 ).
Самые популярные
Иллюстрация: Ретт Аллен
Это означает, что если вы запишете выражение для магнитной постоянной без пи, оно появится в уравнении для скорости света. Так или иначе, число Пи появится.
Пи и колебания
А теперь совсем о другом.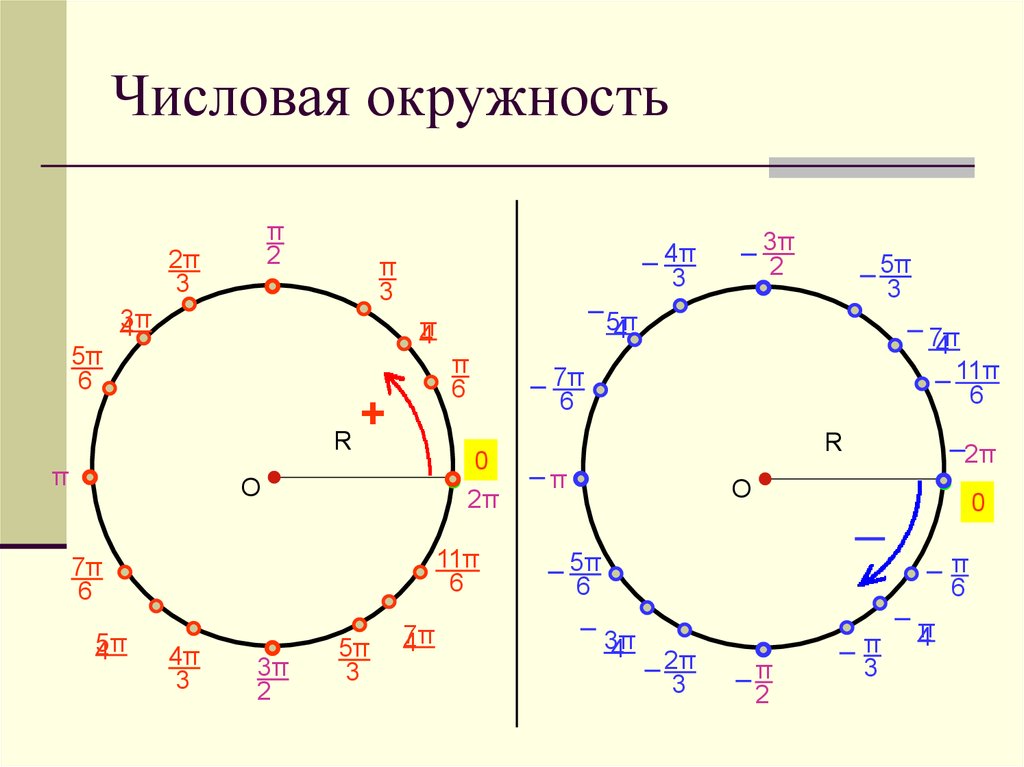
Возьмите груз и повесьте его вертикально на пружину. Теперь немного потяните эту массу вниз и отпустите. Это заставит массу колебаться вверх и вниз. Если вы измерите значение массы (m) и силы пружины (постоянная пружины, k), вы обнаружите, что время, необходимое этой массе для совершения одного полного колебания (период T), согласуется со следующим уравнением :
Иллюстрация: Ретт Аллен
Самые популярные
Вот ваше число Пи. На самом деле, вы можете независимо измерить массу, период и жесткость пружины и использовать это для вычисления числа пи просто для удовольствия.
Однако мы также можем использовать математическую функцию для представления этого колебания. Вот простейшее уравнение, которое дает положение массы как функцию времени, где A — амплитуда движения, а ω — угловая частота.
Иллюстрация: Rhett Allain
Это решение включает косинус тригонометрической функции. Если ваша тригонометрия туманна, просто помните, что все тригонометрические функции сообщают нам об отношении сторон прямоугольных треугольников.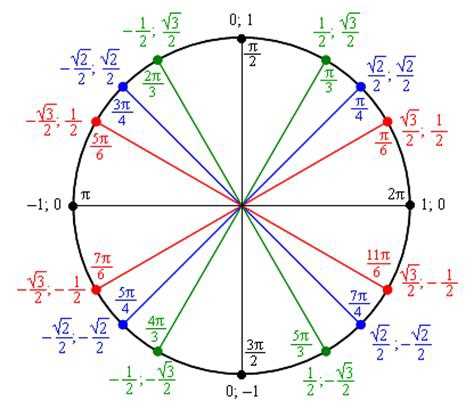
Например, косинус 30 градусов говорит о том, что если у вас есть прямоугольный треугольник с одним углом в 30 градусов, длина стороны, прилегающей к этому углу, деленная на длину гипотенузы, будет некоторым значением. (В данном случае это будет 0,866).
(Вам может показаться странным, что нам нужна математическая функция, которая также используется для треугольников, чтобы понять движение пружины, которая, в конце концов, является круглым объектом. Но, в конце концов, эта функция оказывается решение нашего уравнения. Короче говоря, мы используем его, потому что он работает. В любом случае, оставайтесь со мной.)
Теперь представьте, что угол прямоугольного треугольника постоянно увеличивается. (Это термин ωt.) Поскольку угол меняется, у вас, по сути, есть треугольник, который вращается по кругу. Если вы посмотрите только на одну сторону этого прямоугольного треугольника и на то, как она меняется со временем, вы увидите свою тригонометрическую функцию. Вот как это выглядит:
Видео: Ретт Аллен
Поскольку это колебание связано с кругом, кажется очевидным, что там должно быть число «пи».
На самом деле, вы можете найти пи в любом другом виде колебаний, которые можно смоделировать с помощью триггерной функции, содержащей синусы или косинусы. Например, подумайте о маятнике, представляющем собой массу, раскачивающуюся на струне, или о колебаниях двухатомной молекулы (молекулы с двумя атомами, например азота), или даже об изменении электрического тока в чем-то вроде цепи внутри радиоприемника. что делает колебание.
Принцип неопределенности
Среди фанатов физики, пожалуй, самый популярный фундаментальный принцип называется h-bar (ħ). По сути, это просто постоянная Планка (h), деленная на 2π.
Постоянная Планка дает соотношение между энергией и частотой для сверхмалых объектов, таких как атомы, и вы можете сами измерить эту постоянную с помощью некоторых светодиодов. На самом деле число «пи» так часто встречается в моделях, имеющих дело с крошечными квантовыми вещами, что физики объединили число «пи» и «h» и получили столбец «h».
Самые популярные
Одно место, где вы увидите эту черту (и, следовательно, число Пи), связано с принципом неопределенности, который в основном говорит, что вы не можете точно измерить положение (x) и импульс (p) частицы.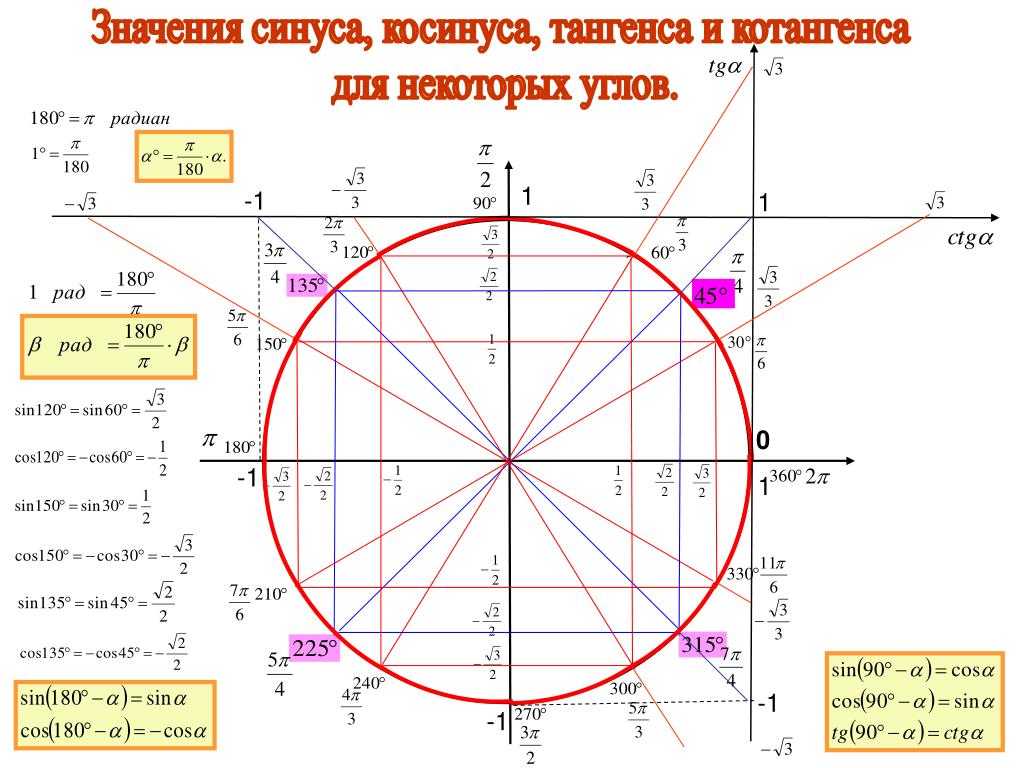
На самом деле у этих измерений есть фундаментальный предел. (Это принцип неопределенности.) Это выглядит так:
Иллюстрация: Ретт Аллен
Это говорит о том, что произведение неопределенности в x (Δx) и импульсе (Δy) должно быть больше, чем значение, зависящее от pi (h- бар).
Почему вы не можете знать положение и импульс ? Лучшее объяснение исходит от волн. Представьте волны, проходящие через воду. Мы можем оценить скорость каждой волны (и ее импульс), взглянув на время, которое требуется нескольким пикам для прохождения стационарной точки. Чем больше волновых пиков проходит через эту точку, тем лучше мы оцениваем скорость каждой волны. Однако, если у вас есть несколько волновых пиков, довольно сложно определить точное местоположение отдельной волны — ее положение.
Теперь представьте, что вместо этого есть только один пик волны. В этом случае у вас будет довольно хорошее представление о том, где находится волна, но теперь вы не знаете, с какой скоростью она движется.
Вы не можете точно определить положение и скорость до точных значений. Это принцип неопределенности — он верен для волн в воде и для поведения мельчайших частиц, таких как электроны и протоны.
Ладно. Но почему там пи? Это будет немного сложно, так что просто задержитесь на мгновение за эту идею: когда мы говорим о частицах, таких как электроны, мы описываем их чем-то, что называется волновой функцией. Эта волновая функция дает нам вероятностную интерпретацию движения, так что мы на самом деле не знаем, где и как движется частица, а только вероятности того, что может произойти.
Самые популярные
нам нужно проинтегрировать эту волновую функцию по всему пространству. В квантовой механике этот интеграл обычно означает, что мы пытаемся найти вероятность найти частицу в любом месте . Для этого мы суммируем вероятности для всех различных значений x, от отрицательной бесконечности до положительной бесконечности.