Векторная алгебра описывает способы выполнения различных операций над векторами, в том числе сложение, вычитание, разные типы перемножения. Здесь приводится лишь часть этого раздела математики, непосредственно относящаяся к задачам, наиболее часто возникающим в физической и инженерной практике. Понятие вектора В геометрическом смысле вектор — это направленный отрезок, определяемый точками своего начала и конца. Ограничения В силу специфики сайта векторные операции рассматриваются для наиболее частого случая — трёхмерного пространства, описываемого в декартовой системе координат (три взаимно ортогональные оси отсчёта). Для пространств меньшей мерности (двухмерной плоскости и одномерной прямой) обычно достаточно обнулить «неиспользуемые» координаты. Пространства большей мерности не рассматриваются, поскольку до сих пор являются физической экзотикой. Для работы с ними следует изучить курс векторной алгебры более серьёзно. В связи с малой практической востребованностью не рассматривается выполнение операций над векторами в полярных и других недекартовых системах координат. Не рассматривается и матричное исчисление, поскольку для трёхмерного пространства алгебраическая форма векторных операций является достаточно простой и удобной, хотя и не столь универсальной. Кроме того, матричное исчисление требует довольно специфического подхода, что затрудняет его применение теми, кто с прежде с матрицами не сталкивался. Основные понятияРассмотрим основные понятия, используемые на этой странице. Проекции и координаты вектора Любой трёхмерный вектор можно спроецировать на три взаимно перпендикулярные оси отсчёта, пересекающиеся в одной точке (декартовы оси координат). Выбор точки отсчёта и положение осей (базис системы координат) теоретически непринципиален, но на практике обычно выбирается так, чтобы как можно большее число участвующих в расчёте векторов было направлено вдоль какой-либо из осей координат — это упрощает вычисления. Каждый вектор можно охарактеризовать координатами двух точек — его начала и конца, — либо проекциями на оси координат и координатами точки привязки (обычно точкой привязки является начало вектора, но иногда бывает удобнее использовать в этом качестве его конец). В физике чаще применяется второй подход. В этом случае в трёхмерном пространстве вектор a описывается шестью величинами — координатами его точки привязки xa, ya, za и проекциями на оси ax, ay и az. Иногда точка привязки не имеет принципиального значения либо подразумевается неявно, и тогда обходятся тремя значениями — проекциями векторной величины на оси координат ( ax, ay, az). Некоторые определения Модулем вектора |a| в геометрии называется его длина, а в физике — абсолютное значение направленной величины (т.е. значение, измеренное вдоль направления её действия). Среди всевозможных взаимных ориентаций векторов выделяют коллинеарные и ортогональные вектора. Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направлеными строго в противоположные стороны. Ортогональными называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны. Понятие равных векторов менее однозначно. Иногда под этим понимают любые сонаправленные вектора одного размера, расположение точки привязки которых безразлично и может быть в любом месте пространства. Более строгое определение подразумевает и совпадение точек привязки. В физике под «равенством векторов» обычно имеют в виду первый случай (величины и направления одинаковы, положение точки привязки произвольно). Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления. Иногда нулевой вектор трактуют как всенаправленный, хотя в строгом смысле это не так. Операции над векторамиСложение векторовВ алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака: сx = ax + bx ;сy = ay + by ; сz = az + bz . Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). Вычитание векторовВычитание векторов с = a – b можно представить как сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак: сx = ax – bx ;сy = ay – by ; сz = az – bz . Умножение вектора на числоПри умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число: bx = k · ax ;by = k · ay ; bz = k · az .  В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи. Операция умножения на число является коммутативной a · k = k · a (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет нулевой вектор, говорить о направлении которого некорректно. Операция умножения на число является дистрибутивной k · (a + b) = k · a + k · b (произведение суммы векторов на число равно сумме произведений слагаемых на это же число). Скалярное произведение векторовРезультатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними. Вычисление скалярного произведенияВ алгебраической форме скалярное произведение d = a · b вычисляется как d = ax · bx + ay · by + az · bz .Свойства скалярного произведенияКоммутативность: a · b = b · a . Дистрибутивность: a · (b + c) = a · b + a · c . Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) . Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора). Векторное произведение векторов
Результатом векторного перемножения двух векторов a и b является вектор c, длина которого равна произведению их модулей, умноженному на синус угла между ними, а сам вектор ориентирован таким образом, что перпендикулярен обоим исходным векторам, и тройка a b c является правой. Вычисление векторного произведенияВ алгебраической форме векторное произведение c = [a × b] в правой системе координат вычисляется как сx = ay · bz – az · by ;сy = az · bx – ax · bz ; сz = ax · by – ay · bx . В левой системе координат знаки слагаемых меняются на противоположные. В физике обычно подразумевается, что точки привязки всех перемножаемых векторов и результирующего вектора совпадают (и вектора-сомножители, и результат их векторного произведения действуют в одной и той же точке пространства). Свойства векторного произведенияАнтикоммутативность: [a × b] = –[b × a] . Дистрибутивность: [a × (b + c)] = [a × b] + [a × c] . Сочетательность относительно скалярного множителя: k · [a × b] = [(k · a) × b] = [a × (k · b)] . Смешанное произведение: a · [b × c] = [a × b] · c . Векторный квадрат вектора всегда является нулевым вектором: [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора). ♦ | |
| последняя правка 27.01.2011 21:01:52 |
В ортогональной системе координат модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Если же одинаковы и точки привязки, то речь идёт о совпадающих (эквивалентных) векторах.
В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или к одной и той же материальной точке).
Скалярное произведение векторов. Профильный уровень 11 класс онлайн-подготовка на Ростелеком Лицей
Длина вектора. Расстояние между точками
Мы продолжаем расширять модель вектора для трехмерного пространства. На прошлом уроке мы рассмотрели определение вектора с использованием двух подходов (геометрического и алгебраического), ввели основные операции (сложение и вычитание векторов, умножение вектора на число), рассмотрели некоторые свойства.
Также мы определили длину вектора как длину соответствующего отрезка с использованием теоремы Пифагора: длина вектора равна корню из суммы квадратов его координат (утверждение остается верным, независимо от количества этих самых координат) (см.
рис. 1):
Рис. 1. Вектор
Если вектор задан координатами начала и конца, то его собственные координаты находятся как разности координат этих точек (см. рис. 2):
Рис. 2. Вектор
Таким образом, формула длины вектора через его координаты эквивалентна утверждению, что расстояние между двумя точками находится как корень из суммы квадратов попарных разностей их координат:
Для трехмерного пространства ситуация повторяется абсолютно. Т. к. длина вектора – это длина диагонали прямоугольного параллелепипеда с измерениями, равными координатам вектора, то его длина находится как корень квадратный из суммы квадратов его координат (см. рис. 3):
Рис. 3. Вектор
Если две точки заданы своими координатами, то мы можем их рассматривать как начало и конец вектора (см. рис. 4):
Тогда мы можем найти координаты вектора и его длину, т. е. расстояние между точками:
Рис. 4. Вектор
Скалярное произведение векторов
Вспомним задачу о нахождении работы силы по перемещению объекта.
Задача 1. Мальчик тащит санки за веревку по горизонтальной поверхности. Чему равна работа силы натяжения по перемещению санок (см. рис. 5)?
Рис. 5. Иллюстрация к задаче 1
Решение
Если мы умножим силу на расстояние, то ответ будет верным только в том случае, если веревка натянута строго горизонтально, т. е. векторы силы и перемещения сонаправлены (см. рис. 6).
Рис. 6. Иллюстрация к задаче 1
Если же веревка натянута под углом, то за перемещение отвечает не сама сила, а ее проекция на вектор перемещения (грубо говоря, помогает тянуть нам только та часть силы, которая действует вдоль перемещения, она и совершает работу) (см. рис. 7):
Рис. 7. Иллюстрация к задаче 1
Длина проекции равна длине вектора силы, умноженной на косинус угла между силой и перемещением (см. рис. 8):
Рис. 8. Иллюстрация к задаче 1
Тогда:
Ответ: .
Рассуждая таким образом, в планиметрии мы ввели понятие скалярного произведения двух векторов.
Произведение двух векторов равно произведению модуля одного вектора на проекцию второго вектора на первый (см. рис. 9):
Рис. 9. Векторы и
Если нам известны длины векторов и угол между ними, то формула для вычисления скалярного произведения имеет вид:
Часто для обозначения модуля вектора используют просто букву , подчеркивая, что длина вектора и длина соответствующего отрезка – это одно и то же:
Результатом скалярного произведения является число. В примере с санками – это работа силы, величина скалярная. Очевидно, для скалярного произведения справедлив переместительный закон (если поменять местами сомножители, то результат не изменится):
Все вышесказанное нам известно из планиметрии. Если мы возьмем два вектора в пространстве и совместим их начала, то они будут лежать в одной плоскости (см. рис. 10).
Рис 10. Векторы и лежат в одной плоскости
Следовательно, для них будет справедливо то же самое определение скалярного произведения:
Физический смысл скалярного произведения остается тем же самым.
Разница появляется только в описании через координаты, т. к. в планиметрии у вектора две координаты, а в пространстве – три:
Произведение вектора на себя называют скалярным квадратом. Подставим его в формулу скалярного произведения:
Таким образом, скалярный квадрат вектора равен квадрату его длины.
Скалярное произведение в координатах
Если вектор задан координатами, то мы можем найти его скалярный квадрат, так как уже умеем искать его длину:
Итак, скалярный квадрат вектора равен сумме квадратов его координат:
Рассмотрим теперь, как выражается скалярное произведение двух произвольных векторов через их координаты. Мы это уже делали в планиметрии, и результат будет аналогичным. Тем не менее повторим эти рассуждения.
Пусть два вектора, и не коллинеарны. Совместим их в общее начало. Построим вектор (см. рис. 11).
Рис. 11. Вектор
По теореме косинусов имеем:
Если векторы коллинеарны, то данное равенство окажется верным и для него.
Таким образом, дальнейшие рассуждения верны для любой пары векторов.
Выражение – это скалярное произведение векторов. Тогда имеем:
Выразим скалярное произведение:
В правой части равенства у нас только скалярные квадраты векторов. Мы умеем находить их через координаты. Сделаем это:
Упростим выражение и получим:
Итак, мы получили формулу, знакомую нам из планиметрии: скалярное произведение векторов равно сумме попарных произведений их соответствующих координат.
Если в формулу скалярного произведения подставить один и тот же вектор , то получим знакомую уже формулу скалярного квадрата.
Итак, повторим:
1. С геометрической точки зрения скалярное произведение двух векторов равно произведению их длин на косинус угла между ними:
2. С алгебраической точки зрения скалярное произведение равно сумме попарных произведений их соответствующих координат:
Теперь мы можем сформулировать основные свойства скалярного произведения:
, причем , при .
Оно непосредственно следует из того:
Переместительный закон, который следует как из геометрической, так и из алгебраической интерпретации произведения:
Распределительный закон, который следует из координатной формы записи скалярного произведения:
Сочетательный закон, который очень легко доказать, используя как геометрическую, так и координатную формы скалярного произведения (сделайте это самостоятельно):
В самом деле: в формуле для вычисления скалярного произведения фигурирует косинус угла между векторами. Т. к. данный угол может принимать значения только от до , то единственное значение, при котором косинус равен , это .
Угол между векторами
Если мы знаем длины векторов и угол между ними, то мы можем найти скалярное произведение по формуле:
Пример. Найти скалярное произведение двух векторов, длины которых равны и , а угол равен .
Решение
:
Вспоминаем: если сила и перемещение сонаправлены, то работа силы (которая и равна скалярному произведению векторов силы и перемещения) максимальна и равна произведению их модулей.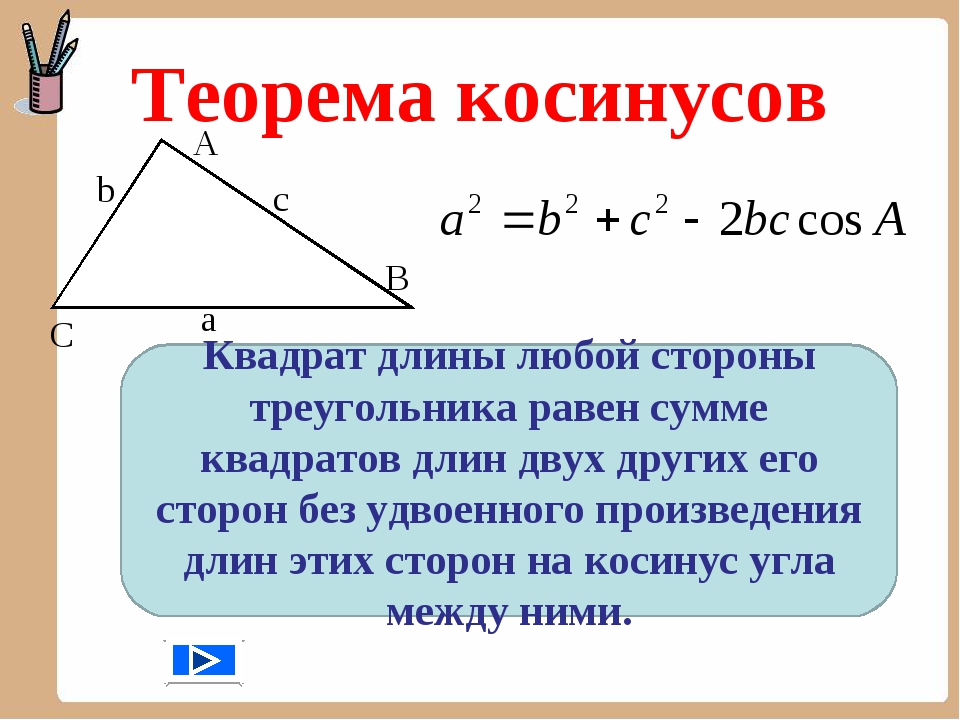
:
Как только веревка санок поднимается, проекция силы на перемещение уменьшается, уменьшается и работа силы. В данном случае в два раза.
:
Если сила направлена вертикально вверх, то работа такой силы по перемещению санок равна нулю.
:
Веревка направлена вверх и назад, горизонтальная проекция силы препятствует движению, работа отрицательна.
:
Сила направлена прямо противоположно перемещению. Работа отрицательна и максимальна по модулю (мы мешали движению как могли сильно) (см. рис. 12).
Рис. 12. Иллюстрация к примеру
Ответ: .
Задача может быть и обратной. Известны длины векторов и скалярное произведение. Тогда мы можем найти угол между векторами. В самом деле:
Тогда:
Эта формула позволяет найти угол между векторами. Проблема в том, что если длина векторов часто может быть известна из постановки задачи, то скалярное произведение вряд ли. Другое дело, если нам известны координаты векторов.
Тогда мы можем найти и их длины, и их скалярное произведение.
Задача 2. Найти угол между ребром куба и диагональю.
Решение
В силу симметрии куба не важно, между каким ребром и диагональю искать угол.
Найдем угол между ребром и диагональю , а для этого рассмотрим соответствующие векторы. Свяжем с кубом систему координат так, чтобы точка совместилась с началом координат (см. рис. 13).
Рис. 13. Иллюстрация к задаче 2
Координаты вектора , координаты вектора . Найдем косинус угла между векторами:
Найдем угол:
Ответ: .
Рассмотрим еще одну задачу на применение скалярного произведения, а более подробно сделаем это уже на практическом уроке.
Задача 3. Доказать, что четыре точки являются вершинами квадрата (см. рис. 14). Найти его площадь:
Рис. 14. Иллюстрация к задаче 3
Решение
Для начала докажем, что данный четырехугольник – параллелограмм.
Рассмотрим векторы противоположных сторон:
Векторы противоположных сторон равны, следовательно, они имеют равную длину и параллельны. Но это признак параллелограмма.
Осталось показать, что смежные стороны перпендикулярны. Найдем координаты вектора:
Перемножим векторы и :
Скалярное произведение векторов равно нулю, следовательно, векторы перпендикулярны.
Осталось найти площадь. Перемножим длины смежных сторон:
Ответ: .
Список литературы
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
- Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал webmath.ru
- Интернет-портал math34.ru
Домашнее задание
- Найти длину вектора , если и .
- Даны векторы и . Найти значение , при котором .
- Доказать, что четырехугольник с вершинами есть параллелограмм.
Возведение вектора в квадрат? — Математический стек Exchange
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 96 тысяч раз
$\begingroup$
Итак, это базовый. И должно быть довольно быстро.
Допустим, у меня есть вектор $\vec{r}$: 92$, когда понятно, что ты не имеешь в виду
$$
{\ bf r} {\ bf r} = \ sum_ {i, j} r_i r_j {\ bf e} _i {\ bf e} _j
$$
что равно вполне допустимой величине [1].
Что касается ${\bf r} = {\bf x} + {\bf y} + {\bf z}$,
$$
\begin{выравнивание}
{\bf r} \cdot {\bf r} &=& {\bf x} \cdot {\bf x} + {\bf x} \cdot {\bf y} + {\bf x} \cdot {\ bf z} + {\bf y} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf y} \cdot {\bf z} + {\bf z} \cdot {\bf x} + {\bf z} \cdot {\bf y} + {\bf z} \cdot {\bf z} \\
&=& {\bf x} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf z} \cdot {\bf z} + 2\left( {\bf x } \cdot {\bf y} + {\bf x} \cdot {\bf z} + {\bf y} \cdot {\bf z}\right)
\end{эквнаррай}
$$
равно ${\bf x} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf z} \cdot {\bf z}$ для всех $\bf x$, $ \bf y$, $\bf z$ тогда и только тогда, когда ${\bf x} \cdot {\bf y} + {\bf x} \cdot {\bf z} + {\bf y} \cdot {\bf z} = 0$ — особый случай, когда ${\bf x} \cdot {\bf y} = {\bf x} \cdot {\bf z} = {\bf y} \cdot {\bf z} = 0$.
2 + 2 \left((\vec{x} \cdot\vec{z}) +(\vec{y}\cdot\vec{z}) + (\vec{x} \cdot\vec{y}) \ справа)$$ 92$$
$\endgroup$
$\begingroup$
Существует два основных способа умножения вектора, скалярного произведения, как показано в ссылке Скалярное произведение, которое дает скаляр, независимо от того, умножаете ли вы A.B или возводите его в квадрат, A.A.
Или у вас может быть перекрестное произведение, то есть A X B, которое дает вам другой вектор, перпендикулярный обоим перекрестным произведениям.
Причина, по которой существуют два разных способа умножения векторов, заключается в том, что они имеют дело с различными физическими ситуациями, поэтому скалярное произведение может использоваться для работы, которая является скалярной, F.D, а векторное произведение используется для крутящего момента, скажем, или углового скорости, которые являются векторами.
$\endgroup$
4
r — Составление списка векторов по сумме квадратов каждого элемента
Задай вопрос
спросил
Изменено
3 года, 10 месяцев назад
92 = 2.