Квадратные неравенства, примеры, решения
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Определение 1Квадратное неравенство – это такое неравенство, которое имеет вид a·x2+b·x+c<0, где a, b и c – некоторые числа, причем aне равно нулю. x – это переменная, а на месте знака < может стоять любой другой знак неравенства.
Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y=a·x2+b·x+c.
Приведем пример квадратного неравенства:
Пример 1Возьмем 5·x2−3·x+1>0. В этом случае a=5, b=−3 и c=1.
Или вот такое неравенство:
−2,2·z2−0,5·z−11≤0, где a=−2,2, b=−0,5 и c=−11.
Покажем несколько примеров квадратных неравенств:
Пример 3Здесь коэффициенты этого квадратного неравенства есть ; 123·x2-x+57<0, в этом случае a=123, b=-1, c=57.
Особое внимание нужно обратить на тот факт, что коэффициент при x2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b·x+c>0, так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.
Пример 4Пример такого неравенства x2−5≥0.
Способы решения квадратных неравенств
Основным метода три:
Определение 2- графический;
- метод интервалов;
- через выделение квадрата двучлена в левой части.

Графический метод
Метод предполагает проведение построения и анализа графика квадратичной функции y=a·x2+b·x+c для квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥). Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a·x2+b·x+c при их наличии.
Для неравенства a·x2+b·x+c<0 решениями являются промежутки со знаком минус, для неравенства a·x2+b·x+c>0, промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.
Выделение квадрата двучлена
Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида (x−p)2<q (≤, >, ≥), где p и q – некоторые числа.
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Приведем пример. Рассмотрим равносильное преобразование неравенства 5≤2·x−3·x2. Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3·x2−2·x+5≤0.
Пример 5Необходимо найти множество решений неравенства 3·(x−1)·(x+1)<(x−2)2+x2+5.
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
3·(x−1)·(x+1)−(x−2)2−x2−5<0, 3·(x2−1)−(x2−4·x+4)−x2−5<0, 3·x2−3−x2+4·x−4−x2−5<0, x2+4·x−12<0.
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
D’=22−1·(−12)=16, x1=−6, x2=2
Построив график, мы можем увидеть, что множеством решений является интервал (−6, 2).
Ответ: (−6, 2).
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2·x2+5<x2+6·x+14
равносильно квадратному неравенству x2−6·x−9<0, а логарифмическое неравенство log3(x2+x+7)≥2 – неравенству x2+x−2≥0.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Квадратные неравенства, примеры, решения
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Определение 1Квадратное неравенство – это такое неравенство, которое имеет вид a·x2+b·x+c<0, где a, b и c – некоторые числа, причем aне равно нулю. x – это переменная, а на месте знака < может стоять любой другой знак неравенства.
Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y=a·x2+b·x+c.
Приведем пример квадратного неравенства:
Пример 1Возьмем 5·x2−3·x+1>0. В этом случае a=5, b=−3 и c=1.
В этом случае a=5, b=−3 и c=1.
Или вот такое неравенство:
Пример 2−2,2·z2−0,5·z−11≤0, где a=−2,2, b=−0,5 и c=−11.
Покажем несколько примеров квадратных неравенств:
Пример 3Здесь коэффициенты этого квадратного неравенства есть ; 123·x2-x+57<0, в этом случае a=123, b=-1, c=57.
Особое внимание нужно обратить на тот факт, что коэффициент при x2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b·x+c>0, так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.
Пример такого неравенства x2−5≥0.
Способы решения квадратных неравенств
Основным метода три:
Определение 2- графический;
- метод интервалов;
- через выделение квадрата двучлена в левой части.
Графический метод
Метод предполагает проведение построения и анализа графика квадратичной функции y=a·x2+b·x+c для квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥). Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a·x2+b·x+c при их наличии.
Для неравенства a·x2+b·x+c<0 решениями являются промежутки со знаком минус, для неравенства a·x2+b·x+c>0, промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.
Выделение квадрата двучлена
Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида (x−p)2<q (≤, >, ≥), где p и q – некоторые числа.
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Приведем пример. Рассмотрим равносильное преобразование неравенства 5≤2·x−3·x2. Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3·x2−2·x+5≤0.
Пример 5Необходимо найти множество решений неравенства 3·(x−1)·(x+1)<(x−2)2+x2+5.
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
3·(x−1)·(x+1)−(x−2)2−x2−5<0, 3·(x2−1)−(x2−4·x+4)−x2−5<0, 3·x2−3−x2+4·x−4−x2−5<0, x2+4·x−12<0.
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
D’=22−1·(−12)=16, x1=−6, x2=2
Построив график, мы можем увидеть, что множеством решений является интервал (−6, 2).
Ответ: (−6, 2).
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2·x2+5<x2+6·x+14
равносильно квадратному неравенству x2−6·x−9<0, а логарифмическое неравенство log3(x2+x+7)≥2 – неравенству x2+x−2≥0.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Квадратные неравенства, примеры, решения
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Определение 1Квадратное неравенство – это такое неравенство, которое имеет вид a·x2+b·x+c<0, где a, b и c – некоторые числа, причем aне равно нулю. x – это переменная, а на месте знака
Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y=a·x2+b·x+c.
Приведем пример квадратного неравенства:
Пример 1Возьмем 5·x2−3·x+1>0. В этом случае a=5, b=−3 и c=1.
В этом случае a=5, b=−3 и c=1.
Или вот такое неравенство:
Пример 2−2,2·z2−0,5·z−11≤0, где a=−2,2, b=−0,5 и c=−11.
Покажем несколько примеров квадратных неравенств:
Пример 3Здесь коэффициенты этого квадратного неравенства есть ; 123·x2-x+57<0, в этом случае a=123, b=-1, c=57.
Особое внимание нужно обратить на тот факт, что коэффициент при x2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b·x+c>0, так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.
Пример 4Пример такого неравенства x2−5≥0.
Способы решения квадратных неравенств
Основным метода три:
Определение 2- графический;
- метод интервалов;
- через выделение квадрата двучлена в левой части.
Графический метод
Метод предполагает проведение построения и анализа графика квадратичной функции y=a·x2+b·x+c для квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥). Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a·x2+b·x+c при их наличии.
Для неравенства a·x2+b·x+c<0 решениями являются промежутки со знаком минус, для неравенства a·x2+b·x+c>0, промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.
Выделение квадрата двучлена
Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида (x−p)2<q (≤, >, ≥), где p и q – некоторые числа.
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Приведем пример. Рассмотрим равносильное преобразование неравенства 5≤2·x−3·x2. Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3·x2−2·x+5≤0.
Пример 5Необходимо найти множество решений неравенства 3·(x−1)·(x+1)<(x−2)2+x2+5.
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
3·(x−1)·(x+1)−(x−2)2−x2−5<0, 3·(x2−1)−(x2−4·x+4)−x2−5<0, 3·x2−3−x2+4·x−4−x2−5<0, x2+4·x−12<0.
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
D’=22−1·(−12)=16, x1=−6, x2=2
Построив график, мы можем увидеть, что множеством решений является интервал (−6, 2).
Ответ: (−6, 2).
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2·x2+5<x2+6·x+14
равносильно квадратному неравенству x2−6·x−9<0, а логарифмическое неравенство log3(x2+x+7)≥2 – неравенству x2+x−2≥0.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Квадратные неравенства — Математика GCSE
Здесь мы узнаем о квадратных неравенствах, в том числе о том, как решать квадратные неравенства, определять наборы решений с использованием записи интервалов и представлять решения на числовой прямой.
Существуют также рабочие листы квадратичных неравенств, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое квадратные неравенства?
Квадратные неравенства 9{2}+ 6x +5 \leq 0 означает, что нам нужно знать значения x, когда график на меньше, чем 0 .
Это соответствует тому, где кривая находится на ниже оси x .
Из графика видно, что значения x должны быть между -1 и -5.
Следовательно, решение этого неравенства можно записать, используя интервальную запись,
-5\leq x \leq-1 .
Например,
9{2}+ 6x +5 > 0 означает, что нам нужно знать значения x, когда график на больше, чем 0 .
Это соответствует кривой над осью x .
Из графика видно, что значения x должны быть больше -1 и меньше -5 .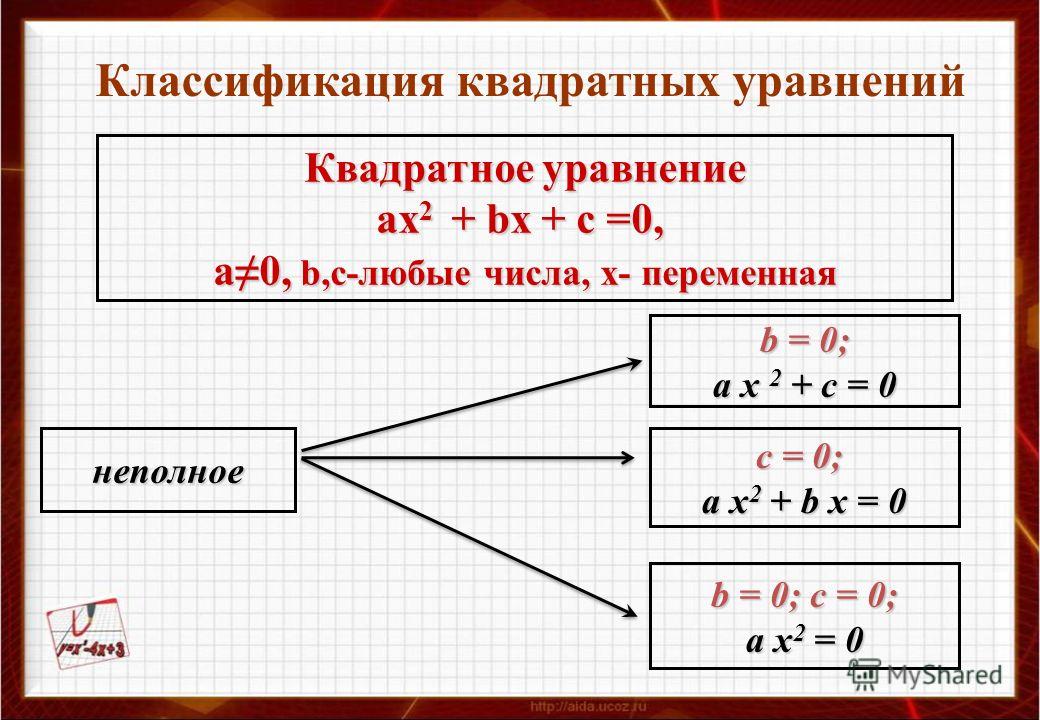
Таким образом, решение этого неравенства может быть записано с использованием интервальной записи в виде двух неравенств x > -1 и x < -5 .
Что такое квадратные неравенства?
Как решать квадратные неравенства
Чтобы решить квадратные неравенства путем разложения на множители:
- Факторизируйте квадратное выражение.
- Найдите значения x , при которых каждая скобка равна нулю.
- Запишите решение, используя интервальную запись.
Для решения квадратных неравенств по квадратной формуле:
- Определите значения a, b и c , чтобы подставить их в квадратичную формулу.
- Решите квадратное неравенство по квадратной формуле.
- Упрощение для вычисления решения неравенства.
- Запишите решение, используя интервальную запись.

Как решать квадратные неравенства
Таблица квадратичных неравенств
Получите бесплатную таблицу квадратичных неравенств, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист квадратного неравенства
Получите бесплатный рабочий лист квадратного неравенства, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Связанные уроки по неравенствам
Квадратные неравенства являются частью нашей серии уроков по пересмотру неравенств . Возможно, вам будет полезно начать с основного урока о неравенстве, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя: 9{2}+7x+10<0 .
Другие уроки в этой серии включают в себя: 9{2}+7x+10<0 .
- Факторизация квадратного выражения.
(х + 2) (х + 5) < 0
2 Найдите значения x, при которых каждая скобка равна нулю.
(x + 2) = 0, если x = -2
(x + 5) = 0, если x = -5
3 Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на меньше, чем 0 и, следовательно, на ниже x 9{2}+3x+10\leq0 .
Факторизация квадратного выражения.
(x-2)(x+5)\leq0
Найдите значения x, при которых каждая скобка равна нулю.
(x — 2) = 0, если x = 2
(x + 5) = 0, если x = -5
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на меньше или равен 0 и, следовательно, на ниже оси x . 9{2}-6x+8\geq0 .
9{2}-6x+8\geq0 .
Факторизация квадратного выражения.
(x-2)(x-4)\geq0
Найдите значений x, при которых каждая скобка равна нулю .
(x -2) = 0, если x = 2
(x -4 ) = 0, если x = 4
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на больше или равен 0 и, следовательно, на выше x 9{2} + 9x + 4\leq0 .
Факторизация квадратного выражения.
(2x+1)(x+4)\leq0
Найдите значений x, при которых каждая скобка равна нулю .
(2x + 1) = 0, когда x = -\frac{1}{2}
(x +4 ) = 0, когда x = -4
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на меньше или равен 0 и, следовательно, на ниже 9{2}-9>0 .
Факторизация квадратного выражения.
(x -3)(x + 3) > 0
Найдите значений x, при которых каждая скобка равна нулю .
(x +3) = 0, когда x = -3
(x -3 ) = 0, когда x = 3
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на больше, чем 0 и, следовательно, на выше оси x . 9{2}-16< 0
Разложите неравенство на множители.
(x — 4)(x + 4) = 0
Найдите значений x, при которых каждая скобка равна нулю .
(x +4) = 0, когда x = -4
(x -4 ) = 0, когда x = 4
Запишите решение, используя интервальную запись .
Нам нужны значения x, которые создают график, который на меньше, чем 0, и поэтому {2}-4 \times 5 \times-12}}{2 \times 5} \\ х \leq \frac{-6 \pm \sqrt{36–240}}{10} \\ x \leq \frac{-6 \pm \sqrt{276}}{10}\]
\[x\leq \frac{-6+2\sqrt{69}}{10} \quad и \quad x \frac{-6-2\sqrt{69}}{10}\\ x\leq \frac{-3+2\sqrt{69}}{5} \quad и \quad x\frac{-3-2\sqrt{69}}{5}\]
В этом случае ответ дается в грубой форме, но вас могут попросить оставить ответы округленными до определенной степени точности.
Запишите решение, используя интервальную запись. 9{2}-4 \times 2 \times-4}}{2 \times 2} \\ х<\frac{3 \pm \sqrt{9–32}}{4} \\ x<\frac{3 \pm \sqrt{41}}{4}\]
\[x<\frac{3+6.4}{4} \quad и \quad x<\frac{3-6.4}{ 4}\\ x < 2,4 \quad и \quad x < -0,9\]
В этом случае ответ дается с точностью до одного десятичного знака, но вы можете оставить решение в грубой форме.
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, равный {2}
Найдите значения x, при которых каждая скобка равна нулю.
Поскольку обе скобки равны, существует только одно решение.
(x +3) = 0, когда x = -3
Запишите решение, используя интервальную запись.
Нам нужны значения x, которые создают график, который на меньше или равен 0 и, следовательно, на ниже оси x . Это происходит только тогда, когда x = -3 .
Это происходит только тогда, когда x = -3 .
Распространенные заблуждения
- Квадратный корень числа имеет два решения
Распространенной ошибкой при вычислении квадратного корня числа является запись только положительного решения. Отрицательное число в квадрате также даст положительное решение.
Например,
\sqrt{16} =4 и -4 . 4 х 4 = 16 и -4 х 4 = 16.
- Несоблюдение исходного знака неравенства
Распространенной ошибкой является случайное изменение направления знака неравенства или непрописывание знака неравенства в решении. 9{2} + 13x +30 < 0
Факторизируем квадратное число, (x + 3)(x +10) < 0 .
Найдите значения x, при которых скобка равна нулю, x = -10 и x = -3 .
Запишите решение, используя интервальную запись, -10 < x < -3 .
5\leq x \leq-2
-5\leq x \leq 2
-5 и -2
-5\leq x \leq -2
х^{2}+3x-10 \leq 0 9{2}-7x+6\geq 0
Факторизация квадратного числа, (x-6)(x-1)\geq 0 . {2} < 1
9{2}-4 \times 3 \times-2}}{2 \times 3} .
{2} < 1
9{2}-4 \times 3 \times-2}}{2 \times 3} .
Упростим неравенство, x \leq \frac{-4 \pm \sqrt{16–24}}{6} .
Упростим еще раз, x \leq \frac{-4 \pm \sqrt{40}}{6} .
Можно упростить до грубой формы, x \leq \frac{-4 \pm 2 \sqrt{10}}{6} .
Упростите дробь. Вы можете уйти в грубой форме, x \leq \frac{-2 \pm \sqrt{10}}{3} .
Исправить до 2 знаков после запятой, x \leq 0,39{2}+3x – 10 < 0 .
(b) Представьте свое решение части (a) в числовой строке ниже.
(6 баллов)
Показать ответ
(a)
(х -2)(х + 5) < 0
1 балл, если есть одна или две ошибки.
(2)
x <2 и x < -5
(1)
-5 < х < 2
(1)
(б)
9{2} – 4x – 21< 0 .(1)
(х – 7)(х + 3) < 0 . {2}-5x+6\ge 0\)
{2}-5x+6\ge 0\)
Факторизация квадратного числа
\[(x-3)(x-2) \geq 0\]Определить критические значения \(х\)
Из факторизованного квадратичного уравнения мы видим, что значения, для которых выполняется неравенство равными нулю являются \(x=3\) и \(x=2\). Они называются критическими значениями неравенство, и они используются для заполнения таблицы знаков.
Заполните таблицу знаков
Мы должны определить, где каждый фактор неравенства положительный и отрицательный на числовая строка:
- влево (в отрицательном направлении) от критического значения
- равно критическому значению
- вправо (в положительном направлении) от критического значения
В последней строке таблицы определяем, где неравенство положительное, а где
отрицательное путем нахождения произведения факторов и их соответствующих знаков.
| Критические значения | \(х=2\) | \(х=3\) | |||
| \(х-3\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(х-2\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) |
| \(f(x)=(x-3)(x-2)\) | \(+\) | \(\текст{0}\) | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что \(f(x)\) больше или равно нулю для \(x\le 2\)
или \(х\ge 3\). 2 — 5x + 6\), \(a>0\) и, следовательно, график
представляет собой «улыбку» и имеет минимальную точку поворота. 92 — 4x + 1\), \(а > 0\) и, следовательно,
график представляет собой «улыбку» и имеет минимальную точку поворота.
2 — 5x + 6\), \(a>0\) и, следовательно, график
представляет собой «улыбку» и имеет минимальную точку поворота. 92 — 4x + 1\), \(а > 0\) и, следовательно,
график представляет собой «улыбку» и имеет минимальную точку поворота.
Обратите внимание, что никакая часть графика не лежит ниже оси \(x\).
9{2}-4\влево(1\вправо)\влево(-5\вправо)}}{2\влево(1\вправо)} \\ &= \frac{-3±\sqrt{29}}{2} \\ x_1 &= \frac{-3-\sqrt{29}}{2} \приблизительно -\text{4,2} \\ x_2 &= \frac{-3+\sqrt{29}}{2} \приблизительно \text{1,2} \конец{выравнивание*}Следовательно, мы можем написать, с точностью до одного десятичного знака, \начать{выравнивать*} х^2+3х-5 &< 0 \\ \text{as} (x-\text{1,2})(x+\text{4,2}) &< 0 \end{выравнивание*}
Определить критические значения \(x\)
Из факторизованного квадратичного уравнения мы видим, что критические значения равны \(x=\text{1,2}\)
и \(х=-\текст{4,2}\).
Заполнить таблицу признаков
| Критические значения | \(х=-\текст{4,2}\) | \(х=\текст{1,2}\) | |||
| \(х+\текст{4,2}\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) |
| \(х-\текст{1,2}\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(f(x)=(x+\text{4,2})(x-\text{1,2})\) | \(+\) | \(\текст{0}\) | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что функция отрицательна при \(-\text{4,2} < x <
\текст{1,2}\). 92+3x-5\), \(a > 0\) и, следовательно, граф
представляет собой «улыбку» и имеет минимальную точку поворота.
92+3x-5\), \(a > 0\) и, следовательно, граф
представляет собой «улыбку» и имеет минимальную точку поворота.
Из графика видно, что функция лежит ниже оси \(x\) между \(-\text{4,2}\) и \(\text{1,2}\). 92 + 3x — 5 < 0 \text{ for } -\text{4,2} < x < \text{1,2}\]
Важно: При работе с неравенством, в котором переменная находится в знаменателя, нужен другой подход. Всегда не забывайте проверять наличие ограничений.
Рабочий пример 19: Решение квадратных неравенств с дробями
Найдите \(x\):
\(\dfrac{2}{x+3} = \dfrac{1}{x-3}\), \(x \ne \pm 3\)
\(\dfrac{2}{x+3} \le \dfrac{1}{x-3}\), \(x \ne \pm 3\)
Решение уравнения
Чтобы решить это уравнение, мы умножаем обе части уравнения на \((x+3)(x-3)\) и просто: \начать{выравнивать*} \frac{2}{x+3} \times (x+3)(x-3) &= \frac{1}{x-3} \times (x+3)(x-3)\\ 2(х-3) &= х+3\\ 2х-6 &= х+3\\ х &= 9\конец{выравнивание*}
Решение неравенства
Очень важно признать, что мы не можем использовать тот же метод, что и выше, для
решить неравенство. Если мы умножим или разделим неравенство на отрицательное
число, то знак неравенства меняет направление. Мы должны скорее упростить
неравенство, чтобы иметь наименьший общий знаменатель и использовать таблицу знаков для
определить значения, удовлетворяющие неравенству.
Если мы умножим или разделим неравенство на отрицательное
число, то знак неравенства меняет направление. Мы должны скорее упростить
неравенство, чтобы иметь наименьший общий знаменатель и использовать таблицу знаков для
определить значения, удовлетворяющие неравенству.
Вычесть \(\dfrac{1}{x-3}\) из обеих частей неравенства
\[\frac{2}{x+3} — \frac{1}{x-3} \le 0\]Найдите наименьший общий знаменатель и упростите дробь
\начать{выравнивать*} \frac{2(x-3) — (x+3)}{(x+3)(x-3)} &\le 0 \\ \frac{x-9}{(x+3)(x-3)} &\le 0 \конец{выравнивание*}
Оставьте знаменатель, потому что он влияет на окончательный ответ.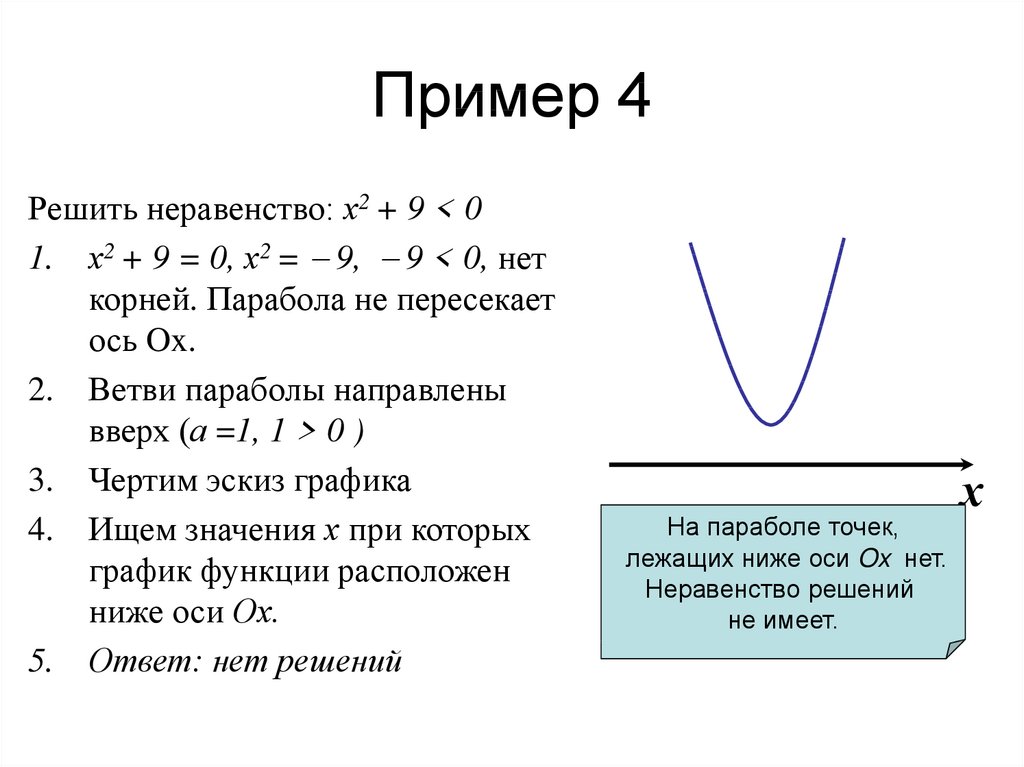
Определить критические значения \(x\)
Из факторизованного неравенства мы видим, что критические значения равны \(x=-3\), \(x=3\) и \(х=9\).
Заполнить таблицу признаков
| Критические значения | \(х=-3\) | \(х=3\) | \(х=9\) | ||||
| \(х+3\) | \(-\) | неопределенный | \(+\) | \(+\) | \(+\) | \(+\) | \(+\) |
| \(х-3\) | \(-\) | \(-\) | \(-\) | неопределенный | \(+\) | \(+\) | \(+\) |
| \(х-9\) | \(-\) | \(-\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(f(x)=\dfrac{x-9}{(x+3)(x-3)}\) | \(-\) | неопределенный | \(+\) | неопределенный | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что функция меньше или равна нулю при \(x <
-3\) или \(3 < x \leq 9\). Мы не включаем \(x = -3\) или \(x = 3\) в
решение из-за ограничений на знаменатель.
Мы не включаем \(x = -3\) или \(x = 3\) в
решение из-за ограничений на знаменатель.
Запишите окончательный ответ и изобразите в числовой строке
\[x < -3 \quad\text{или}\quad 3 < x \le 9\]
Решение квадратных неравенств
Учебник Упражнение 2.8 9{2} — х — 12 & < 0 \\ (х - 4)(х + 3) & < 0 \конец{выравнивание*}
| Критические значения | \(х=-3\) | \(х=4\) | |||
| \(х — 4\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(х + 3\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) |
| \(f(x)= (x — 4)(x + 3)\) | \(+\) | \(\текст{0}\) | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что \(f(x)\) меньше, чем \(\text{0}\) когда \(-3 < х < 4\) 9{2} + х - 4 & > 0 \\ (3x + 4)(x — 1) & > 0 \конец{выравнивание*}
| Критические значения | \(х=-\фракция{4}{3}\) | \(х=1\) | |||
| \(х — 1\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(3x + 4\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) |
| \(f(x)= (3x + 4)(x — 1)\) | \(+\) | \(\текст{0}\) | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что \(f(x)\) больше, чем \(\text{0}\), когда \(x < -\frac{4}{3}\) или когда \(x > 1\) 9{2} + у + 2 < 0\]
Реальных решений нет.
График лежит выше оси \(x\) и не пересекает \(x\) — ось, поэтому функция никогда не бывает отрицательной. Есть нет значений \(y\), которые решат это неравенство.
\((3-t)(1+t) > 0\)
\[(3 — t)(1 + t) > 0\]
| Критические значения | \(t = -1\) | \(t = 3\) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(3 — т\) | \(+\) | \(+\) | \(+\) | \(\текст{0}\) | \(-\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(1 + т\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(f(x)= (3 — t)(1 + t)\) | \(-\) | \(\текст{0}\) | \(+\) | \(\текст{0}\) | 92 — 4(1)(6)}}{2(1)} \\ & = \frac{4 \pm \sqrt{16- 24}}{2 } \\ & = \frac{4 \pm \sqrt{-8}}{2} \конец{выравнивание*}
| Критические значения | \(х = -\фракция {1}{4}\) | \(х = 0\) | |||
| \(х\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) |
| \(4x + 1\) | \(-\) | \(\текст{0}\) | \(+\) | \(+\) | \(+\) |
| \(f(x)=x(4x + 1)\) | \(+\) | \(\текст{0}\) | \(-\) | \(\текст{0}\) | \(+\) |
Из таблицы видно, что \(f(x)\) больше, чем
\(\text{0}\), когда \(x \leq -\frac{1}{4}\) или \(x \geq
0\). 9{2} + х + 6 \le 0\]
9{2} + х + 6 \le 0\]
Действительных корней нет и граф не пересекает \(x\)-ось. График лежит выше оси \(x\), поэтому это неравенство никогда не верно.
\(\dfrac{x}{x-3}<2\), \(x\ne 3\)
Сначала решим уравнение:
\начать{выравнивать*} \dfrac{x}{x-3} & < 2 \\ \dfrac{x}{x-3} - 2 & < 0 \\ \dfrac{х - 2(х-3)}{х-3}& < 0 \\ \dfrac{x - 2x + 6}{x-3}& < 0 \\ \dfrac{-x + 6}{x-3}& < 0 \\ \dfrac{-(x - 6)}{x-3}& < 0 \\ \dfrac{х - 6}{х-3}& > 0 \\ х & = 6 \конец{выравнивание*}
| Критические значения | \(х = 3\) | \(х = 6\) | |||||||||||||||||||||||||||||||||||||||||||
| \(х — 3\) | \(-\) | неопределенный | \(+\) | \(+\) | \(+\) | ||||||||||||||||||||||||||||||||||||||||
| \(х — 6\) | \(-\) | \(-\) | \(-\) | \(\текст{0}\) | \(+\) | ||||||||||||||||||||||||||||||||||||||||
| \(f(x)=x — 6\) | \(+\) | неопределенный | \(-\) | \(\текст{0}\) | \(+\) 92 + 4}{x — 7} \geq 0\), \(x \ne 7\) Сначала упростим дробь: \[\dfrac{(x + 2)(x — 2)}{x — 7} \geq 0\]
Из таблицы видно, что \(f(x)\) больше, чем
\(\text{0}\), когда \(-2 \leq x \leq 2\) и \(x > 7\)
с \(х\ne 7\). Мы можем представить это на числовой прямой: \(\dfrac{x + 2}{x} — 1 \geq 0\), \(x \ne 0\) Сначала упростим уравнение: \начать{выравнивать*} \frac{x + 2}{x} — 1 & \ge 0 \\ \frac{x + 2 — x}{x}& \ge 0 \\ \frac{2}{x} & \ge 0 \\ \text{Поэтому } x & > 0 \конец{выравнивание*} 92 — 5 и \geq 0 \\ \text{Поэтому } x & > 0 \конец{выравнивание*} Рисуем параболу: А теперь отметим, что ищем части
параболы, которые меньше или равны \(\text{0}\). Рисуем параболу: Видим, что парабола никогда не касается оси \(х\) и всегда позитивный. Поэтому неравенство верно для все действительные значения \(x\). Решение квадратных неравенств – алгебра среднего уровняКвадратные уравнения и функции Цели обученияК концу этого раздела вы сможете:
Прежде чем начать, пройдите этот тест на готовность.
Ранее мы научились решать линейные неравенства и рациональные неравенства. Некоторые из методов, которые мы использовали для их решения, были одинаковыми, а некоторые отличались. Теперь мы научимся решать неравенства, имеющие квадратное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений. Квадратные неравенства будем решать двумя способами — и графически, и алгебраически. Решить квадратное неравенство графическиКвадратное уравнение имеет стандартную форму, если записать его в виде x 2 + bx + c = 0. Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме. Квадратное неравенство Квадратное неравенство — это неравенство, содержащее квадратное выражение. Стандартная форма квадратного неравенства записывается: График квадратичной функции f ( x ) = ax 2 + bx + c = 0 является параболой. Когда мы спрашиваем, когда x 2 + bx + c < 0, мы спрашиваем, когда f( x ) < 0. Мы хотим знать, когда парабола ниже x — ось. Когда мы спрашиваем, когда ax 2 + bx + c > 0, мы спрашиваем, когда f ( x ) > 0. Мы хотим знать, когда парабола выше оси y . Как решить квадратное неравенство графически Решить графически. ⓐ Решите графически и ⓑ запишите решение в интервальной записи. ⓐ ⓑ ⓐ Решите графически и ⓑ запишите решение в интервальной записи. ⓐ ⓑ Перечислим шаги, необходимые для графического решения квадратного неравенства. Решите квадратное неравенство графически.
В последнем примере парабола открылась вверх, а в следующем — вниз. В обоих случаях мы ищем часть параболы, которая находится ниже оси x , но отмечаем, как положение параболы влияет на решение. Решить графически. Запишите решение в интервальной записи. 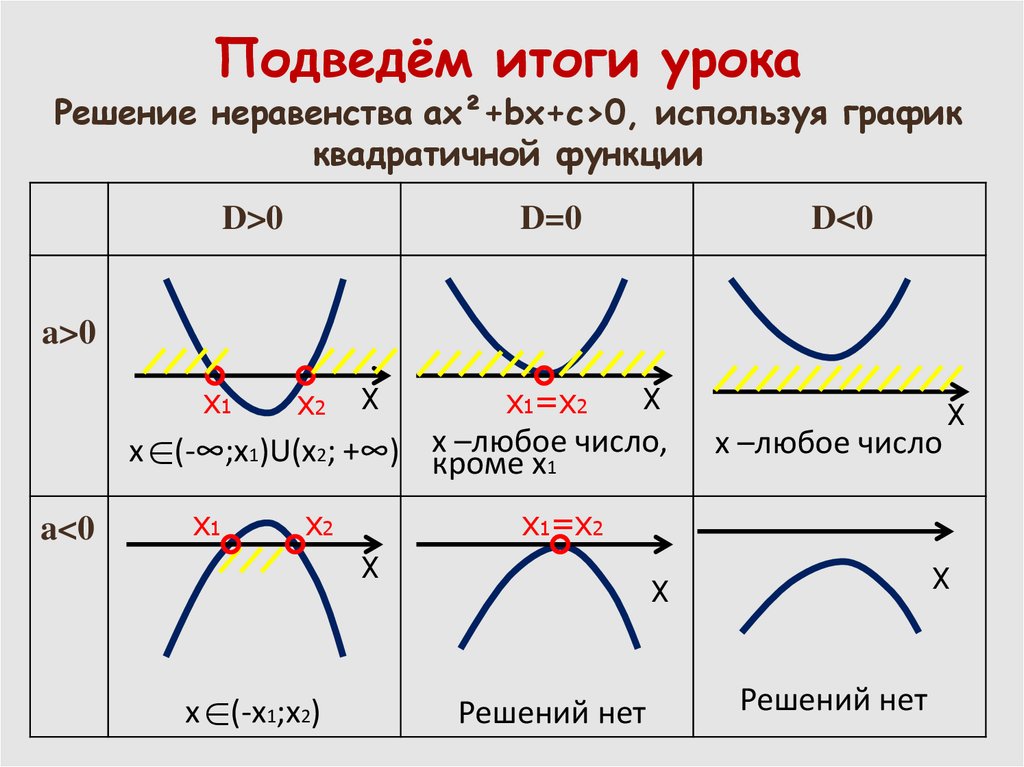 The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»> The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»> | ||||||||||||||||||||||||||||||||||||||||
| Квадратное неравенство в стандартной форме. | |||||||||||||||||||||||||||||||||||||||||||||
| График функции . | Парабола открывается вниз. | ||||||||||||||||||||||||||||||||||||||||||||
| Найдите линию симметрии. | |||||||||||||||||||||||||||||||||||||||||||||
| Найдите вершину. | Вершина | ||||||||||||||||||||||||||||||||||||||||||||
Найдите точки пересечения x . Позволять . Позволять . | |||||||||||||||||||||||||||||||||||||||||||||
| Фактор. Использовать свойство нулевого продукта. | |||||||||||||||||||||||||||||||||||||||||||||
| Постройте параболу. | x -перехваты | ||||||||||||||||||||||||||||||||||||||||||||
| Определите решение по графику. Мы включаем x -отрезков как неравенство — «меньше или равно». |
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
Алгебраическое решение квадратных неравенств
Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств. Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Мы будем использовать критические точки, чтобы разделить числовую прямую на интервалы, а затем определить, будет ли квадратное выражение положительным или отрицательным в интервале. Затем находим решение неравенства.
Алгебраическое решение квадратных неравенств
Алгебраическое решение. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
В этом примере, поскольку выражение хорошо учитывается, мы также можем найти знак в каждом интервале так же, как мы делали это при решении рациональных неравенств. Находим знак каждого из сомножителей, а затем знак произведения. Наша числовая строка будет выглядеть так:
Результат будет таким же, как и при использовании другого метода.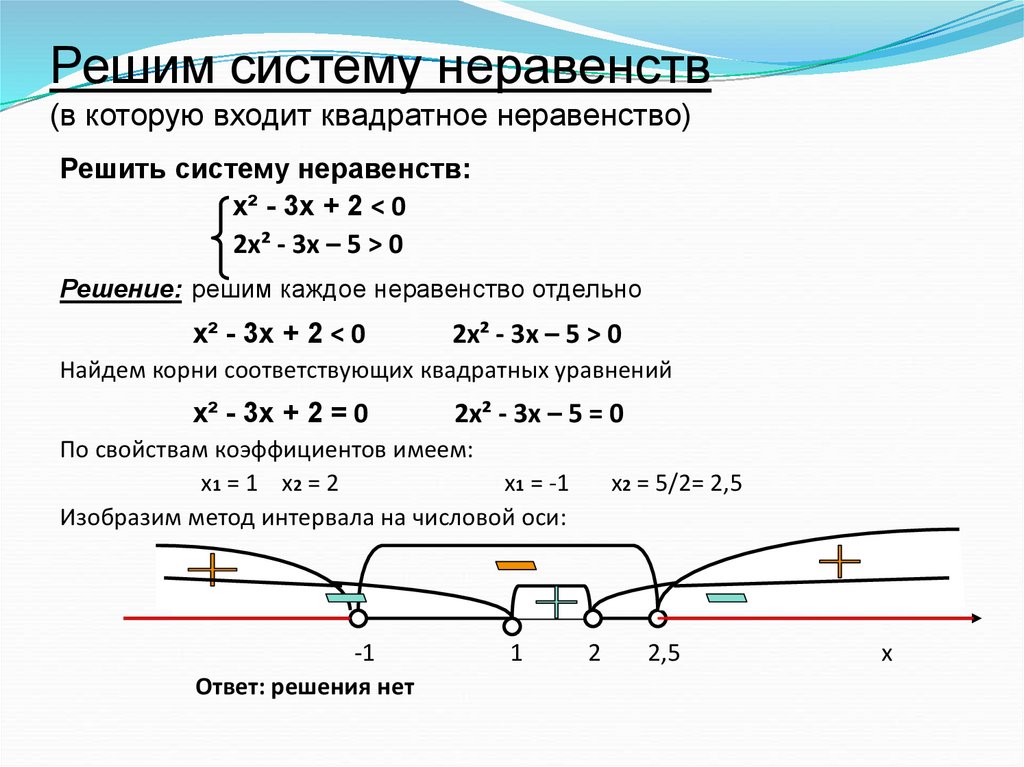
Здесь мы суммируем шаги.
Алгебраически решить квадратное неравенство.
- Запишите квадратное неравенство в стандартной форме.
- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
 On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>
On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>Не забудьте поменять знак неравенства.
соответствующее квадратное уравнение.

номер строки на интервалы.
Тестовые номера из каждого интервала
в исходном неравенстве.
неравенство верно. Напишите решение
в интервальной нотации.
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решениями квадратных неравенств в каждом из предыдущих примеров были либо интервал, либо объединение двух интервалов. Это произошло из-за того, что в каждом случае было найдено два решения соответствующего квадратного уравнения x 2 + bx + c = 0. Затем эти два решения дали нам либо две точки пересечения x- для графика, либо две критические точки для деления числовой прямой на интервалы.
Это коррелирует с нашим предыдущим обсуждением количества и типа решений квадратного уравнения с использованием дискриминанта.
Для квадратного уравнения вида ах 2 + bx + с = 0,
Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось x .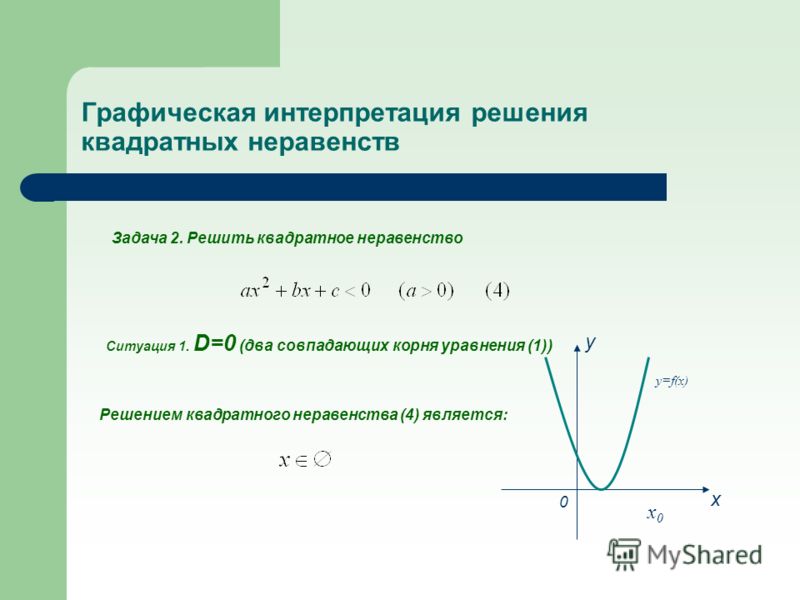 Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
В следующем примере решения квадратного неравенства будут получены в результате комплексного решения квадратного уравнения.
Решите, записав любое решение в интервальной записи:
ⓐⓑ
ⓐ
соответствующее квадратное уравнение.

парабола не пересекает x -ось.
Также парабола открывается вверх. Это
говорит нам, что парабола находится полностью над осью x .
Требуется найти решение задачи Поскольку для всех значений графика выше оси x , все значения x делают неравенство верным. В интервальной записи запишем
ⓑ
Поскольку соответствующее квадратное уравнение такое же, как в части (а), парабола будет такой же. Парабола открывается вверх и находится полностью над 9Ось 1894 x — ни одна из ее частей не находится ниже оси x .
Парабола открывается вверх и находится полностью над 9Ось 1894 x — ни одна из ее частей не находится ниже оси x .
Нам нужно найти решение задачи Поскольку для всех значений x график никогда не находится ниже оси x , никакие значения x не делают неравенство верным. Неравенство не имеет решения.
Решить и записать любое решение в интервальной записи:
ⓐ ⓑ
ⓐ
ⓑ нет решения
Решить и записать любое решение в интервальной записи:
ⓐ ⓑ
ⓐ нет решения
ⓑ
Основные понятия
- Графическое решение квадратного неравенства
- Запишите квадратное неравенство в стандартной форме.
- Постройте график функции, используя свойства или преобразования.
- Определите решение по графику.
- Как решить квадратное неравенство алгебраически
- Запишите квадратное неравенство в стандартной форме.

- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
- Запишите квадратное неравенство в стандартной форме.
Раздельные упражнения
Практика делает совершенным
Решайте квадратные неравенства графически
В следующих упражнениях ⓐ решите графически и ⓑ запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
0003. алгебраически.
алгебраически.
Ответы будут разными.
Решите как графически, так и алгебраически. Какой метод вы предпочитаете и почему?
Опишите шаги, необходимые для графического решения квадратного неравенства.
Ответы будут разными.
Опишите шаги, необходимые для алгебраического решения квадратного неравенства.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ По шкале от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
Упражнения на обзор глав
Решение квадратных уравнений с использованием свойства квадратного корня
Решение квадратных уравнений вида x 2 = k Использование свойства квадратного корня
В следующих упражнениях решите, используя свойство квадратного корня.
11.
Соль Квадратичная Уравнения формы с использованием квадратного корневого свойства
Solve Quadrative уравнения формы с использованием квадратного корневого свойства 0002 В следующих упражнениях решите, используя свойство Square Root.. , завершите квадрат так, чтобы получился идеальный квадратный трехчлен. Затем запишите результат в виде бинома в квадрате.В следующих упражнениях решите, заполнив квадрат.
Solve Quadratic Equations of the form ax 2 + bx + c = 0, заполнив квадрат
В следующих упражнениях решите, заполнив квадрат.
СОЗДАТЕЛЬНЫЕ Уравнения, используя квадратичную формулу
В следующих тренировках, Соль, с использованием квадратичной формулы
В следующих тренировках.
Use the Discriminant to Predict the Количество решений квадратного уравнения
В следующих упражнениях определите количество решений для каждого квадратного уравнения.
ⓐ 1 ⓑ 2 ⓒ 2 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения решить каждое квадратное уравнение. Не решить.
ⓐ множитель ⓑ Квадратная формула ⓒ квадратный корень
Решение уравнений в квадратной форме
Решение уравнений в квадратной форме
В следующих упражнениях решите.
Solve Solvation упражнения, решите, используя метод факторинга, принцип квадратного корня или квадратную формулу. Округлите свои ответы до десятых, если необходимо.
Найдите два последовательных нечетных числа, произведение которых равно 323.
Найдите два последовательных четных числа, произведение которых равно 624.
Два последовательных четных числа, произведение которых равно 624, это 24 и 26, а также -24 и -26.
Треугольный баннер имеет площадь 351 квадратный сантиметр. Длина основания на два сантиметра больше, чем в четыре раза больше высоты. Найдите высоту и длину основания.
Юлий построил треугольную витрину для своей коллекции монет. Высота витрины на шесть дюймов меньше, чем удвоенная ширина основания. Площадь задней части корпуса составляет 70 квадратных дюймов. Найдите высоту и ширину корпуса.
Высота 14 дюймов, ширина 10 дюймов.
Плитка-мозаика в форме прямоугольного треугольника используется в качестве угла прямоугольной дорожки. Гипотенуза мозаики равна 5 футам. Одна сторона мозаики в два раза длиннее другой. Каковы длины сторон? Округлите до десятых.
Прямоугольный кусок фанеры имеет диагональ на два фута больше ширины. Длина фанеры в два раза больше ширины. Какова длина диагонали фанеры? Округлите до десятых.
Длина диагонали 3,6 фута.
Проход от улицы к дому Пэм имеет площадь 250 квадратных футов. Его длина в два раза меньше ширины в четыре раза. Найдите длину и ширину тротуара. Округлите до десятых.
Для выпускного вечера Софии несколько столов одинаковой ширины будут расставлены встык, чтобы получился сервировочный стол общей площадью 75 квадратных футов. Общая длина столов будет в два раза больше ширины. Найдите длину и ширину сервировочного стола, чтобы София могла купить скатерть нужного размера. Ответ округлить до десятых.
Ширина сервировочного стола 4,7 фута, а длина 16,1 фута.
Мяч брошен вертикально в воздух со скоростью 160 футов/сек. Используйте формулу ч = -16 t 2 + v 0 t , чтобы определить, когда мяч будет на высоте 384 фута от земли. Округлите до десятых.
Пара на маленьком самолете совершила быстрый полет в винную страну для романтического ужина, а затем вернулась домой. Самолет летел в общей сложности 5 часов и в одну сторону расстояние составило 360 миль. Если самолет летел со скоростью 150 миль в час, какова была скорость ветра, действовавшего на самолет?
Скорость ветра составляла 30 миль в час.
Эзра плыл вверх по реке и обратно в общей сложности за 6 часов. Путь был 4 мили в одну сторону, и течение было трудным. Если Рой плыл на байдарке со скоростью 5 миль в час, какова была скорость течения?
Два мастера могут сделать ремонт дома за 2 часа, если они будут работать вместе. Одному из мужчин требуется на 3 часа больше, чем другому, чтобы закончить работу самостоятельно. Сколько времени требуется каждому мастеру на ремонт дома индивидуально?
Одному из мужчин требуется на 3 часа больше, чем другому, чтобы закончить работу самостоятельно. Сколько времени требуется каждому мастеру на ремонт дома индивидуально?
Одному человеку требуется 3 часа, а другому 6 часов, чтобы закончить ремонт в одиночку.
График квадратичных функций с использованием свойств
Распознавание графика квадратичной функции
В следующих упражнениях постройте график по точкам.
График
График
В следующих упражнениях определите, раскрываются ли следующие параболы вверх или вниз.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ вверх ⓑ вниз
Найдите ось симметрии и вершину параболы
В следующих упражнениях найдите ⓐ уравнение оси симметрии и ⓑ вершину.
Найдите пересечения параболы
В следующих упражнениях найдите пересечения x – и y .
График квадратичных функций с использованием свойств
В следующих упражнениях постройте график, используя его свойства.
Решайте максимальное значение и минимальное значение
В следующих упражнениях найдите минимальное значение или максимальное значение.
Максимальное значение равно 2, когда x = 2,
В следующих упражнениях решите. Округление ответов до десятых.
Мяч брошен вверх с земли с начальной скоростью 112 футов/сек. Используйте квадратное уравнение ч = -16 t 2 + 112 t , чтобы найти, сколько времени потребуется мячу, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
Детский сад ограждает прямоугольную площадку вдоль стены своего здания, чтобы дети могли играть на открытом воздухе. Им нужно максимально увеличить площадь, используя 180-футовое ограждение с трех сторон двора. Квадратное уравнение A = −2 x 2 + 180 x дает площадь A двора для длины x здания, которое будет граничить с двором. Найдите длину здания, которое должно граничить с двором, чтобы площадь была максимальной, а затем найдите максимальную площадь.
Примыкающая к зданию длина составляет 90 футов, что дает максимальную площадь 4050 квадратных футов.
График квадратичных функций с использованием преобразований
Постройте график квадратичных функций вида
В следующих упражнениях постройте график каждой функции, используя сдвиг по вертикали.
В следующих упражнениях постройте график каждой функции, используя сдвиг по горизонтали.
В следующих упражнениях постройте график каждой функции, используя преобразования.
График квадратичных функций вида
В следующих упражнениях постройте график каждой функции.
График квадратичных функций с использованием преобразований
В следующих упражнениях перепишите каждую функцию в форме, заполнив квадрат.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя преобразования.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя свойства.
Найдите квадратичную функцию по ее графику
В следующих упражнениях запишите квадратичную функцию в форме.
Решение квадратных неравенств
Решение квадратных неравенств графически
В следующих упражнениях решите графически и запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
нет решения
Практический тест
Использование свойства «Квадратный корень» для решения квадратного уравнения
Использование «Заполнение квадрата» для решения квадратного уравнения
Использование квадратной формулы для решения квадратного уравнения
Решите следующие квадратные уравнения. Используйте любой метод.
Используйте дискриминант для определения количества и типа решений каждого квадратного уравнения.
2 комплекса
Решите каждое уравнение.
Для каждой параболы найти ⓐ направление, в котором она раскрывается, ⓑ уравнение оси симметрии, ⓒ вершину, ⓓ x- и y -максимальные пересечения, и e) или минимальное значение.
ⓐ вниз ⓑ
ⓒ ⓓ
ⓔ минимальное значение, когда
Постройте график каждой квадратичной функции, используя точку пересечения, вершину и уравнение оси симметрии.
В следующих упражнениях постройте график каждой функции, используя преобразования.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
Смоделируйте ситуацию квадратным уравнением и решите любым методом.
Найдите два последовательных четных числа, произведение которых равно 360.
Длина диагонали прямоугольника в три раза больше ширины. Длина прямоугольника в три раза больше ширины.



 График лежит над осью \(x\) и
поэтому это неравенство верно для всех действительных значений \(s\).
92 — 4(7)(8)}}{2(7)} \\
& = \frac{1 \pm \sqrt{1- 224}}{14} \\
& = \frac{1 \pm \sqrt{-223}}{14}
\конец{выравнивание*}
График лежит над осью \(x\) и
поэтому это неравенство верно для всех действительных значений \(s\).
92 — 4(7)(8)}}{2(7)} \\
& = \frac{1 \pm \sqrt{1- 224}}{14} \\
& = \frac{1 \pm \sqrt{-223}}{14}
\конец{выравнивание*}
 Эти части отмечены красным ниже: 92\)
Эти части отмечены красным ниже: 92\)

 Запишите решение в интервальной записи.
Запишите решение в интервальной записи.